Characteristics of Particle Size Distributions of Falling Volcanic Ash Measured by Optical Disdrometers at the Sakurajima Volcano, Japan
Abstract
1. Introduction
2. Measurements of Volcanic Ash Particles
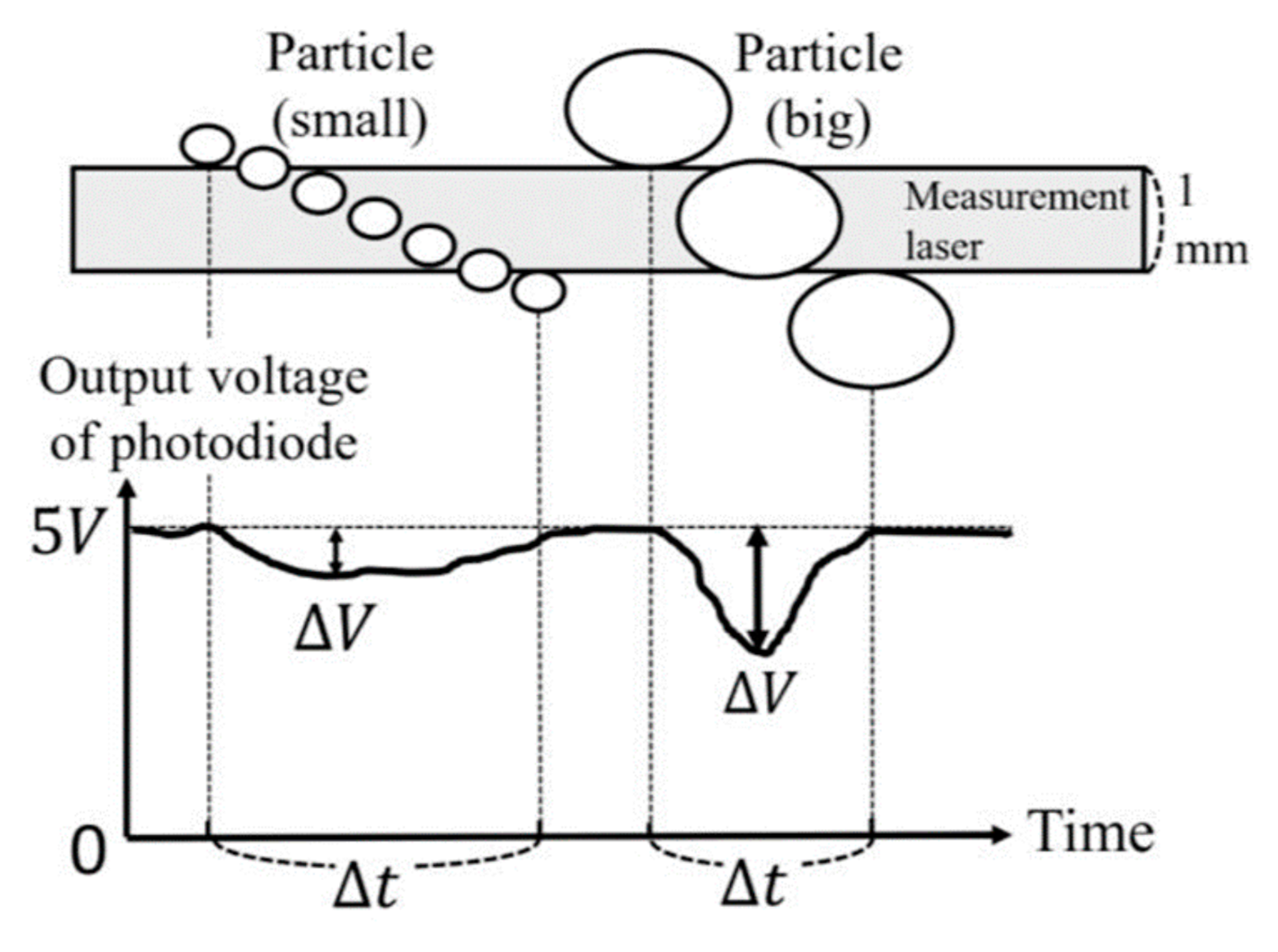
2.1. Parsivel2
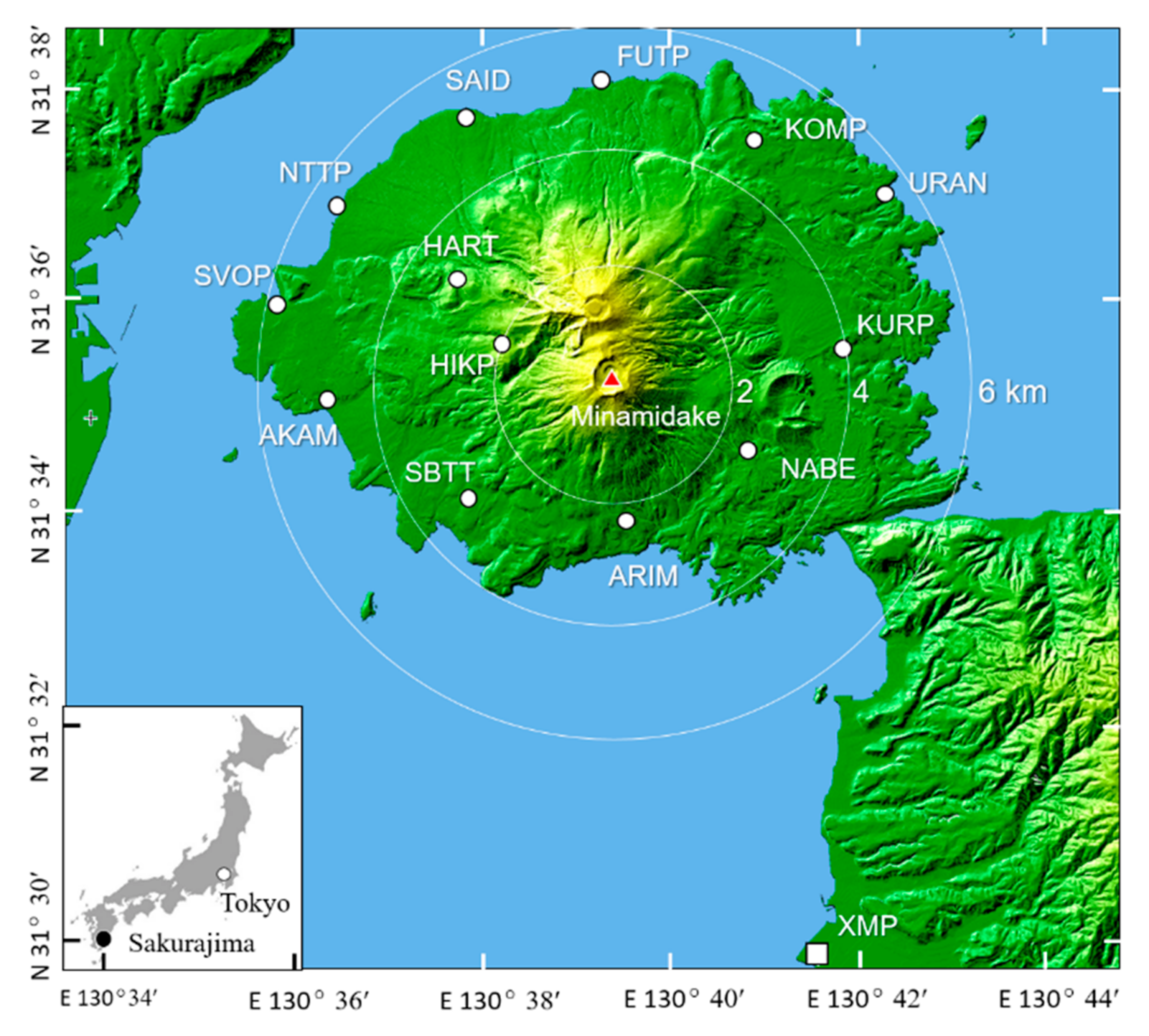
2.2. Data Collection
2.3. Data Processing
3. Functional Representation of Falling Ash Particles
3.1. Radar Meteorological Approach
3.2. Gamma PSD Model
3.3. Normalized Gamma PSD Model
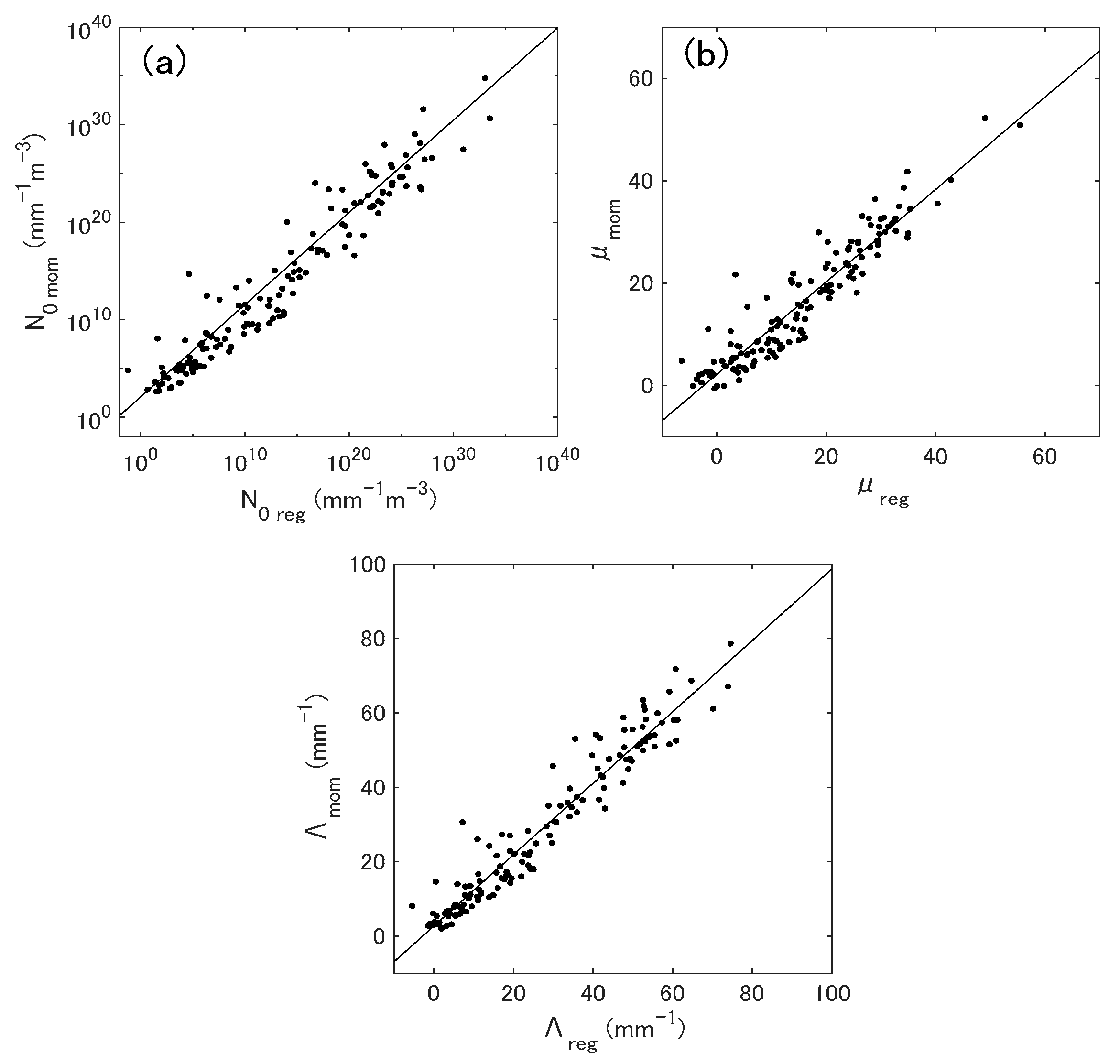
3.4. Calculation of PSD Parameters
3.5. Integrated PSD Parameters
4. Results
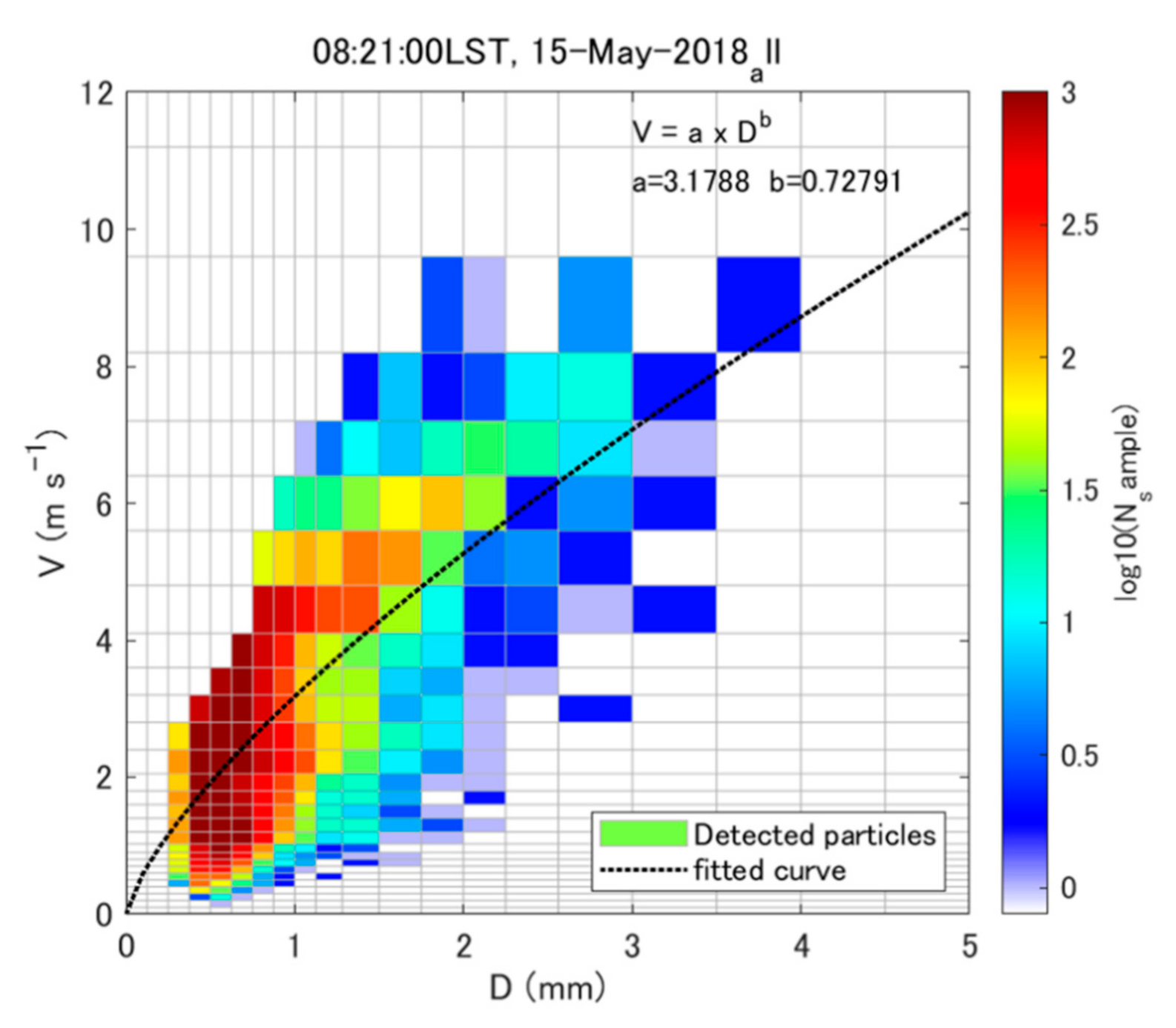
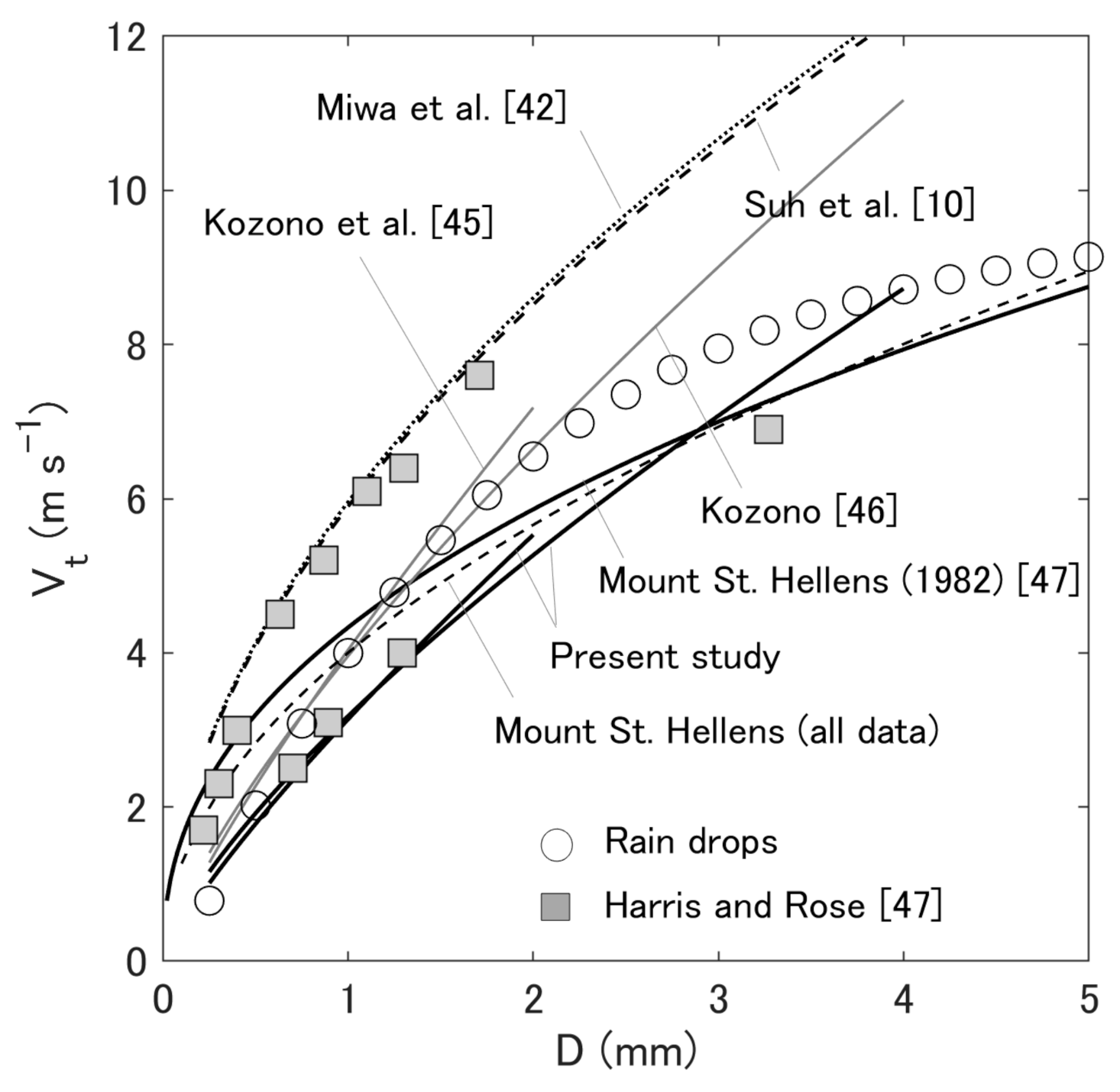
4.1. Fall Speed of Volcanic Ash Particles
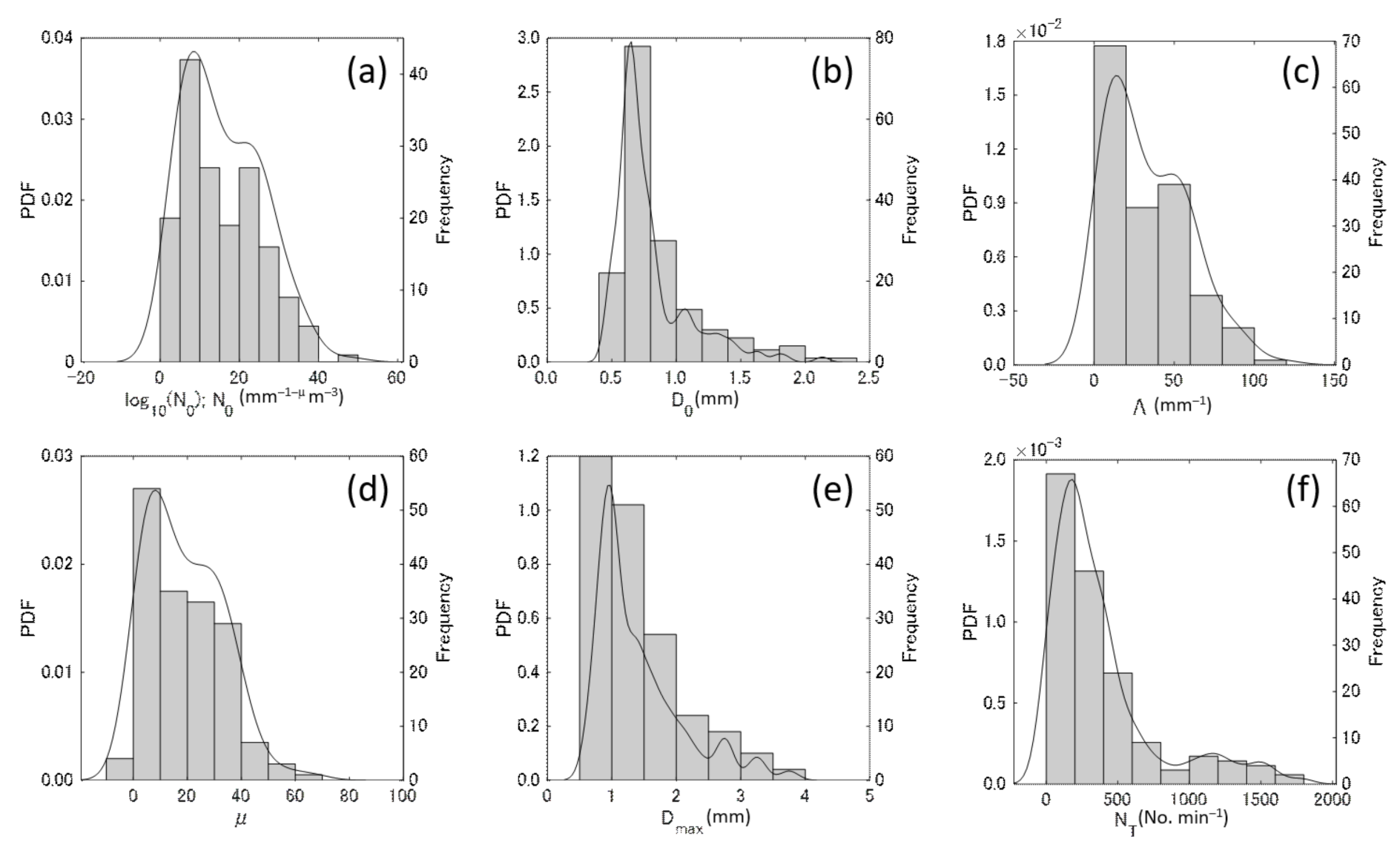
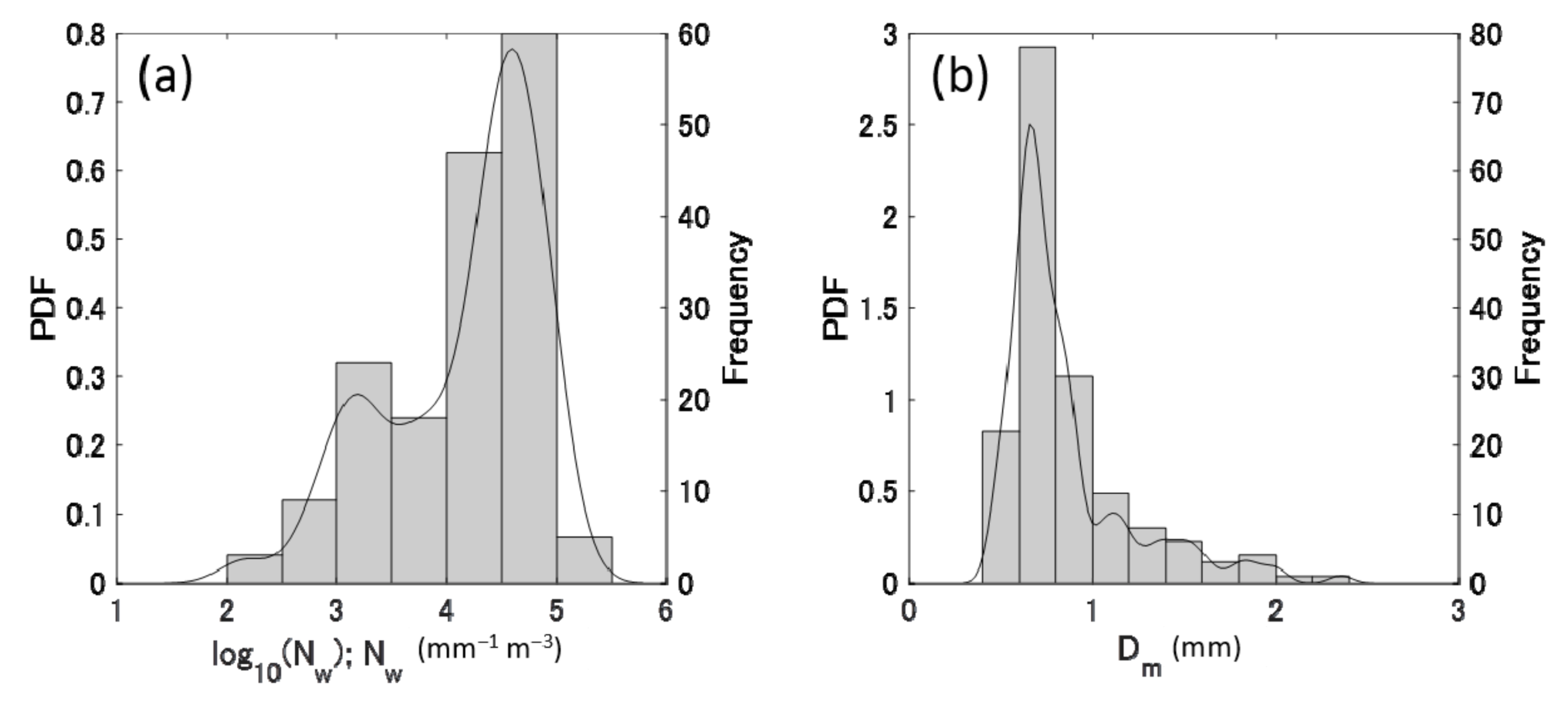
4.2. PSD Parameters
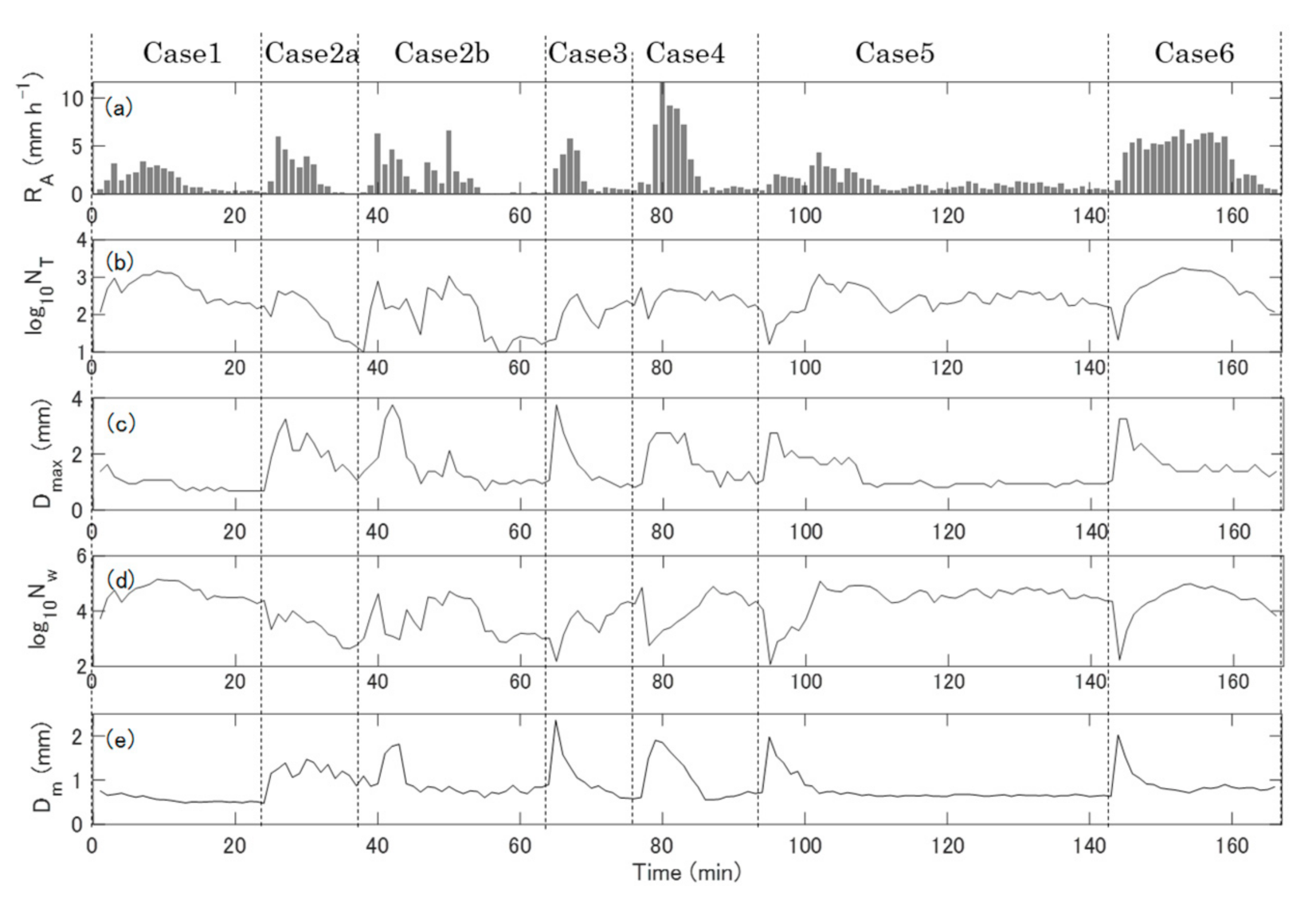
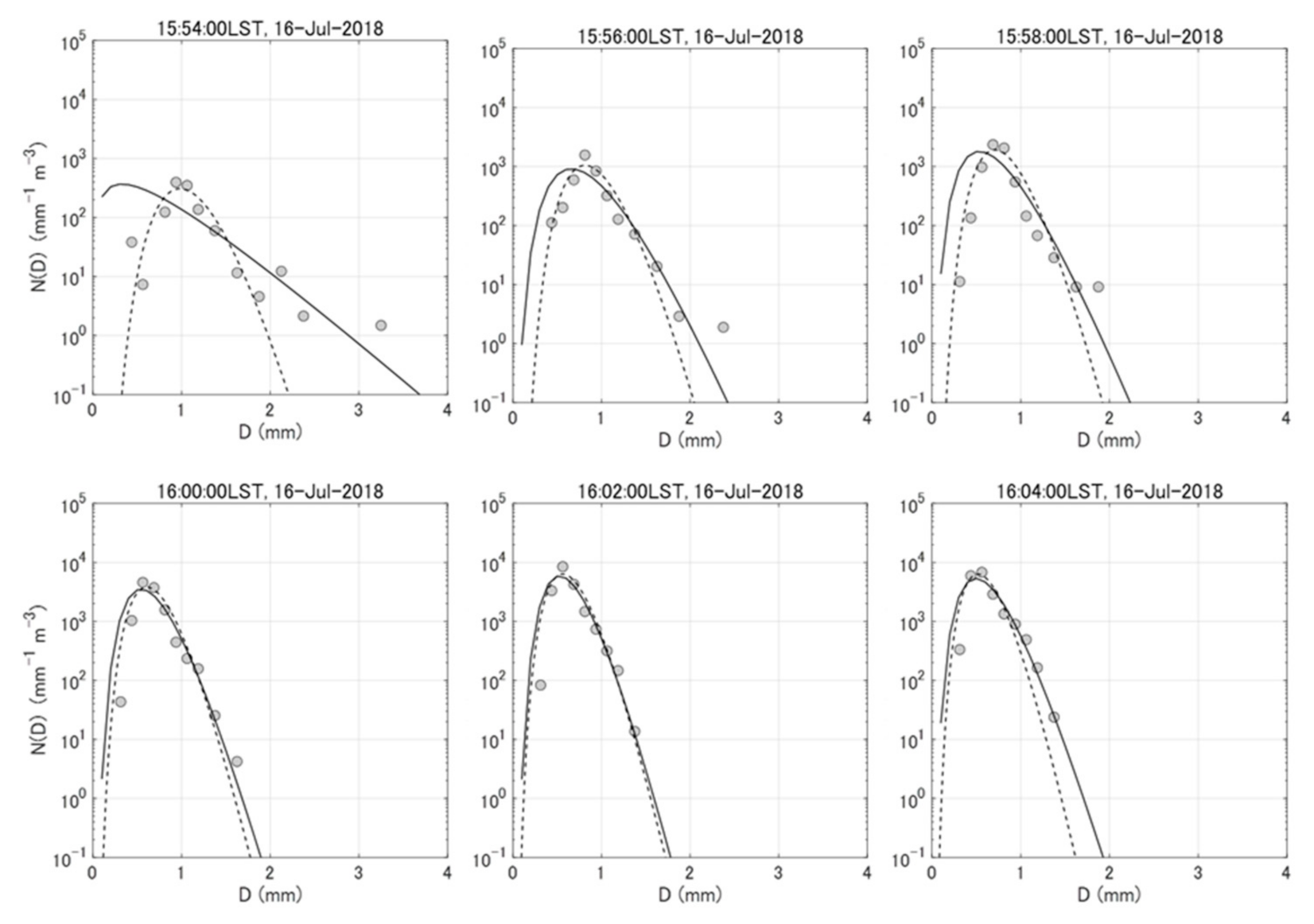
4.2.1. Temporal Changes in PSD
4.2.2. Gamma PSD Parameters
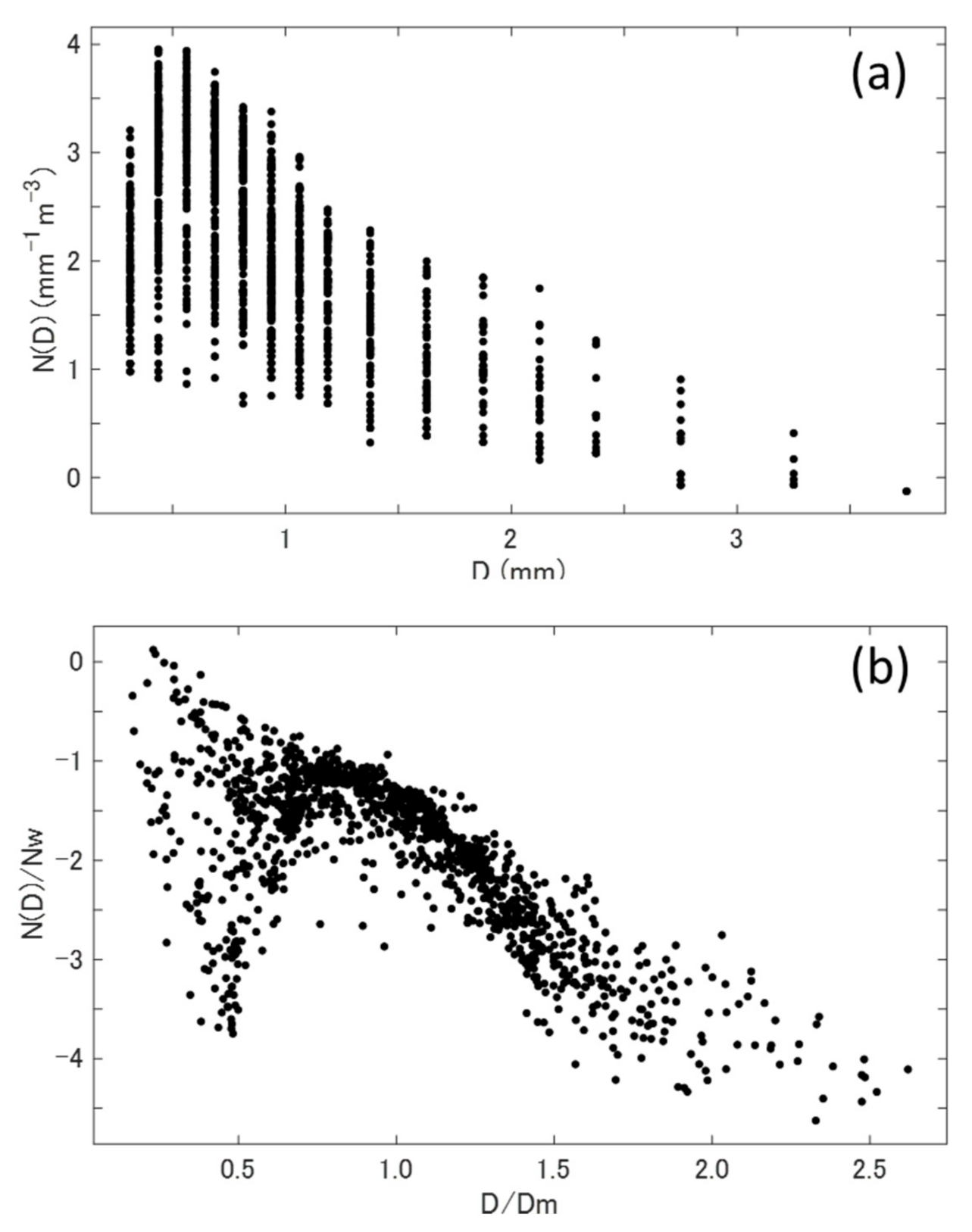
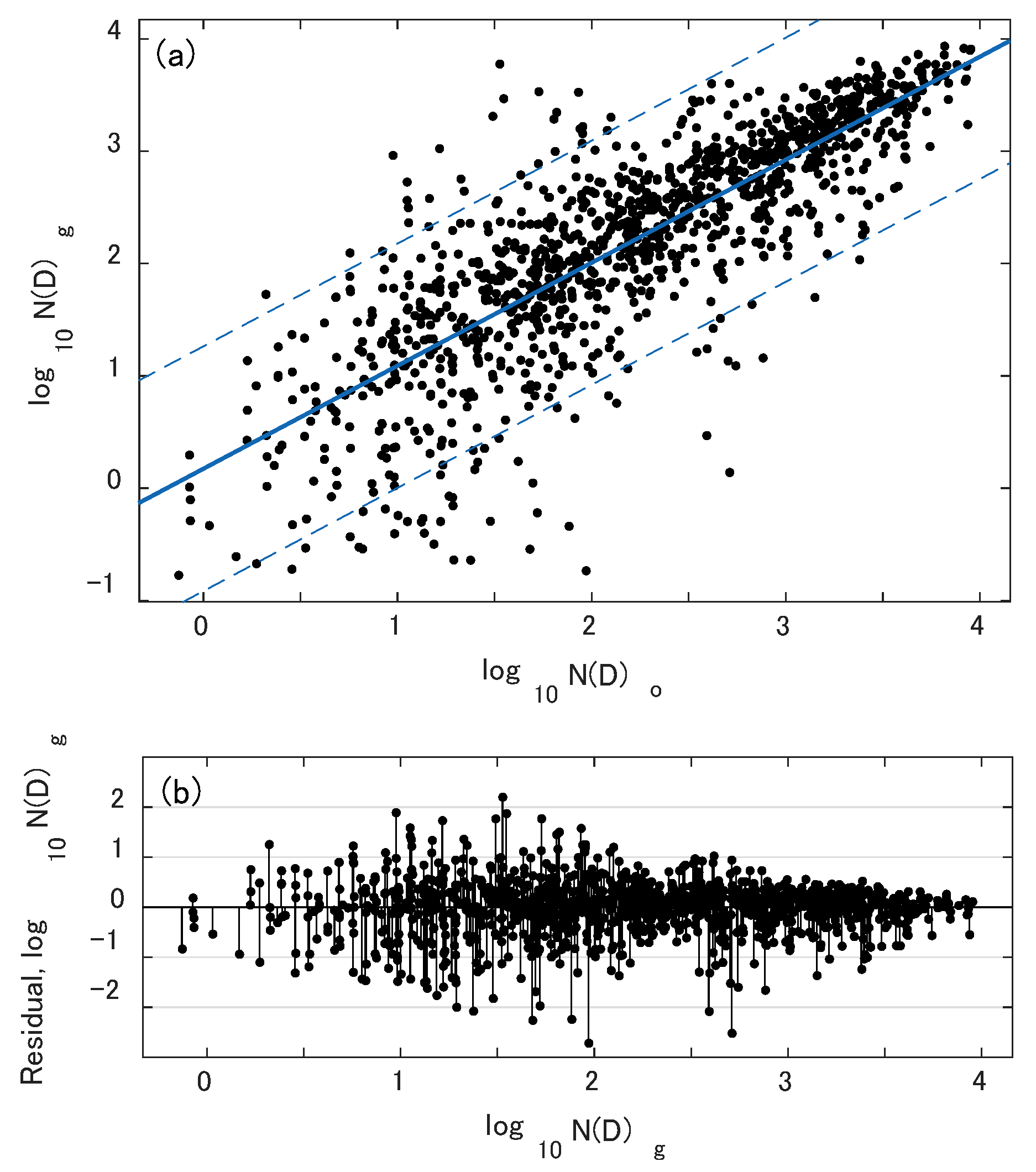
4.2.3. Normalized PSD
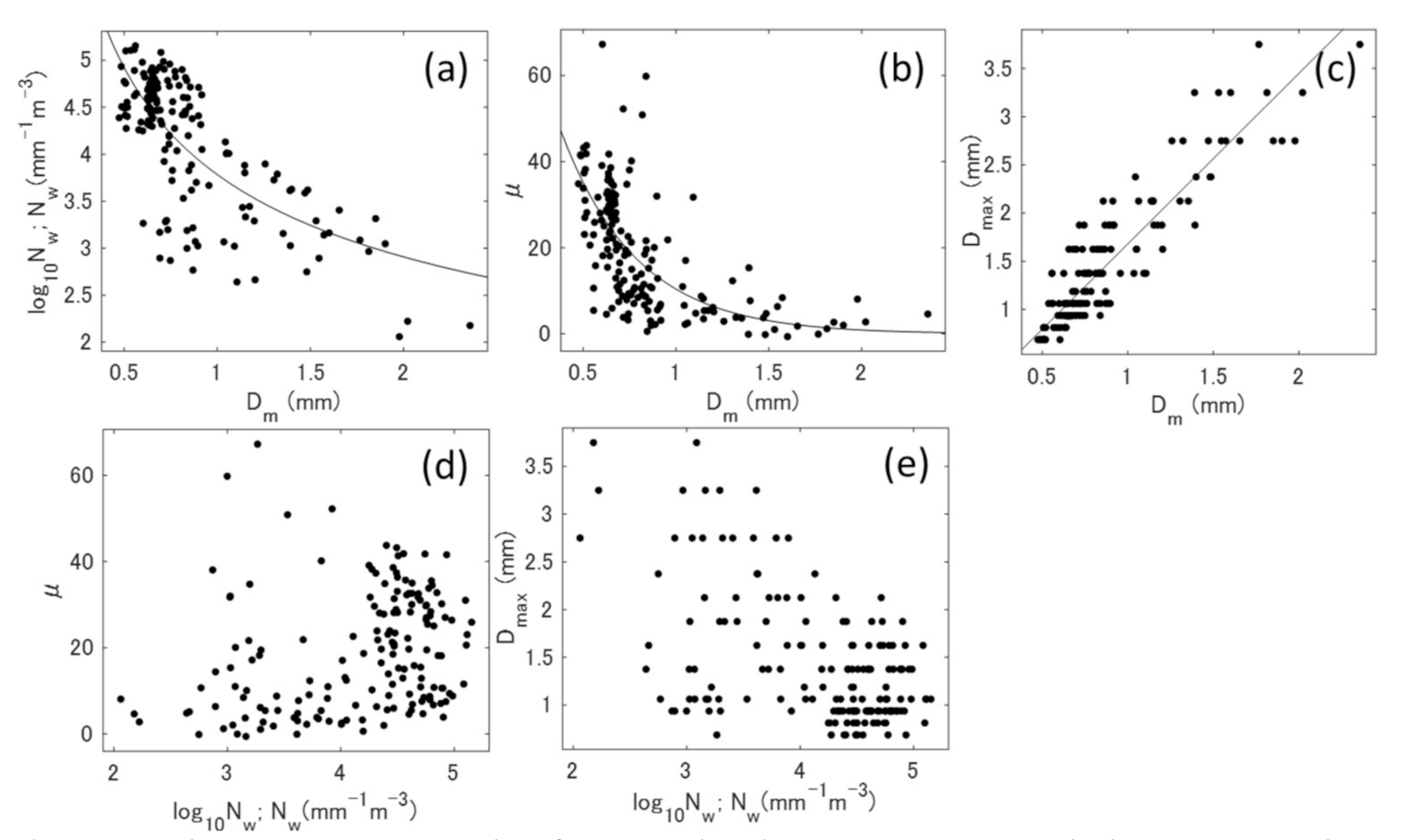
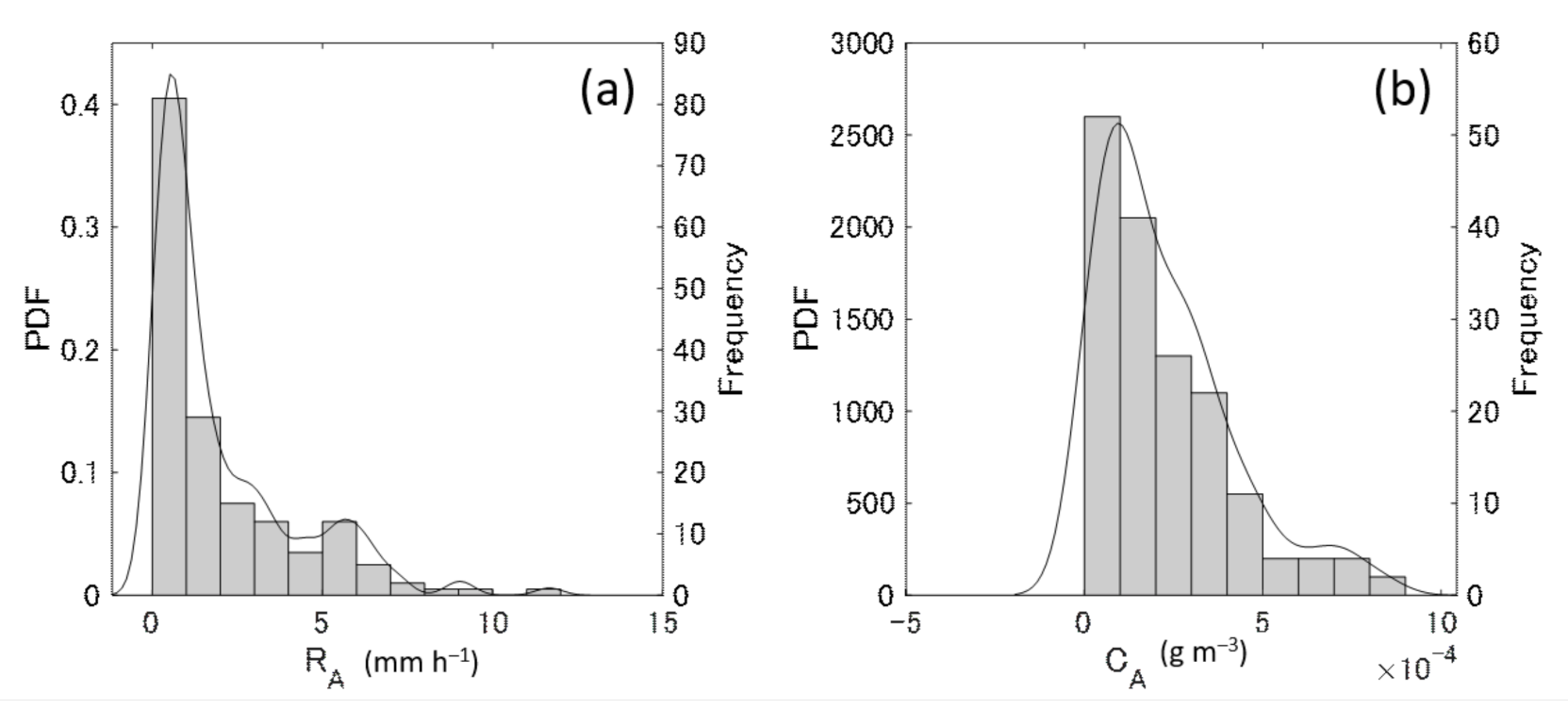
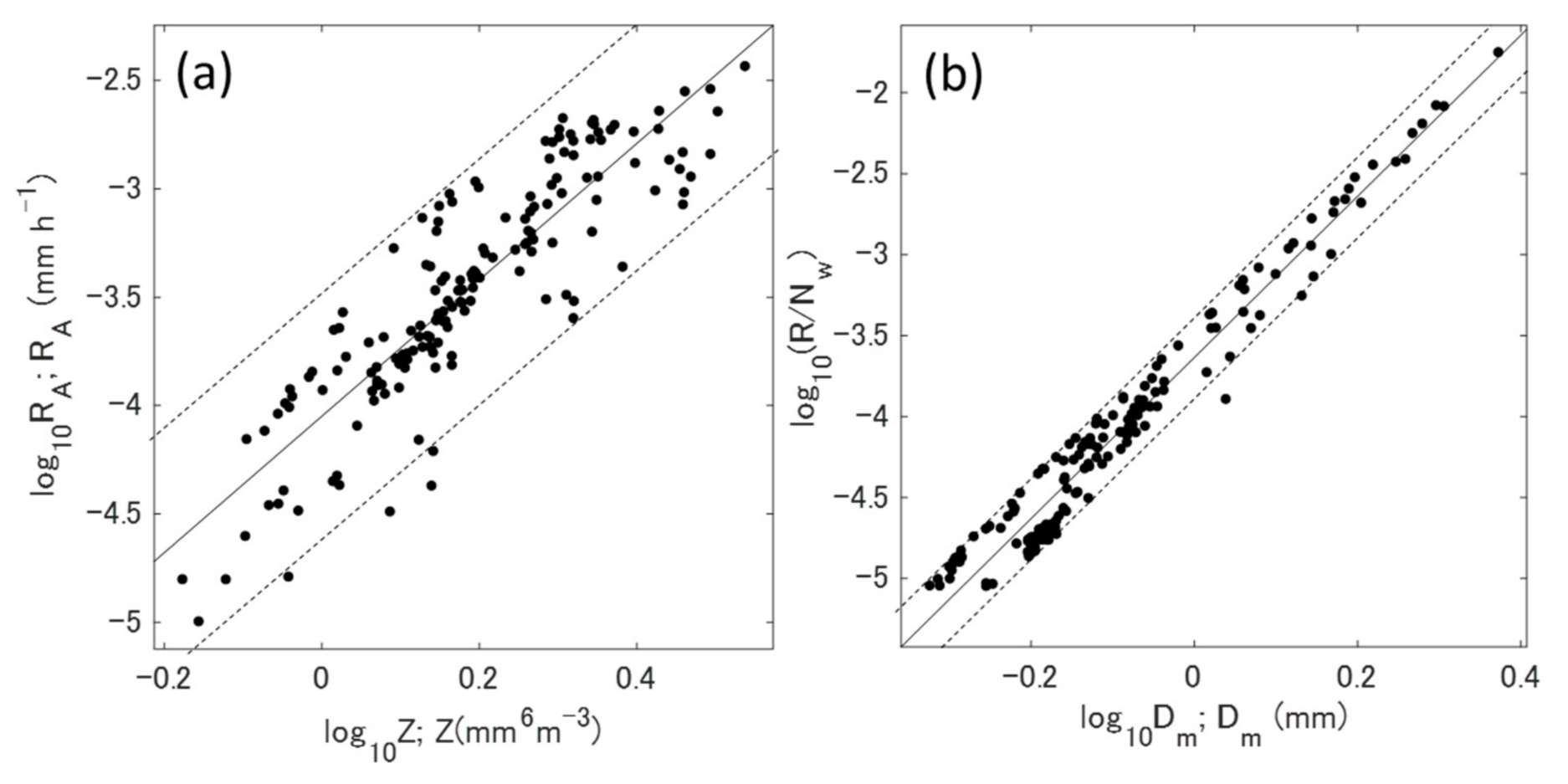
4.2.4. Quantitative Ash Fall Estimation Using Normalized PSD Parameters
4.3. Conventional Relationship for Quantitative Ash Fall Estimation
5. Discussion
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Symbol | Description | Unit |
| Ai | Effective measured area of the i-th size bin | mm2 |
| CA | Volcanic ash mass concentration | kg m−3 |
| Cij | Number of particles measured in i-th diameter bin and j-th Velocity bin | - |
| D | Particle diameter | mm |
| D0 | Median volume diameter | mm |
| Dm | Mass-weighted mean diameter | mm |
| Dmax | Maximum particle diameter | mm |
| Dmin | Minimum particle diameter | mm |
| ΔDi | Bin size of the i-th diameter channel | mm |
| N(D) | Particle size distribution (PSD) | mm−1 m−3 |
| N(Di) | Number of particles from Di to Di + ΔDi per unit volume | mm−1 m−3 |
| N0 | Intercept parameter of gamma PSD | mm–1–μ m−3 |
| NT | Total number of volcanic ash particles | m−3 |
| Nw | Normalized intercept parameter of gamma PSD | mm−1 m−3 |
| nd | Number of diameter bins | - |
| nv | Number of velocity bins | - |
| RA | Ash fall rate; 1 (kg m−2h−1) = ρp/ρb (mm h−1) | mm h−1 |
| Δt | Sampling time (60 s) | s |
| Vj | Fall velocity measured at the j-th velocity bin | m s−1 |
| Vt | Fall velocity of a volcanic ash particle | m s−1 |
| Z | Equivalent reflectivity factor | mm6 m−3 |
| Λ | Slope parameter of gamma PSD | mm−1 |
| μ | Shape parameter of gamma PSD | - |
| ρb | Bulk density of ash deposits (= 1.25 × 103 kg m−3) | kg m−3 |
| ρp | Density of a solid ash particle (= 2.5 × 103 kg m−3) | kg m−3 |
References
- Kaminski, E.; Jaupart, C. The size distribution of pyroclasts and the fragmentation sequence in explosive volcanic eruptions. J. Geophys. Res. 1998, 103, 29759–29779. [Google Scholar] [CrossRef]
- Costa, A.; Pioli, L.; Bonadonna, C. Insights into tephra total grain-size distribution from field data analysis. Earth Planet. Sci. Lett. 2016, 443, 90–107. [Google Scholar] [CrossRef]
- Kueppers, U.; Scheu, B.; Spieler, O. Fragmentation efficiency of explosive volcanic eruptions: A study of experimentally generated pyroclasts. J. Volcanol. Geoth. Res. 2006, 153, 125–135. [Google Scholar] [CrossRef]
- Rust, A.C.; Cashman, K.V. Permeability controls on expansion and size distributions of pyroclasts. J. Geophys. Res. 2011, 116, B11202. [Google Scholar] [CrossRef]
- Cashman, K.V.; Scheu, B. Magmatic fragmentation. In The Encyclopedia of Volcanoes, 2nd ed.; Sigurdsson, H., Houghton, B., McNutt, S., Rymer, H., Stix, J., Eds.; Academic Press: Cambridge, MA, USA, 2015; pp. 459–472. [Google Scholar]
- Webley, P.; Mastin, L. Improved prediction and tracking of volcanic ash clouds. J. Volcanol. Geotherm. Res. 2009, 186, 1–9. [Google Scholar] [CrossRef]
- Mastin, L.G.; Guffanti, M.; Servranckx, R.; Webley, P.W.; Barsotti, S.; Dean, K.; Denlinger, R.; Durant, A.; Ewert, J.W.; Gardner, C.A.; et al. A multidisciplinary effort to assign realistic source parameters to model of volcanic ash-cloud transport and dispersion during eruptions. J. Volcanol. Geotherm. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
- Cashman, K.; Rust, A. Introduction: Part 2: Volcanic ash: Generation and spatial variations. In Volcanic Ash Hazard Observation; Mackie, S., Cashman, K., Ricketts, H., Rust, A., Watson, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 5–22. [Google Scholar]
- Pioli, L.; Bonadonna, C.; Pistolesi, M. Reliability of total grain-size distribution of tephra deposits. Sci. Rep. 2019, 9, 10006. [Google Scholar] [CrossRef]
- Suh, S.-H.; Maki, M.; Iguchi, M.; Lee, D.-I.; Yamaji, A.; Momotani, T. Free-fall experiments of volcanic ash particles using a 2-D video disdrometer. Atmos. Meas. Tech. 2019, 12, 5363–5379. [Google Scholar] [CrossRef]
- Kozono, T.; Iguchi, M.; Miwa, T.; Maki, M.; Maesaka, T.; Miki, D. Characteristics of tephra fall from eruptions at Sakurajima volcano, revealed by optical disdrometer measurements. Bull. Volcanol. 2019, 81. [Google Scholar] [CrossRef]
- Iguchi, M.; Nakamichi, H.; Tanaka, H.; Ohta, Y.; Shimizu, A.; Miki, D. Integrated monitoring of volcanic ash and forecasting at Sakurajima volcano, Japan. J. Disast. Res. 2019, 14, 798–809. [Google Scholar] [CrossRef]
- Schönhuber, M.; Lammer, G.; Randeu, W.L. The 2D video disdrometer. In Precipitation: Advances in Measurement, Estimation and Prediction; Michaelides, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–31. [Google Scholar]
- Kruger, A.; Krajewski, W.F. Two-dimensional video disdrometer: A description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of 852 hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the new version of the laser-optical disdrometer, OTT Parsivel2. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- OTT. Operating Instructions, Present Weather Sensor, OTT Parsivel2; Document Number 70.210.001.B.E 04-0911; Hydromet GmbH: Kempten, Germany, 2011; 46p. [Google Scholar]
- Krajewski, W.F.; Kruger, A.; Caracciolo, C.; Golé, P.; Barthes, L.; Creutin, J.-D.; Delahaye, J.-Y.; Nikolopoulos, E.I.; Ogden, F.; Vinson, J.-P. DEVEX—Disdrometer evaluation experiment: Basic results and implications for hydrologic studies. Adv. Water Resour. 2006, 29, 311–325. [Google Scholar] [CrossRef]
- Lanza, L.G.; Vuerich, E. The WMO field intercomparison of rain intensity gauges. Atmos. Res. 2009, 94, 534–543. [Google Scholar] [CrossRef]
- Thurai, M.; Petersen, W.A.; Tokay, A.; Schultz, C.; Gatlin, P. Drop size distribution comparisons between Parsivel and 2-D video disdrometers. Adv. Geosci. 2011, 30, 3–9. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A. Ein spektrograph für niederschlagstropfen mit automatischer auswertung (A spectrograph for raindrops with automatic interpretation). Pure Appl. Geophys. 1967, 68, 240–246. [Google Scholar] [CrossRef]
- Kagoshima Local Meteorological Observatory, 2019. List of Sakurajima Eruptions in 2013. Available online: https://www.jma-net.go.jp/kagoshima/vol/data/skr_exp_list/skr_exp_2019.html (accessed on 23 April 2021). (In Japanese)
- JMA. Available online: https://www.jma-net.go.jp/kagoshima/vol/data/skr_exp_2013.html (accessed on 3 October 2019).
- Maki, M.; Kim, Y.; Kobori, T.; Hirano, K.; Lee, D.-I.; Iguchi, M. Analyses of three-dimensional weather radar data from volcanic eruption clouds. J. Volcanol. Geotherm. Res. 2021. [Google Scholar] [CrossRef]
- DIAS. XRAIN Precipitation Original Data search and Download System. Available online: https://auth.diasjp.net/cas/login?service=http://xrain.diasjp.net/original/&locale=en (accessed on 13 March 2019).
- Guyot, A.; Pudashine, J.; Protat, A.; Uijlenhoet, R.; Pauwels, V.R.N.; Seed, A.; Walker, J.P. Effect of disdrometer type on rain drop size distribution characterisation: A new dataset for south-eastern Australia. Hydrol. Earth Syst. Sci. 2019, 23, 4737–4761. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the drop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Assessment of the contribution of differential polarization to improved rainfall measurements. Radio Sci. 1984, 19, 49–57. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bringi, V.N. Simulation of radar reflectivity and surface measurements of rainfall. J. Atmos. Ocean. Technol. 1987, 4, 464–478. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Miwa, T.; Maki, M.; Kozono, T.; Fujita, E.; Tanada, T.; Iguchi, M. Experimental measurement on falling velocity of volcanic ash from Sakurajima volcano by using PARSIVEL disdrometer. Annu. Disas. Prev. Res. Inst. Kyoto Univ. 2015, 58, 91–94. Available online: http://hdl.handle.net/2433/210085 (accessed on 23 April 2021). (In Japanese with English abstract).
- Kozono, T.; Miwa, T.; Maki, M.; Maesaka, T.; Miki, D.; Iguchi, M. PARSIVEL tephra-fall observations at Sakurajima Volcano. Annu. Disast. Prev. Res. Inst. Kyoto Univ. 2015, 58B, 86–90, (In Japanese with English abstract). Available online: http://hdl.handle.net/2433/210086 (accessed on 23 April 2021). (In Japanese with English abstract).
- Kozono, T. (Tohoku University, Sendai, Miyagi, Japan). Personal communication, 2020.
- Harris, D.M.; Rose, W.I. Estimating particle sizes, concentrations, and total mass of ash in volcanic clouds using weather radar. JGR Oceans 2019, 88, 10969–10983. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Doppler radar observations of drop-size distributions in a thunderstorm. J. Atmos. Sci. 1971, 28, 983–994. [Google Scholar] [CrossRef]
- Willis, P.T. Functional fits to some observed drop size distributions and parameterization of rain. J. Atmos. Sci. 1984, 41, 1648–1661. [Google Scholar] [CrossRef]
- Sempere Torres, D.; Porrà, J.M.; Creutin, J.-D. 1998: A general formulation for raindrop size distribution. J. Geophys. Res. 1998, 103, 1785–1797. [Google Scholar] [CrossRef]
- Testud, J.; Le Bouar, E.; Obligis, E.; Ali Mehenni, M. The rain profiling algorithm applied to polarimetric weather radar. J. Atmos. Ocean. Technol. 2000, 17, 332–356. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Delanoë, J.; Protat, A.; Testud, J.; Bouniol, D.; Heymsfield, A.J.; Bansemer, A.; Brown, P.R.A.; Forbes, R.M. Statistical properties of the normalized ice particle size distribution. J. Geophys. Res. 2005, 110, D10201. [Google Scholar] [CrossRef]
- Kozu, T.; Nakamura, K. Rainfall parameter estimation from dual-radar measurements combining reflectivity profile and path-integrated attenuation. J. Atmos. Ocean. Technol. 1991, 8, 251–271. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Rainfall microphysics and radar properties: Analysis methods for drop size spectra. J. Appl. Meteorol. 1998, 37, 912–923. [Google Scholar] [CrossRef]
- Ulbrich, C.W. The effects of drop size distribution truncation on rainfall integral parameters and empirical relations. J. Climate Appl. Meteorol. 1985, 24, 580–590. [Google Scholar] [CrossRef][Green Version]
- Sekhon, R.S.; Srivastava, R.C. Snow size spectra and radar reflectivity. J. Atmos. Sci. 1970, 28, 983–994. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. Aerodynamics of volcanic particles: Characterization of size, shape, and settling velocity. In Volcanic Ash Hazard Observation; Mackie, S., Cashman, K., Ricketts, H., Rust, A., Watson, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 39–52. [Google Scholar] [CrossRef]
- Manzella, I.; Bonadonna, C.; Phillips, J.C.; Monnard, H. The role of gravitational instabilities in deposition of volcanic ash. Geology 2015, 43, 211–214. [Google Scholar] [CrossRef]
- Freret-Lorgeril, V.; Gilchri, J.; Donnadieu, F.; Jellinek, A.M.; Delanoë, J.; Latchimy, T.; Vinson, J.P.; Caudoux, C.; Peyrin, F.; Hervier, C.; et al. Ash sedimentation by fingering and sediment thermals from wind-affected volcanic plumes. Earth Planet. Sci. Lett. 2020, 534. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R.; Iguchi, T.; Tokay, A. Characteristics of DSD bulk parameters: Implication for radar rain retrieval. Atmosphere 2020, 11, 670. [Google Scholar] [CrossRef]
- Bringi, V.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001; pp. 378–426. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Jayalakshmi, J.; Seela, B.K.; Lin, P.-L.; Wang, P.K.; Tseng, C.-H.; Reddy, K.K.; Hashiguchi, H.; Feng, L.; Das, S.K.; Unnikrishnan, C.K. Raindrop size distribution characteristics of Indian and Pacific Ocean tropical cyclones observed at India and Taiwan sites. J. Meteorol. Soc. Japan 2020, 98, 299–317. [Google Scholar] [CrossRef]
- Coata, A.; Folch, A.; Macedonio, G. A model for wet aggregation of ash particles in volcanic plumes and clouds: 1. Theoretical formulation. J. Geophys. Res. 2010, 115, B09201. [Google Scholar] [CrossRef]
- Folch, A.; Costa, A.; Durant, A.; Macedonio, G. A model for wet aggregation of ash particles in volcanic plumes and clouds: 2. Model application. J. Geophys. Res. 2010, 115, B09202. [Google Scholar] [CrossRef]
- Brown, R.J.; Bonadonna, C.; Durant, A.J. A review of volcanic ash aggregation. Phys. Chem. Earth Parts A/B/C 2012, 45–46, 65–78. [Google Scholar] [CrossRef]
- Markowitz, A.H. Raindrop size distribution experiments. J. Appl. Meteorol. 1976, 15, 1029–1166. [Google Scholar] [CrossRef]
- Feingold, G.; Levin, Z. Application of the lognormal rain-drop distribution to differential reflectivity radar measurements (ZDR). J. Atmos. Ocean. Technol. 1987, 4, 377–382. [Google Scholar] [CrossRef]
- Cornford, S.G. Sampling errors in measurements of raindrop and cloud droplet concentrations. Meteorol. Mag. 1967, 96, 271–282. [Google Scholar]
- Best, A. The size distribution of raindrops. Quart. J. Roy. Meteorol. Soc. 1950, 76, 16–36. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J. Appl. Meteorol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Shoji, D.; Noguchi, R.; Otsuki, S.; Hino, H. Classification of volcanic ash particles using a convolutional neural network and probability. Sci. Rep. 2018, 8, 8111. [Google Scholar] [CrossRef]
| Category | Subcategory | Specification |
|---|---|---|
| Sensor | Type | Laser diode |
| Wavelength | 650 nm | |
| Output rating | 0.2 mW | |
| Laser class | 1 (IEC/EN 60825-1: 2014) | |
| Sampling | Light strip (W × D) | 30 × 1 mm (54 cm2) |
| Area (W × D) | 180 × 30 mm (54 cm2) | |
| Interval | 10 s to 60 min | |
| Output | Particle size | 32 classes: 0.2, …, 8 mm (liquid particles) 32 classes: 0.2, …, 25 mm (solid particles) |
| Fall velocity | 32 classes: 0.2, …, 20 m s−1 | |
| Precipitation intensity (accuracy) | 0.001, …, 1200 mm h−1 (±5% for liquid, ±20% for solid) | |
| Precipitation type | 8 types (drizzle, drizzle/rain, rain, snow, mixed rain/snow, snow grains, sleet, hail) | |
| Radar reflectivity factor | −9.999, …, 99.999 dBZ ± 20% | |
| Kinetic energy | 0, …, 999.999 J/(m2 h) | |
| Visibility in precipitation | 0, …, 20,000 m |
| Case | Eruption Onset (LST) | Cloud Top Height (m) | Movement | Disdrometer Code |
|---|---|---|---|---|
| 1 | 08:08, 15 May 2018 | 2500 | Top | NABE |
| 2 | 19:48, 22 May 2018 | Unknown | Unknown | HIKP, HART |
| 3 | 08:01, 30 May 2018 | 2500 | Eastward | KURP |
| 4 | 11:35, 10 June 2018 | 3500 | Top | HART |
| 5 | 07:19, 16 June 2018 | 4700 | Westward | SBTT |
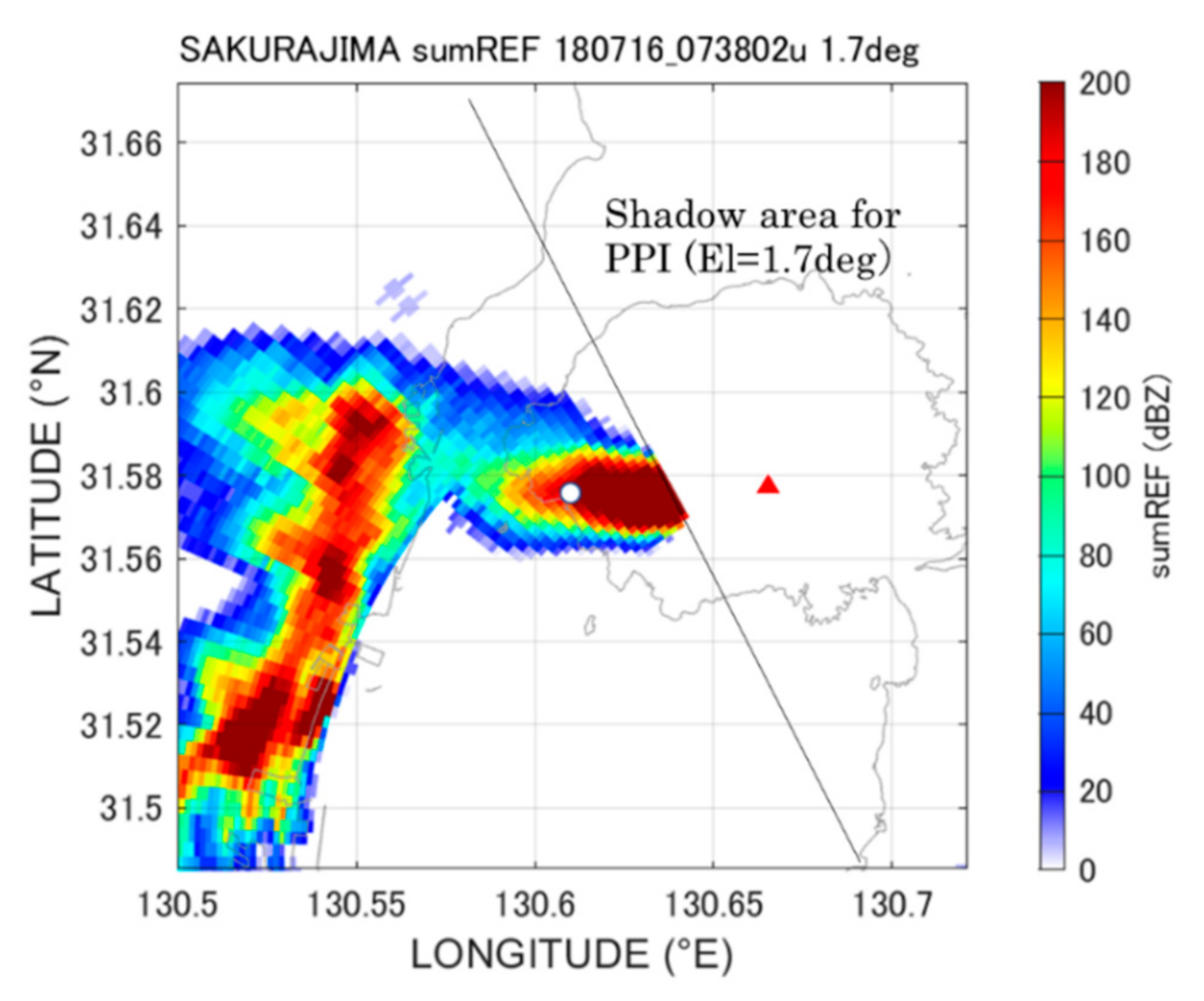
| 6 | 15:38, 16 July 2018 | 4600 | Westward | AKAM |
| a | b | Note | Reference |
|---|---|---|---|
| 5.90 | 0.530 | 0.25 ≤ D < 4 mm (free fall experiments, Parsivel2) | Miwa et al. [31] |
| 5.96 | 0.530 | 0.25 ≤ D < 4 mm (free fall experiments, 2DVD) | Suh et al. [10] |
| 4.04 | 0.830 | 0.25 ≤ D < 2 mm (Sakurajima, Parsivel2, 26,075 particles) | Kozono et al. [32] |
| 3.96 | 0.748 | 0.25 ≤ D < 4 mm (Sakurajima, Parsivel2, 79,170 particles) | Kozono [33] |
| 3.18 | 0.728 | 0.25 ≤ D < 4 mm (Sakurajima, Parsivel2, 63,237 particles) | Present study |
| 3.14 | 0.817 | 0.25 ≤ D < 2 mm (Sakurajima, Parsivel2, 63,237 particles) | Present study |
| 3.42 | 0.371 | 0.2 ≤ D ≤ 6.0 mm (Mt. St. Helens, 19 March 1982) | Harris and Rose [34] |
| 5.02 | 0.335 | 0.22 ≤ D ≤ 1.3 mm (Mt. St. Helens, 19 March 1982) | Harris and Rose [34] |
| 6.87 | 1.0 | 0.02 ≤ D ≤ 0.38 mm (Mt. St. Helens, 18 May 1980) | Harris and Rose [34] |
| 4.33 | 0.437 | 0.02 ≤ D ≤ 6.0 mm (Mt. St. Helens, all data) | Present study (average) |
| Parameter | Unit | Mode | Med | Mean | SD | Max | Skew | D10 | D90 |
|---|---|---|---|---|---|---|---|---|---|
| log10 N0 | mm−1 m−3 | 8.83 | 9.64 | 15.8 | 9.64 | 47.9 | 0.581 | 4.79 | 28.2 |
| L | mm−1 | 13.4 | 27.2 | 33.5 | 25.0 | 118 | 0.742 | 6.05 | 65.4 |
| D0 | mm | 0.65 | 0.69 | 0.79 | 0.292 | 2.13 | 1.88 | 0.54 | 1.21 |
| m | – | 8.3 | 17.1 | 18.9 | 13.7 | 67.3 | 0.661 | 3.10 | 36.8 |
| Dmax | mm | 0.97 | 1.19 | 1.42 | 0.679 | 3.75 | 1.42 | 0.81 | 2.36 |
| log10Nw | mm−1 m−3 | 4.60 | 4.42 | 4.15 | 0.704 | 5.15 | −0.875 | 3.07 | 4.87 |
| Dm | mm | 0.853 | 1.19 | 0.853 | 0.350 | 2.36 | 1.83 | 0.559 | 139 |
| NT | m−3 | 182 | 252 | 381 | 380 | 1788 | 1.75 | 26 | 998 |
| RA | mm h−1 | 0.52 | 1.08 | 2.01 | 2.17 | 11.7 | 1.64 | 0.23 | 5.43 |
| CA | g m−3 | 0.0931 | 0.180 | 0.225 | 0.189 | 0.845 | 1.21 | 0.0323 | 0.478 |
| 10log10Z | dBZ | 17.1 | 18.2 | 19.3 | 7.43 | 36.9 | 0.087 | 9.28 | 28.8 |
| log10N0 | Λ | μ | Dmax | |
|---|---|---|---|---|
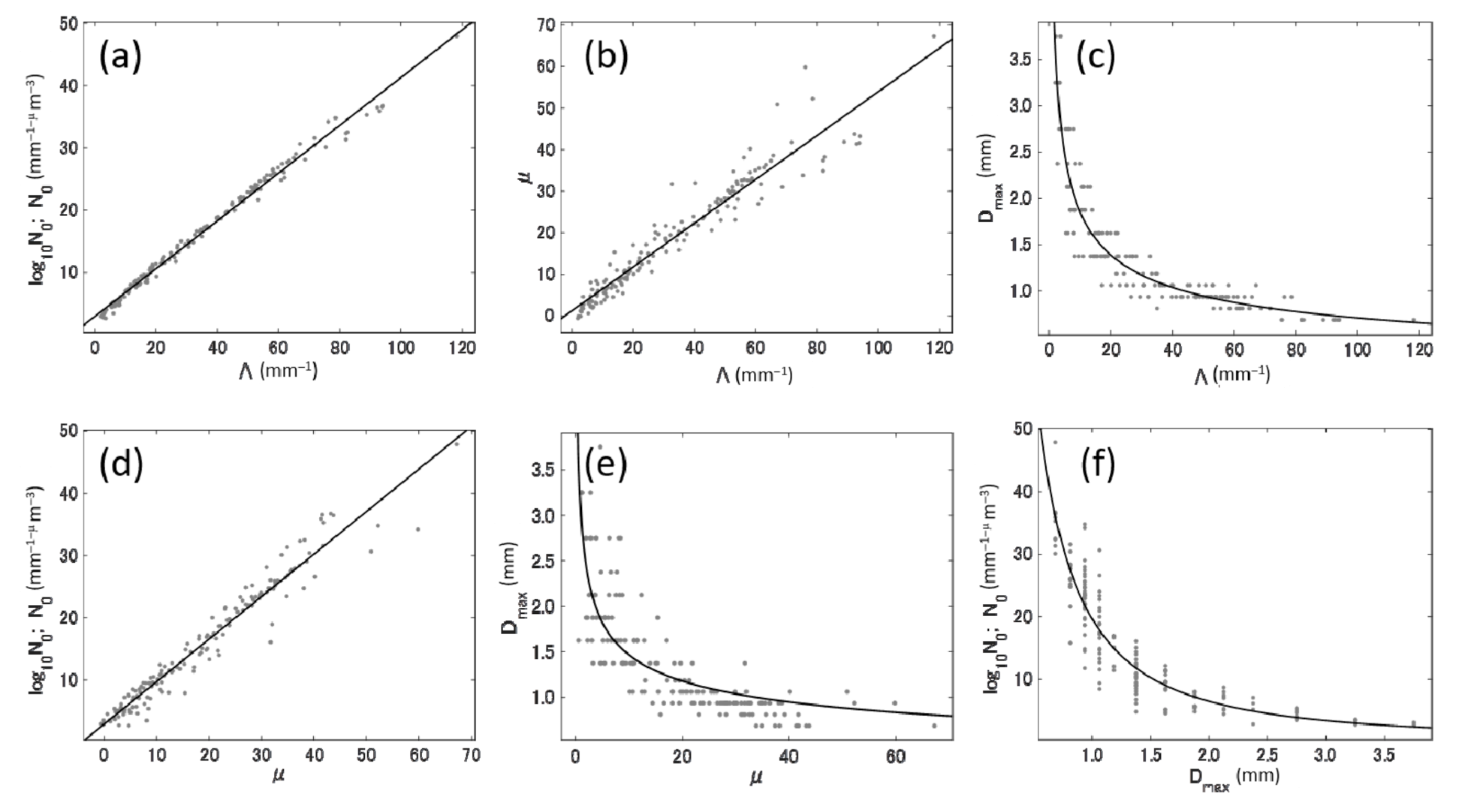
| log10N0 | - | log10N0 = 0.383 Λ + 2.942 (0.995, 0.91) | log10N0 = 0.684 μ + 2.89 (0.973, 2.211) | log10N0 = 19.67 Dmax −1.606 (0.920, 3.784) |
| Λ | Λ = 2.585 log10N0 − 7.308 (0.995, 2.361) | - | Λ = 1.751 μ + 0.469 (0.960, 7.005) | Λ = 42.23 Dmax−2.046 (0.937, 8.76) |
| μ | μ = 1.386 log10N0 − 3.02 (0.974, 3.148) | μ = 0.527 Λ + 1.222 (0.960, 3.842) | - | μ = 23.87 Dmax−1.713 (0.853, 7.178) |
| Dmax | Dmax = 5.863 log10N0 − 0.595 (0.922, 0.263) | Dmax = 4.862 Λ−0.418 (0.937, 0.238) | Dmax = 3.018 μ−0.314 (0.779, 0.393) | - |
| Case | Site | Sampling Period (LST) | (min) | RA–Z Relationship (R, RMSE) | CA–Z Relationship (R, RMSE) | Range |
|---|---|---|---|---|---|---|
| 1 | NABE | 08:22–08:35, 15 May 2018 | 14 | RA = 8.62 × 10−2 Z 0.809 (0.963, 0.300) | CA = 1.51 × 10−2 Z 0.680 (0.912, 0.046) | 0 ≤ Z ≤ 1 × 102 |
| 2 | HART | 20:03–20:11, 22 May 2018 | 9 | RA = 5.44 × 10−2 Z 0.595 (0.910, 0.907) | CA = 0.629 × 10−2 Z 0.569 (0.950, 0.058) | 0 ≤ Z ≤ 2 × 103 |
| HIKP | 20:00–20:14, 22 May 2018 | 12 | RA = 3.03 × 10−2 Z 0.826 (0.977, 0.397) | CA = 0.496 × 10−2 Z 0.770 (0.980, 0.043) | 0 ≤ Z ≤ 1 × 103 | |
| 3 | KURP | 08:09–08:13, 30 May 2018 | 4 | RA = 14.6 × 10−2 Z 0.522 (0.959, 0.613) | CA = 1.72 × 10−2 Z 0.423 (0.903, 0.055) | 0 ≤ Z ≤ 1 × 103 |
| 4 | HART | 12:03–12:20, 10 June 2018 | 12 | RA = 9.45 × 10−2 Z 0.568 (0.972, 0.929) | CA = 4.49× 10−2 Z 0.294 (0.899, 0.073) | 0 ≤ Z ≤ 5 × 103 |
| 5 | SBTT | 07:35–08:21, 16 June 2018 | 31 | RA = 3.55 × 10−2 Z 0.778 (0.917, 0.339) | CA = 1.20 × 10−2 Z 0.692 (0.960, 0.036) | 0 ≤ Z ≤ 4 × 102 |
| 6 | AKAM | 15:53–16:12, 16 July 2018 | 18 | RA = 10.0 × 10−2 Z 0.653 (0.851, 1.123) | CA = 0.553 × 10−2 Z 0.782 (0.913, 0.100) | 0 ≤ Z ≤ 7 × 102 |
| All | - | - | 88 | RA = 22.8 × 10−2 Z 0.436 (0.819, 1.247) | CA = 6.56 × 10−2 Z 0.261 (0.634, 0.147) | 0 ≤ Z ≤ 5 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maki, M.; Takaoka, R.; Iguchi, M. Characteristics of Particle Size Distributions of Falling Volcanic Ash Measured by Optical Disdrometers at the Sakurajima Volcano, Japan. Atmosphere 2021, 12, 601. https://doi.org/10.3390/atmos12050601
Maki M, Takaoka R, Iguchi M. Characteristics of Particle Size Distributions of Falling Volcanic Ash Measured by Optical Disdrometers at the Sakurajima Volcano, Japan. Atmosphere. 2021; 12(5):601. https://doi.org/10.3390/atmos12050601
Chicago/Turabian StyleMaki, Masayuki, Ren Takaoka, and Masato Iguchi. 2021. "Characteristics of Particle Size Distributions of Falling Volcanic Ash Measured by Optical Disdrometers at the Sakurajima Volcano, Japan" Atmosphere 12, no. 5: 601. https://doi.org/10.3390/atmos12050601
APA StyleMaki, M., Takaoka, R., & Iguchi, M. (2021). Characteristics of Particle Size Distributions of Falling Volcanic Ash Measured by Optical Disdrometers at the Sakurajima Volcano, Japan. Atmosphere, 12(5), 601. https://doi.org/10.3390/atmos12050601






