Evaluation of ENSO Prediction Skill Changes since 2000 Based on Multimodel Hindcasts
Abstract
1. Introduction
2. Materials and Methods
3. Results
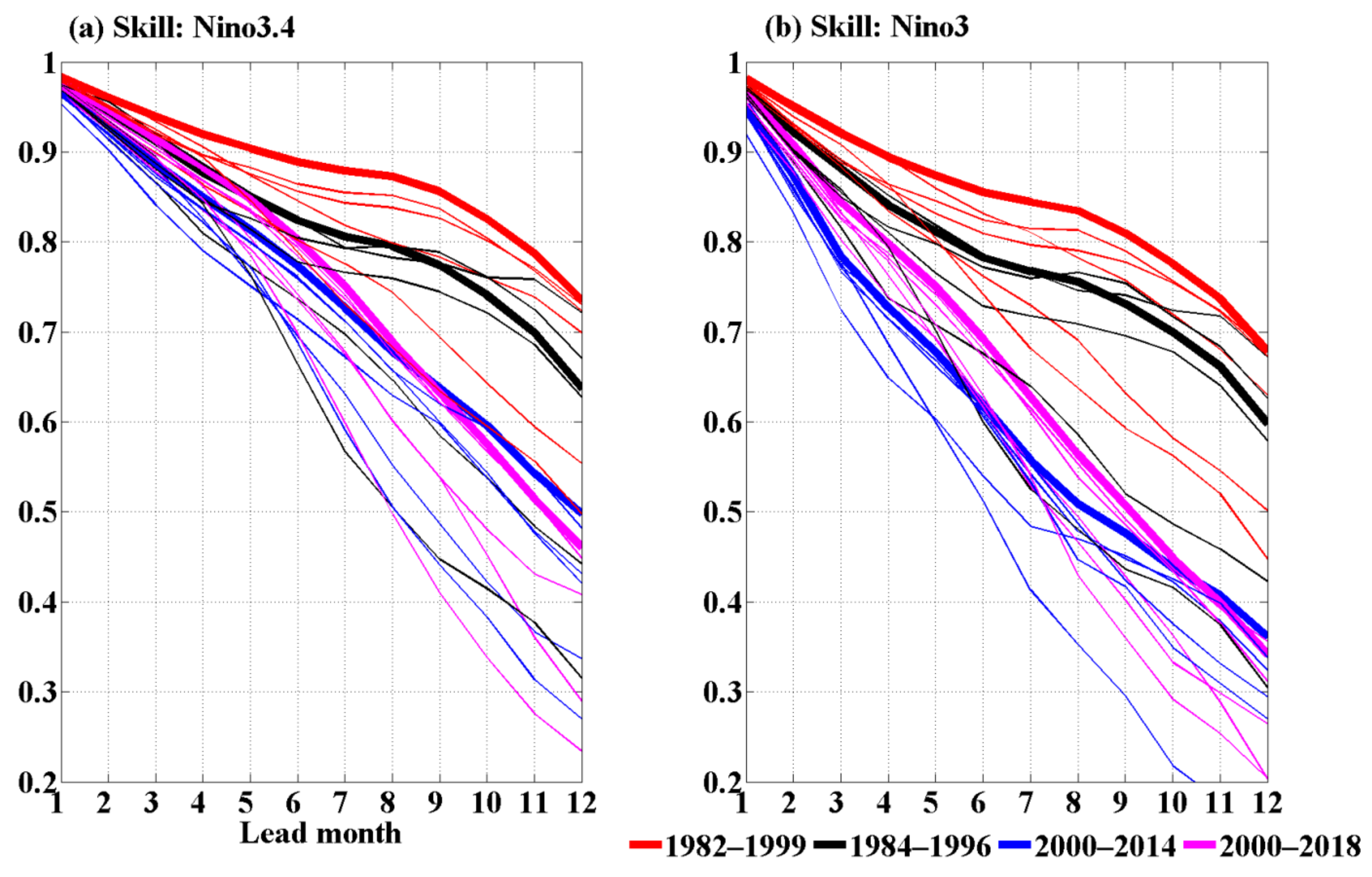
3.1. Changes in the Deterministic and Persistence Predictability
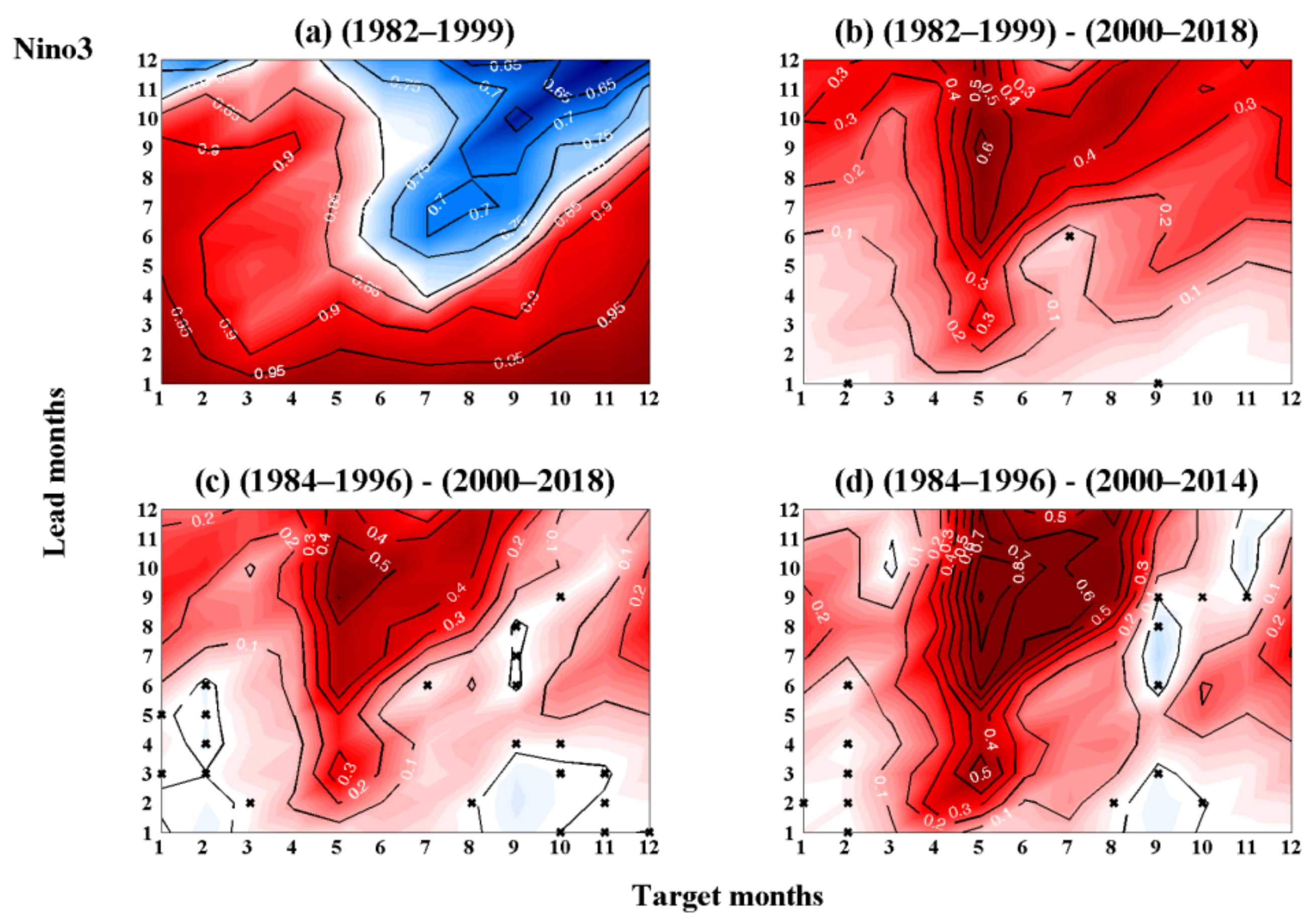
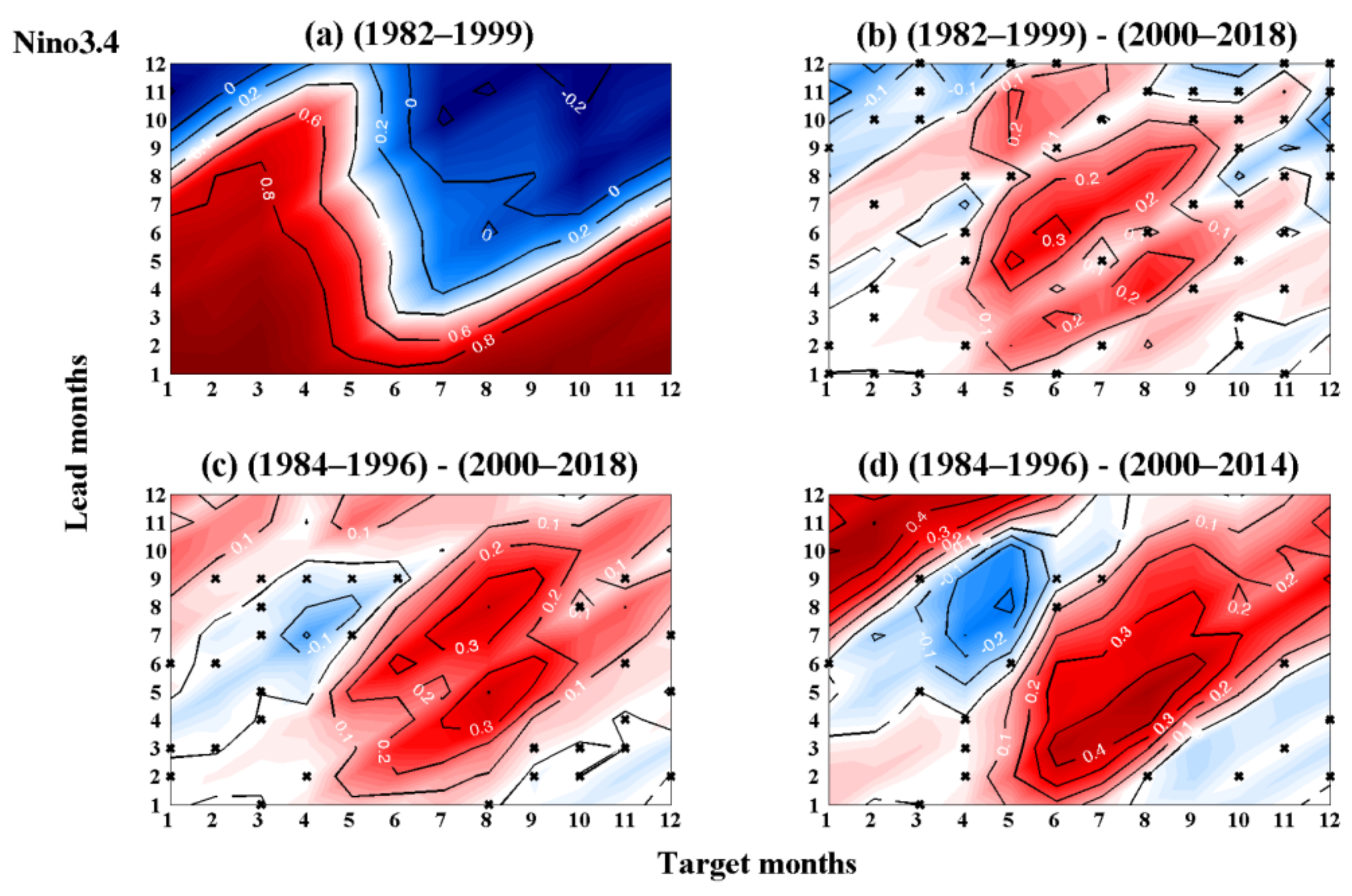
3.2. Main Causes of the Changes in the Deterministic and Persistence Predictability
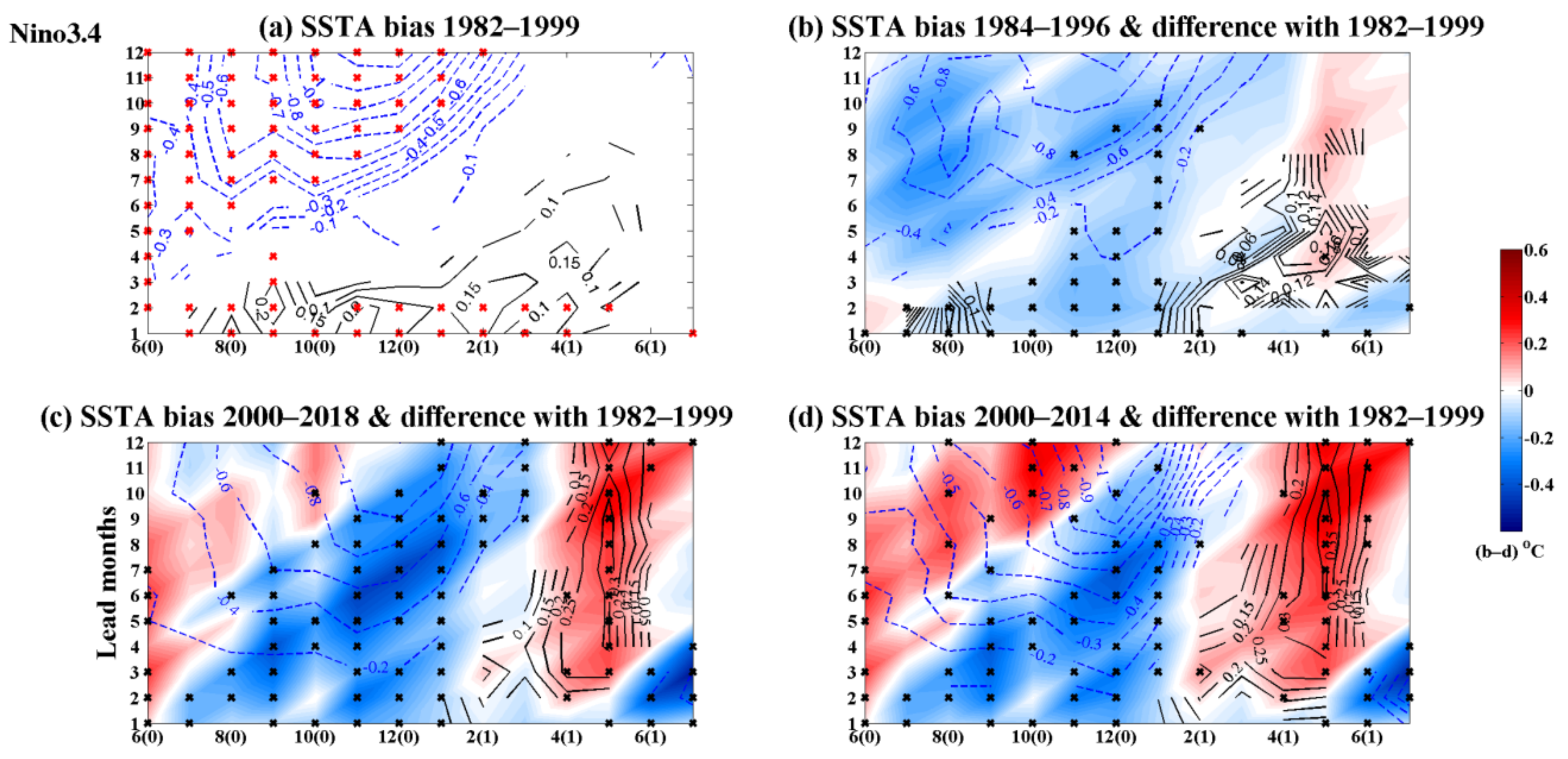
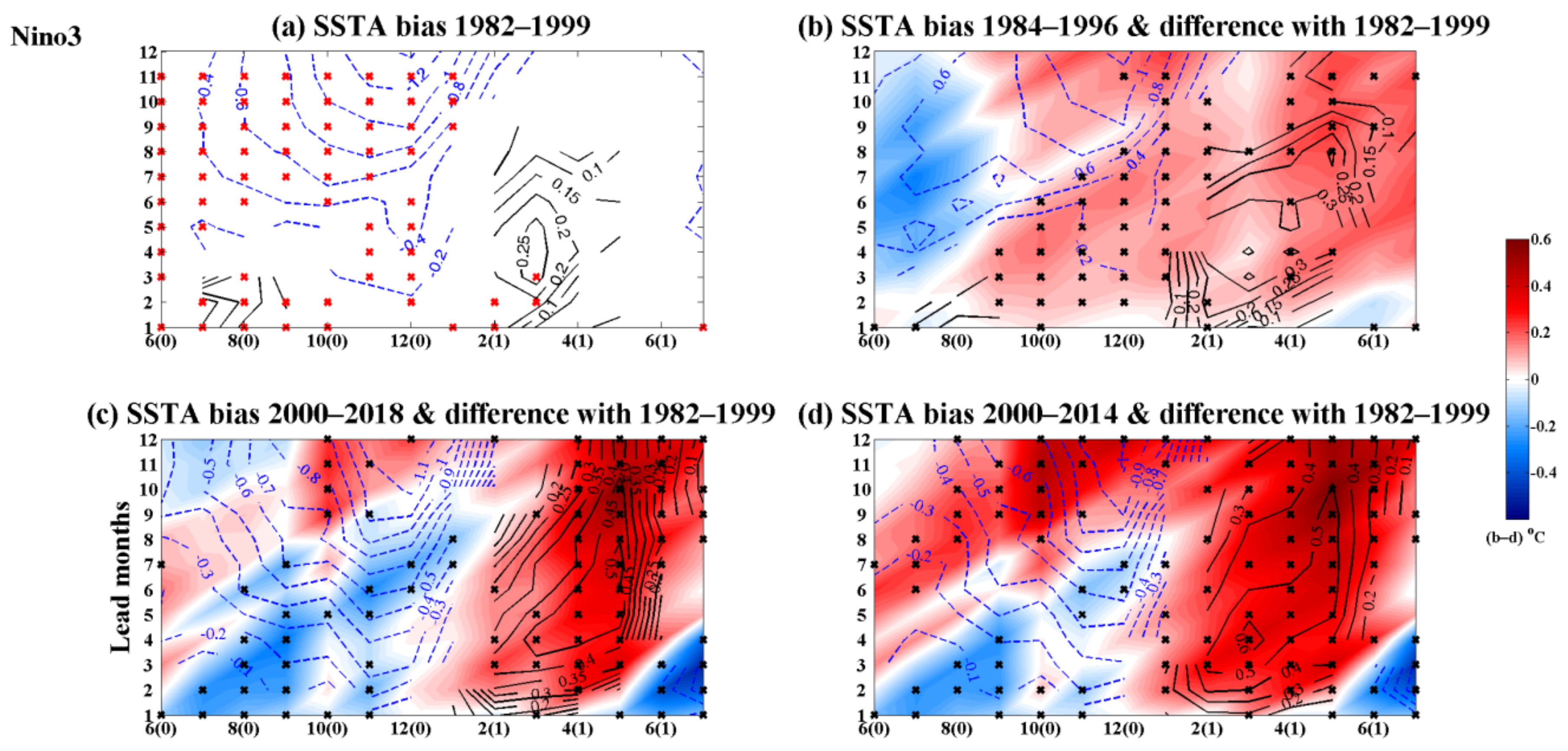
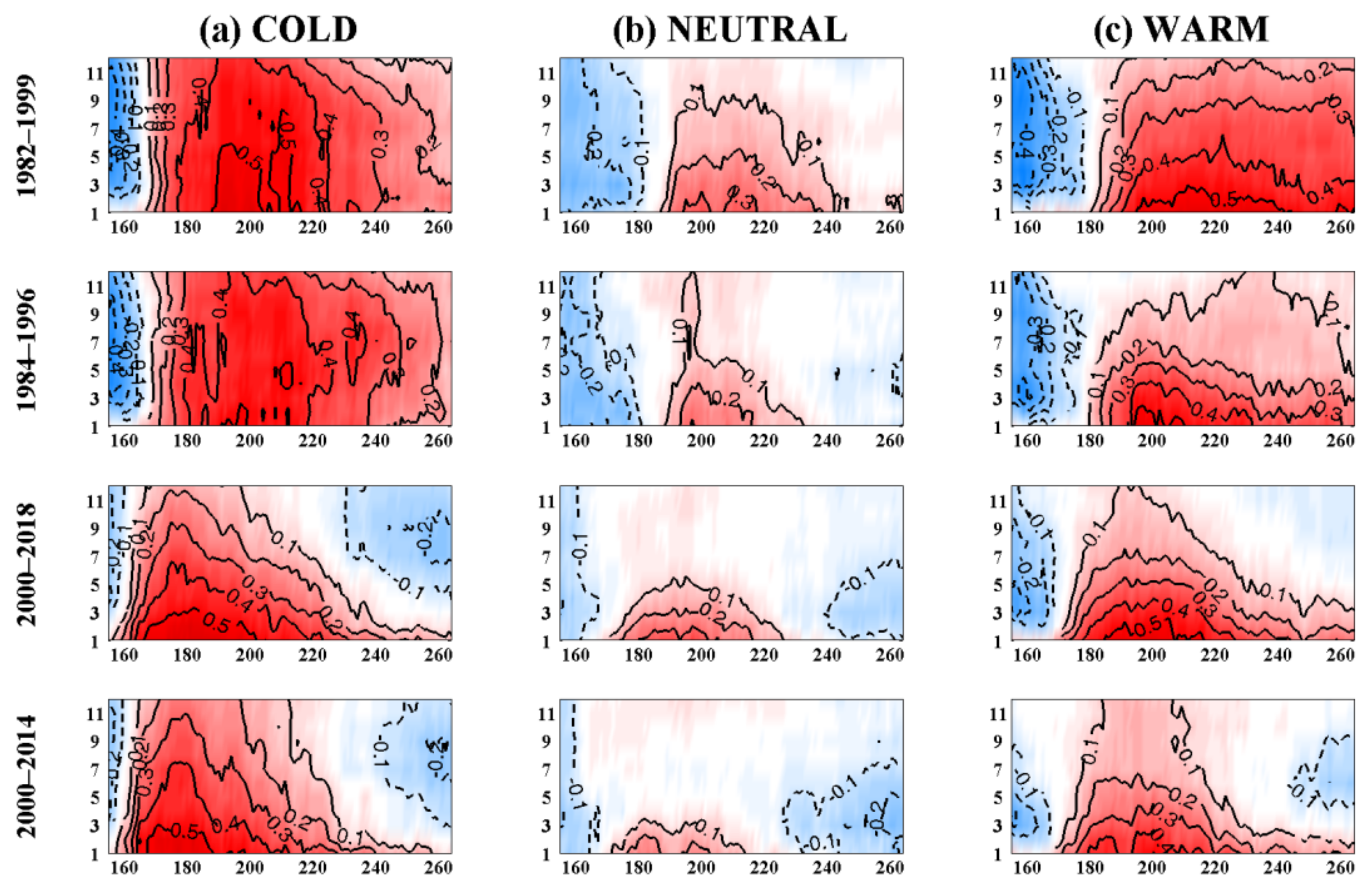
3.3. Changes in the Forecasting of the SSTA Bias during El Niño Events
3.4. Changes in the Probabilistic Predictability
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an intriguing concept in Earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Jin, F.F.; Zhao, J.X.; Qi, L.; Ren, H.L. The possible influence of a nonconventional El Niño on the severe autumn drought of 2009 in southwest China. J. Clim. 2013, 26, 8392–8405. [Google Scholar] [CrossRef]
- Tang, Y.M.; Zhang, R.H.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D.; et al. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
- Balmaseda, M.; Anderson, D.; Vidard, A. Impact of Argo on analyses of the global ocean. Geophys. Res. Lett. 2007, 34, L16605. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of real-time seasonal ENSO model predictions during 2002-11: Is our capability increasing? Bull. Am. Meteor. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Kumar, A.; Ren, H.L.; Wang, H.; L’Heureux, M.; Jin, F.F. Weakened interannual variability in the tropical Pacific Ocean since 2000. J. Clim. 2013, 26, 2601–2613. [Google Scholar] [CrossRef]
- Kumar, A.; Hu, Z.Z. Interannual and interdecadal variability of ocean temperature along the equatorial Pacific in conjunction with ENSO. Clim. Dyn. 2014, 42, 1243–1258. [Google Scholar] [CrossRef]
- Zhao, M.; Hendon, H.H.; Alves, O.; Liu, G.; Wang, G. Weakened Eastern Pacific El Niño Predictability in the Early Twenty-First Century. J. Clim. 2016, 29, 6805–6822. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Kumar, A.; Huang, B.; Zhu, J.; Ren, H.L. Interdecadal variations of ENSO around 1999/2000. J. Meteor. Res. 2017, 31, 73–81. [Google Scholar] [CrossRef]
- McPhaden, M.J. Tropical Pacific Ocean heat content variations and ENSO persistence barriers. Geophys. Res. Lett. 2003, 30, 1480. [Google Scholar] [CrossRef]
- Horii, T.; Ueki, I.; Hanawa, K. Breakdown of ENSO predictors in the 2000s: Decadal changes of recharge/discharge-SST phase relation and atmospheric intraseasonal forcing. Geophys. Res. Lett. 2012, 39, L10707. [Google Scholar] [CrossRef]
- McPhaden, M.J. A 21st century shift in the relationship between ENSO SST and warm water volume anomalies. Geophys. Res. Lett. 2012, 39, L09706. [Google Scholar] [CrossRef]
- Kao, H.Y.; Yu, J.Y. Contrasting Eastern-Pacific and Central-Pacific Types of ENSO. J. Clim. 2009, 22, 615–632. [Google Scholar] [CrossRef]
- Kug, J.S.; Jin, F.F.; An, S.I. Two types of El Niño events: Cold tongue El Niño and warm pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Wen, C.; Kumar, A.; Xue, Y.; McPhaden, M.J. Changes in tropical Pacific thermocline depth and their relationship to ENSO after 1999. J. Clim. 2014, 27, 7230–7249. [Google Scholar] [CrossRef]
- Lai, A.W.C.; Herzog, M.; Graf, H.F. Two key parameters for the El Niño continuum: Zonal wind anomalies and western Pacific subsurface potential temperature. Clim. Dyn. 2015, 45, 3461–3480. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Hu, S.; Lengaigne, M.; Guilyardi, E. The impact of westerly wind bursts and ocean initial state on the development, and diversity of El Niño events. Clim. Dyn. 2015, 44, 1381–1401. [Google Scholar] [CrossRef]
- Chen, D.; Lian, T.; Fu, C.B.; Cane, M.A.; Tang, Y.; Murtugudde, R.; Song, X.; Wu, Q.; Zhou, L. Strong influence of westerly wind bursts on El Niño diversity. Nat. Geosci. 2015, 8, 339–345. [Google Scholar] [CrossRef]
- Wang, R.; Ren, H.L. The linkage between two ENSO types/modes and the interdecadal changes of ENSO around the year 2000. Atmos. Ocean. Sci. Lett. 2017, 10, 168–174. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Kumar, A.; Zhu, J.S.; Peng, P.; Huang, B. On the Challenge for ENSO Cycle Prediction: An Example from NCEP Climate Forecast System, Version 2. J. Clim. 2019, 32, 183–194. [Google Scholar] [CrossRef]
- Vimont, D.J.; Wallace, J.M.; Battisti, D.S. The Seasonal Footprinting Mechanism in The Pacific: Implications for ENSO. J. Clim. 2003, 16, 2668–2675. [Google Scholar] [CrossRef]
- Chang, P.; Zhang, L.; Saravanan, R.; Vimont, D.J.; Chiang, J.C.H.; Ji, L.; Seidel, H.; Tippett, M.K. Pacific meridional mode and El Niño-Southern Oscillation. Geophys. Res. Lett. 2017, 34, L16608. [Google Scholar] [CrossRef]
- Larson, S.M.; Kirtman, B.P. The Pacific meridional mode as an ENSO precursor and predictor in the North American multimodel ensemble. J. Clim. 2014, 27, 7018–7032. [Google Scholar] [CrossRef]
- Amaya, D.J. The Pacific Meridional Mode and ENSO: A Review. Curr. Clim. Change Rep. 2019, 5, 296–307. [Google Scholar] [CrossRef]
- Bond, N.A.; Overland, J.E.; Spillane, M.; Stabeno, P. Recent shifts in the state of the North Pacific. Geophys. Res. Lett. 2003, 30, 2183. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P.; Tseng, Y.; Sun, C.; Guo, Y. The Victoria Mode in the North Pacific Linking Extratropical Sea Level Pressure Variations to ENSO. J. Geophys. Res. Atmos. 2015, 120, 27–45. [Google Scholar] [CrossRef]
- Ballester, J.; Rodríguez-Arias, M.À.; Rodó, X. A new extratropical tracer describing the role of the western Pacific in the onset of El Niño: Implications for ENSO understanding and forecasting. J.Clim. 2011, 24, 1425–1437. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P.; Tseng, Y.H. The Impact of South Pacific Extratropical Forcing on ENSO and Comparisons with the North Pacific. Clim. Dyn. 2014, 44, 2017–2034. [Google Scholar] [CrossRef]
- Kirtman, B.P.; Min, D.H.; Infanti, J.M. The North American Multimodel Ensemble: Phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Meteor. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Merryfield, W.J.; Lee, W.S.; Boer, G.J.; Kharin, V.V.; Scinocca, J.F.; Flato, G.M.; Ajayamohan, R.S.; Fyfe, J.C.; Tang, Y.; Polavarapu, S. The Canadian seasonal to interannual prediction system. Part I: Models and initialization. Mon. Weather. Rev. 2013, 141, 2910–2945. [Google Scholar] [CrossRef]
- Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC-MRB Global Environmental Multiscale (GEM) model. Part I: Design considerations and formulation. Mon. Wea. Rev. 1998, 126, 1373–1395. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Peng, P.; Kumar, A.; van den Dool, H.; Barnston, A.G. An analysis of multi-model ensemble predictions for seasonal climate anomalies. J. Geophys. Res. 2002, 107, 4710. [Google Scholar] [CrossRef]
- Min, Y.M.; Kryjov, V.N.; Oh, S.M. Skill of real-time operational forecasts with the APCC multi-model ensemble prediction system during the period 2008–2015. Clim. Dyn. 2017, 49, 4141–4156. [Google Scholar] [CrossRef]
- Min, Y.M.; Kryjov, V.N.; Oh, S.M. Assessment of APCC multimodel ensemble prediction in seasonal climate forecasting: Retrospective (1983–2003) and real-time forecasts (2008–2013). J. Geophys. Res. Atmos. 2014, 119, 12132–12150. [Google Scholar] [CrossRef]
- Rodrigues, L.R.L.; Doblas-Reyes, F.J.; Coelho CA dos, S. Multi-model calibration and combination of tropical seasonal sea surface temperature forecasts. Clim. Dyn. 2014, 42, 597–616. [Google Scholar] [CrossRef]
- Yang, D.; Yang, X.Q.; Xie, Q.; Zhang, Y.; Ren, X.; Tang, Y. Probabilistic versus deterministic skill in predicting the western North Pacific-East Asian summer monsoon variability with multimodel ensembles. J. Geophys. Res. Atmos. 2016, 121, 1079–1103. [Google Scholar] [CrossRef]
- Tippett, M.K.; Barnston, A.G.; Li, S. Performance of recent multimodel ENSO forecasts. J. Appl. Meteorol. Climatol. 2012, 51, 637–654. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Neske, S.; McGregor, S. Understanding the warm water volume precursor of ENSO events and its interdecadal variation. Geophys. Res. Lett. 2018, 45, 1577–1585. [Google Scholar] [CrossRef]
- Clarke, A.J.; Zhang, X. On the physics of the warm water volume and El Niño/La Niña predictability. J. Phys. Oceanogr. 2019, 49, 1541–1560. [Google Scholar] [CrossRef]
- Chen, H.C.; Sui, C.H.; Tseng, Y.H.; Huang, B. Combined Role of High- and Low-Frequency Processes of Equatorial Zonal Transport in Terminating an ENSO Event. J. Clim. 2018, 31, 5461–5483. [Google Scholar] [CrossRef]
- Tseng, Y.H.; Hu, Z.Z.; Ding, R.Q.; Chen, H.C. An ENSO prediction approach based on ocean conditions and ocean-atmosphere coupling. Clim. Dyn. 2017, 48, 2025–2044. [Google Scholar] [CrossRef]
- Anderson, B.T.; Perez, R.C.; Karspeck, A. Triggering of El Niño Onset through Trade Wind-induced Charging of the Equatorial Pacific. Geophys. Res. Lett. 2013, 40, 1212–1216. [Google Scholar] [CrossRef]
- Chen, H.C.; Tseng, Y.H.; Hu, Z.Z.; Ding, R.Q. Enhancing the ENSO Predictability beyond the spring barrier. Sci. Rep. 2020, 10, 984. [Google Scholar] [CrossRef]
- Trenberth, K.E. The definition of El Niño. Bull. Am. Meteor. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Ren, H.L.; Zuo, J.Q.; Deng, Y. Statistical predictability of Niño indices for two types of ENSO. Clim. Dyn. 2019, 52, 5361–5382. [Google Scholar] [CrossRef]
- Petrova, D.; Koopman, S.J.; Ballester, J.; Rodó, X. Improving the long-lead predictability of El Niño using a novel forecasting scheme based on a dynamic components model. Clim. Dyn. 2017, 48, 1249–1276. [Google Scholar] [CrossRef]
- Petrova, D.; Ballester, J.; Koopman, S.J.; Rodó, X. Multiyear Statistical Prediction of ENSO Enhanced by the Tropical Pacific Observing System. J. Clim. 2020, 33, 163–174. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wang, H.; Jiang, H.; Ma, W. Evaluation of ENSO Prediction Skill Changes since 2000 Based on Multimodel Hindcasts. Atmosphere 2021, 12, 365. https://doi.org/10.3390/atmos12030365
Zhang S, Wang H, Jiang H, Ma W. Evaluation of ENSO Prediction Skill Changes since 2000 Based on Multimodel Hindcasts. Atmosphere. 2021; 12(3):365. https://doi.org/10.3390/atmos12030365
Chicago/Turabian StyleZhang, Shouwen, Hui Wang, Hua Jiang, and Wentao Ma. 2021. "Evaluation of ENSO Prediction Skill Changes since 2000 Based on Multimodel Hindcasts" Atmosphere 12, no. 3: 365. https://doi.org/10.3390/atmos12030365
APA StyleZhang, S., Wang, H., Jiang, H., & Ma, W. (2021). Evaluation of ENSO Prediction Skill Changes since 2000 Based on Multimodel Hindcasts. Atmosphere, 12(3), 365. https://doi.org/10.3390/atmos12030365





