Recent Increases in Winter Snowfall Provide Resilience to Very Small Glaciers in the Julian Alps, Europe
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. Topography-Related Glacier Data and Analysis
3.2. LiDAR Data Acquisition and Processing
3.3. Theodolite-Generated Ground Control Points (GCPs)
3.4. Ice Body Measurements
3.5. Climate Data and Analysis
3.5.1. ERA Interim Dataset
3.5.2. NAO and AMO Index Data
3.5.3. Local Temperature, Precipitation and Glacier Length
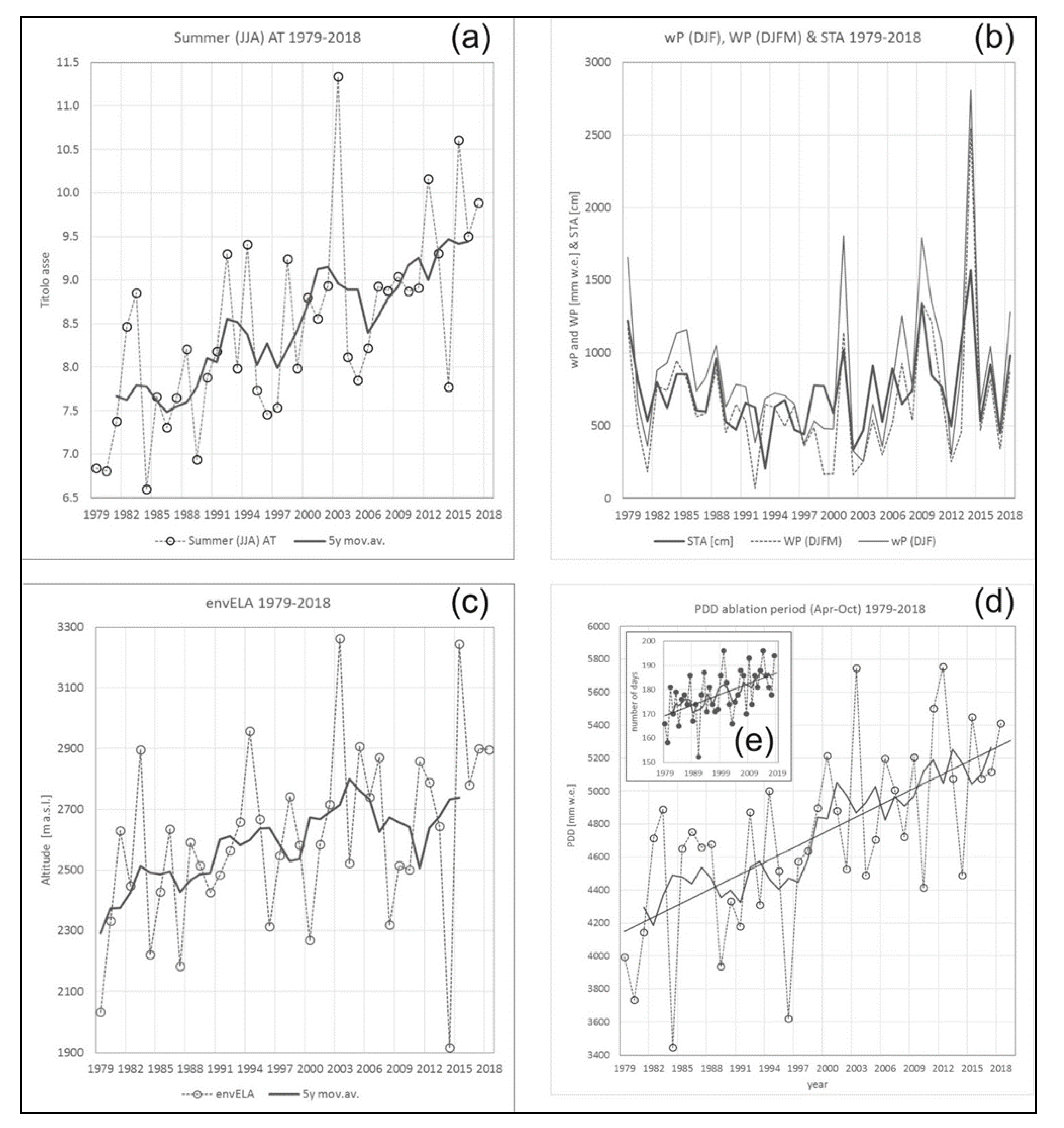
4. Results
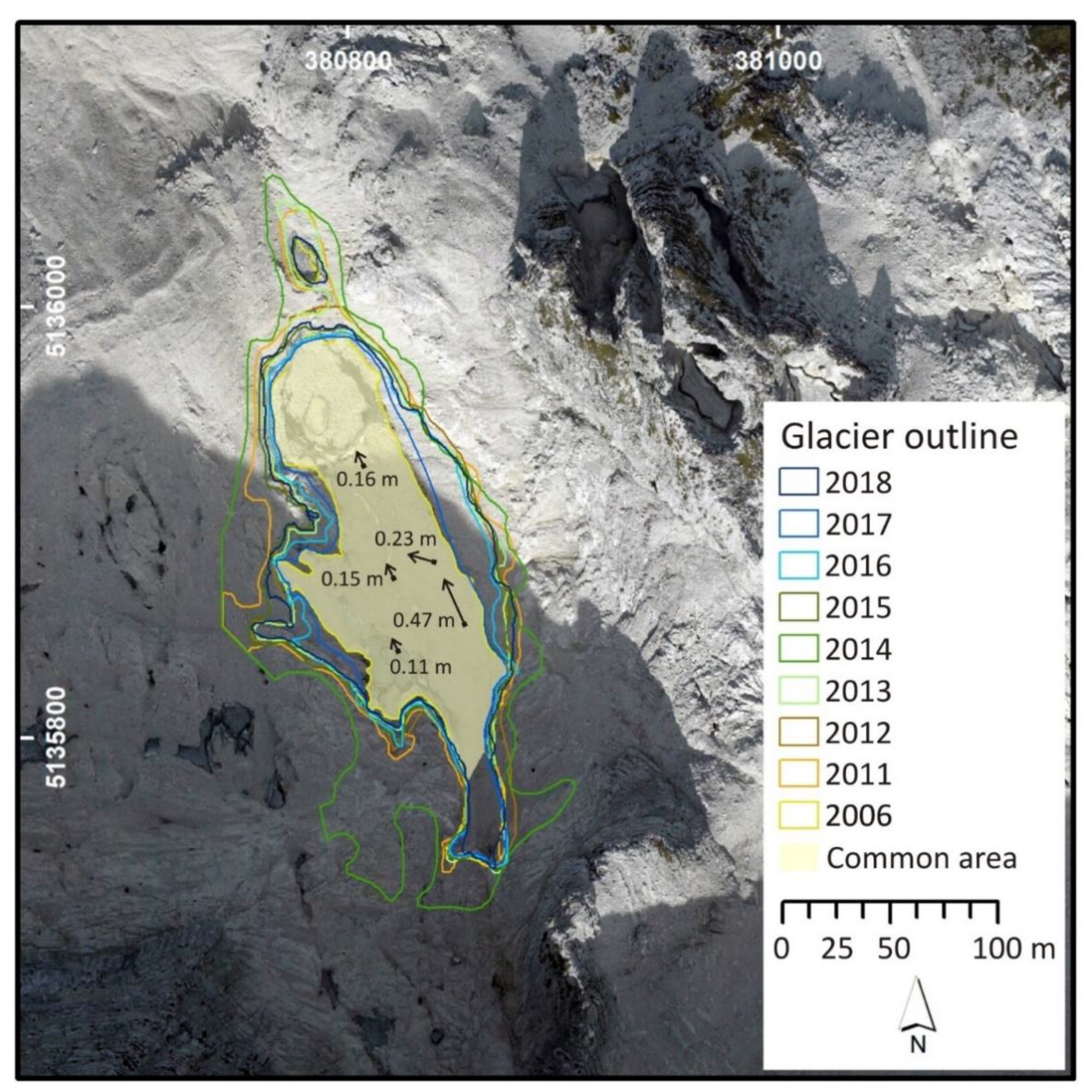
4.1. Glacier Area
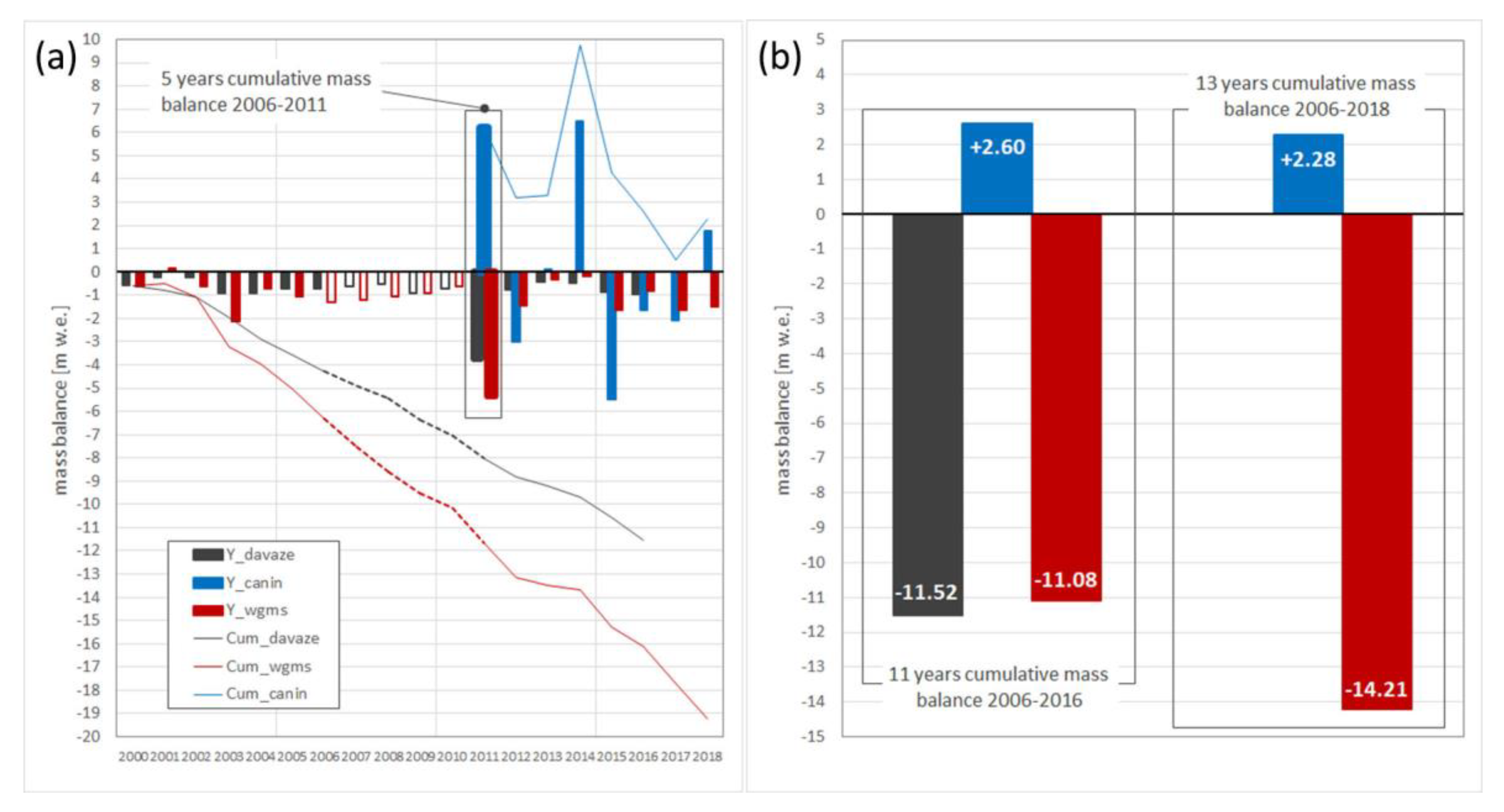
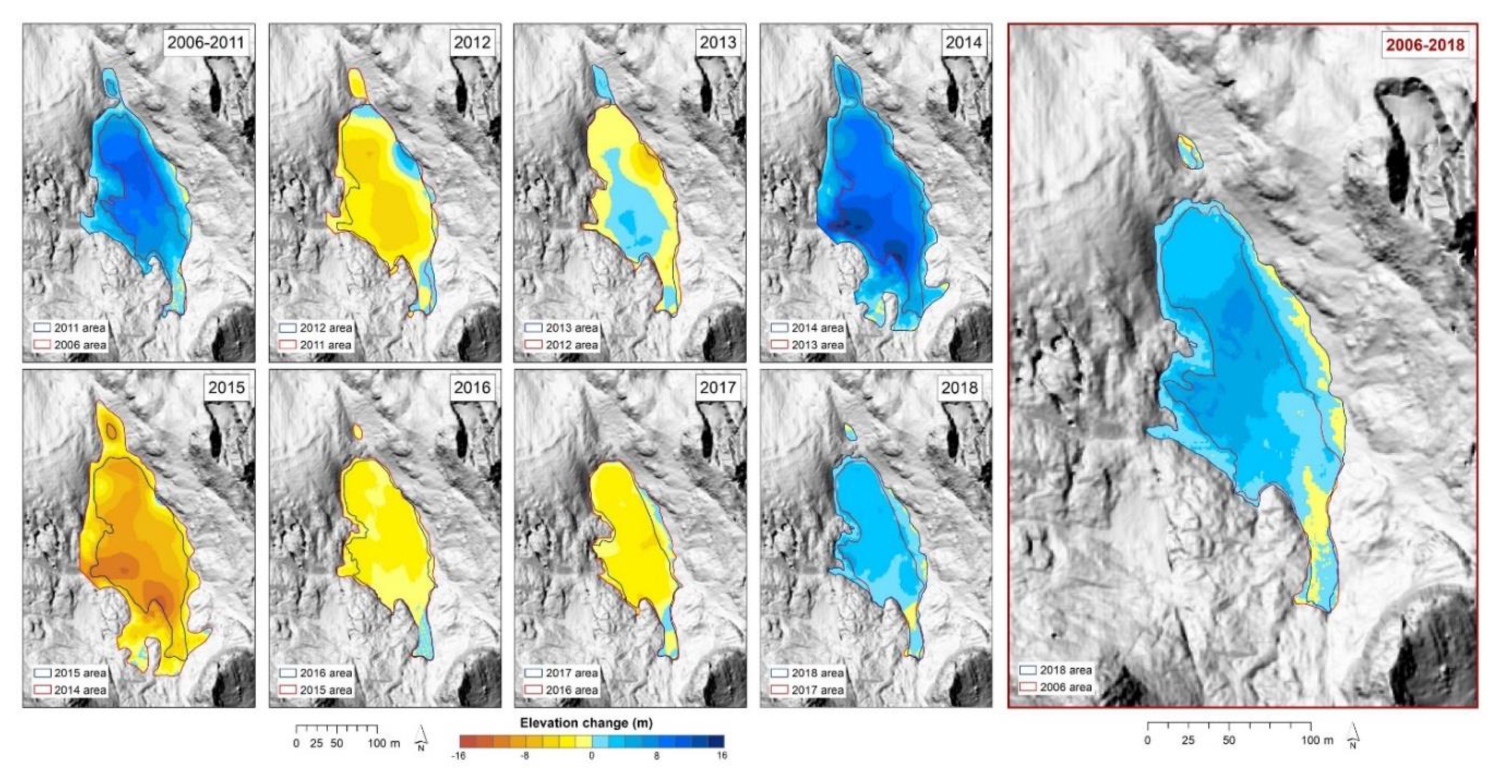
4.2. Geodetic Mass Balance and Volume Change
4.3. Winter Meteorological Patterns in Dry and Wet Winters
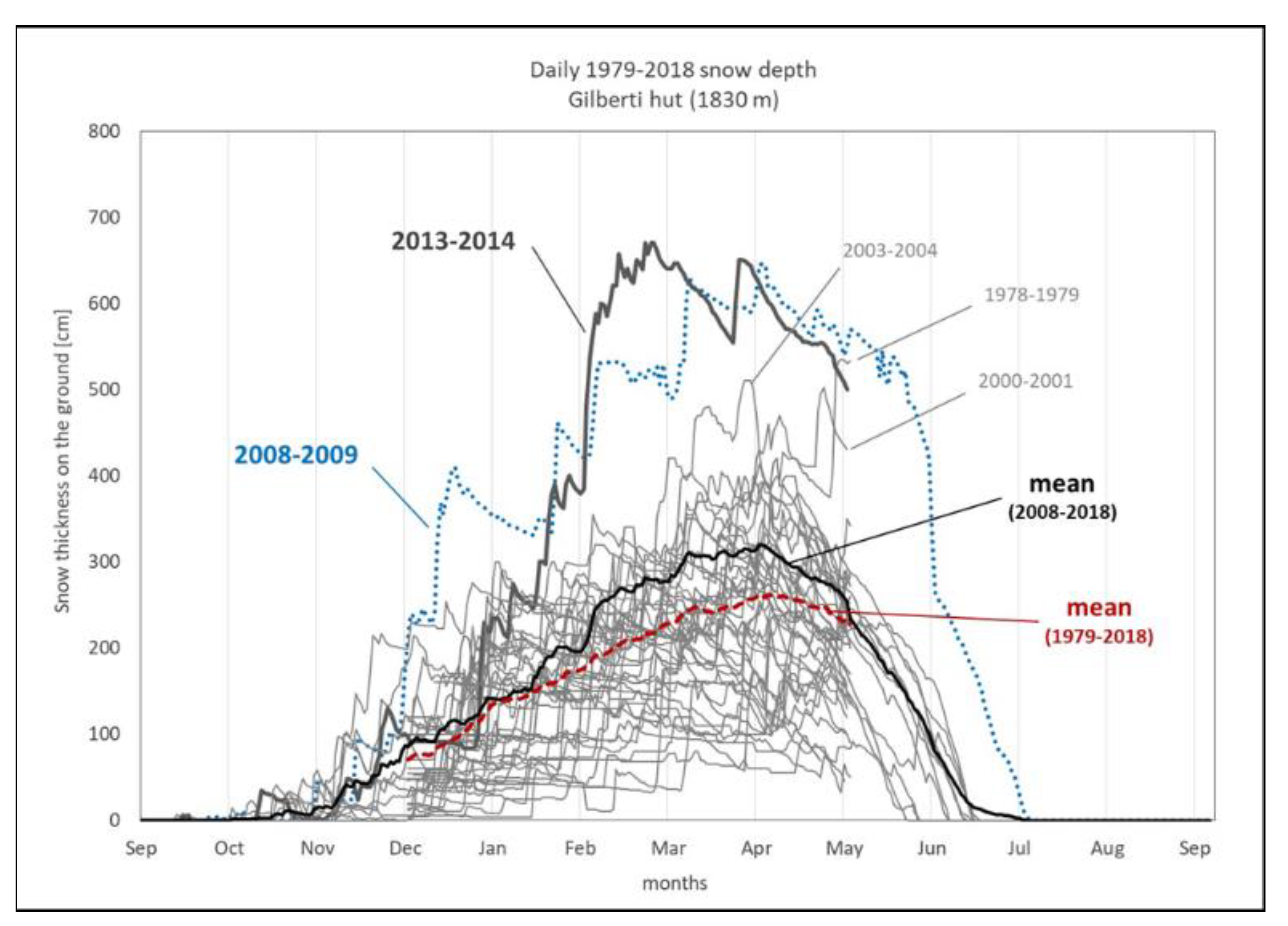
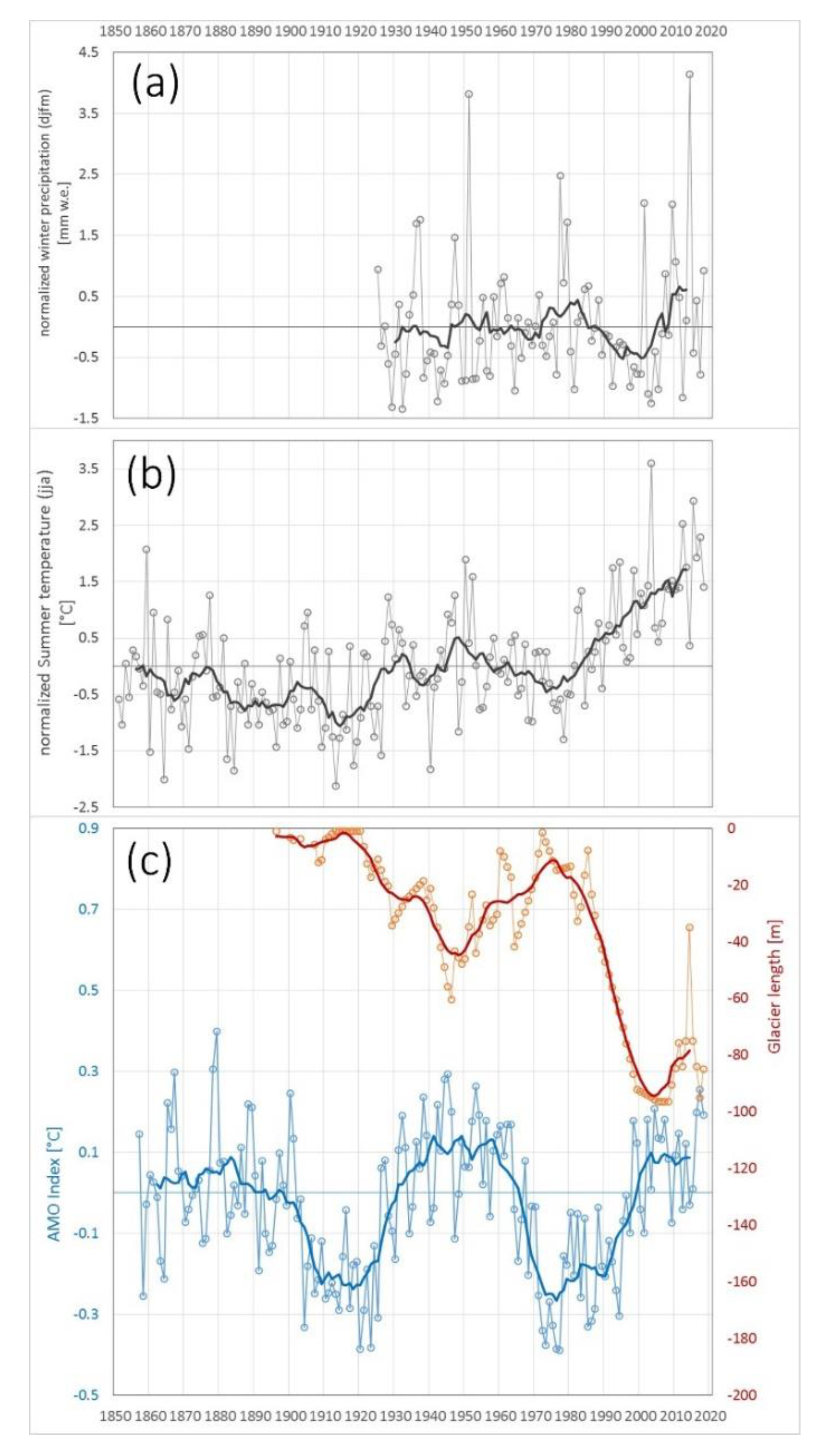
4.4. Climate Data from Local Observations
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serrano, E.; González-Trueba, J.J.; Sanjosé, J.J.; Del Río, L.M. Ice patch origin, evolution and dynamics in a temperate high mountain environment: The jou negro, picos de europa (nw spain). Geogr. Ann. Ser. A Phys. Geogr. 2011, 93, 57–70. [Google Scholar] [CrossRef]
- Carturan, L.; Baldassi, G.A.; Bondesan, A.; Calligaro, S.; Carton, A.; Cazorzi, F.; Fontana, G.D.; Francese, R.; Guarnieri, A.; Milan, N.; et al. Current behaviour and dynamics of the lowermost italian glacier (montasio occidentale, julian alps). Geogr. Ann. Ser. A Phys. Geogr. 2013, 95, 79–96. [Google Scholar] [CrossRef]
- Huss, M.; Fischer, M. Sensitivity of Very Small Glaciers in the Swiss Alps to Future Climate Change. Front. Earth Sci. 2016, 4. [Google Scholar] [CrossRef]
- Hughes, P. Little Ice Age glaciers and climate in the Mediterranean mountains: A new analysis. Cuad. Investig. Geogr. 2018, 44, 15. [Google Scholar] [CrossRef]
- Bahr, D.B.; Radić, V. Significant contribution to total mass from very small glaciers. Cryosphere 2012, 6, 763–770. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Leigh, J.R.; Stokes, C.R.; Carr, R.J.; Evans, I.S.; Andreassen, L.M.; Evans, D.J.A. Identifying and mapping very small (<0.5 km2) mountain glaciers on coarse to high-resolution imagery. J. Glacial. 2019, 65, 873–888. [Google Scholar] [CrossRef]
- Carturan, L.; Baroni, C.; Becker, M.; Bellin, A.; Cainelli, O.; Carton, A.; Casarotto, C.; Fontana, G.D.; Godio, A.; Martinelli, T.; et al. Decay of a long-term monitored glacier: Careser Glacier (Ortles-Cevedale, European Alps). Cryosphere 2013, 7, 1819–1838. [Google Scholar] [CrossRef]
- Fischer, A.; Seiser, B.; Waldhuber, M.S.; Mitterer, C.; Abermann, J. Tracing glacier changes in Austria from the Little Ice Age to the present using a lidar-based high-resolution glacier inventory in Austria. Cryosphere 2015, 9, 753–766. [Google Scholar] [CrossRef]
- Santin, I.; Colucci, R.; Žebre, M.; Pavan, M.; Cagnati, A.; Forte, E. Recent evolution of Marmolada glacier (Dolomites, Italy) by means of ground and airborne GPR surveys. Remote Sens. Environ. 2019, 235, 111442. [Google Scholar] [CrossRef]
- Huss, M.; Bookhagen, B.; Huggel, C.; Jacobsen, D.; Bradley, R.; Clague, J.; Vuille, M.; Buytaert, W.; Cayan, D.; Greenwood, G.; et al. Toward mountains without permanent snow and ice. Earth’s Futur. 2017, 5, 418–435. [Google Scholar] [CrossRef]
- Sommer, C.; Malz, P.; Seehaus, T.C.; Lippl, S.; Zemp, M.; Braun, M.H. Rapid glacier retreat and downwasting throughout the European Alps in the early 21st century. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef]
- Rabatel, A.; Letreguilly, A.; Dedieu, J.-P.; Eckert, N. Changes in glacier equilibrium-line altitude in the western Alps from 1984 to 2010: Evaluation by remote sensing and modeling of the morpho-topographic and climate controls. Cryosphere 2013, 7, 1455–1471. [Google Scholar] [CrossRef]
- Anderson, R.S.; Anderson, L.S.; Armstrong, W.H.; Rossi, M.W.; Crump, S.E. Glaciation of alpine valleys: The glacier-debris-covered glacier-rock glacier continuum. Geomorphology 2018, 311, 127–142. [Google Scholar] [CrossRef]
- Ohmura, A.; Boettcher, M. Climate on the equilibrium line altitudes of glaciers: Theoretical background behind Ahlmann’sP/Tdiagram. J. Glaciol. 2018, 64, 489–505. [Google Scholar] [CrossRef]
- Žebre, M.; Colucci, R.R.; Giorgi, F.; Glasser, N.F.; Racoviteanu, A.E.; Del Gobbo, C. 200 years of equilibrium-line altitude variability across the European Alps (1901−2100). Clim. Dyn. 2020, 1–19. [Google Scholar] [CrossRef]
- Colucci, R.R. Geomorphic influence on small glacier response to post-Little Ice Age climate warming: Julian Alps, Europe. Earth Surf. Process. Landf. 2016, 41, 1227–1240. [Google Scholar] [CrossRef]
- IPCC. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Intergov. Panel Clim. Chang. 2019, in press. Available online: https://www.ipcc.ch/srocc/cite-report/ (accessed on 17 February 2021).
- Davaze, L.; Rabatel, A.; Dufour, A.; Hugonnet, R.; Arnaud, Y. Region-Wide Annual Glacier Surface Mass Balance for the European Alps From 2000 to 2016. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Bosson, J.; Huss, M.; Osipova, E. Disappearing World Heritage Glaciers as a Keystone of Nature Conservation in a Changing Climate. Earth’s Futur. 2019, 7, 469–479. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A.; Mulligan, M.; Scatena, F.N. Hydrometeorology of tropical montane cloud forests: Emerging patterns. Hydrol. Process. 2010, 25, 465–498. [Google Scholar] [CrossRef]
- Buytaert, W.; Vuille, M.; Dewulf, A.; Urrutia, R.; Karmalkar, A.; Célleri, R. Uncertainties in climate change projections and regional downscaling in the tropical Andes: Implications for water resources management. Hydrol. Earth Syst. Sci. 2010, 14, 1247–1258. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of Himalayan rivers. Nat. Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef]
- Kuhn, M. The mass balance of very small glaciers. Z. Gletscherkd. Glazialgeol. 1995, 31, 171–179. [Google Scholar]
- Hughes, P.D. Recent behaviour of the Debeli Namet glacier, Durmitor, Montenegro. Earth Surf. Process. Landf. 2007, 32, 1593–1602. [Google Scholar] [CrossRef]
- Hughes, P.D. Response of a montenegro glacier to extreme summer heatwaves in 2003 and 2007. Geogr. Ann. Ser. A Phys. Geogr. 2008, 90, 259–267. [Google Scholar] [CrossRef]
- Scotti, R.; Brardinoni, F.; Crosta, G.B. Post-LIA glacier changes along a latitudinal transect in the Central Italian Alps. Cryosphere 2014, 8, 2235–2252. [Google Scholar] [CrossRef]
- Colucci, R.R.; Guglielmin, M. Precipitation-temperature changes and evolution of a small glacier in the southeastern European Alps during the last 90 years. Int. J. Clim. 2014, 35, 2783–2797. [Google Scholar] [CrossRef]
- Scotti, R.; Brardinoni, F. Evaluating millennial to contemporary time scales of glacier change in Val Viola, Central Italian Alps. Geogr. Ann. Ser. A Phys. Geogr. 2018, 100, 319–339. [Google Scholar] [CrossRef]
- De Marco, J.; Carturan, L.; Piermattei, L.; Cucchiaro, S.; Moro, D.; Fontana, G.D.; Cazorzi, F. Minor Imbalance of the Lowermost Italian Glacier from 2006 to 2019. Water 2020, 12, 2503. [Google Scholar] [CrossRef]
- Colucci, R.R.; Žebre, M. Late Holocene evolution of glaciers in the southeastern Alps. J. Maps 2016, 12, 289–299. [Google Scholar] [CrossRef]
- Debeer, C.M.; Sharp, M.J. Topographic influences on recent changes of very small glaciers in the Monashee Mountains, British Columbia, Canada. J. Glaciol. 2009, 55, 691–700. [Google Scholar] [CrossRef]
- Evans, I.S. Glacier distribution in the alps: Statistical modelling of altitude and aspect. Geogr. Ann. Ser. A Phys. Geogr. 2006, 88, 115–133. [Google Scholar] [CrossRef]
- Isotta, F.A.; Frei, C.; Weilguni, V.; Tadić, M.P.; Lassègues, P.; Rudolf, B.; Pavan, V.; Cacciamani, C.; Antolini, G.; Ratto, S.M.; et al. The climate of daily precipitation in the Alps: Development and analysis of a high-resolution grid dataset from pan-Alpine rain-gauge data. Int. J. Clim. 2013, 34, 1657–1675. [Google Scholar] [CrossRef]
- Crespi, A.; Brunetti, M.; Lentini, G.; Maugeri, M. 1961–1990 high-resolution monthly precipitation climatologies for Italy. Int. J. Clim. 2018, 38, 878–895. [Google Scholar] [CrossRef]
- Reale, M.; Lionello, P. Synoptic climatology of winter intense precipitation events along the Mediterranean coasts. Nat. Hazards Earth Syst. Sci. 2013, 13, 1707–1722. [Google Scholar] [CrossRef]
- Hofstätter, M.; Lexer, A.; Homann, M.; Blöschl, G. Large-scale heavy precipitation over central Europe and the role of atmospheric cyclone track types. Int. J. Clim. 2017, 38, e497–e517. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Herceg-Bulić, I.; Kucharski, F. North Atlantic SSTs as a Link between the Wintertime NAO and the Following Spring Climate. J. Clim. 2014, 27, 186–201. [Google Scholar] [CrossRef]
- Dijkstra, H.A. Interaction of SST Modes in the North Atlantic Ocean. J. Phys. Oceanogr. 2006, 36, 286–299. [Google Scholar] [CrossRef]
- Börgel, F.; Frauen, C.; Neumann, T.; Meier, H.E.M. The Atlantic Multidecadal Oscillation controls the impact of the North Atlantic Oscillation on North European climate. Environ. Res. Lett. 2020, 15, 104025. [Google Scholar] [CrossRef]
- Peings, Y.; Magnusdottir, G. Forcing of the wintertime atmospheric circulation by the multidecadal fluctuations of the North Atlantic ocean. Environ. Res. Lett. 2014, 9, 034018. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R.; Bauder, A.; Funk, M. 100-year mass changes in the Swiss Alps linked to the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Napoli, A.; Crespi, A.; Ragone, F.; Maugeri, M.; Pasquero, C. Variability of orographic enhancement of precipitation in the Alpine region. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Woollings, T.; Barriopedro, D.; Methven, J.; Son, S.-W.; Martius, O.; Harvey, B.; Sillmann, J.; Lupo, A.R.; Seneviratne, S. Blocking and its Response to Climate Change. Curr. Clim. Chang. Rep. 2018, 4, 287–300. [Google Scholar] [CrossRef]
- Woollings, T. Storm tracks, blocking, and climate change: A review. In Dynamics and Predictability of Large-Scale, High-Impact Weather and Climate Events; Amsterdam University Press: Cambridge, MA, USA, 2016; pp. 113–121. [Google Scholar]
- Colucci, R.R.; Giorgi, F.; Torma, C. Unprecedented heat wave in December 2015 and potential for winter glacier ablation in the eastern Alps. Sci. Rep. 2017, 7, 1–7. [Google Scholar] [CrossRef]
- Sousa, P.M.; Trigo, R.M.; Barriopedro, D.; Soares, P.M.M.; Ramos, A.M.; Liberato, M.L.R. Responses of European precipitation distributions and regimes to different blocking locations. Clim. Dyn. 2016, 48, 1141–1160. [Google Scholar] [CrossRef]
- Van Bebber, W. Die Zugstrassen der barometrischen Minima nach den Bahnenkarten der deutschen Seewarte für den Zeitraum 1875–1890. Meteorol. Z. 1891, 8, 361–366. [Google Scholar]
- Žebre, M.; Stepišnik, U. Glaciokarst landforms and processes of the southern Dinaric Alps. Earth Surf. Process. Landf. 2015, 40, 1493–1505. [Google Scholar] [CrossRef]
- Turk, J.; Malard, A.; Jeannin, P.-Y.; Petrič, M.; Gabrovšek, F.; Ravbar, N.; Vouillamoz, J.; Slabe, T.; Sordet, V. Hydrogeological characterization of groundwater storage and drainage in an alpine karst aquifer (the Kanin massif, Julian Alps). Hydrol. Process. 2014, 29, 1986–1998. [Google Scholar] [CrossRef]
- Colucci, R.R.; Monegato, G.; Žebre, M. Glacial and proglacial deposits of the Resia valley (NE Italy): New in-sights on the onset and decay of the last alpine glacial maximum in the Julian Alps. Alp. Mediterr. Quat. 2014, 27, 85–104. [Google Scholar]
- Colucci, R.R.; Forte, E.; Boccali, C.; Dossi, M.; Lanza, L.; Pipan, M.; Guglielmin, M. Evaluation of Internal Structure, Volume and Mass of Glacial Bodies by Integrated LiDAR and Ground Penetrating Radar Surveys: The Case Study of Canin Eastern Glacieret (Julian Alps, Italy). Surv. Geophys. 2014, 36, 231–252. [Google Scholar] [CrossRef]
- Fitzharris, B.B.; Chinn, T.J.; Lamont, G.N. Glacier balance fluctuations and atmospheric circulation pat-terns over the Southern Alps, New Zealand. Int. J. Climatol. 1997, 17, 745–763. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Cogley, J.G.; Hock, R.; Rasmussen, L.A.; Arendt, A.A.; Bauder, A.; Braithwaite, R.J.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of Glacier Mass Balance and Related Terms; IHP-VII Technical Documents in Hydrology No. 86, IACS Contribution No. 2; UNESCO-IHP: Paris, France, 2011. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Baroni, C.; Bondesan, A.; Carturan, L.; Chiarle, M. Annual glaciological survey of italian glaciers (2018). Cineca IRIS 2019, 42-2, 113–202. Available online: http://www.glaciologia.it/wp-content/uploads/FullText/full_text_campagne_GFDQ/GFDQ_42_2_Campagna_Glaciologica_2018_113_202.pdf (accessed on 17 February 2021).
- Hughes, P.D.; Braithwaite, R.J. Application of a degree-day model to reconstruct Pleistocene glacial climates. Quat. Res. 2008, 69, 110–116. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Valt, M.; Cianfarra, P.; Moro, D.; Zasso, R. Recent snow cover variations and avalanche activities in the Southern Alps. In Proceedings of the International Snow Science Workshop, Davos, Suisse, 27 September–2 October 2009. [Google Scholar]
- Van Oldenborgh, G.J.; Haarsma, R.; De Vries, H.; Allen, M.R. Cold Extremes in North America vs. Mild Weather in Europe: The Winter of 2013–14 in the Context of a Warming World. Bull. Am. Meteorol. Soc. 2015, 96, 707–714. [Google Scholar] [CrossRef]
- Frei, P.; Kotlarski, S.; Liniger, M.A.; Schär, C. Future snowfall in the Alps: Projections based on the EURO-CORDEX regional climate models. Cryosphere 2018, 12, 1–24. [Google Scholar] [CrossRef]
- Nesje, A.; Matthews, J.A. The Briksdalsbre Event: A winter precipitation-induced decadal-scale glacial advance in southern Norway in the ad 1990s and its implications. Holocene 2011, 22, 249–261. [Google Scholar] [CrossRef]
- Bonan, D.B.; Christian, J.E.; Christianson, K. Influence of North Atlantic climate variability on glacier mass balance in Norway, Sweden and Svalbard. J. Glaciol. 2019, 65, 580–594. [Google Scholar] [CrossRef]
- Marzeion, B.; Nesje, A. Spatial patterns of North Atlantic Oscillation influence on mass balance variability of European glaciers. Cryosphere 2012, 6, 661–673. [Google Scholar] [CrossRef]
- Ardito, D. The geometrical evolution of the glaciers. Alto 1927, 39, 1–12. [Google Scholar]
- Serandrei, Z.S.; Barbero, R.; Rabagliati, R. Statystical analysis of hystorical data at the Giulie Alps glacier temrini and their correlation to climatic data. Geogr. Fis. Din. Quat. 1989, 12, 139–149. [Google Scholar]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character of Precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy precipitation events over the Euro-Mediterranean region in a warmer climate: Results from CMIP5 models. Reg. Environ. Chang. 2014, 16, 595–602. [Google Scholar] [CrossRef]
- Giorgi, F.; Im, E.-S.; Coppola, E.; Diffenbaugh, N.S.; Gao, X.J.; Mariotti, L.; Shi, Y. Higher Hydroclimatic Intensity with Global Warming. J. Clim. 2011, 24, 5309–5324. [Google Scholar] [CrossRef]
- Giorgi, F.; Torma, C.; Coppola, F.G.C.T.E.; Ban, N.; Schär, N.B.C.; Somot, S. Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nat. Geosci. 2016, 9, 584–589. [Google Scholar] [CrossRef]
- Rotunno, R.; Houze, R.A. Lessons on orographic precipitation from the Mesoscale Alpine Programme. Q. J. R. Meteorol. Soc. 2007, 133, 811–830. [Google Scholar] [CrossRef]
- Peterson, T.C.; Grant, L.O.; Cotton, W.R.; Rogers, D.C. The effect of decoupled low-level flow on winter oro-graphic clouds and precipitation in the Yampa River Valley. J. Appl. Meteorol. 1991, 30, 368–386. [Google Scholar] [CrossRef]
- Lascaux, F.; Richard, E.; Pinty, J.-P. Numerical simulations of three different MAP IOPs and the associated microphysical processes. Q. J. R. Meteorol. Soc. 2006, 132, 1907–1926. [Google Scholar] [CrossRef]
- Rainaud, R.; Brossier, C.L.; Ducrocq, V.; Giordani, H.; Nuret, M.; Fourrié, N.; Bouin, M.-N.; Legain, D.; Taupier-Letage, I. Characterization of air-sea exchanges over the Western Mediterranean Sea during HyMeX SOP1 using the AROME-WMED model. Q. J. R. Meteorol. Soc. 2015, 142, 173–187. [Google Scholar] [CrossRef]
- Dorman, C.E.; Carniel, S.; Cavaleri, L.; Sclavo, M.; Chiggiato, J.; Doyle, J.; Haack, T.; Pullen, J.; Grbec, B.; Vilibić, I.; et al. February 2003 marine atmospheric conditions and the bora over the northern Adriatic. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Pullen, J.; Doyle, J.D.; Haack, T.; Dorman, C.; Signell, R.P.; Lee, C.M. Bora event variability and the role of air-sea feedback. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Barbi, A.; Monai, M.; Racca, R.; Rossa, A. Recurring features of extreme autumnall rainfall events on the Veneto coastal area. Nat. Hazards Earth Syst. Sci. 2012, 12, 2463–2477. [Google Scholar] [CrossRef]
- Manzato, A.; Davolio, S.; Miglietta, M.M.; Pucillo, A.; Setvak, M. 12 September 2012: A supercell outbreak in NE Italy? Atmos. Res. 2015, 153, 98–118. [Google Scholar] [CrossRef]
- Davolio, S.; Volonté, A.; Manzato, A.; Pucillo, A.; Cicogna, A.; Ferrario, M.E. Mechanisms producing different precipitation patterns over north-eastern Italy: Insights from HyMeX-SOP1 and previous events. Q. J. R. Meteorol. Soc. 2016, 142, 188–205. [Google Scholar] [CrossRef]
- Stocchi, P.; Davolio, S. Intense air-sea exchange and heavy rainfall: Impact of the northern Adriatic SST. Adv. Sci. Res. 2016, 13, 7–12. [Google Scholar] [CrossRef][Green Version]
- Stocchi, P.; Davolio, S. Intense air-sea exchanges and heavy orographic precipitation over Italy: The role of Adriatic sea surface temperature uncertainty. Atmos. Res. 2017, 196, 62–82. [Google Scholar] [CrossRef]
- Raicich, F.; Colucci, R.R. A near-surface sea temperature time series from Trieste, northern Adriatic Sea (1899–2015). Earth Syst. Sci. Data 2019, 11, 761–768. [Google Scholar] [CrossRef]
- Petoukhov, V.; Rahmstorf, S.; Petri, S.; Schellnhuber, H.J. Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl. Acad. Sci. USA 2013, 110, 5336–5341. [Google Scholar] [CrossRef]
- Kornhuber, K.; Osprey, S.; Coumou, D.; Petri, S.; Petoukhov, V.; Rahmstorf, S.; Gray, L. Extreme weather events in early summer 2018 connected by a recurrent hemispheric wave-7 pattern. Environ. Res. Lett. 2019, 14, 054002. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat. Clim. Chang. 2014, 4, 704–709. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barrett, A.P.; Stroeve, J.C.; Kindig, D.N.; Holland, M.M. The emergence of surface-based Arctic amplification. Cryosphere 2009, 3, 11–19. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Serreze, M.C.; Holland, M.M.; Kay, J.E.; Malanik, J.; Barrett, A.P. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Chang. 2011, 110, 1005–1027. [Google Scholar] [CrossRef]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]



| 2006 | 2011 | 2013 | |
| Date | 13 Sep 2006 | 29 Sep 2011 | 19 Sep 2018 |
| Average Flight Height | 800 m a.g.l. | 800 m a.g.l. | 1000 m a.g.l. |
| Point Density | 4.0 points m2 | 4.7 points m2 | 6.5 points m2 |
| LiDAR System | Optech ALTM 3100 EA | Optech ALTM 3100 EA | Optech ALTM 3100 EA |
| Field of View | 46° | 46° | 46° |
| Pulse Repetition Frequency | 100 kHz | 100 kHz | 100 kHz |
| Acquisition Mode | Up to 4 range measurements | Up to 4 range measurements | Up to 4 range measurements |
| Vertical Accuracy | <0.15 m up to 1200 m a.g.l. | <0.15 m up to 1200 m a.g.l. | <0.15 m up to 1200 m a.g.l. |
| Horizontal Accuracy | 1/2000 x altitude | 1/2000 x altitude | 1/2000 x altitude |
| 2015 | 2016 | 2018 | |
| Date | 22 Sep 2015 | 28 Sep 2016 | 19 Sep 2018 |
| Average Flight Height | 1000 m a.g.l. | 1000 m a.g.l. | 1000 m a.g.l. |
| Point Density | 6.5 points m2 | 6.5 points m2 | 6.5 points m2 |
| LiDAR System | Riegl LMS-Q780 | Riegl LMS-Q780 | Riegl LMS-Q780 |
| Field of View | 60° | 60° | 60° |
| Pulse Repetition Frequency | 350 kHz | 350 kHz | 350 kHz |
| Acquisition Mode | Full-waveform | Full-waveform | Full-waveform |
| Vertical Accuracy | 0.02 m at 250 m range | 0.02 m at 250 m range | 0.02 m at 250 m range |
| Horizontal Accuracy | 0.02 m at 250 m range | 0.02 m at 250 m range | 0.02 m at 250 m range |
| Acquisition Date | Number of GCPs Used in Interpolation |
|---|---|
| 05 October 2012 | 10 |
| 01 October 2013 | 7 |
| 28 October 2014 | 23 |
| 20 October 2015 | 84 |
| 04 October 2016 | 54 |
| 10 October 2017 | 96 |
| 03 October 2018 | 174 |
| Year | Time Difference (in days) between LiDAR and GCP Surveys | LIDAR DEM—GCP DEM Natural Neighbour | LiDAR DEM—GCP DEM Spline | LiDAR DEM—GCP DEM Inverse Distance Weighted | LiDAR DEM—GCP DEM Topo to Raster |
|---|---|---|---|---|---|
| 2013 | 0 | −0.44 | −0.09 | −1.01 | −0.28 |
| 2015 | 28 | 0.19 | 0.39 | 0.05 | 0.27 |
| 2016 | 6 | −0.08 | 0.13 | −0.18 | 0.24 |
| 2018 | 14 | 0.33 | 0.44 | 0.14 | 0.42 |
| Average of Absolute Values | 0.26 | 0.26 | 0.35 | 0.3 |
| Year | Area (m2) | Observation Period | Volume Change (m3) | Average Surface Elevation Change (m) * | Average Surface Elevation Change (m) Common Area ** |
|---|---|---|---|---|---|
| 2006 | 11,310 | ||||
| 2011 | 19,425 | 2006–2011 | 108,842 | 5.56 | 7.85 |
| 2012 | 17,136 | 2011–2012 | −50,788 | −2.53 | −3.8 |
| 2013 | 16,589 | 2012–2013 | −5183 | −0.29 | 0.16 |
| 2014 | 27,448 | 2013–2014 | 194,702 | 7.09 | 9.93 |
| 2015 | 15,799 | 2014–2015 | −173,588 | −6.32 | −8.46 |
| 2016 | 14,511 | 2015–2016 | −32,714 | −1.95 | −2.1 |
| 2017 | 12,016 | 2016–2017 | −31,636 | −2.18 | −2.64 |
| 2018 | 15,914 | 2017–2018 | 35,190 | 2.19 | 2.73 |
| 2006–2018 | 43,198 | 2.67 | 3.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colucci, R.R.; Žebre, M.; Torma, C.Z.; Glasser, N.F.; Maset, E.; Del Gobbo, C.; Pillon, S. Recent Increases in Winter Snowfall Provide Resilience to Very Small Glaciers in the Julian Alps, Europe. Atmosphere 2021, 12, 263. https://doi.org/10.3390/atmos12020263
Colucci RR, Žebre M, Torma CZ, Glasser NF, Maset E, Del Gobbo C, Pillon S. Recent Increases in Winter Snowfall Provide Resilience to Very Small Glaciers in the Julian Alps, Europe. Atmosphere. 2021; 12(2):263. https://doi.org/10.3390/atmos12020263
Chicago/Turabian StyleColucci, Renato R., Manja Žebre, Csaba Zsolt Torma, Neil F. Glasser, Eleonora Maset, Costanza Del Gobbo, and Simone Pillon. 2021. "Recent Increases in Winter Snowfall Provide Resilience to Very Small Glaciers in the Julian Alps, Europe" Atmosphere 12, no. 2: 263. https://doi.org/10.3390/atmos12020263
APA StyleColucci, R. R., Žebre, M., Torma, C. Z., Glasser, N. F., Maset, E., Del Gobbo, C., & Pillon, S. (2021). Recent Increases in Winter Snowfall Provide Resilience to Very Small Glaciers in the Julian Alps, Europe. Atmosphere, 12(2), 263. https://doi.org/10.3390/atmos12020263







