Abstract
Many modern ionospheric studies rely on incoherent scatter radars (ISR) since this kind of radar is able to detect various ionospheric parameters over very long ranges. The performance of ISR significantly depends on its coding system. In recent decades, a new type of coding system, which is the so-called composite coding, was presented. It used to be constructed by using a certain code to modulate alternating code to achieve better detection resolution and anti-noise performance for ISRs. In the present study, a new composite coding system was presented, which is constructed based on complementary codes and alternating codes. In this paper, the performance of the new composite code will be compared with that of several traditional codes to show that the new composite code can help to improve the detection performance of the ISR. According to the analysis based on the ambiguity function, the present composite coding system helps to improve the range resolution and detection range for ISR detections. In addition, numerical tests on anti-noise performance show that the complementary composite coding system has a good anti-noise performance and helps to reduce the necessary times of incoherent integration. As a result, the composite coding system can improve the time resolution.
Incoherent scatter radar (ISR) [1,2] is one of the most effective instruments for detecting the ionosphere. Its detection generally ranges from 60 km to 1000 km. It is also able to detect various physical parameters of the ionosphere, for example, electron density, electron temperature, ion temperature, ion drift velocity. Hagfors [3] observed plasma lines with incoherent scatter radar in 1981, and ion-neutral collision frequency was measured with incoherent scatter radar by Nygrén [4] in 1987. Many coding systems, such as the long pulse code and the Barker code [5], are frequently employed in incoherent scattering detection. Hysell [6] used the two types of codes to measure different parameters of the E- and F-region of the ionosphere. In 1987, Lehtinen proposed another coding system called the alternating codes [7]. Markkanen, Nygrén and Sulzer [8,9,10] further developed the alternating code on that basis. Haeggstroem [11] used the alternating code to measure ion composition. Additionally, another system, which is the so-called “complementary code” has been frequently utilized in space environment detection in recent years [12]. In recent decades, in order to improve the range resolution and anti-noise performance, a new concept for the coding system, which is called the “composite code”, has been presented [13,14]. After that, Guo et al. adopted a composite coding scheme, which is the alternating code modulated by the Baker code [15]. The range resolution and anti-noise performance of the composite code strengthens obviously with the increasing number of bits of the Barker code. Both the range resolution and the anti-noise performance are better than that of the Barker code or the alternating code. Unfortunately, it is impossible to further improve the range resolution and anti-noise performance for that type of composite code since the maximum number of Barker codes is only 13 bits. In order to solve this defect, a new composite code, the alternating code modulated by the complementary code, is proposed to improve the detection performance of radar. The complementary code is not limited by the number of code bits such as the Barker codes. In other words, the present coding scheme has great potential to improve its capability of range resolution and anti-noise performance. In the present paper, the performance of traditional strong alternating codes, long pulse and composite codes are compared in the following aspects—the two-dimensional ambiguity function (TDAF), the range ambiguity function and the autocorrelation function. According to these performance comparisons, it can be seen that the performance of the composite code is improved comparing to the previous codes. In such a case, the proposed composite code can help to improve the detection performance of incoherent scattering radar.
1. Complementary Code, Alternating Code and Composite Code
1.1. Complementary Code
The complementary code, which is also called the Golay code, was first proposed by Golay in 1949 [16]. In 1961 and 1962, Golay proposed a method to construct long complementary codes [17]. A complementary code is composed of two sequences, which are called the A code and the B code, respectively. The lengths of the two sequences must be equivalent. Once the aperiodic autocorrelation functions (AACF) for the two sequences are added, the side lobe levels cancel each other, that is, the side lobes are zero. Meanwhile, the main lobe level doubles, that is, supposing that the lengths of the A code and the B code are P, the main lobe level would be 2P. That is the main characteristic of the complementary code. It requires the A code and the B code to be transmitted simultaneously, that is, normally it is applicable to dual-frequency radars or the radars, which are able to simultaneously transmit signals in different polarizations. Another way to use the complementary code by single-frequency radars is to transmit the A code and the B code in sequence, that is, the coded radar signals are transmitted in the sequence of A, B, A, B, A...
So far, there are 2-bit, 10-bit and 26-bit complementary codes, which are called the cores of the complementary codes. The number of complementary codes is limited. Nevertheless, a longer complementary code can be constructed with the tandem method and the interpolation method on the basis of the cores of complementary codes. Both methods use two complementary codes of length P to make the length become 2P, so that as long as the construction principle is satisfied, more and longer complementary codes can be constructed.
1.2. Alternating Code
Alternating codes are also frequently utilized codes for incoherent detections [18]. In addition, it is the basis for the composite coding. In other words, alternating codes usually involve the modulation of a composite code. In the present study, the 4-bit strong alternating code with its code number was employed to construct the composite coding system. Its bitmap is shown in Figure 1a, while its autocorrelation function is shown in Figure 1b.
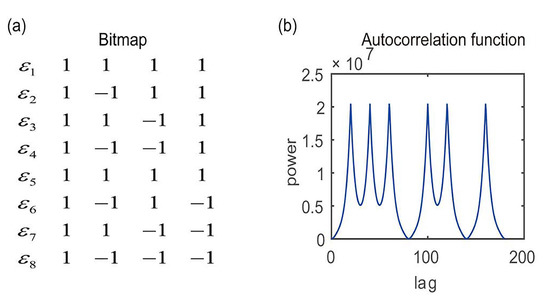
Figure 1.
The 4-bit strong alternating code bitmap and autocorrelation function.
1.3. Composite Code
The composite code is modulated by two or more different types of code. The composite code was first proposed by Damtie et al and Lehtinen et al. [12,14]. In Lehtinen’s work, the 5-bit Barker code and the 22-bit alternating code were employed to form the composite code. After that, the distance resolution and anti-noise performance of the composite coding (alternating code modulated by Barker code) were studied by Guo et al. [15]. According to Guo’s study, the range resolution and the anti-noise performance of the composite code are better than that of the alternating code. It is noticeable that the range resolution and the anti-noise performance of the composite code could be improved by increasing the number of bits of the Barker codes. However, the maximum code position of Barker codes is only 13 bits. The potential to further improve the range resolution and the noise immunity is limited.
2. Performance of the Composite Code
2.1. Two-Dimensional Ambiguity Function
According to the theory of the ambiguity function [19], the carrier wave is first modulated by the 4-bit strong alternating code, and then the A code of the complementary code is used to modulate every chip of the 4-bit strong alternating code to obtain the A code of the composite code. The B code is obtained with a similar method. It makes each element of the alternating code wider. In this letter, it is assumed that the width of the filter is equal to the chip width of the complementary code, and the filter is ideal. It must be noted that the impulse response matches the complementary code. In the time domain, the autocorrelation of the amplitude ambiguity function is a two-dimensional ambiguity function (TDAF), which can reflect the weighted average of the autocorrelation function of the detection target in the lag-range space. Figure 2, Figure 3 and Figure 4 illustrate the 4-bit strong alternating code modulated by 4-bit complementary codes, 8-bit complementary codes and 16-bit complementary codes, respectively. According to those figures, there are some differences that reflect different performances. The first difference is that the peaks of the main lobes are not the same. The longer the bits of the complementary code, the higher the peaks of the main lobes. The peaks of the main lobes can reflect the detection range. The higher the peaks of the main lobes, the farther the detection range. So the detection range increases with the bits of the composite code. The second difference is the width of the main peaks in the corresponding contour plot of the two-dimensional ambiguity function. The longer the bits of the complementary code, the narrower the width of the main peaks in the corresponding contour plot of the two-dimensional ambiguity function. The width of the main peaks in the corresponding contour plot reflect the range resolution. The narrower the width of the main peaks in the corresponding contour plot, the higher the range resolution. So the range resolution increases with the bits of the composite code. In such a case, the three figures illustrate that the detection range and the range resolution could increase with the bits of the composite code. According to those figures, the peak values of the TDAF increase with the increasing number of complementary bits. As the results, the peaks of TDAF sharpen with the increasing number of complementary bits. Compared with that of the composite code based on Barker codes [15], the projection of the ambiguity function on the delay axis of the alternating codes modulated by the complementary is narrower. In such a case, the range resolution and detection range increases with the number of complementary bits.
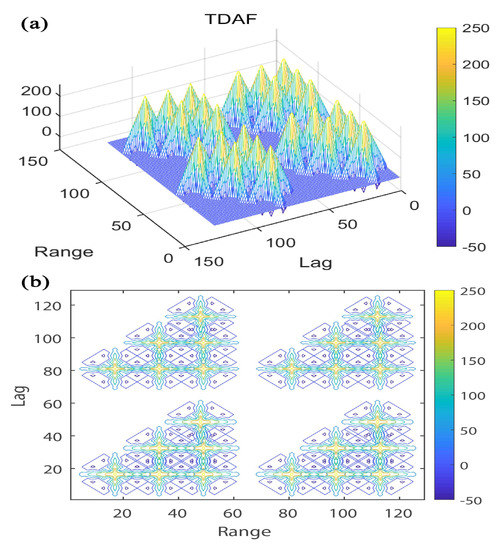
Figure 2.
(a) TDAF of 4-bit strong alternating code modulated by 4-bit complementary code and (b) corresponding contour plot.
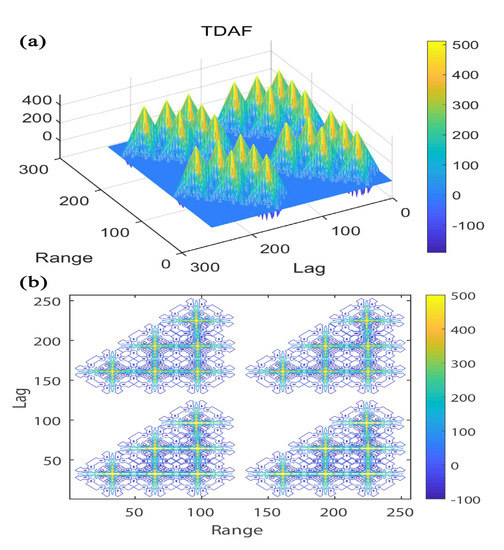
Figure 3.
(a) TDAF of 4-bit strong alternating code modulated by 8-bit complementary code and (b) corresponding contour plot.
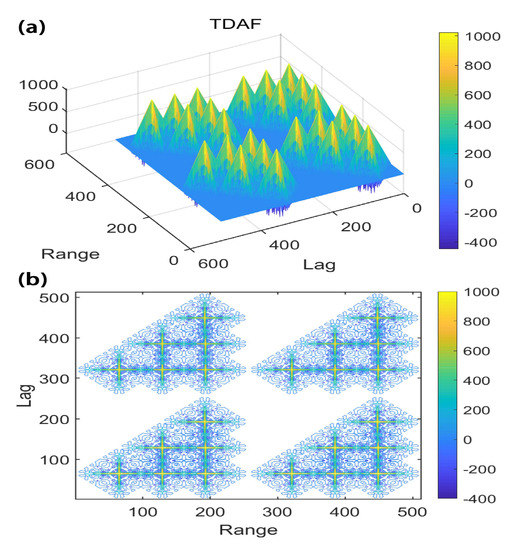
Figure 4.
(a) TDAF of 4-bit strong alternating code modulated by 16-bit complementary code and (b) corresponding contour plot.
The TDAF of the long pulse and the 4-bit strong alternating code are shown in Figure 5 and Figure 6. According to Figure 5, it is obvious that the peaks of the TDAF for the long pulse are all connected without any sharp peaks, and the range resolution is poor. It can be seen from Figure 6 that the TDAF of the 4-bit strong alternating code has six sharp peaks, while there are 24 sharp peaks in composite codes. Therefore, the range resolutions of composite codes are better than that of the alternating code and the long pulse.
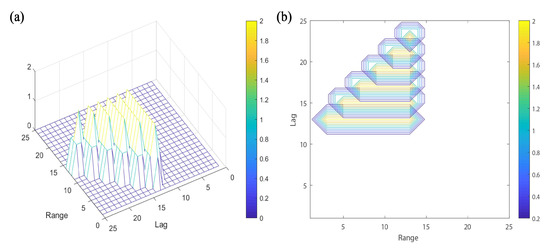
Figure 5.
(a) TDAF of long pulse and (b) corresponding contour plot.
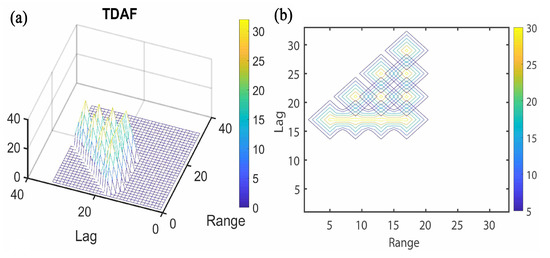
Figure 6.
(a) TDAF of 4-bit strong alternating code and (b) corresponding contour plot.
2.2. Range Ambiguity Function
The range ambiguity function, which can reflect the range resolution, is the integral of the TDAF over the lag [20]. The minimum distance at which a radar can distinguish two targets is called the range resolution [21].
Figure 7a shows the range ambiguity function for the composite codes based on the 16-bit complementary code, with the complementary code slice width of 5 s and the range resolution of 0.75 km. Figure 7b shows the range ambiguity function of the 16-bit strong alternating codes, with the alternating code slice width of 20 s and the range resolution of 3 km. According to Figure 7a,b, the main peak of the 16-bit strong alternating code is wider than that of the composite codes based on the 16-bit complementary code, indicating that its range resolution is poor. The height of the main peak indicates the power of the code. Comparing the two codes, the power of the composite codes is also higher than that of the alternating code, indicating that its detection range is longer. However, there is only one main peak in the traditional alternating code, while there are few side lobes in composite codes, which enables the clutters generated by the target at some ranges to affect the detection of the radar. This is called the radar range ambiguity. Due to the large difference between the peak value of the main lobe and the side lobe, the side lobe will be drowned in the noise, so it is less likely to cause range ambiguity, but some attention should be paid to it. In summary, the composite codes are superior to the traditional strong alternating code in both range resolution and detection range, but it has a small possibility of causing range ambiguity at some points.
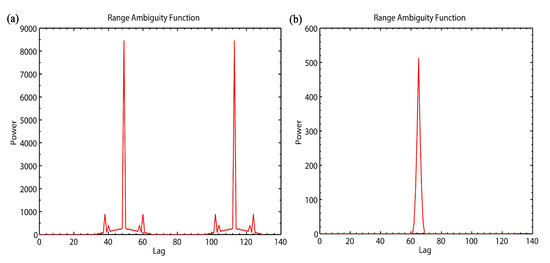
Figure 7.
(a) Range ambiguity function of 4-bit strong alternating code modulated by 16-bit complementary code and (b) Range ambiguity function of 16-bit strong alternating code.
2.3. Anti-Noise Performance
For ISR detections, the echo signals used to be very weak. In such a case, good anti-noise performance is very significant for an incoherent scattering radar system. The range ambiguity function and the autocorrelation function could reflect the anti-noise performance for a coding system in general. Nevertheless, the noise in ionospheric detection could be complicated. In the present subsection, the anti-noise performance of the composite coding system will be evaluated in more detail.
The clutter noise from the neutral atmosphere/ionosphere is considered in this paper. The clutter noise can be considered Rayleigh clutter [22]. In order to simulate the anti-noise performance of the present composite codes, the Rayleigh clutter was added with the composite coded signals. The SNRs were assumed to be −5 dB. The incoherent integration was utilized since the incoherent echo signals are very weak. Figure 8a,b shows the autocorrelation functions for the composite codes and the strong alternating code, respectively. In Figure 8, the black line represents the autocorrelation function without noise. The cyan line represents the autocorrelation function with the added noise, whose corresponding SNR is −5 dB, and the red line represents the autocorrelation function after incoherent accumulation. It can be seen from Figure 8 that the deformation of the autocorrelation function of the alternating code with the added noise is relatively large. There is still deformation between the autocorrelation function after 100 times of incoherent accumulation and the autocorrelation function without noise. When the noise is added to the autocorrelation function of composite codes, its deformation degree is small, indicating that the composite codes have a good anti-noise performance. Moreover, after ten times of incoherent accumulation, the degree of deformation between the autocorrelation function and that without noise is less than that of the alternating code, indicating that the time of radar detection is reduced and the time resolution is improved. To summarize, the anti-noise performance of composite codes is better than that of the traditional alternating code, and the time resolution is improved.
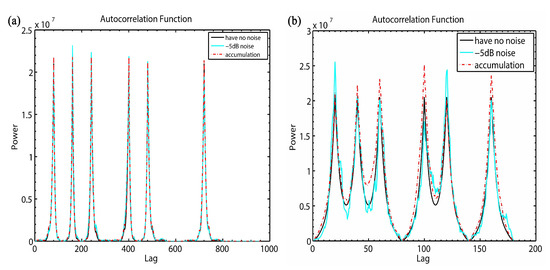
Figure 8.
(a) Autocorrelation function of 4-bit strong alternating code modulated by 16-bit complementary code and (b) Autocorrelation function of 16-bit strong alternating code.
In order to further compare the anti-noise performances of the strong alternating code and the composite code, the SNR of the echo signal after two kinds of coding is continuously improved, and the range ambiguity functions with the SNR of −5 dB, −10 dB and −12 dB were simulated. The results are shown in Figure 9. In the figure, it can be seen that, when the SNR decreases into −12 dB, the main peak of the range ambiguity function of the composite codes can still be clearly distinguished, so the target information can be extracted from the echo signal. However, the main peak of the range ambiguity function of the 16-bit strong alternating code is submerged in the noise, which could yield the ambiguity of the target information. In conclusion, the anti-noise performance of the present composite codes is better than that of the strong alternating code, which greatly improves the detection ability of weak signals of the radar. Therefore, effective target information can be extracted by using the composite codes in some harsh space environment.
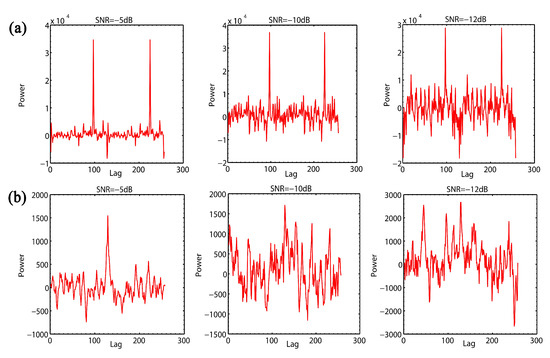
Figure 9.
(a) Range ambiguity function of the composite codes of the 4-bit strong alternatig code modulated by 16-bit complementary code with SNR of −5 dB, −10 dB and −12 dB and (b) Range ambiguity function of the 16-bit alternating code with SNR of −5 dB, −10 dB and −12 dB.
3. Summary and Conclusions
In this paper, a new composite coding system, which is constructed by a complementary code modulation alternating code, was proposed for incoherent scattering radar. The new composite code can help improve the detection performance of ISR by increasing the bits of the composite code, because the detection range and the range resolution could increase with the bits of the composite code. Comparing the TDAF of the composite code with that of the long pulse and the 4-bit strong alternating code, the peak of the TDAF of the long pulse are all connected without any sharp peaks and the TDAF of the 4-bit strong alternating code has six sharp peaks, while there are 24 sharp peaks in the composite code. Therefore, the range resolution and the detection range of the composite code is the best in the three types of codes. In order to analyze the anti-noise performance of the composite code, the alternating code and the composite code were compared in Figure 8 and Figure 9. By comparing these two figures, it can be concluded that the anti-noise performance and the time resolution of the composite code are better than those of the alternating code.
In summary, the present composite code has better range resolution, detection range, anti-noise performance and time resolution than those of the traditional alternating code. In addition, the resolution and the anti-noise performance of the complementary composite coding system are easy to improve by extending the bits number of the elementary complementary code. However, some attention should be paid to the small possibility of causing range ambiguity at some points.
Author Contributions
Conceptualization, K.Y.; software, H.C. and J.X.; validation, K.Y.; investigation, M.Y.; resources, K.Y.; data curation, M.Y. and J.X.; writing—original draft preparation, H.C.; writing—review and editing, H.C.; funding acquisition, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China: 41427901 and 41727804.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gordon, W.E. Incoherent scattering of radio waves by free electrons with applications to space exploration by radar. Proc. Ire 1958, 46, 1824–1829. [Google Scholar] [CrossRef]
- Li, L.; Lu, Y.; Wang, Y.; Ji, H.; Ding, Z. A modified parameter model-based spectrum estimation method for incoherent scatter radar. In Proceedings of the 2017 2nd International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 June 2017. [Google Scholar]
- Hagfors, T. Incoherent scatter radar observations of the plasma line with a chirped pulse system. Radio Sci. 1982, 17, 727–734. [Google Scholar] [CrossRef]
- Nygrén, T.; Jalonen, L.; Huuskonen, A. A new method of measuring the ion-neutral collision frequency using incoherent scatter radar. Planet. Space Sci. 1987, 35, 337–343. [Google Scholar] [CrossRef]
- Farley, D.T. Multiple-Pulse Incoherent-Scatter Correlation Function Measurements. Radio Sci. 1972, 7, 661–666. [Google Scholar] [CrossRef]
- Hysell, D.L.; Larsen, M.F.; Zhou, Q.H. Common volume coherent and incoherent scatter radar observations of mid-latitude sporadic E-layers and QP echoes. Ann. Geophys. 2004, 22, 3277–3290. [Google Scholar] [CrossRef]
- Lehtinen, M.S. Ingemar Häggström A new modulation principle for incoherent scatter measurements. Radio Sci. 1987, 22, 625–634. [Google Scholar] [CrossRef]
- Sulzer, M.P. A new type of alternating code for incoherent scatter measurements. Radio Sci. 1993, 28, 995–1001. [Google Scholar] [CrossRef]
- Nygrén, T.; Markkanen, M. Long alternating codes 1. Search byplaying dominoes. Radio Sci. 1997, 32, 1–8. [Google Scholar] [CrossRef]
- Lehtinen, M.S.; Huuskonen, A.; Markkanen, M. Randomization ofalternating codes: Improving incoherent scatter measurements byreducing correlations of gated autocorrelation function estimates. Radio Sci. 1997, 32, 2271–2282. [Google Scholar] [CrossRef]
- Häggström, I. Incoherent Scatter Studies of Upper Atmmosphere Dynamics and Coding Techniques. Ph.D. Thesis, Swedish Institute of Space Physics, Kiruna, Sweden, 1990. [Google Scholar]
- Yang, G.; Duan, P.; Jiang, C.; Liu, T.; Lan, T.; Zhao, Z.; Shi, S.; Xu, C. Application of biphase complete complementary code for ionospheric sounding. Sensors 2018, 18, 2811. [Google Scholar] [CrossRef] [PubMed]
- Damtie, B.; Nygrén, T.; Lehtinen, M.S.; Huuskonen, A. High resolution observation of sporadic-E layers within the polar cap ionosphere using a new incoherent scatter radar experiment. Ann. Geophys. 2002, 20, 1429–1438. [Google Scholar] [CrossRef][Green Version]
- Lehtinen, M.; Markkanen, J.; Vaananen, A.; Huuskonen, A.; Damtie, B.; Nygrén, T.; Rahkola, J. A new incoherent scatter technique in the EISCAT Svalbard Radar. Radio Sci. 2002, 37, 1050. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, Y.; Kai, Y.; Deng, X. Simulation and Performance Evaluation of Three Types of ISR Coding Systems. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1–4. [Google Scholar] [CrossRef]
- Golay, M. Multi-silt spectrometry. J. Opt. Soc. Am. 1949, 39, 437–444. [Google Scholar] [CrossRef] [PubMed]
- Golay, M. Complementary series. IRE Trans. Inf. Theory 1961, 7, 82–87. [Google Scholar] [CrossRef]
- Markkanen, M.; Nygrén, T. A 64-bit strong alternating code discovered. Radio Sci. 1996, 31, 241–243. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Ji, H.; Ding, Z.; Jin, W. Research on signal modulation and processing for incoherent scatter radar. In Proceedings of the 2015 10th International Conference on Information, Communications and Signal Processing (ICICS), Singapore, 2–4 December 2015; pp. 1–4. [Google Scholar]
- Lehtinen, M.; Huuskonen, A. General incoherent scatter analysis and GUISDAP. J. Atmos. Terr. Phys. 1996, 58, 435–452. [Google Scholar] [CrossRef]
- Trunk, V. Range Resolution of Targets Using Automatic Detectors. IEEE Trans. Aerosp. Electron. Syst. 2007, 14, 750–755. [Google Scholar] [CrossRef]
- Foreman, T.L.; Wilson, S.G. Multiple pulse detection in distributed rayleigh clutter. In Proceedings of the Record of the IEEE 2000 International Radar Conference [Cat. NO. 00CH37037], Alexandria, VA, USA, 12 May 2000; pp. 637–642. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).