An Overall Uniformity Optimization Method of the Spherical Icosahedral Grid Based on the Optimal Transformation Theory

Abstract

The improvement of overall uniformity and smoothness of spherical icosahedral grids, the basic framework of atmospheric models, is a key to reducing simulation errors. However, most of the existing grid optimization methods have optimized grid from different aspects and not improved overall uniformity and smoothness of grid at the same time, directly affecting the accuracy and stability of numerical simulation. Although a well-defined grid with more than 12 points cannot be constructed on a sphere, the area uniformity and the interval uniformity of the spherical grid can be traded off to enhance extremely the overall grid uniformity and smoothness. To solve this problem, an overall uniformity and smoothness optimization method of the spherical icosahedral grid is proposed based on the optimal transformation theory. The spherical cell decomposition method has been introduced to iteratively update the grid to minimize the spherical transportation cost, achieving an overall optimization of the spherical icosahedral grid. Experiments on the four optimized grids (the spring dynamics optimized grid, the Heikes and Randall optimized grid, the spherical centroidal Voronoi tessellations optimized grid and XU optimized grid) demonstrate that the grid area uniformity of our method has been raised by 22.60% of SPRG grid, −1.30% of HR grid, 38.30% of SCVT grid and 38.20% of XU grid, and the grid interval uniformity has been improved by 2.50% of SPRG grid, 2.80% of HR grid, 11.10% of SCVT grid and 11.00% of XU grid. Although the grid uniformity of the proposed method is similar with the HR grid, the smoothness of grid deformation has been enhanced by 79.32% of grid area and 24.07% of grid length. To some extent, the proposed method may be viewed as a novel optimization approach of the spherical icosahedral grid which can improve grid overall uniformity and smoothness of grid deformation.

1. Introduction

Spherical icosahedral grid is often used as the basic framework of atmospheric models, such as the ICosahedral Nonhydrostatic model (ICON) [1,2,3], Models for Predication Across Scales (MPAS) [4], the Non-hydrostatic ICosahedral Atmospheric Model (NICAM) [5], DYNAMICO [6], Ocean–Land–Atmosphere Model (OLAM) [7,8], etc. These models are wieldy used for polar lows simulation [9], monsoon simulation [10], ocean tides dissipation [11], etc. Recently, the Spectral Radiation Transport Model for Aerosol Species coupled with NICAM (NICAM-SPRINTARS) [12] has been developed for studying and simulating atmosphere-aerosols interactions and their effects on atmospheric pollution and climate change. Related studies include simulating the annual aerosol characteristics over China [13], capturing the horizontal distribution of aerosol optical thickness fields [14], studying the resolution dependency of the transport process of black carbon from Siberia to Japan [15], and assimilating global aerosol vertical observations [16], among others.

The accuracy of numerical simulations is affected by the quality of the spherical icosahedral grid [17,18,19]. Low-quality grids may cause large numerical approximation errors. Some noises are leaded by slight irregularities of the grid, which the long-term simulation will become unstable [20]. This is because nonuniform grids may bring grid imprinting in the numerical solutions and speed up their spread in meteorological models [21,22]. In this way, the nonuniformity of the control volume becomes the main source of numerical simulation error [23]. For example, the non-orthogonality of the grid edge and its dual edge, and the non-coincidence of the midpoints of the two edges increases the truncation error of the spherical differential operators [22,23]. Grid misalignment also leads to errors in some low-order algorithms of the spherical surface [19,24], resulting in discretization of differential operators to only meet first-order convergence [17]. The grid with good quality can reduce the truncation error of these operators on the sphere [25].

At present, some grid optimization methods have been proposed to improve grid quality and to reduce the simulation errors [26]. The spring dynamics method (i.e., the SPRing dynamics Grid optimization (SPRG) method) [27,28] is utilized to improve grid interval uniformity and to reduce geometric variations [19]. Iga [29] found that the interval distributions of grids near the icosahedron vertices, optimized by the SPRG method with a zero natural spring length (SPR0), are inversely proportional to the map factor of the Lambert conformal conic projection. An analytical transformation was proposed to stretch the grids near the icosahedral vertices to decrease grid aggregations [30]. Heikes and Randall [31,32] (HR) have minimized the distances between the midpoints of hexagonal/pentagonal grids edges and their dual (triangles) edges to optimize grid. Then, they have re-optimized the grid (named tweaked grid [33]) based on previous result to avoid the hemispheric twisting, where the grid quality and the convergence of PDE operators have been further improved. Spherical Centroidal Voronoi Tessellations (SCVT) [34,35,36] has been put forward, in which grids’ centers were iteratively moved by Llyod’s method [37] to their mass centroids to minimize the distances between these two points. Xu [25] has updated iteratively grids based on the Laplace-Beltrami solution, and the optimization grid and SCVT grid are very close to each other.

Comparations have been done with the main optimization grids, such as HR grid, SCVT grid, SPRG grid, etc. for grid quality [23,33]. Some indicators, for instance the ratios between minimum and maximum grid area, the ratios between minimum and maximum grid intervals, the grid area ranges, grid interval ranges, area relative deviations, length relative deviations, etc. are used to evaluate grid quality. The grid interval ratio of SPRG grid is bigger than HR grid, that means SPRG grid’s interval uniformity is better than that of HR grid. However, its grid area ratio and grid interval ratio are all less than the non-optimized grid (NOPT grid). Its grid quality is limited by the spring constant. When the spring constant is large, some grids near the icosahedral vertices may collapse at high resolutions. When the constant is small, grids do not collapse, but some grids near the icosahedral vertices may aggregate, such that grid intervals are shortened and the amount of calculation is increased [29]. The grid intervals by Iga [29] only be increased along the stretch paths, decreasing the regularity of the grids near the icosahedral vertices. Although area uniformity of HR gird has been enhanced to the most extent, its grid interval ratio is slightly smaller than SPRG grid and NOPT grid. Among these grids, the quality of SCVT grid is the worst, its two ratios are divergent with the increasing grid resolution, and discretization accuracy of basic operator is also lowest. There is none of them being clearly better than the others [19].

Tomita [27] has implied that simulation error appears in regions with high gradient of grid area and interval deviations, and the smoothness is important for high-accuracy and stable simulation [29]. The node interpolation can follow a second-order convergence on a uniform spherical grid, but if there is any deformation, it has only a first-order convergence [38]. The grid uniformity is also important to determine the maximum time step for numerical integration [20] and to maintain the consistency of physical parameterization in atmospheric simulations [23]. Meanwhile, improvement of the uniformity is helpful for wavelet transform to improve the compression technique for weather and climate data [39,40]. The grid uniformity has been quantified from grid area and grid interval deviations in some reviews [20,23,33]. The grid area uniformity and interval uniformity are not independent of each other. As the spherical surface is non-Euclidean, a well-defined grid with more than 12 points, meting the two attributes simultaneously, cannot be constructed on a sphere [20]. However, the area uniformity and the interval uniformity of the spherical grid can be trade off to enhance extremely the overall grid uniformity and smoothness of the spherical distribution of the grid area and interval deviation.

The present study is devoted to the investigation of a novel grid overall uniformity and smoothness optimization approach rooted in the optimal transportation theory. The spherical cell decomposition method was introduced to iteratively update the grid to minimize the spherical transportation cost, achieving an optimization grid. We discuss the details of the proposed method and its effectiveness from the grid geometry quality and numerical accuracy. Unlike existing optimization approaches, the proposed method is optimal in that it does not only improve the grid overall uniformity but also reduce the grid deformation, enhancing the smoothness of grid deformation. Both the smoothness of deformation and uniformity of grid interval have been greatly improved. The smoothness of grid area deformation has also been heightened even the grid area uniformity is comparable to those obtained by the Heikes and Randall grid.

The rest of this paper is organized as follows: the optimal transportation theory, grid uniformity optimization method and the core algorithm are introduced in the Theory and Methods section. The Results and Discussions section presents the comparative results and discussions from the grid quality and numerical accuracy. The conclusions are shown in the last section.

2. Theory and Methods

Optimal transportation theory is used for the measure-preserving mapping between two probability measure spaces, such that the target probability measure is infinitely close to the source (or true) probability measure. In all measure-preserving mappings, a mapping minimizing the transportation cost is an optimal transportation mapping [41]. Gu [41] proposed a discrete spherical optimal transportation mapping based on a purely geometric method and defined the measures as areas to achieve an area-preserving mapping from the topological sphere to the unit sphere [42,43]. The mapping is global and has been applied in biomedicine [44,45], face recognition [46], generative adversarial networks [47], and other fields.

Given a continuous space Rⁿ, two subspaces with measures, (X, ψ) ∈ Rⁿ and (Y, φ) ∈ Rⁿ, having the same total measures, that is ${\displaystyle {\int }_{\mathit{X}}^{}\psi dx}={\displaystyle {\int }_{\mathit{Y}}^{}\phi dy}$, there is a measure-preserving mapping T: X → Y to make φ(B) = ψ(T⁻¹(B)), where B ⊂ Y, T⁻¹(B) ⊂ X. Then the transportation cost can be formalized as in Equation (1):

$$C(T)={\displaystyle {\int }_{\mathit{X}}^{}c(x,T(x))d\psi (x)}$$

(1)

where C: X × Y → R is a cost function of T; T_opt = argmin{C(T)} is the optimal transportation mapping.

Spherical optimal transportation mapping realizes the area-preserving mapping from the topological sphere to the unit sphere. There is a probability measure ψ in the continuous space defined on the unit sphere and a Dirac measure φ = {φ₁, φ₂, …, φ_nv} corresponding to the point set {p_i} ⊂ S², which cannot be covered by any hemisphere, such that $\psi (S^2)={\displaystyle {\sum }_{i=1}^{nv}{\phi }_i}$. A set of cells, W = {w_i}, decomposing the unit sphere, that is $S^2={\displaystyle {\cup }_{i=1}^{nv}{w}_i}$, can be found to make φ(w_i) = ψ_i. Then a mapping T: w_i → p_i is the optimal transportation mapping minimizing the transportation cost. The existence and uniqueness of the complete solutions in the continuous space have been proved by Gu (2013). Surfaces can be discretized by triangular meshes. The discrete spherical optimal transportation mapping is an approximate preserved area mapping from a topological spherical triangular mesh to a spherical triangular mesh. A topological spherical triangular mesh is M {V, E, F}, with point set V = {v₁, v₂, …, v_nv}, edge set E = {e₁, e₂, …, e_ne} and face set F = {f₁, f₂, …, f_nf}. ∀v_i ∈ V, there is a set of first-order adjacent vertices v_adj = {$v_{i_1}$, $v_{i_2}$, …, $v_{i_{Ns}}$}, Ns is the number of first-order adjacent vertices. 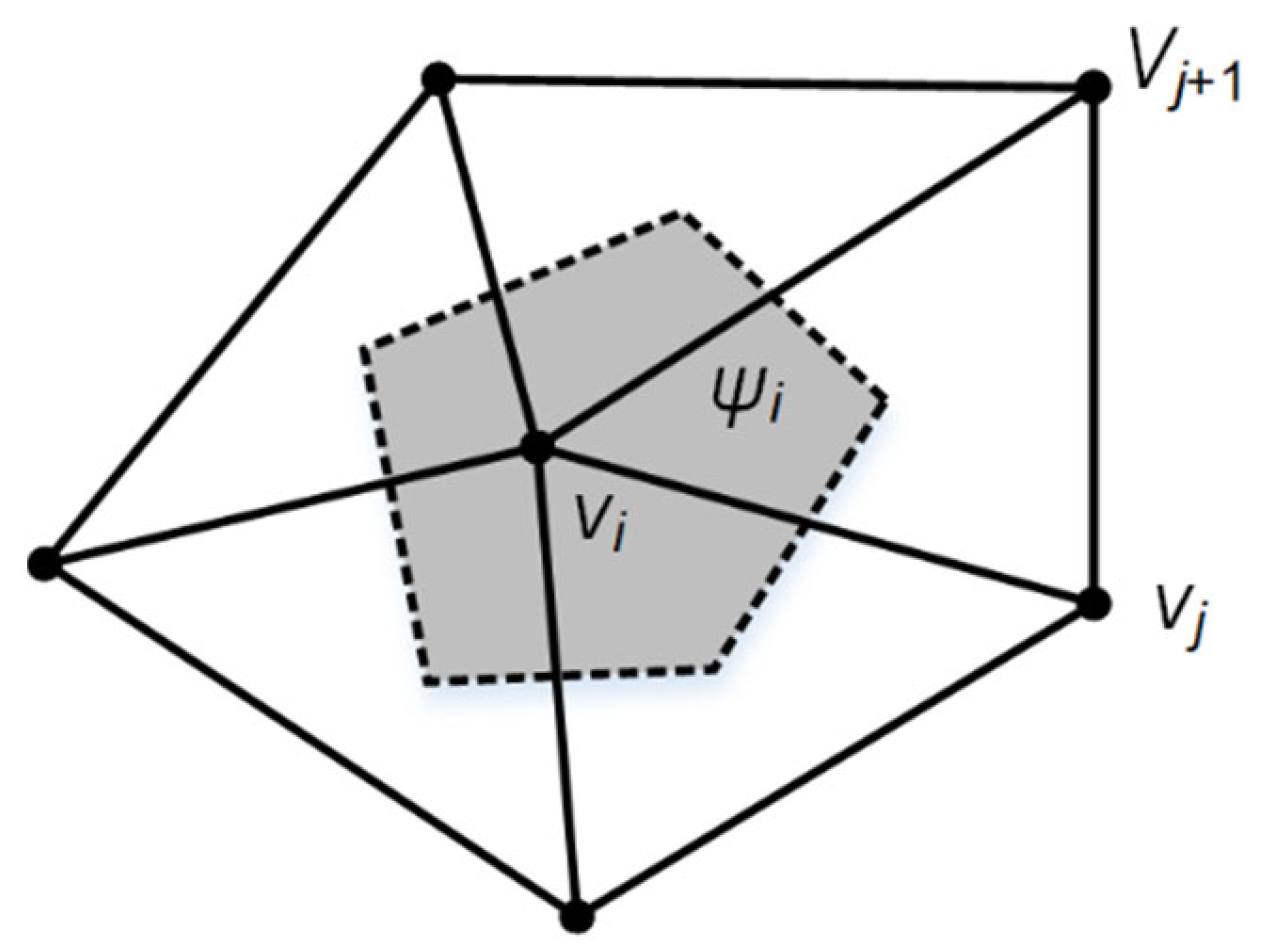∀ψ_i ∈ ψ, it can be defined as one-third of total area of triangles formed by v_i and v_adj, its construction is illustrated in Figure 1 and its formulization is defined in Equation (2),

$${\psi }_i=\frac{1}{3}{\displaystyle {\sum }_{j=1}^{Ns}{S}_{\Delta v_i{v}_j{v}_{j+1}}}$$

(2)

where S is the spherical area of ∆v_iv_jv_j+1.

There is an optimal transportation mapping T: (M, ψ) → (N, φ), such that φ_i = ψ_i and C(T) in Equation (3) is minimal, in which N {V*, E, F} is the image of M, φ is a measure set of N.

$$C(T)=\frac{1}{2}{\displaystyle {\sum }_{i=1}^{nv}{\left({\phi }_i-{\psi }_i\right)}^2}$$

(3)

Based on the point set V, a cell decomposition set W = {w_i} can be constructed, where w_i’s area is φ_i. When φ_i equals ψ_i, the transportation cost is minimal equal to zero. Updating the center of cell w_i as $v_i^{\ast }$ obtains the image of the approximate preserved area mapping.

Cell decomposition on a sphere is a spherical power diagram generation. There is a point set V = {v₁, v₂, …, v_nv} ∈ S² and its weight set r = {r₁, r₂, …, r_nv} ∈ R, c_i(v_i, r_i) is a circle on a sphere with center v_i and radius r_i. Spherical power distance between any point p ∉ V and c_i is defined in Equation (4):

$$\mathrm{pow}(p,v_i)=\frac{\cos d(p,v_i)}{\cos r_i}$$

(4)

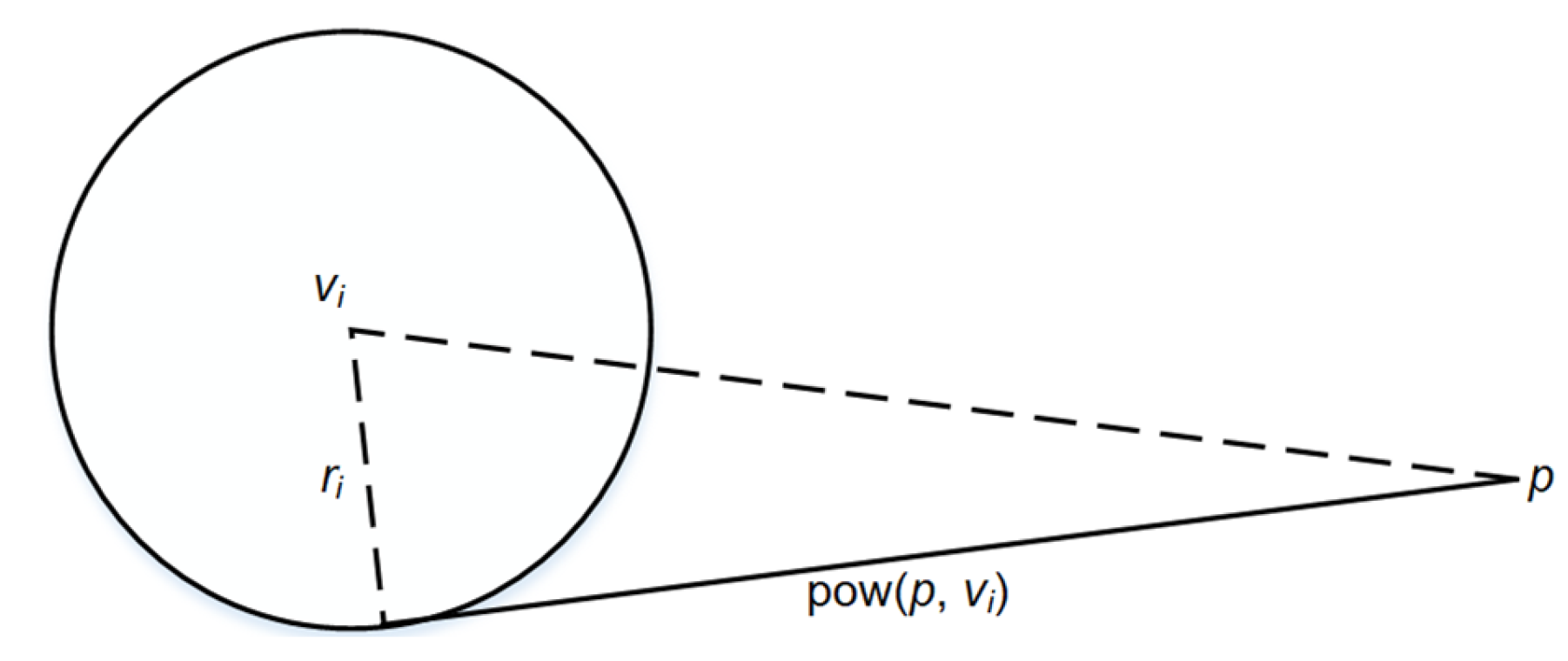
where d(∙) means the spherical great circle, pow(p, v_i) is a geodesic distance between p and tangent point, intersection of a line through p tangent to circle and the circle, as shown in Figure 2.

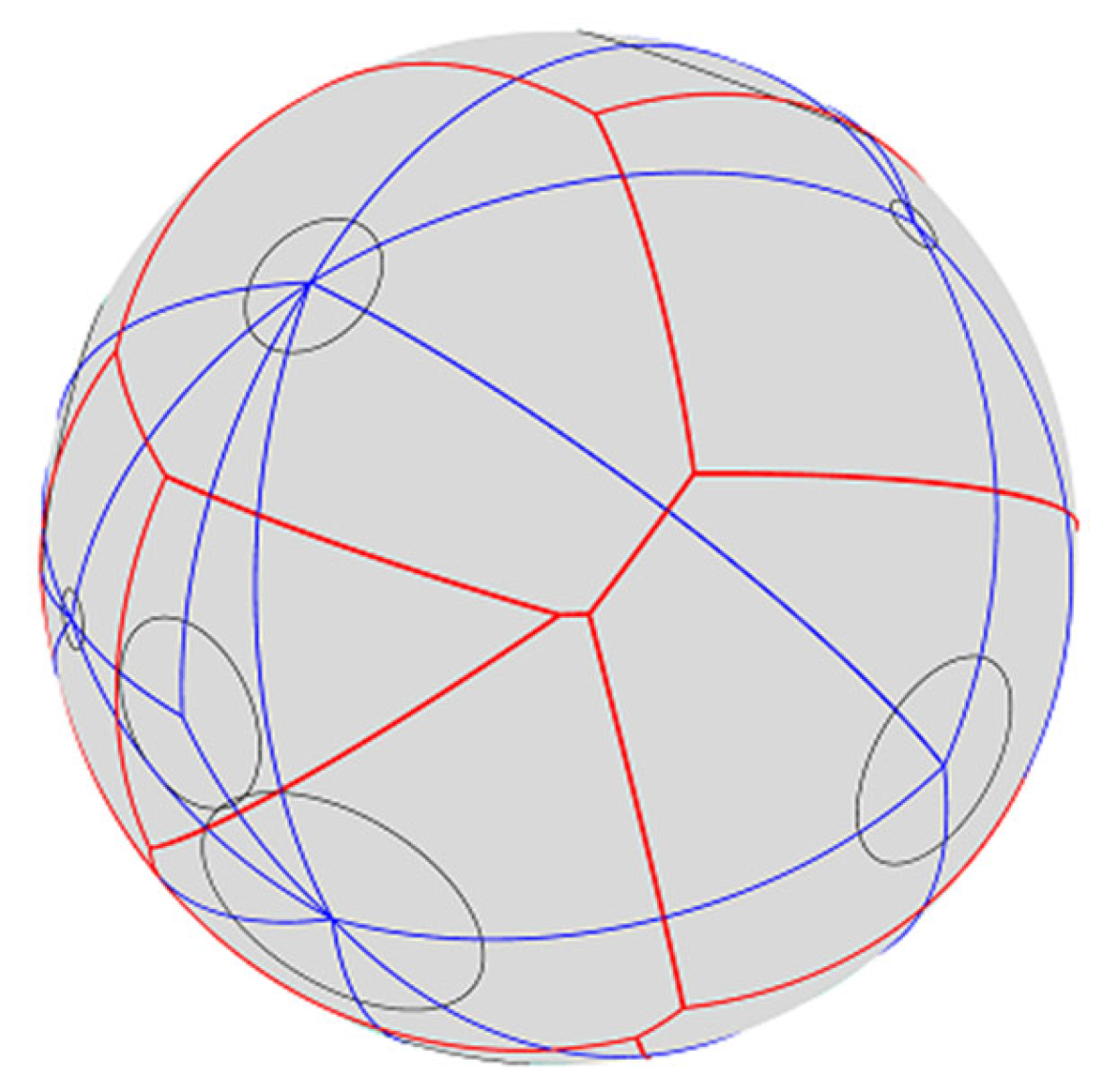
The spherical power diagram of {(p_i, r_i)} is a cell decomposition of sphere, that is $S^2={\displaystyle {\cup }_{i=1}^{nv}{w}_i}$, where w_i = {v_i ∈ V | pow(p, v_i) < pow(p, v_j), ∀v_j ∈ V−{v_i}}. A spherical power diagram of a random point set is shown in Figure 3.

Where the green circle is spherical circle of each point with center v_i and radius r_i, the red spherical polygon is spherical power cell of each point, and the blue spherical triangle is cell’s dual triangle.

It has been proved that the optimal transportation mapping can be achieved by adjusting the weight of the spherical power diagram. When the area of each power cell is equal the predefined weight, defined by the area measure, the optimal transportation mapping can be obtained. According to the spherical power diagram, the transportation cost can be defined as follows:

$$C(\mathit{h})=\frac{1}{2}{{\displaystyle {\sum }_{i=1}^{nv}\left(\phi (\omega (h_i))-{\psi }_i\right)}}^2$$

(5)

where h is a function of radius, h = −ln(cos(r)), φ is the power cell area.

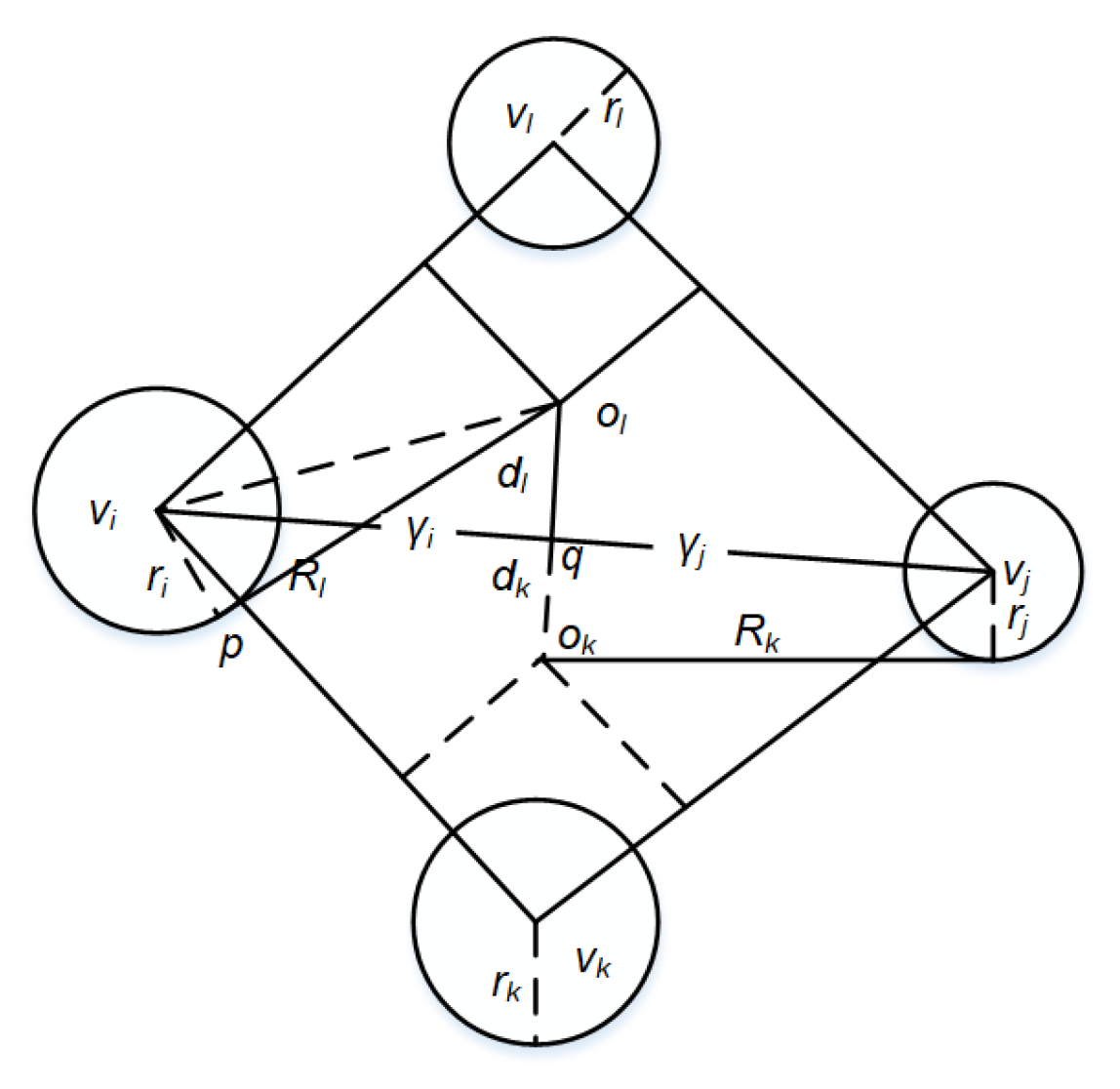
The power cell area is an analytic function of radius [42]. Let q is a center point of line between v_i and v_j, there is pow (q, v_i) = pow (q, v_j) (Figure 4), then:

$$\cos d(q,v_i)e^{h_i}=\cos d(q,v_j)e^{h_j}$$

(6)

Where R_l and R_k are triangle power radius of ∆v_iv_jv_k and ∆v_iv_jv_l.. d_l and d_k are vertical distances from the triangle center o_l and o_k to edge [v_i, v_j], respectively. γ_i and γ_j are the distances between v_i and q, v_j and q, respectively.

Let γ_i = d(q, v_i), γ_j = d(q, v_j), and γ_i + γ_j = γ_ij, there is:

$$\cos ({\gamma }_{ij}-{\gamma }_j)e^{h_i}=\cos {\gamma }_j{e}^{h_j}$$

(7)

$$\tan {\gamma }_j=\frac{1}{\sin {\gamma }_{ij}}(e^{h_j-h_i}-\cos {\gamma }_j)$$

(8)

According to the partial derivative of tanγ_j with respect to h_i, there is:

$$\begin{array}{l}\frac{d{\gamma }_j}{d{h}_i}={\cos }^2{\gamma }_j{\frac{\partial \tan {\gamma }_j}{\partial h_i}}^{}=-{\cos }^2{\gamma }_j\frac{1}{\sin {\gamma }_{ij}}{e}^{h_j-h_i}\\ \begin{array}{cc}& =\end{array}-\frac{1}{\sin {\gamma }_{ij}}{e}^{-h_j-h_i}{({\cos }^2{\gamma }_j{e}^{h_j})}^2=-\frac{1}{\sin {\gamma }_{ij}}\cos r_i\cos r_j{(\frac{\cos R_l}{\cos d_l})}^2\end{array}$$

(9)

According to area of infinitesimal spherical quadrilateral, ${\phi }_i^{jl}$ = area(w_i ∩ ∆v_iv_jv_l), ${\phi }_i^{jk}$ = area(w_i ∩ ∆v_iv_jv_k), φ is the power cell area. There is:

$$\frac{\partial {\phi }_{jk}}{\partial h_i}=-\frac{{\cos }^2{R}_l\sin d_l}{\sin {\gamma }_{ij}{\cos }^2{d}_l}\cos r_i\cos r_j$$

(10)

$$\frac{\partial {\phi }_i^{ik}}{\partial h_j}=-\frac{{\cos }^2{R}_k\sin d_k}{\sin {\gamma }_{ij}{\cos }^2{d}_k}\cos r_i\cos r_j$$

(11)

$$\frac{\partial {\phi }_i}{\partial h_j}=\frac{\partial {\phi }_j}{\partial h_i}=-\frac{\cos r_i\cos r_j}{\sin {\gamma }_{ij}}\left(\frac{{\cos }^2{R}_l\sin d_l}{{\cos }^2{d}_l}+\frac{{\cos }^2{R}_k\sin d_k}{{\cos }^2{d}_k}\right)$$

(12)

The convexity of the transportation cost has been proved by Gu (2013) and it can be minimized by means of Newton’s method. The gradient of cost can be defined as ∇C = (φ(w₁) − ψ₁, φ(w₂) − ψ₂, …, φ(w_nv) − ψ_nv), and the Hessian matrix can be expressed as follows:

$$H=\left[\begin{array}{cccc}-{\displaystyle \sum _{i\ne 1}\frac{\partial {\phi }_i}{\partial h_1}}& \frac{\partial {\phi }_2}{\partial h_1}& \dots & \frac{\partial {\phi }_{nv}}{\partial h_1}\\ \frac{\partial {\phi }_1}{\partial h_2}& -{\displaystyle \sum _{i\ne 2}\frac{\partial {\phi }_i}{\partial h_2}}& \cdots & \frac{\partial {\phi }_{nv}}{\partial h_2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial {\phi }_1}{\partial h_{nv}}& \frac{\partial {\phi }_2}{\partial h_{nv}}& \cdots & -{\displaystyle \sum _{i\ne nv}\frac{\partial {\phi }_i}{\partial h_{nv}}}\end{array}\right]$$

(13)

For the spherical icosahedral grid, the measure-preserving mapping becomes a self-mapping. The measure is replaced by a virtual measure ψ_virtual, where ψ_{i_virtual} = 4πR²/nv for any spherical icosahedral grid point; R is the earth radius. There is a mapping T: (Ico-Grid, ψ_virtual) → (AREA-Ico-Grid, φ), where Ico-Grid is composed of a grid point set V = {v_i}, a grid edge set E, a grid set F and a grid point set of AREA-Ico-Grid, V* = {$v_i^{\ast }$} is the image of V under the mapping T, its grid edge set and grid set are the same as Ico-Grid’s. When the areas of the grids by cell decomposition are equal to each other, that is φ(v*) = ψ_virtual(T⁻¹(v*)), v* ⸦ AREA-Ico-Grid, T⁻¹(v*) ⸦ Ico-Grid, T is the approximate area-preserved mapping. The Algorithm 1 of area quasi-uniformity optimization for the spherical icosahedral grid is described as follows.

Algorithm 1: Area Uniformity Optimization for the Spherical Icosahedral Grid

Input: a spherical icosahedral grid Ico-Grid {V, E, F}, step λ, initial height vector h0, threshold δC

Output: a spherical icosahedral grid with area quasi-uniformity AREA-Ico-Grid {V*, E, F}

(1) Compute the virtual measure ψvirtual = {ψi_virtual};

(2) According to h0 and V, decompose the sphere into a cell set W = {wi}, and calculate each power cell area to get the original measure φ of Ico-Grid by, φ0 ← φ;

(3) Calculate the transportation cost C between φ0 and ψvirtual by Equation (3). If C < δC, V* ← V and move to step 5. If not, move to the next step;

(4) Update cell decomposition of S2

(4.1) Calculate gradient ∇C = (φ(w1) − ψ1, φ(w2) − ψ2, …, φ(wnv) − ψnv)T;

(4.2) Compute the transportation cost C via ∇C. If C<δC, move to step 5. If not, move to step 4.3;

(4.3) According to Equations (10)–(13), calculate a Hessian matrix H;

(4.4) Establish the relationship between hessian matrix and gradient, that is Hδh = ∇C;

(4.5) Update height vector, h = h + λδh;

(4.6) Decompose the sphere into a new cell set W = {wi} based on h; compute cells’ area φW = {φwi};

(5) Compute the centers of cells in W, and obtain CW = {cwi};

(6) V* ← CW, and output result;

(7) End.

3. Results and Discussions

To verify the effectiveness of this algorithm, tests were performed to compare the grid quality and numerical accuracy among the proposed algorithm optimized grid (OURS grid), the non-optimized grid (NOPT grid), the spring dynamic method optimized grid (SPRG grid), tweaked grid optimized by Heikes and Randall grid (HR grid) Spherical Centroidal Voronoi Tessellations grid (SCVT grid) and grid optimized by Xu (XU grid). Here, the construction of the NOPT grid was through recursive division, and the parameter β in the SPRG grid was set to 1.1 according to [33]. All experiments were implemented in C++ and executed on a PC with Intel Core i5-6400 [email protected] GHz, 8 GB RAM.

3.1. The Grid Quality Evaluation

3.1.1. The Grid Area Uniformity

The relative area deviation D_area was used to measure the grid area uniformity, which can be calculated with Equation (14):

$$D_{\mathrm{area}}=\frac{A-A_{\mathrm{avg}}}{A_{\mathrm{avg}}}$$

(14)

where A is the area of a grid; A_avg is the average area of the spherical icosahedral grid; earth radius was set to 6, 371.007 km.

Maximum grid area A_max and minimum grid area A_min and average area A_avg of NOPT grid and OURS grid at certain resolutions are listed in

Table 1. A_min, A_max of spherical icosahedral grids (unit: km²).

Level	nv	Aavg	NOPT		OURS
			Amin	Amax	Amin	Amax
0	12	42, 505, 466.06	42, 505, 466.06	42, 505, 466.06	42, 505, 466.06	42, 505, 466.06
1	42	12, 144, 418.88	11, 115, 261.91	12, 556, 071.10	11, 115, 254.48	12, 556, 081.85
2	162	3, 148, 553.04	2, 812, 532.18	3, 339, 347.67	2, 885, 170.41	3, 216, 806.64
3	642	794, 494.69	705, 296.93	923, 852.78	735, 897.42	799, 720.75
4	2, 562	199, 088.83	176, 460.40	237, 913.42	185, 750.43	199, 596.50
5	10, 242	49, 801.37	44, 123.63	59, 942.43	46, 638.43	49, 880.62
6	40, 962	12, 452.17	11, 031.44	15, 015.28	11, 700.00	12, 500.00
7	163, 842	3, 113.16	2, 757.89	3, 755.66	2, 919.71	3, 114.73
8	655, 362	778.30	689.48	939.35	729.62	778.67
9	2, 621, 442	194.57	172.37	234.84	182.34	194.60

.

The grid area was normalized according to Equation (15) to compare the differences at various resolutions.

$$\tilde{A}=\frac{A\times nv}{12\times R^2}$$

(15)

The normalized minimum area ${\tilde{A}}_{\min }$ and maximum area ${\tilde{A}}_{\max }$ of different spherical icosahedral grids are listed in

Table 2. The normalized area and the ratios between the A_min and A_max.

Level		3	4	5	6	7	8	9
${\tilde{A}}_{\mathrm{avg}}$		1.047	1.047	1.047	1.047	1.047	1.047	1.047
NOPT	${\tilde{A}}_{\min }$	0.930	0.928	0.930	0.928	0.928	0.928	0.928
	${\tilde{A}}_{\max }$	1.218	1.251	1.260	1.263	1.263	1.264	1.264
	rA	0.764	0.742	0.740	0.735	0.735	0.734	0.734
SPRG	${\tilde{A}}_{\min }$	0.879	0.848	0.820	0.803	0.791	0.781	0.776
	${\tilde{A}}_{\max }$	1.080	1.079	1.080	1.081	1.083	1.087	1.092
	rA	0.814	0.786	0.760	0.743	0.730	0.718	0.711
HR	${\tilde{A}}_{\min }$	0.998	1.008	1.012	1.014	1.013	1.016	1.016
	${\tilde{A}}_{\max }$	1.062	1.066	1.068	1.068	1.069	1.070	1.070
	rA	0.940	0.946	0.950	0.949	0.948	0.950	0.950
SCVT	${\tilde{A}}_{\min }$	0.861	0.812	0.760	0.719	0.677	0.639	0.599
	${\tilde{A}}_{\max }$	1.082	1.081	1.080	1.081	1.081	1.081	1.081
	rA	0.796	0.751	0.710	0.665	0.626	0.591	0.554
XU	${\tilde{A}}_{\min }$	0.861	0.812	0.760	0.719	0.676	0.638	0.600
	${\tilde{A}}_{\max }$	1.082	1.081	1.080	1.081	1.082	1.082	1.082
	rA	0.796	0.751	0.710	0.665	0.625	0.590	0.555
OURS	${\tilde{A}}_{\min }$	0.970	0.977	0.981	0.984	0.982	0.982	0.981
	${\tilde{A}}_{\max }$	1.054	1.050	1.049	1.051	1.048	1.048	1.047
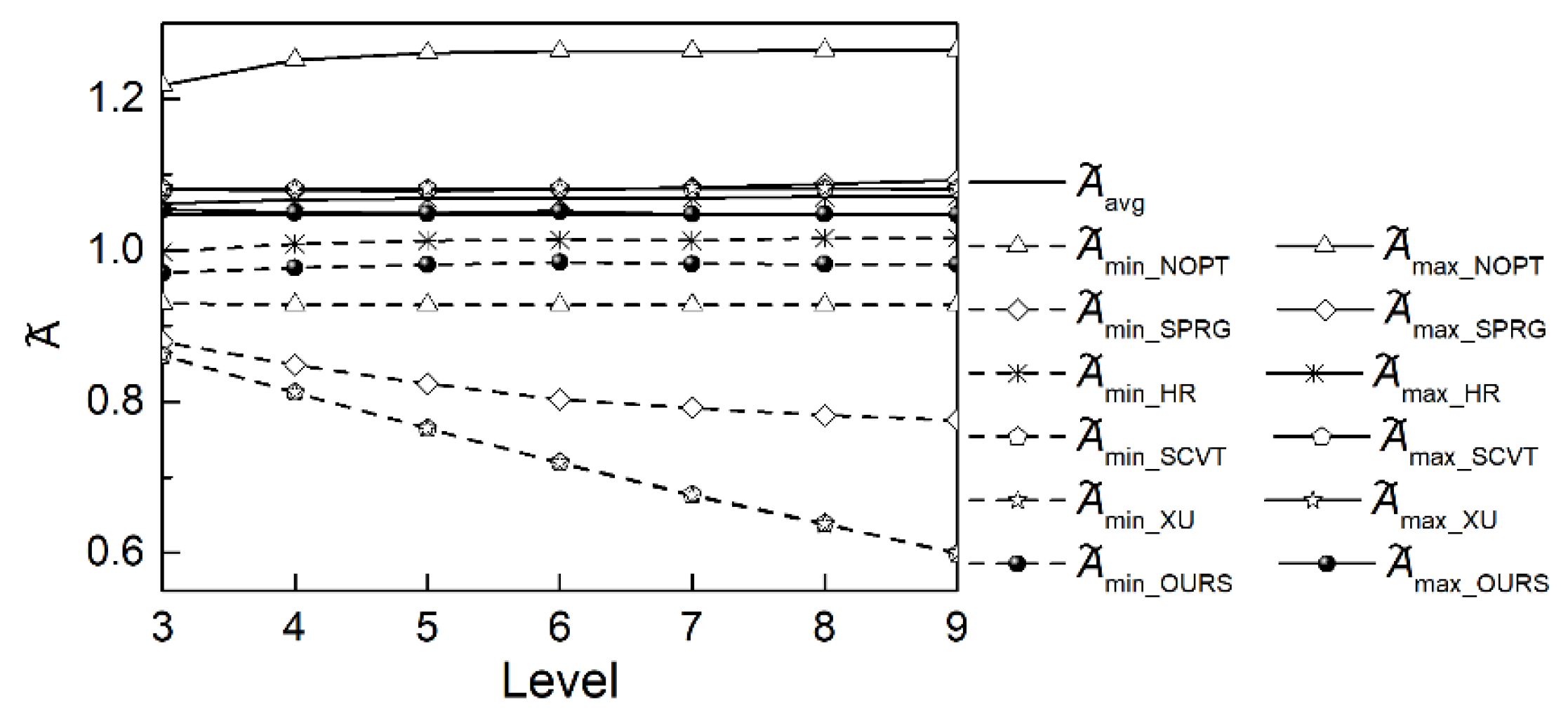
	rA	0.920	0.930	0.940	0.936	0.937	0.937	0.937

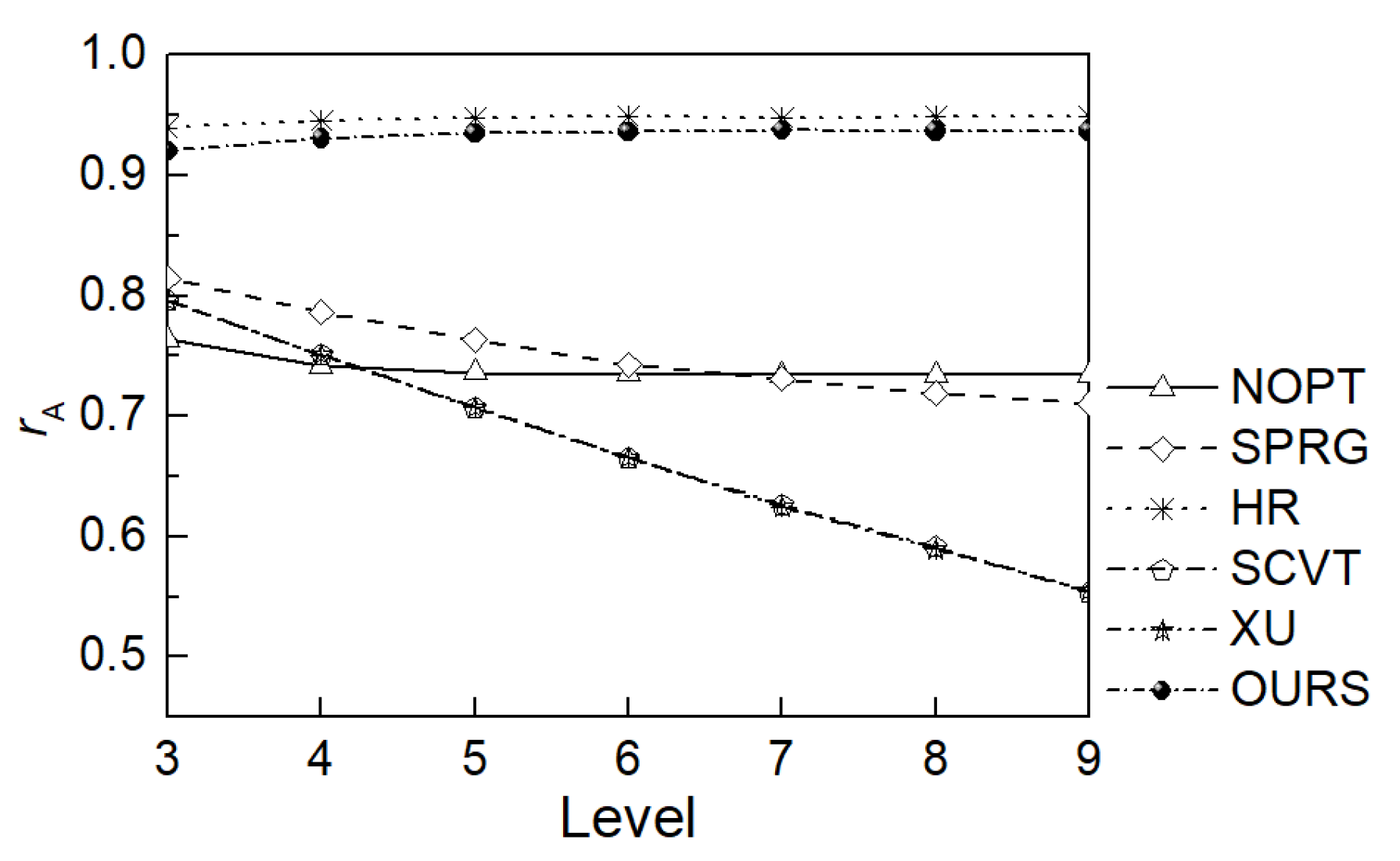
, and their curves are illustrated in Figure 5. Ratios between the minimum and maximum area, r_A = A_min/A_max, of different spherical icosahedral grids at different resolutions are presented in Figure 6.

The maximum grid area, minimum grid area and their ratios indicate the ranges of grid area. The closer the ratio is to one, the smaller the area range is, which indicates a more uniform grid area. The normalized minimum and maximum areas of all grids except the SCVT grid and XU grid gradually have converged as the resolution increases (Figure 5 and Figure 6 and Table 1 and Table 2). The area range of SCVT grid and XU grid are the same and the biggest among all grids at level 9. The one of NOPT grid is followed and that of HR grid is the smallest. The range of OURS grid is only expanded by 1.20% compared with HR grid. Same as the range, ratios of SCVT grid and XU grid are non-convergence as resolution increases and have decreased to 0.554 and 0.555 at level 9, respectively. The ratios of SPRG grid and NOPT grid have converged slowly to 0.711 and 0.734, respectively. On the contrary, the ones of HR grid and OURS grid have increased as resolution increases and converged to 0.950 and 0.937, respectively at the same resolution.

To further emphasize the spherical distribution characteristic of grid area uniformity, taking the grid at level 9 as an example, the number of grids in different intervals of grid area relative deviation calculated by Equation (15) are counted in

Table 3. The number of grids in different D_area interval of different grids.

Interval (%)	NOPT	SPRG	HR	SCVT	XU	OURS
[−100, −38.0]	0	0	0	0	0	0
(−38.0, −34.0)	0	0	0	162	162	0
(−34.0, −30.0)	0	0	0	0	0	0
(−30.0, −26.0)	0	0	0	960	960	0
(−26.0, −22.0)	0	162	0	1, 920	1, 920	0
(−22.0, −18.0)	0	960	0	2, 880	3, 840	0
(−18.0, −14.0)	0	4, 800	0	14, 400	13, 440	0
(−14.0, −10.0)	192	34, 560	0	42, 240	42, 240	0
(−10.0, −6.0)	436, 770	180, 480	0	112, 320	115, 200	12
(−6.0, −2.0)	1, 132, 800	630, 720	22, 786	314, 880	317, 760	0
(−2.0, 2.0)	366, 240	887, 520	2598, 480	1, 403, 040	1, 341, 584	2, 621, 430
(2.0, 6.0)	60, 480	647, 040	176	728, 640	784, 336	0
(6.0, 10.0)	0	235, 200	0	0	0	0
(10.0, 14.0)	380, 160	0	0	0	0	0
(14.0, 18.0)	96, 000	0	0	0	0	0
(18.0, 22.0)	148, 800	0	0	0	0	0
(22.0, 100.0)	0	0	0	0	0	0
total	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442

.

Refine these intervals to further demonstrate the area features of OURS grid (

Table 4. The number of grids in refined D_area interval of OURS grid.

Interval (%)	N	p (%)
[−100, −0.18)	72	0.00
[−0.18, −0.14)	60	0.00
[−0.14, −0.10)	17, 695	0.68
[−0.10, −0.06)	44, 733	1.71
[−0.06, −0.02)	495, 834	18.91
[−0.02, 0.02)	1, 342, 129	51.20
(−0.02, 0.60)	720, 919	27.50
(0.06, 100]	0	0
total	2, 621, 442	100.00

). Where, N is the number of grids in different intervals, and p is grid proportions.

The cumulative grid proportions of |D_area| are depicted in

Table 5. The cumulative proportion of |D_area| of different grids (%).

Interval (%)	NOPT	SPRG	HR	SCVT	XU	OURS
[0, 0.004)	0	0	1.07	0	0.26	12.57
[0.004, 0.012)	0.02	0.07	3.27	0.07	0.59	33.35
[0.012, 0.02)	0.02	0.22	5.87	0.07	0.73	51.20
[0.02, 0.028)	0.02	0.22	8.63	0.22	0.93	66.98
[0.028, 0.036)	0.02	0.51	11.06	0.22	1.25	81.04
[0.036, 0.044)	0.02	0.62	13.24	0.37	1.25	92.56
[0.044, 0.052)	0.02	0.77	15.10	0.66	1.39	96.17
[0.052, 0.06)	0.02	0.99	16.73	0.92	1.39	97.61
[0.06, 0.068)	0.02	1.65	22.95	2.38	1.76	99.32
[0.068, 0.076)	0.02	2.23	28.11	3.04	2.16	99.99
[0.076, 0.3)	0.02	4.69	43.54	6.23	5.35	99.99
[0.3, 0.5)	0.02	7.87	56.64	10.25	9.87	99.99
[0.5, 0.7)	0.02	11.17	66.66	14.39	14.25	99.99
[0.7, 0.9)	0.02	14.39	74.64	18.82	18.53	99.99
[0.9, 2)	13.97	33.86	99.12	53.52	51.18	99.99
[6, 26)	59.49	82.6	100	93.33	93.32	100
[26, 100]	100	100	100	100	100	100

, and Figure 7 (|D_area| < 0.08%).

The D_area of all grids are in [−38.0%, 22.0%] (Table 3). The ones of HR grid and OURS grid are mainly in (−2.0%, 2.0%), which is smaller than other four grids. There are more than 90% grids with D_area in (−0.06%, 0.06%) in OURS grid. The cumulative proportions have increased logarithmically as |D_area| increases, in which the increasing rate of OURS grid is the fastest and that of NOPT grid is the slowest (Figure 7). The cumulative proportions of OURS grid with |D_area| of less than 0.044% is more than 90.00%, and the ones of other five grids are only 0.02% (NOPT grid), 0.62% (SPRG grid), 13.24% (HR grid), 0.37% (SCVT grid), and 1.25% (XU grid). Although the area ratio of HR grid is bigger than OURS grid, the proportion of grid with smaller is far less than that of OURS grid.

Meanwhile, the spherical distributions of the area relative deviations at level 9 are shown in Figure 8, where the lighter the color is, the closer the grid area deviation is to zero.

From Figure 8, the grids with maximum area deviation are the pentagons, and spherical distributions patterns of D_area are symmetry. The distribution of NOPT grid has fractal characteristics and is not continuous. Because of the larger number of grids with larger D_area, its distribution is shown by darker color. The distributions of the SPRG grid, SCVT grid and XU grid are similar. As the larger number of grids with smaller D_area (−0.06%, 0.06%) in OURS grid, its distribution is shown by the lightest color and some grids with larger D_area are mainly located along the triangular boundaries. Grids with larger D_area are also located around these boundaries, however, these regions are far larger than that of OURS grid.

3.1.2. The Grid Interval Uniformity

The geodesic distance, d, between grid points, the minimum distance, d_min and the maximum distance d_max (

Table 6. d_min, d_max, d_avg of different grids (unit: km).

Level	NOPT			OURS
	davg	dmin	dmax	davg	dmin	dmax
0	7529.85	7529.85	7529.85	7529.85	7529.85	7529.85
1	3764.92	3526.83	4003.02	3764.92	3526.83	4003.02
2	1914.33	1763.41	2079.28	1915.30	1739.23	2087.62
3	961.22	881.71	1050.16	961.85	866.34	1059.12
4	481.12	440.85	526.42	481.47	432.15	532.56
5	240.62	220.43	263.38	240.81	215.84	267.18
6	120.32	110.21	131.71	120.42	107.83	134.40
7	60.16	55.11	65.86	60.20	54.13	67.12
8	30.08	27.55	32.93	30.10	27.06	33.56
9	15.04	13.78	16.47	15.05	13.53	16.78

), the ratios between them (

Table 7. Normalized distance and ratios between the d_min and d_max of different grids.

Level		3	4	5	6	7	8	9
${\tilde{d}}_{\mathrm{avg}}$		1.182	1.182	1.182	1.182	1.182	1.182	1.182
NOPT	${\tilde{d}}_{\min }$	1.107	1.107	1.107	1.107	1.107	1.107	1.107
	${\tilde{d}}_{\max }$	1.319	1.322	1.323	1.323	1.323	1.323	1.323
	rd	0.839	0.837	0.837	0.837	0.837	0.837	0.837
SPRG	${\tilde{d}}_{\min }$	1.077	1.059	1.043	1.017	1.017	0.999	0.983
	${\tilde{d}}_{\max }$	1.276	1.279	1.279	1.284	1.285	1.279	1.259
	rd	0.844	0.828	0.815	0.802	0.791	0.781	0.781
HR	${\tilde{d}}_{\min }$	1.076	1.074	1.074	1.074	1.074	1.074	1.075
	${\tilde{d}}_{\max }$	1.351	1.361	1.364	1.364	1.365	1.364	1.382
	rd	0.796	0.789	0.787	0.787	0.787	0.787	0.778
SCVT	${\tilde{d}}_{\min }$	1.065	1.035	1.005	0.975	0.946	0.917	0.890
	${\tilde{d}}_{\max }$	1.275	1.277	1.277	1.277	1.277	1.277	1.280
	rd	0.835	0.810	0.787	0.763	0.741	0.718	0.695
XU	${\tilde{d}}_{\min }$	1.065	1.035	1.005	0.975	0.945	0.916	0.888
	${\tilde{d}}_{\max }$	1.275	1.277	1.277	1.277	1.277	1.277	1.276
	rd	0.835	0.810	0.787	0.763	0.740	0.717	0.696
OURS	${\tilde{d}}_{\min }$	1.088	1.085	1.084	1.083	1.087	1.091	1.091
	${\tilde{d}}_{\max }$	1.330	1.337	1.342	1.350	1.349	1.354	1.353
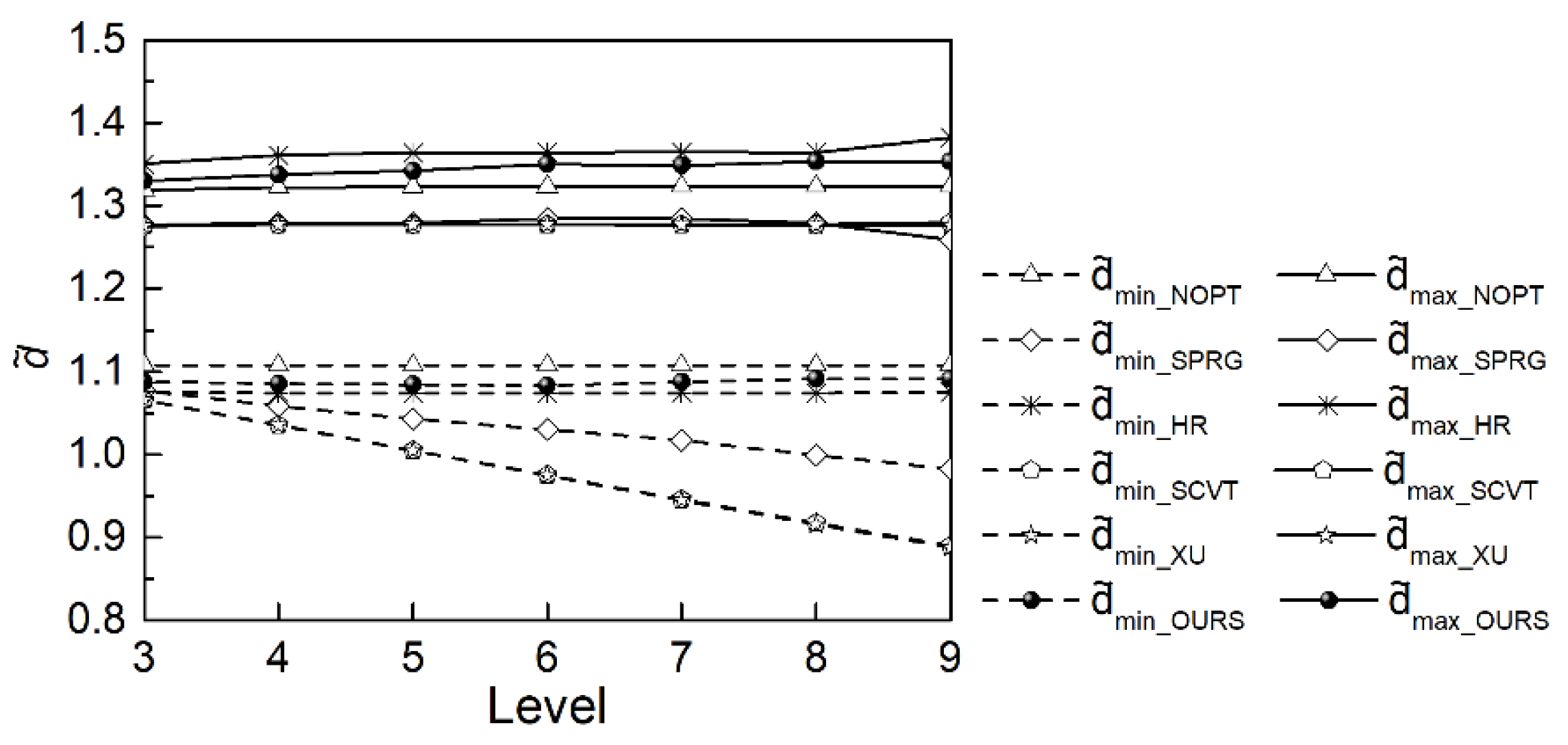
	rd	0.818	0.812	0.808	0.802	0.806	0.806	0.806

) and the grid length relative deviation (as Equation (16)) are calculated to describe the grid interval uniformity.

$$D_{\mathrm{length}}=\frac{L-L_{\mathrm{avg}}}{L_{\mathrm{avg}}}$$

(16)

The grid distance was normalized according to Equation (17) to compare the differences at various resolutions (Table 7 and Figure 9).

$$\tilde{d}=\frac{d\times 2^{Level}}{R}$$

(17)

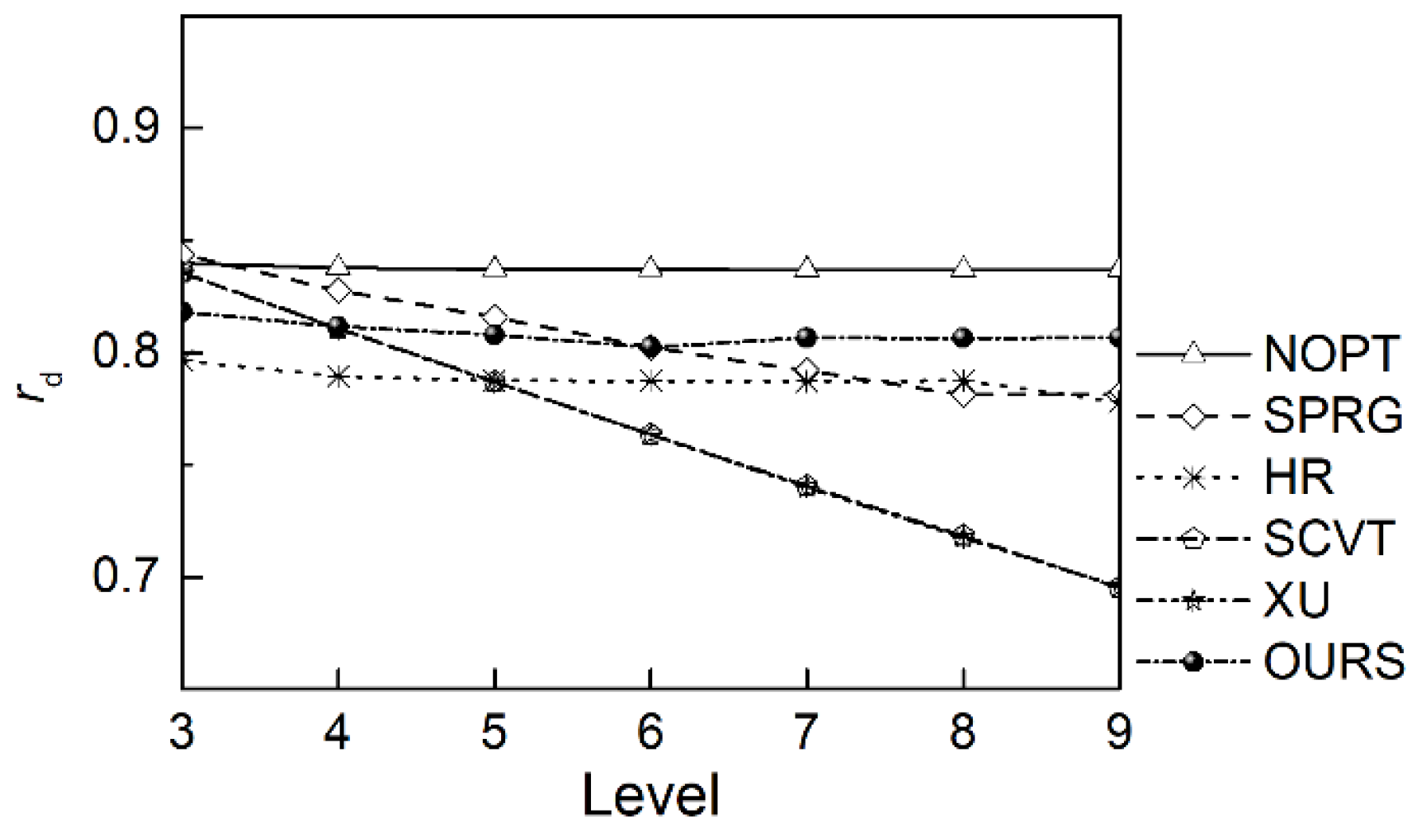
Ratios between the minimum and maximum distances, r_d = d_min/d_max, of different grids at different resolutions are calculated in Table 7 and presented in Figure 10.

Same as the normalized area, ${\tilde{d}}_{\min }$, ${\tilde{d}}_{\max }$ and ratios indicate the ranges of grid interval. The closer the ratio is to one, the smaller the interval range is, which indicates a more uniform grid interval. The ${\tilde{d}}_{\min }$, ${\tilde{d}}_{\max }$ of the all grids except the SCVT grid and XU grid have gradually converged as the resolution increases (Figure 9 and Figure 10 and Table 6 and Table 7). The ratios of SCVT grid and XU grid are non-convergence as resolution increases, and ones of SPRG grid and HR grid have converged to 0.781 and 0.778 at level 9, respectively, the ratio of OURS grid is larger than them.

The number of grids in different intervals of grid length relative deviation have been counted (

Table 8. The number of grids with different D_length interval of different grids.

	NOPT	SPRG	HR	SCVT	XU	OURS
[−100, −15]	0	0	0	0	0	0
(−15, −13]	0	0	0	60	60	0
(−13, −11]	0	0	0	120	120	0
(−11, −9]	0	0	0	360	420	0
(−9, −7]	0	5, 730	0	720	1, 020	0
(−7, −5]	0	28, 800	0	2, 640	2, 280	0
(−5, −3]	0	151, 680	0	100, 800	106, 030	0
(−3, −1]	1, 488, 960	620, 160	0	301, 632	301, 632	0
(−1, 1)	446, 880	966, 240	2, 447, 056	1, 536, 160	1, 471, 680	2, 621, 430
[1, 3)	60, 480	679, 680	174, 374	678, 950	738, 200	0
[3, 5)	0	168, 960	0	0	0	0
[5, 7)	446, 400	192	0	0	0	0
[7, 9)	144, 960	0	0	0	0	0
[9, 11)	33, 750	0	0	0	0	0
[11, 13)	0	0	0	0	0	0
[13, 15)	0	0	0	0	0	0
[15, 17)	12	0	0	0	0	0
[17, 19)	0	0	0	0	0	12
[19, 21)	0	0	12	0	0	0
[21, 100]	0	0	0	0	0	0
total	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442	2, 621, 442

) to emphasize the spherical distribution characteristic of grid interval uniformity.

There are the similar characteristics of HR and OURS grid from Table 8, so the intervals is refined to further reveal their differences in

Table 9. The number of grids with refined D_length interval of HR and OURS grid.

Interval (%)	HR		OURS
	N	p (%)	N	p (%)
[−100, −1.1]	16	0.00	0	0
(−1.1, −0.9]	46, 592	1.78	0	0
(−0.9, −0.7]	137, 776	5.26	0	0
(−0.7, −0.5]	835, 680	31.88	0	0
(−0.5, −0.3]	468, 576	17.87	325, 328	12.41
(−0.3, −0.1]	288, 704	11.01	659, 536	25.16
(−0.1,0.1)	211, 232	8.06	676, 512	25.81
[0.1, 0.3)	166, 432	6.35	705, 728	26.92
[0.3, 0.5)	134, 192	5.12	234, 528	8.95
[0.5, 0.7)	110, 118	4.20	19, 798	0.76
[0.7, 0.9)	91, 328	3.48	0	0
[0.9, 1.0)	73, 328	2.80	0	0
[1.1, 1.3)	50, 640	1.93	0	0
[1.3, 1.5)	6, 816	0.26	0	0
[1.5, 1.7)	0	0	0	0
[1.7, 2.3)	0	0	12	0
[2.3, 100]	12	0	0	0
total	2, 621, 442	100	2, 621, 442	100

. Where, N is the number of grids in different intervals, and p is grid proportions.

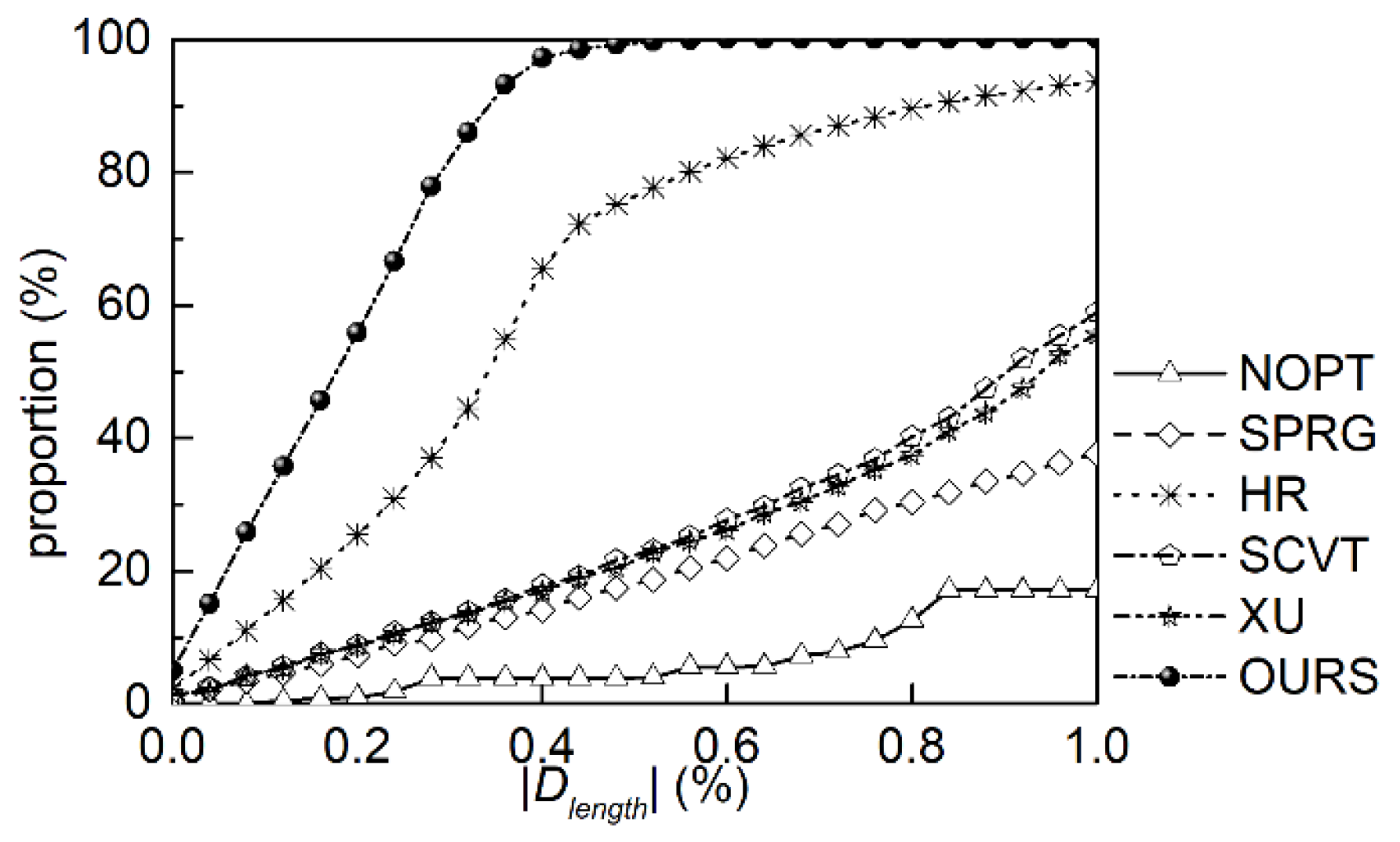
The cumulative proportions of grid with |D_length| are depicted in

Table 10. The cumulative proportion of |D_length| of different grids (%).

Interval (%)	NOPT	SPRG	HR	SCVT	XU	OURS
[0, 0.02)	0	0.51	2.20	0.73	1.32	5.02
[0.02, 0.10)	0.02	3.41	11.01	4.06	4.32	25.81
[0.10, 0.18)	0.79	5.93	20.37	7.54	7.47	45.63
[0.18, 0.26)	1.78	9.01	30.87	10.77	10.33	66.58
[0.26, 0.34)	3.86	11.65	44.40	13.84	13.40	86.02
[0.34, 0.42)	3.86	14.10	65.49	17.80	16.96	97.28
[0.42, 0.50)	3.86	17.36	75.17	21.64	20.47	99.24
[0.50, 0.58)	5.51	20.43	80.03	25.20	24.45	99.96
[0.58, 0.66)	5.58	23.80	83.90	29.66	28.66	99.99
[0.66, 0.74)	7.82	26.97	87.00	34.42	32.75	99.99
[0.74, 0.82)	12.54	30.34	89.58	40.17	37.39	99.99
[0.82, 2.00)	22.72	66.59	99.99	90.00	89.23	99.99
[2.00, 5.00)	76.15	98.67	99.99	97.62	97.62	99.99
[5.00, 7.00)	92.30	99.63	99.99	98.97	98.83	99.99
[7.00, 100]	100	100	100	100	100	100

and Figure 11. Because of higher cumulative proportion in OURS grid in a smaller interval, only a part of results with |D_length| < 1.00% are demonstrated.

The D_length of all grids are in [−15%, 21%] (Table 8), and the ones of HR grid and OURS grid are mainly in (−1%, 1%). The proportion of grid in this range of OURS grid is about 7 times that of NOPT grid, although the interval ratio of NOPT grid is bigger than that of OURS grid. The cumulative proportions also increase logarithmically as |D_length| increases, in which the increasing rate in OURS grid is the fastest and that of NOPT grid is the slowest. The cumulative proportions of OURS grid is more than 99.00% with |D_length| less than 0.50%. Ones of other grids are only 3.86% (NOPT grid) 17.36% (SPRG grid), 75.17% (HR grid), 21.64% (SCVT grid), and 20.47% (XU grid) in the same range.

Meanwhile, the spherical distributions of D_length are shown in Figure 12 at level 9.

Same as spherical distribution of grid area, the grids with maximum D_length are these pentagons, and distributions of all grids are symmetry. Near these pentagons, the lengths of grids are less than the average length and shown by darker color in all grids. The distribution of NOPT grid has fractal characteristics and is not continuous, too. The D_length in the remaining grids are reduced from the pentagons to triangular centers. The grids with larger D_length are mainly located along the triangular boundaries in OURS grid, and those grids are spread like pentagon or star from these pentagons.

3.2. The Numerical Accuracy Evaluation

Spherical Laplacian operators of scalar field (as Equation (18)) is discretized to evaluate numerical accuracy on different grids.

$$f(\lambda ,\phi )=\cos \lambda \times {\cos }^4\phi$$

(18)

where λ and φ are the longitude and latitude of point on the sphere, respectively.

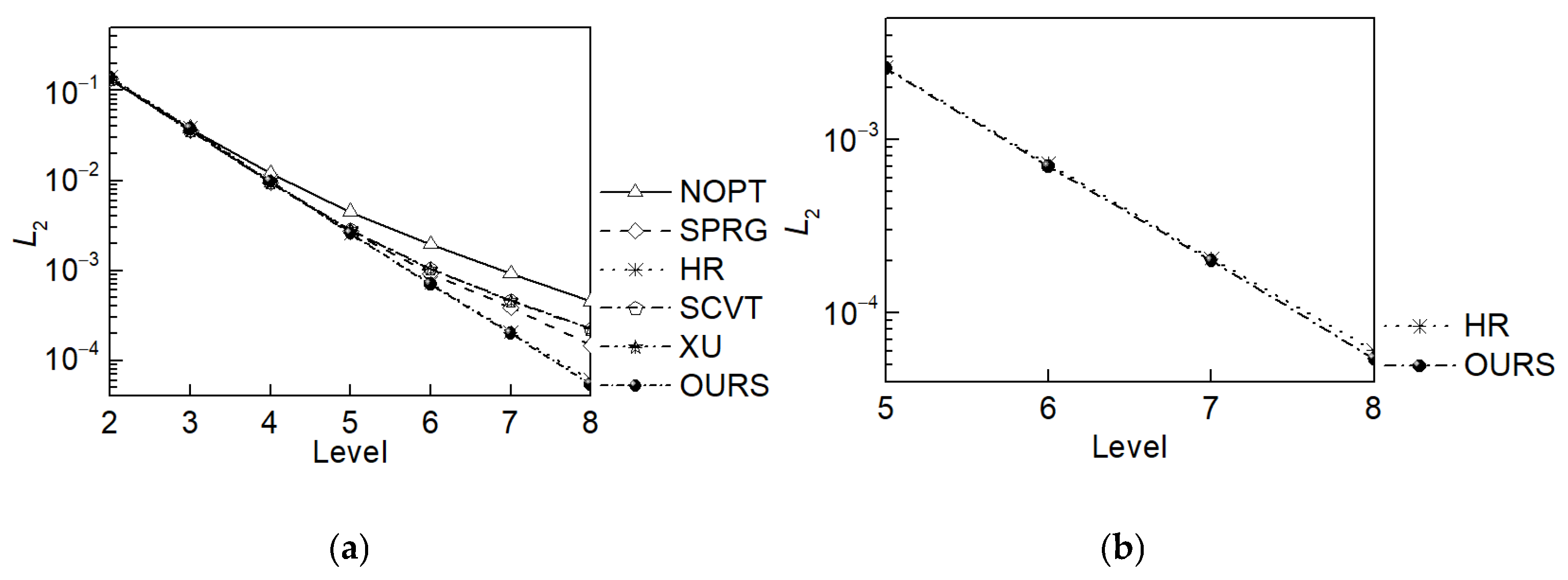
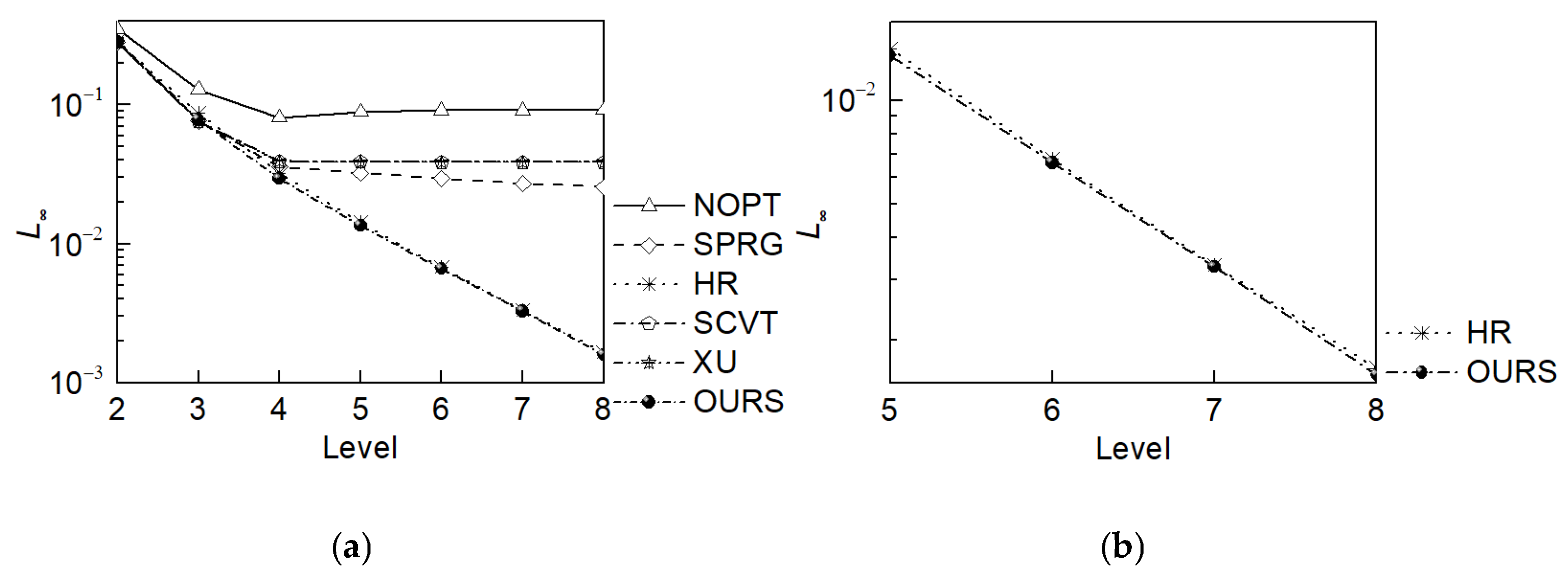
The L₂-norm error (as Equation (19)), L_∞-norm error (as Equation (20)) of discretization have been calculated (

Table 11. L₂-norm error of Laplacian operator of different grids.

	2	3	4	5	6	7	8
NOPT	1.31 × 10−1	3.78 × 10−2	1.20 × 10−2	4.49 × 10−3	1.96 × 10−3	9.26 × 10−4	4.52 × 10−4
SPRG	1.33 × 10−1	3.56 × 10−2	9.47 × 10−3	2.74 × 10−3	9.30 × 10−4	3.84 × 10−4	1.47 × 10−4
HR	1.41 × 10−1	3.79 × 10−2	9.85 × 10−3	2.58 × 10−3	7.23 × 10−4	2.05 × 10−4	6.05 × 10−5
SCVT	1.33 × 10−1	3.55 × 10−2	9.47 × 10−3	2.81 × 10−3	1.04 × 10−3	4.61 × 10−4	2.23 × 10−4
XU	1.33 × 10−1	3.55 × 10−2	9.47 × 10−3	2.81 × 10−3	1.04 × 10−3	4.61 × 10−4	2.23 × 10−4
OURS	1.38 × 10−1	3.75 × 10−2	9.78 × 10−3	2.57 × 10−3	6.98 × 10−4	1.99 × 10−4	5.42 × 10−5

and

Table 12. L_∞-norm error of Laplacian operator of different grids.

	2	3	4	5	6	7	8
NOPT	3.52 × 10−1	1.28 × 10−1	8.08 × 10−2	8.89 × 10−2	9.10 × 10−2	9.10 × 10−2	9.15 × 10−2
SPRG	2.81 × 10−1	7.62 × 10−2	3.56 × 10−2	3.23 × 10−2	3.00 × 10−2	2.70 × 10−2	2.57 × 10−2
HR	2.84 × 10−1	8.67 × 10−2	3.23 × 10−2	1.41 × 10−2	6.75 × 10−3	3.31 × 10−3	1.66 × 10−3
SCVT	2.81 × 10−1	7.61 × 10−2	3.92 × 10−2	3.88 × 10−2	3.87 × 10−2	3.87 × 10−2	3.87 × 10−2
XU	2.81 × 10−1	7.61 × 10−2	3.92 × 10−2	3.88 × 10−2	3.87 × 10−2	3.87 × 10−2	3.87 × 10−2
OURS	2.85 × 10−1	7.81 × 10−2	2.93 × 10−2	1.35 × 10−2	6.59 × 10−3	3.27 × 10−3	1.59 × 10−3

and Figure 13 and Figure 14).

$$L_2=\sqrt{\left(\frac{1}{{\displaystyle {\sum }_{i=1}^{nv}{A}_i}}\left({\displaystyle {\sum }_{i=1}^{nv}{A}_i{\left(f_i^{\mathrm{num}}-f_i^{\mathrm{ana}}\right)}^2}\right)\right)}$$

(19)

$$L_{\infty }=\underset{i=1,nv}{\max }\left|f_i^{\mathrm{num}}-f_i^{\mathrm{ana}}\right|$$

(20)

where f^ana and f^num are the analytical and numerical solutions of Laplacian operator, respectively.

The L₂-norm errors and L_∞-norm errors of all grids have been reduced as resolution increase, ones of OURS grid and HR grid are smaller than the others. The L_∞-norm error (meaning the maximal error) of OURS grid has been reduced from 9.15 × 10⁻² (NOPT grid), 2.57 × 10⁻² (SPRG grid), 1.66 × 10⁻² (HR grid), 3.87 × 10⁻² (SCVT and XU grid) to 1.59 × 10⁻² at level 8. The L₂-norm error (meaning the RMS error) of OURS grid has been reduced from 4.52 × 10⁻⁴ (NOPT grid), 2.03 × 10⁻⁴ (SPRG grid), 6.05 × 10⁻⁵ (HR grid), 2.33 × 10⁻⁴ (SCVT and XU grid) to 5.86 × 10⁻⁴ at the same grid resolution, in which the enhancement of average accuracy is nearly 8 times that of NOPT grid and has more than 11.62% compared to the HR grid.

Meanwhile, the spherical distributions of the Laplacian operator error on different grids are shown in Figure 15 at level 5.

Grids in NOPT grid with larger errors are mainly located the boundaries of refined icosahedral triangular cells, and that of all optimization grids are mainly located on the icosahedral triangular boundaries. In OURS grid, there are some fluctuations near icosahedral vertices and the middle part of boundaries, grids’ error in these regions are smaller than that of HR grid. In addition, the error range of OURS grid is the smallest among all grids, and it has been narrowed to 84.81% of NOPT grid and 12.00% of HR grid.

3.3. Discussion

The raw grid (non-optimized grid) has been optimized by the proposed method. The area quasi-uniformity can be achieved by minimizing the grid area deviation cost, which improve the smoothness of grid area deviation to some extent. Although the grid area range of OURS grid is comparable to those of Heikes and Randall grid, the deformations of grid area and intervals of OURS grid are smoother, which is conducive to error control in simulation. In addition, the maximum error and RMS error of discritization of Laplacian operator have been decreased and converged as the resolution increases.

The grid quality is one of the aspects affecting the simulation accuracy. There is no high gradient of grid area and interval deformation in the optimized grid by our method, which can be helpful to improve the accuracy of discritization of Laplacian operator. A more extensive analysis of Laplace operator in a diffusion problem and some numerical experiments in terms of the accuracy and the numerical efficiency will be carried out in the future.

4. Conclusions

In this study, an overall uniformity and smoothness optimization method of the spherical icosahedral grid has been proposed based on the optimal transportation theory. The effectiveness of the proposed method was evaluated for grid uniformity and smoothness and the following conclusions may be drawn: (1) the area uniformity measured by the ratio between minimum and maximum grid area has been improved by 22.6% (SPRG grid), 38.3% (SCVT grid) and 38.2% (XU grid), and can be comparable to the HR grid. The interval uniformity has also been increased by 2.5% (SPRG grid), 2.8% (HR grid), 11.1% (SCVT grid) and 11.0% (XU grid). (2) the smoothness of grid area deformation measured by the number of grids with grid area deviation of less than 0.05% has been enhanced by 79.32% (HR grid) and more than 90% compared to the SPRG grid, SCVT grid and XU grid. The smoothness of grid length deformation has also been increased by 24.07% (HR grid) and more than 75% compared to other three grids. Although the uniformity of grid optimized by the proposed method is comparable to the HR grid, the smoothness of grid deformation is improved. In addition, the average accuracy of Laplacian operator is slightly better than the HR grid.

In this study, we only evaluated the geometric uniformity of the optimized grid, and the truncation error of Laplacian operator. Future work will focus on the accuracy of Laplacian operator of different grids in a diffusion equation problem and some numerical experiments in terms of the accuracy and the numerical efficiency.