Abstract
In recent years, frequent severe haze weather has formed in China, including some of the most populated areas. We found that these smog-prone areas are often relatively a “local climate” and aim to explore this series of scientific problems. This paper uses remote sensing and data mining methods to study the correlation between haze weather and local climate. First, we select Beijing, China and its surrounding areas (East longitude 115°20′11″–117°40′35″, North latitude 39°21′11″–41°7′51″) as the study area. We collected data from meteorological stations in Beijing and Xianghe from March 2014 to February 2015, and analyzed the meteorological parameters through correlation analysis and a grey correlation model. We study the correlation between the six influencing factors of temperature, dew point, humidity, wind speed, air pressure and visibility and PM2.5, so as to analyze the correlation between haze weather and local climate more comprehensively. The results show that the influence of each index on PM2.5 in descending order is air pressure, wind speed, humidity, dew point, temperature and visibility. The qualitative analysis results confirm each other. Among them, air pressure (correlation 0.771) has the greatest impact on haze weather, and visibility (correlation 0.511) is the weakest.
1. Introduction
With the progress of technology and industry development, the term “haze” has gradually entered the news media’s vision and the general public in recent years. Haze often occurs when dust and smoke particles accumulate in relatively dry air. In recent years, with the frequent occurrence of haze weather, people’s health, daily life, production, and labor have been affected to varying degrees [1,2,3,4,5]. Due to the increasingly severe air pollution, the number of haze days in China has increased. As a result, China’s Meteorological Bureau has added haze in the severe weather warning and forecast [6,7,8,9,10].
In the current studies of haze weather impact factors, they use source analysis technology to analyze. Analytical technology includes two aspects: the source diffusion model and receptor model, including a diffusion model based on pollution sources as the research object, due to the diffusion model needing to know the advanced list of sources of pollution, thus to some extent hindered its application in the field of haze weather factor [11,12]. The receptor model is based on contaminated areas. The source analysis technology can obtain the types, chemical component characteristics, and contribution of different pollution sources in the haze. The influence degree of each impact factor on haze weather can be measured accordingly. The receptor model can be subdivided into two different methods: chemical method and microscope method [13,14,15,16,17], in which the chemical method also includes enrichment factor method, chemical mass balance method, factor analysis method, UNMIX model, and rough set theory [18,19,20,21]. Although a small part of research on haze factors has adopted the microscope method, the chemical method in the receptor model is more widely used in researching haze impact factors.
Globally speaking, there are still few studies on particulate matter impact factors using the microscope. As a result, many scholars are still more inclined to focus on the conservation of chemical mass and combine mathematical statistics with chemical methods to study haze impact factors.
The scholars [22] adopted the chemical mass balance method to conduct the research. They determined that the main influencing factors of atmospheric particulate matter in cities Zhejiang Province were urban dust and motor vehicle exhaust. Lu et al. [23] used a chemical transport model to investigate the response of secondary inorganic aerosols (SIA) to chemical processes and their precursor emissions over northern and southern city-clusters of China in January 2014. Unexpectedly, SIA concentrations with low precursor emissions were much higher over the southern regions than those over the northern region with high precursor emissions, based on ground observations and high-precision simulations.
The factor analysis model is another method widely used in haze research. The main principle is to extract the common factor in variable data and then calculate the load by correlating the chemical composition of particulate matter. Based on factor weight and knowledge of characteristic elements, the influence degree of each factor in the particulate matter on haze weather is judged. Taking four Chinese cities (Beijing, Tianjin, Shanghai, and Chongqing) as examples [24], Yao et al. studied the reasons for fog and haze caused by multi-factor coupling. Firstly, the contribution of four factors to fog and haze in Tianjin was analyzed. Then, these four cities were compared to explore the impact of the same factor on fog and haze in different regions. Secondly, the functional relationships between these four factors and the air quality index (AQI) were obtained based on statistical data. Finally, a sensitivity analysis was carried out to get the dominant factor of fog and haze in these four cities. Gan et al. [25] used 287 cities’ panel data from 1998 to 2016, and PM 2.5 represents haze pollution. The spatial Durbin model explores the role of the economy and population agglomeration on smog pollution. Wu et al. [26] propose using the improved method of the degree of grey slope incidence to analyze the weight factors of the effects of haze on irradiance. The exponential-linear model is used to describe the impact of haze on the amount of irradiance.
The UNMIX model, enrichment factor method, and rough set theory in the chemical method have also made corresponding contributions to the study of influence factors of particulate matter. Zheng et al. [27,28] analyzed the source of haze. They found the classification relation of the element content of haze particles. Thus, they could determine the impact of emission sources on haze weather.
In addition to using a single model for the study of particulate matter, the above methods can also be combined to discuss the impact factors of particulate matter. For example, to quantify regional sources contributing to submicron particulate matter (PM1) pollution in haze episodes, Tang et al. [29] conducted online measurements combining two modeling methods, namely, positive matrix factorization (PMF) and backward Lagrangian particle dispersion modeling (LPDM), for one month in urban Nanjing, a city located in the western part of Yangtze River Delta (YRD) region of China. When Baosheng Z. et al. [30] studied the haze particles, they adopted diffusion and comprehensive receptor models. They found that the coking, sintering, and smelting dust sources of iron and steel had the most significant impact on the haze particles influencing factors. Cai et al. [31] calculated and decomposed the regional differences of haze pollution intensity distribution in China using the index method. At the same time, they established the convergence model of haze pollution intensity to test the regional differences of haze pollution intensity distribution in China.
At present, there are many kinds of research on haze particulate matter around the world, but these researches have their limitations. For example, the diffusion model takes the pollution source as the research object. Using the WRF-FLEXPART atmospheric diffusion model, He et al. [32] simulated the pollutant diffusion processes of two steel industries from October 2018 to March 2019 in Caofeidian district, and then analyzed the pollutant diffusion characteristics, the impacts of atmospheric circulation and local circulation on pollutants diffusion, the contribution of steel industry emissions on air quality nearby emission sources and air quality observation stations. As the diffusion model needs to know the list of pollution sources in advance, its application in haze weather impact factors is hindered to some extent [11].
The method of studying haze pollution through satellite data has also been widely used in academia [33]. Sorek-Hamer et al. [34] proposed the strategy of using satellite products to simulate PM2.5 and short-term pollution events in 2020. Mishra, R.K. et al. [35] uses Landsat 8 satellite data to predict the ground PM2.5 concentration in Delhi.
The pollution source determines the formation of haze weather. It is closely related to the meteorological parameters of the research area during the research time in certain factors. Meteorological parameters have an impact on the dispersion and transformation of pollutants in the atmosphere. Under relatively stable pollution sources, meteorological parameters are an essential factor for aerodynamics studying haze weather.
This paper studies the influencing factors of haze weather starting from the influence of aerodynamics and meteorological conditions. First, through the correlation analysis between the hourly concentration difference data of the smog component PM2.5 (the difference between the observation points in the main urban area and the observation points in the outer suburbs) and the meteorological factor data difference (the difference between the observation points in the main urban area and the observation points in the outer suburbs), we get the influence relationship between the temperature difference, humidity difference, dew point difference, wind speed difference, and PM2.5 difference. Then, using gray correlation analysis from the perspective of multi-factor interaction, it is found that the impact of each indicator on PM2.5 from large to small is air pressure, wind speed, humidity, dew point, temperature, and visibility. This result mutually confirms the results of qualitative analysis.
2. Data and Study Area
In this paper, Beijing and its surrounding areas (115°20′11″–117°40′35″, 39°21′11″–41°7′51″) were selected as the study area. In addition, two meteorological stations (urban station and Xianghe station) were selected. The monitoring data are divided into eight categories: air temperature, air pressure, evaporation, precipitation, wind speed and direction, sunshine duration, 0 cm ground temperature, and relative humidity. Limited by monitoring conditions, only Beijing and Xianghe stations had continuous AOD detection values in the study area.
As a whole, the selected study area is flat in the southeast and higher in the northwest. Beijing in the study area is located at the junction of plain and mountain terrain, surrounded by mountains in the west, north, and northeast. The plain facing Bohai Sea in the southeast constitutes a special terrain of sea back mountains. Its climatic conditions are short in spring and autumn, high temperature and rainy in summer, cold and dry in winter, characterized by a warm temperate sub-humid continental monsoon climate.
In this paper, the data were selected from the temperature, humidity, dew point, wind speed, and PM2.5 concentration of Beijing urban area and Xianghe monitoring station at 10 and 16 o’clock every day from March 2014 to February 2015. Since grades monitor the observed values of wind speed indicators, a random number method is adopted to preprocess them according to the wind speed range represented by each grade.
Source of data set: daily observation data set of China Meteorological Element station, resource and environmental science data center of Chinese Academy of Sciences (https://www.resdc.cn/data.aspx?DATAID=230, accessed on 10 October 2016).
3. Methods
This section introduces the spatial autocorrelation method and the gray correlation analysis model, which are used to analyze the influence of meteorological factors on the haze in the study area.
3.1. Spatial Autocorrelation
The research entities are interrelated, and the degree of such association is gradually enhanced with the shortening of distance [36]. Haze weather also follows the first law of geography. The haze weather in the research area will be spatially affected by the surrounding area.
Spatial autocorrelation refers to the correlation and dependence between a unit of a research area and the observed data of the surrounding area within a specific research area, which can generally be divided into global spatial positive correlation and local spatial positive correlation. At the same time, spatial autocorrelation can be divided into positive and negative correlations [37,38,39].
Global Spatial Autocorrelation
Global autocorrelation refers to the spatial patterns and characteristics of the research parameters reflected in the whole research area. In the study of this section, we choose the most common Moran’s I index to represent the changes of global spatial autocorrelation characteristics in the study area.
Moran’s I index represents the similarity of research parameters in adjacent regions in space in the research area, similar to the correlation coefficient. The range of this index is (−1, 1). When the index range is (0, 1), then the research area in the whole research space for positive correlation, and the index value is close to 1, the stronger the positive correlation, namely the research area of observation properties displayed on the spatial pattern of “the areas surrounding the high concentrations of pollutants-high concentrations of pollutants” (later referred to as “high-high”) “the areas surrounding the high concentrations of pollutants-high concentrations of pollutants” (hereinafter referred to as “low-”) after the agglomeration pattern; When the index range of (1, 0), then the research area in the whole research space for negative correlation, and the index value, the closer to 1, the stronger the negative correlation, the observed attributes of the study area in the whole space pattern present in high concentrations of pollutants—“study area around the low pollutant concentration” (later referred to as “high-low”) research area pollutant concentration low-high concentrations of pollutants around “(later referred to as “low-high”)” of agglomeration pattern; if the index is 0, then there is no autocorrelation. Global autocorrelation Moran’s I index calculation Formula (1) as shown below:
In the formula, I is the global autocorrelation Moran’s I index, is the observed value in the study area, is the spatial weight matrix, , .
The calculated global autocorrelation Moran’s I index must also be tested, as shown in Formula (2), where Z is a standardized statistic.
If the null hypothesis is Y, there is no autocorrelation between all the study parameters in the study area. Calculate the standardized statistic Z to test the significance of Y.
3.2. Grey Relational Analysis Model
Grey relational analysis belongs to the grey system, which means to quantitatively analyze the development trend of the dynamic process and judge the degree of correlation by comparing and analyzing the correlation of the change of factor curve. The closer the change rate and direction of the experimental sequence and the theoretical curve are, the more significant the correlation between the experimental sequence and the theoretical value will be. Thus, many factors cause the increase of haze weather frequency, and the secondary and primary factors can be identified through gray correlation analysis.
In order to find out the main influence factors and the interrelation of each factor, we need to analyze the distance between comparison sequence and reference sequence by grey correlation and then determine the difference and relation between them.
When gray correlation analysis is adopted, the system characteristic sequence can be expressed as Equation (3) [37]:
The correlation factor sequence is as Equation (4):
Firstly, dimensionless processing is applied to the sequence of related factors and system feature sequences. is used to represent the grey relational degree of and , and is used to represent the correlation between and in as shown in Equation (5):
Any two behavior sequences correlate with the gray system, therefore
When = , gamma . The grey relational degree varies with different environments, so it may not satisfy the principle of symmetry. Then, we have Equations (7) and (8).
where
However, for the grey correlation set with only two sequences, the sequences are more symmetric, as Equation (9):
According to the above principle, the grey relational degree of two sequences is closely related to the closeness of sequence curves. According to the basic principle of grey relational analysis, the grey relational degree depends on the closeness of two sequence curves. The smaller is, the larger is. Equation (10) is the calculation of the correlation coefficient:
Write , then we can get Equation (11)
where ρ represents the resolution coefficient, which generally varies with the specific situation. When less than or equal to 0.5463, take ρ = 0.5, at which point the best resolution is obtained.
4. Results
4.1. Correlation Analysis of PM2.5 and Aerodynamic Factors
Due to the dimensionality of significant differences among all kinds of data, Formula (12) is first used to normalize the data. At the same time, considering that a large number of point data are used in the analysis, we set the sliding step K to process the mean value of the original point data. First, we calculate the mean value of K with K as the count. Then, we take the mean value successively increasing to form a series of continuous observation mean values. In this section, we take the step size K = 35.
4.1.1. Temperature Difference
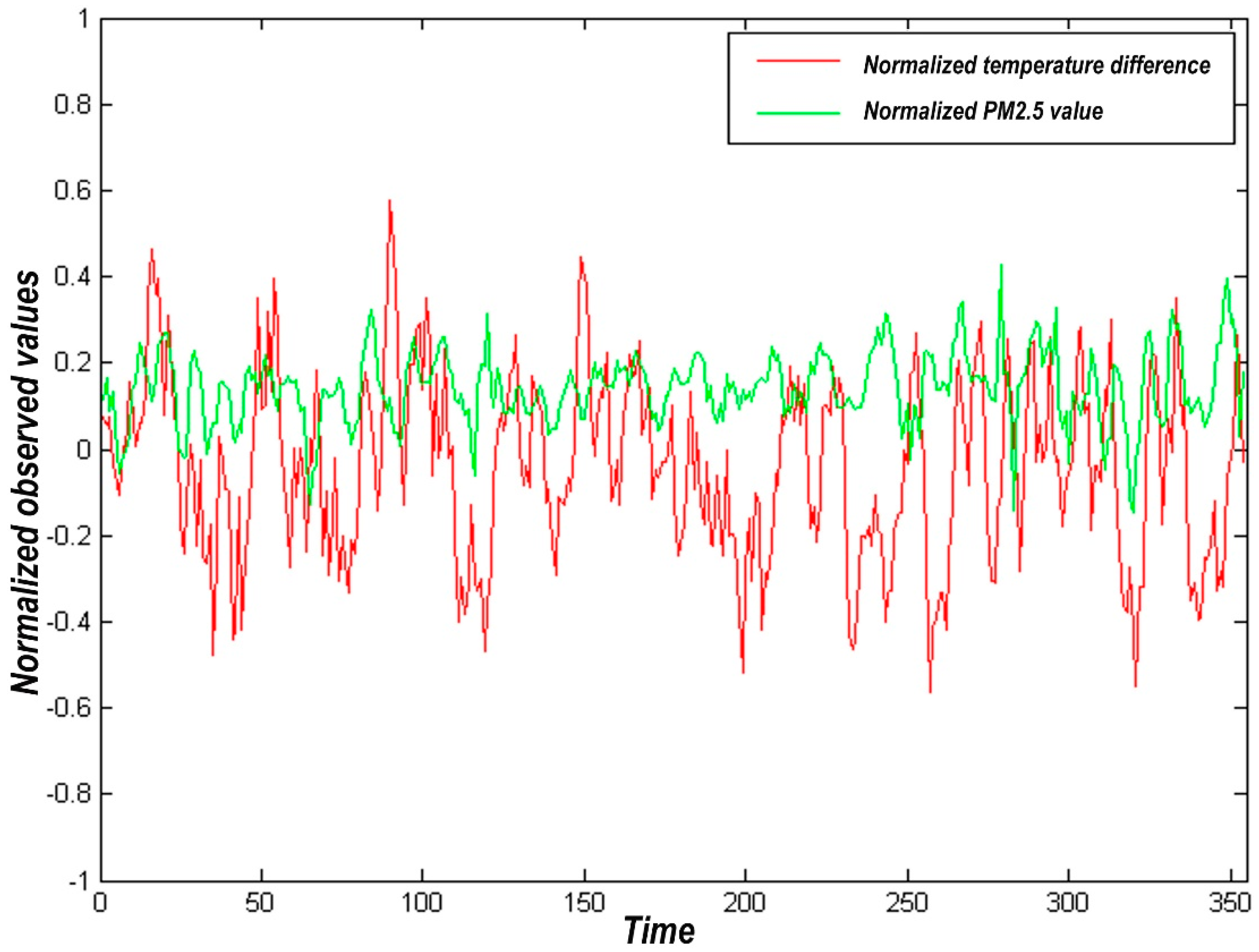
Usually, there is no direct physical correlation between PM2.5 and air temperature. The correlation between air temperature and haze weather affects the migration and diffusion of PM2.5 by affecting atmospheric stability. The exchange intensity between upper air and lower air increases with the increase of atmospheric temperature. The concentration of PM2.5 also decreases with the increase of its diffusion in the vertical direction of the atmosphere. Conversely, the concentration of PM2.5 increases as its diffusion decreases. The correlation between temperature difference and PM2.5 difference is shown in Figure 1.
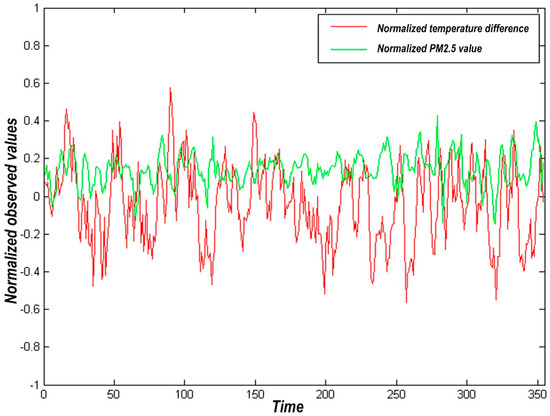
Figure 1.
Correlation between temperature difference and PM2.5 difference.
As shown in Figure 1, the correlation analysis of the difference between the temperature and PM2.5 data collected by the two stations in the study area (data collected by the urban stations minus data collected by the Xianghe station) shows that the correlation coefficient R = 0.1334, showing a weak positive correlation between the two. The main reason is that the concentration of inhalable particulates in the atmosphere is different from the optical thickness of aerosol. Furthermore, the concentration of inhalable particulates is also related to other characteristic weather in the study area (Beijing) and specific human activity factors, such as sand-prone weather in Beijing in spring and central heating in autumn and winter. In addition, the annual general temperature of urban stations is higher than that of suburban stations, and the PM2.5 concentration detected by urban stations is also higher than that of suburban stations in most of the study time.
4.1.2. Dew Point Difference
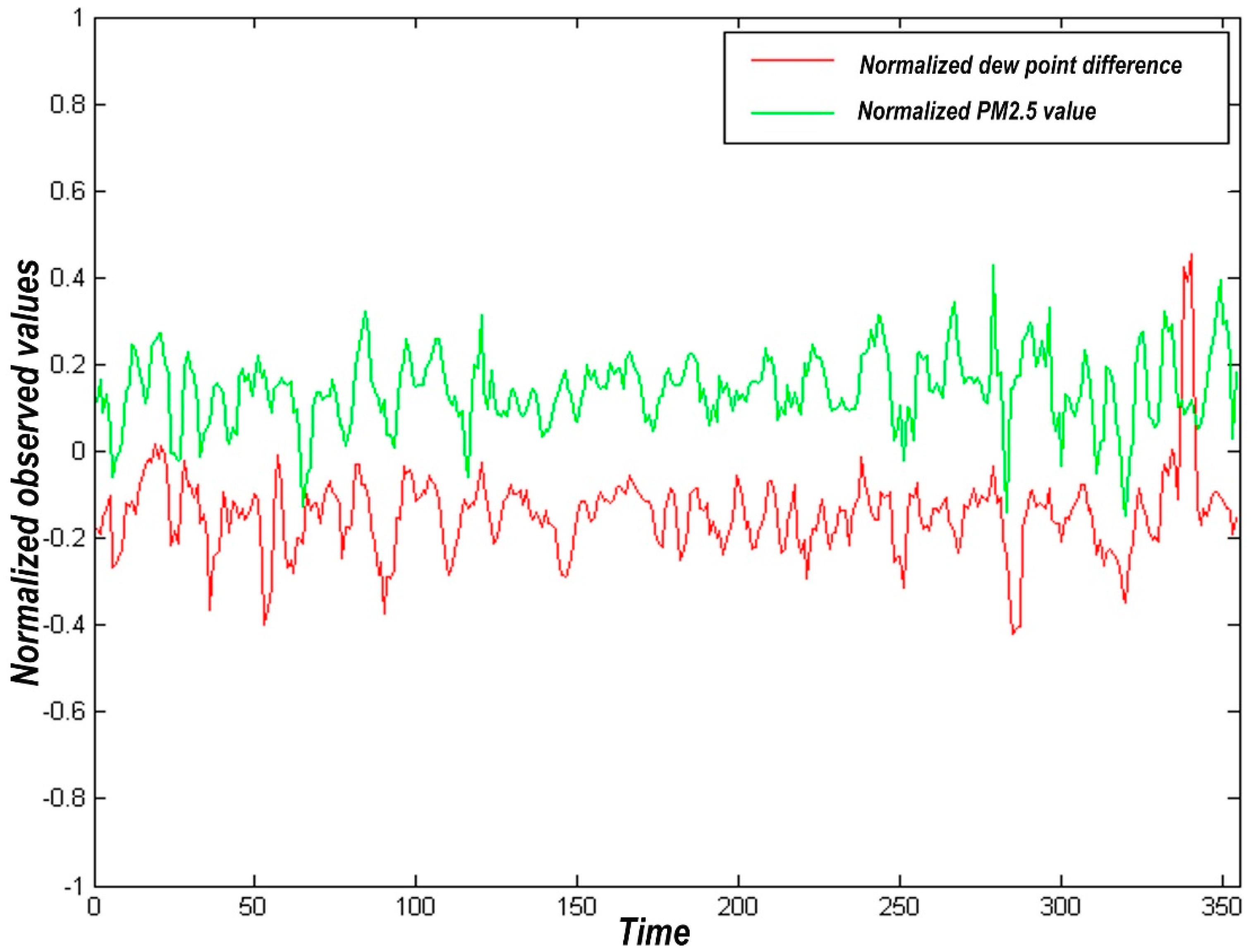
When the pressure is fixed, the temperature at which gaseous water in the atmosphere is converted to a liquid state by saturation is the dew point. The dew point is often associated with relative humidity, and the dew point approaches the temperature gradually with the increase of relative humidity. Thus, when the dew point is constant, the temperature is inversely proportional to the relative humidity. The correlation between the dew point difference and PM2.5 difference is shown in Figure 2.
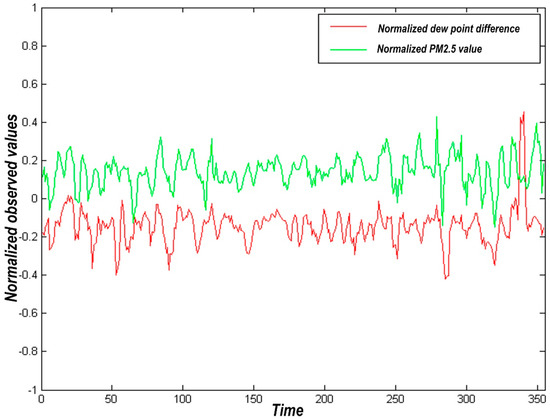
Figure 2.
Correlation between dew point difference and PM2.5 difference.
By observing Figure 2, the law of dew point and PM2.5 concentrations are relatively significant, with the correlation coefficient R = 0.3046, which may be due to the effect of this factor and other parameters on pollutant concentration.
4.1.3. Humidity Difference
In aerodynamics, humidity is a measure of the amount of water vapor in the atmosphere. Generally, low atmospheric humidity means that the weather is clear and the air is dry, the atmosphere is stable, the diffusion is poor, and the concentration of PM2.5 tends to be high. Conversely, higher air humidity leads to a decrease in PM2.5 concentrations. The analysis results in this section are not consistent with this. However, some studies also believe there is a positive correlation between PM2.5 concentration and humidity, with the correlation coefficient R = 0.3128. In this regard, we make the following analysis:
- Humidity influences the diffusion and migration of PM2.5 and the composition of PM2.5.
- When the composition of PM2.5 is different, humidity has different effects on its concentration. Secondary particles such as nitrate and sulfate are more likely to be generated when humidity is high. Some studies have pointed out that the culprit for haze weather is such secondary particles.
- When the atmospheric state is relatively stable, water vapor in the high-humidity atmosphere is adsorbed on the suspended PM2.5, causing haze weather.
- The influence of humidity on PM2.5 concentration exists complex and different mechanisms in different threshold ranges.
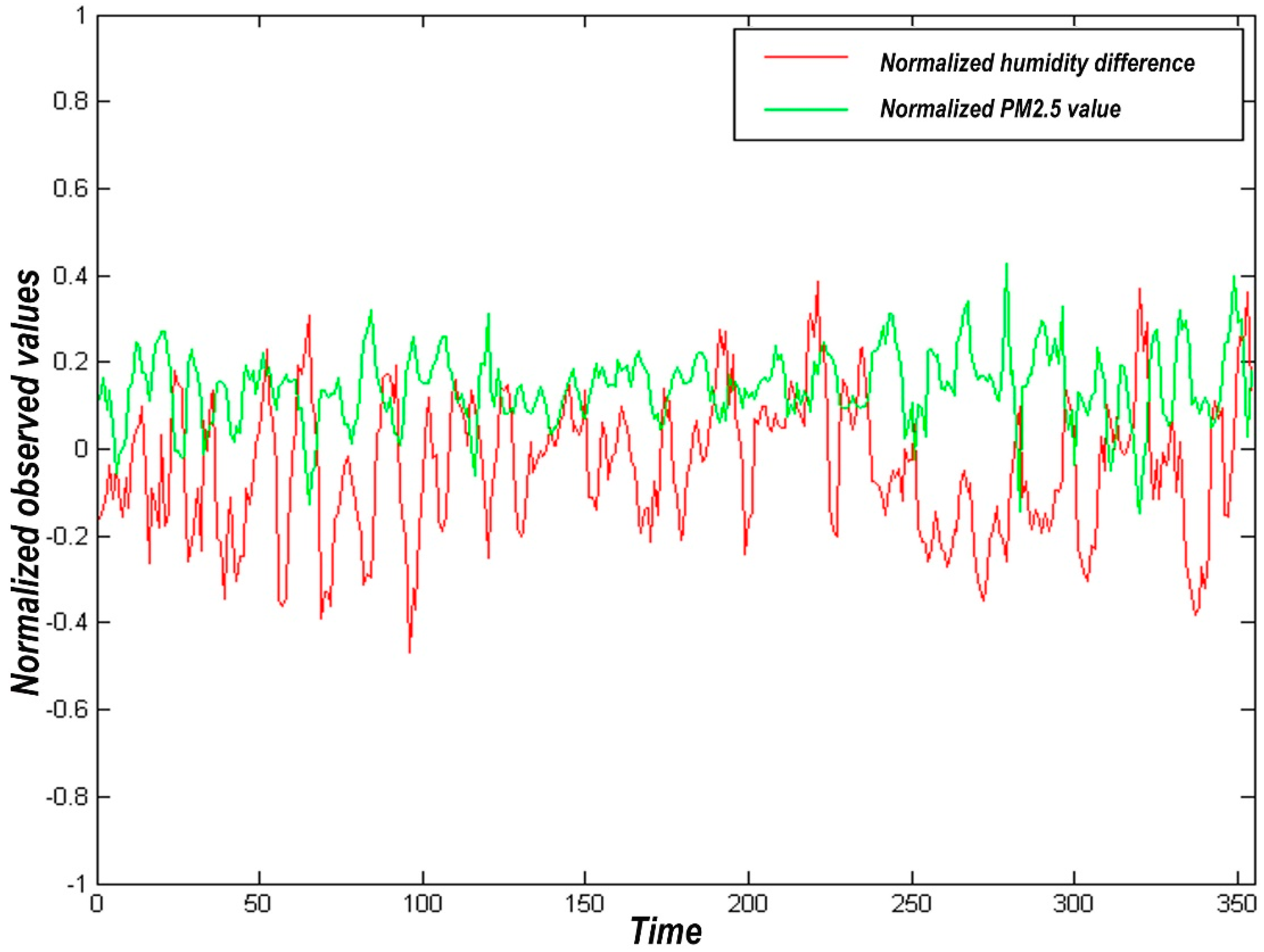
Then, we made the humidity difference according to the different humidity of the two stations and made a correlation analysis with the corresponding difference of PM2.5 to further analyze the correlation between local climate and haze weather. The correlation between humidity difference and PM2.5 difference is shown in Figure 3.
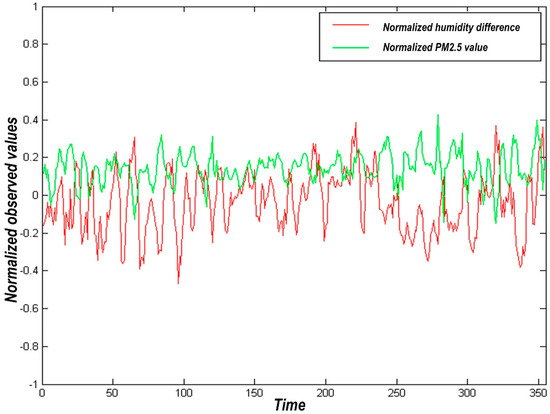
Figure 3.
Correlation between humidity difference and PM2.5 difference.
In Figure 3, the correlation analysis of the difference between the humidity and PM2.5 data collected by the two stations in the study area shows the correlation coefficient R = 0.3128, showing a positive correlation between the two. The difference in humidity showed that it increased to the peak and immediately began to decline within the whole year. The concentration of particulate matter fluctuated within the range of higher values throughout the year. In the early summer, the difference of PM2.5 gradually decreases and then starts to rise again after the end of summer. Since then, humidity difference data and particulate concentration values show a trend of up and down oscillation.
4.1.4. Wind Speed Difference
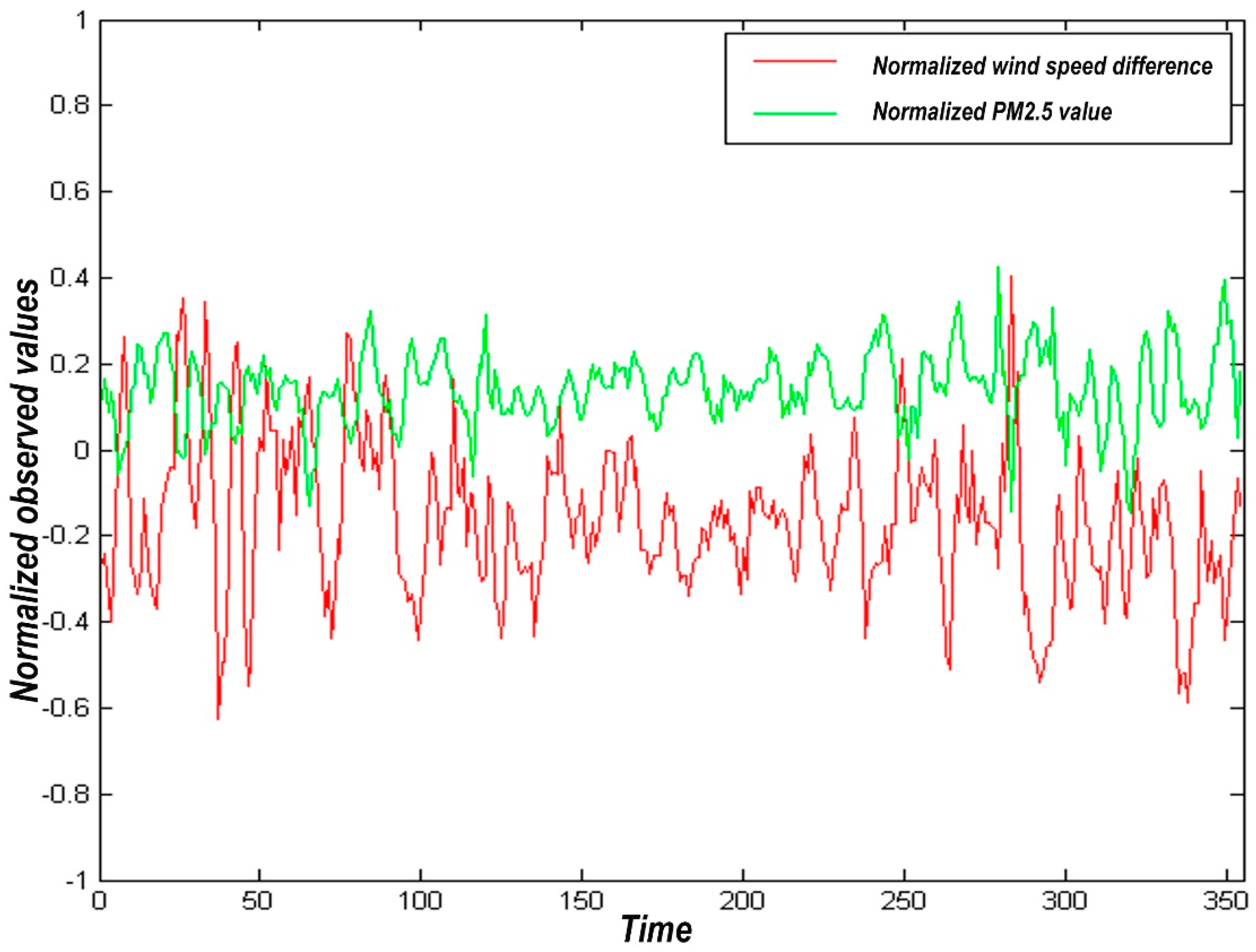
From the perspective of aerodynamics, the essential factor affecting PM2.5 is wind speed. In contrast, other factors affect it through wind speed, manifested as diffusion, transmission, and re-dusting. With the enhancement of wind speed, the PM2.5 concentration increases. In diffusion and dilution, the concentration of PM2.5 decreases. On the contrary, a large amount of PM2.5 is easy to gather under the condition of low wind speed, forming haze weather. However, when the wind speed is in a higher range, the PM2.5 that sinks on the ground will be blown up again, forming a re-dusting effect. The correlation between wind speed difference and PM2.5 difference is shown in Figure 4.
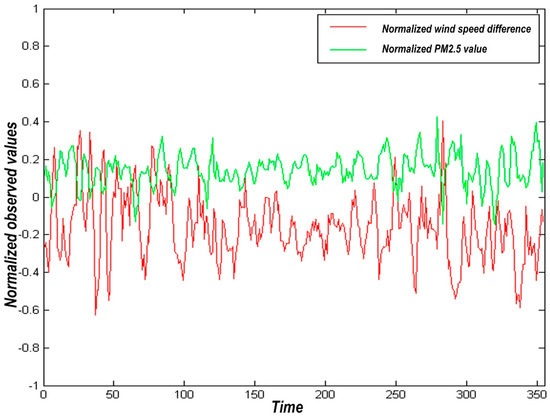
Figure 4.
Correlation between wind speed difference and PM2.5 difference.
Correlation analysis of the difference between wind speed and PM2.5 data collected by two stations in the study area (data collected by urban stations minus data collected by Xianghe station) shows a strong positive correlation between the two, with the correlation coefficient R = 0.3456. As shown in Figure 4, the wind speed difference fluctuates back and forth throughout the year. Meanwhile, the difference of PM2.5 concentration increases with the increase of wind speed. In other words, when the urban wind speed is high, the concentration of PM2.5 is relatively low. Conversely, the concentration of PM2.5 is relatively high when the urban wind speed is low.
4.2. Grey Correlation Analysis of PM2.5 and Aerodynamic Factors
The above uses a variety of impact factors to analyze the correlation between local climate and haze weather. Next, we study the most critical and meteorological factors that can most affect haze weather.
Different ground meteorological impact factors have different aerodynamic principles on PM2.5, which results in their varying degrees of influence on PM2.5. This section uses the grey correlation method to analyze the joint influence of humidity, air pressure, wind speed, dew point, temperature, and visibility on PM2.5 concentrations. The system’s characteristic sequence and influencing factor sequence are, respectively, hourly concentration of PM2.5 and the observed values of humidity, air pressure, wind speed, dew point, temperature, and visibility in the same period. After considering the dimensionality of the significant difference between the data, Formula (15) was used to conduct range normalization processing of the data before analysis.
4.2.1. Grey Correlation Analysis Based on Time Window
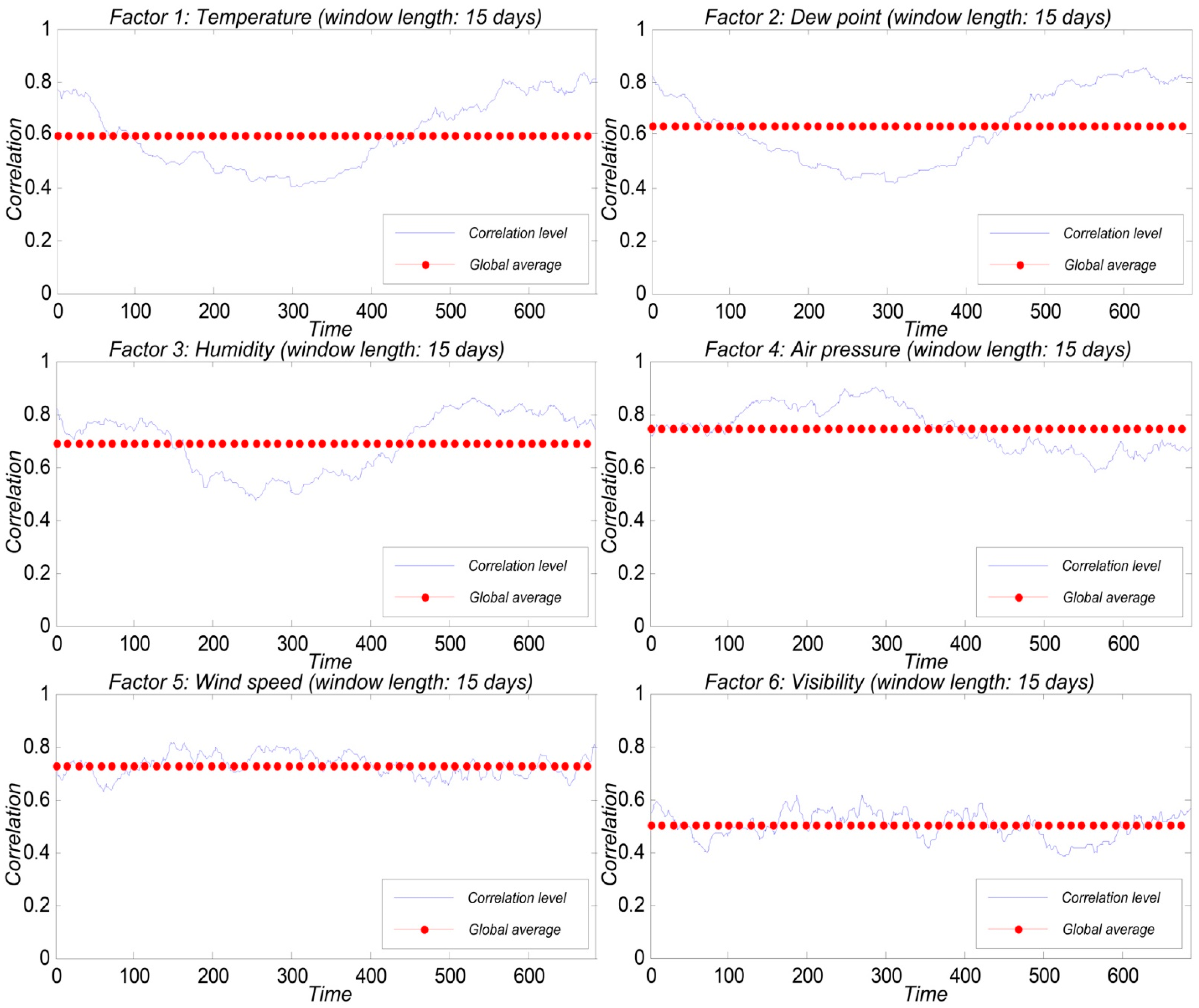
After analysis, we found that the influence of various parameters on the concentrations of PM2.5 in different seasons is not consistent, so in this section, we use “time window value” grey correlation analysis: specify the first gray analysis sample size K as “time window”, starting from the first observation, with K as the sample size calculation correlation K1, again from the second set of observations, in turn, calculating correlation K2, and then through the analysis of (K1 Smoothing and mean processing of correlation degree sequence of Kn). Finally, the average value of the daily data of the two stations is taken as the meteorological parameter. Then, the correlation analysis between each meteorological parameter and PM2.5 is carried out based on the grey correlation of the time window, as shown in Figure 5.
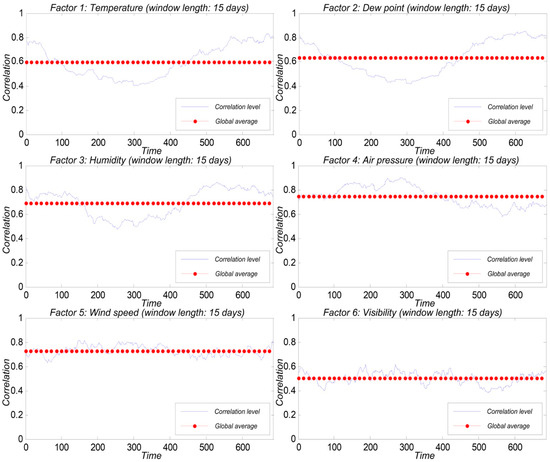
Figure 5.
Grey correlation analysis of time window between meteorological parameters and PM2.5.
In the whole year, the influence of temperature on PM2.5 concentration fluctuates greatly, manifested as a strong influence in spring and winter, gradually increasing influence in autumn with the decrease of temperature and low influence in summer. Among the four seasons, the influence degree of winter is the highest.
Among the remaining factors, the influence of dew point on PM2.5 is close to the temperature, shows strong influence in spring and winter, and low influence in summer. The influence of humidity on PM2.5 concentrations is shown as a sharp weakening and strengthening in late spring and early autumn, while it is always in a high influence area in spring. The influence of air pressure on PM2.5 concentration fluctuates greatly. Spring and summer are always within the high influence range. As the temperature drops into autumn and winter, the influence degree gradually falls into the low-value region. The influence of wind speed on PM2.5 concentration has no significant difference with seasonal changes in the whole year. It is always in the high influence area, with an average of around 0.7 and slightly higher than the other three seasons in summer. Visibility has a different effect on PM2.5 concentrations than other aerodynamic factors: the level of PM2.5 concentrations directly affects visibility. However, visibility does not directly affect the concentration of PM2.5, and visibility appears only as a metric. Therefore, its influence on PM2.5 concentration ranks the last and only fluctuates within the range of 0.5 in the whole year.
4.2.2. Average Grey Correlation
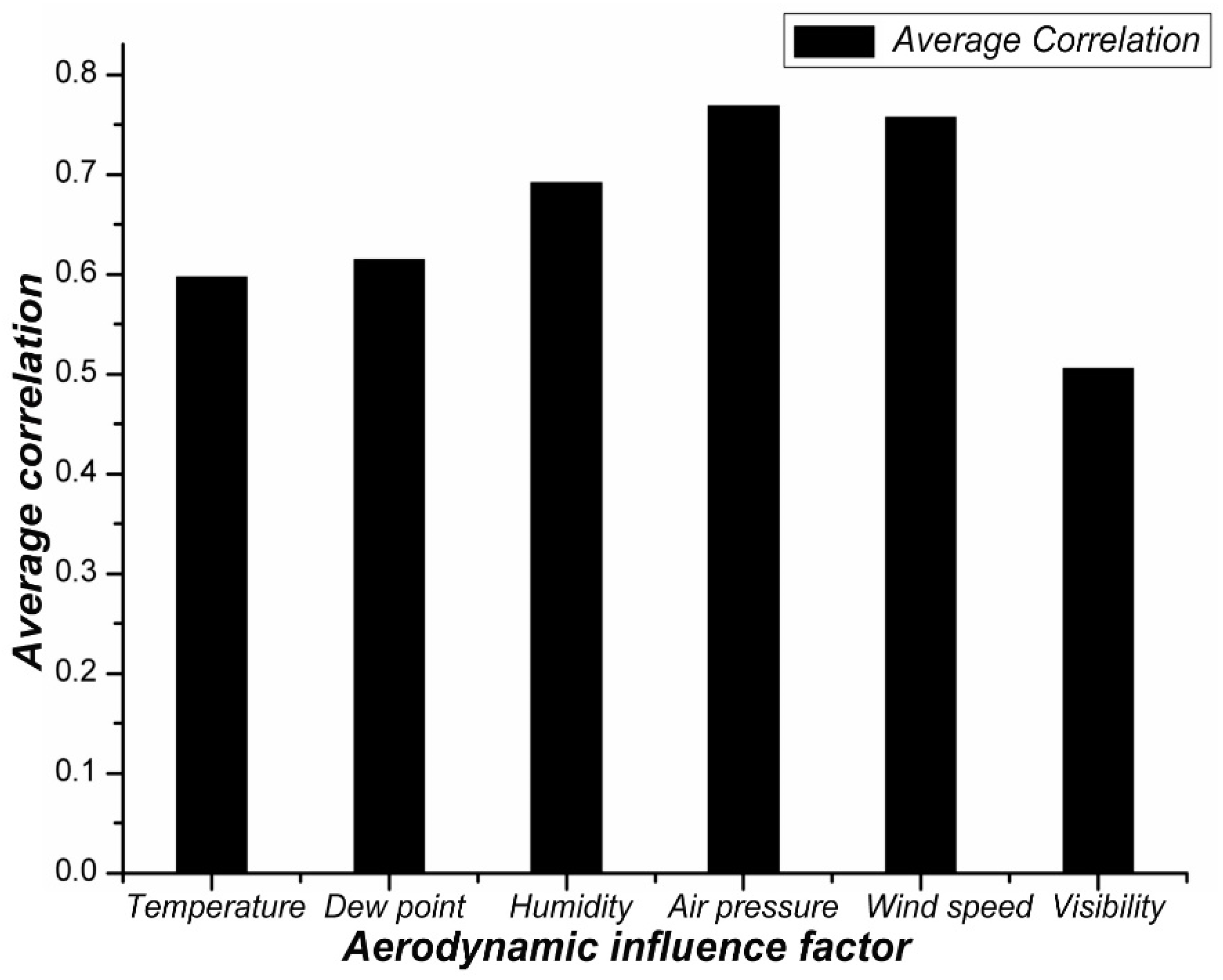
In order to calculate the degree of influence of various meteorological parameters on haze weather, the grey correlation method was used to calculate the correlation degree, which were R1 = 0.587 (temperature), R2 = 0.621 (dew point), R3 = 0.689 (humidity), R4 = 0.771 (pressure), R5 = 0.762 (wind speed), and R6 = 0.511 (visibility). Figure 6 shows that haze weather strongly influences air pressure and wind speed, and the weakest correlation between visibility.
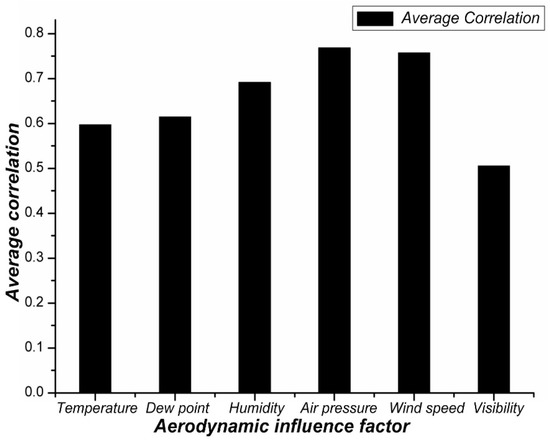
Figure 6.
Correlation between meteorological parameters and PM2.5 average.
Air pressure had the most potent effect on PM2.5 concentrations, but this was not consistent with previous single-correlation analyses. From the perspective of aerodynamics, atmospheric pressure is closely related to the stability of the atmospheric structure. When low pressure plays a leading role, the airflow rises, pushing the low-pressure center with the surrounding high pressure. At this time, the atmosphere is extremely unstable and prone to strong wind speed, promoting the diffusion of PM2.5. On the contrary, it is not conducive to the dilution of PM2.5 in the atmosphere and a relatively high concentration, causing haze weather.
Wind speed is the leading cause of PM2.5 dilutions, diffusion, and re-dust, and its influence on PM2.5 concentrations is also complex. When the wind speed is low, PM2.5 gradually spreads, and the concentration decreases due to the push of the wind. However, when the wind speed exceeds a specific range, PM2.5 is picked up again by the strong wind. As a result, it enters the atmosphere, resulting in higher concentrations and haze whether—the correlation between the two changes into a positive correlation.
The effect of humidity on PM2.5 concentrations is more complicated than that of wind speed. At present, there are two opinions: first, a large amount of precipitation caused by high humidity will significantly reduce the concentration of PM2.5 in the atmosphere due to the scouring effect, presenting a negative correlation; on the other hand, sulfate and nitrate and other secondary particles are generated in large quantities with higher air humidity, which plays a significant role in promoting the formation of haze weather, showing a positive correlation.
Temperature acts on the horizontal and vertical diffusion of PM2.5 in the atmosphere through its influence on atmospheric stability. In particular, when there is a temperature inversion phenomenon of low temperature on the lower ground and high temperature on the upper, the vertical movement of the atmosphere almost stops. PM2.5 agglomerates in one place and causes haze weather. When temperatures are low in winter, heavy coal consumption is also a significant source of PM2.5.
5. Discussion
This study takes Beijing as the main object. It uses grey relational analysis model to study the correlation of meteorological parameters to haze weather and local climate. Based on aerodynamics and data mining methods, we analyze the four meteorological data (temperature difference, dew point difference, humidity difference, and wind speed difference) in the local climate to comprehensively study its relevance and relevance to haze weather. By analyzing and calculating the correlation coefficient between the variation trend chart of meteorological parameters and PM2.5 difference, we found a weak positive correlation between temperature, dew point, and PM2.5 concentration. There was a strong positive correlation between humidity difference, wind speed difference, and PM2.5 concentration difference. The haze weather is most affected by air pressure and wind speed, mainly on the diffusion of inhalable particles. The haze weather’s weakest degree of influence is visibility. The correlation between the analysis and PM2.5 concentration difference is not listed separately because the atmospheric pressure difference is insignificant in the local climate.
This paper takes Beijing as the main object, using remote sensing methods, spatial autocorrelation, gray correlation analysis, and other methods to study the correlation between haze weather and local climate. However, due to limited conditions, there are still many shortcomings in the research process, and we will continue to improve these shortcomings in the future:
- The research mainly focuses on PM2.5, but NOx is also an essential part of the haze pollution components. As accurate data cannot be obtained in this paper, the analysis of this influence factor is abandoned. However, with the escalation of environmental monitoring in my country, we will continue participating in NOx research [37].
- In future research, we will try to use the technology of combining PM2.5 and satellite data [31,32,33,34,35,36,40] to obtain data, and study the correlation of more factors with PM2.5.
- This article analyzes the impact of human activities on smog pollution. However, there is a lack of in-depth discussion on developing the social economy rationally, and further research is needed in future research [41].
6. Conclusions
This paper analyzes various meteorological data in the local climate and studies its relevance to haze weather based on aerodynamics. Using the data mining method, this study starts with the hourly concentration data of PM2.5 and conventional meteorological data, avoids the more complex process of chemical experiment in the general haze research, saves a lot of time.
Through the analysis of the change trend graph of the difference of various meteorological parameters and the difference of PM2.5 and the calculation of its correlation coefficient, we found that there is a weak positive correlation between the temperature difference, the dew point difference, the PM2.5 concentration difference, the humidity difference, and wind speed difference, and there is a strong positive correlation between the difference in PM2.5 concentrations. Therefore, the grey correlation analysis is carried out again. The strongest influence on haze weather is air pressure and wind speed, which mainly affect the diffusion of inhalable particles. The weakest influence on haze weather is visibility. As there is little difference in air pressure in the local climate, the correlation between the analysis and the difference in PM2.5 concentrations are not separately listed.
Compared with traditional mathematical statistical methods such as variance analysis, regression analysis, and principal component analysis, grey relational analysis has the following characteristics:
- (1)
- The requirements for the amount of data are broad. The gray relational analysis can use fewer data to obtain relevant results. The minimum amount of data that can be calculated is 4, which can be applied to irregular random data.
- (2)
- Traditional methods such as analysis of variance have requirements for the sequence itself. For example, the sample sequence must have probability distribution characteristics. There is no correlation between the sequences, which significantly limits the range of sequences that can be analyzed.
- (3)
- Grey relational analysis is relatively concise in modeling, and the amount of calculation is small.
- (4)
- Grey relational analysis has high accuracy and can be highly consistent with the results of qualitative analysis. That is, the quantitative results will fit the objective laws of the system and the interrelationships between elements.
Given the current status of statistical data: the gray scale of the data is large, the amount of data is limited, and there is no typical probability distribution characteristic. Due to the large fluctuations in the data caused by human activities, the effect of using traditional data statistical methods is poor, while the gray correlation analysis can be greatly improved. To overcome the above problems and improve the accuracy of statistical analysis.
Author Contributions
Conceptualization, W.Z. and Y.G.; methodology, J.X. and Z.L.; software, L.Y.; validation, Y.L. and J.T.; formal analysis, Y.L. and S.L.; investigation, J.T.; resources, Z.L.; data curation, J.T.; writing—original draft preparation, Y.L.; writing—review and editing, L.Y.; supervision, W.Z.; project administration, W.Z. and B.Y.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was jointly supported by the Sichuan Science and Technology Program (2021YFQ0003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this paper are obtained from the Chinese Academy of Sciences at https://www.resdc.cn/data.aspx?DATAID=230, (accessed on 10 October 2021). The data is only available under request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, X.; Yin, L.; Yao, L.; Yu, W.; She, X.; Wei, W. Seismic spatiotemporal characteristics in the Alpide Himalayan Seismic Belt. Earth Sci. Inform. 2020, 13, 883–892. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Zheng, W.; Yin, Z.; Song, L.; Ge, L.; Zeng, Q. Fractal dimension analysis for seismicity spatial and temporal distribution in the circum-Pacific seismic belt. J. Earth Syst. Sci. 2019, 128, 22. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Yin, L.; Fan, Y.; Song, L.; Ji, T.; Liu, Y.; Tian, J.; Zheng, W. Temporal evolution characteristics of PM2. 5 concentration based on continuous wavelet transform. Sci. Total Environ. 2020, 699, 134244. [Google Scholar] [CrossRef]
- Zheng, W.; Li, X.; Yin, L.; Wang, Y. Spatiotemporal heterogeneity of urban air pollution in China based on spatial analysis. Rend. Lincei 2016, 27, 351–356. [Google Scholar] [CrossRef]
- Han, Y.; Bandowe, B.A.M.; Schneider, T.; Pongpiachan, S.; Ho, S.S.H.; Wei, C.; Wang, Q.; Xing, L.; Wilcke, W. A 150-year record of black carbon (soot and char) and polycyclic aromatic compounds deposition in Lake Phayao, north Thailand. Environ. Pollut. 2021, 269, 116148. [Google Scholar] [CrossRef]
- Guo, B.; Wang, Y.; Zhang, X.; Che, H.; Zhong, J.; Chu, Y.; Cheng, L. Temporal and spatial variations of haze and fog and the characteristics of PM2. 5 during heavy pollution episodes in China from 2013 to 2018. Atmos. Pollut. Res. 2020, 11, 1847–1856. [Google Scholar] [CrossRef]
- Li, Q.; Xia, M.; Guo, X.; Shi, Y.; Guan, R.; Liu, Q.; Cai, Y.; Lu, H. Spatial characteristics and influencing factors of risk perception of haze in China: The case study of publishing online comments about haze news on Sina. Sci. Total Environ. 2021, 785, 147236. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, S.; Deng, Y.; Zhang, Y.; Yin, L.; Zheng, W. Construction of force haptic reappearance system based on Geomagic Touch haptic device. Comput. Methods Programs Biomed. 2020, 190, 105344. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Huang, W.; Liu, S.; Yang, B.; Zheng, W. Spatiotemporal Analysis of Haze in Beijing Based on the Multi-Convolution Model. Atmosphere 2021, 12, 1408. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, W.; Yin, L.; Zheng, W.; Liu, S. A Haze Prediction Method Based on One-Dimensional Convolutional Neural Network. Atmosphere 2021, 12, 1327. [Google Scholar] [CrossRef]
- Wang, X.; Yin, C.; Shao, C. Relationships among haze pollution, commuting behavior and life satisfaction: A quasi-longitudinal analysis. Transp. Res. Part D Transp. Environ. 2021, 92, 102723. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Liu, H.; Su, H.; Li, X.; Zheng, W. Deriving bathymetry from optical images with a localized neural network algorithm. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5334–5342. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, S.; Deng, Y.; Zhang, Y.; Yin, L.; Zheng, W. An improved method for soft tissue modeling. Biomed. Signal. Process. Control 2021, 65, 102367. [Google Scholar] [CrossRef]
- Ma, Z.; Zheng, W.; Chen, X.; Yin, L. Joint embedding VQA model based on dynamic word vector. PeerJ Comput. Sci. 2021, 7, e353. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, W.; Liu, X.; Mou, Y.; Yin, L.; Yang, B. Research and improvement of feature detection algorithm based on FAST. Rend. Lincei Sci. Fis. E Nat. 2021, 1–15. [Google Scholar] [CrossRef]
- Deng, Y.; Tang, Y.; Yang, B.; Zheng, W.; Liu, S.; Liu, C. A Review of Bilateral Teleoperation Control Strategies with Soft Environment. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 459–464. [Google Scholar]
- Wu, X.; Liu, Z.; Yin, L.; Zheng, W.; Song, L.; Tian, J.; Yang, B.; Liu, S. A Haze Prediction Model in Chengdu Based on LSTM. Atmosphere 2021, 12, 1479. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, X.; Yin, L. Sentence Representation Method Based on Multi-Layer Semantic Network. Appl. Sci. 2021, 11, 1316. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, X.; Ni, X.; Yin, L.; Yang, B. Improving Visual Reasoning Through Semantic Representation. IEEE Access 2021, 9, 91476–91486. [Google Scholar] [CrossRef]
- Zheng, W.; Yin, L.; Chen, X.; Ma, Z.; Liu, S.; Yang, B. Knowledge base graph embedding module design for Visual question answering model. Pattern Recognit. 2021, 120, 108153. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, X.; Yin, L. Research on image classification method based on improved multi-scale relational network. PeerJ Comput. Sci. 2021, 7, e613. [Google Scholar] [CrossRef]
- Li, M.; Hu, M.; Guo, Q.; Tan, T.; Du, B.; Huang, X.; He, L.; Guo, S.; Wang, W.; Fan, Y. Seasonal source apportionment of PM2. 5 in Ningbo, a coastal city in southeast China. Aerosol Air Qual. Res. 2018, 18, 2741–2752. [Google Scholar] [CrossRef]
- Lu, M.; Tang, X.; Feng, Y.; Wang, Z.; Chen, X.; Kong, L.; Ji, D.; Liu, Z.; Liu, K.; Wu, H. Nonlinear response of SIA to emission changes and chemical processes over eastern and central China during a heavy haze month. Sci. Total Environ. 2021, 788, 147747. [Google Scholar] [CrossRef]
- Yao, W.; Zheng, Z.; Zhao, J.; Wang, X.; Wang, Y.; Li, X.; Fu, J. The factor analysis of fog and haze under the coupling of multiple factors—Taking four Chinese cities as an example. Energy Policy 2020, 137, 111138. [Google Scholar] [CrossRef]
- Gan, T.; Yang, H.; Liang, W.; Liao, X. Do economic development and population agglomeration inevitably aggravate haze pollution in China? New evidence from spatial econometric analysis. Environ. Sci. Pollut. Res. 2021, 28, 5063–5079. [Google Scholar] [CrossRef]
- Wu, Q.; Jiang, Y.; Shi, T.; Miao, J.; Qi, B.; Du, R.; Luo, Y.; Chi, X. Quantifying Analysis of the Impact of Haze on Photovoltaic Power Generation. IEEE Access 2020, 8, 215977–215986. [Google Scholar] [CrossRef]
- Zheng, W.; Li, X.; Xie, J.; Yin, L.; Wang, Y. Impact of human activities on haze in Beijing based on grey relational analysis. Rend. Lincei 2015, 26, 187–192. [Google Scholar] [CrossRef]
- Li, X.; Zheng, W.; Yin, L.; Yin, Z.; Song, L.; Tian, X. Influence of social-economic activities on air pollutants in Beijing, China. Open Geosci. 2017, 9, 314–321. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Yu, H.; Ding, A.; Zhang, Y.; Qin, W.; Wang, Z.; Chen, W.; Hua, Y.; Yang, X. Regional contribution to PM1 pollution during winter haze in Yangtze River Delta, China. Sci. Total Environ. 2016, 541, 161–166. [Google Scholar] [CrossRef]
- Zhang, B.; Zhe, H.; Wang, J.; Wu, H. Study on the total amount control of atmospheric environment based on CALPUFF atmospheric diffusion model. North. Environ. 2011, 6, 95–96. [Google Scholar]
- Cai, H.-Y.; Xu, Y.-Z.; Sun, W.-Y. Regional differences and convergence of haze pollution intensity distribution in China—The empirical analysis based on provincial panel data. J. Shanxi Univ. Financ. Econ. 2017, 39, 1–14. [Google Scholar]
- He, J.; Zhao, M.; Zhang, B.; Wang, P.; Zhang, D.; Wang, M.; Liu, B.; Li, N.; Yu, K.; Zhang, Y. The impact of steel emissions on air quality and pollution control strategy in Caofeidian, North China. Atmos. Pollut. Res. 2020, 11, 1238–1247. [Google Scholar] [CrossRef]
- Di Nicolantonio, W.; Cacciari, A.; Petritoli, A.; Carnevale, C.; Pisoni, E.; Volta, M.; Stocchi, P.; Curci, G.; Bolzacchini, E.; Ferrero, L. MODIS and OMI satellite observations supporting air quality monitoring. Radiat. Prot. Dosim. 2009, 137, 280–287. [Google Scholar] [CrossRef] [PubMed]
- Sorek-Hamer, M.; Chatfield, R.; Liu, Y. Strategies for using satellite-based products in modeling PM2. 5 and short-term pollution episodes. Environ. Int. 2020, 144, 106057. [Google Scholar] [CrossRef] [PubMed]
- Mishra, R.K.; Agarwal, A.; Shukla, A. Predicting Ground Level PM2.5 Concentration over Delhi Using Landsat 8 Satellite Data. Int. J. Remote Sens. 2021, 42, 827–838. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, X.; Liu, Y. Spatial autocorrelation analysis of Chinese inter-provincial industrial chemical oxygen demand discharge. Int. J. Environ. Res. Public Health 2012, 9, 2031–2044. [Google Scholar] [CrossRef] [Green Version]
- Tsai, V.C.; Moschetti, M.P. An explicit relationship between time-domain noise correlation and spatial autocorrelation (SPAC) results. Geophys. J. Int. 2010, 182, 454–460. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Liu, J.; Zhu, X.; Liu, J.; Liu, Z. The experiment study of frost heave characteristics and gray correlation analysis of graded crushed rock. Cold Reg. Sci. Technol. 2016, 126, 44–50. [Google Scholar] [CrossRef]
- Ren, C.; Huang, X.; Wang, Z.; Sun, P.; Chi, X.; Ma, Y.; Zhou, D.; Huang, J.; Xie, Y.; Gao, J. Nonlinear response of nitrate to NOx reduction in China during the COVID-19 pandemic. Atmos. Environ. 2021, 264, 118715. [Google Scholar] [CrossRef]
- Shi, X.; Liu, Y. Sample Contribution Pattern Based Big Data Mining Optimization Algorithms. IEEE Access 2021, 9, 32734–32746. [Google Scholar] [CrossRef]
- Gan, T.; Yang, H.; Liang, W. How do urban haze pollution and economic development affect each other? Empirical evidence from 287 Chinese cities during 2000–2016. Sustain. Cities Soc. 2021, 65, 102642. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).