Next Article in Journal
Effect of Humidity on the Reactive Uptake of Ammonia and Dimethylamine by Nitrogen-Containing Secondary Organic Aerosol
Previous Article in Journal
Implications of COVID-19 Restriction Measures in Urban Air Quality of Thessaloniki, Greece: A Machine Learning Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 12
Issue 11
10.3390/atmos12111501
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluating Quantitative Precipitation Forecasts Using the 2.5 km CReSS Model for Typhoons in Taiwan: An Update through the 2015 Season

by
Chung-Chieh Wang
1,
Chih-Sheng Chang
1,*,
Yi-Wen Wang
1,
Chien-Chang Huang
1,2,
Shih-Chieh Wang
1,3,
Yi-Shin Chen
4,
Kazuhisa Tsuboki
5,
Shin-Yi Huang
1,
Shin-Hau Chen
1,
Pi-Yu Chuang
1 and
Hsun Chiu
1
1
Department of Earth Sciences, National Taiwan Normal University, Taipei 11677, Taiwan
2
National Tainan First Senior High School, Tainan 701005, Taiwan
3
Meteorological Satellite Center, Central Weather Bureau, Taipei 100006, Taiwan
4
Department of Natural Science Education, National Taipei University of Education, Taipei 10671, Taiwan
5
Institute for Space-Earth Environmental Research, Nagoya University, Nagoya 464-8601, Japan
*
Author to whom correspondence should be addressed.
Atmosphere 2021, 12(11), 1501; https://doi.org/10.3390/atmos12111501
Submission received: 26 October 2021 / Revised: 9 November 2021 / Accepted: 12 November 2021 / Published: 14 November 2021
(This article belongs to the Section Atmospheric Techniques, Instruments, and Modeling)
Browse Figures
Versions Notes

Abstract

:
In this study, 24 h quantitative precipitation forecasts (QPFs) by a cloud-resolving model (with a grid spacing of 2.5 km) on days 1–3 for 29 typhoons in six seasons of 2010–2015 in Taiwan were examined using categorical scores and rain gauge data. The study represents an update from a previous study for 2010–2012, in order to produce more stable and robust statistics toward the high thresholds (typically with fewer sample points), which is our main focus of interest. This is important to better understand the model’s ability to predict such high-impact typhoon rainfall events. The overall threat scores (TS, defined as the fraction among all verification points that are correctly predicted to reach a given threshold to all points that are either observed or predicted to reach that threshold, or both) were 0.28 and 0.18 on day 1 (0–24 h) QPFs, 0.25 and 0.16 on day 2 (24–48 h) QPFs, and 0.15 and 0.08 on day 3 (48–72 h) QPFs at 350 mm and 500 mm, respectively, showing improvements over 5 km models. Moreover, as found previously, a strong dependence of higher TSs for larger rainfall events also existed, and the corresponding TSs at 350 and 500 mm for the top 5% of events were 0.39 and 0.25 on day 1, 0.38 and 0.21 on day 2, and 0.25 and 0.12 on day 3. Thus, for the top typhoon rainfall events that have the highest potential for hazards, the model exhibits an even higher ability for QPFs based on categorical scores. Furthermore, it is shown that the model has little tendency to overpredict or underpredict rainfall for all groups of events with different rainfall magnitude across all thresholds, except for some tendency to under-forecast for the largest event group on day 3. Some issues associated with categorical statistics to be aware of are also demonstrated and discussed.

1. Introduction

The quantitative precipitation forecast (QPF) is one of the most challenging areas in modern numerical weather prediction (e.g., [1,2,3,4,5]), as precipitation is considered the end product of all nonlinear processes involved in the atmosphere. This is especially true for heavy and extreme rainfall events (≥200 and 500 mm in 24 h, respectively), where the responsible weather systems are mostly of mesoscale and can evolve rapidly with time (e.g., [6,7]). One such system of great importance is the tropical cyclone (TC) or typhoon in the western North Pacific, which can bring flash floods, landslides, and other types of weather hazards such as destructive winds and storm surges to the affected areas. Therefore, while other aspects of TC predictions (such as tracks and intensity, e.g., [8,9,10]) are also vital, verification in model QPFs for TCs is critical in many tropical and subtropical regions around the world.
Traditionally, the categorical scores based on the 2 × 2 contingency table (e.g., [11,12,13,14]) have been widely used to verify model QPFs, as they are intuitive and easy to compute. While more details are given in Section 2.3 the threat score (TS), a major parameter in this method, is the fraction of area to reach a specified rainfall threshold in both the observation and the model (correctly predicted to occur, called a “hit”) among all union areas of either observed or predicted to meet the same threshold. Thus, the value of TS is bounded by 0 and 1, and a higher score is better. It is also clear that hits are required in the prediction in order for TS to be greater than zero; otherwise, one would not be able to tell how closely the prediction missed the observed rain area. As model resolution increases to make QPFs for migratory mesoscale systems (such as squall lines or rainbands), hits are difficult to achieve, and issues such as “double penalty” become more serious, especially at longer lead times; thus, the TS may no longer be effective in evaluating model QPFs (e.g., [6,15,16]). Thus, various new methods that do not require hits, such as attribute- or object-oriented methods, have been developed and used for rainfall verification in recent years (e.g., [16,17,18,19,20]). However, if the model has the ability to produce some “hits”, i.e., to predict rainfall at the correct amount, location, and time simultaneously, this would still be much desired in many important applications, such as hazard prevention and mitigation linked to flooding, landslide, or water reservoir management. After all, accurate QPFs including timing and location still represent a goal that should be sought.
Past studies used the categorical scores to evaluate QPFs for typhoons in Taiwan, but they were few until more recently (within a decade). Chen et al. [21] showed that the official forecasts issued by the Central Weather Bureau (CWB) prior to heavy rainfall (≥50 mm per day) had TSs of 0.38–0.59 in five subregions in Taiwan from 1977–1989. More recently, the CWB and the Taiwan Typhoon and Flood Research Institute (TTFRI) also perform routine (point-to-point) verification for the QPFs using their 5 km models based on rain-gauge observations (see Figure 1). While these regional models have consistently demonstrated a better ability than the coarser global models to predict rainfall at higher thresholds (e.g., [22,23]), their TS values on day 1 (0–24 h) are below 0.4 at 100 mm and about 0.16 at 350 mm [23,24]. Particularly informative are perhaps the results for the 2014 season (two TCs). Two studies [23,25] have shown that the TSs of 5 km models at the CWB and TTFRI, mostly the Weather Research and Forecasting (WRF) Model [26] members, on day 1 dropped from roughly 0.5–0.6 at low thresholds to below 0.2 at 350 mm, with some over-forecast across low thresholds, but serious under-forecasts (i.e., the model-predicted rain areas are much smaller than those observed) at 350 mm, which is the highest threshold routinely verified at the TTFRI. With time, their annual reports also show a gradual improvement in the overall TS from 2011–2015, from about 0.1 to 0.24 at 350 mm (in the range of 6–30 h; personal communication).
At the CWB, the highest threshold verified is 500 mm (per 24 h), and the TSs of day-1 (0–24 h) QPFs were at most ~0.05 for July–September 2014 [23]. However, a few members using the Hurricane WRF (HWRF) Model [10,27] at the TTFRI performed better in 2014, as the highest TS on day 1 reached 0.16 at 500 mm [28], but decreased rapidly to 0.08 and 0.03 on days 2 and 3. Thus, while some variations exist among the TS values (due to different cases and data periods, and perhaps also methodology), the above studies overall indicate that the grid size of 5 km is not fine enough to produce rainfall as heavy as in the observations and, subsequently, to produce hits at high and extreme thresholds. Thus, the QPF performance at thresholds above 350 mm was rather limited in past studies. In addition, only a few of the above studies performed QPF evaluation at forecast ranges beyond day 1 (up to 24 or 30 h). In those that did [22,28], the TSs at most thresholds decreased considerably on day 2 and dropped further on day 3, whereas poor performance existed above ~150 mm.
Since 2010, the Cloud-Resolving Storm Simulator (CReSS) [29,30] at a grid size of 2.5 km has been used to perform routine forecasts at the National Taiwan Normal University (NTNU), Taiwan [31] (referred to as W15 hereafter), and provided to the TTFRI as a forecast member. In [31], results of 24 h QPFs within 3 days for 15 typhoons during 2010–2012 were reported. The overall TSs for all events at 350 and 500 mm were 0.26 and 0.16 on day 1, 0.21 and 0.12 on day 2, and 0.08 and 0.01 on day 3, respectively. These scores from deterministic forecasts over three seasons at least match the best results for single seasons reported above, if not better, and show that typhoon heavy-rainfall QPFs in Taiwan at high thresholds can be improved using a higher model resolution and a larger fine-grid domain. Moreover, W15 [31] also reported a strong positive dependence of categorical scores on the observed rainfall amount, i.e., event size or magnitude. That is, a larger rainfall area meeting a given threshold results in a higher TS and a greater inferred QPF performance at that threshold. Because of this property, for the rainiest top 5% of typhoon events, the TSs at 350 and 500 mm are 0.32 and 0.34 on day 1 and 0.22 and 0.04 on day 3. Therefore, the skill scores for the top events are even higher, and at least higher than those obtained for all events without classification (see [31,32] for details). Toward the high and extreme thresholds, the evaluation of model QPFs for large rainfall events is very important due to their high hazard potential, but such events are rare by definition. This rarity leads to a reduced sample size toward higher thresholds and, therefore, calls for the need to update the data period of verification in order to ensure the robustness of the results.
Thus, the objectives of the present study were threefold. First, the results of W15 [31,32,33] for three seasons of 2010–2012 were updated to include three more seasons (2013–2015) and, thus, the sample size was roughly doubled. As discussed above, this is important and necessary to confirm stable results of QPFs, particularly for the top events toward the extreme thresholds. Furthermore, the results for QPFs at longer ranges of days 2–3 were also augmented. Second, a classification scheme different from that of W15 [31] is introduced to isolate increasingly larger events to assess model QPFs for them. This method is simple and easier to implement for operational use, if needed. Third, some of the issues associated with categorical scores in model QPFs are also be demonstrated and discussed using examples, such that future researchers will be more aware of these issues. In Section 2, the model, data, and methodology used in this study are described. In Section 3, a few selected examples of CReSS forecasts during 2013–2015 are presented and discussed, so that a general ability of this model to predict rainfall in Taiwan under normal conditions can be assessed. The categorical scores for all events and the top events are updated in Section 4; lastly, the summary and conclusion are given in Section 5.

2. The CReSS Model, Data and Methodology

2.1. The CReSS Model and Its Forecasts

As an extension of work from W15 [31], the same version and configuration of CReSS was used in this study. Thus, only a brief description is provided below, and the readers are referred to W15 [31] for more details. The CReSS model [29,30] is a cloud-resolving model suitable to simulate convective storms at high resolution with parallel computation (e.g., [34,35,36,37,38,39]). The model utilizes a terrain-following vertical coordinate based on height, and it has neither nesting nor cumulus parameterization [29]. Instead, clouds are treated fully explicitly using a bulk cold-rain scheme following the studies of [40,41,42,43,44], with a total of six species (vapor, cloud water, cloud ice, rain, snow, and graupel). Sub-grid scale processes parameterized include turbulent mixing in the planetary boundary layer [30,45] and surface radiation and momentum/energy fluxes with a substrate model [46,47,48].
As shown in Table 1, a horizontal grid size of 2.5 km (with 40 levels) has been used since 2010, comparable to typical resolutions used for research (e.g., [6,7,49,50,51]). From 1080 × 900 km2 in 2010–2011, the model domain size has been increased to 1500 × 1200 km2 since 2012 (see Figure 2). Run in real time, the model is initialized four times a day (at 12:00 a.m., 6:00 a.m., 12:00 p.m., and 6:00 p.m. UTC) using the National Centers for Environmental Prediction (NCEP) Global Forecasting System (GFS) real-time analyses and forecasts [52,53,54,55] as initial and boundary conditions (IC/BCs). Since 2013, the resolution of the GFS data has also been increased from 1° to 0.5° (Table 1). Digital terrain data on a (1/120)° grid and the NCEP-analyzed sea-surface temperature are also provided at the lower boundary for the CReSS runs.

2.2. Data and Methodology

Observational data used in this study were also similar to those used in W15 [31]. Mostly from the CWB, these include the best-track data, weather maps, and radar reflectivity composites. For QPF verification, hourly rainfall data from more than 400 automated rain gauges over Taiwan [56] were used. Figure 1 shows the topography of Taiwan and the locations of these gauges, which are denser in coastal plains than in the mountain interiors.
To extend the results of W15 [31] for three more typhoon seasons in a consistent manner, the methodology to select and classify verification periods also followed the same approach closely. Thus, only 24 h QPFs, either from 12:00–12:00 a.m. UTC or 12:00–12:00 p.m. UTC, covering the warning period issued by the CWB for each typhoon (land and/or sea warning), were selected as our target periods for evaluation. While all typhoons must be included, these periods were checked to confirm that the rainfall in Taiwan was at least partially caused by or linked to the TCs, using weather maps and radar/satellite loops. As a result, a total of 193 time segments from 29 typhoons were selected, as shown in Figure 2, and the 24 h QPFs on day 1 (0–24 h), day 2 (24–48 h), and day 3 (48–72 h) by the CReSS runs at 12:00 a.m. and 12:00 p.m. UTC covering these periods were evaluated. Compared to the 99 segments from 15 typhoons in W15 [31], the sample size here was nearly doubled.
Next, the 193 segments were classified into four groups (A to D) on the basis of the observed 24 h rainfall using the same criteria as W15 [31]. That is, when at least 50 gauge sites in Taiwan reached 100, 50, or 25 mm, the segment was classified as group A, B, or C, respectively. Segments that failed to reach the group C standard were classified as group D. Thus, the magnitude of the rainfall decreases from group A to D. Given in Table 2, the numbers of segments following the order A–D were 55, 39, 47, and 52, respectively; thus, they are quite comparable. The total data points were 86,016 for the 193 segments, averaging near 446 points (gauge sites) per segment. While the four groups were exclusive to each other, a top 10 group (denoted as T10) was also selected from group A as a subset for the top 10 segments (Table 2). Thus, T10 is the rainiest part of group A and represents roughly the top 5% of all samples (out of 193 segments). The above classification allowed for a proper examination on the dependence of QPF skill on rainfall magnitude, and the related results are presented in Section 4.

2.3. Categorical Scores for Model QPFs

Again, as in W15 [31], the categorical scores based on the 2 × 2 contingency table [11,12,13,14] were employed to verify model QPFs. At any verification point, the outcome of a prediction to reach a given rainfall threshold over an accumulation period (called an event) can be one of four possibilities: hit (H, event predicted and occurred), miss (M, event occurred but not predicted), false alarm (FA, event predicted but not occurred), and correct negative (CN, event neither predicted nor occurred). By counting the number of points falling into each category among a total of N points (N = H + M + FA + CN) in the verification domain, the TS mentioned in Section 1 and the bias score (BS) can be computed as
TS = H/(H + M + FA),
BS = (H + FA)/(H + M).
Thus, TS is the fraction of successful prediction of event occurrences (rainfall ≥ the threshold) among all events that are observed and/or predicted, where 0 ≤ TS ≤ 1 (the higher, the better). On the other hand, BS is the ratio of the number of events in model prediction (F = H + FA) to that which actually occurred (O = H + M), thus reflecting overprediction if BS > 1 and underprediction if BS < 1. Obviously, the most ideal value of BS is unity. Typically, at least both TS and BS need to be inspected to allow for a better understanding of how the model performs in QPFs, and this is what we do below. Here, a wide range of 24 h rainfall thresholds were used, from 0.05 to 1000 mm. Lastly, it was noted that the TS and BS are computed at the rain-gauge sites where correct observations are available (see Figure 1), by interpolating model QPFs onto these locations as in W15 [31].

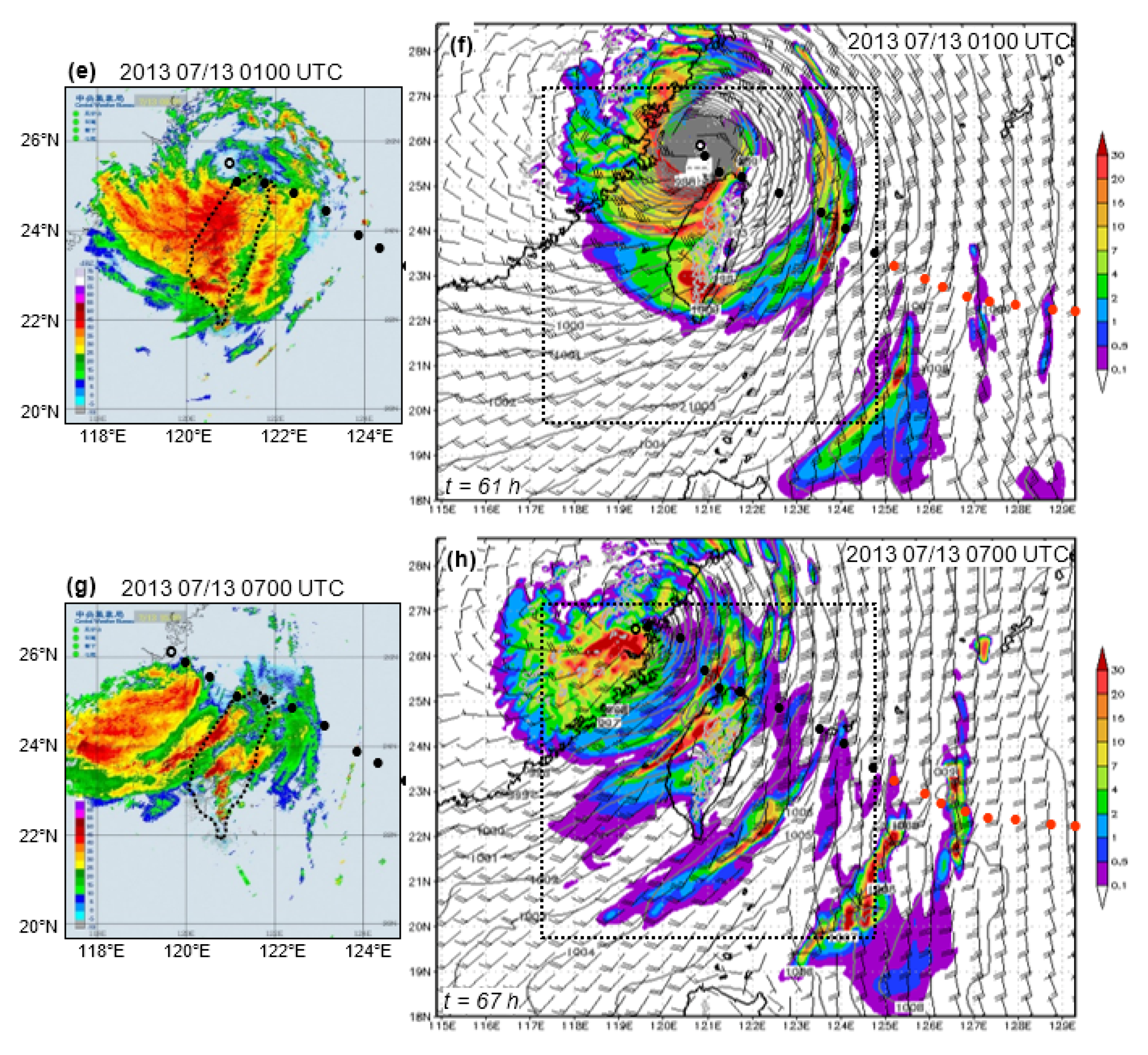
3. Examples of CReSS Forecasts

A few examples of CReSS forecasts during the added period are shown and discussed in this section. These examples are from Typhoon (TY) Soulik (2013), which approached Taiwan from the east-southeast with a typical track more commonly seen. From the examples, a general idea can be obtained about the model’s capability in simulating typhoons and their evolution near Taiwan, and subsequently in the 24 h QPFs over Taiwan.
Figure 3 depicts the track of TY Soulik (2013) and the reflectivity composites from land-based radars in Taiwan at selected times every 5–6 h during its passage over 12–13 July 2013 (left column), as well as compares them to the model prediction (of track and rainfall structure) made at the initial time (t0) of 12:00 p.m. UTC 10 July 2013. On the left panels of Figure 3, one can see that TY Soulik (2013) approached northern Taiwan from the southeast at a speed of close to 30 km·h−1, and its center made landfall across the northernmost part of Taiwan. Despite being more limited in the field of view at longer distances farther away, the radar composites nonetheless indicate that the rainfall associated with Soulik was somewhat asymmetric and more to the south than the north of its center during approach (Figure 3a), and became more concentrated over the windward slopes of Taiwan (see Figure 1) during and shortly after landfall (Figure 3c,e). As Soulik moved away and the overall rainfall gradually weakened, rainbands that aligned in a northeast–southwest direction were present across Taiwan (Figure 3g). The forecast initialized at 12:00 p.m. UTC 10 July (right column, Figure 3), while not always at the same time of the radar observations shown, suggests that the CReSS model captured the evolution of TY Soulik quite well, even in a range of 48–67 h on day 3. One can see that the track was well produced (with a timing difference within 2 h), and the rainfall structure of the TC and around Taiwan also compared quite favorably with the radar observations, including the heavy rainfall over the windward slopes around landfall (Figure 3d,f) and the rainbands at the wake of the storm (Figure 3h).
The 24 h total rainfall distributions over Taiwan from rain-gauge observations for five segments from 12:00 p.m. UTC 10 to 12:00 p.m. UTC 15 July 2013 are shown in Figure 4a–e, and they indicate that the rainfall from TY Soulik was most concentrated from 12:00 p.m. UTC 12 to 12:00 p.m. UTC 13 July, with a peak amount of 875.5 mm (Figure 4c) over the Snow Mountain Range (SMR, cf. Figure 1). While this 24 h segment belonged to group T10 (and group A), other adjacent segments, being much less rainy, could only be classified as group C or D at most. In the second row, Figure 4f–h depict the rainfall distributions on days 1–3 from the run starting at 12:00 p.m. UTC 10 July, i.e., the one shown in Figure 3 (right column). One can see that, on the third day (48–72 h) of this run, the overall rainfall pattern predicted by the 2.5 km CReSS was very good, with a peak amount of 957.9 mm and only some minor disagreements with the observation. The results from the two runs 24 and 48 h later (with t0 at 12:00 p.m. UTC 11 and 12:00 p.m. UTC 12 July, respectively) are shown in the third and fourth rows of Figure 4; therefore, the rainiest target periods were on day 2 and day 1, respectively. Again, the model performed quite well in its rainfall prediction for this period, with peak amounts just over 1000 mm (Figure 4j,l). For other days where it was less rainy, the agreement between forecasts and observations could not be judged as well by visual inspection. However, the QPFs for these less rainy segments carry less significance, as the most important ones should be those made for the rainiest period (i.e., 12:00 p.m. UTC 12 to 12:00 p.m. UTC 13 July) in the event of TY Soulik (2013).
The TS and BS across 15 thresholds from 0.05 to 1000 mm from the three experiments are shown in Figure 4 (rows 2–4), i.e., those made at 12:00 p.m. UTC on 10, 11, and 12 July, are shown and examined in Figure 5. As mentioned, these three runs all resulted in a fairly good rainfall forecast for the rainiest 24 h, i.e., on day 3 of the run on 10 July (Figure 5a, blue), day 2 of the run on 11 July (Figure 5b, red), and day 1 of the run on 12 July (Figure 5c, black). These TSs were high and at least close to 0.7 up to 250 mm and above 0.4 at 750 mm. Such scores were much higher compared to those of the QPFs made for other 24 h segments, which decreased to zero at or before 130 mm without exception. Similarly, the BS curves were also the most ideal when the period from 12:00 p.m. UTC 12 to 12:00 p.m. UTC 13 July was targeted (Figure 5, right column). For other days that were less rainy, the BS tended to more easily go much higher or lower than unity. With the added information in Figure 5, including the classification group and hit rate H/N (left column), the peak 24 h rainfall amount, and the observed base rate O/N (i.e., rainfall area size) and where it reaches 10%, one can readily recognize that, in the case of TY Soulik (2013), the model QPFs could be verified to be of high quality, and they performed substantially better when the magnitude of the rainfall event during the target period was greater, i.e., with large rainfall area at a relatively high threshold.
Another typhoon, TY Fung-Wong (2014) was also examined. It approached Taiwan from the south very slowly, and this track type is less frequent. Although the TS values were somewhat lower, the overall results for Fung-Wong (figures not shown) were similar to those obtained earlier for TY Soulik (2013). From the above discussion and the TS and BS curves shown in the examples (Figure 3, Figure 4 and Figure 5), one can see that, in successive runs where the typhoon was captured by the model in a more-or-less similar way (i.e., no major differences in the simulations), the magnitude of the rainfall event appeared to exert a strong control on the categorical statistics (and the performance of derived model QPFs), especially in the TS. This dependence is an important aspect investigated in this study, and it is further elaborated below. As stressed by W15 [31], these examples also show that computing the scores for individual segments first and then taking the arithmetic average is problematic, as this creates biases toward the smaller and less important events. This is particularly true for the BS, which can be very unstable in small events with few points reaching a given threshold.

4. Evaluation of Overall Model Performance in QPFs

4.1. Updated Results of 2010–2015

Following the methodology in Section 2, the overall TSs from CReSS QPFs starting at 12:00 a.m. and 12:00 p.m. UTC for the 193 segments and 29 typhoons (denoted as “all”) and those for individual groups A–D and T10 (see Table 2) in the three ranges of days 1–3 are presented in Figure 6. For each group, the entries from all 24 h periods are combined to form one contingency table to compute the scores (so that each of the 86,016 data points carries the same weight). As in W15 [31], one can immediately see that, while each curve nearly always decreased with rainfall threshold, the TSs were higher in group A than B, higher in group B than C, etc., following the order among the four exclusive groups (in black, red, blue, and green), regardless of forecast range or lead time (Figure 6a–c). Naturally, the “all group” (gray) had TS values somewhere in between those of A and D, whereas they became closer to those from the larger events (i.e., group A) toward the high thresholds. Compared to the TSs of group A, the T10 curve (orange) was even higher as expected. In the range of day 1 and 2, the TSs from two earlier forecasts by the 4 km CReSS for TY Morakot (2009) at the time (from [36,57]) and targeted for the 24 h on 8 August (in UTC) are also plotted as purple dots at available thresholds. As TY Morakot (2009) was an even larger and more extreme event (over 1650 mm on 8 August), the TSs were higher. Thus, it is confirmed that rainfall area size or event magnitude (see Figure 6d) exerted a strong control on the TS, and the larger events tended to have higher TSs at the same set of rainfall thresholds for the typhoon regime in Taiwan. Recently, the same dependence in the Mei-yu regime was also confirmed [58].
While the overall curves (similar to “all group” here) are often the only ones examined, it is clear in Figure 6a–c that the larger events (group A, group T10, and for Morakot) had considerable higher TSs across the low and middle thresholds, as well as even the high thresholds at times (Figure 6b). For instance, the “all” curve on day 1 started from 0.73 at 0.05 mm and reached 0.34 at 250 mm and 0.18 at 500 mm, whereas the T10 curve was at 1.00, 0.50, and 0.25 at the same three thresholds (Figure 6a). Over a longer range involving day 2 (where all forecasts started 24 h earlier than those for day 1), the TS values remained the same or were only barely lower (Figure 6b) than those on day 1. This phenomenon indicates that the model exhibited nearly the same performance on day 2 (24–48 h) as day 1 (0–24 h); thus, this is impressive compared to the results of 5 km models reviewed in Section 1. The decrease in performance was more visible only on day 3 (Figure 6c), where the overall TSs (all group) were 0.20 at 250 mm and 0.08 at 500 mm (0.33 and 0.12 at the same thresholds in the T10 group). Typically, the QPFs can be considered to have a certain level of skill when the TS reaches 0.2 [58]. Using this value, one can say that the 2.5 km CReSS possesses a skill above this level up to 500 mm on day 1, around 450 mm on day 2, and around 250 mm on day 3 in typhoon QPFs in Taiwan. For the top 10% of rainiest events (T10), these values increased to 600, 500, and 400 mm on days 1–3, respectively. Again, we note that the TS values across the high thresholds in Figure 6 were considerably higher than those by 5 km models reviewed in Section 1, especially on days 2–3, and they were, in general, also slightly higher than those reported in W15 [31]. This latter improvement over the seasons of 2010–2012 may presumably be linked to the larger model domain since 2012 (Figure 2 and Table 2) and better quality of IC/BCs from the NCEP GFS with time.

4.2. Results from a Simple Classification Scheme Using Peak Rainfall Amount

While the above results using exclusive groups of A–D in Section 4.1 are informative and clearly demonstrate the dependence of TSs on event magnitude, a different classification scheme was used in this section. Here, the classification beyond the “all” group simply used the observed peak rainfall amount in the 24 h segments to filter out those reaching 200, 350, 500, and 750 mm, respectively. Therefore, these groups were inclusive, and the group of a higher class (larger group) was a subset from the class below it. Using this simple method for classification, the results are presented in Figure 7. As indicated in the inserts, the classes with a peak rainfall reaching 200, 350, 500, and 750 mm had 98, 52, 26, and 14 segments; thus, their sample sizes were all roughly half of the next class below them.
In Figure 7, one can again see that the larger events exhibited higher TSs across the same set of thresholds, regardless of whether the range was day 1 (0–24 h), day 2 (24–48 h), or day 3 (48–72 h). Because these groups were inclusive, the differences in TSs between curves were not as large compared to Figure 6. Toward the highest threshold, the “all” curves became closer and closer to those from the highest class (i.e., with a peak amount reaching 750 mm), because such big events were almost the only ones to provide data points into the categorical statistics at these high thresholds. While the TS curves for all events (“all group”) and TY Morakot (days 1–2 only) were the same as in Figure 6, those for segments with a peak amount ≥750 mm were only slightly lower than the T10 curves (at the corresponding range) since the former contained a few more time segments (at 14). Since Figure 7 shows the TS results using a simple and intuitive classification method, it is perhaps a good way to examine the performance of model QPFs for increasingly larger events, especially as a routine practice.
Figure 8 shows the BS curves corresponding to the groups in Figure 7 using the inclusive classification method. Overall, these curves indicate that the BS values for the “all group” were quite stable across the thresholds within 500 mm, with slight overprediction (1 ≤ BS ≤ 1.2) on day 1 (Figure 8a) and nearly perfect values (1 ≤ BS ≤ 1.1) on days 2 and 3 (Figure 8b,c). Only toward the extreme thresholds where the data points become fewer did the BS values become more unstable and show some overprediction on days 1 and 3, but not much on day 2 (Figure 8). As pointed out earlier, the total number of data points was 86,016 from all segments; for example, 50,325 of them in observation reached 2.5 mm, but only 278, 33, and three points reached 500, 750, and 1000 mm, respectively. To put this in perspective, the probability of reaching 1000 mm in our study period for 29 TCs was extremely low (0.0035%). At 1000 mm, since the denominator (i.e., O = H + M) in Equation (2) is so small, one can see how a BS of 3.33 is completely understandable (Figure 8a) if the model produces a total of 10 points reaching 1000 mm. Such a BS value, however, would be interpreted as serious overprediction at a low threshold, where the data points are ample. Due to its unstable nature with small sample size, the BS is not suitable to compute when using small samples (such as individual segments) as discussed, and special caution must also be exercised in the interpretation of its results.
In Figure 8, for the larger events, the overprediction on day 1 was less, the BSs were very good on day 2, and some under-forecasts occurred on day 3. This indicates that, over the longer range, there is a tendency to under-forecast the rainfall if the event turns out to be one of high accumulation. In any case, the BS curves overall indicated good model performance across the thresholds in rainfall amount, especially in the range of 24–48 h (day 2). As discussed and shown earlier in the examples, since the data points tend to be too few (or even none) toward the high thresholds in groups B–D (see Figure 6d), the results in BS from the exclusive classification method are not representative (in some threshold ranges), and Figure 8 shown here is a more suitable way to evaluate the BSs.

4.3. Dependence of TS on Rainfall Area Size

From previous sections, we confirmed that the larger rainfall events from typhoons tend to possess higher TSs across a fixed set of thresholds than those from all events during the same verification period in Taiwan (Figure 6 and Figure 7). In this section, we further investigate the influence of rain-area size on the TSs among groups A–D and T10. If the TSs for the same rain-area size (instead of at a fixed rainfall threshold) among different groups are comparable, it would imply that the above phenomenon of dependence results solely from the variation in rain-area size. On the other hand, if the TSs are still higher in larger groups for events with the same rain-area size, this would indicate that the model indeed possesses a higher ability to predict events of greater accumulation, which are typically under stronger forcing at the synoptic scale and the mesoscale. To do this, a procedure similar to W15 [31,32] was used. For each 24 h segment (Table 2), the observed rainfall amounts at all sites were sorted and ranked to identify a set of new thresholds that gave certain percentages of rain-gauge sites, i.e., areal coverage (O/N) in Taiwan, from 99%, 95%, 90–10% (every 10%), 5%, 3%, 2%, and 1%, respectively. From 99% to 1% in size, these 15 percentiles correspond to rainfall thresholds from low to high for each segment. Using this new set of thresholds (different for each segment), the numbers of H, M, FA, and CN could be obtained at each rain-area size in terms of the percentages of O/N, and the TSs could eventually be computed at these rain-area sizes from one combined 2 × 2 contingency table for each group (A–D or T10) as before. Essentially, the rainfall thresholds were standardized using the fixed rain-area sizes in the above process.
After the standardization, the TSs for A–D and T10 groups are presented in Figure 9a–c. Now, the horizontal axis is the rain-area size (O/N in %) from large to small; thus, the impact of different rain-area sizes in events of different groups is eliminated. Even so, the TSs were higher in the larger accumulation groups across the thresholds of rain-area sizes in all three ranges of days 1–3, following the order of T10 ≥ A ≥ B ≥ C ≥ D almost exclusively (Figure 9a–c). The “all” curves from all segments were between those for groups B and C. Over the longer range of day 3, the differences among the groups also became smaller, especially across the middle thresholds, from roughly 80% to 40% in rain-area sizes. In Figure 9a–c, the TS results also indicate that the model is considerably more capable of predicting the T10 events toward the high thresholds (with smaller rain areas) compared to lower accumulation groups. For example, for rain areas that occupied only 10% and 2% of Taiwan (in terms of the percentages of verification points) in the T10 group, the TSs on day 1 were 0.38 and 0.19, respectively, where the mean rainfall thresholds were about 350 and 530 mm (Figure 9d). Similarly, the TSs for the same targets on day 2 were 0.35 and 0.21 (even higher than on day 1), but dropped to 0.25 and 0.10 on day 3. Even on day 3, the value of 0.25 at a threshold of 350 mm, which is the same as in Figure 6c, still suggests a certain skill level that is quite high. In Figure 9d, the mean rainfall thresholds in different groups as a function of rain-area size are shown, and they were much higher in larger groups, especially toward the high threshold (smaller rain-area size). Overall, Figure 9 indicates that the 2.5 km CReSS model is indeed more skillful in predicting larger typhoon rainfall events, and more factors than just the rain-area size are involved in this dependence. Some aspects were discussed in W15 [31,58] but are beyond the scope of the present update study.

5. Conclusion and Summary

In this study, 24 h QPFs by the cloud-resolving 2.5 km CReSS model (initialized at 12:00 a.m. and 1200 p.m. UTC) over three ranges of day 1 (0–24 h), day 2 (24–48 h), and day 3 (48–72 h) during warning periods of 29 typhoons in Taiwan in six seasons of 2010–2015 (193 24 h time segments in observation) were verified and examined using categorical skill scores. The study is an update from W15 [31,32,33] for 15 typhoons during 2010–2012 (99 segments), and the sample size was roughly doubled in order to produce more stable statistics toward the high and extreme thresholds (up to 1000 mm per 24 h) and to better understand the capability of the model to predict these high-impact rainfall events. The major conclusions are summarized below.
(i)
The overall TS values of day 1 (0–24 h) QPFs for all events were 0.34, 0.28, and 0.18 at 250, 350, and 500 mm, respectively, and the corresponding scores at the three thresholds were 0.31, 0.25, and 0.16 on day 2, and 0.20, 0.15, and 0.08 on day 3. Compared to results from contemporary studies of 5 km models (often from fewer samples for a single season), the above TS values at these high thresholds are higher and represent considerable improvement, especially toward the high thresholds and at ranges beyond day 1. In particular, the day 2 scores are only slightly lower than those of day 1, suggesting a comparable model QPF skill at 24–48 h in relation to 0–24 h.
(ii)
The dependence found in W15 [31], i.e., higher TSs in larger rainfall events, was also evident in our results here, as expected, and this means a further improved ability to produce QPFs for typhoons with greater rain accumulations in Taiwan. After classification, the TSs for the T10 group (roughly top 5% of events) on day 1, again at 250, 350, and 500 mm, were 0.50, 0.39, and 0.25, respectively, while the corresponding scores were 0.49, 0.38, and 0.21 on day 2, and 0.34, 0.25, and 0.12 on day 3. Using a different and simple classification scheme based on the observed peak rainfall amount, the TSs for the top class (about top 7%, with peak rainfall ≥750 mm) were also similar or slightly lower, indicating that these results are stable and robust. Thus, for the top typhoon rainfall events that have the highest potential for hazards, the 2.5 km CReSS exhibits an improved ability to produce QPFs on the basis of categorical statistics.
(iii)
The classification method based on the observed peak rainfall amount successively filters out subsets of samples with heavier rainfall, and the situations of insufficient points in samples are avoided (as much as possible) even toward the high thresholds. The resultant groups are inclusive and, thus, better suited for categorical statistics, particularly the BS. Overall, the BSs of the 2.5 km CReSS are quite good and especially ideal on day 2, and they show stable results close to unity for all groups across all thresholds with sufficient data points. Thus, the model does not have a tendency to underpredict rainfall toward even the highest threshold, and it is, thus, capable of producing extreme rainfall. For the larger events, nonetheless, there is a slight tendency to under-forecast rainfall toward the higher thresholds.
Overall, the 2.5 km CReSS herein shows improved typhoon QPFs over coarser 5 km models in Taiwan. Therefore, a further increase in model resolution, perhaps down to a grid size at the kilometer or finer scale, similar to the HWRF model [59,60], may potentially further improve the QPF performance (in categorical statistics) in Taiwan to some extent. While this question remains to be answered, some related studies are currently ongoing, and their results will be reported when available.

Author Contributions

Conceptualization, C.-C.W.; formal analysis, C.-C.W., C.-S.C., Y.-W.W., C.-C.H., S.-C.W., Y.-S.C., S.-Y.H., S.-H.C., P.-Y.C. and H.C.; funding acquisition, C.-C.W.; investigation, C.-C.W., C.-S.C., Y.-W.W., C.-C.H., S.-C.W. and Y.-S.C.; methodology, C.-C.W., C.-S.C. and Y.-W.W.; project administration, C.-C.W.; software, C.-S.C., Y.-W.W. and K.T.; supervision, C.-C.W.; visualization, Y.-W.W., C.-C.H., S.-C.W. and Y.-S.C.; writing—original draft, C.-C.W. and C.-S.C.; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the Ministry of Science and Technology (MOST) of Taiwan (grants MOST-105-2625-M-003-001, MOST-106-2625-M-003-001, MOST-108-2111-M-003-005-MY2, MOST-110-2111-M-003-004, and MOST-110-2625-M-003-001).

Data Availability Statement

The CReSS model and its user guide are open to researchers and available at http://www.rain.hyarc.nagoya-u.ac.jp/~tsuboki/cress_html/index_cress_eng.html, and the CReSS forecasts are available for viewing at http://cressfcst.es.ntnu.edu.tw/ accessed on 1 October 2021.

Acknowledgments

The authors thank the two anonymous reviewers for their valuable comments and suggestions, as well as the assistance from K.-Y. Chen. The GFS analysis and forecasts used to drive the CReSS forecasts are produced and made available by the NCEP.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Olson, D.A.; Junker, N.W.; Korty, B. Evaluation of 33 Years of Quantitative Precipitation Forecasting at the NMC. Wea. Forecast. 1995, 10, 498–511. [Google Scholar] [CrossRef] [Green Version]
  2. Golding, B.W. Quantitative Precipitation Forecasting in the UK. J. Hydrol. 2000, 239, 286–305. [Google Scholar] [CrossRef]
  3. Mullen, S.L.; Buizza, R. Quantitative Precipitation Forecasts over the United States by the ECMWF Ensemble Prediction System. Mon. Wea. Rev. 2001, 129, 638–663. [Google Scholar] [CrossRef]
  4. Fritsch, J.M.; Carbone, R.E. Improving quantitative precipitation forecasts in the warm season. A USWRP research and development strategy. Bull. Amer. Meteor. Soc. 2004, 85, 955–965. [Google Scholar] [CrossRef] [Green Version]
  5. Cuo, L.; Pagano, T.C.; Wang, Q.J. A review of quantitative precipitation forecasts and their use in short-to medium-range streamflow forecasting. J. Hydormeteor. 2011, 12, 713–728. [Google Scholar] [CrossRef]
  6. Clark, A.J.; Gallus, W.A., Jr.; Chen, T.-C. Comparison of the diurnal precipitation cycle in convection-resolving and non-convection-resolving mesoscale models. Mon. Wea. Rev. 2007, 135, 3456–3473. [Google Scholar] [CrossRef] [Green Version]
  7. Clark, A.J.; Gallus, W.A., Jr.; Xue, M.; Kong, F. A comparison of precipitation forecast skill between small convection-allowing and large convection-parameterizing ensembles. Wea. Forecast. 2009, 24, 1121–1140. [Google Scholar] [CrossRef] [Green Version]
  8. DeMaria, M.; Knaff, J.A.; Sampson, C. Evaluation of long-term trends in tropical cyclone intensity forecasts. Meteor. Atmos. Phys. 2007, 97, 19–28. [Google Scholar] [CrossRef]
  9. Rogers, R.; Aberson, S.; Aksoy, A.; Annane, B.; Black, M.; Cione, J.; Dorst, N.; Dunion, J.; Gamache, J.; Goldenberg, S.; et al. NOAA’s Hurricane Intensity Forecasting Experiment: A Progress Report. Bull. Amer. Meteor. Soc. 2013, 94, 859–882. [Google Scholar] [CrossRef] [Green Version]
  10. Tallapragada, V.; Kieu, C.; Trahan, S.; Liu, Q.; Wang, W.; Zhang, Z.; Tong, M.; Zhang, B.; Zhu, L.; Strahl, B. Forecasting Tropical Cyclones in the Western North Pacific Basin Using the NCEP Operational HWRF Model: Model Upgrades and Evaluation of Real-Time Performance in 2013. Wea. Forecast. 2016, 31, 877–894. [Google Scholar] [CrossRef]
  11. Schaefer, J.T. The critical success index as an indicator of warning skill. Wea. Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef] [Green Version]
  12. Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 1995; p. 467. [Google Scholar]
  13. Ebert, E.E.; Damrath, U.; Wergen, W.; Baldwin, M.E. The WGNE assessment of short-term quantitative precipitation forecasts (QPFs) from operational numerical weather prediction models. Bull. Amer. Meteor. Soc. 2003, 84, 481–492. [Google Scholar] [CrossRef]
  14. Jolliffe, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner’s Guide in Atmospheric Science; Wiley and Sons: Hoboken, NY, USA, 2003; p. 240. [Google Scholar]
  15. Ebert, E.E.; McBride, J.L. Verification of precipitation in weather systems: Determination of systematic errors. J. Hydrol. 2000, 239, 179–202. [Google Scholar] [CrossRef]
  16. Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Wea. Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef] [Green Version]
  17. Marzban, C.; Sandgathe, S. Cluster analysis for verification of precipitation fields. Wea. Forecast. 2006, 21, 824–838. [Google Scholar] [CrossRef] [Green Version]
  18. Wernli, H.; Paulat, M.; Hagen, M.; Frei, C. SAL—A novel quality measure for the verification of quantitative precipitation forecasts. Mon. Wea. Rev. 2008, 136, 4470–4487. [Google Scholar] [CrossRef] [Green Version]
  19. Wang, C.-C.; Paul, S.; Lee, D.-I. Evaluation of rainfall forecasts by three mesoscale models during the Mei-yu season of 2008 in Taiwan. Part II: Development of an object-oriented method. Atmosphere 2020, 11, 939. [Google Scholar] [CrossRef]
  20. Wang, C.-C.; Paul, S.; Lee, D.-I. Evaluation of rainfall forecasts by three mesoscale models during the Mei-yu season of 2008 in Taiwan. Part III: Application of an object-oriented verification method. Atmosphere 2020, 11, 705. [Google Scholar] [CrossRef]
  21. Chen, G.T.J.; Shieh, S.L.; Chen, L.F.; Chen, C.D. On the forecast skill of heavy rainfall in Taiwan. Atmos. Sci. 1991, 19, 177–188. [Google Scholar]
  22. Hsu, J.C.-S.; Wang, C.-J.; Chen, P.-Y.; Chang, T.-H.; Fong, C.-T. Verification of quantitative precipitation forecasts by the CWB WRF and ECMWF on 0.125 grid. In Proceedings of the 2014 Conference on Weather Analysis and Forecasting, Central Weather Bureau, Taipei, Taiwan, 16–18 September 2014; pp. A2–A24. [Google Scholar]
  23. Huang, T.-H.; Yeh, S.-H.; Lu, G.-C.; Hong, J.-S. A synthesis and comparison of QPF verifications at the CWB and major NWP guidance. In Proceedings of the 2015 Conference on Weather Analysis and Forecasting, Central Weather Bureau, Taipei, Taiwan, 15–17 September 2015; pp. 7–11. [Google Scholar]
  24. Tsai, C.-C.; Hsiao, L.-F.; Chen, D.-S.; Bao, C.-W.; Lee, C.-S. Evaluation of the Performance of Hurricane WRF Model over the Western North Pacific in 2013. In Proceedings of the 2014 Conference on Weather Analysis and Forecasting, Central Weather Bureau, Taipei, Taiwan, 16–18 September 2014; pp. A2–A45. [Google Scholar]
  25. Wang, C.-J.; Huang, L.-J.; Hsiao, L.-F.; Lee, C.-S. Analysis and Discussion on the Results of Taiwan-Area Precipitation Ensemble Experiment (TAPEX) in 2014. In Proceedings of the 2014 Conference on Weather Analysis and Forecasting, Central Weather Bureau, Taipei, Taiwan, 16–18 September 2014; pp. A2–A22. [Google Scholar]
  26. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2; NCAR Technical Note: Boulder, CO, USA, 2005; p. 88. [Google Scholar] [CrossRef]
  27. Biswas, M.K.; Abarca, S.; Bernardet, L.; Ginis, I.; Grell, E.; Iacono, M.; Kalina, E.; Liu, B.; Liu, Q.; Marchok, T.; et al. Hurricane Weather Research and Forecasting (HWRF) Model: 2018 Scientific Documentation. Developmental Testbed Center; Developmental Testbed Center: Boulder, CO, USA, 2018; p. 112. Available online: http://www.dtcenter.org/sites/default/files/community-code/hwrf/docs/scientific_documents/HWRFv4.0a_ScientificDoc.pdf (accessed on 1 October 2021).
  28. Tsai, C.-C.; Hsiao, L.-F.; Chen, D.-S.; Bao, C.-W.; Lee, C.-S. Evaluation of the performance of hurricane WRF and typhoon WRF models in track and rainfall over the Western North Pacific. In Proceedings of the 2014 Conference on Weather Analysis and Forecasting, Central Weather Bureau, Taipei, Taiwan, 16–18 September 2014; pp. 2–11. [Google Scholar]
  29. Tsuboki, K.; Sakakibara, A. Large-scale parallel computing of cloud resolving storm simulator. In High Performance Computing; Zima, H.P., Joe, K., Sato, M., Seo, Y., Shimasaki, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 243–259. [Google Scholar]
  30. Tsuboki, K.; Sakakibara, A. Numerical Prediction of High-Impact Weather Systems—The Textbook for the Seventeenth IHP Training Course in 2007; Hydrospheric Atmospheric Research Center: Nagoya, Japan, 2007; p. 273. [Google Scholar]
  31. Wang, C.-C. The More Rain, the Better the Model Performs—The Dependency of Quantitative Precipitation Forecast Skill on Rainfall Amount for Typhoons in Taiwan. Mon. Wea. Rev. 2015, 143, 1723–1748. [Google Scholar] [CrossRef]
  32. Wang, C.-C. Corrigendum. Mon. Wea. Rev. 2016, 144, 3031–3033. [Google Scholar] [CrossRef]
  33. Wang, C.-C. Paper of Notes: The More Rain from Typhoons, the Better the Models Perform. Bull. Amer. Meteor. Soc. 2016, 97, 16–17. [Google Scholar]
  34. Liu, A.Q.; Moore, G.W.K.; Tsuboki, K.; Renfrew, I.A. A High-Resolution Simulation of Convective Roll Clouds During a Cold-Air Outbreak. Geophys. Res. Lett. 2004, 31, L03101. [Google Scholar] [CrossRef] [Green Version]
  35. Wang, C.-C.; Kuo, H.-C.; Chen, Y.-H.; Huang, H.-L.; Chung, C.-H.; Tsuboki, K. Effects of Asymmetric Latent Heating on Typhoon Movement Crossing Taiwan: The Case of Morakot (2009) with Extreme Rainfall. J. Atmos. Sci. 2012, 69, 3172–3196. [Google Scholar] [CrossRef]
  36. Wang, C.-C.; Kuo, H.-C.; Yeh, T.-C.; Chung, C.-H.; Chen, Y.-H.; Huang, S.-Y.; Wang, Y.-W.; Liu, C.-H. High-Resolution Quantitative Precipitation Forecasts and Simulations by the Cloud-Resolving Storm Simulator (CReSS) for Typhoon Morakot (2009). J. Hydrol. 2013, 506, 26–41. [Google Scholar] [CrossRef]
  37. Akter, N.; Tsuboki, K. Numerical Simulation of Cyclone Sidr Using a Cloud-Resolving Model: Characteristics and Formation Process of an Outer Rainband. Mon. Wea. Rev. 2012, 140, 789–810. [Google Scholar] [CrossRef]
  38. Kuo, H.-C.; Tsujino, S.; Huang, C.-C.; Wang, C.-C.; Tsuboki, K. Diagnosis of the Dynamic Efficiency of Latent Heat Release and the Rapid Intensification of Supertyphoon Haiyan (2013). Mon. Wea. Rev. 2019, 147, 1127–1147. [Google Scholar] [CrossRef]
  39. Wang, C.-C.; Chen, Y.-H.; Li, M.-C.; Kuo, H.-C.; Tsuboki, K. On the Separation of Upper and Low-Level Centres of Tropical Storm Kong-Rey (2013) near Taiwan in Association with Asymmetric Latent Heating. Quart. J. Roy. Meteor. Soc. 2021, 147, 1135–1149. [Google Scholar] [CrossRef]
  40. Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk Parameterization of the Snow Field in a Cloud Model. J. Climate Appl. Meteor. 1983, 22, 1065–1092. [Google Scholar] [CrossRef] [Green Version]
  41. Cotton, W.R.; Tripoli, G.J.; Rauber, R.M.; Mulvihill, E.A. Numerical Simulation of the Effects of Varying Ice Crystal Nucleation Rates and Aggregation Processes on Orographic Snowfall. J. Clim. Appl. Meteor. 1986, 25, 1658–1680. [Google Scholar] [CrossRef] [Green Version]
  42. Murakami, M. Numerical Modeling of Dynamical and Microphysical Evolution of an Isolated Convective Cloud—The 19 July 1981 CCOPE Cloud. J. Meteor. Soc. Jpn. 1990, 68, 107–128. [Google Scholar] [CrossRef] [Green Version]
  43. Ikawa, M.; Saito, K. Description of a nonhydrostatic model developed at the Forecast Research Department of the MRI. MRI Tech. Rep. 1991, 28, 238. [Google Scholar]
  44. Murakami, M.; Clark, T.L.; Hall, W.D. Numerical Simulations of Convective Snow Clouds over the Sea of Japan: Two-Dimensional Simulation of Mixed Layer Development and Convective Snow Cloud Formation. J. Meteor. Soc. Jpn. 1994, 72, 43–62. [Google Scholar] [CrossRef] [Green Version]
  45. Deardorff, J.W. Stratocumulus-Capped Mixed Layers Derived from a Three-Dimensional Model. Bound. -Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
  46. Kondo, J. Heat balance of the China Sea during the air mass transformation experiment. J. Meteor. Soc. Jpn. 1976, 54, 382–398. [Google Scholar] [CrossRef] [Green Version]
  47. Louis, J.F.; Tiedtke, M.; Geleyn, J.F. A Short History of the Operational PBL Parameterization at ECMWF. Workshop on Planetary Boundary Layer Parameterization; ECMWF: Reading, UK, 1981; pp. 59–79. [Google Scholar]
  48. Segami, A.; Kurihara, K.; Nakamura, H.; Ueno, M.; Takano, I.; Tatsumi, Y. 1989: Operational Mesoscale Weather Prediction with Japan Spectral Model. J. Meteor. Soc. Jpn. 1989, 67, 907–924. [Google Scholar] [CrossRef] [Green Version]
  49. Done, J.; Davis, C.A.; Weisman, M. The Next Generation of NWP: Explicit Forecasts of Convection Using the Weather Research and Forecasting (WRF) Model. Atmos. Res. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
  50. Liu, C.; Moncrieff, M.W.; Tuttle, J.D.; Carbone, R.E. Explicit and Parameterized Episodes of Warm-Season Precipitation over the Continental United States. Adv. Atmos. Sci. 2006, 23, 91–105. [Google Scholar] [CrossRef]
  51. Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Wea. Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
  52. Kanamitsu, M. Description of the NMC Global Data Assimilation and Forecast System. Wea. Forecast. 1989, 4, 335–342. [Google Scholar] [CrossRef] [Green Version]
  53. Kalnay, E.; Kanamitsu, M.; Baker, W.E. Global Numerical Weather Prediction at the National Meteorological Center. Bull. Amer. Meteor. Soc. 1990, 71, 1410–1428. [Google Scholar] [CrossRef]
  54. Moorthi, S.; Pan, H.L.; Caplan, P. Changes to the 2001 NCEP Operational MRF/AVN Global Analysis/Forecast System. Tech. Proced. Bull. 2001, 484, 14. [Google Scholar]
  55. Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Wu, W.S.; Lord, S. 2009: Introduction of the GSI into the NCEP global data assimilation system. Wea. Forecast. 2009, 24, 1691–1705. [Google Scholar] [CrossRef] [Green Version]
  56. Hsu, J. ARMTS up and running in Taiwan. Väisälä News 1998, 146, 24–26. [Google Scholar]
  57. Wang, C.-C. On the calculation and correction of equitable threat score for model quantitative precipitation forecasts for small verification areas: The example of Taiwan. Wea. Forecast. 2014, 29, 788–798. [Google Scholar] [CrossRef]
  58. Wang, C.-C.; Chuang, P.-Y.; Chang, C.-S.; Tsuboki, K.; Huang, S.-Y.; Leu, G.-C. Evaluation of mei-yu heavy-rainfall quantitative precipitation forecasts in Taiwan by a cloud-resolving model for three seasons of 2012–2014. Nat. Hazards Earth Syst. Sci. 2021. [Google Scholar]
  59. Feng, J.; Wang, X.G. Impact of assimilating upper-level dropsonde observations collected during the TCI field campaign on the prediction of intensity and structure of Hurricane Patricia (2015). Mon. Wea. Rev. 2019, 147, 3069–3089. [Google Scholar] [CrossRef]
  60. Feng, J.; Wang, X.G. Impact of increasing horizontal and vertical resolution during the HWRF hybrid EnVar data assimilation on the analysis and prediction of Hurricane Patricia (2015). Mon. Wea. Rev. 2021, 149, 419–441. [Google Scholar] [CrossRef]
Atmosphere 12 01501 g001 550
Figure 1. The topography of Taiwan (m, color) and distribution of rain gauges (dots). The Central Mountain Range (CMR) and Snow Mountain Range (SMR) of Taiwan are indicated.
Figure 1. The topography of Taiwan (m, color) and distribution of rain gauges (dots). The Central Mountain Range (CMR) and Snow Mountain Range (SMR) of Taiwan are indicated.
Atmosphere 12 01501 g001
Atmosphere 12 01501 g002a 550Atmosphere 12 01501 g002b 550
Figure 2. CWB best tracks of (a) 15 typhoons in 2010–2012, (b) eight typhoons in 2013–2014, and (c) six typhoons in 2015. Typhoon center positions are given every 6 h (dots; at 12:00 a.m., 6:00 a.m., 12:00 p.m., and 6:00 p.m. UTC), and the month and date at 12:00 a.m. UTC are labeled (and enlarged in (b,c)) as needed. The track segments for which QPFs are included for evaluation are thickened. The forecast domain (white area) in 2010–2011 is shown in (a), and that in 2012–2015 is shown in (b,c).
Figure 2. CWB best tracks of (a) 15 typhoons in 2010–2012, (b) eight typhoons in 2013–2014, and (c) six typhoons in 2015. Typhoon center positions are given every 6 h (dots; at 12:00 a.m., 6:00 a.m., 12:00 p.m., and 6:00 p.m. UTC), and the month and date at 12:00 a.m. UTC are labeled (and enlarged in (b,c)) as needed. The track segments for which QPFs are included for evaluation are thickened. The forecast domain (white area) in 2010–2011 is shown in (a), and that in 2012–2015 is shown in (b,c).
Atmosphere 12 01501 g002aAtmosphere 12 01501 g002b
Atmosphere 12 01501 g003a 550Atmosphere 12 01501 g003b 550
Figure 3. (a) Radar VMI reflectivity composite (dBZ, scale at lower left, every 5 dBZ from −10 to 75 dBZ) at 2:00 p.m. UTC 12 July (provided by the CWB) and (b) CReSS forecast (t0 at 12:00 p.m. UTC 10 July) of sea-level pressure (hPa, every 1 hPa, over ocean only), surface wind (kts, barbs) at 10 m height, terrain elevation (gray contours at 1 and 2 km, over land only), and 1 h rainfall (mm, color, scale to the right) valid at 12:00 p.m. UTC 12 July 2013. (c,e,g) As in (a), but for radar reflectivity at (c) 7:00 p.m. UTC 12, and (e) 1:00 a.m. and (g) 7:00 a.m. UTC 13 July 2013. (d,f,h) As in (b), but for forecast valid at (d) 5:00 p.m. UTC 12, and (f) 1:00 a.m. and (h) 7:00 a.m. UTC 13 July 2013. The current typhoon center is marked by an open dot, and the earlier positions every 3 h (at 12:00 a.m. UTC, 3:00 a.m. UTC, etc.) are marked by solid dots (in orange prior to 6:00 a.m. UTC 12 July). The dotted box in model plots corresponds to the region of radar plots.
Figure 3. (a) Radar VMI reflectivity composite (dBZ, scale at lower left, every 5 dBZ from −10 to 75 dBZ) at 2:00 p.m. UTC 12 July (provided by the CWB) and (b) CReSS forecast (t0 at 12:00 p.m. UTC 10 July) of sea-level pressure (hPa, every 1 hPa, over ocean only), surface wind (kts, barbs) at 10 m height, terrain elevation (gray contours at 1 and 2 km, over land only), and 1 h rainfall (mm, color, scale to the right) valid at 12:00 p.m. UTC 12 July 2013. (c,e,g) As in (a), but for radar reflectivity at (c) 7:00 p.m. UTC 12, and (e) 1:00 a.m. and (g) 7:00 a.m. UTC 13 July 2013. (d,f,h) As in (b), but for forecast valid at (d) 5:00 p.m. UTC 12, and (f) 1:00 a.m. and (h) 7:00 a.m. UTC 13 July 2013. The current typhoon center is marked by an open dot, and the earlier positions every 3 h (at 12:00 a.m. UTC, 3:00 a.m. UTC, etc.) are marked by solid dots (in orange prior to 6:00 a.m. UTC 12 July). The dotted box in model plots corresponds to the region of radar plots.
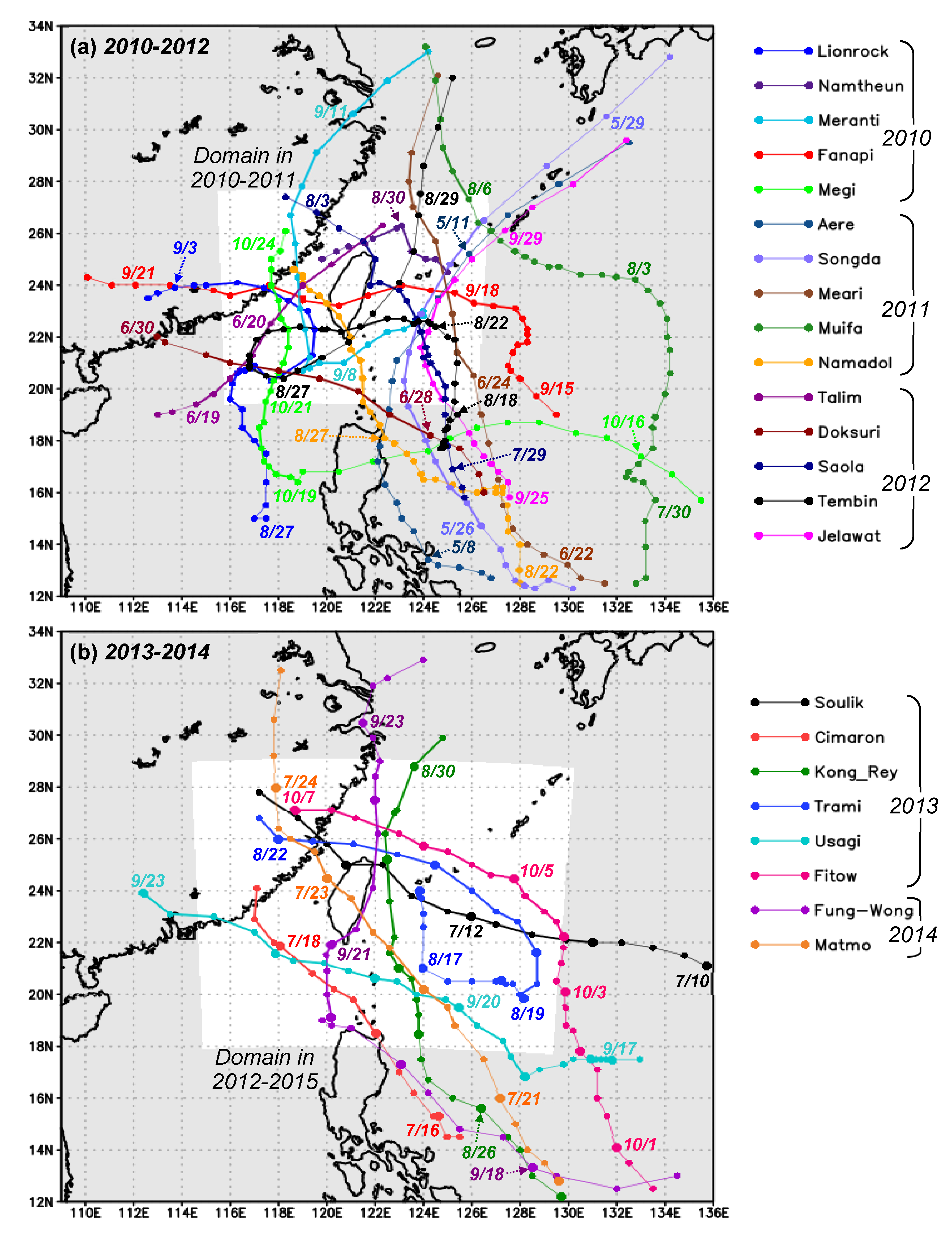
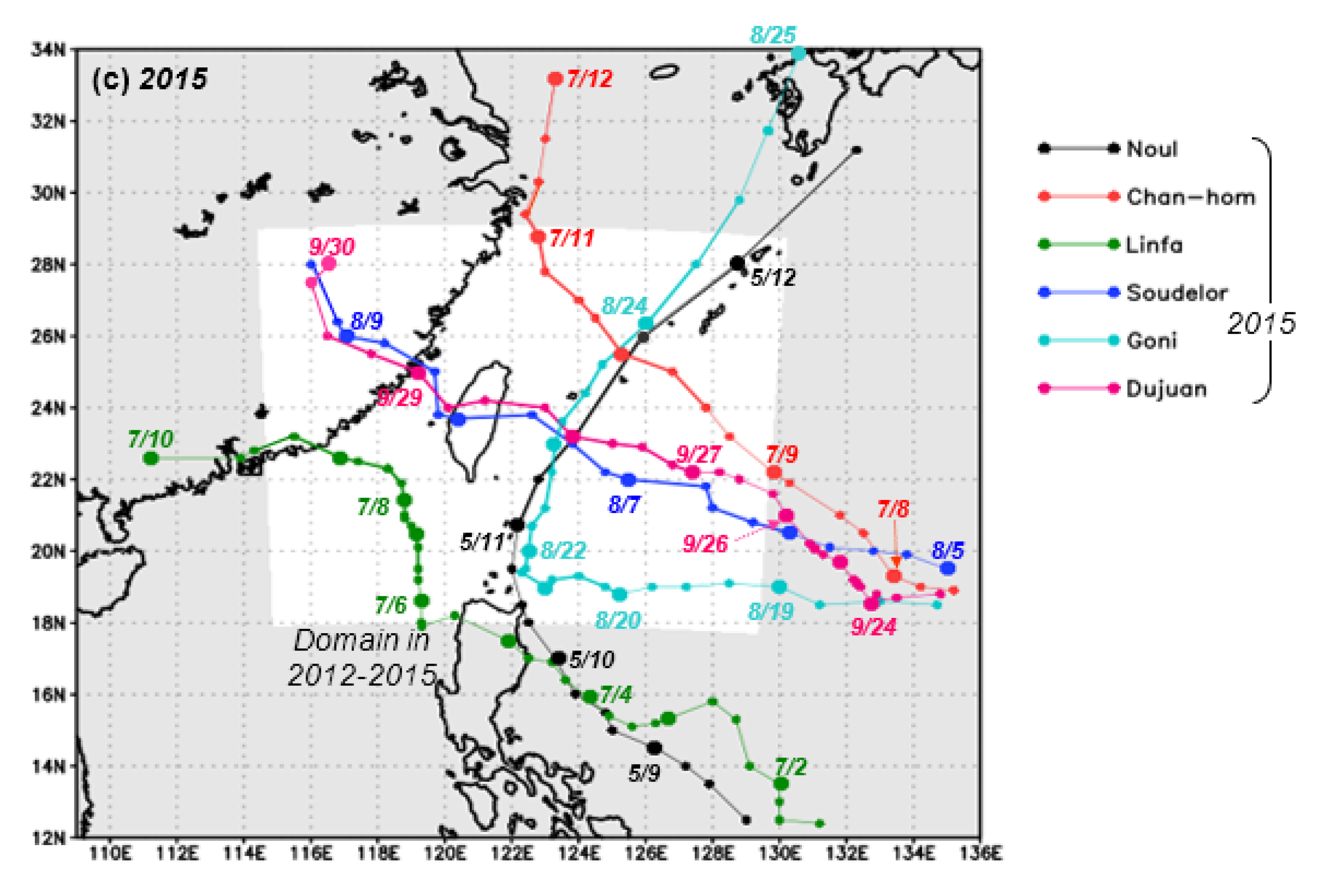
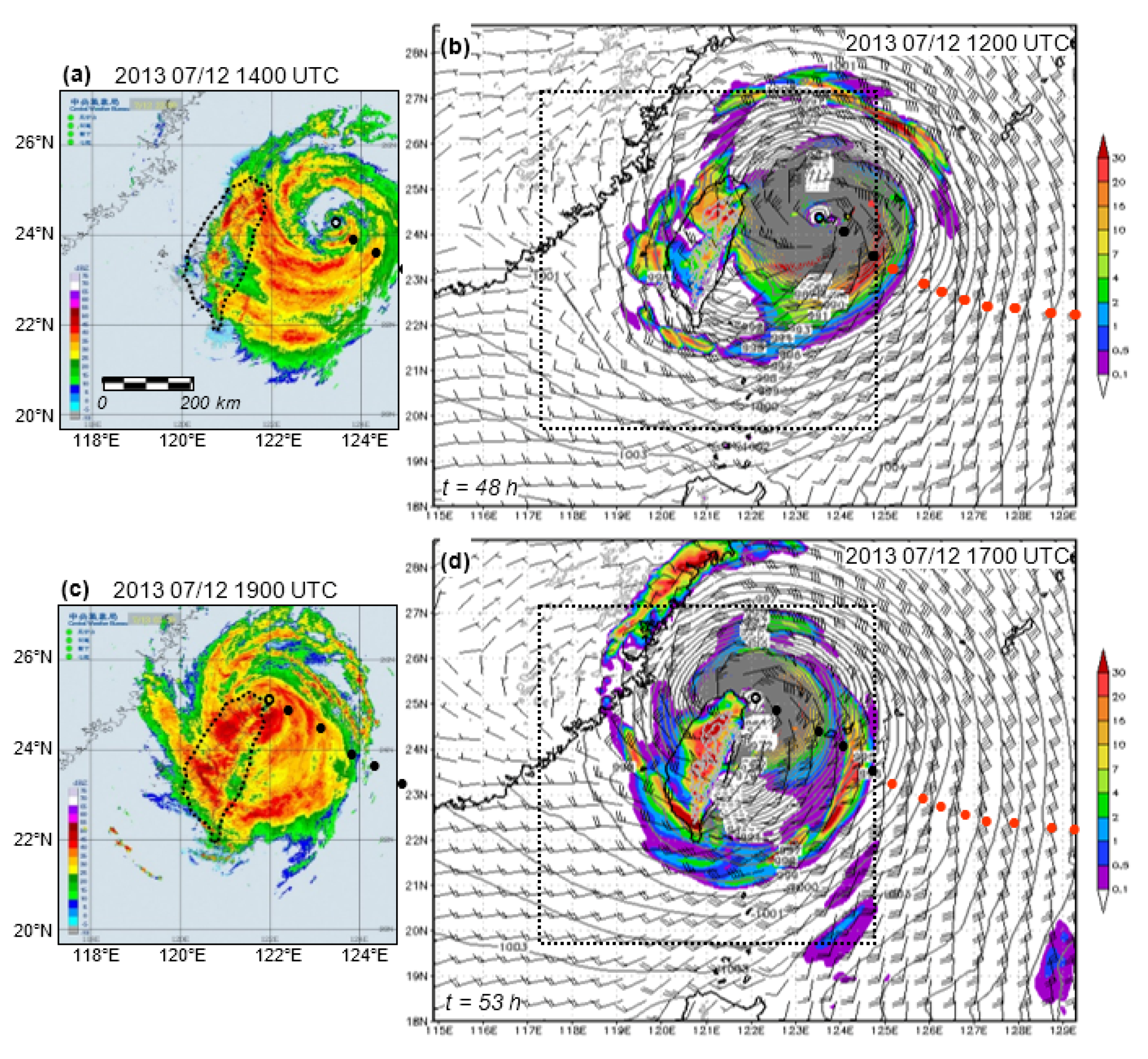
Atmosphere 12 01501 g003aAtmosphere 12 01501 g003b
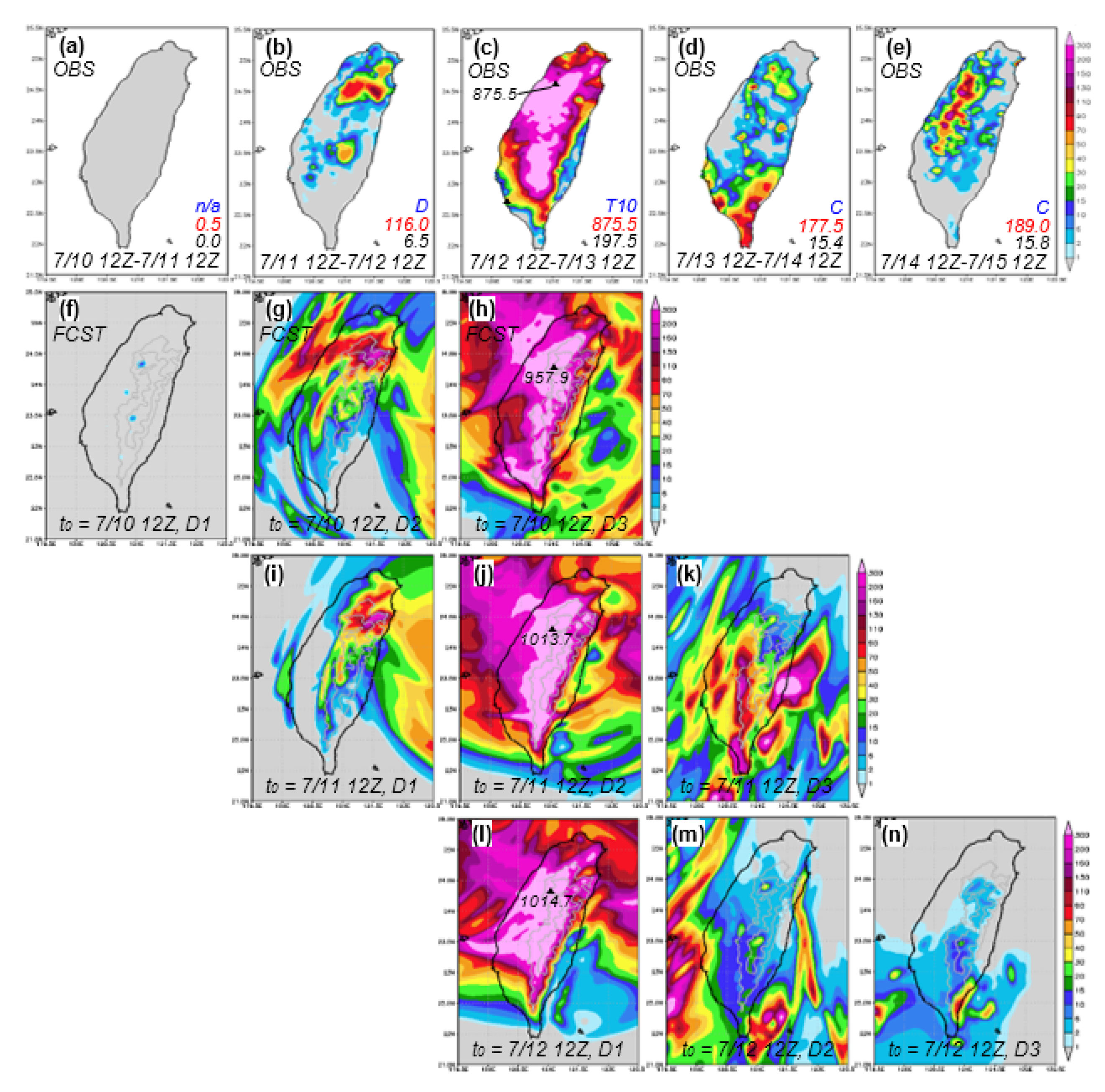
Atmosphere 12 01501 g004 550
Figure 4. Observed 24 h rainfall distributions (mm, 12:00–1200 p.m. UTC) over Taiwan starting from 12:00 p.m. UTC of (a) 10 to (e) 14 July 2013, and corresponding CReSS 24 h QPFs made at 12:00 p.m. UTC 10 July for (f) day 1 (0–24 h), (g) day 2 (24–48 h), and (h) day 3 (48–72 h), during TY Soulik. (i–k) and (l–n) As in (f–h), but showing day 1 to day 3 QPFs made at 12:00 p.m. UTC 11 and 12 July 2013, respectively. The classification group (see text for details) and observed maximum and averaged amounts are given in the lower right corner in (a–e) and are also marked in (c). The color scales are identical for all panels.
Figure 4. Observed 24 h rainfall distributions (mm, 12:00–1200 p.m. UTC) over Taiwan starting from 12:00 p.m. UTC of (a) 10 to (e) 14 July 2013, and corresponding CReSS 24 h QPFs made at 12:00 p.m. UTC 10 July for (f) day 1 (0–24 h), (g) day 2 (24–48 h), and (h) day 3 (48–72 h), during TY Soulik. (i–k) and (l–n) As in (f–h), but showing day 1 to day 3 QPFs made at 12:00 p.m. UTC 11 and 12 July 2013, respectively. The classification group (see text for details) and observed maximum and averaged amounts are given in the lower right corner in (a–e) and are also marked in (c). The color scales are identical for all panels.
Atmosphere 12 01501 g004
Atmosphere 12 01501 g005 550
Figure 5. (a) TS and (b) BS of CReSS 24 h QPFs for day 1 (black), day 2 (red), and day 3 (blue) from the forecast made at 12:00 p.m. UTC 10 July 2013 as a function of threshold (mm). (c,d) and (e,f) As in (a,b), but from the forecasts made at 12:00 p.m. UTC 11 and 12 July 2013, respectively. The hit rate (H/N) and observed base rate (O/N) as percentages (%, rounded to integer) are labeled for selected points inside the panels for TS (left) and BS (right), where the base rate at 10% is marked (vertical dashed line). The classification group of T (for T10) or A–D (left, n/a for not available) and the observed maximum 24 h rainfall (right, mm, rounded to integer) are also given in the upper right corner inside the panels.
Figure 5. (a) TS and (b) BS of CReSS 24 h QPFs for day 1 (black), day 2 (red), and day 3 (blue) from the forecast made at 12:00 p.m. UTC 10 July 2013 as a function of threshold (mm). (c,d) and (e,f) As in (a,b), but from the forecasts made at 12:00 p.m. UTC 11 and 12 July 2013, respectively. The hit rate (H/N) and observed base rate (O/N) as percentages (%, rounded to integer) are labeled for selected points inside the panels for TS (left) and BS (right), where the base rate at 10% is marked (vertical dashed line). The classification group of T (for T10) or A–D (left, n/a for not available) and the observed maximum 24 h rainfall (right, mm, rounded to integer) are also given in the upper right corner inside the panels.
Atmosphere 12 01501 g005
Atmosphere 12 01501 g006 550
Figure 6. The TS of 24 h QPFs for (a) day 1 (0–24 h), (b) day 2 (24–48 h), and (c) day 3 (48–72 h) by the CReSS model for 29 typhoons from 2010–2015 in Taiwan as a function of rainfall threshold (mm) for group T10, groups A to D, and all segments. For each group at a threshold, a single 2 × 2 contingency table was used. The scores of single forecasts for TY Morakot in 2009 (MRK, target period: 12:00 a.m.–12:00 p.m. UTC 8 Aug 2009, days 1–2 only) are also plotted. (d) Total numbers of verification points involved to compute the TS (H + M + FA) in day 1 QPFs for the various groups and MRK across the thresholds (in logarithmic scale).
Figure 6. The TS of 24 h QPFs for (a) day 1 (0–24 h), (b) day 2 (24–48 h), and (c) day 3 (48–72 h) by the CReSS model for 29 typhoons from 2010–2015 in Taiwan as a function of rainfall threshold (mm) for group T10, groups A to D, and all segments. For each group at a threshold, a single 2 × 2 contingency table was used. The scores of single forecasts for TY Morakot in 2009 (MRK, target period: 12:00 a.m.–12:00 p.m. UTC 8 Aug 2009, days 1–2 only) are also plotted. (d) Total numbers of verification points involved to compute the TS (H + M + FA) in day 1 QPFs for the various groups and MRK across the thresholds (in logarithmic scale).
Atmosphere 12 01501 g006
Atmosphere 12 01501 g007 550
Figure 7. As in Figure 6a–c, but showing the TS computed for (a) day 1, (b) day 2, and (c) day 3 for all segments and the groups with observed peak 24 h rainfall reaching 200, 350, 500, and 750 mm for typhoons in 2010–2015, as well as for Morakot (days 1–2 only). The total numbers of 24 h segments in each group are given in the parentheses, and the scores for all events and Morakot are identical to those in Figure 6.
Figure 7. As in Figure 6a–c, but showing the TS computed for (a) day 1, (b) day 2, and (c) day 3 for all segments and the groups with observed peak 24 h rainfall reaching 200, 350, 500, and 750 mm for typhoons in 2010–2015, as well as for Morakot (days 1–2 only). The total numbers of 24 h segments in each group are given in the parentheses, and the scores for all events and Morakot are identical to those in Figure 6.
Atmosphere 12 01501 g007
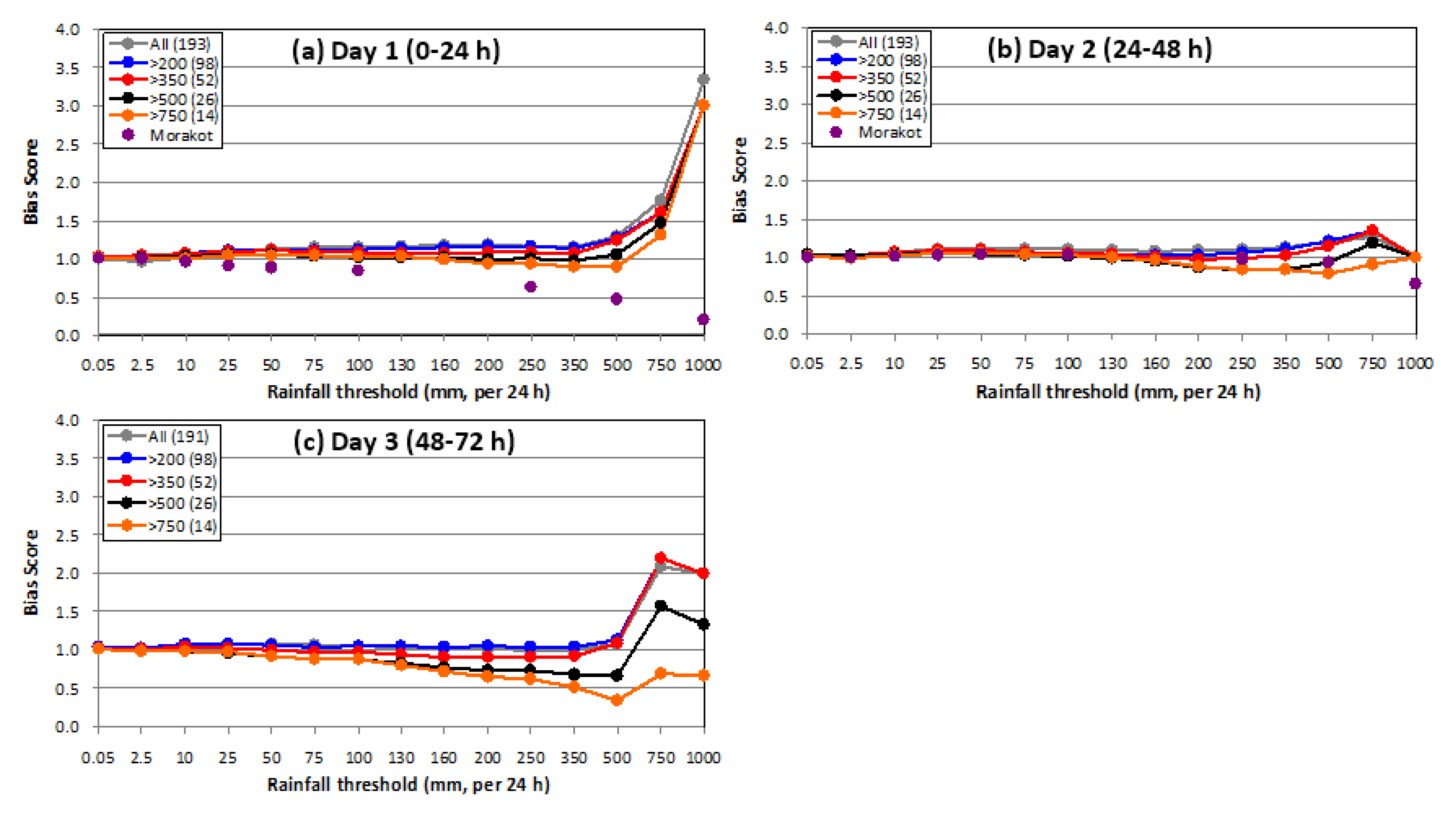
Atmosphere 12 01501 g008 550
Figure 8. As in Figure 7, but showing the BS for (a) day 1, (b) day 2, and (c) day 3 for the groups with different observed peak 24 h rainfall for typhoons in 2010–2015 and for Morakot (days 1–2 only).
Figure 8. As in Figure 7, but showing the BS for (a) day 1, (b) day 2, and (c) day 3 for the groups with different observed peak 24 h rainfall for typhoons in 2010–2015 and for Morakot (days 1–2 only).
Atmosphere 12 01501 g008
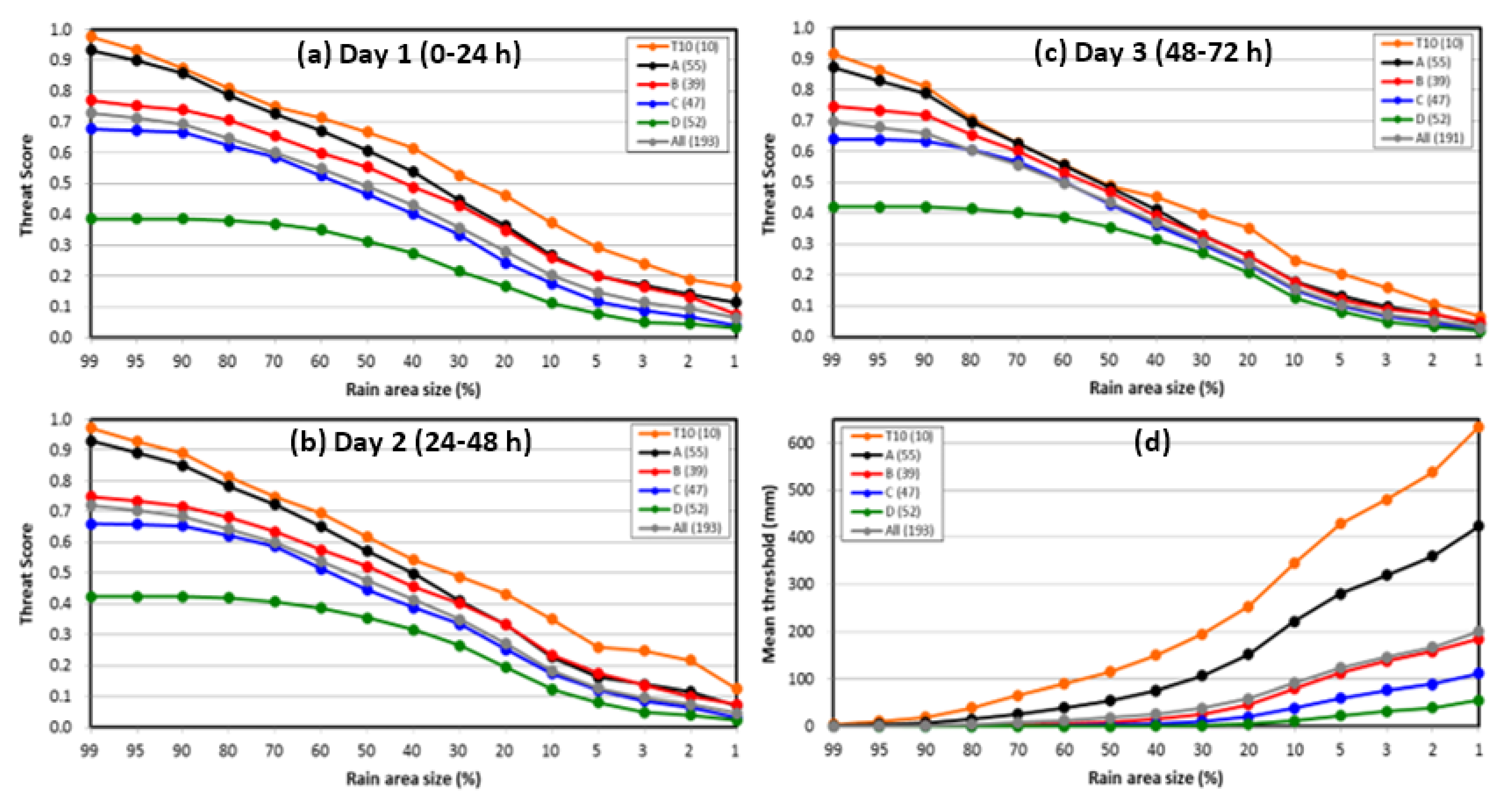
Atmosphere 12 01501 g009 550
Figure 9. (a–c) As in Figure 6a–c, but showing the TS for groups A–D, group T10, and all typhoon events as a function of observed rain-area size (%), instead of rainfall threshold, for (a) day 1, (b) day 2, and (c) day 3. (d) As in (a), but for mean threshold of the six groups (same for days 1–3). The total numbers of 24 h segments in each group are given in parentheses.
Figure 9. (a–c) As in Figure 6a–c, but showing the TS for groups A–D, group T10, and all typhoon events as a function of observed rain-area size (%), instead of rainfall threshold, for (a) day 1, (b) day 2, and (c) day 3. (d) As in (a), but for mean threshold of the six groups (same for days 1–3). The total numbers of 24 h segments in each group are given in parentheses.
Atmosphere 12 01501 g009
Table
Table 1. The basic domain and configuration of the 2.5 km CReSS in 2010–2015.
Table 1. The basic domain and configuration of the 2.5 km CReSS in 2010–2015.
Season2010–201120122013–2015
Grid spacing (km)2.5 × 2.5 × 0.2−0.663 (0.5) *
Grid dimension (x, y, z)432 × 360 × 40600 × 480 × 40
Domain size (km)1080 × 900 × 201500 × 1200 × 20
Forecast interval and rangeEvery 6 h (initial times at 12:00 a.m., 6:00 a.m., 12:00 p.m., and 6:00 p.m. UTC), 72/78 h
IC/BCsNCEP GFS analyses and forecasts (26 levels)
Grid spacing of IC/BCs1.0° × 1.0°0.5° × 0.5°
* The vertical grid spacing of CReSS is uneven and stretched (smallest at bottom), and the parentheses give the averaged value.
Table
Table 2. List of the 29 typhoon cases, their data period, number of 24 h segments (12:00–12:00 a.m. and 12:00–12:00 p.m. UTC), and classification (group A–D or T10, in chronical order) included in this study. The 10 segments in group T10 are denoted by “T” in the classification, and this group is a subset of group A. TY Lionrock shares a period (brackets) with Namtheun, and it is counted only once. A summary of the sample size is given at the bottom. The cases in 2010–2012 were the same as W15 [31].
Table 2. List of the 29 typhoon cases, their data period, number of 24 h segments (12:00–12:00 a.m. and 12:00–12:00 p.m. UTC), and classification (group A–D or T10, in chronical order) included in this study. The 10 segments in group T10 are denoted by “T” in the classification, and this group is a subset of group A. TY Lionrock shares a period (brackets) with Namtheun, and it is counted only once. A summary of the sample size is given at the bottom. The cases in 2010–2012 were the same as W15 [31].
NameData PeriodNo. of SegmentsClassification
Lionrock (2010)12:00 a.m. UTC 28 August–12:00 p.m. UTC 3 September8CC[CBAB]CBACDD
Namtheun (2010)12:00 a.m. UTC 29–12:00 p.m. UTC 31 August4CBAB
Meranti (2010)12:00 a.m. UTC 6–12:00 p.m. UTC 11 September10DDDDCBBCDC
Fanapi (2010)12:00 a.m. UTC 16–12:00 p.m. UTC 21 September10DDDDBATACD
Megi (2010)12:00 a.m. UTC 19–12:00 p.m. UTC 24 October10BBBATABCDD
Aere (2011)12:00 a.m. UTC 9–12:00 a.m. UTC 10 May1D
Songda (2011)12:00 a.m. UTC 26–12:00 p.m. UTC 29 May6CCBCDD
Meari (2011)12:00 a.m. UTC 24–12:00 p.m. UTC 26 June4BABC
Muifa (2011)12:00 a.m. UTC 6–12:00 p.m. UTC 7 August2DD
Nanmadol (2011)12:00 a.m. UTC 27 August–12:00 p.m. UTC 1 September10BAAAAAACCC
Talim (2012)12:00 a.m. UTC 19–12:00 p.m. UTC 22 June6BAABCC
Doksuri (2012)12:00 a.m. UTC 28–12:00 p.m. UTC 30 June4CCDD
Saola (2012)12:00 a.m. UTC 30 Jul–12:00 p.m. UTC 3 August8BAAAATAA
Tembin (2012)12:00 a.m. UTC 22–12:00 p.m. UTC 28 August12CCBAABCDDDBB
Jelawat (2012)12:00 a.m. UTC 27–12:00 p.m. UTC 29 September4DCCD
Soulik (2013)12:00 a.m. UTC 11–12:00 p.m. UTC 16 July10DDATACCCDD
Cimaron (2013)12:00 a.m. UTC 17–12:00 p.m. UTC 20 July6CCDDDD
Trami (2013)12:00 a.m. UTC 19–12:00 p.m. UTC 24 August10DBAATAABBB
Kong-Rey (2013)12:00 a.m. UTC 27–12:00 p.m. UTC 31 August8DDATAAAA
Usagi (2013)12:00 a.m. UTC 19–12:00 p.m. UTC 24 September10DDBAAABCDD
Fitow (2013)12:00 a.m. UTC 4–12:00 p.m. UTC 9 October10DCCBCDDDDD
Matmo (2014)12:00 p.m. UTC 21–12:00 p.m. UTC 24 July5BATAC
Fung-Wong (2014)12:00 a.m. UTC 20–12:00 p.m. UTC 23 September6BTABDC
Noul (2015)12:00 a.m. UTC 11–12:00 a.m. UTC 12 May1C
Linfa (2015)12:00 p.m. UTC 6–12:00 a.m. UTC 10 July6CBBCCB
Chan-Hom (2015)12:00 p.m. UTC 9–12:00 p.m. UTC 11 July3BBC
Souledor (2015)12:00 a.m. UTC 6–12:00 p.m. UTC 9 August6DCATAA
Goni (2015)12:00 a.m. UTC 20–12:00 p.m. UTC 24 August8DDCBBBCD
Dujuan (2015)12:00 a.m. UTC 27–12:00 a.m. UTC 30 September5CATAD
Total 193A: 55, B: 39, C: 47, D: 52
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wang, C.-C.; Chang, C.-S.; Wang, Y.-W.; Huang, C.-C.; Wang, S.-C.; Chen, Y.-S.; Tsuboki, K.; Huang, S.-Y.; Chen, S.-H.; Chuang, P.-Y.; et al. Evaluating Quantitative Precipitation Forecasts Using the 2.5 km CReSS Model for Typhoons in Taiwan: An Update through the 2015 Season. Atmosphere 2021, 12, 1501. https://doi.org/10.3390/atmos12111501

AMA Style

Wang C-C, Chang C-S, Wang Y-W, Huang C-C, Wang S-C, Chen Y-S, Tsuboki K, Huang S-Y, Chen S-H, Chuang P-Y, et al. Evaluating Quantitative Precipitation Forecasts Using the 2.5 km CReSS Model for Typhoons in Taiwan: An Update through the 2015 Season. Atmosphere. 2021; 12(11):1501. https://doi.org/10.3390/atmos12111501

Chicago/Turabian Style

Wang, Chung-Chieh, Chih-Sheng Chang, Yi-Wen Wang, Chien-Chang Huang, Shih-Chieh Wang, Yi-Shin Chen, Kazuhisa Tsuboki, Shin-Yi Huang, Shin-Hau Chen, Pi-Yu Chuang, and et al. 2021. "Evaluating Quantitative Precipitation Forecasts Using the 2.5 km CReSS Model for Typhoons in Taiwan: An Update through the 2015 Season" Atmosphere 12, no. 11: 1501. https://doi.org/10.3390/atmos12111501

APA Style

Wang, C. -C., Chang, C. -S., Wang, Y. -W., Huang, C. -C., Wang, S. -C., Chen, Y. -S., Tsuboki, K., Huang, S. -Y., Chen, S. -H., Chuang, P. -Y., & Chiu, H. (2021). Evaluating Quantitative Precipitation Forecasts Using the 2.5 km CReSS Model for Typhoons in Taiwan: An Update through the 2015 Season. Atmosphere, 12(11), 1501. https://doi.org/10.3390/atmos12111501

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop