Abstract
This study describes the process of deriving integrated water vapor (IWV) from (a) a set of 18 GPS receivers that were installed at different airports across India and (b) a pair of GPS receivers located in Ahmedabad situated around 8 km apart. The Zenith Tropospheric Delay was estimated from the GPS observations using the GAMIT software. Further, IWV was estimated from the ZTD values using surface temperature and pressure from ERA-I reanalysis as additional inputs. The IWV estimates for 1 year—March 2013 to February 2014—were compared with ECMWF Reanalysis Interim (ERA-I) reanalysis as well as radiosonde soundings. The Root Mean Squared Error (RMSE) was ≈6 mm or better for most stations. The IWV estimates for July 2013 were assimilated into the WRF model and had a positive impact on model analysis of IWV. The forecasted rain improved by up to 3–4 mm/day in some regions as a result of GPS-derived IWV estimates. For the Ahmedabad receivers, the GPS-derived IWV was compared with IWV from ERA-I reanalysis and was found to have a RMSE of ≈7.7 mm which is <20% of the mean value. The study demonstrates that the observed IWV variation is consistent with rainfall patterns over Ahmedabad. The rise and dips in the IWV correlate well with the active-break cycle in the monsoon rain. The study demonstrates the value of local measurements of IWV with high temporal frequency, as they are more likely to respond to fast-moving weather phenomena such as rainfall. Thus, the GPS-derived IWV measurements are likely to have significant value in the short-term forecasts of precipitation.
1. Introduction
Atmospheric water vapour is a critical atmospheric parameter that plays an important role in the transfer of energy in the atmosphere and to our understanding of weather phenomena [1]. Improved knowledge of its distribution would likely result in significant improvements in weather forecasting, particularly in the tropics. An improvement in short-range cloud and precipitation forecasts is one of the major goals of the atmospheric modeling community, which is restricted by the lack of frequent and accurate water vapour measurements. The deficiency of accurate water vapour observations over a large portion of the globe impedes the skill of precipitation forecasting in numerical weather prediction (NWP) models [2]. Particularly over the south-Asia region, water vapour remains one of the most poorly characterized meteorological parameters [3]. Traditional measurements of water vapour, radiosonde soundings, are temporally and spatially infrequent over the Indian region relative to other developed countries. Atmospheric soundings in Visible and InfraRed bands from geostationary satellites are accurate only over clear-sky conditions. Microwave satellites provide more accurate measurements in cloudy conditions, but have poor temporal sampling over a specific location. Further, the accuracy of microwave frequency instruments over land is poor, as the land surface has high - and highly variable- emissivity over land surfaces. Thus, it is likely that advanced data assimilation schemes like four-dimensional variational (4D-Var) method, implemented in many operational centres, would provide improved weather forecasts if frequent, accurate observations of water vapour were available.
Rainfall and IWV are closely related in the tropics [4]. However, as suggested by earlier studies [5], it is unlikely that the increase in IWV may only be attributed to precipitation. The relationship of IWV with precipitation is quite complex and inhomogeneous; however, it is considered to be reasonably strong in the tropical regions. The peaks of IWV indicate events of strong precipitation, due to tropospheric moistening of convective cells resulting in positive moisture-convection feedback [6]. Due to this positive correlation, the IWV qualifies naturally as a potentially useful parameter for prediction of rain, a hypothesis which is tested later in this manuscript.
Estimation of IWV has been done conventionally with radiosonde balloon sounding at globally distributed network of stations at 00Z and 12Z UTC. While still continuing, these observations, owing to their low temporal sampling (only twice a day) and issues of instrument calibration, are deemed to have limited usefulness in studies related to short-term prediction of IWV. Other ground-based instruments such as Lidars and Fourier transform infrared spectrometer can only profile precipitable water below the clouds [7].
The ground-based GPS sensing of IWV, demonstrated by Rocken et al. [1,8,9] to have an RMSE of 1–2 mm, is an alternative technique with several characteristic advantages over the earlier measurement techniques, discussed in the previous paragraph. The GPS-sensed IWV has a significantly higher temporal sampling, of up to a minute or less, making it principally suitable for the study of high-rate variability of IWV. This, in turn, may be vital to the process of understanding the causal relationship between the build-up and decay of IWV and the likelihood of the occurrence or non-occurrence of convective rain events. This understanding forms a significant first step towards devising a proper approach to model the relationship for the short-term prediction system for IWV based rain events. Additionally, the GPS-based technique is relatively unaffected by instrument calibration, unlike radiosondes and MWR, ensuring signal fidelity and measurement reliability. This is particularly significant when it comes to up-scaling the location-based methodology to a wider network of GPS ground-tracking stations. The concept of network-based analysis of GPS measurements is important as has been revealed in Tregoning et al. (1998) wherein they concluded that better estimates of precipitable water can be obtained with GPS analysis between stations separated by more than 2000 km. Accuracy of the GPS estimates of IWV has been demonstrated by several more studies such as by Emardson et al. (1998) showing 1–2 mm RMSE compared to MWR and of 1.4 mm in Tregoning et al. [10], when compared to either radiosonde or MWR. That the agreement between GPS- and microwave radiometer-sensed IWV depends on the total water vapor loading of the atmosphere at the measurement location has, more recently, been shown in Liou et al. (2000). The impact of high water vapor loading on the RMSE of GPS-sensed IWV compared to MWR measurement of IWV has been shown to dominate even in the case with large baseline of GPS stations [11]. That, high atmospheric inhomogeneity in the humid region may affect the consistency of measurements made by the two techniques with widely different volumetric sampling geometry, is offered as a plausible explanation for the large RMSE. These are important considerations to be factored in when comparing GPS estimates of IWV with either radiosonde or MWR. Since geometry plays an important role in GPS estimates of IWV, it is worthwhile to discuss the fundamental principle of GPS sensing of the atmosphere and the associated estimation of IWV.
The GPS data used in the study have been obtained from the Indian Satellite Based Augmentation System project named—GAGAN (GPS Aided Geo Augmented Navigation). Under this project, 18 dual-frequency GPS receivers were established in India in 2004 to monitor, study, and develop region specific ionospheric models for implementation in GAGAN [12]. The number of GPS receivers under this network was increased to 26 in 2009-10. The dual frequency GPS receivers “GSV4004A/B” have been customized to provide Ionospheric Total Electron Content (TEC) and L-band scintillation measurements (S4 Index) in addition to usual ‘range’ and ‘ephemeris’ logs. The range logs are sampled at 10 s interval which provide pseudo range (m) and carrier phase (cycles) at L1 and L2 bands. The raw data is converted to RINEX format which is the standard format for GPS processing. In this study, we have analysed GPS-derived IWV data for the 1-year time period between March 2013–February 2014. There were a total of 19 receivers (at 18 distinct locations) available during this time period. Additionally, a pair of dual-frequency GPS receivers in Ahmedabad city have been used to explore the correlation of GPS-derived IWV with localized rainfall.
Various sensitivity studies have been performed to assimilate the GPS IWV data to improve the prediction skill of numerical models [13,14,15]. Kuo et al. [14] showed that the assimilation of precipitable water improves the vertical structure of moisture and precipitation predictions. Vedel et al. [15] processed GPS data from Western Europe network and assimilated into the HIRLAM NWP model. Authors found neutral impact in general, but for a severe rain event, assimilation of GPS improved the forecast skill and suggested that the GPS data has excellent potential for improving numerical models in rapidly developing, high moisture flux situations. The most significant finding is that the forecast skill is improved with assimilation of GPS-IWV data each year as the number of stations has increased; this suggests that the increase in the network density can lead to further forecast improvement. In the Indian context, Kumar et al. [16] found a small positive impact on 24-h forecasts upon assimilating observations from a single GPS station in Bangalore. In contrast, the current study analyzes the impact of IWV derived from a network of GPS stations.
In the following section, we describe the procedure used to derive IWV from the GPS data.
2. Estimating Integrated Water Vapour from GPS Network
In this section, we describe the procedure used to estimate IWV from the raw GPS data collected by the network of GPS receivers. In addition, we present the results of inter-comparisons of GPS-derived IWV with corresponding IWV estimates from radiosondes as well as ERA-I reanalysis [17].
2.1. Estimating Zenith Tropospheric Delay Using GAMIT Software
The observed range by a GNSS receiver is combination of the true range between the receiver and the satellite, as well as the ionospheric delay, the tropospheric delay and the error in the range due to the clock offset between the receiver and the satellite.The parameter of our interest, the zenith tropospheric delay (ZTD), was estimated using GAMIT software (Herring et al. [18]). The software was configured to process all available GPS stations, along with IGS reference stations located at Bangalore, Hyderabad, Lhasa, Urumqi, Irkutsk and Kitab. The IGS stations were solely used as a reference for the GAMIT software, and not for any subsequent analysis. GAMIT was configured to generate ZTD estimates at half-hour intervals. The default configuration was used for most other processing parameters.
2.2. IWV Estimation
The GNSS-derived IWV was calculated from the ZTD using the procedure described in Bevis et al. [19]. The main steps in the procedure are described below: The ZTD is modelled as a combination of a zenith hydrostatic delay (ZHD) (which does not depend on atmospheric humidity) and a zenith wet delay (ZWD) which is a function of the IWV. The ZHD (in millimetres) is modelled using the model described in Elgered et al. [20]:
where is the surface pressure (in millibars) at the station, is the latitude of the station (in degrees) and H is the altitude of the station (in kilometres).
The Zenith Wet Delay (ZWD) is obtained by subtracting the ZHD from the total tropospheric delay.
The IWV (in millimeters) is expressed as:
where is the density of water and the parameter k is calculated using the expression:
where is the specific gas constant for water vapour and is pressure-weighted mean temperature of the atmospheric column. The values and 17 are used for the constants and [21]. Bevis expresses as a linear function of the surface temperature Ts using radiosonde profiles over Albany, New York. We use the same linear function for our calculations, though regional differences in the optimal coefficients have been reported. The surface pressure and temperature values required for performing the estimation of IWV from ZTD were obtained from the ERA-I product. These surface estimates are provided every 6 h by ERA-I; the 6-hourly estimates are interpolated linearly to 30 min time intervals corresponding to the GPS ZTD estimates.
2.3. IWV Data Validation
The IWV estimates were compared station-wise both with IWV estimates from ERA-I as well as from radiosonde soundings. We note that the GPS-derived IWV estimates are not completely independent of the ERA-I estimates, as the surface parameters from ERA-I are used in the conversion of ZTD to IWV in our procedure. Figure 1 shows the bias and RMSE between the IWV estimates from GPS and ERA-I. Large positive biases of 20 mm and higher were observed in Mumbai, Bagdogra, Vishakapatnam and Guwahati.
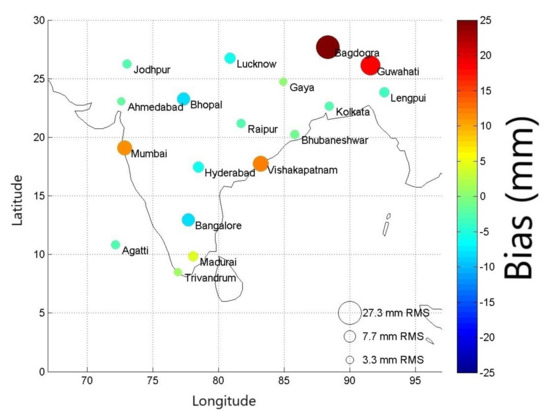
Figure 1.
Bubble plot depicting station-wise comparison between GPS-derived IWV and IWV from ERA-I. (The colors depict the bias in mm for each station, and the size of the bubbles depict the RMSE).
Further analysis revealed that the primary contribution to these biases was from the substantial differences in surface pressure estimates from ERA-I (used in the IWV calculation) compared to estimates from Integrated Global Radiosonde Archive (IGRA) radiosonde data [22]; in some cases the mean surface pressure differences were as high as 60 hPa. The mean biases in the surface pressure between ERA-I and IGRA radiosonde data were calculated station-wise for all available data from 2013 and 2014, and a corresponding bias correction term was applied to each station to eliminate the mean bias in surface pressure. Figure 2 shows the bias and RMSE between the IWV estimates from GPS and ERA-I after applying the bias correction for surface pressure. The IWV biases in Bagdogra and Guwahati reduce from 15–25 mm to under 6 mm. Similar reduction in IWV bias is seen in Vishakapatnam and Mumbai. The median RMSE for the set of GPS stations drops from 7.7 mm to 4.8 mm (i.e., to under 15 percent of the mean value) as a result of the correction of surface pressure. We acknowledge that this is a somewhat ad-hoc solution; Parracho et al. [23] have utilized a more sophisticated interpolation scheme to adjust the surface pressure values for stations which either lie between 2 pressure levels, or which have surface pressure values greater than 1000 hPa. However, since our ad-hoc correction is successful in correcting a significant portion of the error—and since our primary focus is on the highly variable ZWD rather than the hydrostatic delay—we believe that our ad-hoc bias correction is an acceptable solution to the problem.
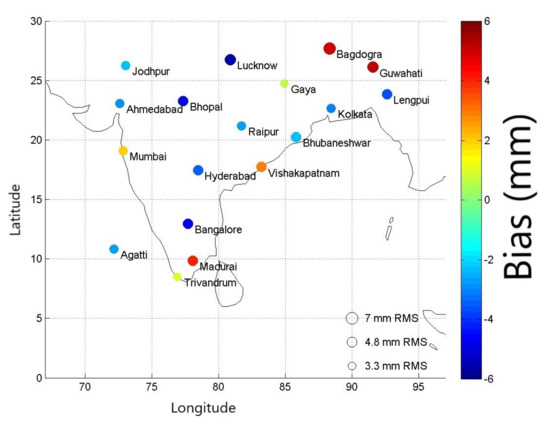
Figure 2.
Bubble plot depicting station-wise comparison between GPS-derived IWV and IWV from ERA-I after bias correction of surface pressure. (The colors depict the bias in mm for each station, and the size of the bubbles depict the RMSE).
The GPS-derived IWV estimates were also compared to IWV from the IGRA radiosonde archives. The comparison was restricted to stations where there were at least 100 matching observations from both IGRA and GPS. There were 7 stations that satisfied this condition; the summary statistics from the comparison are shown in Table 1. The overall bias between GPS-derived and IGRA IWV is close to zero and the RMSE values are generally under 6 mm (around 15% of the mean value of IWV).

Table 1.
Comparison of GPS-derived IWV with IGRA radiosonde data.
3. Local Experiment with Pair of GPS Receivers in Ahmedabad
Another experiment conducted as part of this study was to examine the utility of reducing the baseline distance between GPS receivers for IWV estimation and subsequent short-range forecasts of rainfall. For this purpose, a pair of GPS receivers were installed in Ahmedabad, as shown in the Table 2 below.

Table 2.
Receiver locations in Ahmedabad.
The GPS samples are logged at the rate of 10 samples per second, and the data is processed using the methods described previously. The data from July 2016–September 2016 (corresponding to the peak monsoon season in Ahmedabad) are used for our analysis.The IWV estimates between the different stations were found to match each other to under ≈1 mm both on rainy as well as dry days. This indicates that both GPS receivers are functioning well. However, this also implies that we were unable to discriminate between the signals of the different receivers due to the high spatial density of the cluster. This finding is not entirely unexpected; as the the ZTDs represent the cone average of IWV along different slant paths (based on the location of the different GPS satellites). Thus, each IWV estimate represents the area average of over 30–40 km. Since the distance between both receivers is in the range of ≈10 km, there is significant overlap between the area being observed by the different receivers. Further, IWV is generally a slow-varying parameter and significant variations in IWV are expected only over distances of 100–200 km. Thus, we find negligible benefit of having such dense baselines in the estimation of IWV.
The IWV estimates derived from the GPS cluster were compared to ERA-I reanalysis, and were found to be well correlated as shown in Figure 3. The RMSE is ≈7.7 mm which is consistent with our earlier results. The reanalysis estimates are consistently higher than the GPS IWV by ≈7 mm; this is qualitatively similar to the differences observed in Section 2. However, we find that the IWV estimates derived from radiosonde soundings (which are more accurate than the reanalysis data) lie in between the GPS and the ERA-I values. Since the GPS IWV lies within the range of uncertainty shown by the different reference data, we do not apply any bias corrections on the GPS IWV.
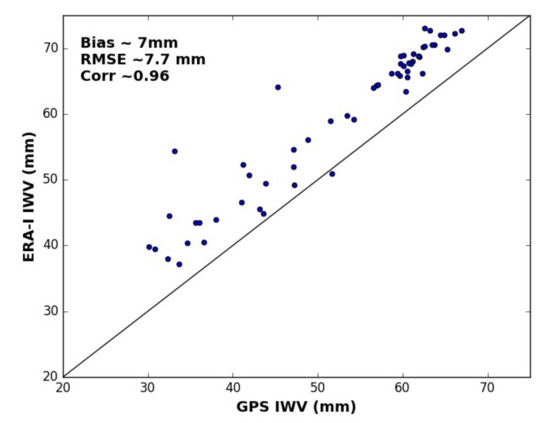
Figure 3.
Comparison of IWV estimates from GPS cluster in Ahmedabad and ERA-I reanalysis data.
Additionally, we show the time series plot of rainfall in conjunction with the estimated IWV values from the Ahmedabad stations for July–September 2016 in Figure 4. The IWV values are generally greater than 60 mm during the rainy phases of the monsoon. The IWV generally peaks during active phases of the monsoon (periods with significant rainfall accumulation); though the correspondence does not hold very strongly on a day-to-day basis. The plot shows the IWV plotted at lead times of 3 h to 36 h relative to the rainfall measurements with the GPS-derived IWV with each lead-time being considered a potential “predictor” of rainfall; however, the different lead times have mostly similar patterns relative to the rainfall accumulation. Overall, we were unable to demonstrate any observable benefit of having GPS receivers at short-baselines in improving either the accuracy of GPS-derived IWV or its potential for short-range forecasts of precipitation.
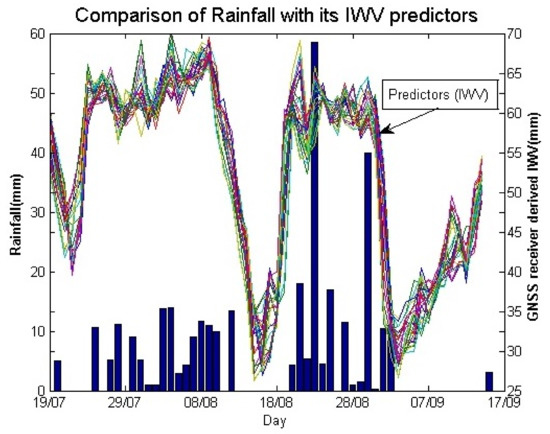
Figure 4.
Time-series plot of GPS IWV estimates and rainfall in Ahmedabad.
4. Short-Range Forecasts of Rainfall Using IWV Estimates
The non-hydrostatic primitive equation Weather Research and Forecasting (WRF) model and its four-dimensional variational data assimilation (4D-Var) scheme are used in this study to assimilate the hourly IWV observations retrieved from the GPS receivers. The Advanced Research WRF (ARW) core-model version 3.4—with WRF single-moment six-class microphysics, the Kain-Fritsch cumulus convection parameterization scheme, and the Yonsei University planetary boundary layer scheme are used in this study. The rapid radiative transfer model and Dudhia scheme are used for longwave and shortwave radiation, respectively. With the availability of high temporal resolution IWV observations, 4D-Var assimilation method uses the model dynamics to compute the model’s equivalent value at the valid report time of the observation. The WRF 4D-Var method is based on incremental 4D-Var formulation to produce the model analysis. The model simulations are performed using nested domain with two-way feedback. The outer domain simulations are performed at 75 km × 75 km spatial resolution covering region (50 E–120 E, 20 S–50 N), and inner domain are performed at 25 km × 25 km spatial resolution covering Indian region (66–100 E, 7–38 N). All results are based on Inner model domain performed at 25 km spatial resolution. A detailed description of the WRF model physics and 4-D-Var system can be found in Kumar et al. [3] and Mandal et al. [24].
Two simultaneous assimilation experiments (GPS and CNT) are performed in this study with and without assimilation of GPS-derived IWV during summer monsoon 2013. The control experiment (CNT) uses conventional data and satellite winds and profiles, while the GPS experiment uses GPS-derived IWV in addition to this data. Six hourly 4D-Var assimilation cycle are performed starting from 0000 UTC 01 July 2013 to 0000 UTC 31 July 2013 to assimilate the hourly GPS data (see Figure 5). Instead of directly starting from the NCEP Global Data Assimilation System (GDAS) analysis, six hourly WRF model forecast valid at 0000 UTC 01 July 2013 is used for initial condition for both the assimilation experiments. In cycling approach, forecast from previous cycle uses as the background for the next cycle, which is more consistent with forecast model. Conventional observations like SONDE, SYNOP, METAR, BUOY, SHIP, etc. are used in all the experiments. Lateral boundary conditions are taken from NCEP GDAS analysis.
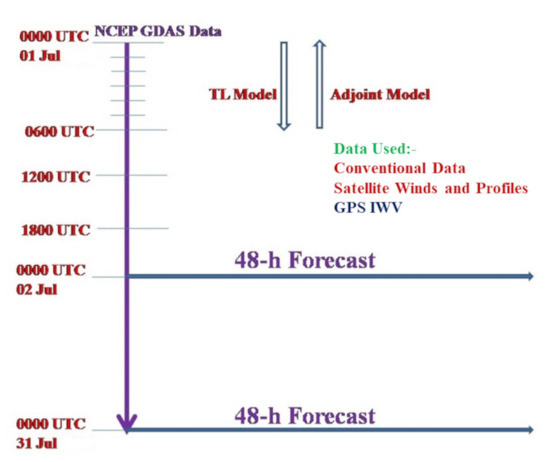
Figure 5.
Schematic diagram depicting the assimilation of GPS-IWV data. Conventional Data as well as Satellite winds are assimilated 6-hourly for the control run (CNT) and GPS-IWV is added for the other experimental run).
Figure 6a shows the IWV first guess (Observation-Background) and analysis (Observation-Analysis) departures for the entire month of the July 2013. The first-guess and analysis departures have a RMSE of 3.78 mm and 1.79 mm, respectively. The mean differences are changed from 0.21 mm (O-B) to 0.38 mm (O-A). The first guess and analysis RMSE show that in all the cases model IWV analysis are better matched with the GPS-IWV data than the background which confirms the successful assimilation of GPS-derived IWV using WRF 4D-Var. Figure 6b shows the percentage change in the RMSE in the model analysis of IWV. The impact on model analysis is largely positive, with many grid points showing improvements of up to 30%. The map only displays the grid points where the change in forecast skill is statistically significant at 95% confidence interval; further, the comparison is carried out only over land.
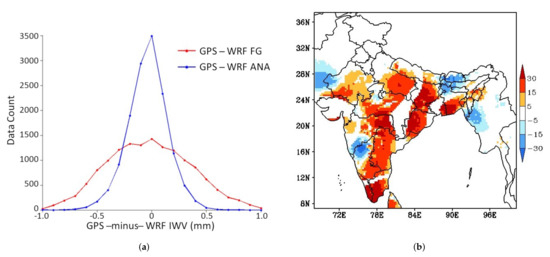
Figure 6.
(a) (left) Comparison of histograms of IWV First-Guess (FG) and Analysis (ANA); and (b) (right) Map showing the change IWV analysis error (in percent) after assimilation. Positive values correspond to decrease in RMSE (improvement in skill) and negative values correspond to increase in RMSE (degradation in skill).
The impact of assimilation of GPS-IWV on 24-h forecasts of IWV as well as rainfall is shown in Figure 7. The impact on IWV is mixed, whereas there is a modest positive impact on the rain forecasts, especially to the east of the Western ghats. In this region, the model significantly overestimates rainfall in the CNT run; this overestimation is reduced by an average of 3–4 mm/day upon assimilation of GPS-derived IWV.
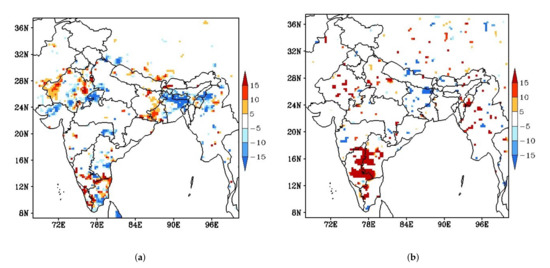
Figure 7.
Map showing the percentage change in 24-h forecast error after assimilation for (a) (left) IWV and (b) (right) Surface Rainfall. Positive values correspond to decrease in RMSE (improvement in skill) and Negative values correspond to increase in RMSE (degradation in skill).
5. Discussion
This manuscript describes an observational study of GPS-derived IWV over India. The Zenith Tropospheric Delay was estimated from the GPS observations using the GAMIT software. Further, IWV was estimated from the ZTD values using surface temperature and pressure from ERA-I reanalysis as additional inputs. The GPS-derived IWV estimates for 1 year—March 2013 to February 2014—were compared station-wise with corresponding IWV from ERA-I reanalysis as well as radiosonde soundings. The RMSE relative to the reference values was ≈6 mm (approximately 15% of the mean) for most stations after applying corrections for surface pressure. While these results are encouraging, further analysis using longer-term data series is desirable to robustly characterize the error characteristics of GPS-derived IWV in the Indian region.
A pair of GPS stations at Ahmedabad were used to derive IWV for the period July–September 2016. The RMSE relative to ERA-I reanalysis was ≈7.5 mm. The IWV variation was found to correspond to the active-break cycle of the monsoon; the IWV peaks generally occurred during periods of high rainfall accumulation. However, we were unable to demonstrate any significant benefits from using data collected from GPS receivers situated at short baselines from each other. The estimates from both receivers tracked each other so closely that we were unable to extract independent information from each instrument.
The GPS-IWV estimates for July 2013 were assimilated into the WRF model and had a strong positive impact on model analysis of IWV. The forecasted rain to the east of the Western ghats improved by 3–4 mm/day as a result of GPS-derived IWV estimation. This finding of a small but significant positive impact on short-range forecasts is consistent with other studies reported in the literature. While Giannaros et al. [25] and Rohm et al. [26] show large improvements in precipitation forecasts over Greece and Central Europe respectively, Kumar et al. [16] and Risanto et al. [27] show modest positive impact of assimilating GPS-derived IWV. This study provides further evidence that GPS-derived weather observations have significant potential for positively impacting weather studies and forecasts in the Indian region.
Author Contributions
Conceptualization, K.G. and A.S.; methodology, K.G., P.K., B.P.S., S.S. (Som Sharma) and A.S.; software, K.G., B.P.S., P.K., S.S. (Surendra Sunda) and A.G.; validation, K.G., S.S. (Som Sharma) and A.G.; data curation, K.G., S.S. (Som Sharma) and S.S. (Surendra Sunda); writing—original draft preparation, K.G., A.S., B.P.S. and P.K.; writing—review and editing, K.G., S.S. (Som Sharma), B.P.S. and P.K.; visualization, K.G., P.K. and B.P.S.; supervision, S.S. (Som Sharma). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The GPS-derived IWV data is available at https://mosdac.gov.in/gps-derived-integrated-water-vapour, accessed on 2 October 2021. WRF model data available from authors upon request. ERA-Interim and IGRA radiosonde data are publicly available from ECMWF and NCEP respectively.
Acknowledgments
Data for this study was provided by the Indian Space Research Organization and the Airports Authority of India.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rocken, C.; Van Hove, T.; Ware, R. Near real-time GPS sensing of atmospheric water vapor. Geophys. Res. Lett. 1997, 24, 3221–3224. [Google Scholar] [CrossRef]
- Filiberti, M.; Eymard, L.; Urban, B. Assimilation of satellite precipitable water in a meteorological forecast model. Mon. Weather Rev. 1994, 122, 486–506. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.; Kishtawal, C.; Pal, P. Impact of satellite rainfall assimilation on Weather Research and Forecasting model predictions over the Indian region. J. Geophys. Res. Atmos. 2014, 119, 2017–2031. [Google Scholar] [CrossRef]
- Muller, C.J.; Back, L.E.; O’Gorman, P.A.; Emanuel, K.A. A model for the relationship between tropical precipitation and column water vapor. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Holloway, C.E.; Neelin, J.D. Temporal relations of column water vapor and tropical precipitation. J. Atmos. Sci. 2010, 67, 1091–1105. [Google Scholar] [CrossRef]
- Moncrieff, M.W. Analytic representation of the large-scale organization of tropical convection. J. Atmos. Sci. 2004, 61, 1521–1538. [Google Scholar] [CrossRef]
- Solheim, F.; Godwin, J.R.; Westwater, E.; Han, Y.; Keihm, S.J.; Marsh, K.; Ware, R. Radiometric profiling of temperature, water vapor and cloud liquid water using various inversion methods. Radio Sci. 1998, 33, 393–404. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Van Hove, T.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the Global Positioning System. Geophys. Res. Lett. 1993, 20, 2631–2634. [Google Scholar] [CrossRef]
- Rocken, C.; Hove, T.V.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. GPS/STORM GPS sensing of atmospheric water vapor for meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Tregoning, P.; Boers, R.; O’Brien, D.; Hendy, M. Accuracy of absolute precipitable water vapor estimates from GPS observations. J. Geophys. Res. Atmos. 1998, 103, 28701–28710. [Google Scholar] [CrossRef]
- Liou, Y.A.; Teng, Y.T.; Van Hove, T.; Liljegren, J.C. Comparison of precipitable water observations in the near tropics by GPS, microwave radiometer, and radiosondes. J. Appl. Meteorol. 2001, 40, 5–15. [Google Scholar] [CrossRef]
- Acharya, R.; Nagori, N.; Jain, N.; Sunda, S.; Regar, S.; Sivaraman, M.; Bandopadhyay, K. Ionospheric studies for the implementation of GAGAN. Indian J. Radio Space Phys. 2007, 36, 394–404. [Google Scholar]
- Smith, T.L.; Benjamin, S.G.; Gutman, S.I.; Sahm, S. Short-range forecast impact from assimilation of GPS-IPW observations into the Rapid Update Cycle. Mon. Weather Rev. 2007, 135, 2914–2930. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Guo, Y.R.; Westwater, E.R. Assimilation of precipitable water measurements into a mesoscale numerical model. Mon. Weather Rev. 1993, 121, 1215–1238. [Google Scholar] [CrossRef]
- Vedel, H.; Huang, X.Y.; Haase, J.; Ge, M.; Calais, E. Impact of GPS zenith tropospheric delay data on precipitation forecasts in Mediterranean France and Spain. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Kumar, P.; Gopalan, K.; Shukla, B.P.; Shyam, A. Impact of single-point GPS integrated water vapor estimates on short-range WRF model forecasts over southern India. Theor. Appl. Climatol. 2017, 130, 755–760. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Elgered, G.; Davis, J.; Herring, T.; Shapiro, I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. Solid Earth 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV trends and variability in atmospheric reanalyses and GPS observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef]
- Mandal, A.K.; Ramakrishnan, R.; Pandey, S.; Rao, A.; Kumar, P. An early warning system for inundation forecast due to a tropical cyclone along the east coast of India. Nat. Hazards 2020, 103, 2277–2293. [Google Scholar] [CrossRef]
- Giannaros, C.; Kotroni, V.; Lagouvardos, K.; Giannaros, T.M.; Pikridas, C. Assessing the impact of GNSS ZTD data assimilation into the WRF modeling system during high-impact rainfall events over Greece. Remote Sens. 2020, 12, 383. [Google Scholar] [CrossRef]
- Rohm, W.; Guzikowski, J.; Wilgan, K.; Kryza, M. 4DVAR assimilation of GNSS zenith path delays and precipitable water into a numerical weather prediction model WRF. Atmos. Meas. Tech. 2019, 12, 345–361. [Google Scholar] [CrossRef]
- Risanto, C.B.; Castro, C.L.; Arellano, A.F., Jr.; Moker, J.M., Jr.; Adams, D.K. The Impact of Assimilating GPS Precipitable Water Vapor in Convective-Permitting WRF-ARW on North American Monsoon Precipitation Forecasts over Northwest Mexico. Mon. Weather Rev. 2021, 149, 3013–3035. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).