The Impact of Utility-Scale Photovoltaics Plant on Near Surface Turbulence Characteristics in Gobi Areas
Abstract
1. Introduction
2. Site Overview and Methods
2.1. Site Overview
2.2. Flux Data Processing and Calculation Methods
3. Results and Discussion
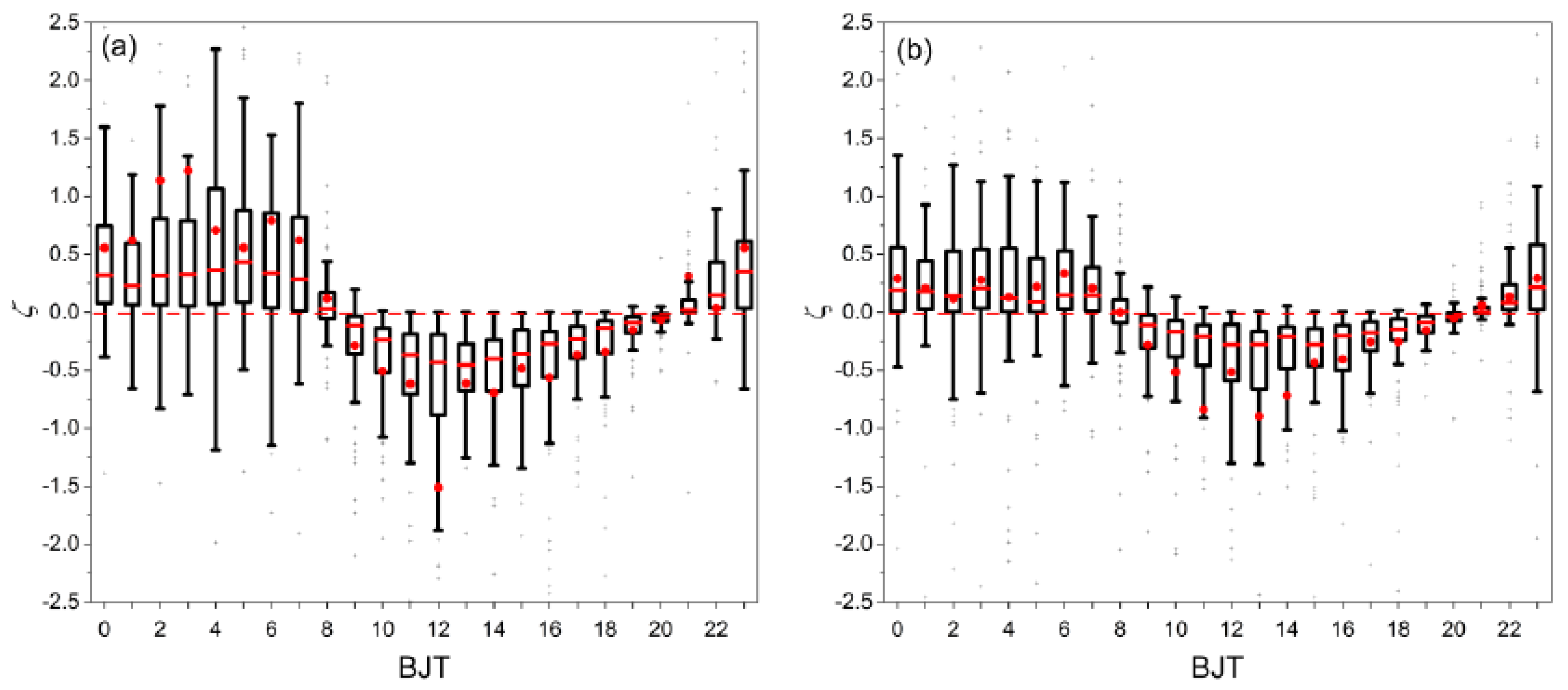
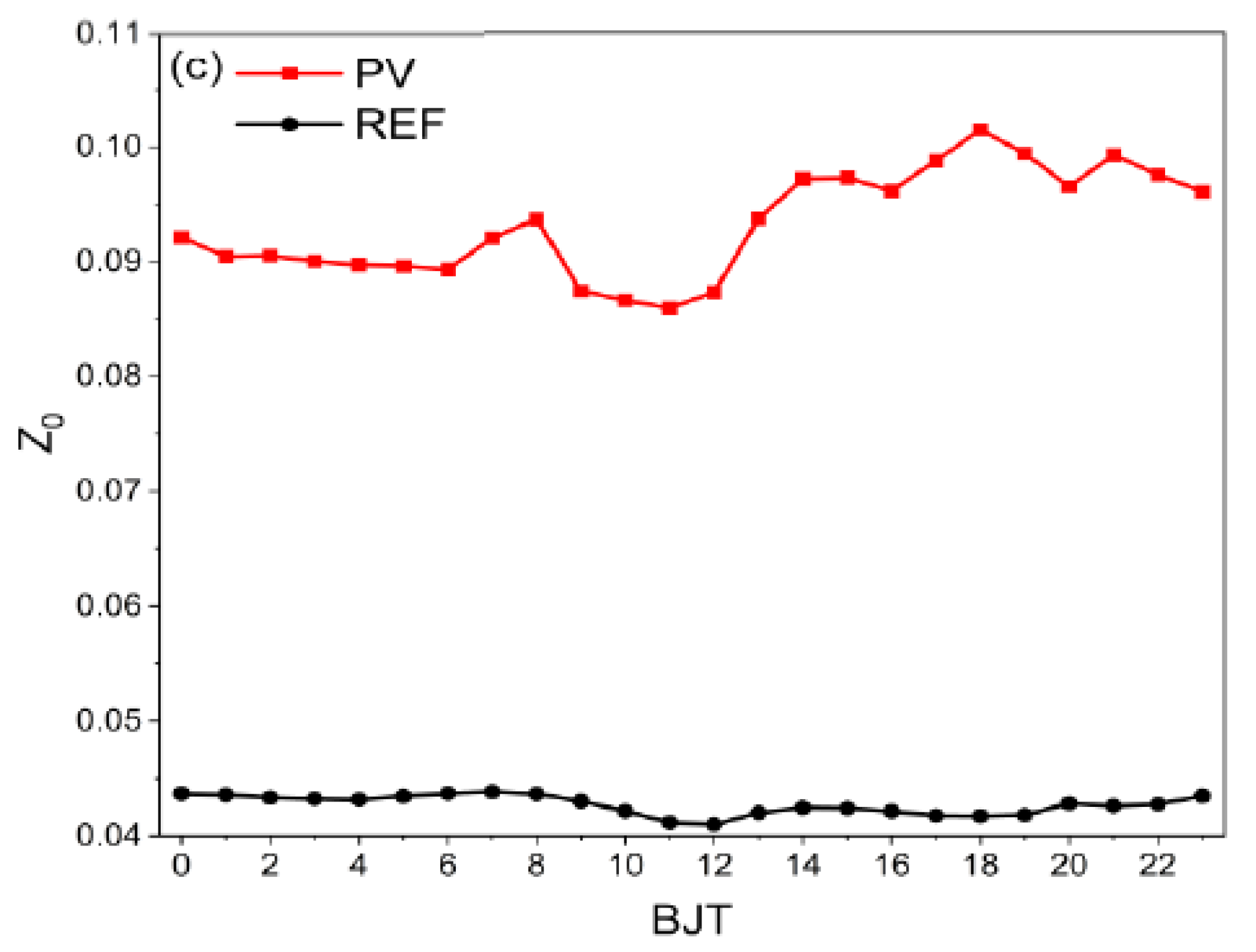
3.1. Atmospheric Stability Parameter and Aerodynamic Roughness
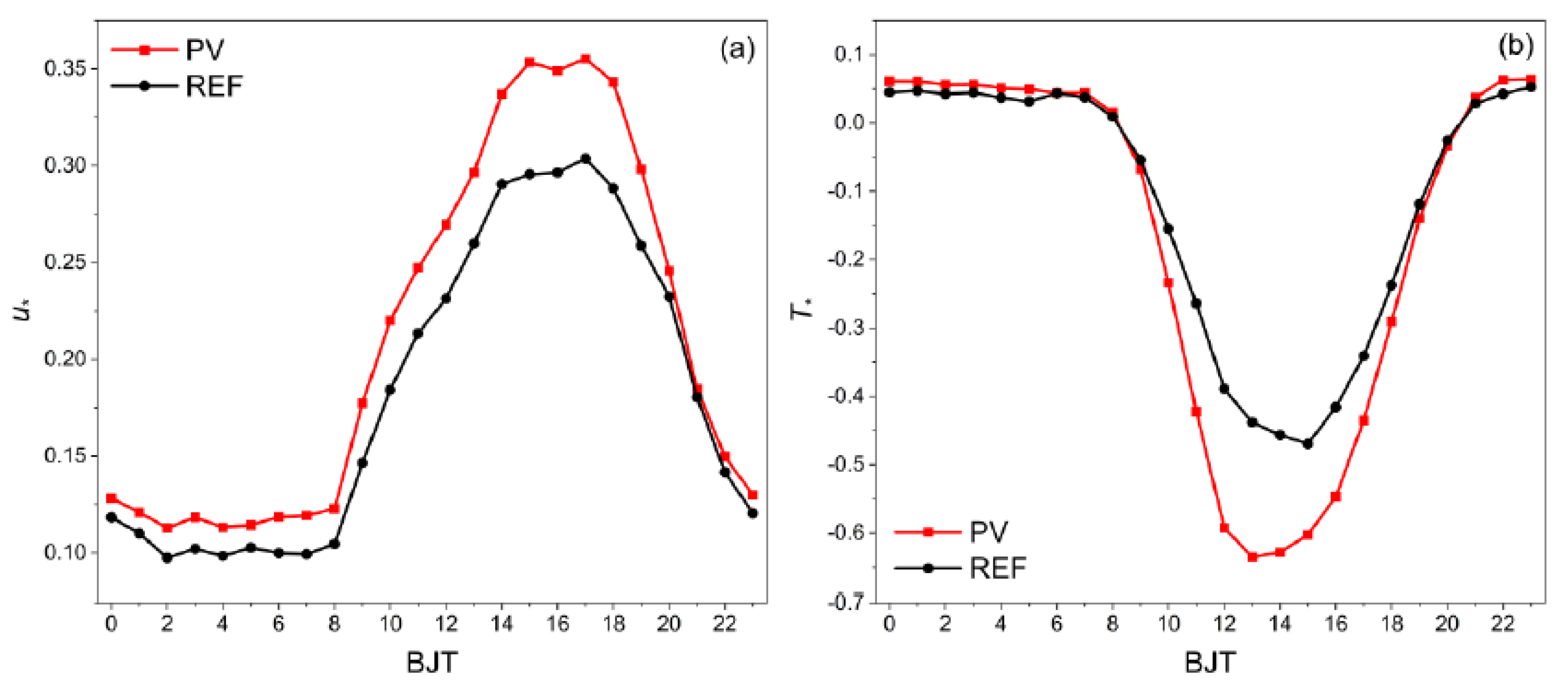
3.2. Scaling Parameters
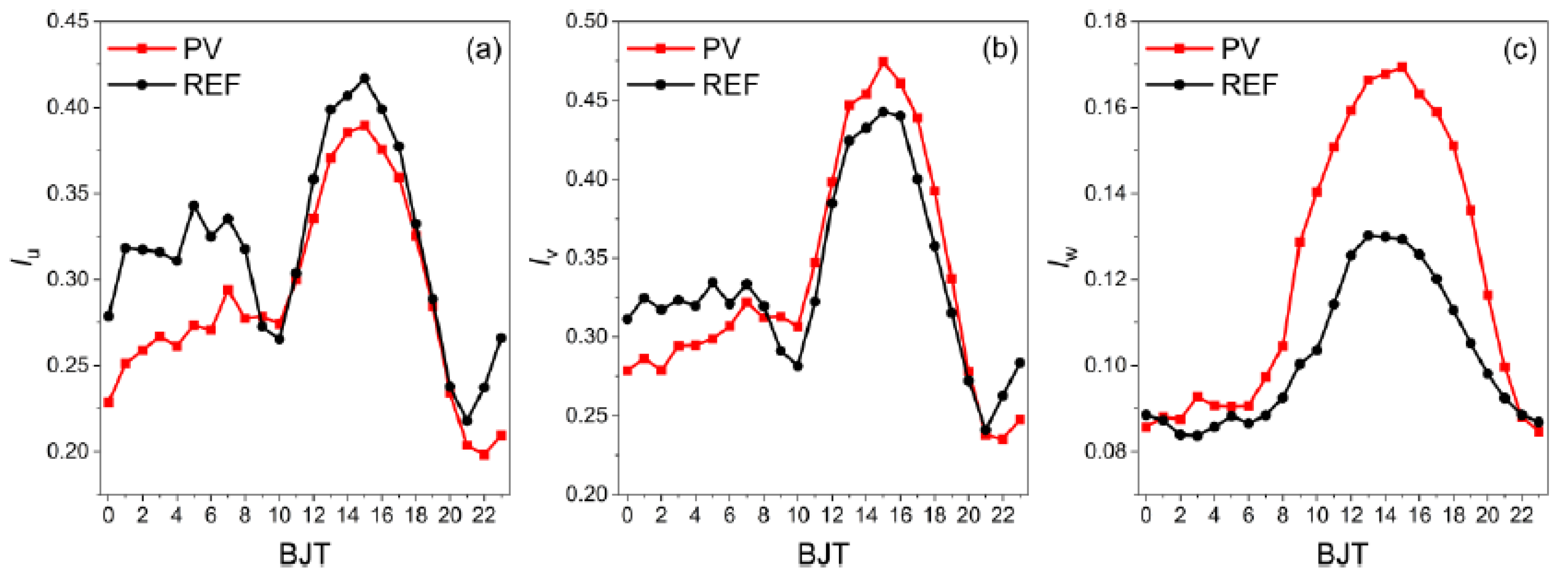
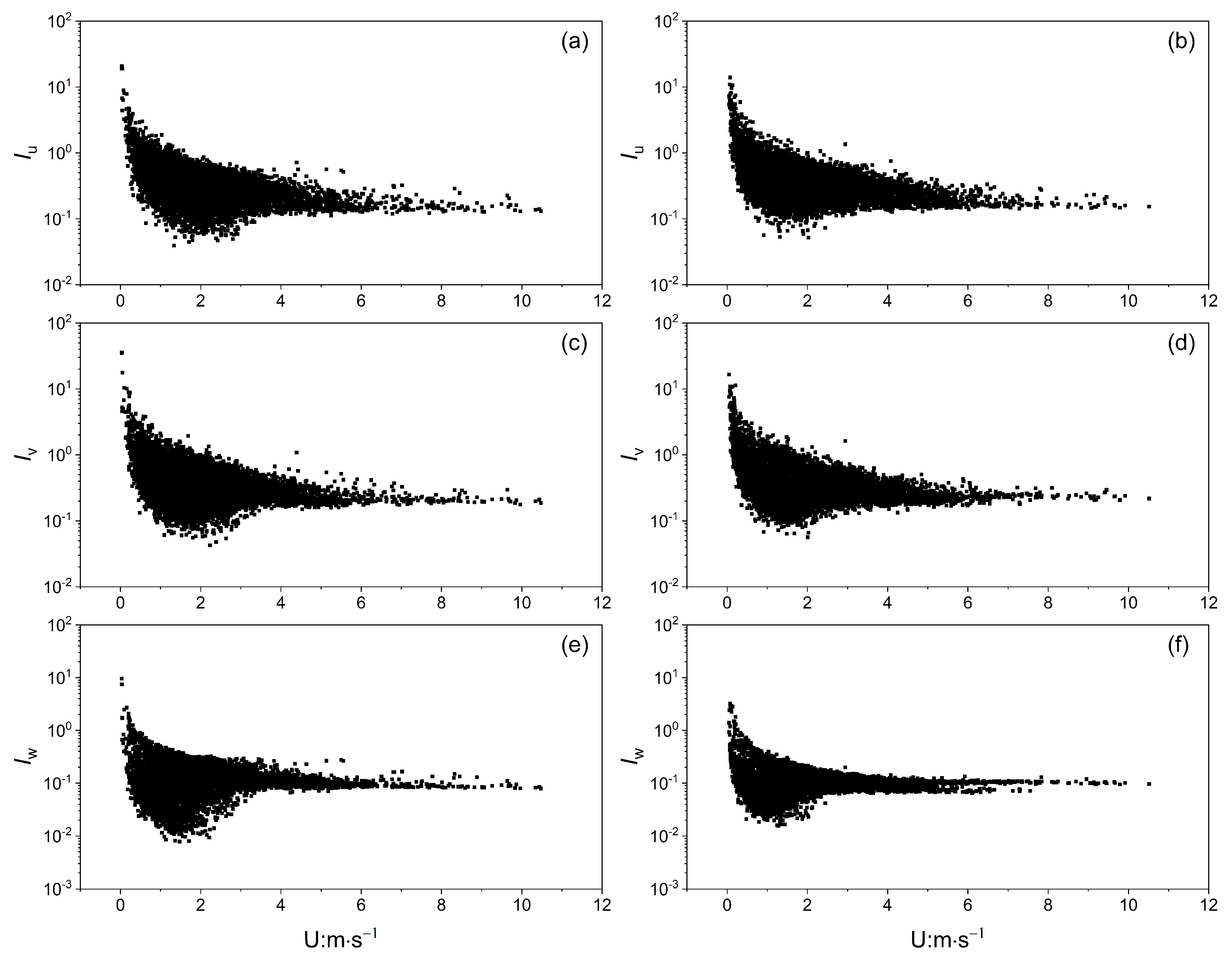
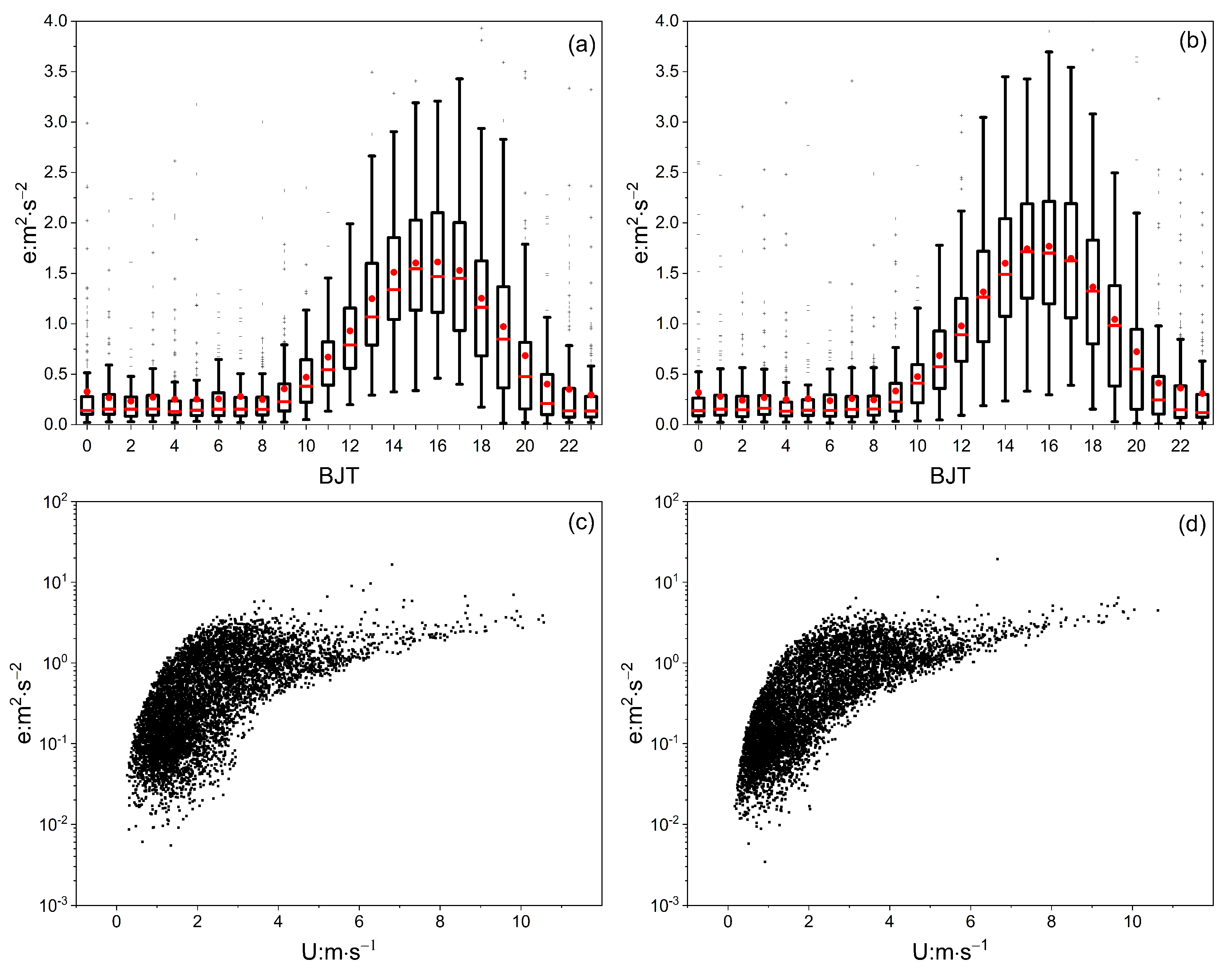
3.3. Turbulence Strength and Turbulent Kinetic Energy
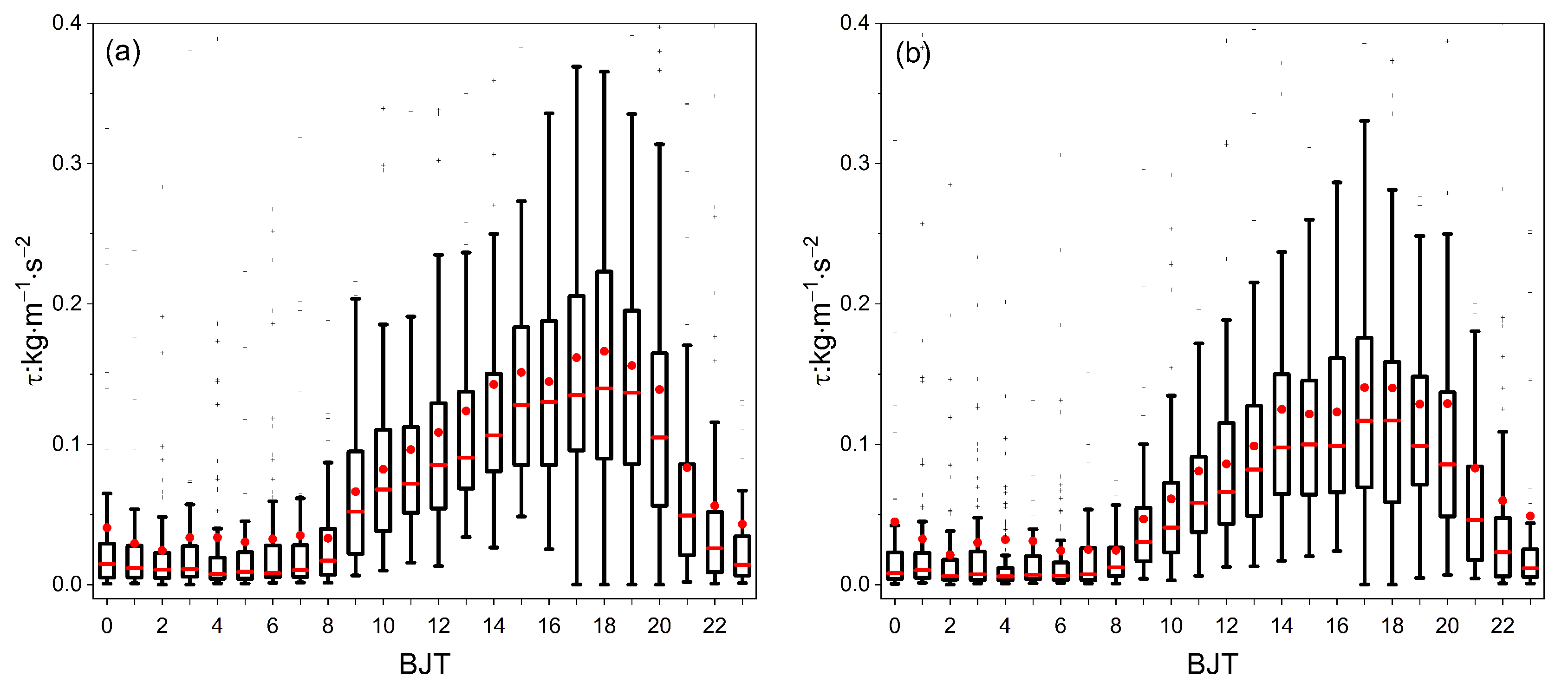
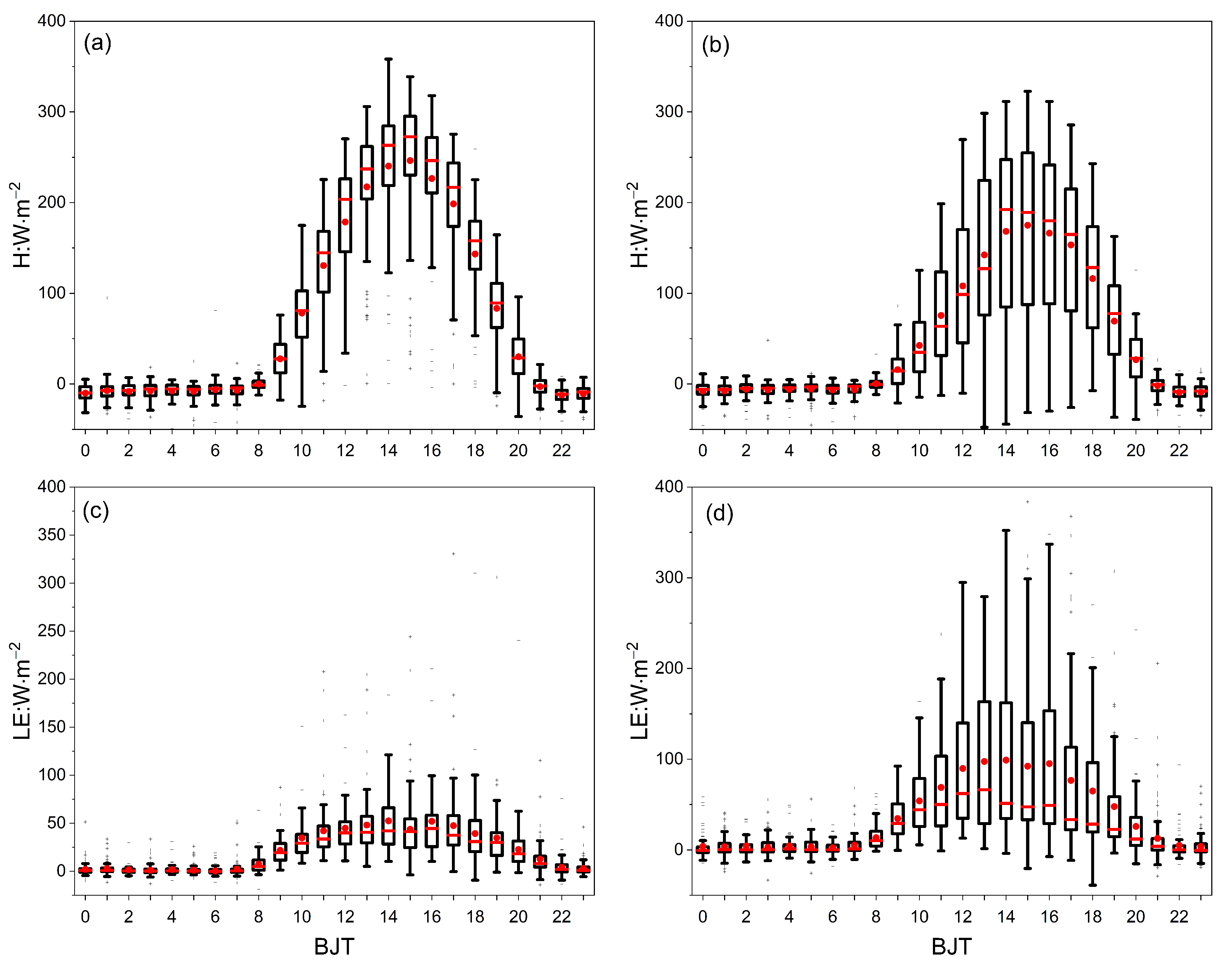
3.4. Momentum Flux and Heat Flux
3.5. The Relationship between Turbulence Variance and Stability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haegel, N.M.; Margolis, R.; Buonassisi, T.; Feldman, D.; Froitzheim, A.; Garabedian, R.; Green, M.; Glunz, S.; Henning, H.-M.; Holder, B.; et al. Terawatt-scale photovoltaics: Trajectories and challenges. Science 2017, 356, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Breyer, C.; Bogdanov, D.; Gulagi, A.; Aghahosseini, A.; Barbosa, L.S.; Koskinen, O.; Barasa, M.; Caldera, U.; Afanasyeva, S.; Child, M.; et al. On the role of solar photovoltaics in global energy transition scenarios. Prog. Photovolt. Res. Appl. 2017, 25, 727–745. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology; Springer: New York, NY, USA, 2008; p. 308. [Google Scholar]
- Brunet, Y. Turbulent Flow in Plant Canopies: Historical Perspective and Overview. Bound. Layer Meteorol. 2020, 1772, 315–364. [Google Scholar] [CrossRef]
- Prasad, K.B.R.R.H.; Srinivas, C.V.; Singh, A.B.; Naidu, C.V.; Baskaran, R.; Venkatraman, B. Turbulence characteristics of surface boundary layer over the Kalpakkam tropical coastal station, India. Theor. Appl. Clim. 2018, 131, 827–843. [Google Scholar] [CrossRef]
- Dyer, A.J.; Garratt, J.R.; Francey, R.J.; McIlroy, I.C.; Bacon, N.E.; Hyson, P.; Bradley, E.F.; Denmead, O.T.; Tsvang, L.R.; Volkov, Y.A.; et al. An international turbulence comparison experiment (ITCE 1976). Bound. Layer Meteorol. 1982, 24, 181–209. [Google Scholar] [CrossRef]
- Shuhua, L.; Jie, L.; Heping, L.; Fuming, L.; Jianhua, W.; .Chan, J.C.L.; CHEN, A.Y.S.; Fei, H.; Huizhi, L. Characteristics of Turbulence Spectra and Local Isotropy in EBEX-2000. Chin. J. Atmos. Sci. 2005, 29, 213–224. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J. The Influence of Topography on Meteorological Variables and Surface-Atmosphere Interactions. J. Hydrol. 1997, 190, 182–213. [Google Scholar] [CrossRef]
- Van Gorsel, E.; Christen, A.; Feigenwinter, C.; Parlow, E.; Vogt, R. Daytime Turbulence Statistics above a Steep Forested Slope. Bound. Layer Meteorol. 2003, 109, 311–329. [Google Scholar] [CrossRef]
- Moraes, O.; Acevedo, O.; DeGrazia, G.; Anfossi, D.; DaSilva, R.; Anabor, V. Surface layer turbulence parameters over a complex terrain. Atmos. Environ. 2005, 39, 3103–3112. [Google Scholar] [CrossRef]
- Solanki, R.; Singh, N.; Kumar, N.V.P.K.; Rajeev, K.; Dhaka, S.K. Time Variability of Surface-Layer Characteristics over a Mountain Ridge in the Central Himalayas During the Spring Season. Bound. Layer Meteorol. 2015, 158, 453–471. [Google Scholar] [CrossRef]
- Pleim, J.E. A Simple, Efficient Solution of Flux–Profile Relationships in the Atmospheric Surface Layer. J. Appl. Meteorol. Clim. 2006, 45, 341–347. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Haugen, D.A.; Kaimal, J.C.; Bradley, E.F. An experimental study of Reynolds stress and heat flux in the atmospheric surface layer. Q. J. R. Meteorol. Soc. 1971, 97, 168–180. [Google Scholar] [CrossRef]
- Shikhovtsev, A.; Kovadlo, P.; Lukin, V.; Nosov, V.; Kiselev, A.; Kolobov, D.Y.; Kopylov, E.A.; Shikhovtsev, M.; Avdeev, F. Statistics of the Optical Turbulence from the Micrometeorological Measurements at the Baykal Astrophysical Observatory Site. Atmosphere 2019, 10, 661. [Google Scholar] [CrossRef]
- Helgason, W.D.; Pomeroy, J.W. Characteristics of the Near-Surface Boundary Layer within a Mountain Valley during Winter. J. Appl. Meteorol. Clim. 2012, 51, 583–597. [Google Scholar] [CrossRef]
- Barman, N.; Borgohain, A.; Kundu, S.S.; Roy, R.; Saha, B.; Solanki, R.; Kumar, N.V.P.K.; Raju, P.L.N. Daytime Temporal Variation of Surface-Layer Parameters and Turbulence Kinetic Energy Budget in Topographically Complex Terrain Around Umiam, India. Bound. Layer Meteorol. 2019, 172, 149–166. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Turbulent Mixing Laws in the Atmospheric Surface Layer. Contrib. Geophys. Inst. Acad. Sci. Ussr 1954, 151, 163–187. [Google Scholar]
- Nosov, V.V.; Emaleev, O.N.; Nosov, E.V. Semiempirical hypotheses of the turbulence theory in anisotropic boundary layer. In Proceedings of the SPIE Proceedings; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5743, pp. 110–131. [Google Scholar]
- Panofsky, H.A.; Tennekes, H.; Lenschow, D.H.; Wyngaard, J.C. The characteristics of turbulent velocity components in the surface layer under convective conditions. Bound. Layer Meteorol. 1977, 11, 355–361. [Google Scholar] [CrossRef]
- Lange, B.; Larsen, S.; Hojstrup, J.; Barthelmie, R. The influence of thermal effects on the wind speed profile of the coastalmarine boundary layer. Bound. Layer Meteorol. 2004, 112, 587–617. [Google Scholar] [CrossRef]
- Huizhi, L.; Zhongxiang, H. Turbulent Characteristics in the Surface Layer over Gerze Area in the Tibetan Plateau. Chin. J. Atmos. Sci. 2000, 24, 289–300. [Google Scholar]
- Yaoming, M.; Weiqiang, M.; Zeyong, H.; Maoshan, L.; Jiemin, W. Similarity Analysis of Atmospheric Turbulent Strength over Grassland Surface of Qinghai-Xizang Plateau. Plateau Meteorol. 2002, 21, 514–517. [Google Scholar]
- Huizhi, L.; Zhongxiang, H. Turbulent Statistical Characteristics over the Urban Surface. Chin. J. Atmos. Sci. 2002, 26, 241–248. [Google Scholar]
- Hedde, T.; Durand, P. Turbulence intensities and bulk coefficients in the surface layer above the sea. Bound. Layer Meteorol. 1994, 71, 415–432. [Google Scholar] [CrossRef]
- Huiwang, G.; Ming, G.; Renlei, W.; Yuhuan, X. Analysis of the Characteristics of the Atmospheric Turbulene Strength and the Similarity of the Standard Deviations of Wind Velocity over the North Yellow Sea. Period. Ocean Univ. China 2009, 39, 563–568+578. [Google Scholar]
- Yaoming, M.; Jieming, W.; Wei, L.; Qingrong, Z.; Boqiang, M. The Study of the Characteristics of Both the Atmospheric Turbulence Structure and the Transfer in the Lower Layer of the Atmosphere above the Nansha Islands Area. Chin. J. Atmos. Sci. 1997, 21, 102–110. [Google Scholar]
- Nosov, V.; Lukin, V.; Torgaev, A. Turbulence Scales of the Monin–Obukhov Similarity Theory in the Anisotropic Mountain Boundary Layer. Russ. Phys. J. 2020, 63, 244–249. [Google Scholar] [CrossRef]
- Nemet, G.F. Net Radiative Forcing from Widespread Deployment of Photovoltaics. Environ. Sci. Technol. 2009, 43, 2173–2178. [Google Scholar] [CrossRef]
- Burg, B.R.; Ruch, P.; Paredes, S.; Michel, B. Placement and efficiency effects on radiative forcing of solar installations. In Proceedings of the 11th International Conference on Concentrator Photovoltaic Systems: Cpv-11; AIP Publishing: Melville, NY, USA, 2015; Volume 1679, p. 090001. [Google Scholar]
- Hernandez, R.R.; Easter, S.; Murphymariscal, M.L.; Maestre, F.T.; Tavassoli, M.; Allen, E.B.; Barrows, C.W.; Belnap, J.; Ochoahueso, R.; Ravi, S.; et al. Environmental impacts of utility-scale solar energy. Renew. Sustain. Energy Rev. 2014, 29, 766–779. [Google Scholar] [CrossRef]
- Chang, R.; Shen, Y.; Luo, Y.; Wang, B.; Yang, Z.; Guo, P. Observed surface radiation and temperature impacts from the large-scale deployment of photovoltaics in the barren area of Gonghe, China. Renew. Energy 2018, 118, 131–137. [Google Scholar] [CrossRef]
- Yang, L.; Gao, X.; Lv, F.; Hui, X.; Ma, L.; Hou, X. Study on the local climatic effects of large photovoltaic solar farms in desert areas. Sol. Energy 2017, 144, 244–253. [Google Scholar] [CrossRef]
- Armstrong, A.; Ostle, N.J.; Whitaker, J. Solar park microclimate and vegetation management effects on grassland carbon cycling. Environ. Res. Lett. 2016, 11, 074016. [Google Scholar] [CrossRef]
- Broadbent, A.M.; Krayenhoff, E.S.; Georgescu, M.; Sailor, D.J. The Observed Effects of Utility-Scale Photovoltaics on Near-Surface Air Temperature and Energy Balance. J. Appl. Meteorol. Clim. 2019, 58, 989–1006. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, A.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Massman, W.J. A simple method for estimating frequency response corrections for eddy covariance systems. Agric. For. Meteorol. 2000, 104, 185–198. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.; De Bruin, H. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound. Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- RB, S. Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Rosenberg, N.J.; Blad, B.B.; Verma, S.B. Microclimate: The Biological Environment, 2nd ed.; John Wiley & Son: New York, NY, USA, 1983; p. 135. [Google Scholar]
- Qiang, Z.; Zeng, J.; Yao, T. Interaction of aerodynamic roughness length and windflow conditions and its parameterization over vegetation surface. Chin. Sci. Bull. 2012, 57, 1559–1567. [Google Scholar] [CrossRef]
- Prueger, J.H.; Kustas, W.P.; Hipps, L.; Hatfield, J.L. Aerodynamic parameters and sensible heat flux estimates for a semi-arid ecosystem. J. Arid. Environ. 2004, 57, 87–100. [Google Scholar] [CrossRef]
- Ao, Y.H.; Lv, S.H.; Han, B.; Li, Z.G. Analysis on Micrometeorology Characteristics in Surface Layer over Badan Jaran Desert in summer. Plateau Meteorol. 2013, 32, 1682–1691. [Google Scholar]
- Xinqian, Z.; Fan, Y.; Chaofan, L.; Honglin, P.; Chunrong, J.; Mamtimin, A.; Wen, H.; Xinghua, Y.; Chenglong, Z. The Turbulence Strength of Surface Layer and Land Surface Processes over Guaizi Lake Shifting Sandy Land on the Northern Margin of Badain Jaran Desert. J. Desert Res. 2019, 39, 103–112. [Google Scholar]
- McBean, G.A. The variations of the statistics of wind, temperature and humidity fluctuations with stability. Bound. Layer Meteorol. 1971, 1, 438–457. [Google Scholar] [CrossRef]
- Singha, A.; Sadr, R. Characteristics of surface layer turbulence in coastal area of Qatar. Environ. Fluid Mech. 2012, 12, 515–531. [Google Scholar] [CrossRef]

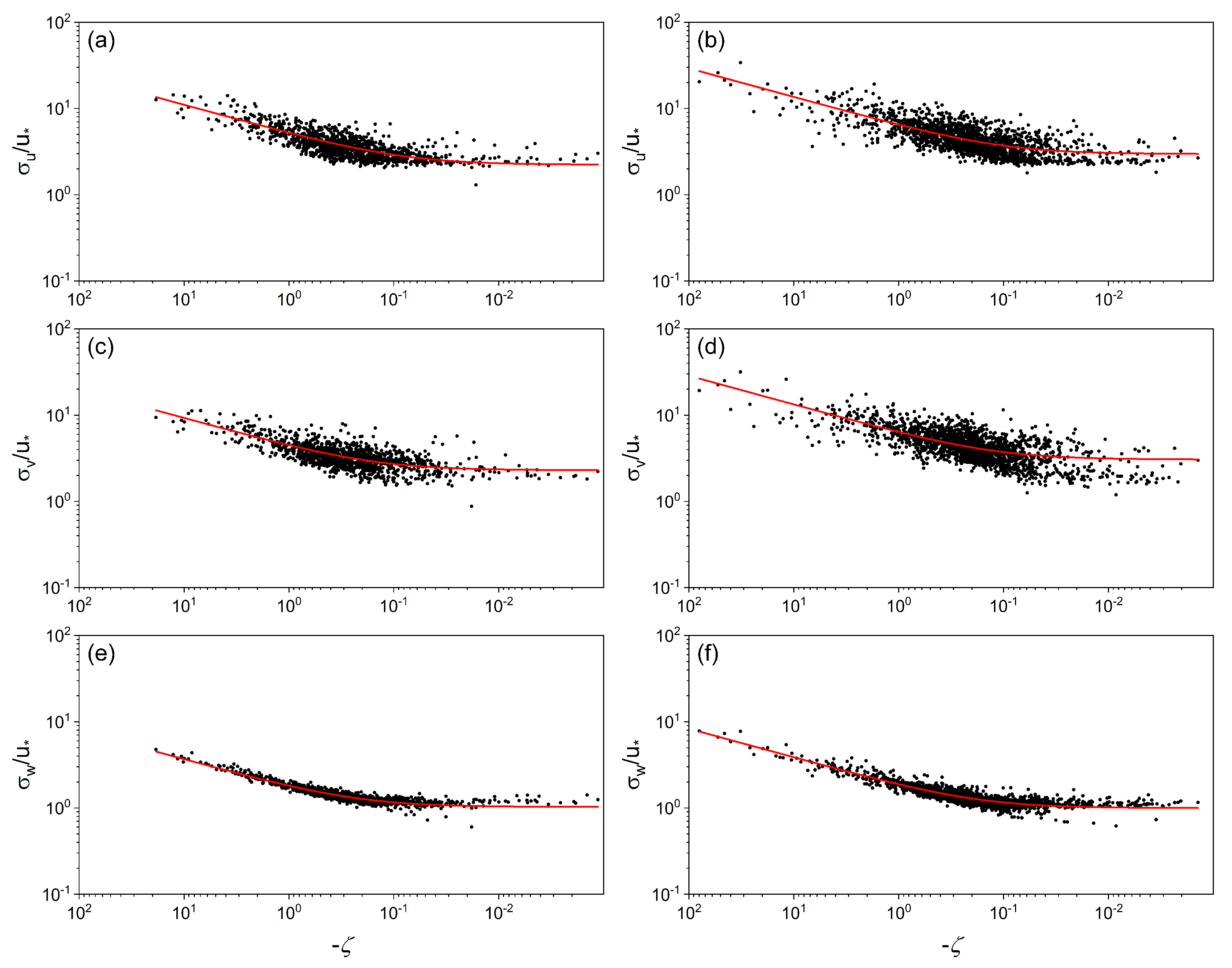
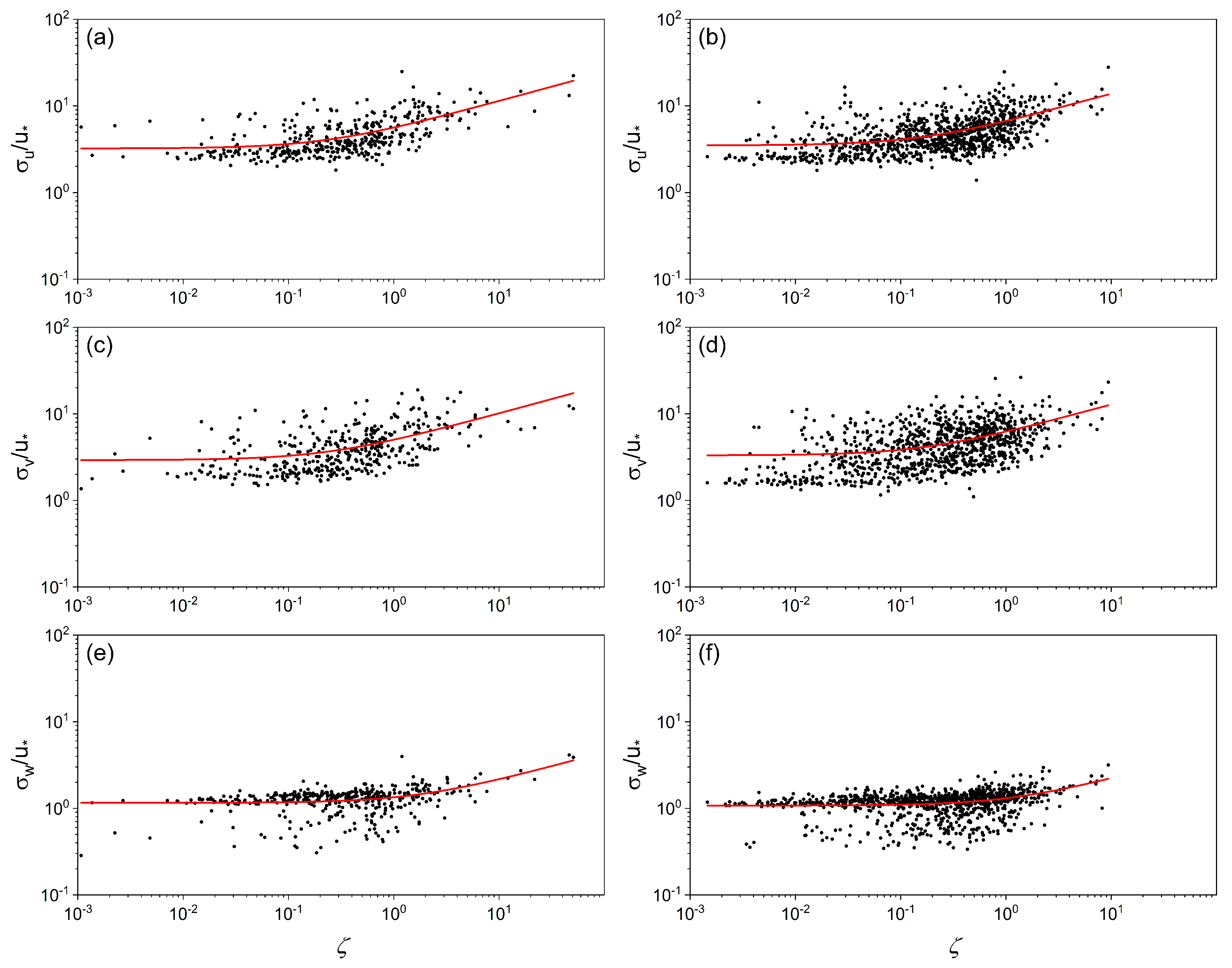
| Unstable | Stable | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | REF | PV | REF | |||||||||
| a | b | R2 | a | b | R2 | a | b | R2 | a | b | R2 | |
| 2.24 | 11.97 | 0.67 | 3.01 | 8.67 | 0.59 | 3.16 | 3.73 | 0.41 | 3.50 | 6.05 | 0.30 | |
| 2.30 | 6.50 | 0.58 | 3.11 | 7.4 | 0.53 | 2.1 | 3.52 | 0.30 | 3.31 | 5.7 | 0.20 | |
| 1.03 | 4.51 | 0.92 | 1.01 | 5.42 | 0.89 | 1.12 | 0.67 | 0.30 | 1.08 | 0.78 | 0.15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Gao, X.; Chen, B. The Impact of Utility-Scale Photovoltaics Plant on Near Surface Turbulence Characteristics in Gobi Areas. Atmosphere 2021, 12, 18. https://doi.org/10.3390/atmos12010018
Jiang J, Gao X, Chen B. The Impact of Utility-Scale Photovoltaics Plant on Near Surface Turbulence Characteristics in Gobi Areas. Atmosphere. 2021; 12(1):18. https://doi.org/10.3390/atmos12010018
Chicago/Turabian StyleJiang, Junxia, Xiaoqing Gao, and Bolong Chen. 2021. "The Impact of Utility-Scale Photovoltaics Plant on Near Surface Turbulence Characteristics in Gobi Areas" Atmosphere 12, no. 1: 18. https://doi.org/10.3390/atmos12010018
APA StyleJiang, J., Gao, X., & Chen, B. (2021). The Impact of Utility-Scale Photovoltaics Plant on Near Surface Turbulence Characteristics in Gobi Areas. Atmosphere, 12(1), 18. https://doi.org/10.3390/atmos12010018





