CNT Parameterization Based on the Observed INP Concentration during Arctic Summer Campaigns in a Marine Environment

Abstract

Aerosol–cloud interactions present a large source of uncertainties in atmospheric and climate models. One of the main challenges to simulate ice clouds is to reproduce the right ice nucleating particle concentration. In this study, we derive a parameterization for immersion freezing according to the classical nucleation theory. Our objective was to constrain this parameterization with observations taken over the Canadian Arctic during the Amundsen summer 2014 and 2016 campaigns. We found a linear dependence of contact angle and temperature. Using this approach, we were able to reproduce the scatter in ice nucleated particle concentrations within a factor 5 of observed values with a small negative bias. This parameterization would be easy to implement in climate and atmospheric models, but its representativeness has to first be validated against other datasets.

1. Introduction

Cloud processes are among the most difficult challenges to represent reliably in large-scale atmospheric models. Ice nucleation is one of the key processes that affects the fate of cloud evolution. Furthermore, nucleation strongly depends on aerosol physico-chemical properties which are, to a good extent, a characteristic of regional environment. Hence, fundamental understanding of ice nucleation processes in clouds is a pertinent field of study. This study focuses on a cloud scheme representation of ice forming nuclei in the Arctic environment during summer, a specific but poorly studied case in polar regional climate models.

The Arctic is the region most affected by climate warming, leading to a decrease in sea ice and land snow cover, altering the regional aerosol composition and sources, which indirectly affect clouds and their properties [1]. During summer, 70 % of the Arctic is covered by mixed-phase clouds, which tend to warm the surface by emitting long-wave radiation towards the surface [2], enhancing evaporation and new cloud formation. Overall, Arctic mixed-phase clouds have a large impact on the surface energy budget, therefore more knowledge on the physical and chemical characteristics of ice nucleating particles (INPs) in this region is required.

Studies have demonstrated that parameterization of cloud microphysics plays a critical role in the simulation of the changing state of atmospheric composition, as well as on the global water budget and climate simulations [3,4]. Compared to homogeneous ice nucleation occurring in liquid solutions, heterogeneous nucleation processes are much more complicated and consist of deposition, condensation, immersion and contact freezing [5]. Deposition freezing is a process in which stable ice clusters form on an ice nucleating particle (INP) directly from the vapour phase. Condensation of water in an INP below 0 $°$C followed by freezing is required for condensation mode. An INP located within a droplet of supercooled liquid can trigger ice nucleation heterogeneously. This is known as the immersion-freezing mode. These INP are rare occurrences in the atmosphere, especially in clean high-latitude marine environments. Finally, contact freezing is initiated by collision of a water droplet and an INP. These processes require the presence of an INP and depend on temperature, humidity, particle surface properties and chemical composition [6].

Earlier parameterizations of heterogeneous ice nucleation often used an empirical approach to predict ice particle concentrations either as a function of temperature [7,8] or ice supersaturation [9] without including aerosol property dependencies. This usually led to very poor estimations of ice crystal concentrations if they were applied outside of the range of measurements on which they were based, such as over the Arctic where measurements are still sparse [10]. In recent years, the representation of aerosol–cloud interactions in atmospheric models has benefited from field measurements and laboratory controlled experiments, having microphysics schemes with prognostic mass and number mixing ratios of hydrometeor categories [11,12,13,14]. Nonetheless, some uncertainties still remain (e.g., which distribution to use, which nucleation mode dominates, composition, mixture, etc.), especially for the ice phase.

To represent the nucleation efficiency of INPs, a freezing process may be treated via a stochastic or deterministic approach. Based on the classical nucleation theory (CNT) [6], ice nucleation is a stochastic approach, dependent on time, temperature and surface area. Deterministic (singular) approach assumes particles have a characteristic number density of surface sites, where ice nucleation occurs at fixed conditions of temperature and humidity [15,16]. Which approach is best is still a matter of debate.

Currently in atmospheric models, detailed microphysics schemes include most of the heterogeneous nucleation modes. According to many laboratory studies [17,18,19,20,21], aerosol types such as mineral dust are very efficient as ice nuclei below −15 $°$C in immersion and deposition nucleation modes [22,23]. Biological particles like bacteria, pollen and diatoms [24] are active INPs at higher temperatures, but in much smaller concentrations [25]. Most laboratory studies use pure mineral dust samples, which may be more efficient INPs than typical soil dust mixture [23]. Due to the long-range transport of dust in the atmosphere, particles can interact with other species like trace gases, acid coating or (in)organic aerosols, which changes their surface properties, decreasing their nucleation temperature and increasing supersaturation values required for initiating ice nucleation [26,27,28].

Clearly, there is a need for parameterizations of heterogeneous ice nucleation based on in-situ observations from the atmosphere bearing characteristics of regional aerosol for predicting ice crystal numbers as a function of multiple species of INPs, similar to Phillips et al. [29]. The importance of model predictions constrained by observational data as well as including temporaland spatial variability of INPs was stressed by DeMott et al. [4] as an urgent need. To better simulate ice crystal concentration, models should be constrained with field measurements, taking into account aerosol size distribution, as ice particle concentration strongly depends on INP surface area [30,31,32,33,34].

The existing empirical nucleation schemes are not applicable to the Arctic marine environment due to unique and characteristic regional conditions. It would be relevant to develop a specific Arctic summer parameterization of INPs based on reliable observations. Girard et al. [35] and Keita and Girard [36] used a stochastic approach based on CNT to simulate ice clouds and aerosol characteristics in the Arctic region during the winter/spring time of the year. According to laboratory studies by Eastwood et al. [20,28], they used a specific contact angle value to investigate acidification properties of ice nuclei and compared it to the singular parameterization approach. Results showed that a stochastic approach with appropriate contact angle can better simulate the formation of Arctic ice clouds in both polluted and pristine air masses compared to field measurements than other approaches. This physically based method can help to interpret model simulations. Extending this successful method into the summer season has motivated us to use the same CNT approach for our study. The main difference is, instead of laboratory assumed values for contact angles, we derived contact angle as a polynomial function of temperature based on the in-situ measurement data.

This study is a part of the larger project Network on Climate and Aerosols: addressing key uncertainties in Remote Canadian Environments (NETCARE) with one of the leading objectives to assess the impact of aerosols on Arctic mixed-phase clouds [37]. Field measurements took place on board the Canadian Coast Guard Services (CCGS) vessel Amundsen in summer 2014 and 2016, studying atmospheric and oceanic compositions throughout the Canadian Arctic. As part of this effort, in our study, we focus on immersion freezing, known to be the dominant freezing mode in mixed-phase clouds [23,38]. Aerosol particles were collected using an inertial impactor and a droplet freezing technique was used to determine the immersion-mode freezing properties [39,40]. Using measured concentrations and aerosol size distribution, we derive a parameterization based on CNT leading to a representation of observations limited within factor 5 of the observed response, a significant uncertainty reduction considering the wide variability reported on the global scale. Section 2 describes the new parameterization scheme and calibration based on the Amundsen campaign measurements and gives detailed information on the field measurements. Results are presented in Section 3 and a discussion and short summary are given in Section 4.

2. Methods

2.1. Parameterization Approach

Immersion freezing can be simulated in models either according to the CNT or the deterministic (singular) approach [6]. In the first approach, ice nucleation is a stochastic process and is time dependent while in the second approach, ice nucleation occurs as a function of specific thermodynamic conditions related to each particle type.

In the CNT the contact angle is used to quantify the ability of a given particle to nucleate ice either by deposition or immersion freezing mode. The contact angle between the ice embryo and the particle in either a vapour (deposition freezing) or liquid (immersion freezing) medium can be parameterized based on field and laboratory measurements. This approach has been used previously in several studies [21,41,42,43]. The concentration of ice crystals nucleated by deposition or immersion freezing (N${}_x$) is given by the following equation:

$$N_x=N_{xt}\left[1-exp\left(-J_x\left({\theta }_x\right)S\Delta t\right)\right]$$

(1)

where N${}_{xt}$ is the number concentration of particles, J${}_x$ is the ice nucleation rate by deposition or immersion freezing per unit surface area of the particle, ${\theta }_x$ is the contact angle for either deposition or immersion freezing, S is the particle surface, x stands for the nucleation process (i.e., deposition or immersion) and t is the time. The equation for J is given in [6] for both deposition and immersion freezing. $\theta$ characterizes single particle species and can be kept constant [17,20,28,35,41,44], have several values according to a probability density function [42,45,46,47] or be parameterized as a function of environmental conditions such as temperature or other variables [15,16,45,48,49].

We developed a new parameterization using INPs and aerosol size distribution measurements from several days of the Amundsen campaigns, which took place during July 2014 and August 2016. A map with sampling locations for both campaigns can be seen in Figure 1, while exact dates and times used in this work are presented in

Table 1. Dates, times and sampling locations from several days of the Amundsen campaigns, which took place during July 2014 and August 2016, used for this study.

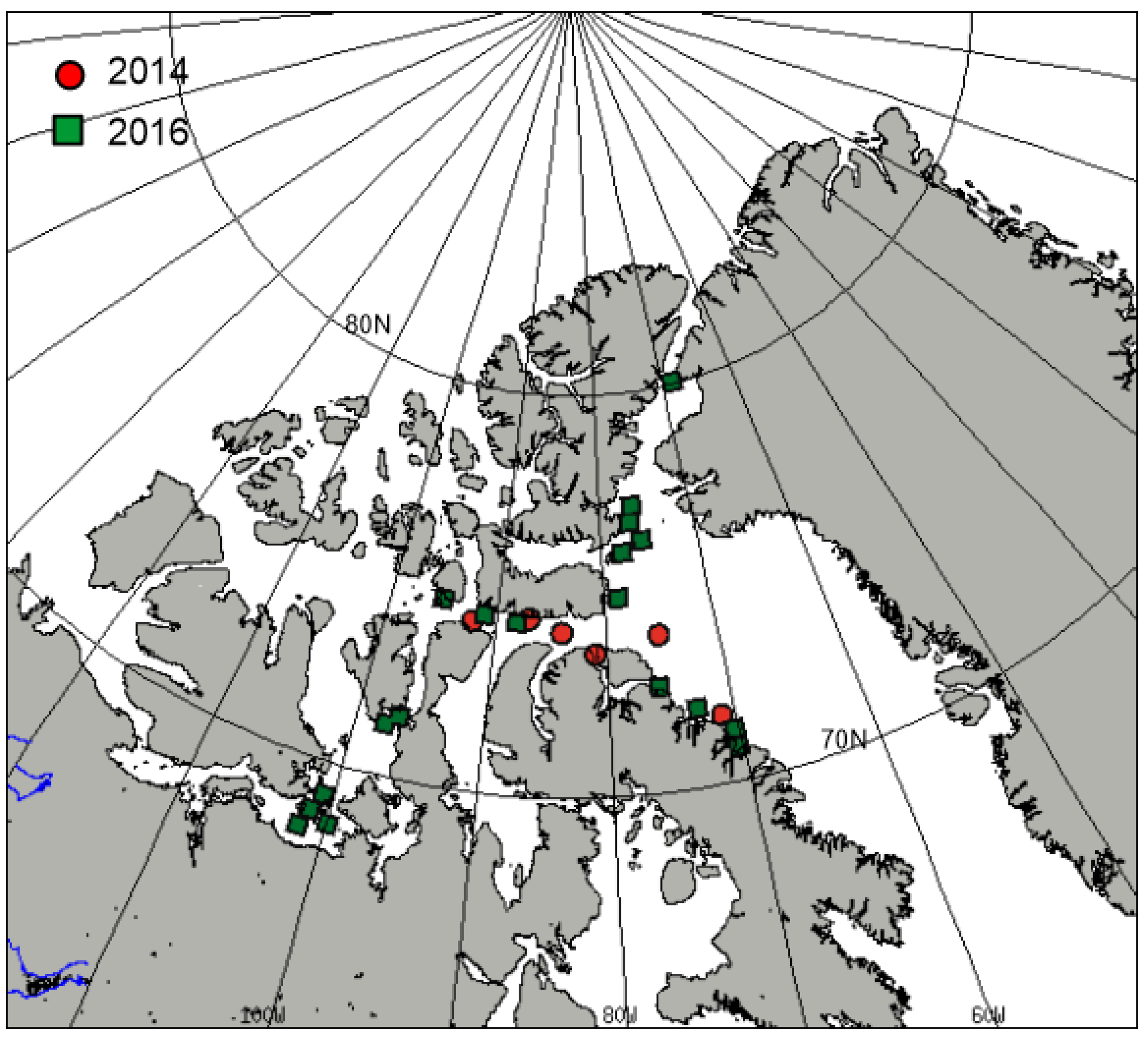
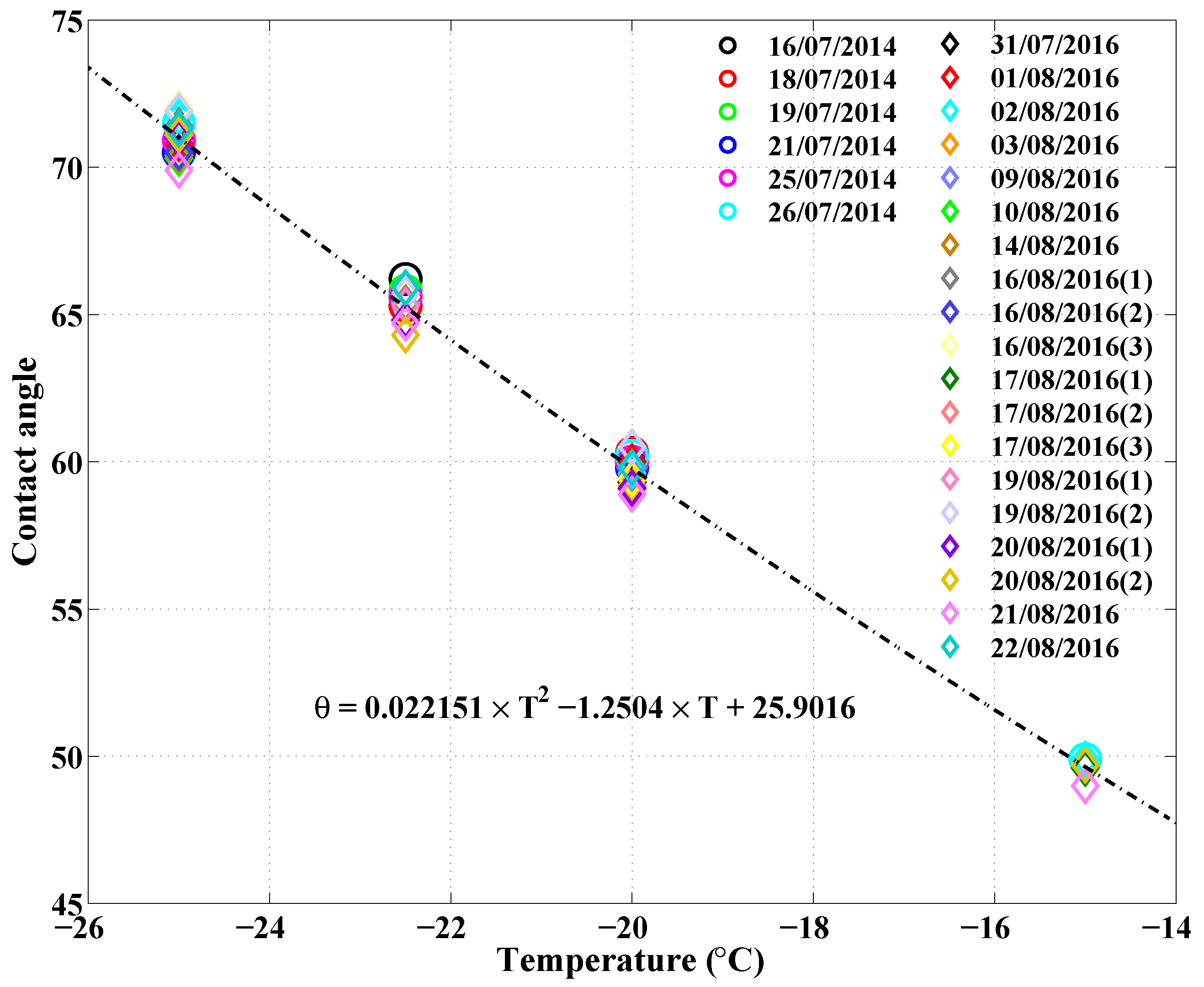
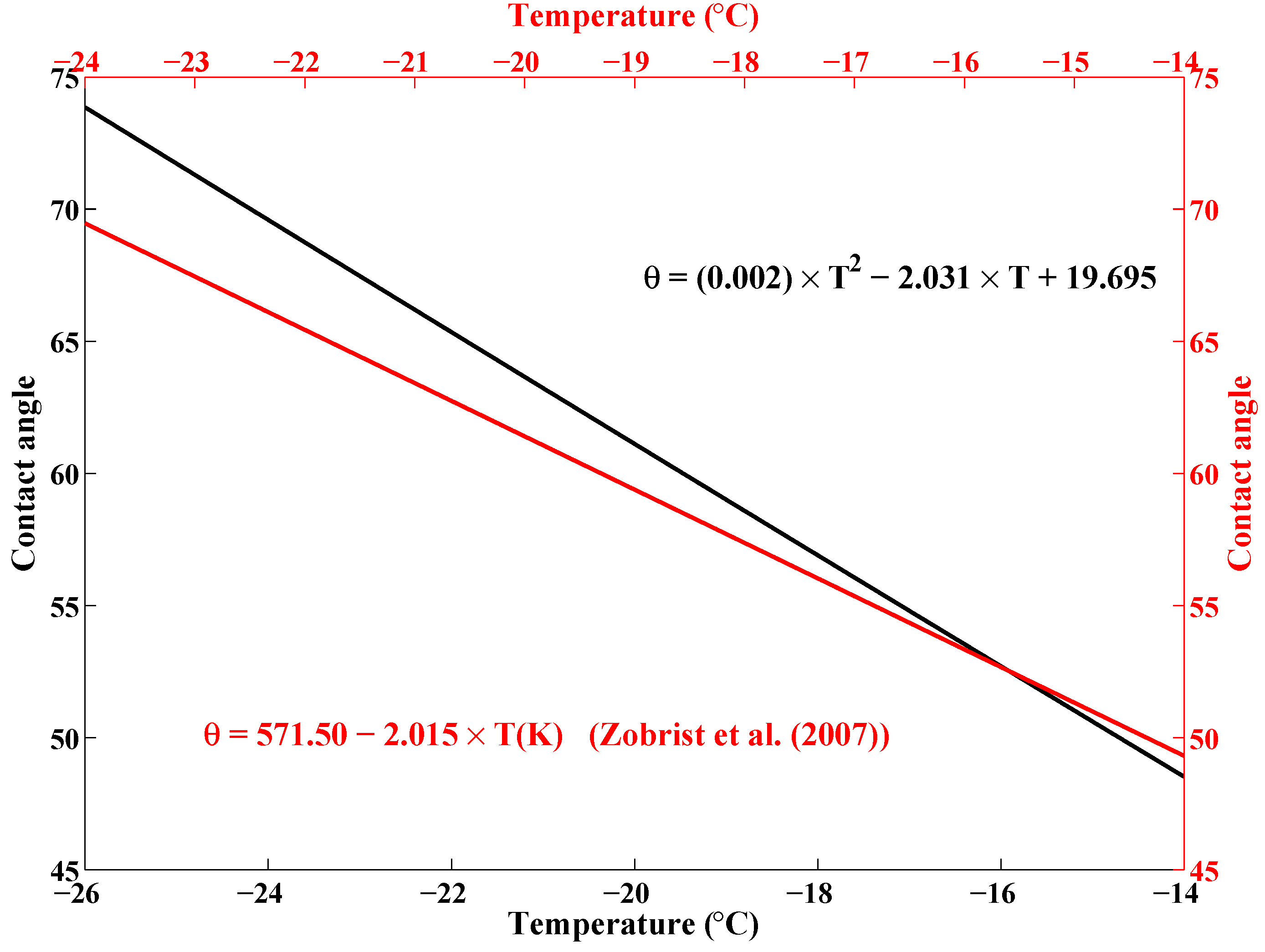
Date	Time Mid-Sample (UTC)	Longitude ($°$)	Latitude ($°$)
16/07/2014	21:52	−71.117	71.702
18/07/2014	20:37	−81.018	73.569
19/07/2014	16:18	−83.976	74.110
21/07/2014	14:21	−92.225	74.237
25/07/2014	19:50	−86.998	74.428
26/07/2014	17:13	−75.270	73.926
31/07/2016	19:42	−70.350	70.846
01/08/2016	22:08	−70.353	71.292
02/08/2016	13:02	−72.960	71.977
03/08/2016	13:46	−75.762	72.638
09/08/2016	13:14	−75.757	76.317
10/08/2016	16:44	−76.436	77.192
14/08/2016	12:54	−68.535	80.047
16/08/2016(1)	12:30	−76.838	76.794
16/08/2016(2)	18:30	−77.875	76.053
16/08/2016(3)	23:40	−78.633	74.940
17/08/2016(1)	12:42	−88.119	74.328
17/08/2016(2)	16:28	−91.054	74.430
17/08/2016(3)	22:08	−95.155	74.659
19/08/2016(1)	12:56	−96.763	71.557
19/08/2016(2)	19:06	−97.699	71.294
20/08/2016(1)	13:48	−100.703	69.172
20/08/2016(2)	19:10	−101.320	68.723
21/08/2016	15:02	−101.802	68.246
22/08/2016	13:18	−99.888	68.492

. The other campaign days were not used for parameterization development due to missing data from a scanning mobility particle sizer (SMPS) or because they were affected by ship emissions [40].

This parameterization is based on CNT following Zobrist et al. [50]. Since the concentration of INPs was determined through the measurement technique based on the immersion freezing mode, the heterogeneous ice nucleation rate is

$$J_{imm}\left(T\right)=\frac{kT}{h}exp\left[\frac{-\Delta F_{diff}\left(T\right)}{kT}\right]\times nexp\left[\frac{-\Delta G\left(T\right)f_{imm}}{kT}\right]\left[{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$$

(2)

which gives the number of frozen particles per unit time and area of particles at a specific temperature. k and h are the Boltzmann and the Planck constants, respectively, while n is the number density of water molecules at the ice/water interface (≈10${}^{15}$ cm${}^{-2}$). $\Delta F_{diff}\left(T\right)$ is the diffusion activation energy necessary for the transfer of water molecule to the ice embryo

$$\Delta F_{diff}\left(T\right)=\frac{k{T}^{2}E}{{(T-T_0)}^2}$$

(3)

In Zobrist et al. [50] it is based on a few fit parameters for diffusivity, experimentally determined by Smith and Kay [51] for the temperature range of 150 K < T < 273 K (E = 892 K, T${}_0$ = 118 K). $\Delta G\left(T\right)$ is the Gibbs free energy necessary for the critical ice embryo formation

$$\Delta G\left(T\right)=\frac{16\pi }{3}\frac{{\upsilon }_{ice}^2\left(T\right){\sigma }_{iw}^3\left(T\right)}{{[kTlnS\left(T\right)]}^2}$$

(4)

where ${\upsilon }_{ice}$(T) is the volume of a H${}_2$O molecule in ice, ${\sigma }_{iw}\left(T\right)$ is the interfacial tension between ice and water and S(T) is the ice saturation ratio. Parameterizations for these variables as a function of temperature are given in Zobrist et al. [50]. The Gibbs free energy is generally influenced by the interfacial tension, and theoretical and molecular-modeling approaches suggest the decrease of Gibbs free energy should be linear with temperature [52,53,54]. Only Zobrist et al. [50] and Pruppacher and Klett [6] refer to a non-linear dependence, based on nucleation measurements extrapolated to the melting point temperature and equilibrium of interfacial tensions (Young relation, 1805), respectively (for more details refer to Zobrist et al. [50] and Ickes et al. [55]). The compatibility factor f${}_{imm}$, characteristic of particles, acts to reduce the Gibbs free energy due to the presence of an ice nucleus. Zobrist et al. [50] uses approximation for a plane surface, assuming that the radius of the INP is significantly larger than the ice germ as follows

$$f_{imm}=\frac{1}{4}\left(2+cos\theta \right){\left(1-cos\theta \right)}^2$$

(5)

where $\theta$ is a contact angle with possible values from 0$°$ to 180$°$ resulting in values from 0 to 1 for f${}_{imm}$.

Contact angle is not easily measurable since it depends on the nucleating vapor, ice nucleus and properties of the forming cluster. In theory, through Young’s equation [6], it only depends on empirical or measured information on surface tensions. There were attempts to determine contact angle experimentally [56,57] through observed critical saturation ratio at nucleation onset using CNT. Caveats that might arise are from dependencies on other variables, which are determined from repeated experiments under different conditions.

2.2. Field Measurements

Quantification of INPs was done by first collecting atmospheric particles on hydrophobic glass slides using a micro-orifice single-stage impactor (MOSSI; MSP corp., Shoreview, MN, USA). The sampling flow rate was 10 L min${}^{-1}$, and collection time was approximately 20 min. After collection, the concentration of INPs was determined from the number of INPs on the slides using the droplet freezing technique. The glass slides were placed in a temperature and RH-controlled flow cell, coupled to an optical microscope [40]. Water droplets were condensed on the collected particles by setting the temperature of the flow cell to 2 $°$C and by flowing helium with a dew point > 2 $°$C over the particles. This resulted in droplets with diameters ranging from 100 to 500 nm condensing on the particles. After the formation of droplets on the slides, the helium flow was stopped and the temperature was decreased (rate of 10 $°$C min${}^{-1}$) until all of the droplets had frozen. The temperature at which each droplet froze was then determined from videos recorded of the droplets while the temperature was decreased.

The average surface area and average aerosol number concentration during sample collection was determined with a scanning mobility particle sizer (SMPS) and aerodynamic particle sizer (APS). The SMPS was used for droplet diameters ≤ 550 nm, and the APS was used for droplet diameters > 550 nm. SMPS data collected at ambient RH was converted to a dry diameter using the hygroscopic growth of a sea spray aerosol and the measured ambient RH, as done previously Ming and Russell [58]. APS data recorded at ambient RH were converted to physical dry diameter using the hygroscopic growth of a sea spray aerosol, the measured ambient RH and a bulk sea spray density of 1.8 g cm${}^{-3}$, as done previously DeMott et al. [32].

3. Results

The ability to nucleate ice crystals in polar clouds currently carries a large error range, depending to a good extent on physico-chemical properties of aerosols. In an attempt to narrow down this uncertainty, we propose to parametrize this relation in terms of direct in-situ measurements taken during extensive campaignes by the CCGS’s Amundsen research ship during summers 2014 and 2016. Our approach is to follow fundamental CNT as a physical base to facilitate the interpretation of aerosol–cloud–climate interaction processes in future simulations and to extend in a consistent way previous successful works [20,28,35,36]. The main idea of the parameterization was to derive a representation of the observed INP concentration, active in the immersion freezing mode at ambient atmospheric measured temperatures during the field experiment (−15, −20, −22.5 and −25 $°$C). These were obtained using the droplet freezing technique, a well supported method with years of application in controlled laboratory environments [39,59]. To remove the effect of variable water uptake on particles, the averaged surface areas and aerosol number concentrations for all sampling times were determined from SMPS and APS measurements after conversion of wet aerosol to dry particle diameter. They were integrated per size bin in the range of sizes relevant from the freezing measurements (0.08–8 $\mathsf{\mu }$m). The determined total values of the aerosol number concentrations and the average surface areas obtained for each day were used as input for the offline code (the offline code consisted of equations from Section 2 and the following integration procedures). An iterative procedure was first applied to a temperature with a prescribed cooling rate of −10 K min${}^{-1}$ and a time step of $\Delta t$ = 1 s, within the same ambient temperature range previously used during controlled laboratory freezing experiments (0 $°$C < T < −40 $°$C) as a reference. Then an iterative procedure for determining the contact angle on each collected sample was performed within the range of 0$°$< $\theta$ < 180$°$, using $\Delta \theta$ = 0.1$°$. By repeating this procedure with all samples, a list of contact angles was obtained from the optimal minimum difference between simulated and observed temperature. After each integration time step, using CNT parameterization equations mentioned in Section 2, the aerosol number concentration was decreased with respect to nucleated aerosol. The entire procedure was repeated for each simulation day and the best fitted contact angle corresponding to the observed temperature was determined from the optimal difference between simulated and observed INP (see Figure 2).

Results show that $\theta$ is remarkably similar for any given temperature on different days. This notable stability in the overall dataset strengthens our confidence in using this method as a general scheme suitable for prevalent mixed-phase clouds ubiquitous in polar ocean environments during summer. Moreover, $\theta$ depends almost linearly on temperature, suggesting a relatively simple dependency on the environmental conditions and supporting our expectation for a representative relationship between INP, aerosol and cloud formation. Results could have been different and very complex since parameters such as aerosol concentration, composition and mean radius change from case to case. This is not the case in our dataset and we were encouraged to apply this property to develop an algorithm in order to parameterize this key process into atmospheric models. To achieve this objective, the Nelder–Mead Simplex Algorithm was used as a minimization optimization technique [60] on a general best fitted trend line, shown in Figure 2, in order to obtain the best fitted contact angle. The set parameter is determined from the sum of square errors between the log of simulated and observed INPs. The log scale is use to accommodate the typical wide range of INPs. Finally, the resulting new optimized function to use in our parameterization is shown in Figure 3.

As a verification, Figure 4 shows a scatter plot of the simulated INPs based on the best estimated optimized contact angle θ = f(T) dependent linearly on temperature versus observed INPs for all analyzed campaign cases. The central 1:1 line represents an ideal perfect simulation. Results from this investigation (Figure 4a) show a consistent and good fit to the observed INP reference values, with most of the points within a factor 5 of observed values, which is an improvement from the typical wider spread often seen in these type of observations. A small negative bias is noted, but it may not constitute a limiting factor in the application of our scheme in simulation models.

As a comparison against other similar parameterizations, Figure 4b–e show results from existing empirical parameterizations by Meyers et al. [9], Fletcher [7], DeMott et al. [4] and McCluskey et al. [61], respectively. Each alternate method gives much larger deviations compared to our parameterization. To further examine the behaviour of our parameterization from another reference point a simplified exponential scheme has been fitted to the field data (Appendix Figure A1) for comparison. Figure 4f shows a similar scatter plot of this simple scheme, as compared to our parameterization. Again, results are consistent with the CNT approach. By applying statistical analysis as shown in

Table 2. Co-variability between simulated and observed ice nucleating particles (INPs) using the newly derived parameterization vs Meyers et al. [9], Fletcher [7], DeMott et al. [4], McCluskey et al. [61] and a simplified parameterization. RMSE stands for root mean square error, while MRE for mean relative error.

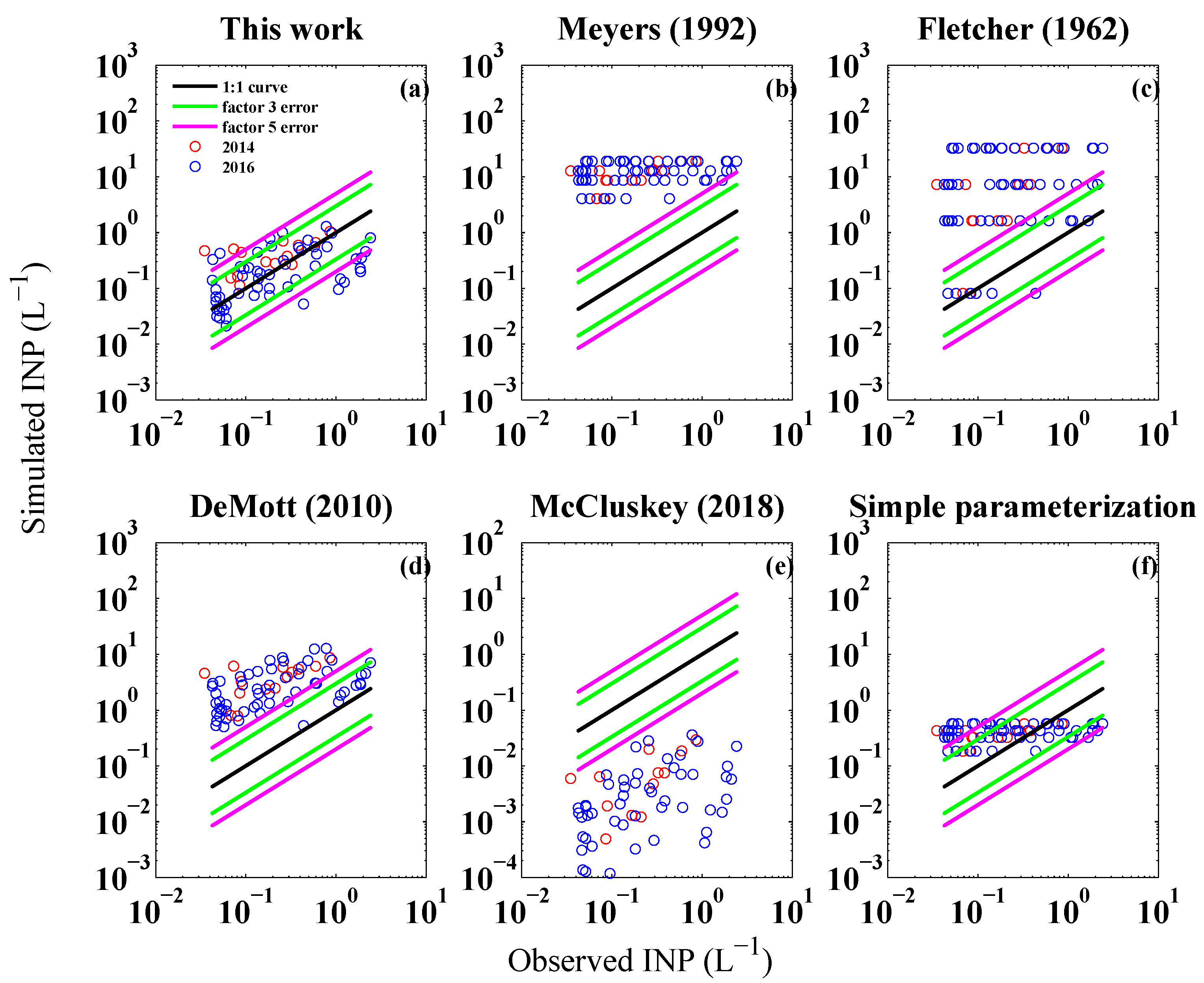
Scheme	Bias	RMSE	MRE
this work	−0.10	0.55	1.16
Meyers et al. [9]	12.26	13.24	97.52
Fletcher [7]	12.86	18.80	85.30
DeMott et al. [4]	3.01	4.00	19.01
McCluskey et al. [61]	−0.41	0.69	0.98
simple parameterization	0.15	0.23	2.07

, the CNT scheme still improves the results. This gives us confidence in the usefulness of the new parameterization in application, a step that we intend to verify in future studies.

To summarize, Table 2 shows statistical analysis of the simulated INPs versus observed INPs, comparing our new scheme to other existing parameterizations. The Meyers et al. [9] method is based primarily on the humidity factor. In this case, the supersaturation with respect to ice is calculated according to Murphy and Koop [62], including a dependence on temperature. The formula of Fletcher [7] estimates the concentration of activated nuclei as a function of temperature, while the deterministic approach by DeMott et al. [4], based on data from nine field studies over 14 years, at various locations, takes into account the number concentration of particles larger than 0.5 $\mathsf{\mu }$m diameter at a given temperature. Those schemes overestimate the observed INP concentrations by one or two orders of magnitude, respectively [4,7], or even larger [9] leading to large statistical errors in applications. Similarly, the McCluskey et al. [61] parameterization, based on the surface area and temperature over marine region, underestimates the observed INP concentrations by two orders of magnitude.

The Arctic is a region where cloud formation processes are the most poorly represented compared to lower latitudes, so it is expected that existing parameterizations based on vastly different environments poorly predict field data measured in the Arctic. Meyers et al. [9] performed a sensitivity test on a wintertime precipitation event over a mountain range in the Western United States, while the Fletcher [7] parameterization was derived for rainy clouds at lower latitudes. Both parameterizations were based on measurements in continental environments, therefore it is not surprising that they do not work adequately in the Arctic marine boundary layer, as concentrations of INPs in continental environments are typically higher than in polar marine environments, especially during summer. DeMott et al. [4] combined data from nine field studies from a variety of locations during a 14 year period. Since field measurements in the marine boundary layer were not considered, we assume that this might be the main reason why their parameterization is not able to reproduce our field measurements. Co-variability between simulated and observed INPs using our parameterization showed the best match since it was fitted directly to the measured Arctic data. Observed data were also compared to the McCluskey et al. [61] parameterization, which was derived from INPs in pristine air masses originating from the North Atlantic. Although derived in a similar regime, based on the marine aerosol surface area and temperature, simulated INPs largely underestimate observed INPs (Figure 4e). This could be due to a lack of large aerosols from wind blown soil particles originating in the Arctic from exposed terrestrial region.

4. Discussion and Summary

The dependence of $\theta$ on T might be linked to variability of chemical composition in the aerosol population: very good ice nuclei will have a smaller contact angle and will nucleate at warmer temperatures, while less effective ice nuclei will have a larger contact angle and nucleate at colder temperatures. Several previous studies have shown that a single contact angle is often not able to describe freezing data [17,20,46]. Ickes et al. [63] stated that compared to the PDF-$\theta$ model, where a distribution of contact angles exists for an ensemble of particles [42,45], and the active site model, where several surface sites with different contact angles are assumed for a single INP [16,42,45], the θ(T) scheme would be a simplified version of those schemes. Therefore, it would be computationally cheaper, because no integration over a contact angle distribution is needed. However, as a drawback of these schemes, they mention the necessity of knowing indirect assumptions of how the aerosol population changes with time and thermodynamic conditions.

Welti et al. [47] found a similar relationship between $\theta$ and temperature using CNT for commercial kaolinite particles of 400 and 800 nm for temperatures between −30 $°$C and −37 $°$C using unimodal size distributions for each case. Increase of $\theta$ for lower temperatures was explained through the Young relationship [6] and the fact that the surface tension between kaolinite and ice increased with lower temperatures, decreasing the ratio of surface tensions. However, they did not discuss the physical meaning of their finding and this conclusion has yet to be verified for particle types other than kaolinite.

Linear increase of contact angle with decreasing temperature is also found by Zobrist et al. [50]. They showed that experimentally determined heterogeneous ice nucleation rate of differently sized droplets coated with a nonadecanol/oil layer can be parameterized with a temperature-dependent $\theta$ using CNT. Our optimized fit is very close to the Zobrist et al. [50] linear fit, as shown in Figure 3.

θ(T) relationship, as derived in our study, has shown that our method provides relatively good results for the summertime Arctic. It is simple to implement in a model and can be used with reasonable errors (up to a factor 5 to 10). So far, this scheme is only applicable for the Arctic summer period and over a marine environment. Aerosols sampled during the two summer campaign periods have both Arctic marine and continental terrestrial origins [40]. Further investigations are needed to validate its behaviour during the rest of the year, especially during wintertime, when abundance of acid coated aerosols is dominant. The robustness of the parameterization for a broader Arctic environment/conditions, such as during winter and spring haze periods and/or near oilfield locations, will need to be further investigated against measurements conducted under these conditions.

The main result of this study indicates that the contact angle is robust and somewhat independent of aerosol types with a simple linear dependency on temperature, at least within the Arctic marine boundary layer. Its broader validity still needs to be tested, but the current results are very encouraging as a guideline. The advantage of using the CNT is that it can be expressed in terms of ice nucleation rate on a physical basis which can be directly incorporated into explicit microphysical schemes. The parameterization from this study can be easily included into numerical models such as NWP, online CTMs and GCMs, for predicting ice nucleation given aerosol number concentration and surface area. A limitation of this scheme is that it does not take into account a specific aerosol type, nor the chemical composition, but assumes a representative marine background aerosol typical of the Arctic summer. Further improvements in this direction are encouraged.