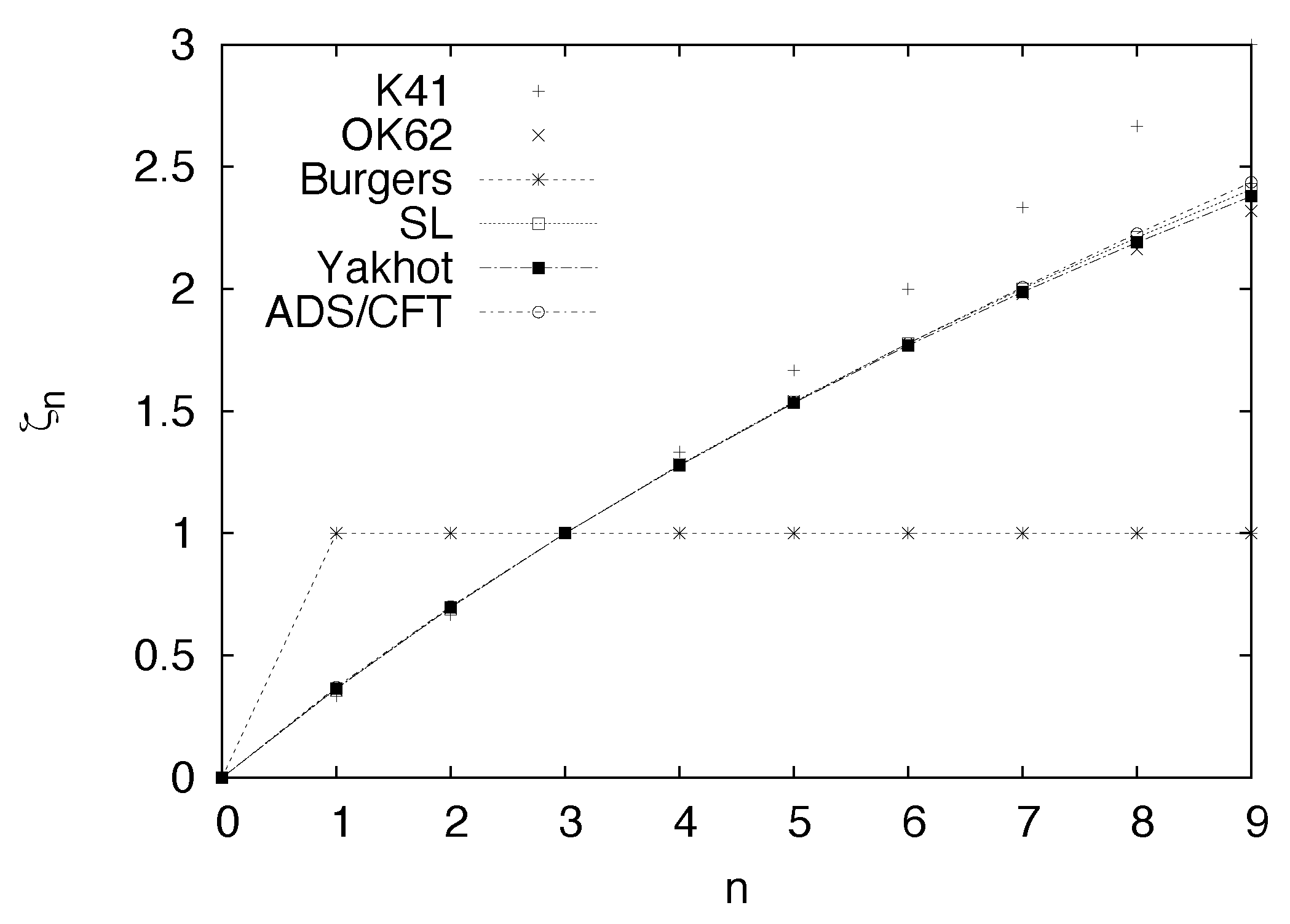1. Introduction
The phenomenon of homogeneous and isotropic turbulence can still be considered as one of the main unsolved problems in classical physics [
1,
2]. An adequate treatment of the underlying Navier–Stokes equation should make an assertion about the small-scale fluctuations of the longitudinal velocity increments
in a statistical sense. Here, deviations from Kolmogorov’s mean field theory [
3] that predicts
are commonly attributed to the intermittent fluctuations of the local energy dissipation rate
and manifest themselves by a non-self-similar probability density function (PDF) of the velocity increments. In turn, this implies a nonlinear order dependence for the scaling exponents
of the moments
. In this context, considerable efforts have been devoted to the development of phenomenological models of turbulence that all try to account for the intermittent character of the local energy dissipation rate such as the log-normal model [
4,
5] or the popular model by She and Leveque [
6] (we also refer the reader to the monograph by Frisch [
7] for further discussion).
In this paper, we follow a different phenomenological approach [
8] that interprets the concept of the turbulent energy cascade, i.e., the transport of energy from large to small scales, as a Markov process of velocity increments
in scale. The vigor of this phenomenology is its capability to reproduce the entire multi-scale velocity increment statistics from the integral length scale down to a scale where the Markov property is violated [
9]. The experimentally and numerically verified Markov property of the velocity increments in the inertial range of scales, however, implies that the increment PDF as well as the transition PDF are governed by the same partial differential equation in scale, the so-called Kramers–Moyal expansion. As it is discussed in
Section 2 of the present paper, the Kramers–Moyal approach allows for a general description of anomalous scaling. Consequently, it is able to reproduce all known phenomenological models of turbulence by the proper choice of the Kramers–Moyal coefficients that enter the Kramers–Moyal expansion.
The result of this paper is that, in order to obtain an accurate description of intermittency effects, higher order Kramers–Moyal coefficients have to be small but non-vanishing. Therefore, the truncation of the Kramers–Moyal expansion as it is done in the usual Fokker–Planck approach [
8,
10,
11] might result in an inaccurate description of the tails of the PDFs. To this end, we investigate the asymptotics of higher-order Kramers–Moyal coefficients of the corresponding phenomenologies in
Section 2.
Section 3 substantiates the existence of higher order coefficients by direct numerical simulations of the Burgers equation. Due to its advantageous properties in comparison to the Navier–Stokes equation (no nonlocal pressure contributions, integrability via the Hopf–Cole transformation [
12,
13]), the Burgers equation has been widely used as a model system for turbulence [
14,
15,
16,
17,
18] and exhibits pronounced intermittency effects due to strong negative velocity gradients occurring in shocks (we also refer the reader to [
19] for further references). Further applications of Burgers equation range from astrophysical problems [
20,
21,
22] to solid surface growth by vapor deposition via the equivalent Kardar–Parisi–Zhang equation [
23]. Moreover, the inclusion of an additional nonlocal term allows for the incorporation of intermittency effects similar to the ones that are encountered in Navier–Stokes turbulence [
24]. Therefore, we will explicitly investigate the influence of the balance between nonlinearity and nonlocality and its consequences for the Kramers–Moyal coefficients. Furthermore, we will give an outlook on the extension of this analysis to ordinary Navier–Stokes turbulence.
2. Interpretation of the Turbulent Energy Cascade as a Markov Process
of Velocity Increments in Scale
A key quantity in the statistical description of turbulence [
2] is the
n-increment PDF of longitudinal velocity increments (
1) defined according to
where the brackets indicate ensemble averaging. The
n-increment PDF is a high-dimensional object whose determination from first principles is inaccessible due to the hierarchical ordering that is inherent in turbulent flows. In the following, we will focus on the spatial properties of the
n-increment PDF at different scales
, i.e., we will assume stationarity. We can further assume homogeneity with respect to the point of reference
. In stochastic processes [
25], the
n-increment PDF can be expressed as a product of the
-increment PDF and a conditional probability according to
In their seminal work, Friedrich and Peinke [
8] investigated the multi-scale velocity increment statistics in a free jet experiment. They could show that longitudinal velocity increments (
1) possess a Markov property
in scale, namely
or more generally
Further experiments [
9] revealed that the Markov property (
4) is valid in the inertial range and is only broken at small scale separations
, where
is termed the Markov–Einstein length. An important consequence of the Markov property is that the
n-increment PDF (
2) can be factorized into products containing only transition probabilities
for all
and
This means a considerable reduction of the complexity of the problem, since the knowledge of the transition probabilities
is sufficient for the determination of the
n-increment PDF (
is presumed to be known at large scales). Moreover, a central notion of a Markov process is that the one-increment PDF and the transition PDF follow the same Kramers–Moyal expansion in scale [
25]
where
is the Kramers–Moyal operator
and
are the Kramers–Moyal coefficients
Here, the minus signs in Equations (
7) and (8) indicate that the process runs from large to small scales. In this interpretation of the turbulent energy cascade, the effects of small-scale intermittency, i.e., non-self-similar (non-Gaussian, if one assumes a Gaussian initial condition
) solutions for the one-increment PDF, are apprehended in terms of an evolution of the one-increment PDF in scale governed by Equation (
7). In the following, we want to relate the Kramers–Moyal expansion to scaling solutions of different phenomenologies of turbulence. To this end, we take the moments
of the one-increment PDF in Equation (
7)
In order to match powers of
v, we choose
and obtain
Furthermore, scaling solutions
fix the scale-dependence of
as
. At this point, we introduce the
reduced Kramers–Moyal coefficients for the order-dependent constant of proportionality according to
. This particular choice leads to a rather simple correspondence between
and
, which can be seen by integrating
from integral scale
L to small scales
rHence, in this alternative formulation of universality in turbulence [
18], scaling exponents
of structure functions
are related to the sequence of reduced Kramers–Moyal coefficients
by a binomial transform
TThe binomial transform is an involution
, and, hence, the sequence of reduced Kramers–Moyal coefficients
can be associated with the scaling exponents
of each phenomenological model of turbulence according to
It should be noted that the binomial transform is usually defined to start from
, which can readily be included in Equations (
16) and (
17) since
. Furthermore, the fact that the reduced Kramers–Moyal coefficients
are determined by the scaling exponents
shows that the Kramers–Moyal expansion (
7) with specific Kramers–Moyal coefficients
is general enough to capture the essence of anomalous scaling. In other words,
all currently known phenomenological models of turbulence—characterized by their corresponding sets of scaling exponents
as depicted in
Figure 1—can be reproduced by the Kramers–Moyal expansion (
7) with Kramers–Moyal coefficients (
18) where reduced Kramers–Moyal coefficients
are related to the scaling exponents
by Equation (
17). In the next subsections, we will describe in detail how these different phenomenological models can be mapped onto the Kramers–Moyal coefficients.
(i.) Kolmogorov’s theory K41:
The monofractal K41 phenomenology [
3] states that
and an evaluation of the reduced Kramers–Moyal coefficients (
17) suggests that it can be reproduced by just a single Kramers–Moyal coefficient
(ii.) Oboukhov–Kolmogorov theory OK62:
A first intermittency model which assumes a log-normal distribution of the local rate of energy dissipation
has been proposed by Kolmogorov [
4] and Oboukhov [
5].
It predicts the scaling of the structure functions according to
where
L is the integral length scale and
is the so-called intermittency coefficient which is of the order
(recent experiments [
26], however, suggest a value of
). As it has been discussed by Friedrich and Peinke [
8], this reduces the Kramers–Moyal expansion to a Fokker–Planck equation with drift and diffusion coefficient
and implies the vanishing of all higher-order coefficients.
(iii.) Burgers scaling:
The velocity structure functions in Burgers turbulence [
19] follow the extreme scaling
Here, the first scaling is due to smooth positive velocity increments in the ramps, whereas the latter scaling corresponds to negative velocity increments dominated by shocks that form due to the compressibility of the velocity field in the vicinity of the viscosity .
The smooth solutions correspond to a single Kramers–Moyal coefficient, whereas the shock solutions can only be reproduced by an infinite number of Kramers–Moyal coefficients and we obtain
(iv.) She–Leveque model:
The She–Leveque model [
6] for 3D Navier–Stokes turbulence predicts scaling exponents
that are in very good agreement with both experimental and numerical data. This yields an infinite set of coefficients [
27] and the reduced Kramers–Moyal coefficients read
where
is the generalized hypergeometric function. It has been shown recently [
28] that this particular model can be apprehended as a jump process of a stochastic process for the velocity increments in scale.
(v.) Yakhot model:
Yakhot [
29,
30] introduced a model for structure function exponents
based on a mean-field approximation. Similar scaling exponents were first derived by Novikov [
31] and subsequently by Castaing [
32]. With the choice of
, structure functions agree equally well with experimental data as the popular She–Leveque model. The translation to the Krames-Moyal coefficients is given by
(vi.) ADS/CFT random geometry model:
Eling and Oz [
33] introduced a structure function scaling model which is motivated by a gravitational Knizhnik–Polyakov–Zamolodchikov (KPZ)-type relation. For 3D Navier–Stokes turbulence, they derive
where experimental data suggest the value
. Unfortunately, we could not obtain an analytical formula for the coefficients of this particular model and have restricted ourselves to a numerical evaluation of Equation (
17).
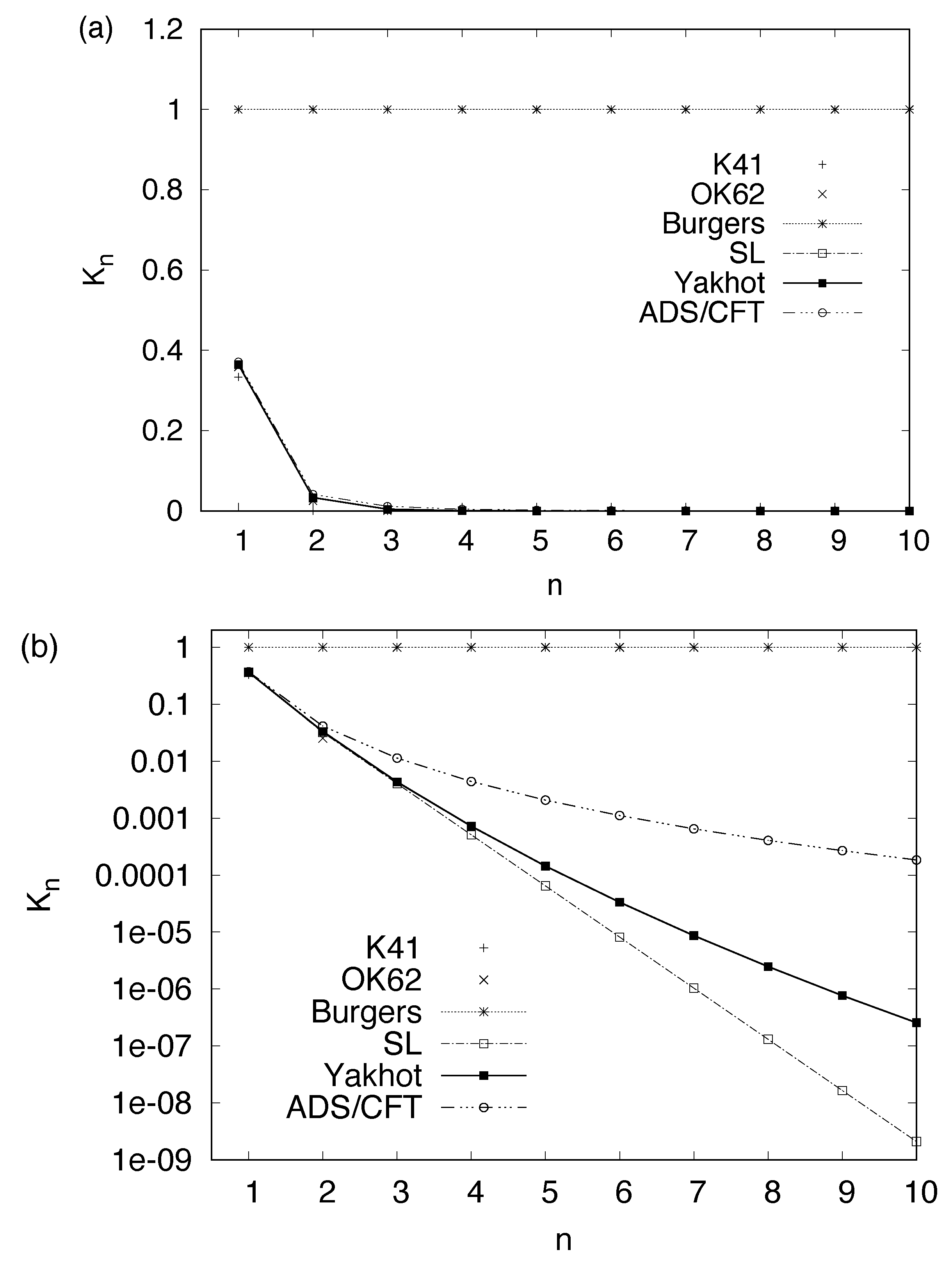
We have plotted the reduced Kramers–Moyal coefficients
for the different models up to the order
in
Figure 2a. As one can see, all models besides K41 and Burgers can hardly be distinguished from one another and the reduced Kramers–Moyal coefficients seem to tend towards zero very quickly. According to a theorem due to Pawula [
34] (see also [
25]), the vanishing of the fourth-order Kramers–Moyal coefficient implies that all higher coefficients are zero as well and the Kramers–Moyal expansion (
7) reduces to an ordinary Fokker–Planck equation. The latter is particularly suitable for modeling approaches via its corresponding Langevin equation as well as the undemanding determination of statistical quantities via the exact short-scale propagator of the Fokker–Planck equation [
25].
In the original work [
8] and also all subsequent works [
9,
10,
35], it was argued in favor of Pawula’s theorem since the experimentally determined Kramers–Moyal coefficient of order four was very close to zero.
Figure 2a seems to agree qualitatively with this finding. However, in order to demonstrate that this can be misleading, we show a semi-logarithmic plot of
Figure 2a in
Figure 2b. It can be seen that the models
(iv.)–(vi.) tend asymptotically towards zero and higher-order Kramers–Moyal are rather small but strictly non-zero. At this point, we want to emphasize that since
, the significant detection of these higher-order coefficients in the experiment might be quite challenging due to the presence of measurement noise or insufficient statistics. Nevertheless, since the models
(iv.)–(vi.) agree quite well with experimental data, an accurate determination of the higher-order coefficients should be within the reach of a spatially and temporarily well-resolved high-Reynolds number experiment. Moreover, Pawula’s theorem directly reduces the velocity increment statistics to families of the OK62 phenomenology
(ii.). It should therefore be noted that the latter is only valid for moments
that do not exceed the order
, due to the convexity condition for
(see also [
7] for further discussion). Consequently, one should bear in mind that, whilst modeling or other purposes of the Fokker–Planck approach, the tails of the PDFs might not be described accurately, although—admittedly—this effect should be rather small. In the following section, we want to quantify the small-scale intermittency behavior on the basis of the reduced Kramers–Moyal cofficients (
17) at the example of a generalized Burgers equation with an additional nonlocality.
3. Direct Numerical Simulations of a Generalized Burgers Equation
We consider the generalized Burgers equation
with forcing that is assumed to be white noise in time
. Here, the spatial correlation of the forcing follows a power law in Fourier space [
36], namely
Moreover,
in Equation (
26) corresponds to the case of Burgers turbulence, whereas
corresponds to a purely nonlocal case that is dominated by self-similar behavior [
24]. The intermediate case
, however, exhibits several similarities to the intermittency behavior of 3D hydrodynamic turbulence. The latter manifest themselves by a skewed velocity gradient PDF, as well as by nonlinear scaling exponents
of the velocity structure functions
which has been reported by Zikanov, Thess, and Grauer [
24]. Apparently, the balance between the nonlinear and nonlocal term results in particular dissipative structures that have considerable influence on the intermittency behavior of the system. Therefore, the model system (
26) seems to be an interesting surrogate for the Navier–Stokes equation that allows for studying the competition between nonlinearity (steepening of velocity gradients) and nonlocality (regularization) in a systematic way, i.e., by controlling the parameter
(we also refer the reader to the monograph by Sagaut and Cambon [
37] for a further discussion of these issues). It has to be stressed that, already due to the restriction to a single dimension in Equation (
26), this cannot be considered as a one-to-one correspondence to 3D Navier–Stokes turbulence but rather corresponds to a model system with similar properties (non-self-similarity of the velocity increment PDF, skewness).
Equation (
26) has been solved with the help of a standard pseudo-spectral code. A third order Runge–Kutta method was used for the time stepping due to its vigor of capturing the temporal evolution of shock-like structures [
38]. Furthermore, aliasing errors that occur due to an insufficient resolution of the quadratic nonlinearities were treated with the help of a filter in Fourier space [
39]. Concerning the realization of the forcing determined by Equation (
27), we assured the white-noise in time condition with a numerical method for the Langevin equation discussed by Higham [
40]. Cheklov and Yakhot [
36] reported that a power law correlation function
results in a Kolmogorov-type spectrum which can also be determined on the basis of a one-loop renormalization group consideration. Here, the nonlinearity directly balances forcing contributions that are acting on all scales. Therefore, the cut-off of the forcing is located in the neighborhood of the dissipation range in all simulations.
Table 1 shows the characteristic parameters of the DNS. The attained Reynolds numbers in the simulations are not as high as the Reynolds numbers attained in references [
24,
36]. This is due to the fact that the latter results were obtained with a so-called hyperviscous term, i.e., replacing
by
, which leads to an efficient damping of the higher wavenumber (small-scale) components of the velocity field. By this method, higher Reynolds numbers can be attained, which leads to an increased inertial range. Apparently, the concept of hyperviscosity has no considerable influence on the inertial range behavior [
36]; therefore, it can be considered as an efficient method to attain higher Reynolds numbers. Nonetheless, in this work, we intend to investigate the original dissipative effects, and thus only the Laplacian viscous term has been considered. Moreover, we chose the resolution
N in a way which allows for the production of a sufficient amount of data. These restrictions lead to the moderate Reynolds numbers in
Table 1.
3.1. Strong Intermittency : Burgers Equation
For the case
, the additional nonlocality in Equation (
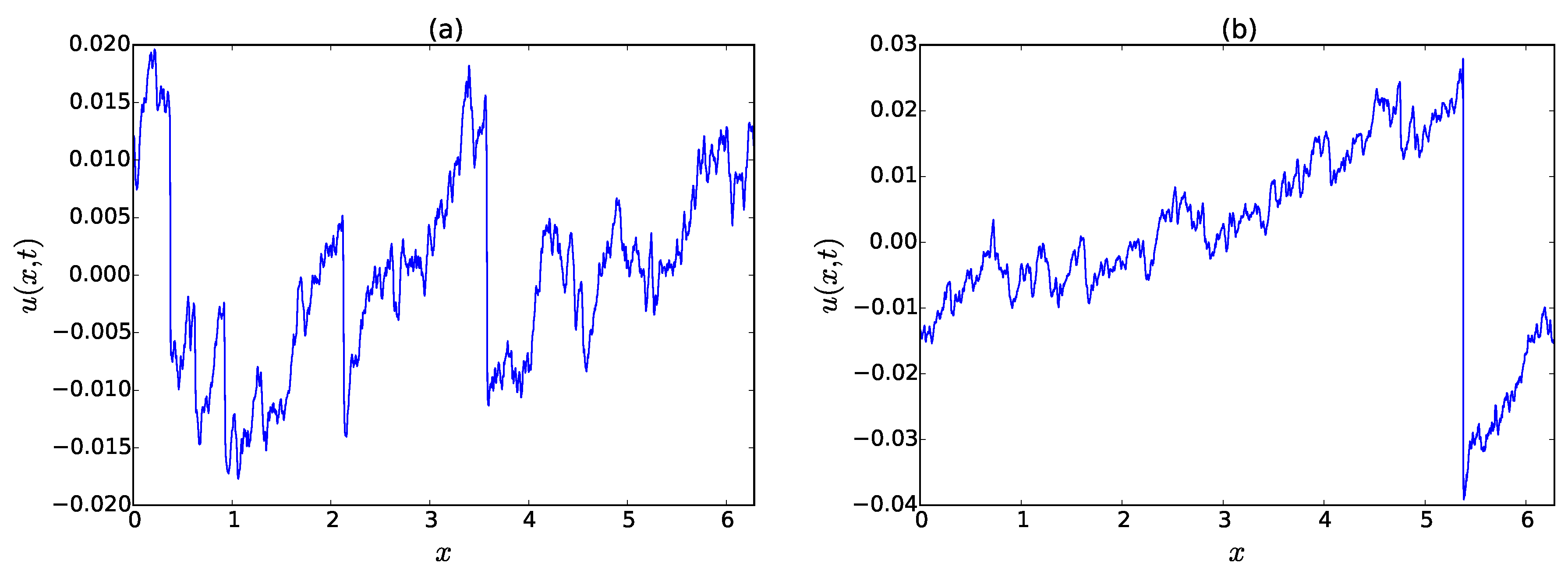
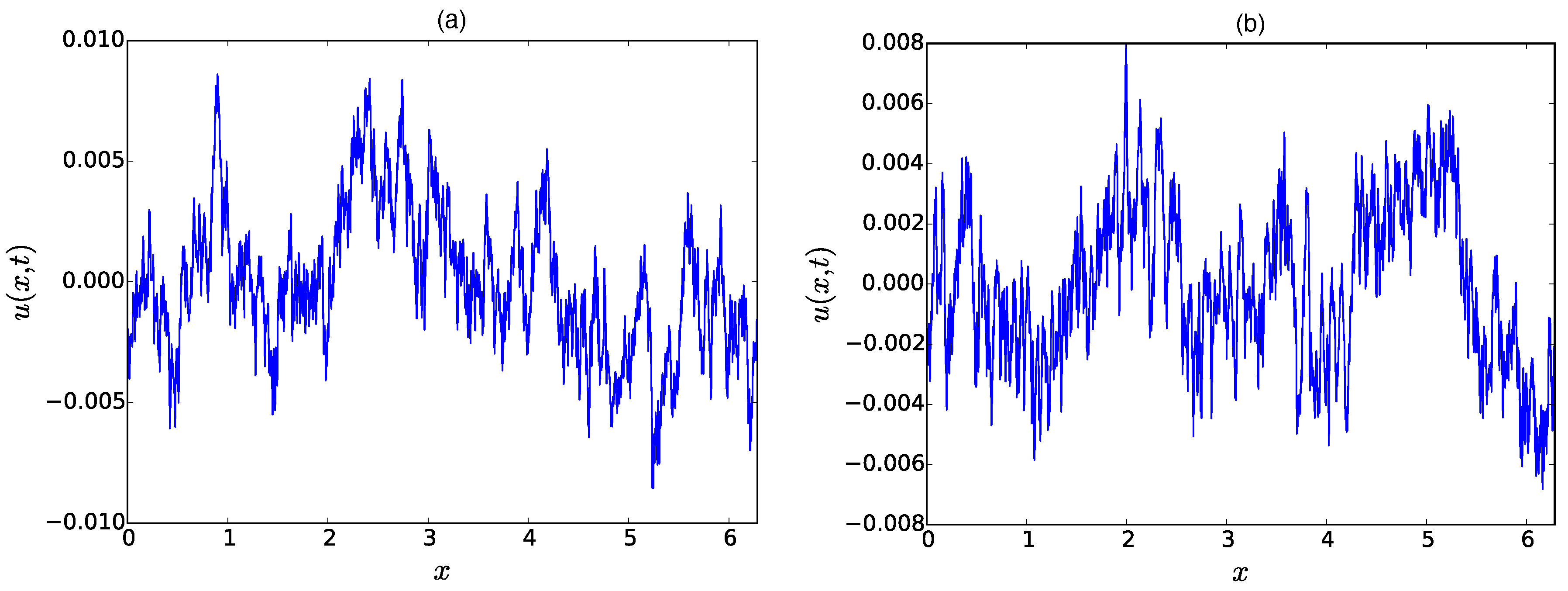
26) vanishes and we recover the ordinary Burgers equation with its shock-type velocity profiles. A typical realization of the velocity field of Burgers turbulence (run #1) is shown in
Figure 3a. The velocity field exhibits a sawtooth-like structure and forms shock fronts consisting of large negative velocity gradients. In this particular snapshot, we can distinguish three or four shocks that are connected via ramps of positive inclination and are superimposed by small-scale structures that also consist of small shocks.
Figure 3b shows the velocity field belonging to the most extreme shock event that occurred during the simulations. It consists of one large negative gradient event that is barely resolved by the corresponding resolution of
grid points. Events such as the one depicted in
Figure 3b are extremely rare, but they do bear a particular statistical significance.
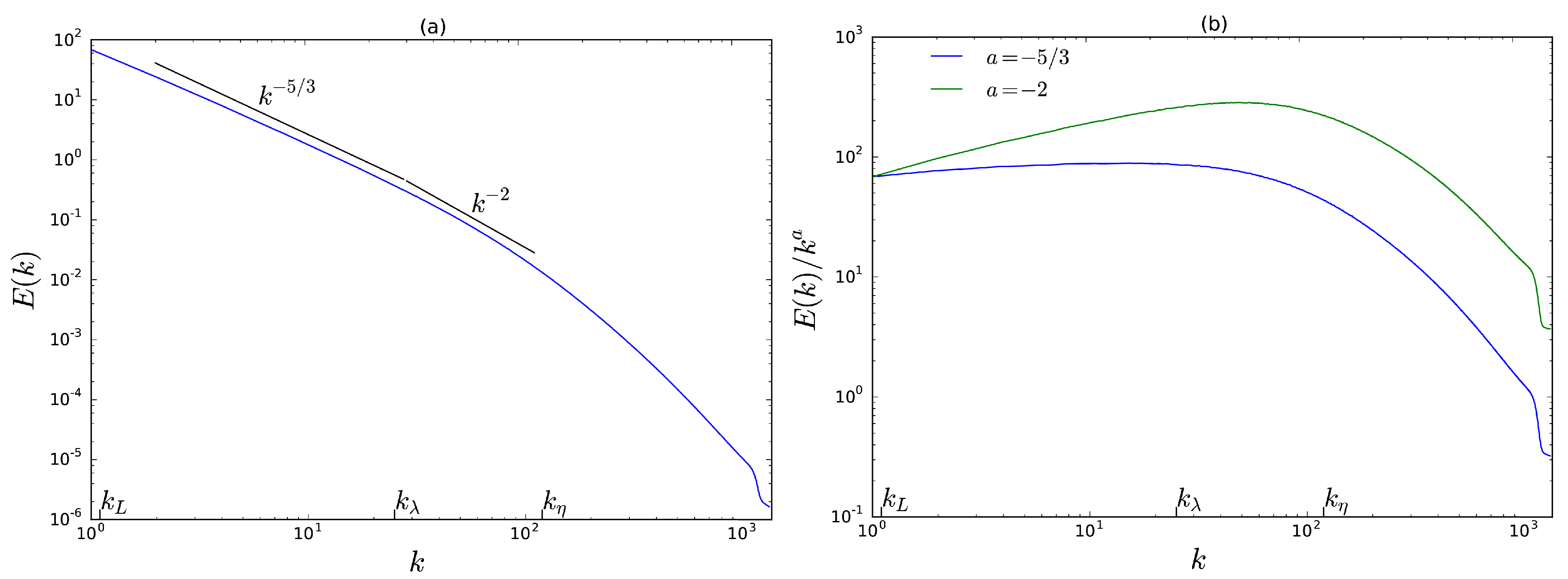
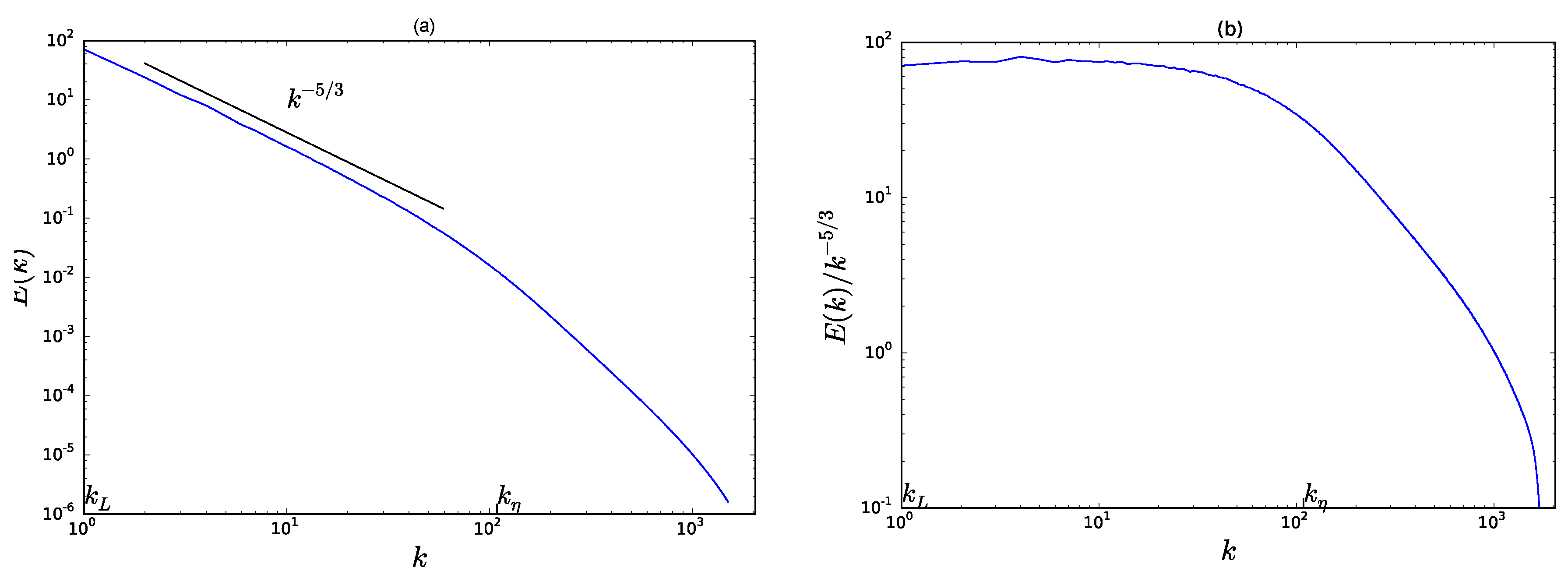
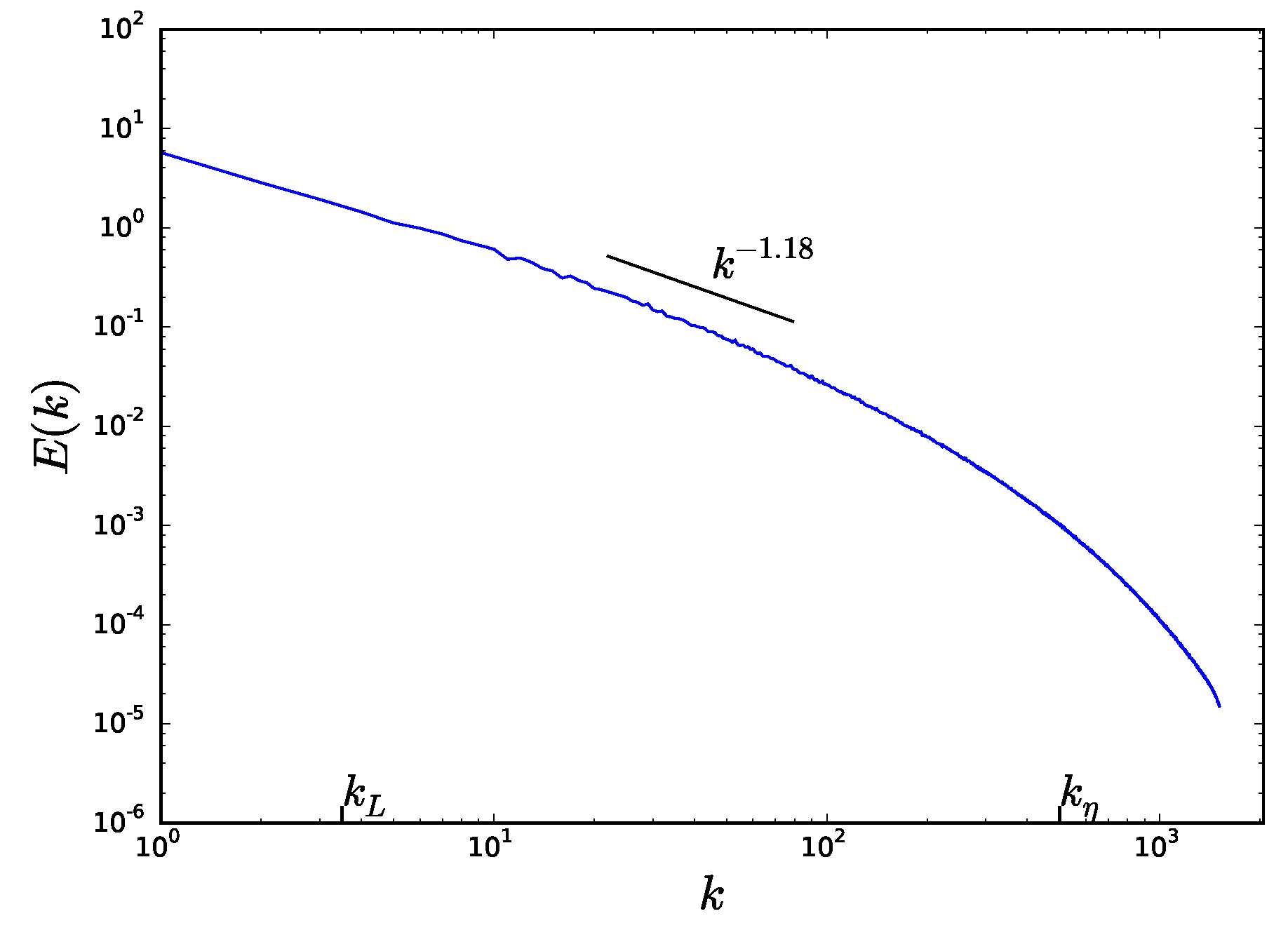
Figure 4a shows the energy spectrum
of simulation #1. Here, the inertial range is limited by the wave numbers
and
which are associated with the integral length scale
L and the Kolmogorov dissipation length
. The small wavenumber regime can be described quite accurately by a Kolmogorov-like spectrum
. However, as the wavenumbers increase, the spectrum drops faster than the Kolmogorov spectrum. It is tempting to propose a shock-like spectrum
for intermediate wavenumbers
that piles up in front of the dissipation range. Obviously, the latter does not manifest itself as clear as the
-part, but since the spectrum drops already in front of the dissipation range and shocks represent a small-scale quantity, it seems to be a convenient explanation. We must emphasize, however, that, in the original work of Cheklov and Yakhot [
36], solely the Kolmogorov-spectrum has been observed. The latter finding might be a result of hyperviscosity and the attained high Reynolds numbers. In order to further quantify these tendencies,
Figure 4b shows compensated spectra
with
and
. Plateaus in the plot correspond to scaling behavior of the spectrum and confirm the Kolmogorov part at small wavenumbers and a small range of the shock-like part as well.
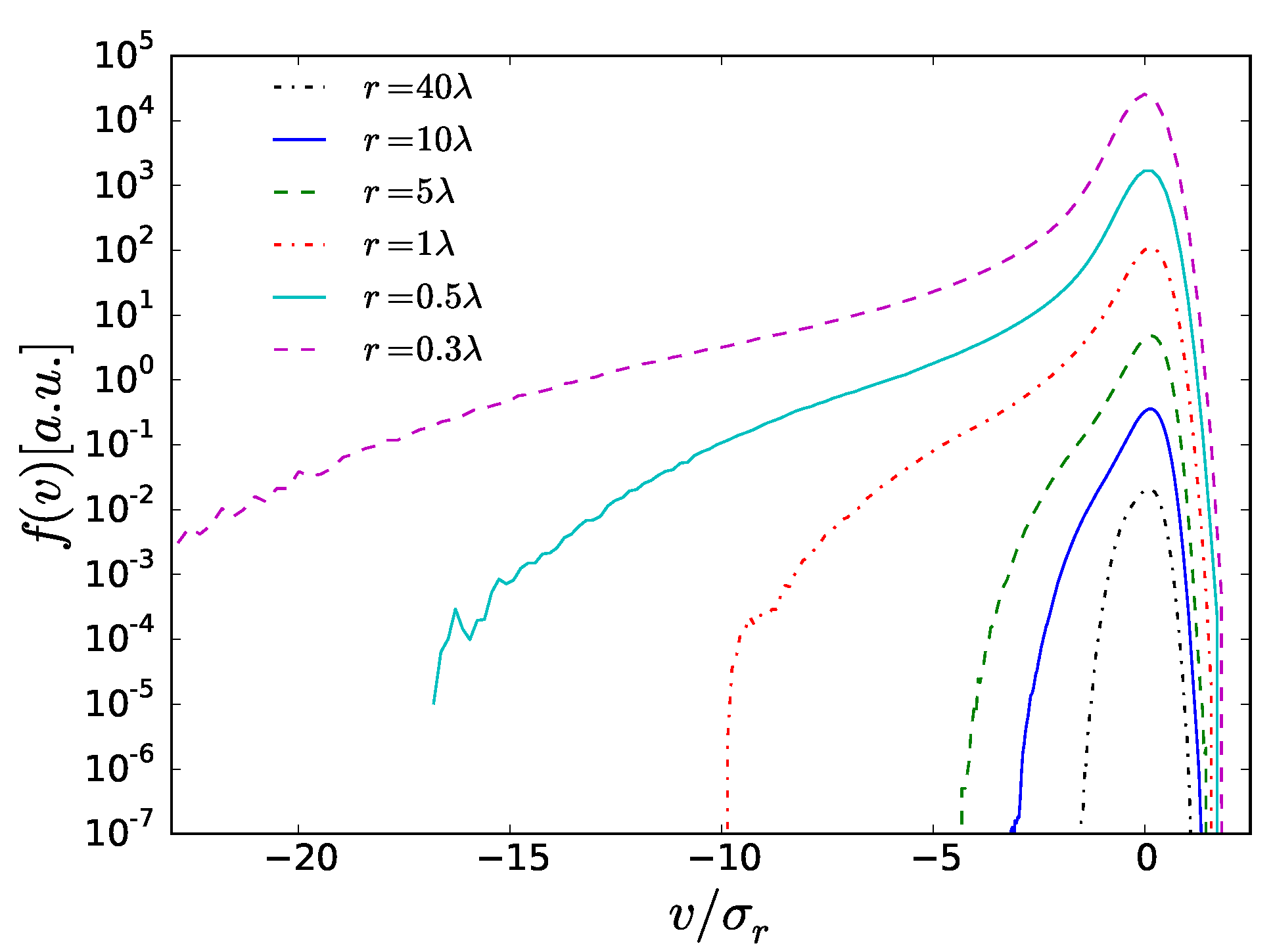
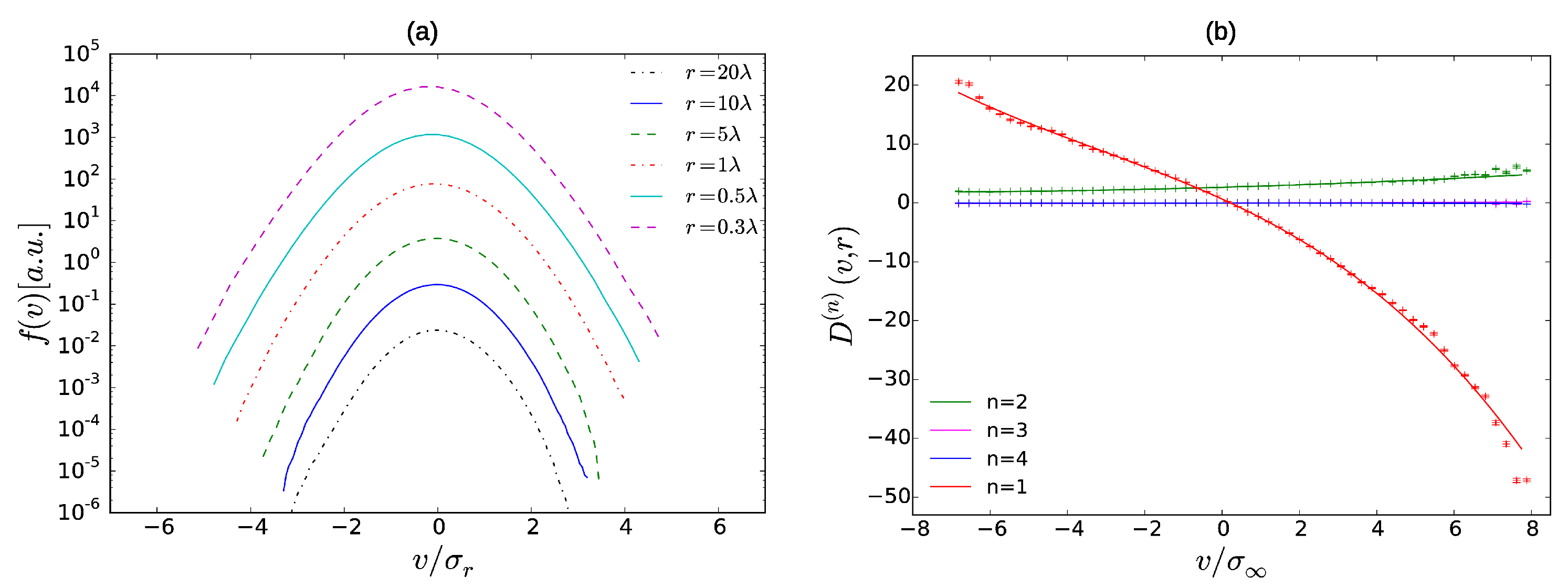
Figure 5 shows the evolution of the one-increment PDF
in scale, where
r is expressed in multiples of the Taylor length
. At small scales, the PDF shows a pronounced left tail due to shock events, whereas it is close to Gaussian on large scales. Here, the PDF for
seems to exhibit an algebraic part for negative increments and drops exponentially for larger negative increments. However, it is not obvious whether the algebraic part corresponds to
as it has been predicted for the gradient PDF [
15]. Due to the moderate Reynolds numbers, it is also not clear whether the exponential decay for large negative velocity increments follows the exponential decay
predicted from instanton calculations [
41].
3.1.1. Examination of the Markov Property
In this section, we seek to examine the Markov property (
4) from DNS of Burgers turbulence. To this end, we briefly mention two possibilities: first, the Markov property can be examined directly in comparing the conditioned PDF with the transition PDF
where the intermediate scale
was chosen to lie well within the inertial range and
can be considered as the variable step width of the process. In general, the intermediate scale can also be chosen at a different inertial range scale, but in the following we will only consider this particular case. At this point, since we are comparing two objects of different complexity, we perform cuts of the doubly conditioned PDF for fixed
. This can be done by the simple choice
, which offers the best statistics. However, for a more critical examination, it is appropriate to put
at least to
, where
The other method is to examine the Chapman–Kolmogorov equation [
25]
which has the advantage that it involves solely transition PDFs.
In the following, we use the first method, i.e., Equation (
28). In order to obtain a sufficient overlap between the two PDFs, we choose
and
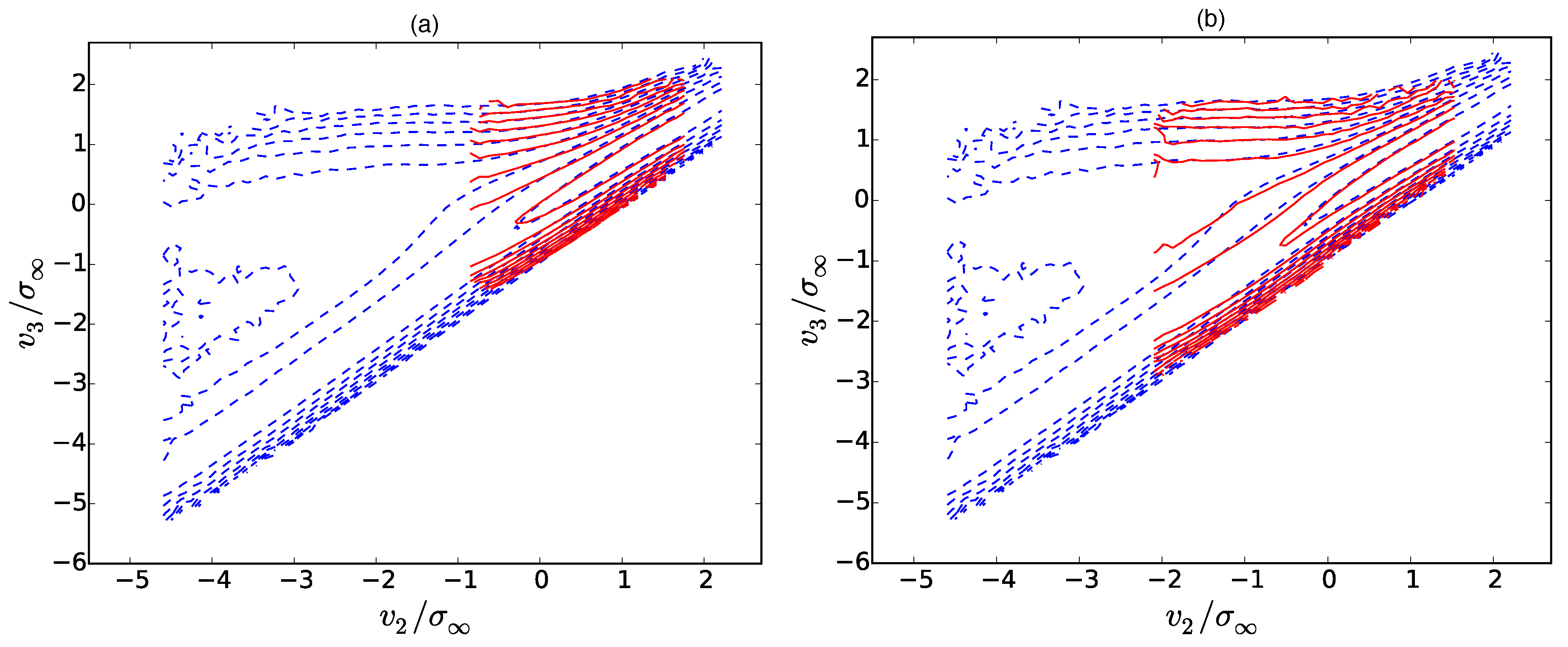
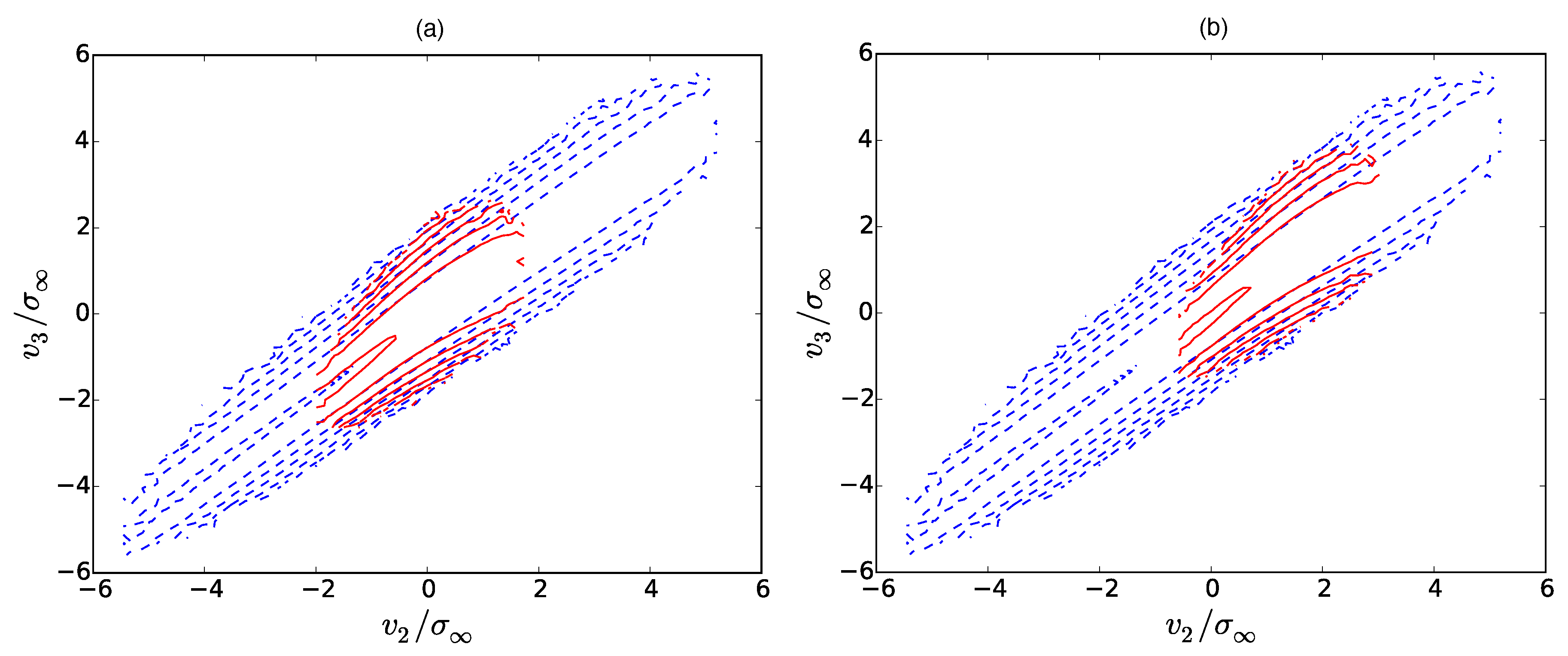
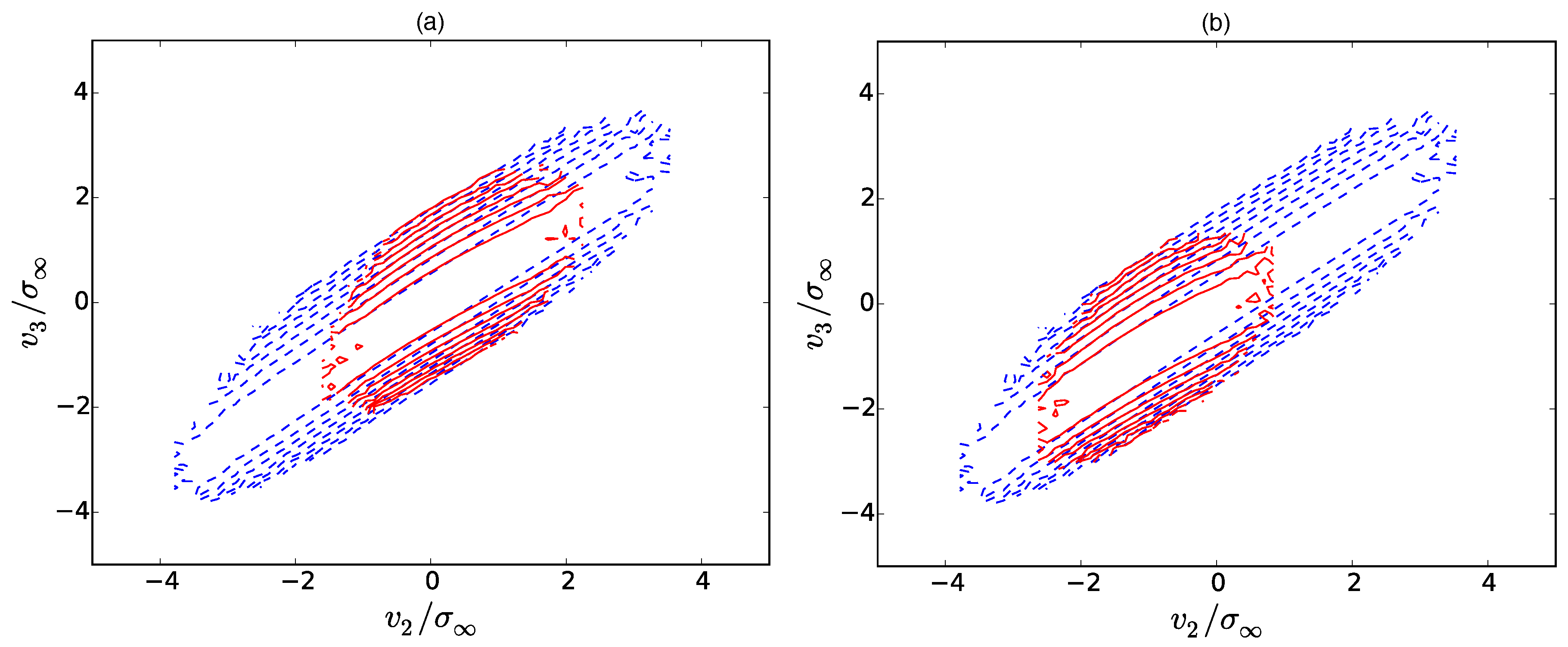
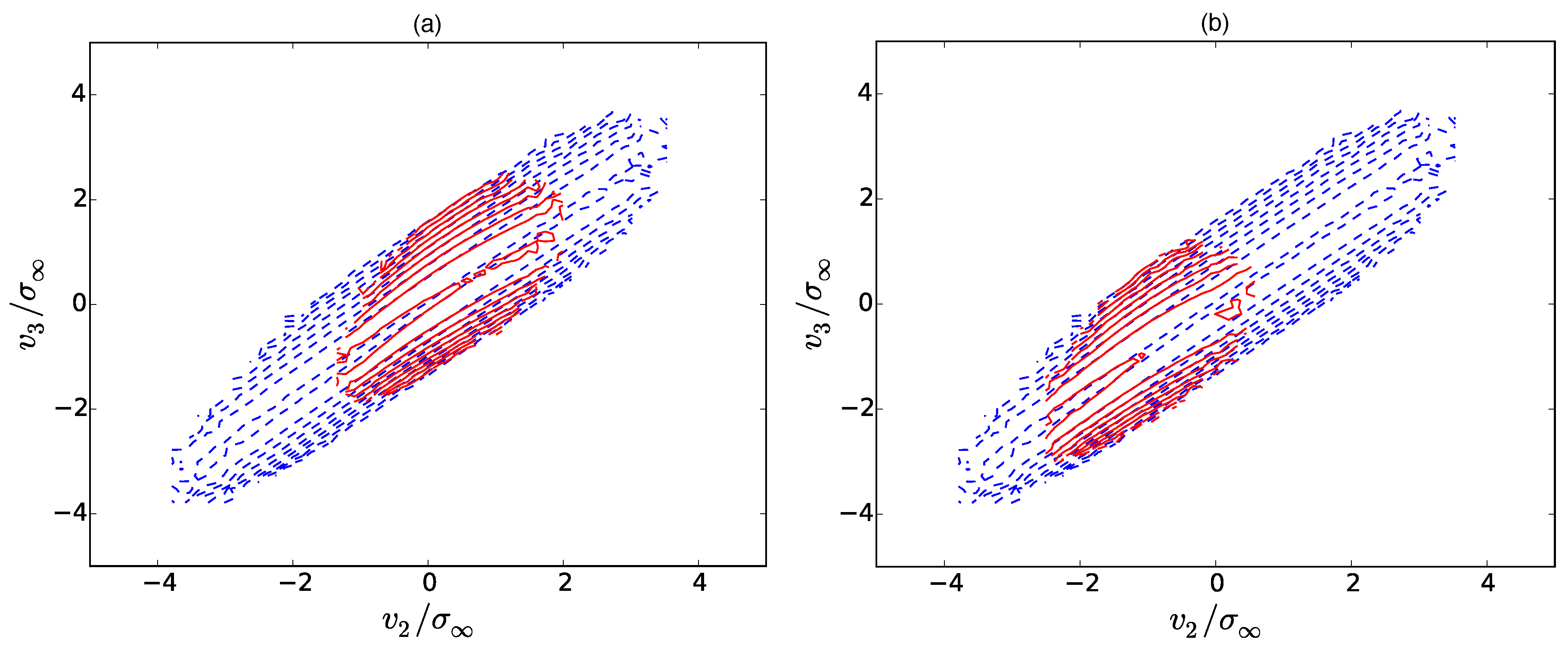
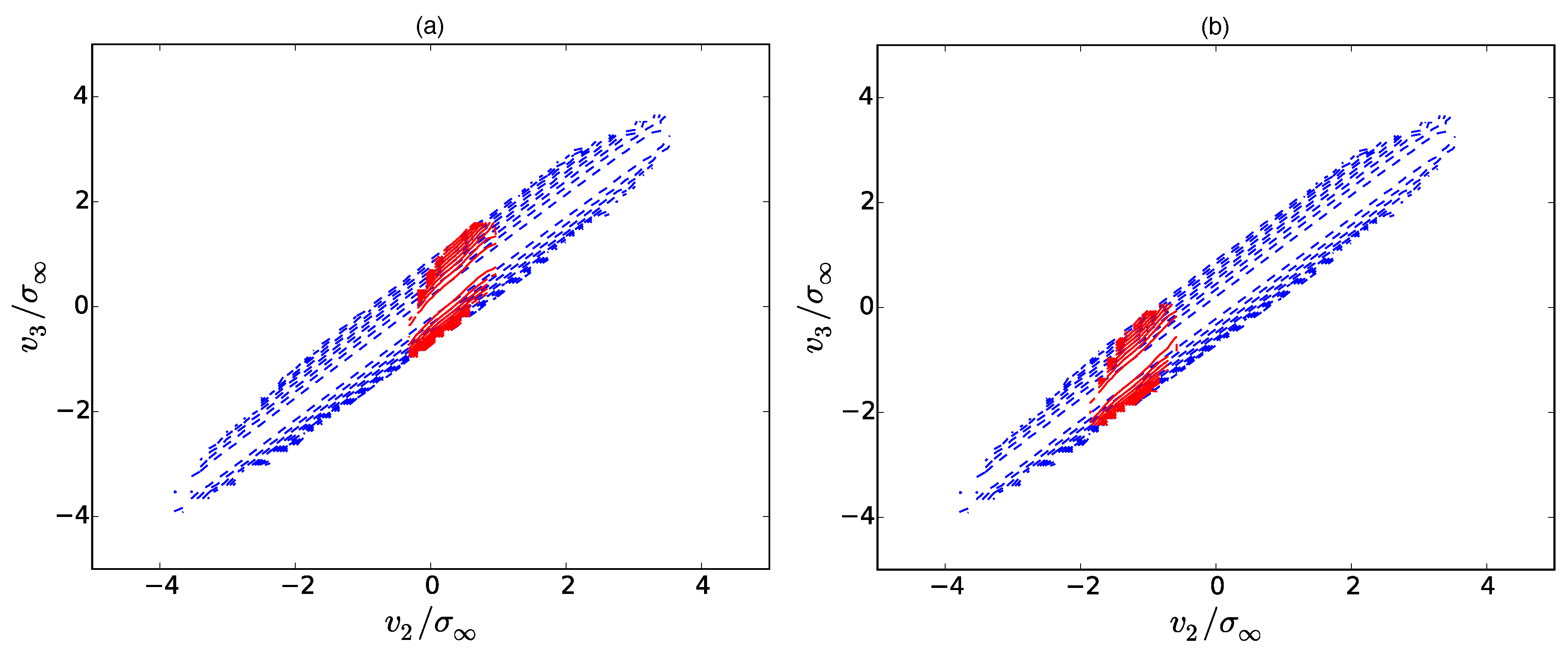
, since the positive increment parts of the PDFs are suppressed by shocks. The resulting contour plots for three different
are depicted in
Figure 6,
Figure 7 and
Figure 8. Here, the dashed blue lines correspond to the transition PDF
, whereas the red lines correspond to the conditional PDF
. At first glance, we can see that the shape of the transition PDF (blue) can be reproduced for the most part by the solution of (8)
which is derived in
Appendix A. For
, the additional branch
appears. Obviously, the contours of the transition PDFs are not pure delta functions, but are rather broad. We want to emphasize that this can be considered as an artifact of the Kramers–Moyal expansion (8): The solution (
31) has been constructed from the initial condition
A second initial condition, which would be a Gaussian transition probability at large scales, cannot be imposed since the Kramers–Moyal expansion is only a first-order differential equation.
Concerning the Markov property itself, it seems to be best fulfilled around the Taylor length, i.e., for
in
Figure 7a. We can also establish this finding for
. However, at larger scale separations
in
Figure 6, the Markov property slightly deteriorates. Although the shape of the transition PDF and the conditional PDF are basically the same, there is a small shift of the contour lines in the
-direction. The effect becomes even stronger for
which can be seen from
Figure 6b. In comparison to the true violation of the Markov property in
Figure 8, however, this effect is rather small. At those smaller scale separations, here for
, both PDFs possess a different shape.
Figure 8a shows that the transition PDF (red) overestimates the
-correlations of the conditional PDF (blue) manifesting itself by a strong steepening of the contour lines of the transition PDF in comparison to the conditional PDF. The effect becomes even more pronounced for
. Nevertheless, for large negative values
, the contour lines seem to overlap again. It is therefore tempting to speculate about whether the Markov property might again be fulfilled inside the shocks, and that only the regions of extreme curvature in the vicinity of the shocks lead to the break-down of the Markov property. In this context, it is important to notice that the Taylor length
is located just in front of the
-part of the spectrum in
Figure 4. In the following section, we aim to quantify the break-down of the Markov property by the introduction of a distance measure between the two distributions in Equation (
28).
3.1.2. Determination of the Markov–Einstein Length
Here, we seek to quantify the break-down of the Markov property (
28). There are a variety of methods for comparing the transition PDF and the conditional PDF [
10]. In the present study, we will restrict ourselves to the so-called Hellinger distance [
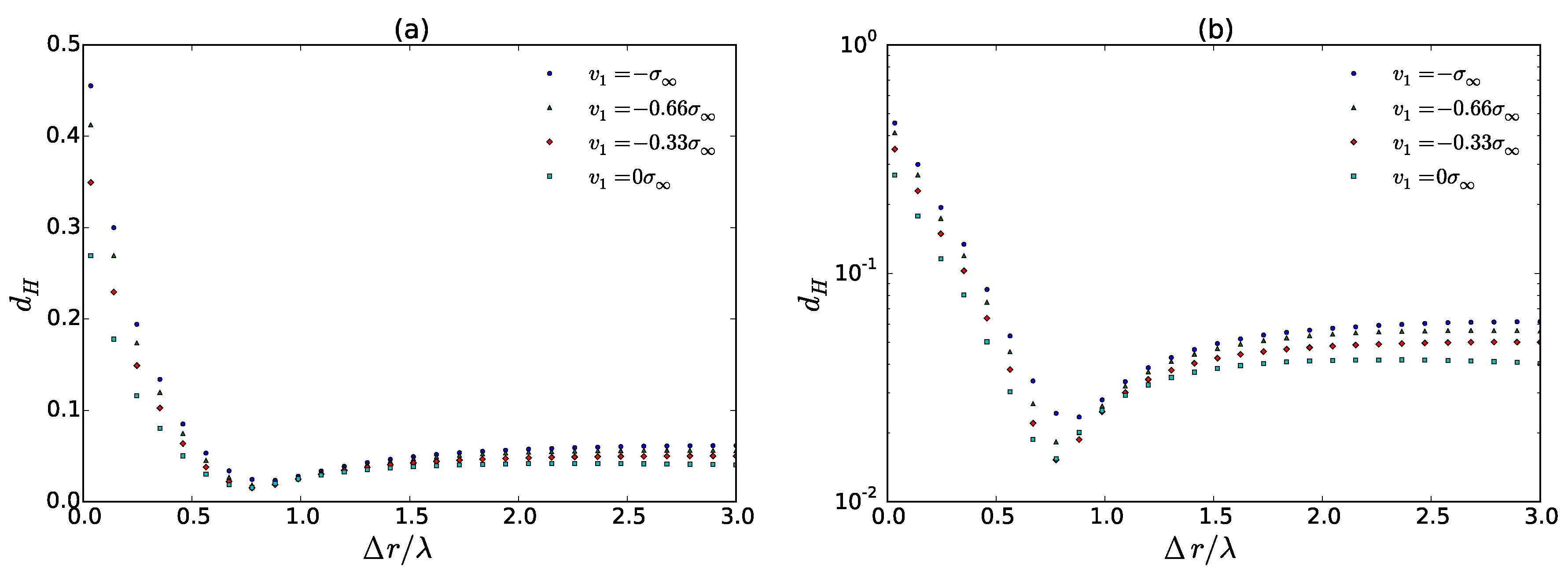
42], although other methods such as the correlation distance or the Kullback–Leibler divergence have also been experimented with. The advantage of the Hellinger distance
H is that it forms a true metric in the space of the PDFs and can therefore be used to decide at which scale separation
the Markov property significantly deteriorates. The Hellinger distance
H for continuous distributions is defined according to
Here, we made use of the identities
in the last step. Hence, the Hellinger distance is symmetric in both probabilities and is restricted to
which is a direct consequence of the Cauchy–Schwarz inequality. Another useful property of the Hellinger distance is that it can be explicitly calculated for certain types of PDFs (normal distribution, beta distribution, exponential distribution, etc.).
In our case, the Hellinger distance still is a function of
if we assume that
is fixed. Therefore, an average of the corresponding
-values is performed in order to obtain a pure correlation measure
The corresponding
dependency in
Figure 9a is expressed in terms of the Taylor length
. Remarkably, the Hellinger distance
is smallest at around
and approaches a small constant that is different from zero for larger
. This corresponds to the observation from
Figure 6 where the contour plots were slightly shifted in the
-direction for larger
. In other words, the Markov property gets slightly better before it gets worse in the process of letting
. The latter observation differs from usual investigations of the Markov property in turbulence [
10]. For smaller
, however, the Hellinger distance shows a more pronounced increase and therefore, the Markov property is clearly violated since it seems to approach 1 in the limit
. These effects become even more unambiguous for
.
Figure 9b shows a semi-logarithmic plot of the Hellinger distance. For
, a quantitatively new behavior emerges. The latter is characterized by a close to exponential increase of the Hellinger distance. Such behavior implies an exponential decay of the correlations of the Markov property Equation (
28). Here, it suffices to estimate the Einstein–Markov length at around the point, where a pronounced increase sets in, i.e.,
.
Hence, the task of an accurate determination of the Markov–Einstein length is far from obvious. However, it can be inferred from
Figure 9 that it lies near the Taylor length as the correlation measure clearly drops at
.
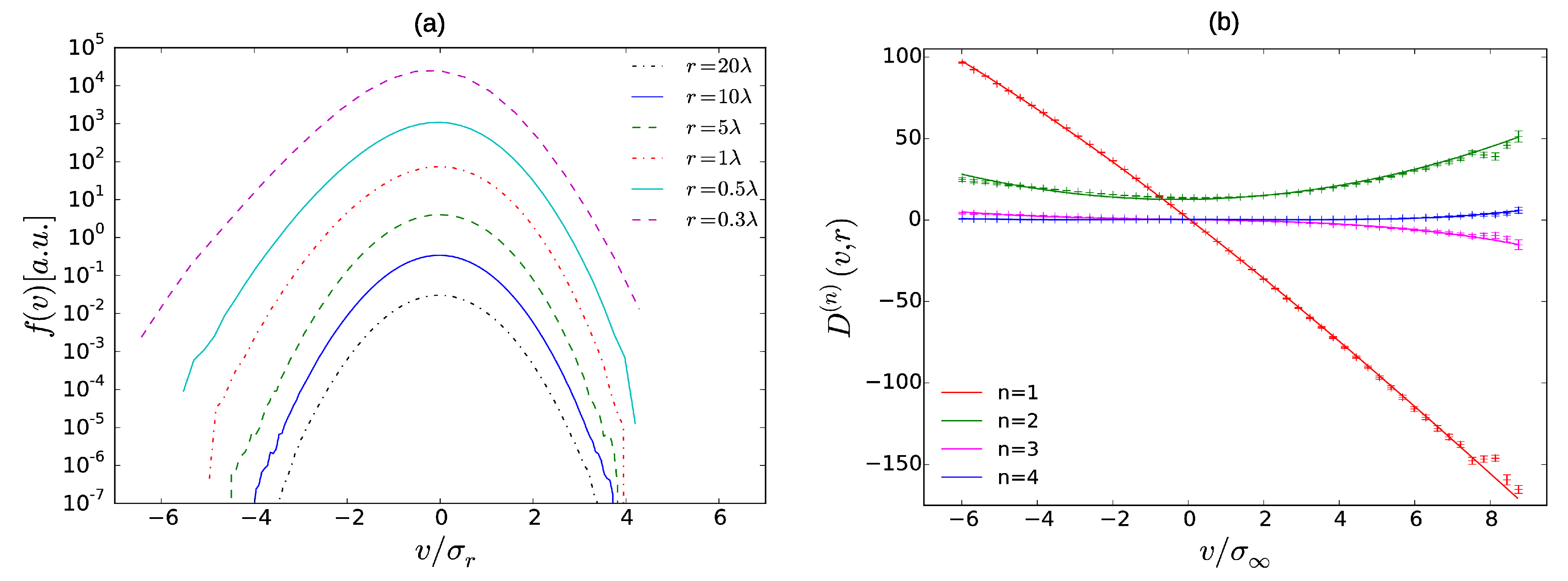
3.1.3. Determination of the Kramers–Moyal Coefficients
In this section, we will outline a procedure which determines the Kramers–Moyal coefficients (
10) from the numerically evaluated transition probabilities similar to
Figure 7.
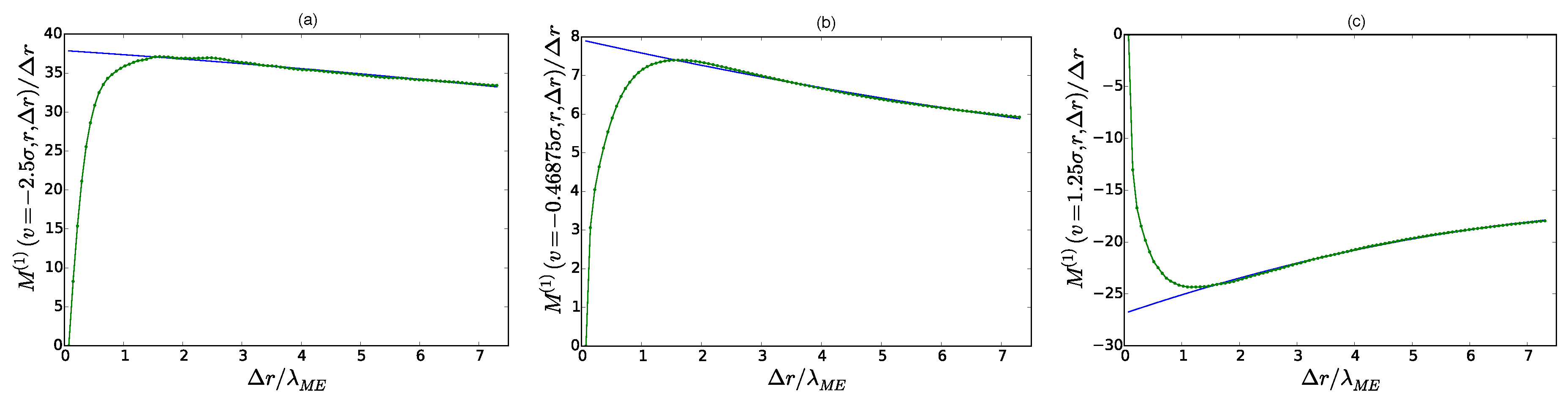
To this end, we devise an appropriate extrapolation method for the conditional moments
as the Markov property becomes violated in the proximity of the Einstein–Markov length. Subsequently, the limit
has to be determined from the extrapolation of the conditional moments in order to obtain the corresponding Kramers–Moyal coefficient [
10]. As an example, we plotted the conditional moments of first order
for three different
in
Figure 10.
drops against zero for
as the Markov property is violated. In order to extrapolate the moments, polynomial fits of second order in
were performed for
(blue lines in the plots). The Kramers–Moyal coefficient for a particular
v, in this case the drift coefficient, can be read off from the
y-intercepts of the fits. Consequently, this procedure has to be repeated for several
v (and in general also different
r) for the sake of obtaining the full functional form of the Kramers–Moyal coefficients. The method was used for the Kramers–Moyal coefficients up to order four in
Figure 11. The corresponding coefficients were fitted with polynomials of order
n. The obtained reduced Kramers–Moyal coefficients
correspond well with the theoretical predictions from Equation (
22) even at such small Reynolds numbers. Kramers–Moyal coefficients of higher order are detectable for negative velocity increments and Pawula’s theorem [
34] is violated. The drift coefficient
possesses an additional cubic
v-dependence that has already been reported in the experiment [
10]. In the Burgers case, only the drift coefficient is different from zero for positive increments, which underlines the self-similarity of the right tail of the PDF in
Figure 5. The diffusion coefficient, however, possesses an additional positive intercept which turns out to be a consequence of the non-conservative forcing procedure. In fact, it can be shown that a conservative force
in Equation (
26) leads to the vanishing of the intercept.
3.2. No Intermittency : Purely Nonlocal Case
In the following, we will discuss the purely nonlocal case (
) of the generalized Burgers Equation (
26).
Figure 12a shows a typical velocity field realization of the DNS of run #2 in
Table 1. In contrast to the case of Burgers turbulence, no clear shock fronts can be detected and the velocity field is organized in cusp-like structures.
Apparently, the nonlocality in the generalized Burgers Equation (
26) leads to entirely different singular structures. The latter manifest themselves also in the spectrum
in
Figure 13 which exhibits a close to Kolmogorov-type inertial range.
3.2.1. Examination of the Markov Property
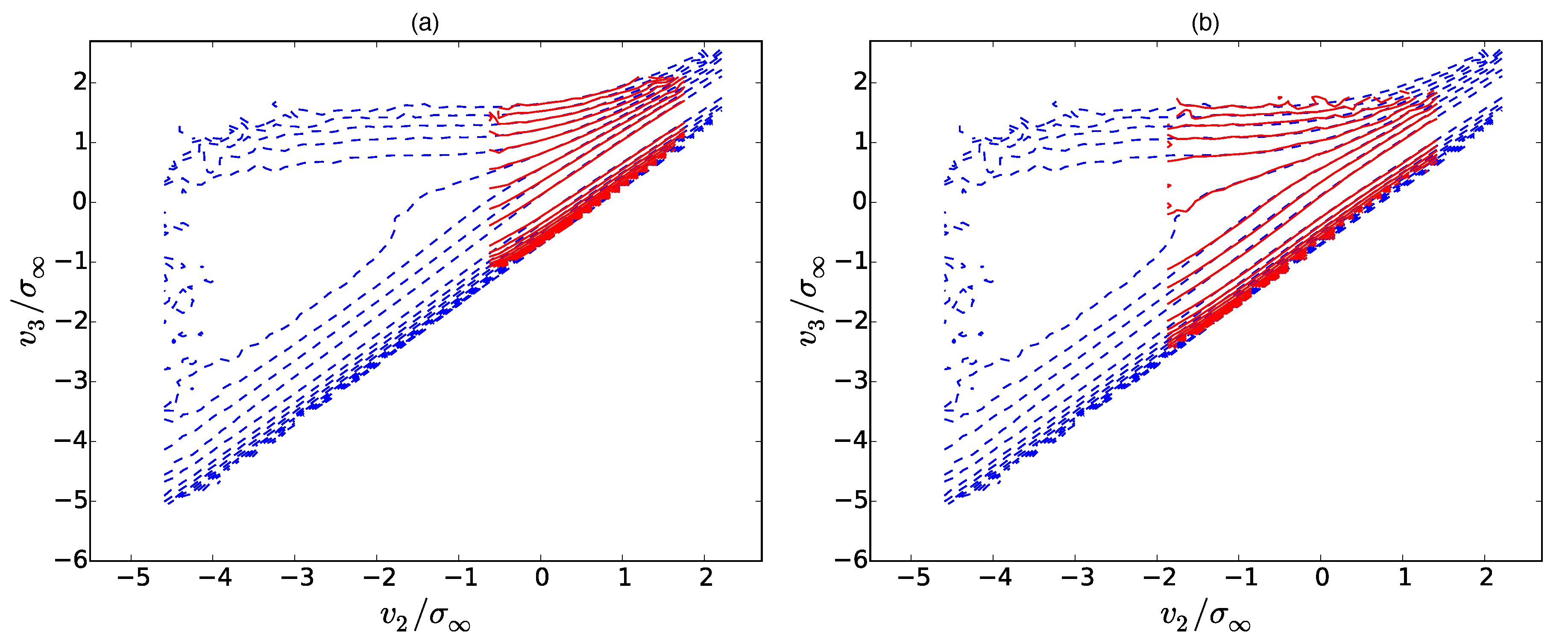
Figure 14,
Figure 15 and
Figure 16 show the contour plots of the one-time conditioned PDF (blue) and the two-time conditioned PDF (red). For this particular case, the transition PDF (blue) possesses a solely diagonal shape in contrast to the pure Burgers case in
Section 3.1.1, which possessed a
-part for negative
.
The Markov property is fulfilled to a great extend for
and
in
Figure 14 and
Figure 15. For smaller scale separations, i.e.,
in
Figure 16, the Markov property is broken: the doubly conditional PDF (red) appears steeper than the transition PDF (blue), which underestimates the correlations between
and
. The contours are shown for two different slices of
, namely
in (a) and
. Contrary to the Burgers case in
Figure 6,
Figure 7 and
Figure 8, the exact
-position of the slice is quite unimportant and only alters the significant statistics, not the shape of the PDFs. For comparison, we also refer to
Appendix B for an explicit solution for the K41 transition probability.
3.2.2. Determination of the Markov–Einstein Length
Figure 17 presents the Hellinger distance
from Equation (
36) for the purely nonlocal case. The Hellinger distance is close to zero for large scale separations
. In contrast to the Burgers case in
Figure 9, which exhibited a clear drop of the Hellinger distance at around
, the Markov property is a good approximation for all larger scale separations.
Here, the Hellinger distances increase at around
. It must be stressed that this behavior differs significantly from the Burgers case: whereas the Hellinger distances in
Figure 9 decrease at around
and then increase, i.e., they exhibit a clear minimum, the nonlocal case exhibits a steady increase at these scales.
Figure 17b shows a semi-logarithmic plot of the Hellinger distance
. Whether the increase of the Hellinger distance is exponential is somewhat hard to anticipate. However, the increase is not as violent as in the Burgers case in
Figure 9b. Accordingly, the Markov property in the nonlocal case is not deteriorating as fast as in the Burgers case. The determination of the Markov–Einstein length
for the nonlocal case proves to be quite challenging since the Hellinger distance is steadily increasing for smaller
. In the following, we estimate
, in order to determine the Kramers–Moyal coefficients of the nonlocal case.
3.2.3. Determination of the Kramers–Moyal Coefficients
The PDFs
at different scales
r in
Figure 18a are purely self-similar functions that are close to Gaussian. Hence, the purely nonlocal case is characterized by the absence of intermittency. The self-similarity of the one-increment PDF is in agreement with the heuristic arguments established in
Section 2 (i.). They can be reproduced by a self-similar function
with
and
g being very close to a Gaussian (not depicted in the figure). Hence, the nonlocal case is in very close correspondence to the K41 phenomenology. This is also reflected in the Kramers-Moyal coefficients depicted in
Figure 18b. Whereas the drift coefficient
possesses a slightly cubic dependence, the linear part with its corresponding reduced Kramers–Moyal coefficient
is close to the K41 prediction
. The diffusion coefficient points further into the direction of the K41 phenomenology: it shows only a slight quadratic dependence on
v and has a rather linear shape. Accordingly, the reduced Kramers–Moyal coefficient of order two is rather small,
. Higher-order coefficients,
are even smaller (
,
). Furthermore, for
, the coefficients strongly deviate from the scaling
, e.g., the reduced Kramers–Moyal coefficients become negative. Hence, the obtained Kramers–Moyal coefficients are in agreement with the self-similarity of the one-increment PDF in
Figure 18a.
3.3. Intermediate Case
Seminal numerical investigations [
24] already highlighted the fact that the intermediate case exhibits statistical behavior that is close to the intermittency behavior encountered in ordinary hydrodynamic turbulence. The latter behavior manifested itself by a skewed velocity gradient PDF as well as by structure function exponents that deviated considerably from the predictions suggested by the K41 theory.
Figure 19a shows a snapshot of the velocity field obtained from DNS run #3. In contrast to run #2 in
Figure 12, the intermediate case reveals a rather saw-tooth like velocity field profile. Nonetheless, no clear shock-like structures can be distinguished.
Figure 20 shows the energy spectrum of run #2. It deviates considerably from the Kolmogorov prediction, i.e.,
. Firstly, no clear power–law behavior could be detected. The fitted line corresponds to
; however, a Kolmogorov spectrum might as well be attained at higher
k-values. Zikanov et al. [
24] propose an energy spectrum of the form
, which is closer to
than the simulations performed here. At this point, it is not clear, whether the small Reynolds numbers attained in run #2 are responsible for the underestimation of the spectral energy decay.
3.3.1. Examination of the Markov Property
The Markov property is fulfilled for the intermediate case as well, provided that the scale separation
is not too small.
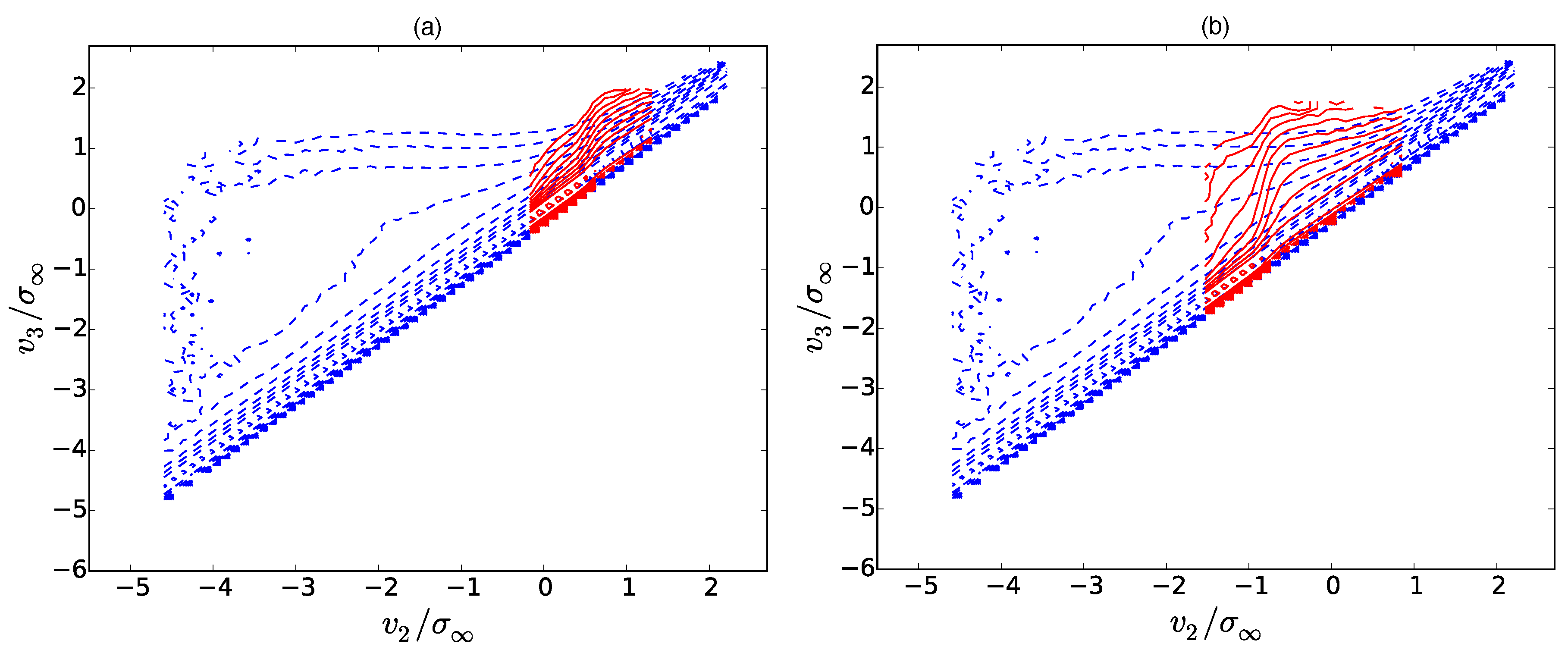
Figure 21 and
Figure 22 show the corresponding contour plots for
and
. The shape of the PDFs qualitatively agree with those of the purely nonlocal case; however, for smaller scale separations, one might guess certain differences. The Markov property is not fulfilled for
, which can be deduced from
Figure 23. The transition PDF (blue) underestimates the
–
–correlations of the doubly conditional PDF (red). For comparison, we also refer to
Appendix C for an explicit solution for the OK62 transition probability.
3.3.2. Determination of the Markov–Einstein Length
Figure 24 shows the Hellinger distance (
36) for five different
. It is remarkable that for
, the Helligner distance is smaller than for
, which only changes for small
r. This is also a first hint on the asymmetry of velocity increments in the intermediate case. The latter can be further quantified in considering the evolution in scale of the one -increment PDF in
Figure 25a which shows that extreme large negative velocity increments at small scales are more common than positive ones.
Concerning the Hellinger distance itself, we can see that, in contrast to the nonlocal case, the Hellinger distance exhibits a rather pronounced minimum at around
. This behavior thus resembles somewhat to the behavior encountered in the pure Burgers case and, hence, can be attributed to nonlinear shock generation. Henceforward, the determination of the Markov–Einstein length is rather simple and it can be estimated according to
. The latter finding is supported by the semi-logarithmic plot in
Figure 24b as well.
3.3.3. Determination of the Kramers–Moyal Coefficients
The Kramers–Moyal coefficients from run #3 are shown in
Figure 25b. The second Kramers–Moyal coefficient exhibits a clear parabolic dependence on
v in contrast to the purely nonlocal case, which revealed a linear dependence. The corresponding reduced Kramers–Moyal coefficient
, hence, is roughly ten times bigger than the one determined from the nonlocal case
. The tendency for these intermittency effects also reflects itself in higher-order Kramers–Moyal coefficients
. The latter coefficients, even though they appear rather flat, follow a clear
v-polynomial of order 3 and 4, respectively.
Moreover, in contrast to the two previous runs #1 and #2, Kramers–Moyal coefficients up to order 9 could significantly be detected and their reduced Kramers–Moyal coefficients could be determined, which will also be discussed in the next section.
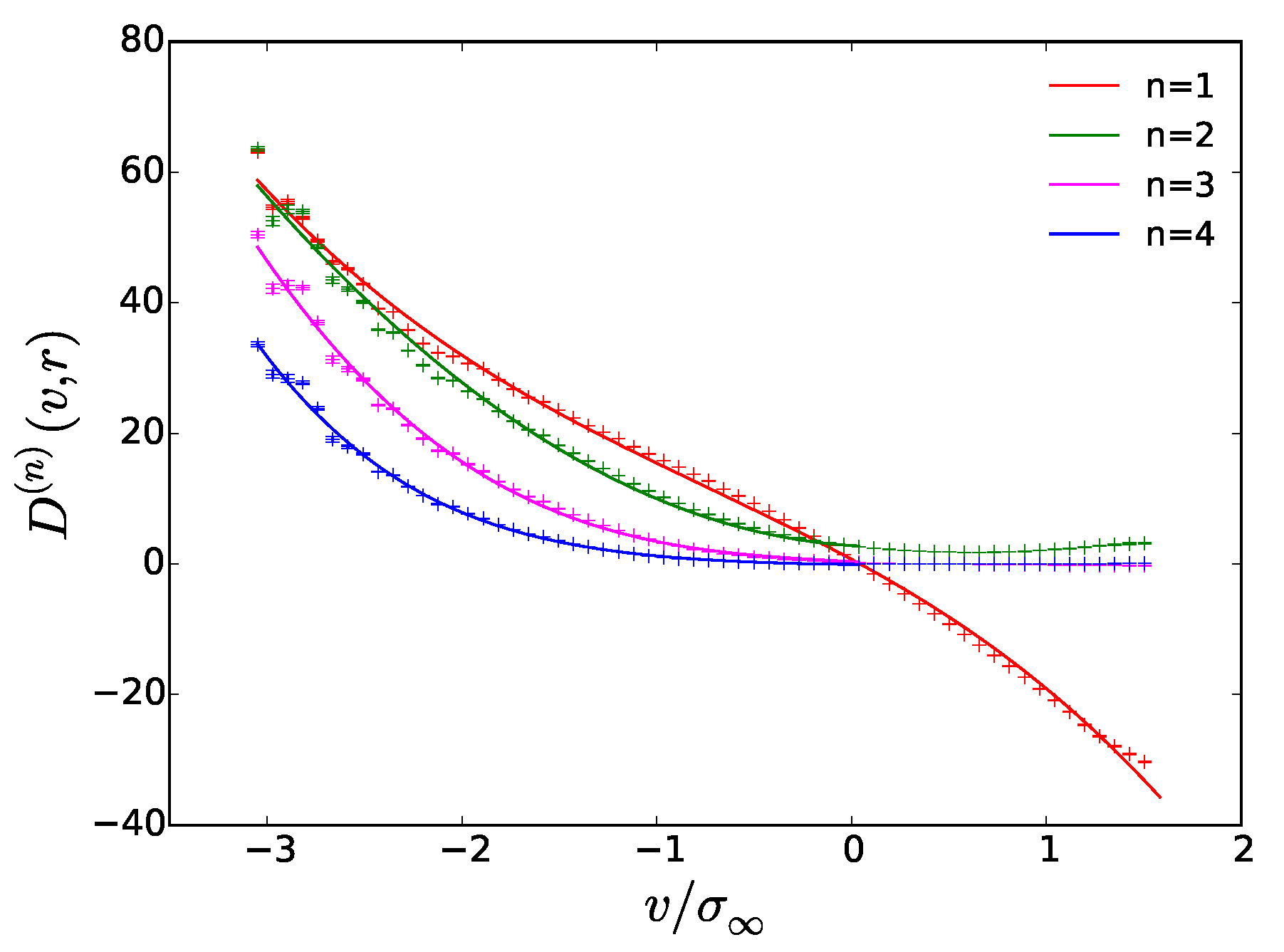
4. Quantification of Small-Scale Intermittency on the Basis of Kramers–Moyal Coefficients
We compare the reduced Kramers–Moyal coefficients from runs #1–3 in
Figure 26 to the ones predicted by the phenomenological models from
Section 2.
For the Burgers case (
), higher-order coefficients (
) can also be detected significantly for negative increments due to rare large-negative gradient events. Moreover, as discussed in
Section 3.1.1, the evolution of the one-increment PDF in scale (
Figure 11) showed a pronounced left tail due to shock events. Nonetheless, we could not verify whether this tail corresponds to the predictions of an algebraic tail
proposed in [
15,
43]. It has to be stressed that these predictions have been obtained in the context of velocity gradients in Burgers turbulence. The proposed Markov approach, however, solely applies to velocity increments
and the limit of velocity gradients
cannot be studied due to the breakdown of the Markov property at small scales (see
Section 3.1.1). It is thus not possible to assess the algebraic tail behavior in terms of a solution of the one-increment PDF on the basis of a Kramers–Moyal expansion (
7).
Concerning the purely nonlocal case (
), we observed a self-similar evolution of the one-increment PDF in scale which can be seen from
Figure 18a. As self-similar behavior is characterized by a single drift coefficient
, higher order Kramers–Moyal coefficients should be close to zero. In fact,
Figure 18b shows that
and
are rather small. Furthermore, the diffusion coefficient
is linear in
v and has only a small reduced Kramers–Moyal coefficient
. Finally,
suggests that the purely nonlocal case can be described quite accurately by the K41 theory
i.), which has already been reported in [
24].
Higher order
of the intermediate case (
) correspond well to Yakhot’s intermittency model. However, it must be stressed that the first three coefficients deviate from Yakhot’s predictions (red curve in
Figure 26). Moreover, in calculating the third-order structure function
, we observe that it does not follow Kolmogorov’s law. Hence, an accurate description via the Kramers–Moyal coefficients has to resolve the spatial dependence of
as well in order to extract the
dependence. Nevertheless, one can clearly distinguish between the green (She–Leveque model) and red curve (Yakhot’s model), which is usually not possibly on the basis of a mere scaling exponent analysis.