Abstract
This study investigates false alarms of a major sudden stratospheric warming (MSSW) by real-time subseasonal-to-seasonal forecast data of the European Centre for Medium-Range Weather Forecasts system for the 2017/2018 Northern Hemisphere winter season. The analysis reveals two false alarm cases in the season, one in early December and the other in early February. Each case is characterized by ensembles of which a considerable part of the members (MSSW members) show an MSSW, that is, reversal of the zonal mean zonal wind in the extratropical stratosphere on similar calendar dates. Ensemble forecasts that are initialized earlier or later basically lack an MSSW, demonstrating clear intraseasonal variability in the frequency of forecasted MSSWs. For each false alarm case, the MSSW member mean field shows equatorward displacement of the polar vortex around the onset date. For both cases, the MSSW members accompany stronger wave activity in the lower stratosphere than other non-MSSW members and reanalysis data. They are further associated with higher geopotential height than the non-MSSW members, in the upper troposphere over northeastern Canada and Greenland before the first case, and lower height over northeastern Eurasia before the second case. These are located over the ridge and trough, respectively, of the climatological planetary wave of zonal wave number one, and are consistent with the increased wave activity.
1. Introduction
It is widely accepted that knowledge of the stratospheric state contributes to enhanced tropospheric predictability over intraseasonal and longer time scales as stratospheric variability influences the troposphere over various time scales [1,2]. A strong downward influence can occur when the stratosphere experiences significant anomalies, such as sudden stratospheric warmings (SSWs) [3]. SSWs are a dramatic phenomenon, during which the polar vortex largely distorts or even breaks down, accompanied by a strong warming in the polar stratosphere [4,5]. An SSW is often classified as a major SSW (MSSW) if the zonal mean zonal wind at 60° N, 10 hPa reverses from westerly to easterly [6,7]. A surge of recent studies investigated the predictability of SSWs or MSSWs [1].
Several previous studies examined the predictability of an MSSW that occurred in mid-February of the 2017/2018 Northern Hemisphere winter season, which is a target season in this study. Analysis of forecasts of the Beijing Climate Center Climate System Model for the MSSW shows that the maximum deterministic predictable time limit is 1–2 weeks, and increased wave activity is well predicted only within this limit [8]. It also suggests that extratropical tropospheric disturbances, such as East Asian and East United States troughs and Alaskan blocking, are important for the upward wave propagation to the stratosphere in the real world and forecast data. Using the subseasonal to seasonal (S2S) multi-system prediction database [9], Karpechko et al. [10] showed that MSSW forecast skill is reduced with errors in the forecast location of a Ural high and underestimated magnitude of upward wave activity flux. Lee et al. [11] further pointed out that an anticyclonic Rossby wave break associated with a cyclone plays an important role in building the Ural high. They showed that the ensemble members that fail to capture the pair underestimated the enhanced vertical wave activity flux and stratospheric polar vortex weakening. The importance of an Ural high in weakening the stratospheric polar vortex is consistent with the numerical experiments [12], although the experiments targeted a stratospheric response in early winter.
The S2S prediction database has been extensively utilized for a multi-system comparison of the predictability of MSSWs. Taguchi [13] compared S2S multi-system forecasts for five characteristic MSSWs, and showed that some systems are more skillful than others. More comprehensive comparisons using more MSSWs obtained consistent results [14,15]. Studies for two recent cases, MSSW in January 2019 and minor SSW in September 2019 in the Southern Hemisphere, revealed prolonged predictable time limits of about 18 days or longer for these cases [16,17], compared with the typical range between 5 and 15 days [1]. A study for final warmings in the Northern Hemisphere, that is, final reversal of the stratospheric circulation toward its easterly state in summer showed that the interannual variability in its timing was well forecasted more than four weeks in advance [18].
A possible role of the February 2018 MSSW in the tropospheric cold spell observed over Eurasia in the late winter season has been also investigated as follows. Karpechko et al. [10] showed that the cold anomaly was predicted more than two weeks ahead with a weaker magnitude, and suggested that this predictability is more associated with persistence of tropospheric anomalies in the forecast, with a smaller role of the MSSW. Kautz et al. [19] conducted forecast experiments (comparing observationally nudged stratosphere versus climatologically nudged stratosphere) and obtained an increased probability of a cold spell for the former, supporting enhanced predictability of surface weather extremes following MSSWs. They also suggested that the subsequent evolution in the lower stratosphere, rather than the MSSW itself, plays a crucial role in coupling to large-scale tropospheric flow patterns. Analysis of the S2S database for the two MSSWs in February 2018 and January 2019 by Rao et al. [20] emphasized the importance of the strength of the MSSWs in determining their downward propagation features.
Previous studies for the MSSW (or SSW) predictability, including the aforementioned studies for the MSSW in February 2018, commonly took an approach to identify target MSSWs that occurred in the real world and then examine how they were forecasted. When forecasts are initialized before the predictable time limit of a target MSSW, which depends on MSSWs and systems, they tend to miss or underestimate zonal wind deceleration to the target MSSW. Such large stratospheric forecast errors occur when the forecasts are unsuccessful in representing enhanced planetary wave activity in the lower stratosphere and troposphere [8,10,21,22].
This study seeks to take a different approach, that is, conducts a case study of false alarms of a MSSW for the NH winter season of 2017/2018 in a S2S prediction system, that is, the European Centre for Medium-Range Weather Forecasts (ECMWF) system. A false alarm here means that an MSSW is forecasted to occur, but no MSSW occurred in reality. For example, a contingency analysis of Japan Meteorological Agency (JMA) forecast data by Taguchi [22] suggested several false alarm cases, but their specific features were not investigated. The 2017/2018 season is targeted here, as it turns out that two clear false alarm cases are found in the S2S ECMWF forecast data. Such an analysis of false alarms, though relatively unpracticed so far, will be useful to better understand the characteristics of forecast data as well as variability in the stratosphere and troposphere in the real world.
2. Data
This study employs daily averages of the Japanese 55-year Reanalysis (JRA-55) data [23] as a representation of the real atmosphere. The data analyzed here extend from January 1979 to June 2018. The seasonally varying climatology of a target quantity is obtained by taking the time (yearly) mean of the quantity for the whole period, and then retaining only low frequency components of its Fourier-series expansion whose periods are longer than about 90 days. The choice of the JRA-55 data will not affect the present assessment, as modern reanalysis datasets, such as the JRA-55 and ECMWF interim reanalysis (ERA-interim) data, yield similar results when diagnosing large-scale features of MSSWs [24,25].
For a forecast dataset, this study targets ECMWF real-time forecasts available in the S2S prediction database [9]. The forecasts analyzed are those initialized in the 2017/2018 Northern Hemisphere winter season, from November to February. We chose the ECMWF system for this study, because it provides relatively abundant data in terms of initialization frequency and ensemble size [9]. The system was also shown to be one of the best systems in the S2S project database in forecasting MSSWs [13,14,15,16]. The initialization frequency is every 3 or 4 days. The ensemble size is 51 for each initialization.
We analyze the following quantities for both JRA-55 and forecast data. The zonal mean zonal wind [U] at 60° N, 10 hPa is used to measure the strength and flow direction of the stratospheric polar vortex. The square brackets denote the zonal mean. The index is also used to identify MSSWs. An MSSW is identified when the wind at the grid point reverses from westerly to easterly [6]. An onset date of an MSSW is defined as the date of the first wind reversal. Synoptic patterns of the stratospheric polar vortex are examined using the geopotential height at 10 hPa. Possible planetary wave forcings to stratospheric dynamical events such as MSSWs are quantified with the poleward heat flux [V*T*] of planetary waves of zonal wave numbers 1–3 (waves 1–3) averaged over 40–90° N, 100 hPa. The asterisks denote waves, or departures from the zonal mean. The poleward heat flux is proportional to the Eliassen–Palm flux for the quasi-geostrophic approximation [4]. When averaged in the extratropical lower stratosphere, it measures wave activity entering the stratosphere. We also seek to relate heat flux variations to planetary wave signatures in the geopotential height at 300 hPa in the upper troposphere.
Statistical significance of a composite difference or correlation coefficient is evaluated using Student’s t-distribution with a confidence level of 95% (two-sided test).
3. Results
3.1. Overview
Figure 1a plots time series of the zonal mean zonal wind at 60° N, 10 hPa and waves 1–3 heat flux in 40–90° N, 100 hPa in the JRA-55 data for the Northern Hemisphere winter season. The zonal wind, or polar vortex strength, is relatively weak between 10 and 40 m/s until late December, before it strengthens mostly above 30 m/s until early February. The zonal wind reverses from westerly to easterly on 12 February, confirming the occurrence of the MSSW. This MSSW and its possible influence on the troposphere were examined by previous studies as introduced in Section 1. This onset date is identical to the result using another reanalysis dataset [10].
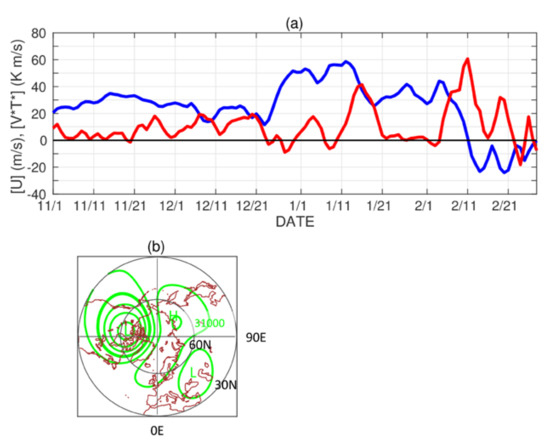
Figure 1.
(a) Time series of the zonal mean zonal wind [U] at 60° N, 10 hPa (blue), and waves 1–3 poleward heat flux [V*T*] in 40–90° N, 100 hPa (red) in the JRA-55 data. Panel (b) plots the 10 hPa geopotential height in the JRA-55 data averaged for 5 days (±2 days) around the major sudden stratospheric warming (MSSW) onset date of 12 February. Thick contour is for 30,000 m, and the contour interval is 500 m.
The heat flux covaries with the zonal wind, as expected (Figure 1a). Specifically, there is a clear tendency that weakenings of the zonal wind occur with increases in the heat flux, and vice versa. Such covariability is a well-known relationship between the mean flow and planetary waves [26,27].
Figure 1b plots the 10 hPa geopotential height in the JRA-55 data averaged for 5 days (±2 days) around the MSSW onset date. The height distribution shows two cyclonic vortices, indicating a split of the polar vortex in the MSSW. The two cyclones are different in strength in the 10 hPa height at this timing.
We examine all ECMWF real-time forecasts available for the season in the S2S database, and find if and when each member of each ensemble set shows a zonal wind reversal during its forecast period. We count only the first wind reversal in each member when it has two or more reversals. Forecasts initialized after the MSSW onset date in the JRA-55 data are excluded. The results are plotted in Figure 2. One can notice that there are clusters of ensemble members showing an MSSW on similar calendar dates. The clusters are around 9 December, 1 February, and 12 February. The first two cases are false alarms, as no MSSW was observed in the real world around the timings (Figure 1a). These two clusters are the focus in the following, and the calendar dates are used as their reference dates (RDs, Table 1). Note that the first and second clusters occur for forecast times around 12 and 21 days, respectively. The former forecast time is within the representative range of the predictable time limits for MSSWs [1], and the latter forecast time is outside it, but close to the predictable limit for the MSSW in January 2019 [16]. The last cluster corresponds to the real MSSW identified in the JRA-55 data. For the last case, the forecasts become more successful as initialized closer to the onset date; all members initialized on 5 and 8 February successfully forecast the onset date. The ensemble set initialized on 1 February includes both successful and unsuccessful members. The difference between these members is likely to be explained by the reproducibility of the Ural high and increased wave activity flux [11].
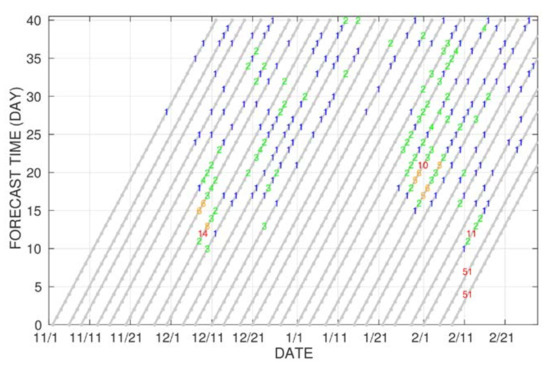
Figure 2.
Number of ensemble members that show a first reversal of the zonal mean zonal wind at 60 °N, 10 hPa on each forecast day and calendar date. Different colors are used to emphasize differences in the numbers. Each slope corresponds to an ensemble set for the same initial time.

Table 1.
Initial dates of ensembles analyzed for two clusters in this study. The initial dates are given in mm/dd format. MSSW, major sudden stratospheric warming.
It is further interesting to note that each of the first two clusters is sandwiched by ensembles that are relatively free from MSSWs. For example, the first cluster is seen especially around the forecast time of 12 days for the ensemble initialized on 27 November. In the following, we adopt a shorter expression for initial dates, such as N27 for 27 November. The N27 initialization has 29 members forecasting MSSWs in the 7-day period around RD. We refer to such members, which show the first zonal wind reversal in the RD ± 3 day window, as MSSW members. In addition, as non-MSSW members, we refer to members that show the first zonal wind reversal only after (inclusive) RD + 4 or show no reversal in the forecast period. Note that there may be other members, called the rest, that show the first zonal wind reversal before the 7-day period. The ensembles of similar initial dates also forecast MSSWs around RD. We refer to such ensembles, which include many MSSW members, as MSSW ensembles. The ensembles initialized further earlier or later hardly forecast MSSWs around RD. We refer to such ensembles as non-MSSW ensembles.
A similar variation is also the case with the second cluster, which is seen for the ensembles initialized on J04 to J15. The ensembles initialized later around late January are relatively free from MSSWs, and those initialized further later (early February) start to forecast the real mid-February MSSW. The forecasted MSSWs in the second cluster are thus different from the real MSSW. They also have different horizontal patterns of the polar vortex from the mid-February MSSW, as shown later.
Such variability of the presence or absence of forecasted MSSWs has been relatively unrecognized, as previous studies were mostly interested in the predictability of real MSSWs, that is, how forecasts are improved with decreasing lead time to the MSSWs that occurred in reality. In the following, we characterize such variability for each of the first and second clusters. For each cluster, we contrast an MSSW ensemble to two sandwiching non-MSSW ensembles, as listed in Table 1. For each MSSW ensemble, we also contrast MSSW members to non-MSSW members.
3.2. First Cluster
Time series of the stratospheric zonal wind in the target and comparison ensembles are plotted in Figure 3a–c for the first cluster. By definition, the target MSSW ensemble includes a large part of MSSW members, that is, members forecasting MSSWs, or negative zonal wind values, around RD, whereas in comparison, the non-MSSW ensembles do not. The JRA-55 zonal wind shows some weakening to about 15 m/s around RD (see also Figure 1a).
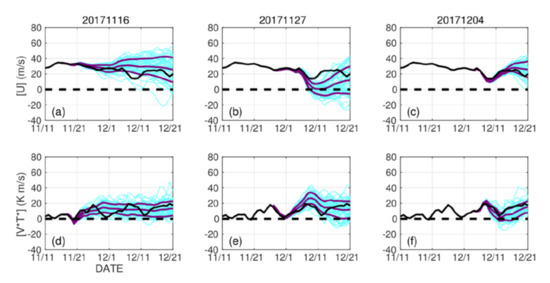
Figure 3.
As in Figure 1, but for the target MSSW and comparison non-MSSW ensembles for the first cluster (Table 1). The initialization dates are indicated above the panels. Top panels (a–c) plot the zonal mean zonal wind, and bottom panels (d–f) plot the heat flux. Cyan lines are for all ensemble members. Purple lines plot the ensemble mean ± one standard deviation. Black line is for the JRA-55 data.
Figure 4a–c plot maps of the 10 hPa height, averaged for 5 days around RD, for the JRA–55 data, MSSW member mean, and non-MSSW member mean of the MSSW ensemble. It is common in the JRA-55 and forecast data that the polar vortex center shifts off from the polar region toward northwestern Eurasia around 30–45° E. An anticyclone is seen over Alaska. A comparison of the MSSW member mean to the JRA-55 data and non-MSSW member mean shows that the MSSW member mean has relatively high height values over the polar region and low values in surrounding latitudes. The height difference pattern is consistent, through the geostrophic wind relationship, with the fact that only the MSSW members have easterly winds at 60° N around RD.
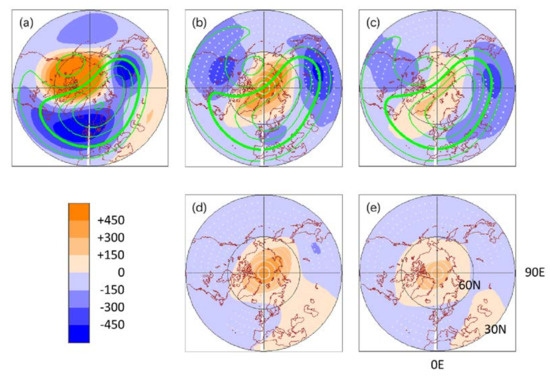
Figure 4.
(a) Map of the JRA-55 10 hPa geopotential height averaged for 5 days around RD (RD ± 2) for the first cluster in green contours, as in Figure 1b. The values inside the 30,000 m thick contour are lower than it. Color shadings plot differences from the JRA-55 climatology in the same period. Panel (b) is similar, but for the mean of the 29 MSSW members for the MSSW ensemble (N27 initialization). Color shadings plot differences from the JRA-55 data (a). Panel (c) is similar, but uses the 22 non-MSSW members. Panel (d) plots the difference of (b) from (c). Panel (e) plots 5-day mean 10 hPa height regressed onto the 7-day mean (RD-6 to RD) heat flux, using all ensemble members. Dots are plotted where the differences in (b–d) or correlations in (e) are statistically significant. The dots are plotted every two grids for each of longitude and latitude at most to avoid too dense plots.
Such stratospheric disturbances are often associated with planetary wave forcings from the troposphere. This is seen in time series of the waves 1–3 heat flux in the lower stratosphere (Figure 3d–f). Many of the ensemble members have stronger heat fluxes than the JRA-55 data around RD for the MSSW ensemble, as the ensemble mean ± 1 standard deviation range is almost above the JRA-55 result. For the non-MSSW ensembles, the JRA-55 heat flux data are basically within the range.
This relationship is further supported in scatter plots between the heat flux and stratospheric zonal wind (Figure 5a–c). The zonal wind is averaged for 5 days around RD. The heat flux is averaged for 7 days before RD, that is, from RD-6 to RD. The 7-day time period is determined to capture the increase in the heat flux (Figure 3e). As expected, the two quantities are linearly (negatively) correlated for all three initializations, as stronger heat fluxes are related to weaker zonal winds. All correlations are statistically significant. Such a relationship was pointed out when verifying forecast data for MSSWs that occurred in reality [8,21,22]. One sees that, only for the MSSW ensemble, many of the members have stronger heat fluxes and weaker zonal winds than the JRA-55 data. The situation is opposite for the N16 initialization. For the D04 initialization, all members are close to the JRA-55 data, far from an MSSW condition.
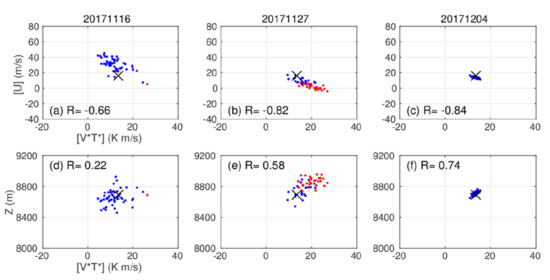
Figure 5.
(a–c) Scatter plots between the waves 1–3 heat flux over 40–90° N, 100 hPa, and the zonal mean zonal wind at 60° N, 10 hPa for all members in the MSSW (b) and non-MSSW (a,c) ensembles for the first cluster. The zonal mean zonal wind is averaged for 5 days around RD. The heat flux is averaged from RD-6 to RD. The forecast data are plotted by dots in different colors, with a black cross for the JRA-55 data. Red dots are for MSSW members, blue dots for non-MSSW members, and black dots for the rest (the rest includes no member for these initial dates). The initial dates are denoted above the panels. The number in each panel denotes the correlation coefficient for all ensemble members. Panels (d–f) are similar, but use the 300 hPa geopotential height averaged over a region of 65 ± 10° N, 305 ± 15° E from RD-6 to RD, instead of the zonal wind.
The difference in the 10 hPa height between the MSSW and non-MSSW members in the MSSW ensemble is well reproduced when applying a regression analysis to all members (Figure 4d,e). In the analysis, the 5-day mean 10 hPa height fields are regressed onto to the 7-day mean lower stratospheric heat flux. The good reproducibility supports a close relationship between the lower stratospheric heat flux, stratospheric zonal wind, and geopotential height.
In order to seek possible tropospheric traces of the lower stratospheric heat flux, Figure 6 examines the 300 hPa height averaged for the same 7-day period (from RD-6 to RD) in the JRA-55 data, MSSW member mean, and non-MSSW member mean. A notable difference of the MSSW members from the JRA-55 data and non-MSSW members is seen in higher height values over northeastern Canada and Greenland around 65° N, 305° E (55° W) for the MSSW members (Figure 6b,d). A similar signal is seen in a regression field of the 300 hPa height onto the heat flux (Figure 6e). Figure 5e shows that, for the MSSW ensemble, the lower stratospheric heat flux is positively correlated to the 300 hPa height averaged over the region of 65 ± 10° N, 305 ± 15° E, where the difference and regression fields have positive values (Figure 6d,e). The correlation is statistically significant. The D04 initialization also shows a significant positive correlation, while the N16 initialization does not (Figure 5d,f).
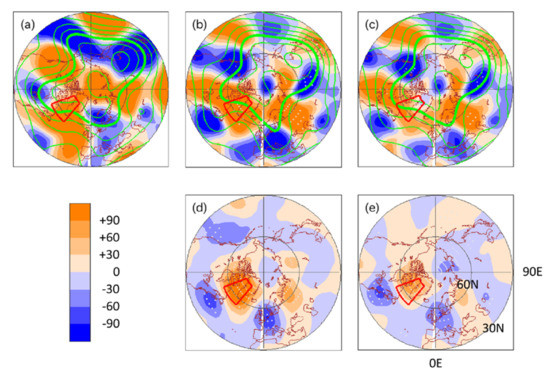
Figure 6.
Same as Figure 4, for the 300 hPa geopotential height averaged from RD-6 to RD. Panel (a) plots the JRA-55 data, (b) MSSW member mean, and (c) non-MSSW member mean. In (a–c), thick green contours denote 8800 m, and contour interval is 200 m. The values generally increase with decreasing latitude. Panel (d) plots the difference of (b) from (c). Panel (e) plots the regression field onto the heat flux. The region used for Figure 5d–f is highlighted in red.
The positive height values over northeastern Canada and Greenland in Figure 6d,e are in phase with the ridge of the climatological wave 1 (Figure 7), and hence are likely to lead to increased wave 1 amplitude and activity through constructive interference. They are also reminiscent of a precursory tropospheric height signal for MSSWs obtained for a reanalysis data set [28,29].
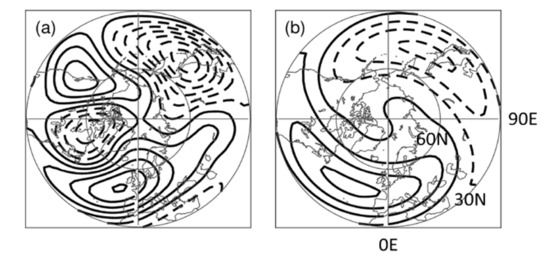
Figure 7.
Maps of 300 hPa height waves in the JRA-55 climatology for Northern Hemisphere winter from December to February: (a) all wave components and (b) wave 1. Contour interval is 50 m. Solid contours are for zero and positive values, and broken contours are for negative values.
Such higher height values appear around the forecast day of 4 days, and amplify with time until the forecast day of about 13 days while being roughly stationary in longitude (Figure 8). It is interesting to further explore a trigger that differentiates the MSSW and non-MSSW members, although it is beyond the scope of the paper.
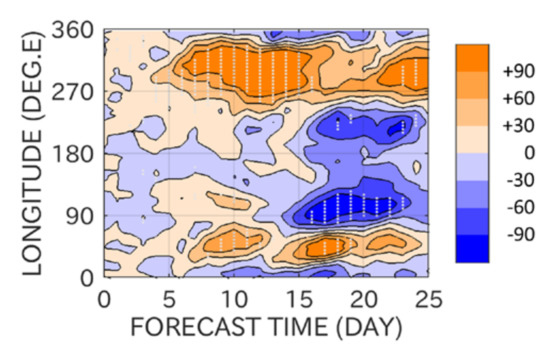
Figure 8.
Forecast time–longitude section of the composite difference of the MSSW members from the non-MSSW members in the MSSW ensemble for the first cluster. The difference is averaged in latitude over 65 ± 10° N. Dots indicate where the difference is significant at the 95% level. The dots are plotted every two longitudinal grids at most to avoid too dense plots.
3.3. Second Cluster
The same methodology is applied to the second cluster (Figure 2 and Table 1). Whereas the JRA-55 zonal wind is above 20 m/s around RD, even the ensemble mean wind for the J11 initialization is close to 0 m/s, with 29 MSSW members (Figure 9b). The JRA-55 heat flux stays around 0 K m/s in late January (Figure 9e). The ensemble mean heat flux increases near the end of January. It is noted that these JRA-55 data states do not outlie compared with the ensemble members of the J11 initialization, but are within the ensemble range.
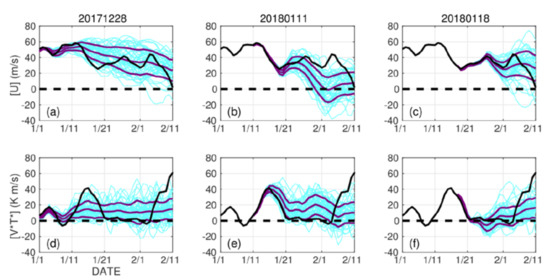
Figure 9.
Same as Figure 3, but for the second cluster. Top panels (a–c) plot the zonal mean zonal wind, and bottom panels (d–f) plot the heat flux.
Such MSSW members are basically absent or much fewer for the comparison non-MSSW ensembles. For the D28 initialization, the ensemble mean wind gradually decreases toward about 20 m/s in early February, whereas the ensemble mean heat flux is almost constant in time (Figure 9a,d). For the J18 initialization, the ensemble mean wind closely follows the JRA-55 data in January, and only a limited number of the members show easterly winds in early February (Figure 9c). Most members overestimate the JRA-55 zonal wind on 11 February, one day before the mid-February MSSW onset date, hinting that they miss the MSSW. It is not until the F01 initialization that the MSSW is more or less forecasted by the system (Figure 2).
The polar vortex in the 10 hPa height shifts equatorward near 0° E in the JRA-55 data, MSSW member mean, and non-MSSW member mean (Figure 10a–c). The polar vortex in the MSSW member mean shows a larger shift than the JRA-55 counterpart, and is much weaker. Note that the MSSW member mean pattern is different from the mid-February MSSW that occurred in reality (Figure 1b). The non-MSSW member mean vortex is also weaker than the JRA-55 data (Figure 10c). These are consistent with Figure 9b, where the JRA-55 zonal wind is close to the edge in the stronger westerly wind side of the ensemble members.
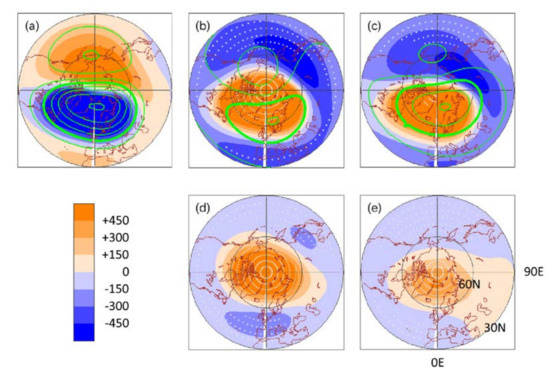
Figure 10.
Same as Figure 4, but using the J11 initialization for the second cluster. Panel (a) plots the JRA-55 data, (b) MSSW member mean, and (c) non-MSSW member mean. Panel (d) plots the difference of (b) from (c). Panel (e) plots the regression field onto the heat flux. There are 29 MSSW members and 21 non-MSSW members.
The second cluster shows similar changes between the MSSW and non-MSSW ensemble, to the first cluster, in scatter plots between the zonal wind and heat flux. For the MSSW ensemble, the data points form a straight line, and a considerable part of them are located below or close to the 0 m/s wind (Figure 11b). The JRA-55 data point is located near the other edge (i.e., stronger westerly wind) of the scatter plot distribution. The distributions for the non-MSSW ensembles are characterized by stronger winds and weaker heat fluxes compared with the MSSW ensemble (Figure 11a,c).
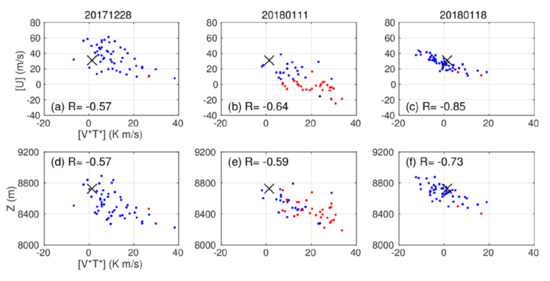
Figure 11.
Same as Figure 5, but for the second cluster. Panels (a–c) plot the heat flux and zonal wind. Panels (d–f) use the 300 hPa height averaged over 65 ± 10 °N, 150 ± 15 °E instead of the zonal wind.
Figure 12b,c compare 300 hPa height fields between the MSSW and non-MSSW member means. The comparison shows lower values, indicating a more pronounced upper-air low or trough, over northeastern Eurasia around 65° N, 150° E (Figure 12d). This location corresponds to where the climatological wave field has a trough (Figure 7). This signal is again reminiscent of the observational result [28,29].
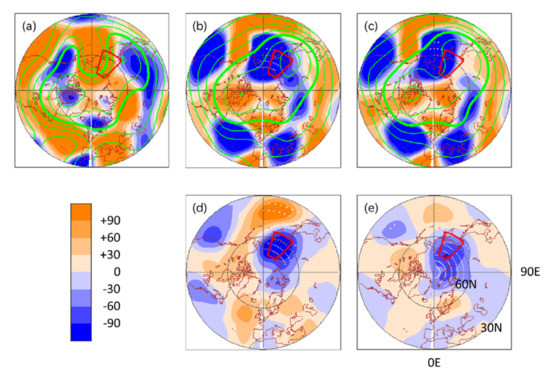
Figure 12.
Same as Figure 6, but using the J11 initialization for the second cluster. Panel (a) plots the JRA-55 data, (b) MSSW member mean, and (c) non-MSSW member mean. Panel (d) plots the difference of (b) from (c). Panel (e) plots the regression field onto the heat flux. The highlighted region in red is used for Figure 11d–f.
This suggests a relationship of the more pronounced low to the larger heat fluxes for the MSSW members. The relationship between the enhanced heat flux and northeastern Euriasia low is supported when comparing the two indices (Figure 11d–f). Both MSSW and non-MSSW ensembles show similar distributions between the two indices, as larger heat fluxes are associated with lower height values. In particular, in the MSSW ensemble, most of the members have stronger heat flux and lower height values than the JRA-55 data.
The lower height for the MSSW member mean develops from the forecast time of about 10 days to RD (Figure 13). It appears roughly stationary in longitude, with some hint of slight westward movement.
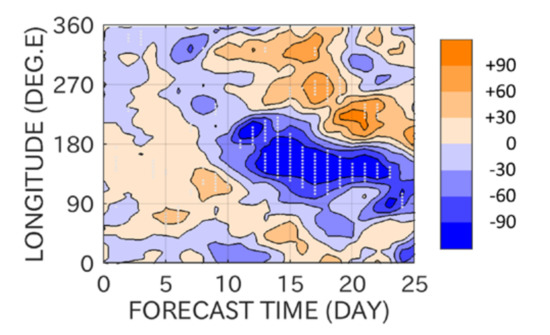
Figure 13.
Same as Figure 8, but using the J11 initialization for the second cluster.
4. Summary and Discussion
While stratospheric predictability, especially MSSW predictability, has drawn a lot of attention, previous studies mostly focused on MSSWs that occurred in reality [1]. The present case study has taken a different approach, that is, investigated false alarms of an MSSW by real-time S2S forecasts for the 2017/2018 Northern Hemisphere winter season. The target ECMWF system is one of the systems that were shown to have relatively good skill in forecasting real MSSWs [13,14,15,16].
Analysis has revealed two false alarm cases in early December and early February of the season, characterized by clusters of ensemble members forecasting an MSSW on similar calendar dates. Each cluster, that is, MSSW ensembles, is sandwiched by non-MSSW ensembles. The MSSW members accompany weaker polar vortex states by definition, and are associated with increased heat fluxes, as expected. In other words, the MSSW members overestimate the zonal wind deceleration seen in the JRA-55 data (Figure 3b and Figure 9b). The MSSW member mean fields also exhibit an equatorward displacement of the polar vortex around RD for both clusters, whereas the real mid-February MSSW is a vortex split type. The MSSW members are further associated with tropospheric traces, that is, higher height (compared with the non-MSSW members) over northeastern Canada and Greenland for the first cluster, and lower height over northeastern Eurasia for the second cluster. These are located over the ridge and trough of climatological wave 1, respectively, and hence are consistent with the increased heat fluxes. For each cluster, the JRA-55 data are located near the edge of the members of the target MSSW ensemble in the stronger wind and weaker heat flux side.
This study leaves a couple of questions and extensions for future research. First, it will be interesting to further explore, for each false alarm case, if there is some trigger phenomenon that differentiates the MSSW and non-MSSW members in the MSSW ensembles. This is also the case with differentiating the MSSW and non-MSSW ensembles. For the MSSW in mid-February 2018, Lee et al. [11] pointed out the importance of an anticyclonic Rossby wave break in building the Ural high and increased wave activity to the stratosphere. The intraseasonal variability (existence and absence of forecasted MSSWs) for the 2017/2018 season is associated with the planetary wave activity and pattern in the extratropical lower stratosphere and upper troposphere (Figure 5, Figure 6, Figure 11 and Figure 12). The extratropical signals may be affected by intraseasonally varying external forcings, with the most important agent being the Madden-Julian Oscillation [30,31], although it is beyond the scope of this paper to examine the possible relationship between the false alarm MSSWs and such external forcings.
Second, it is obvious that one can extend the present approach to other years and systems. Some years are likely to prefer more forecasted MSSWs than others, as various interannually varying external factors, such as the Quasi-Biennial Oscillation and El Niño/Southern Oscillation, are known to affect the occurrence of MSSWs [5]. It is also possible that some systems exhibit different false alarm MSSWs than others.
Finally, the most interesting extension of this study will be to use such false alarms to suggest a possibility that the real atmosphere might have experienced an MSSW, that is, in early December or early February for the 2017/2018 season. This suggestion depends on the fidelity of the forecast data; the ensemble members and real evolution should be equally likely to happen. If the fidelity is guaranteed for the present S2S system, then the existence of the MSSW ensembles, sandwiched by the non-MSSW ensembles, will imply intraseasonal variability of likelihood of a MSSW; an increased MSSW frequency or probability is obtained when forecasts are initialized in only limited periods of time. Conversely, the suggestion can not be made if the false alarms are just artifacts, apart from the real world. The present results do not deny the fidelity of the forecast data, as the JRA-55 data are within the range covered by the ensemble members, although they examine only limited quantities. The suggestion may also depend on the forecast time for which many ensemble members forecast a MSSW and the degree to which the members are clustered in terms of the timing. Future study will further explore these aspects using multi-year forecast data for the suggestion.
Funding
This research received no external funding.
Acknowledgments
The author thanks those who made the analyzed data available. The JRA-55 data used for this study were provided by the JMA. The JRA-55 data were obtained from the Research Data Archive at the National Center for Atmospheric Research, Computational, and Information Systems Laboratory (https://doi.org/10.5065/D6HH6H41). The S2S data were obtained from the ECMWF server (http://apps.ecmwf.int/datasets/data/s2s/). The author acknowledges that comments from three anonymous reviewers improved the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Tripathi, O.P.; Baldwin, M.; Charlton-Perez, A.; Charron, M.; Stephen, D.; Gerber, E.; Harrison, R.G.; Jackson, D.R.; Kim, B.; Kuroda, Y.; et al. The predictability of the extratropical stratosphere on monthly time-scales and its impact on the skill of tropospheric forecasts. Q. J. R. Meteorol. Soc. 2015, 987–1003. [Google Scholar] [CrossRef]
- Butler, A.; Charlton-Perez, A.; Domeisen, D.I.V.; Garfinkel, C.; Gerber, E.P.; Hitchcock, P.; Karpechko, A.Y.; Maycock, A.C.; Sigmond, M.; Simpson, I.; et al. Sub-Seasonal Predictability and the Stratosphere; Elsevier Inc.: Amsterdam, The Netherlands, 2019; ISBN 9780128117149. [Google Scholar]
- Baldwin, M.P.; Dunkerton, T.J. Stratospheric harbingers of anomalous weather regimes. Science 2001, 294, 581–584. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.G.; Holton, J.R.; Leovy, C.B. Middle Atmosphere Dynamics; Academic Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Baldwin, M.P.; Ayarzag, B.; Birner, T.; Butchart, N.; Butler, A.H.; Charlton-Perez, A.J.; Domeisen, D.I.V.; Garfinkel, C.I.; Garny, H.; Gerber, E.P.; et al. Sudden Stratospheric Warmings. Rev. Geophys. 2020. submitted. [Google Scholar]
- Charlton, A.J.; Polvani, L.M. A new look at stratospheric sudden warmings. Part I: Climatology and modeling benchmarks. J. Clim. 2007, 20, 449–469. [Google Scholar] [CrossRef]
- Butler, A.H.; Seidel, D.J.; Hardiman, S.C.; Butchart, N.; Birner, T.; Match, A. Defining sudden stratospheric warmings. Bull. Am. Meteorol. Soc. 2015, 96, 1913–1928. [Google Scholar] [CrossRef]
- Rao, J.; Ren, R.; Chen, H.; Yu, Y.; Zhou, Y. The Stratospheric Sudden Warming Event in February 2018 and its Prediction by a Climate System Model. J. Geophys. Res. Atmos. 2018, 123, 13332–13345. [Google Scholar] [CrossRef]
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M.; et al. The subseasonal to seasonal (S2S) prediction project database. Bull. Am. Meteorol. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- Karpechko, A.Y.; Charlton-Perez, A.; Balmaseda, M.; Tyrrell, N.; Vitart, F. Predicting Sudden Stratospheric Warming 2018 and Its Climate Impacts with a Multimodel Ensemble. Geophys. Res. Lett. 2018, 45, 13538–13546. [Google Scholar] [CrossRef]
- Lee, S.H.; Charlton-Perez, A.J.; Furtado, J.C.; Woolnough, S.J. Abrupt Stratospheric Vortex Weakening Associated With North Atlantic Anticyclonic Wave Breaking. J. Geophys. Res. Atmos. 2019, 124, 8563–8575. [Google Scholar] [CrossRef]
- Peings, Y. Ural Blocking as a Driver of Early-Winter Stratospheric Warmings. Geophys. Res. Lett. 2019, 46, 5460–5468. [Google Scholar] [CrossRef]
- Taguchi, M. Comparison of Subseasonal-to-Seasonal Model Forecasts for Major Stratospheric Sudden Warmings. J. Geophys. Res. Atmos. 2018, 123, 10231–10247. [Google Scholar] [CrossRef]
- Taguchi, M. Verification of Subseasonal-to-Seasonal Forecasts for Major Stratospheric Sudden Warmings in Northern Winter from 1998/99 to 2012/13. Adv. Atmos. Sci. 2020, 37, 250–258. [Google Scholar] [CrossRef]
- Domeisen, D.I.V.; Butler, A.H.; Charlton-Perez, A.J.; Ayarzagüena, B.; Baldwin, M.P.; Dunn-Sigouin, E.; Furtado, J.C.; Garfinkel, C.I.; Hitchcock, P.; Karpechko, A.Y.; et al. The Role of the Stratosphere in Subseasonal to Seasonal Prediction: 1. Predictability of the Stratosphere. J. Geophys. Res. Atmos. 2020, 125, 1–17. [Google Scholar] [CrossRef]
- Rao, J.; Garfinkel, C.I.; Chen, H.; White, I.P. The 2019 New Year Stratospheric Sudden Warming and Its Real-Time Predictions in Multiple S2S Models. J. Geophys. Res. Atmos. 2019, 124, 11155–11174. [Google Scholar] [CrossRef]
- Rao, J.; Garfinkel, C.I.; White, I.P.; Schwartz, C. The Southern Hemisphere Minor Sudden Stratospheric Warming in September 2019 and its predictions in S2S Models. J. Geophys. Res. Atmos. 2020, 1–19. [Google Scholar] [CrossRef]
- Butler, A.H.; Charlton-Perez, A.; Domeisen, D.I.V.; Simpson, I.R.; Sjoberg, J. Predictability of Northern Hemisphere Final Stratospheric Warmings and Their Surface Impacts. Geophys. Res. Lett. 2019, 46, 10578–10588. [Google Scholar] [CrossRef]
- Kautz, L.A.; Polichtchouk, I.; Birner, T.; Garny, H.; Pinto, J.G. Enhanced extended-range predictability of the 2018 late-winter Eurasian cold spell due to the stratosphere. Q. J. R. Meteorol. Soc. 2020, 146, 1040–1055. [Google Scholar] [CrossRef]
- Rao, J.; Garfinkel, C.I.; White, I.P. Predicting the Downward and Surface Influence of the February 2018 and January 2019 Sudden Stratospheric Warming Events in Subseasonal to Seasonal (S2S) Models. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Taguchi, M. Predictability of Major Stratospheric Sudden Warmings of the Vortex Split Type: Case Study of the 2002 Southern Event and the 2009 and 1989 Northern Events. J. Atmos. Sci. 2014, 71, 2886–2904. [Google Scholar] [CrossRef]
- Taguchi, M. Predictability of major stratospheric sudden warmings: Analysis results from JMA operational 1-month ensemble predictions from 2001/02 to 2012/13. J. Atmos. Sci. 2016, 73, 789–806. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA–55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Martineau, P.; Son, S.W.; Taguchi, M.; Butler, A.H. A comparison of the momentum budget in reanalysis datasets during sudden stratospheric warming events. Atmos. Chem. Phys. 2018, 18, 7169–7187. [Google Scholar] [CrossRef]
- Ayarzagüena, B.; Palmeiro, F.M.; Barriopedro, D.; Calvo, N.; Langematz, U.; Shibata, K. On the representation of major stratospheric warmings in reanalyses. Atmos. Chem. Phys. 2019, 19, 9469–9484. [Google Scholar] [CrossRef]
- Shiotani, M.; Hirota, I. Planetary wave-mean flow interaction in the stratosphere: A comparison between northern and southern hemispheres. Q. J. R. Meteorol. Soc. 1985, 111, 309–334. [Google Scholar] [CrossRef]
- Polvani, L.M.; Waugh, D.W. Upward wave activity flux as a precursor to extreme stratospheric events and subsequent anomalous surface weather regimes. J. Clim. 2004, 17, 3548–3554. [Google Scholar] [CrossRef]
- Kolstad, E.W.; Charlton-Perez, A.J. Observed and simulated precursors of stratospheric polar vortex anomalies in the Northern Hemisphere. Clim. Dyn. 2011, 37, 1443–1456. [Google Scholar] [CrossRef]
- Cohen, J.; Jones, J. Tropospheric precursors and stratospheric warmings. J. Clim. 2011, 24, 6562–6572. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Feldstein, S.B.; Waugh, D.W.; Yoo, C.; Lee, S. Observed connection between stratospheric sudden warmings and the Madden-Julian Oscillation. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Schwartz, C. MJO-Related Tropical Convection Anomalies Lead to More Accurate Stratospheric Vortex Variability in Subseasonal Forecast Models. Geophys. Res. Lett. 2017, 44, 10054–10062. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).