Reconciling Chord Length Distributions and Area Distributions for Fields of Fractal Cumulus Clouds
Abstract
1. Introduction
- a higher chance of missing small clouds all together biases towards large chord lengths;
- a high likelihood of hitting clouds off-center biases towards small chord lengths; and
- irregularities in cloud shapes, such as gaps and the fractal dimension of the cloud edge [15], bias toward small chord lengths.
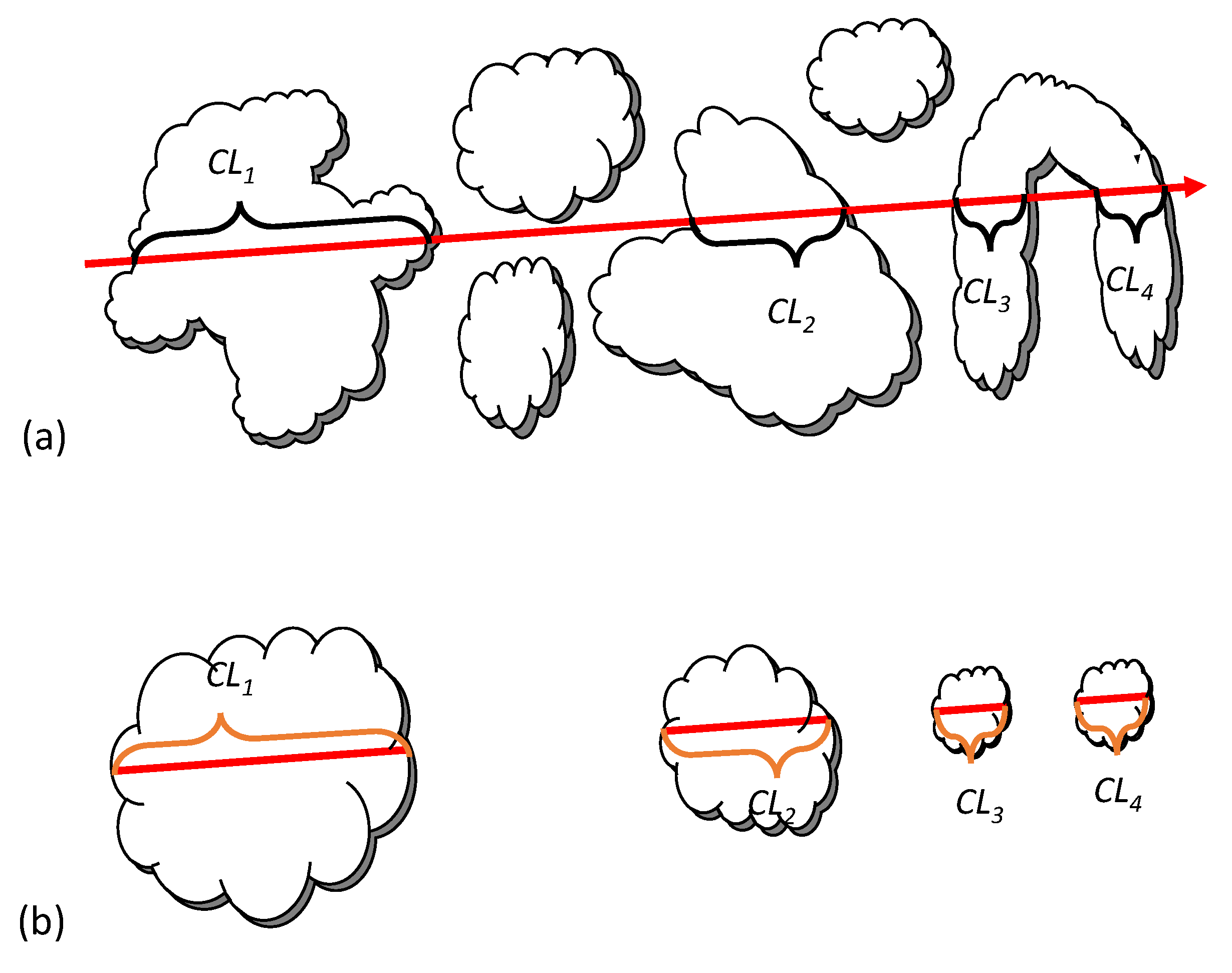
2. Methods
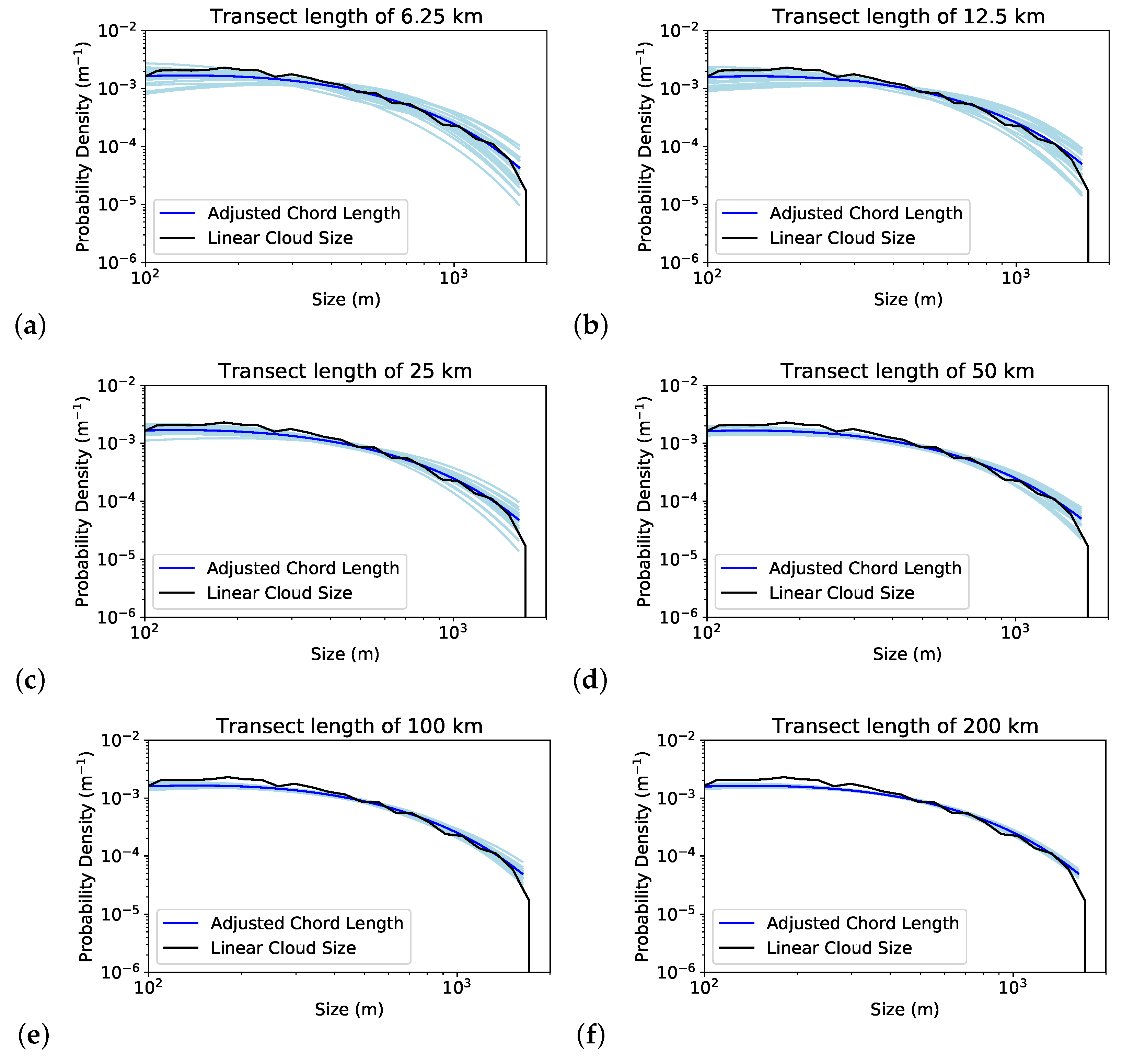
3. Results and Discussion
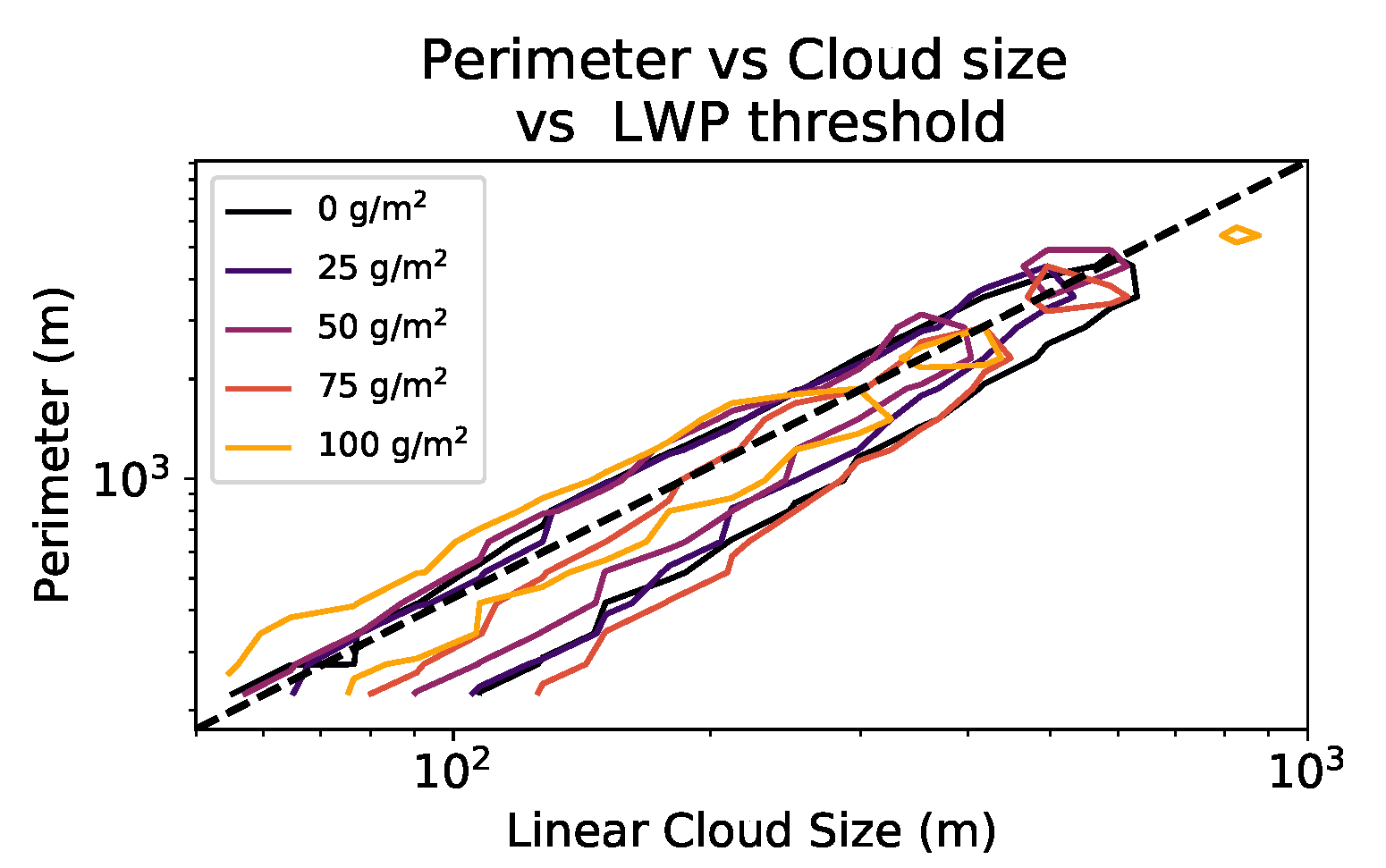
3.1. Sensitivity and Convergence
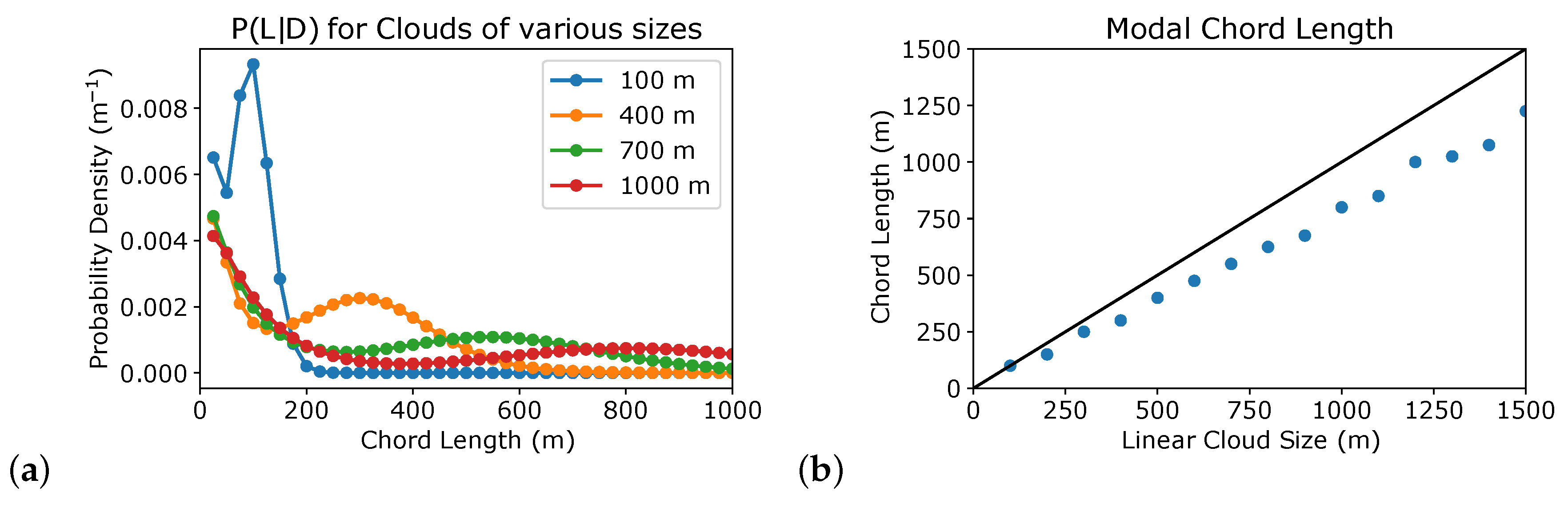
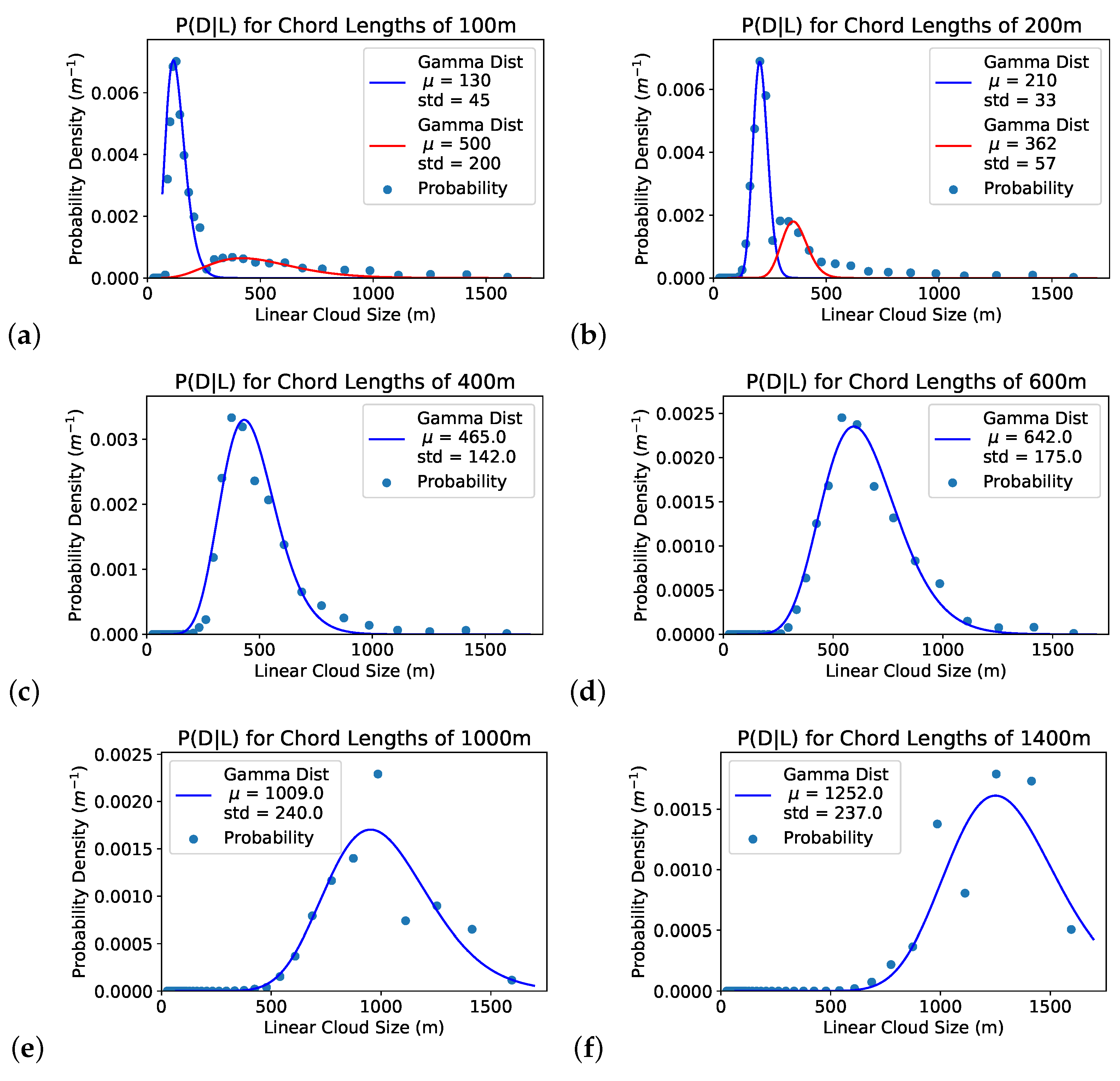
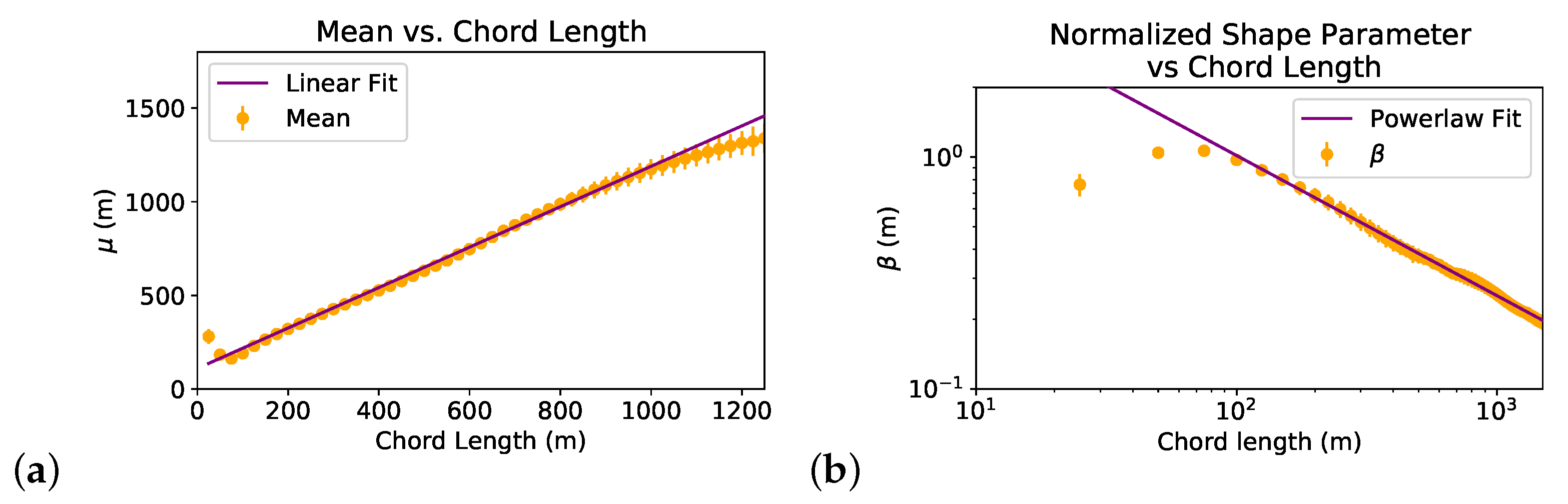
3.2. Chord Length Distribution Conditional on Linear Size
3.3. Linear Cloud Size Distribution Conditional on Chord Length
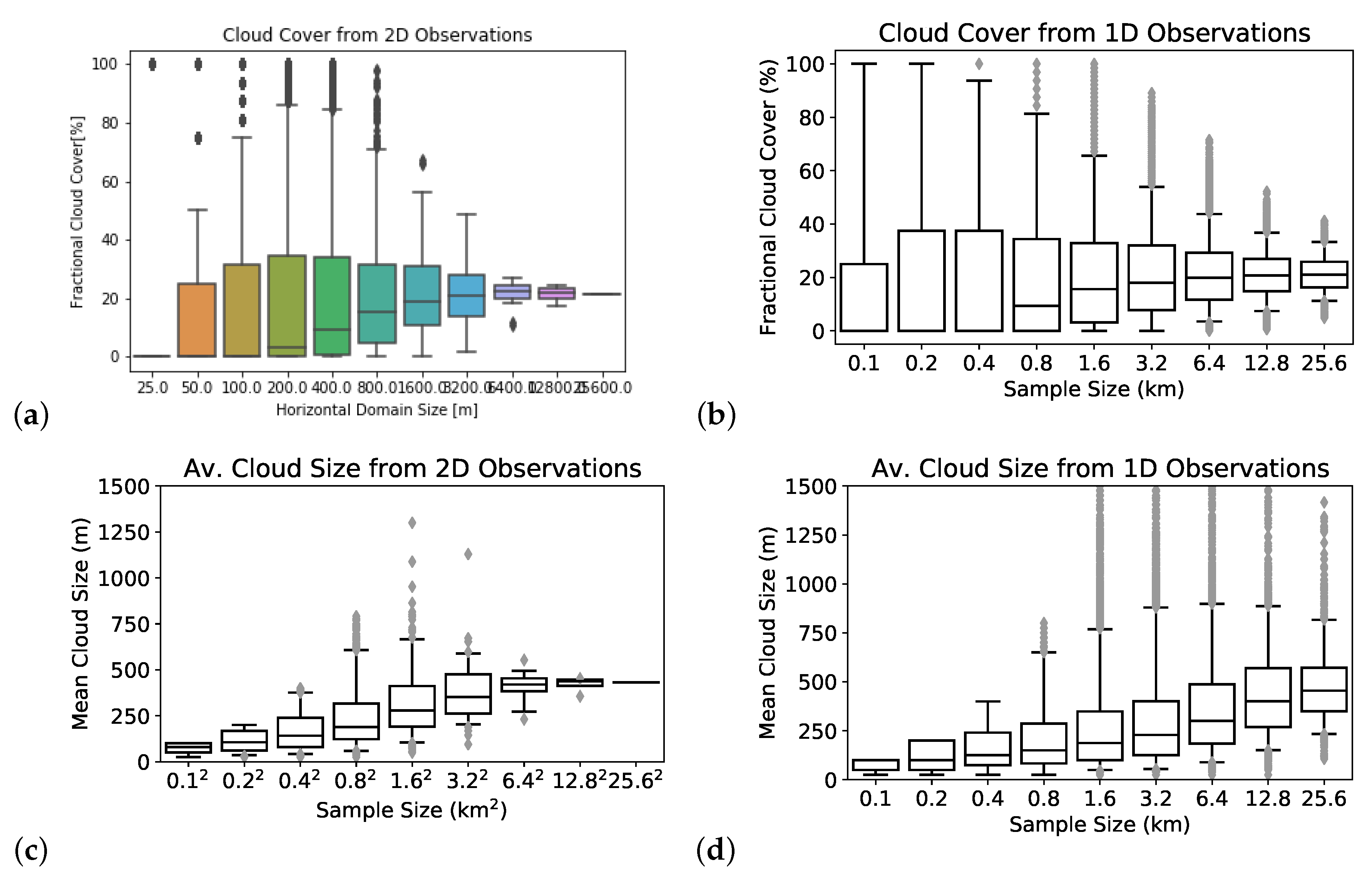
3.4. Robustness for Small Sample Sizes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bony, S.; Stevens, B.; Frierson, D.M.W.; Jakob, C.; Kageyama, M.; Pincus, R.; Shepherd, T.G.; Sherwood, S.C.; Siebesma, A.P.; Sobel, A.H.; et al. Clouds, circulation and climate sensitivity. Nat. Geosci. 2015, 8, 261–268. [Google Scholar] [CrossRef]
- Wyngaard, J. Toward numerical modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Honnert, R.; Masson, V.; Couvreux, F. A Diagnostic for Evaluating the Representation of Turbulence in Atmospheric Models at the Kilometric Scale. J. Atmos. Sci. 2011, 68, 3112–3131. [Google Scholar] [CrossRef]
- Neggers, R.A.J. Exploring bin-macrophysics models for moist convective transport and clouds. J. Adv. Model. Earth Syst. 2015, 7, 2079–2104. [Google Scholar] [CrossRef]
- Sakradzija, M.; Seifert, A.; Heus, T. Fluctuations in a quasi-stationary shallow cumulus cloud ensemble. Nonlinear Process. Geophys. 2015, 22, 65–85. [Google Scholar] [CrossRef]
- Plant, R.S.; Craig, G.C. A Stochastic Parameterization for Deep Convection Based on Equilibrium Statistics. J. Atmos. Sci. 2008, 65, 87–105. [Google Scholar] [CrossRef]
- Rodts, S.M.A.; Duynkerke, P.G.; Jonker, H.J.J. Size distributions and dynamical properties of shallow cumulus clouds from aircraft observations and satellite data. J. Atmos. Sci. 2003, 60, 1895–1912. [Google Scholar] [CrossRef]
- Wood, R.; Field, P.R. The Distribution of Cloud Horizontal Sizes. J. Clim. 2011, 24, 4800–4816. [Google Scholar] [CrossRef]
- Trivej, P.; Stevens, B. The Echo Size Distribution of Precipitating Shallow Cumuli. J. Atmos. Sci. 2010, 67, 788–804. [Google Scholar] [CrossRef]
- Neggers, R.A.J.; Jonker, H.J.J.; Siebesma, A.P. Size statistics of cumulus cloud populations in large-eddy simulations. J. Atmos. Sci. 2003, 60, 1060–1074. [Google Scholar] [CrossRef]
- Van Laar, T.W.; Schemann, V.; Neggers, R.A.J. Investigating the Diurnal Evolution of the Cloud Size Distribution of Continental Cumulus Convection Using Multiday LES. J. Atmos. Sci. 2019, 76, 729–747. [Google Scholar] [CrossRef]
- Chandra, A.S.; Kollias, P.; Albrecht, B.A. Multiyear Summertime Observations of Daytime Fair-Weather Cumuli at the ARM Southern Great Plains Facility. J. Clim. 2013, 26, 10031–10050. [Google Scholar] [CrossRef]
- Sulak, A.; Calabrase, W.; Ryan, S.D.; Heus, T. The Contributions of Shear and Turbulence to Cloud Overlap for Cumulus Clouds. J. Geophys. Res. Atmos. 2020, 125, e2019JD032017. [Google Scholar] [CrossRef]
- Griewank, P.J.; Heus, T.; Lareau, N.P.; Neggers, R.A.J. Size-dependence in chord characteristics from simulated and observed continental shallow cumulus. Atmos. Chem. Phys. Discuss. 2020, 2020, 1–32. [Google Scholar] [CrossRef]
- Siebesma, A.P.; Jonker, H.J.J. Anomalous scaling of cumulus cloud boundaries. Phys. Rev. Lett. 2000, 85, 214–217. [Google Scholar] [CrossRef] [PubMed]
- Romps, D.M.; Vogelmann, A.M. Methods for Estimating 2D Cloud Size Distributions from 1D Observations. J. Atmos. Sci. 2017, 74, 3405–3417. [Google Scholar] [CrossRef]
- Yau, M.K.; Rogers, R.R. An Inversion Problem on Inferring the Size Distribution of Precipitation Areas from Raingage Measurements. J. Atmos. Sci. 1984, 41, 439–448. [Google Scholar] [CrossRef][Green Version]
- Neggers, R.A.J.; Duynkerke, P.G.; Rodts, S.M.A. Shallow cumulus convection: A validation of large-eddy simulation against aircraft and Landsat observations. Q. J. R. Meteorol. Soc. 2003, 129, 2671–2696. [Google Scholar] [CrossRef]
- Van Heerwaarden, C.C.; van Stratum, B.J.H.; Heus, T.; Gibbs, J.A.; Fedorovich, E.; Mellado, J.P. MicroHH 1.0: A computational fluid dynamics code for direct numerical simulation and large-eddy simulation of atmospheric boundary layer flows. Geosci. Model Dev. 2017, 10, 3145–3165. [Google Scholar] [CrossRef]
- Siebesma, A.P.; Bretherton, C.S.; Brown, A.; Chlond, A.; Cuxart, J.; Duynkerke, P.G.; Jiang, H.L.; Khairoutdinov, M.; Lewellen, D.; Moeng, C.H.; et al. A large eddy simulation intercomparison study of shallow cumulus convection. J. Atmos. Sci. 2003, 60, 1201–1219. [Google Scholar] [CrossRef]
- Brown, A.R.; Cederwall, R.T.; Chlond, A.; Duynkerke, P.G.; Golaz, J.C.; Khairoutdinov, M.; Lewellen, D.C.; Lock, A.P.; MacVean, M.K.; Moeng, C.H.; et al. Large-eddy simulation of the diurnal cycle of shallow cumulus convection over land. Q. J. R. Meteorol. Soc. 2002, 128, 1075–1093. [Google Scholar] [CrossRef]
- VanZanten, M.C.; Stevens, B.; Nuijens, L.; Siebesma, A.P.; Ackerman, A.S.; Burnet, F.; Cheng, A.; Couvreux, F.; Jiang, H.; Khairoutdinov, M.; et al. Controls on precipitation and cloudiness in simulations of trade-wind cumulus as observed during RICO. J. Adv. Model. Earth Syst. 2011, 3, M06001. [Google Scholar] [CrossRef]
- Seifert, A.; Heus, T. Large-eddy simulation of organized precipitating trade wind cumulus clouds. Atmos. Chem. Phys. 2013, 13, 5631–5645. [Google Scholar] [CrossRef]
- Seifert, A. On the shape-slope relation of drop size distributions in convective rain. J. Appl. Meteorol. 2005, 44, 1146–1151. [Google Scholar] [CrossRef]
- Gustafson, W.I., Jr.; Vogelmann, A.M.; Li, Z.; Cheng, X.; Dumas, K.K.; Endo, S.; Johnson, K.L.; Krishna, B.; Fairless, T.; Xiao, H. The Large-Eddy Simulation (LES) Atmospheric Radiation Measurement (ARM) Symbiotic Simulation and Observation (LASSO) Activity for Continental Shallow Convection. Bull. Am. Meteorol. Soc. 2020, 101, E462–E479. [Google Scholar] [CrossRef]
- Neggers, R.A.J.; Griewank, P.J.; Heus, T. Power-Law Scaling in the Internal Variability of Cumulus Cloud Size Distributions due to Subsampling and Spatial Organization. J. Atmos. Sci. 2019, 76, 1489–1503. [Google Scholar] [CrossRef]
- Oue, M.; Tatarevic, A.; Kollias, P.; Wang, D.; Yu, K.; Vogelmann, A.M. The Cloud-resolving model Radar SIMulator (CR-SIM) Version 3.3: Description and applications of a virtual observatory. Geosci. Model Dev. 2020, 13, 1975–1998. [Google Scholar] [CrossRef]
- Oue, M.; Kollias, P.; North, K.W.; Tatarevic, A.; Endo, S.; Vogelmann, A.M.; Gustafson, W.I., Jr. Estimation of cloud fraction profile in shallow convection using a scanning cloud radar. Geophys. Res. Lett. 2016, 43, 10,998–11,006. [Google Scholar] [CrossRef]
- Lamer, K.; Puigdomènech Treserras, B.; Zhu, Z.; Isom, B.; Bharadwaj, N.; Kollias, P. Characterization of shallow oceanic precipitation using profiling and scanning radar observations at the Eastern North Atlantic ARM observatory. Atmos. Meas. Tech. 2019, 12, 4931–4947. [Google Scholar] [CrossRef]
- Heus, T.; Pols, C.F.J.; Jonker, H.J.J.; Van den Akker, H.E.A.; Lenschow, D.H. Observational validation of the compensating mass flux through the shell around cumulus clouds. Q. J. R. Meteorol. Soc. 2009, 135, 101–112. [Google Scholar] [CrossRef]
- Romps, D.M.; Öktem, R. Observing Clouds in 4D with Multiview Stereophotogrammetry. Bull. Am. Meteorol. Soc. 2019, 99, 2575–2586. [Google Scholar] [CrossRef]
- Kleiss, J.M.; Riley, E.A.; Long, C.N.; Riihimaki, L.D.; Berg, L.K.; Morris, V.R.; Kassianov, E. Cloud Area Distributions of Shallow Cumuli: A New Method for Ground-Based Images. Atmosphere 2018, 9, 258. [Google Scholar] [CrossRef]

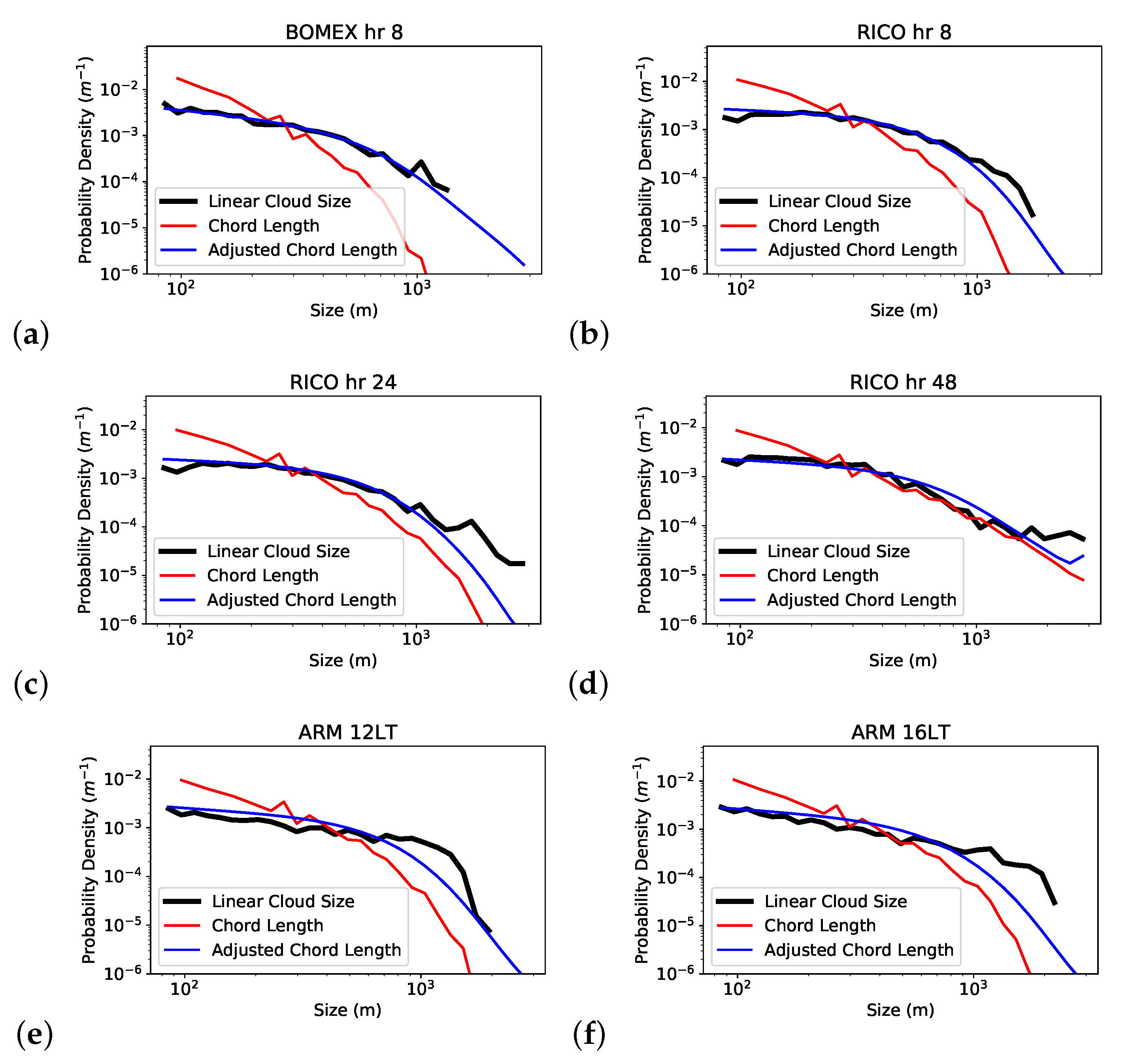
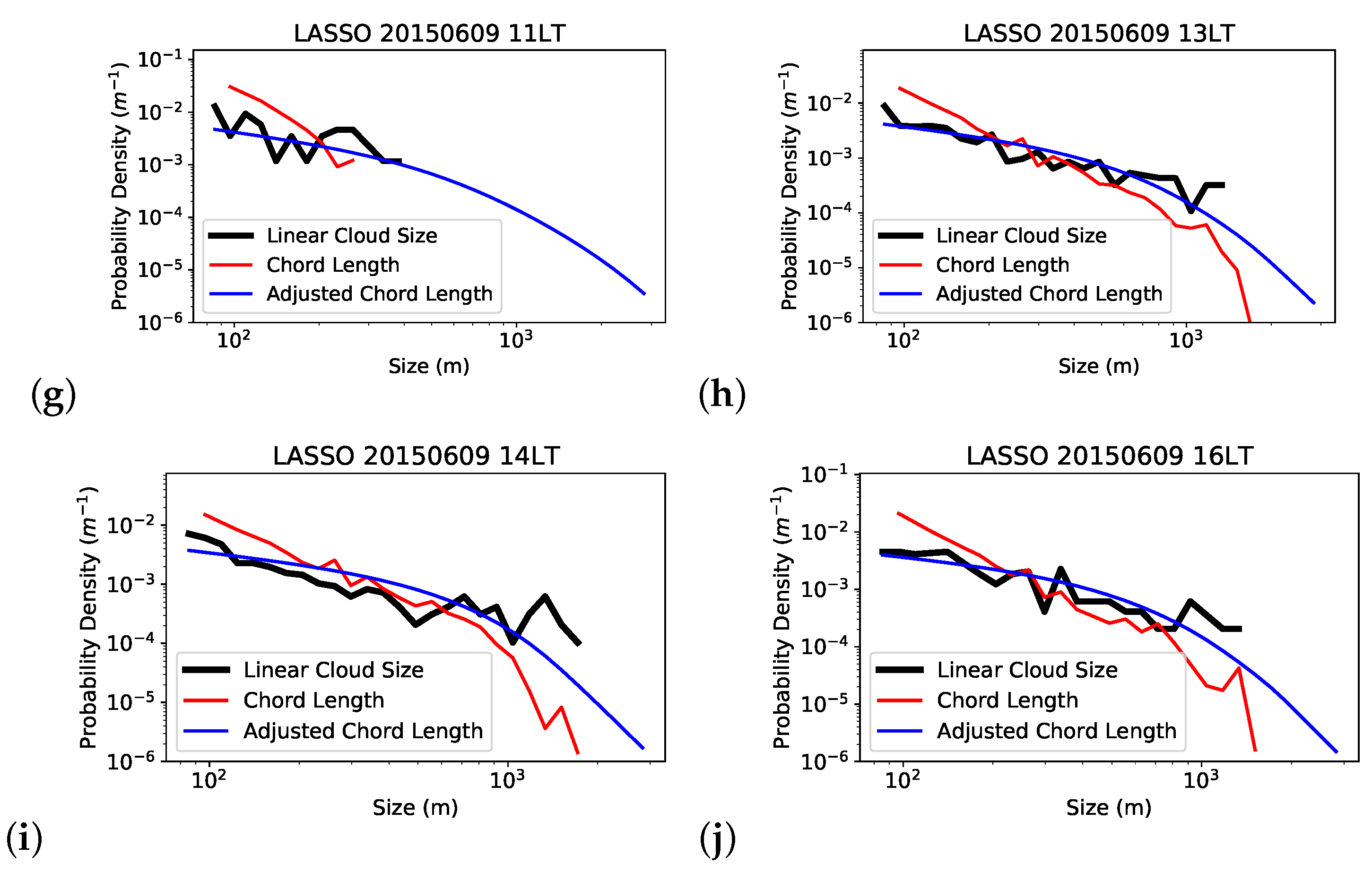
| Linear | Chord Length | pct Change | Adjusted Chord Length | pct Change | |
|---|---|---|---|---|---|
| RICO h8 | 545 | 292 | −47 | 478 | −12 |
| RICO h24 | 741 | 354 | −52 | 524 | −29 |
| RICO h40 | 716 | 506 | −29 | 643 | −10 |
| RICO h48 | 790 | 554 | −30 | 697 | −12 |
| RICO h56 | 656 | 512 | −22 | 649 | −1 |
| BOMEX h4 | 435 | 210 | −52 | 470 | 8 |
| BOMEX h5 | 467 | 227 | −51 | 474 | 1 |
| BOMEX h6 | 446 | 216 | −52 | 470 | 5 |
| BOMEX h7 | 445 | 214 | −52 | 469 | 5 |
| BOMEX h8 | 452 | 227 | −50 | 472 | 4 |
| ARM h11 | 383 | 249 | −35 | 466 | 22 |
| ARM h12 | 713 | 343 | −52 | 518 | −27 |
| ARM h13 | 905 | 376 | −58 | 540 | −40 |
| ARM h14 | 909 | 367 | −60 | 533 | −41 |
| ARM h15 | 888 | 359 | −60 | 526 | −41 |
| ARM h16 | 826 | 358 | −57 | 525 | −37 |
| ARM h17 | 823 | 354 | −57 | 521 | −37 |
| ARM h18 | 744 | 326 | −56 | 502 | −32 |
| LASSO h12.0 | 392 | 219 | −44 | 511 | 30 |
| LASSO h13.0 | 560 | 330 | −41 | 517 | −8 |
| LASSO h14.0 | 743 | 345 | −54 | 515 | −31 |
| LASSO h15.0 | 639 | 324 | −49 | 504 | −21 |
| LASSO h16.0 | 504 | 306 | −39 | 494 | −2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barron, N.R.; Ryan, S.D.; Heus, T. Reconciling Chord Length Distributions and Area Distributions for Fields of Fractal Cumulus Clouds. Atmosphere 2020, 11, 824. https://doi.org/10.3390/atmos11080824
Barron NR, Ryan SD, Heus T. Reconciling Chord Length Distributions and Area Distributions for Fields of Fractal Cumulus Clouds. Atmosphere. 2020; 11(8):824. https://doi.org/10.3390/atmos11080824
Chicago/Turabian StyleBarron, Nicholas R., Shawn D. Ryan, and Thijs Heus. 2020. "Reconciling Chord Length Distributions and Area Distributions for Fields of Fractal Cumulus Clouds" Atmosphere 11, no. 8: 824. https://doi.org/10.3390/atmos11080824
APA StyleBarron, N. R., Ryan, S. D., & Heus, T. (2020). Reconciling Chord Length Distributions and Area Distributions for Fields of Fractal Cumulus Clouds. Atmosphere, 11(8), 824. https://doi.org/10.3390/atmos11080824





