On the Buoyancy Subrange in Stratified Turbulence
Abstract
1. Introduction
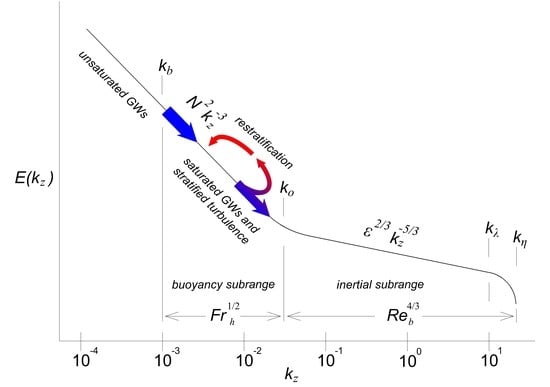
2. An Overview of the Spectral Properties in the Buoyancy Subrange
3. On the Concept of Critical Balance
4. On Scaling Law Constants in the Buoyancy Subrange
5. An Implication to Turbulence Strength Measurements Using Radar
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SST | Strongly Stratified Turbulence |
| GW | Gravity Wave |
Appendix A. On the Derivation of Taylor Microscale
Appendix B. On the Derivation of the Scaling Constant
References
- Lindzen, R.S. Turbulence and stress owing to grawity wave and tidal breakdown. J. Geophys. Res. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Lübken, F.J. Thermal structure of the Arctic summer mesosphere. J. Geophys. Res. 1999, 104, 9135–9149. [Google Scholar]
- Avsarkisov, V.; Strelnikov, B.; Becker, E. Analysis of the vertical spectra of density fluctuation variance in the strongly stratified turbuelence. In Proceedings of the 11th International Symposium on Turbulence and Shear Flow Phenomena (TSFP11), Osaka, Japan, 30 July–2 August 2019; pp. 1–5. [Google Scholar]
- Strelnikov, B.; Eberhart, M.; Staszak, T.; Asmus, H.; Strelnikova, I.; Grygalashvyly, M.; Lübken, F.J.; Latteck, R.; Baumgarten, G.; Höffner, J.; et al. Simultaneous in situ measurements of small-scale structures in neutral, plasma, and atomic oxygen densities during WADIS sounding rocket project. Atmos. Chem. Phys. 2019, 19, 114-43-60. [Google Scholar] [CrossRef]
- Lumley, J.L. The spectrum of nearly inertial turbulence in a stably stratified fluid. J. Atmos. Sci. 1964, 21, 99–102. [Google Scholar] [CrossRef]
- Shur, G.H. Experimental studies of the energy spectrum of atmospheric turbulence. Tr. Tsent. Aerolog. Observ. 1962, 43, 79–90. [Google Scholar]
- Richardson, L.F. The supply of energy from and to atmospheric eddies. Proc. R. Soc. 1920, 97, 354–373. [Google Scholar]
- Ozmidov, R.V. On the turbulent exchange in a stably stratified ocean. Izv. Akad. Nauk. SSSR Atmos. Oceanic Phys. Ser. 1 1965, 853, 1950–1954. [Google Scholar]
- Dougherty, J.P. The anisotropy of turbulence at the meteor level. J. atmos. terr. Phys. 1961, 21, 210–213. [Google Scholar] [CrossRef]
- Gregg, M.C. A Comparison of Finestructure Spectra from the Main Thermocline. J. Phys. Oceanogr. 1977, 7, 33–40. [Google Scholar] [CrossRef]
- Dewan, E.M. Stratospheric Wave Spectra Resembling Turbulence. Science 1979, 204, 832–835. [Google Scholar] [CrossRef]
- VanZandt, T.E. A universal spectrum of buoyancy waves in the atmosphere. J. Atmos. Sci. 1982, 9, 575–578. [Google Scholar] [CrossRef]
- Garrett, C.; Munk, W. Space-time scales of internal waves. Geophys. Fluid Dyn. 1972, 2, 225–268. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Fritts, D.C. Gravity wave saturation in the middle atmosphere: A review of theory and observations. Rev. Geophys. 1984, 22, 275–308. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, T.; Zhao, Y.; Pautet, P.D.; Taylor, M.J.; Pendleton, W.R., Jr. A coordinated investigation of the gravity wave reaking and the associated dynamical instability by a Na lidar and an Advanced Mesosphere Temperature Mapper over Logan, UT (41.7∘ N, 111.8∘ W). J. Geophys. Res. Space Phys. 2014, 119, 6852–6864. [Google Scholar] [CrossRef]
- Yuan, T.; Heale, C.J.; Snively, J.B.; Cai, X.; Pautet, P.D.; Fish, C.; Zhao, Y.; Taylor, M.J.; Pendleton, W.R., Jr.; Wickwar, V.; et al. Evidence of dispersion and refraction of a spectrally broad gravity wave packet in the mesopause region observed by the Na lidar and Mesospheric Temperature Mapper above Logan, Utah. J. Geophys. Res. Atmos. 2016, 121, 579–594. [Google Scholar] [CrossRef]
- Chau, J.L.; Urco, J.M.; Avsarkisov, V.; Vierinen, J.P.; Latteck, R.; Hall, C.M.; Tsutsumi, M. Four-Dimensional Quantification of Kelvin-Helmholtz Instabilities in the Polar Summer Mesosphere Using Volumetric Radar Imaging. Geophys. Res. Lett. 2020, 47, e2019GL086081. [Google Scholar] [CrossRef]
- Smith, S.A.; Fritts, D.C.; VanZandt, T.E. Comparison of mesospheric wind spectra with a gravity wave model. Radio Sci. 1985, 20, 1331–1338. [Google Scholar] [CrossRef]
- Smith, S.A.; Fritts, D.C.; Zandt, T.E.V. Evidence for a saturated spectrum of atmospheric gravity waves. J. Atmos. Sci. 1987, 44, 1404–1410. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E. Saturation and the “universal” spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res.: Atmos. 1986, 91, 2742–2748. [Google Scholar] [CrossRef]
- Weinstock, J. On the theory of turbulence in the buoyancy subrange of stably stratified flows. J. Atmos. Sci. 1978, 35, 634–649. [Google Scholar] [CrossRef]
- Munk, W. Internal waves and small-scale processes. In Evolution of Physical Oceanography; Warren, B.A., Wunsch, C., Eds.; MIT Press: Cambridge, MA, USA, 1981; pp. 264–291. [Google Scholar]
- Weinstock, J. Vertical wind shears, turbulence and non-turbulence in the troposphere and stratosphere. Geophys. Res. Lett. 1980, 7, 749–752. [Google Scholar] [CrossRef]
- Osborn, T.R. Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 1980, 10, 83–89. [Google Scholar] [CrossRef]
- Maffioli, A.; Brethouwer, G.; Lindborg, E. Mixing efficiency in stratified turbulence. J. Fluid Mech. 2016, 794, R3. [Google Scholar] [CrossRef]
- Weinstock, J. On the theory of temperature spectra in a stably stratified fluid. J. Phys. Oceanogr. 1985, 15, 475–477. [Google Scholar] [CrossRef]
- Dalaudier, F.; Sidi, C. Evidence and interpretation of a spectral gap in the turbulent atmospheric temperature spectra. J. Atmos. Sci. 1987, 44, 3121–3126. [Google Scholar] [CrossRef][Green Version]
- Holloway, G. The buoyancy flux from internal gravity wave breaking. Dyn. Atmos. Oceans 1988, 12, 107–125. [Google Scholar] [CrossRef]
- Riley, J.J.; Metcalfe, R.W.; Weissman, M.A. Direct numerical simulations of homogeneous turbulence in density-stratified fluids. AIP Conf. Proc. 1981, 76, 79–112. [Google Scholar] [CrossRef]
- Brethouwer, G.; Billant, P.; Lindborg, E.; Chomaz, J.M. Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 2007, 585, 343–368. [Google Scholar] [CrossRef]
- Waite, M.L. Stratified turbulence at the buoyancy scale. Phys. Fluids 2011, 23, 1–12. [Google Scholar] [CrossRef]
- Bouruet-Aubertot, P.; Sommeria, J.; Staquet, C. Stratified turbulence produced by internal wave breaking: two-dimensional numerical experiments. Dyn. Atmos. Oceans 1996, 23, 357–369. [Google Scholar] [CrossRef]
- Gerz, T.; Schumann, U. A Possible Explanation of Countergradient Fluxes in Homogeneous Turbulence. Theoret. Comput. Fluid Dyn. 1996, 8, 169–181. [Google Scholar] [CrossRef][Green Version]
- Sidi, C. Wave-turbulence coupling. In Coupling Processes in the Lower and Middle Atmosphere; Thrane, E.W., Blix, T.A., Fritts, D.C., Eds.; Kluwer Academic Publishers: Berlin, Germany, 1993; pp. 291–304. [Google Scholar]
- Holloway, G. A conjecture relating oceanic internal waves and small-scale processes. Atmos. Ocean 1983, 21, 107–122. [Google Scholar] [CrossRef]
- Smyth, W.D.; Moum, J.N. Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 2000, 12, 1343–1362. [Google Scholar] [CrossRef]
- Billant, P.; Chomaz, J.M. Self-similarity of strongly stratified inviscid flows. Phys. Fluids 2001, 13, 1645–1651. [Google Scholar] [CrossRef]
- Lindborg, E. The energy cascade in a strongly stratified fluid. J. Fluid Mech. 2006, 550, 207–242. [Google Scholar] [CrossRef]
- Holmboe, J. On the behaviour of symmetric waves in stratified shear layers. Geophys. Publ. 1962, 24, 67–113. [Google Scholar]
- Browand, F.K.; Winant, C.D. Laboratory observations of shear-layer instability in a stratified fluid. Bound.-Layer Meteor. 1973, 5, 67–77. [Google Scholar] [CrossRef]
- Salehipour, H.; Peltier, W.R.; Caulfield, C.P. Self-organized criticality of turbulence in strongly stratified mixing layers. J. Fluid Mech. 2018, 856, 228–256. [Google Scholar] [CrossRef]
- Smyth, W.D.; Nash, J.D.; Moum, J.N. Self-organized criticalityin geophysical turbulence. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Mater, B.D.; Venayagamoorthy, S.K. A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 2014, 26, 036601-1-18. [Google Scholar] [CrossRef]
- Yamazaki, H.; Osborn, T. Dissipation estimates for stratified turbulence. J. Geophys. Res. 1990, 95, 9739–9744. [Google Scholar] [CrossRef]
- Nazarenko, S.V.; Schekochihin, A.A. Critical balance in megnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 2011, 677, 134–153. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence in Rotating, Stratified and Electrically Conducting Fluids; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Nastrom, G.D.; Gage, K.S. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950–960. [Google Scholar] [CrossRef]
- Liu, H.L. Quantifying gravity wave forcing using scale invariance. Nature Comm. 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Vierinen, J.; Chau, J.L.; Charuvil, H.; Urco, J.M.; Clahsen, M.; Avsarkisov, V.; Marino, R.; Volz, R. Observing Mesospheric Turbulence With Specular Meteor Radars: A Novel Method for Estimating Second-Order Statistics of Wind Velocity. Earth Space Sci. 2019, 6, 1171–1195. [Google Scholar] [CrossRef]
- Fukao, S.; Yamanaka, M.D.; Ao, N.; Hocking, W.K.; Sato, T.; Yamamoto, M.; Nakamura, T.; Tsuda, T.; Kato, S. Seasonal variability of vertical eddy diffusivity in the middle atmosphere 1. Three-year observations by the middle and upper atmosphere radar. J. Geophys. Res. 1994, 99, 18973–18987. [Google Scholar] [CrossRef]
- Sreenivasan, K. On the universality of the Kolmogorov constant. Phys. Fluids 1995, 7, 2778–2784. [Google Scholar] [CrossRef]
- Weinstock, J. Energy dissipation rates of turbulence in a the stable free atmosphere. J. Atmos. Sci. 1981, 38, 880–883. [Google Scholar] [CrossRef][Green Version]
- Hocking, W.K. The dynamical parameters of turbulence theory as they apply to middle atmosphere studies. Earth Planets Space 1999, 51, 525–541. [Google Scholar] [CrossRef]
- Hocking, W.K.; Roettger, J.; Palmer, R.D.; Sato, T.; Chilson, P.B. Atmospheric Radar; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Kantha, L.; Luce, H.; Hashiguchi, H. Shigaraki UAV-radar experiment (ShUREX): overview of the campaign with some preliminary results. Earth Planets Space 2017, 4, 1–26. [Google Scholar] [CrossRef]
- Luce, H.; Kantha, L.; Hashiguchi, H.; Lawrence, D.; Doddi, A. Turbulence kinetic energy dissipation rates estimated from concurrent UAV and MU radar measurements. Earth Planets Space 2018, 70, 1–19. [Google Scholar] [CrossRef]
- Kantha, L.; Luce, H.; Hashiguchi, H. On a numerical model for extracting TKE dissipation rate from very high frequency (VHF) radar spectral width. Earth Planets Space 2018, 70, 1–18. [Google Scholar] [CrossRef]
- Dauxois, T.; Peacock, T.; Bauer, P.; Caulfield, C.P.; Cenedese, C.; Gorlé, C.; Haller, G.; Ivey, G.N.; Linden, P.F.; Meiburg, E.; et al. Confronting Grand Challenges in Environmental Fluid Dynamics. arXiv 2019, arXiv:1911.09541. [Google Scholar]
- Caccamo, M.T.; Magazú, S. A physical-mathematical approach to climate change effects through stochastic resonance. Climate 2019, 7, 1–16. [Google Scholar] [CrossRef]
- Sukoriansky, S.; Galperin, B. An analytical theory of the buoyancya-Kolmogorov subrange transition in turbulent flows with stable stratification. Phil. Trans. R. Soc. A 2013, 371, 20120212. [Google Scholar] [CrossRef] [PubMed]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; The MIT Press: Berlin, Germany, 1972. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avsarkisov, V. On the Buoyancy Subrange in Stratified Turbulence. Atmosphere 2020, 11, 659. https://doi.org/10.3390/atmos11060659
Avsarkisov V. On the Buoyancy Subrange in Stratified Turbulence. Atmosphere. 2020; 11(6):659. https://doi.org/10.3390/atmos11060659
Chicago/Turabian StyleAvsarkisov, Victor. 2020. "On the Buoyancy Subrange in Stratified Turbulence" Atmosphere 11, no. 6: 659. https://doi.org/10.3390/atmos11060659
APA StyleAvsarkisov, V. (2020). On the Buoyancy Subrange in Stratified Turbulence. Atmosphere, 11(6), 659. https://doi.org/10.3390/atmos11060659