Initial Results of Meteor Wind with Langfang Medium Frequency Radar
Abstract
1. Introduction
2. Principles of Meteor Wind Measurement
3. Experimental Setup of Meteor Observations
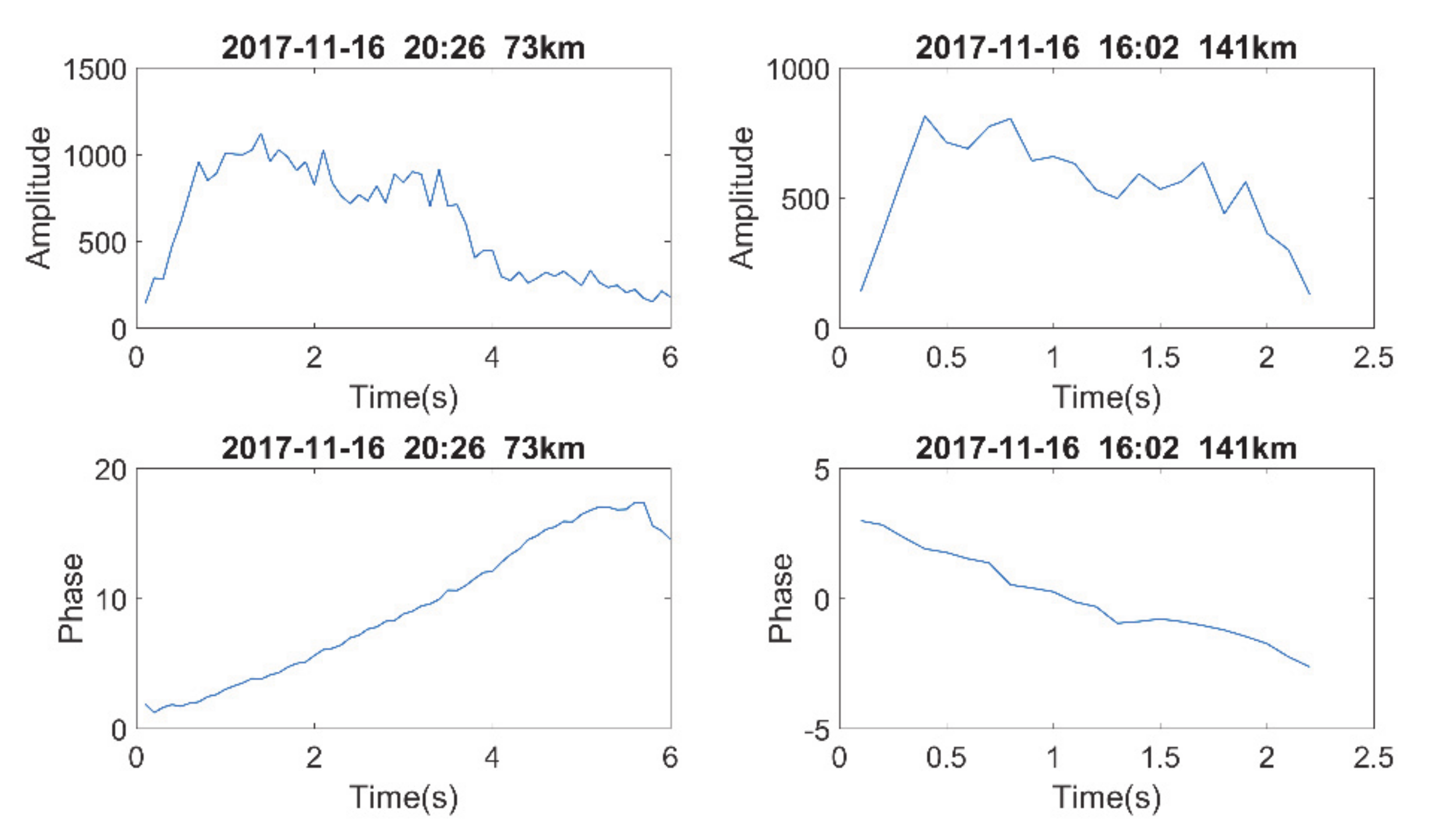
4. Meteor Echo Detection and Data Analysis
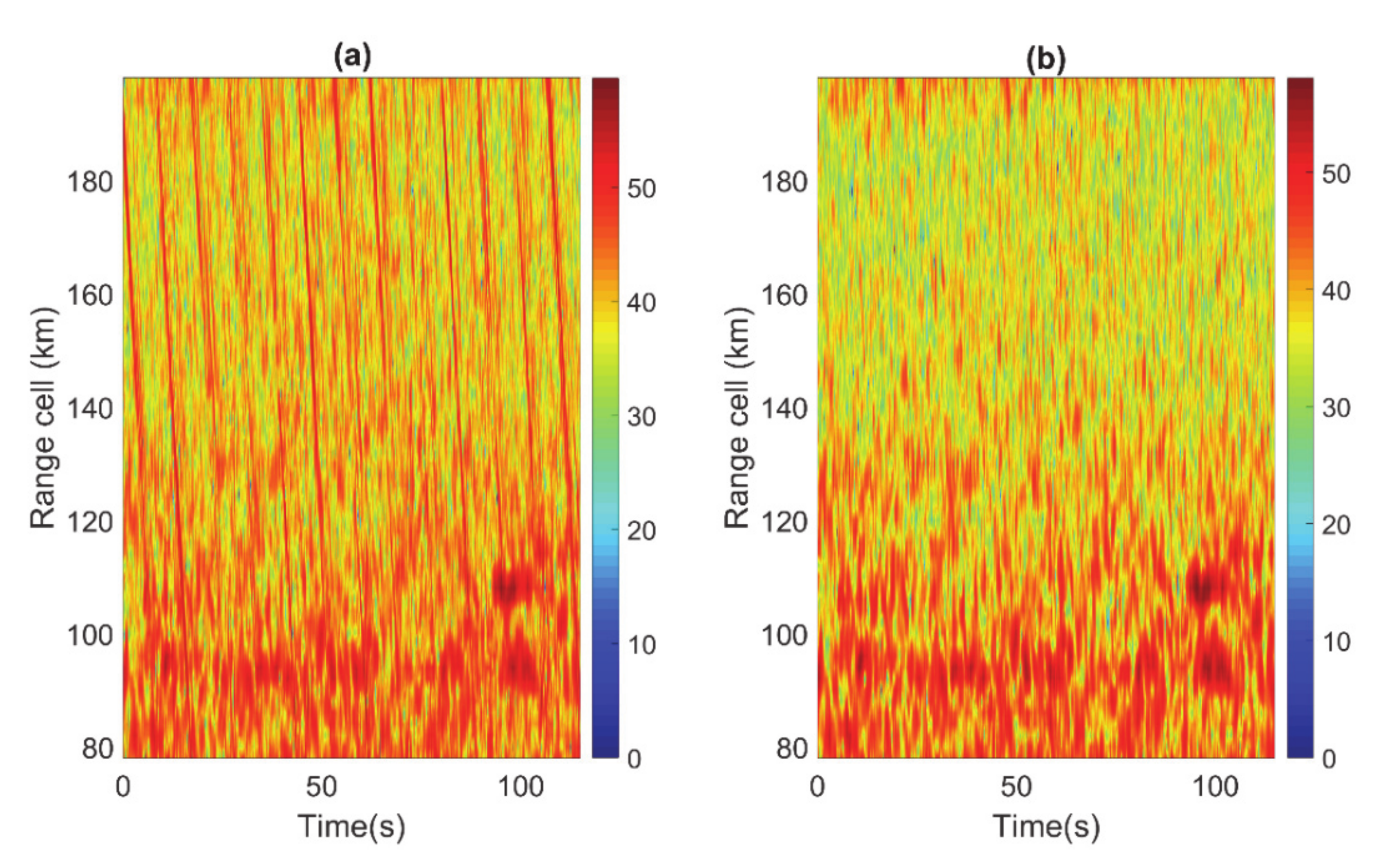
4.1. Detection Algorithms
4.2. Parameteor Estimation
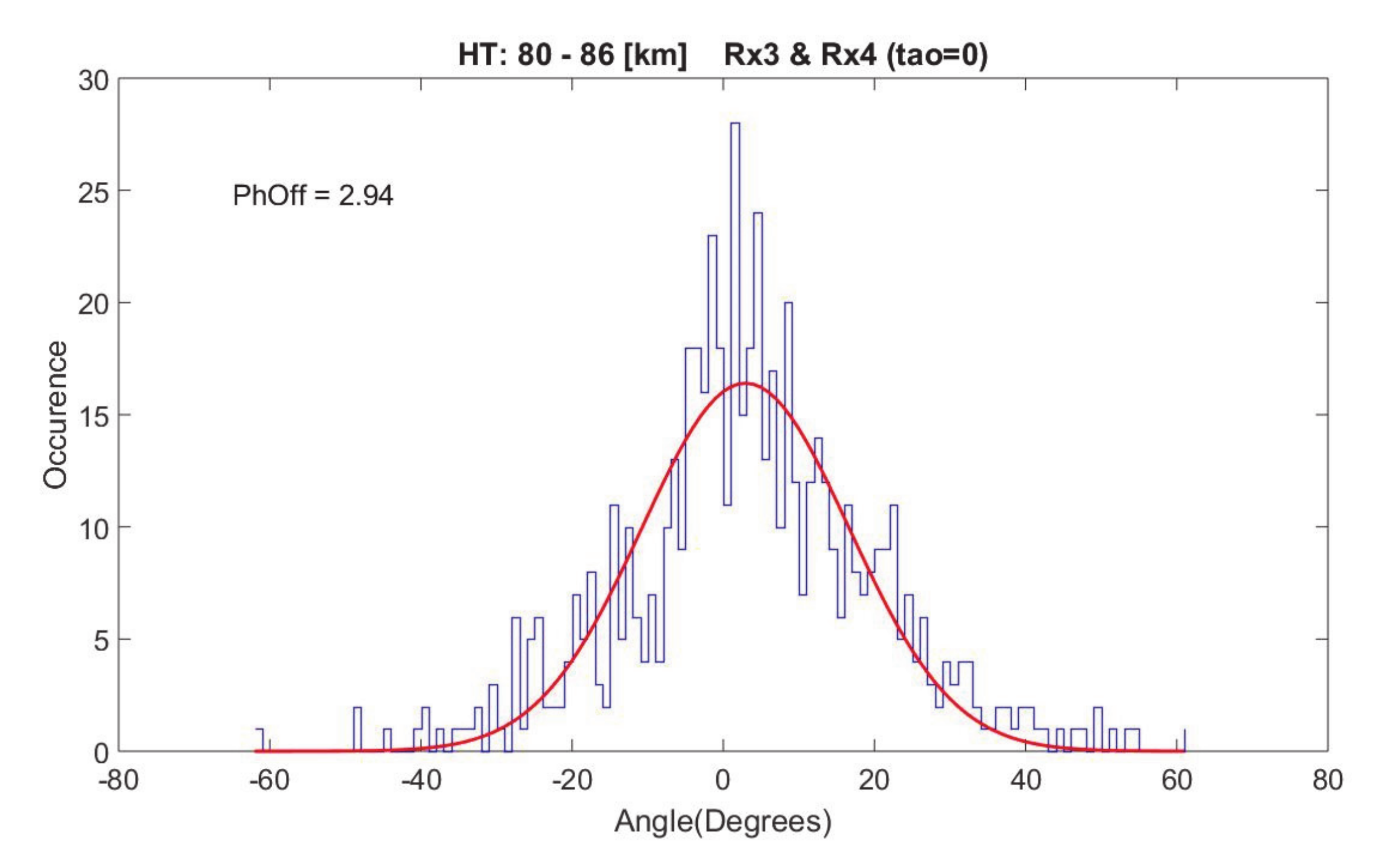
4.2.1. AOA
4.2.2. Meteor Height
4.2.3. Radial Drifted Velocity
4.3. Horizontal Wind Calculation
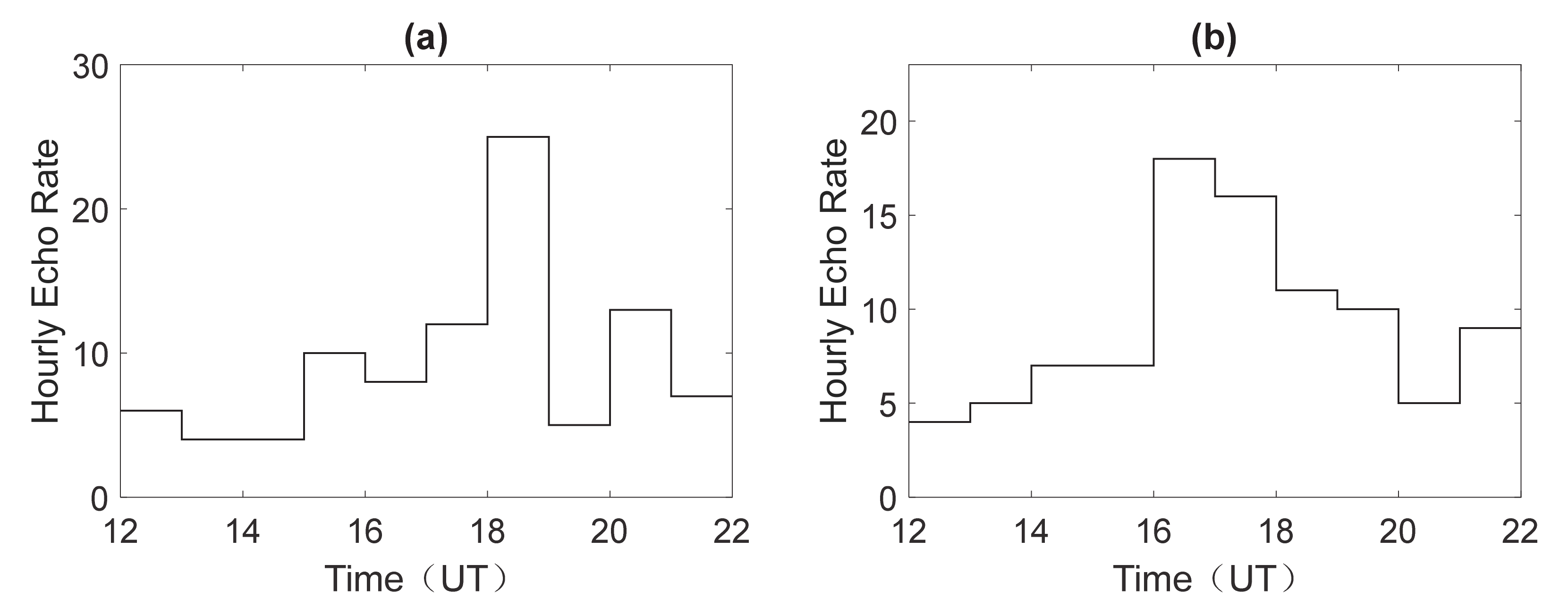
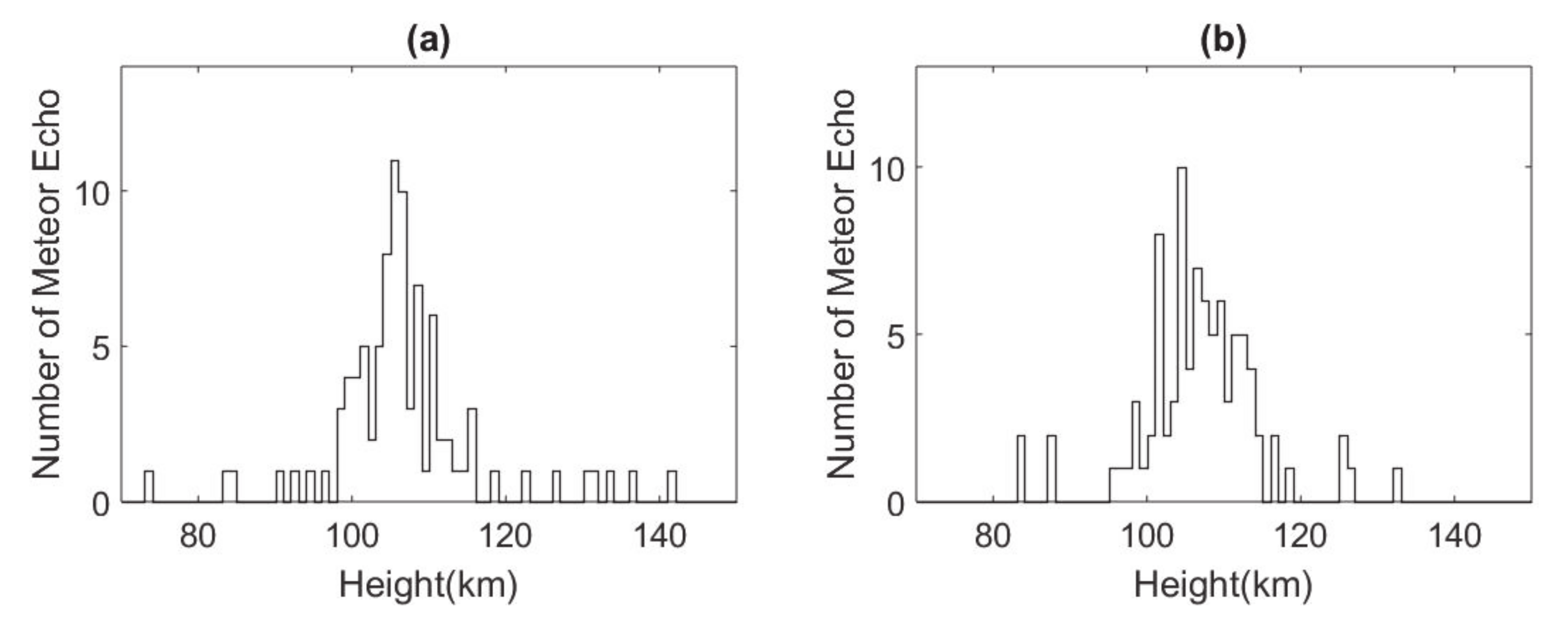
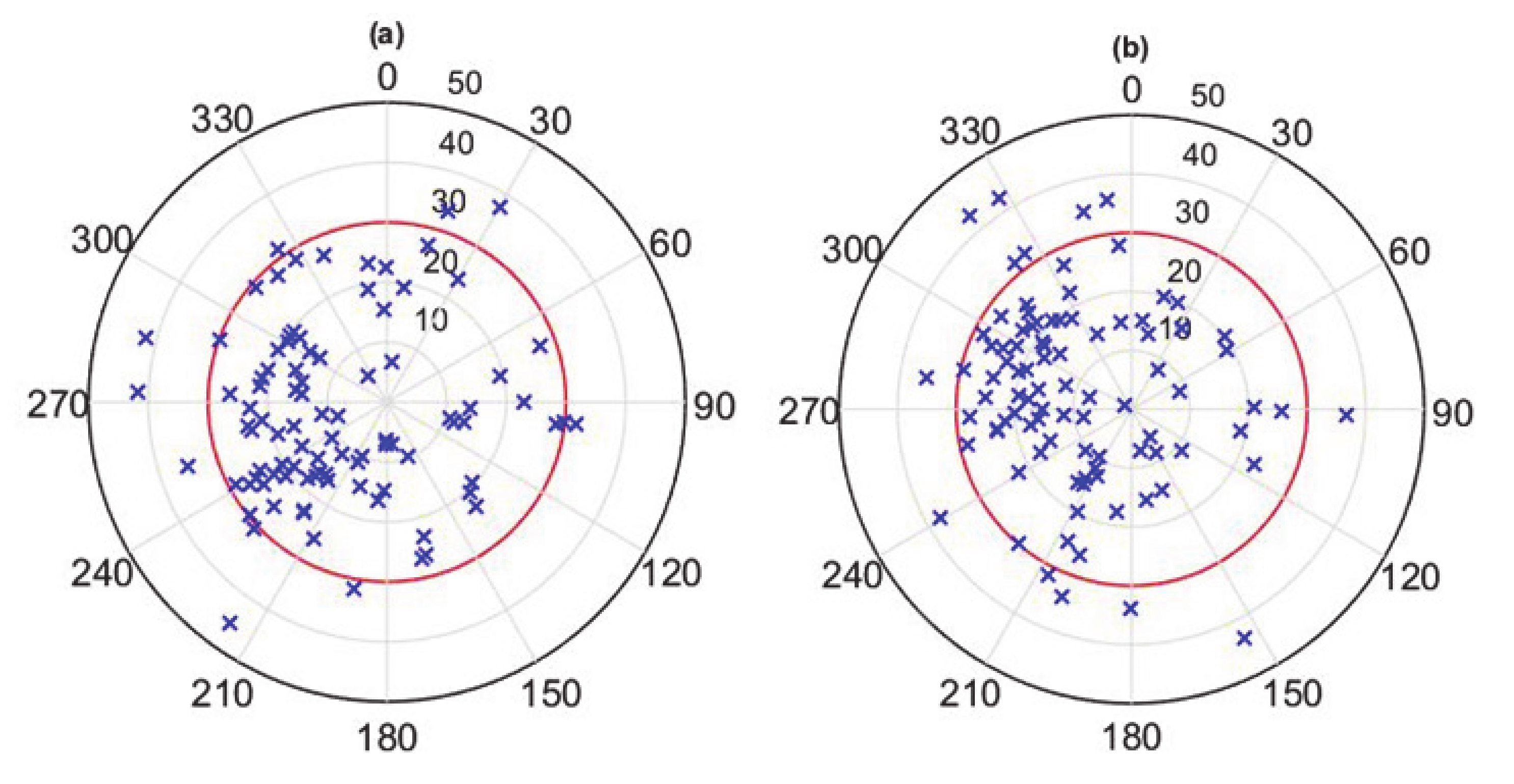
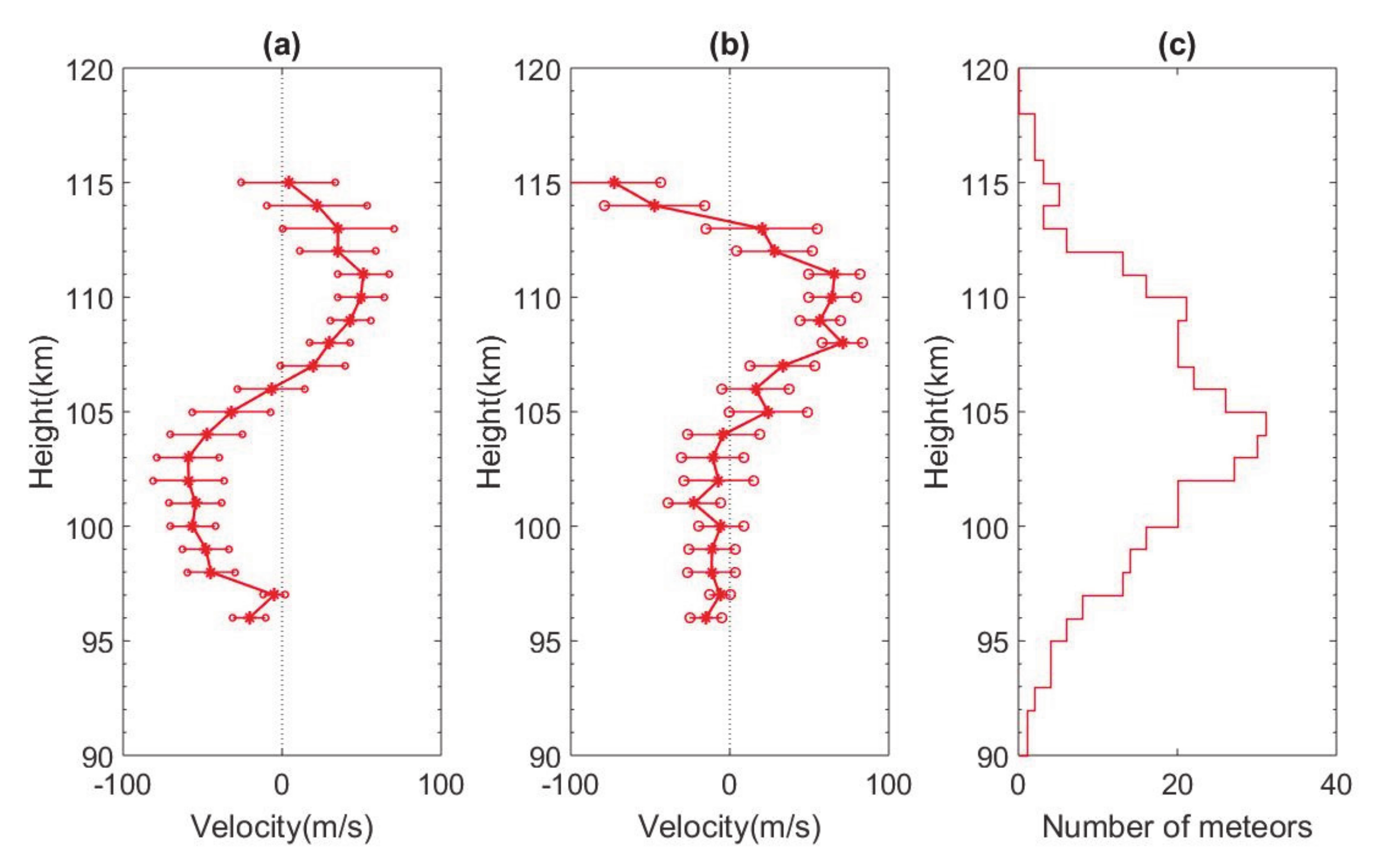
5. Meteor Distribution
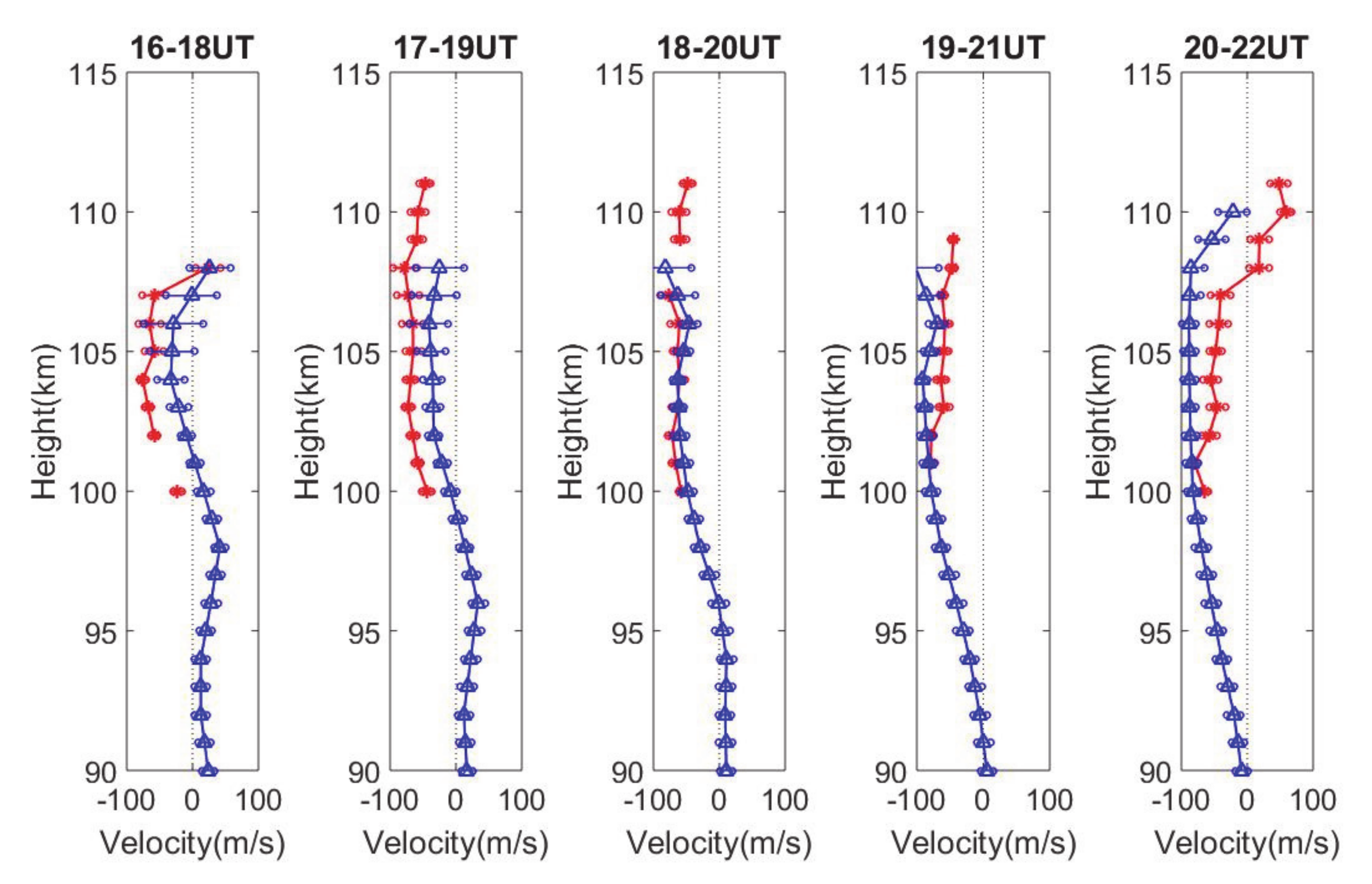
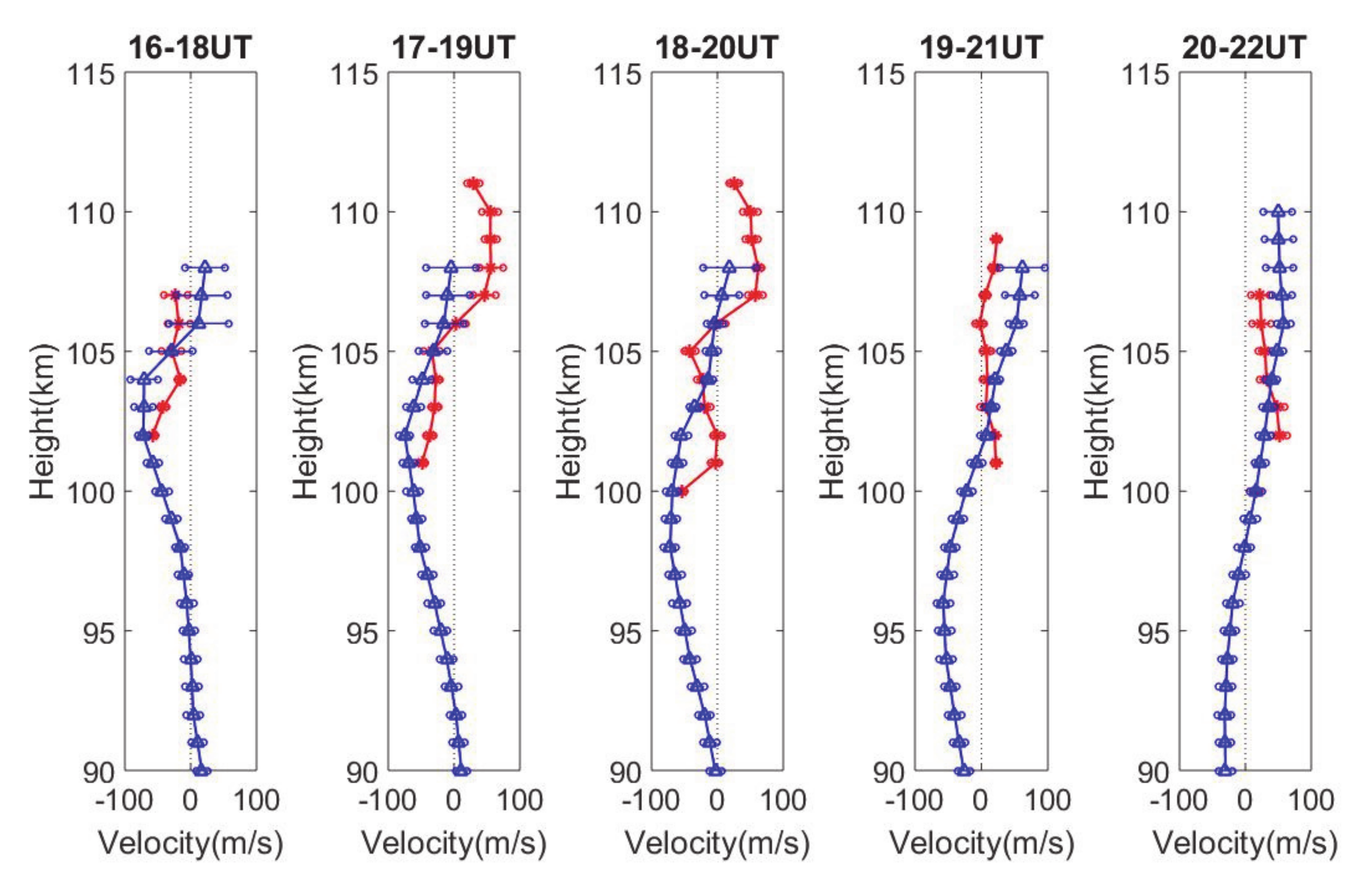
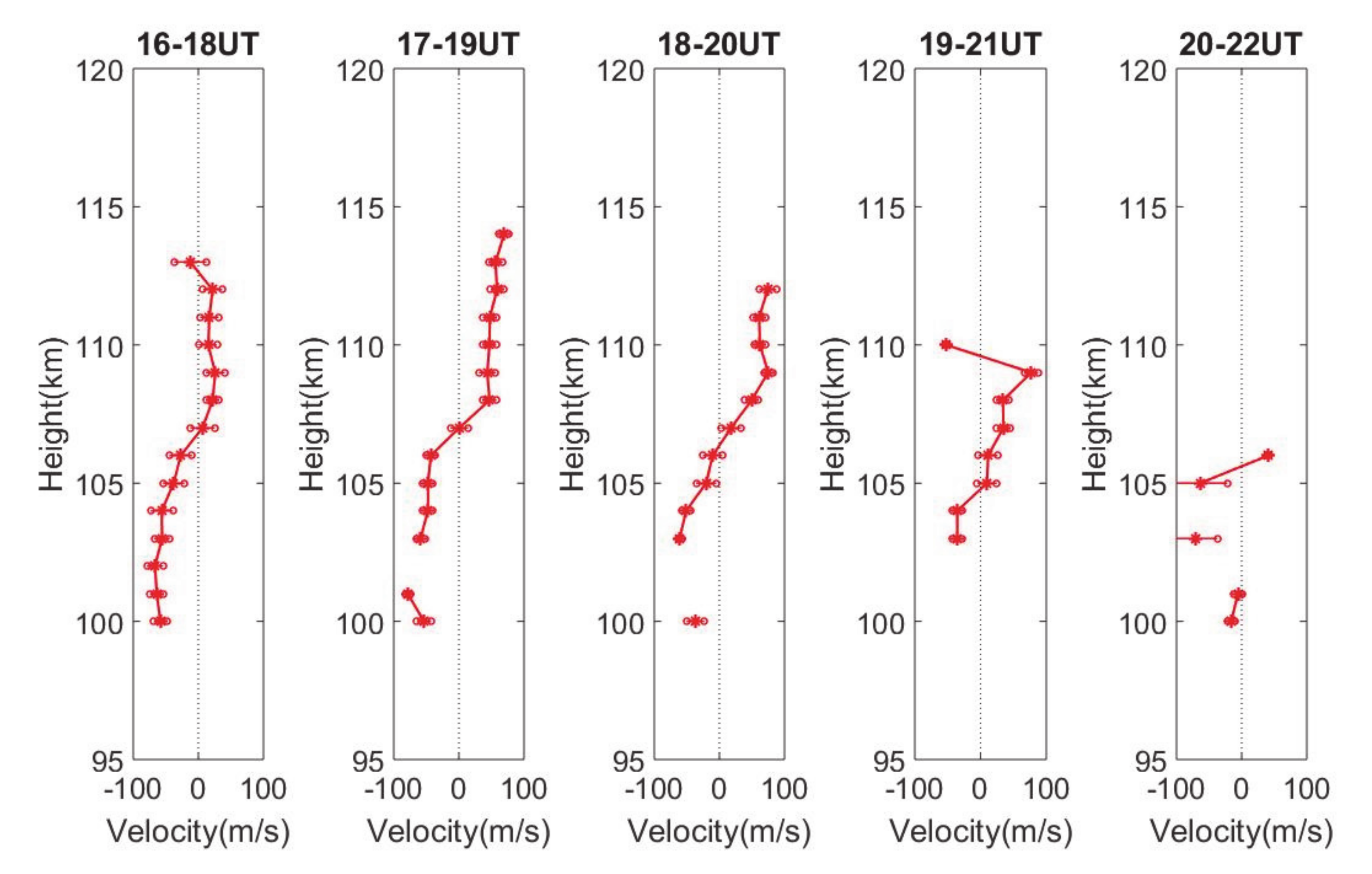
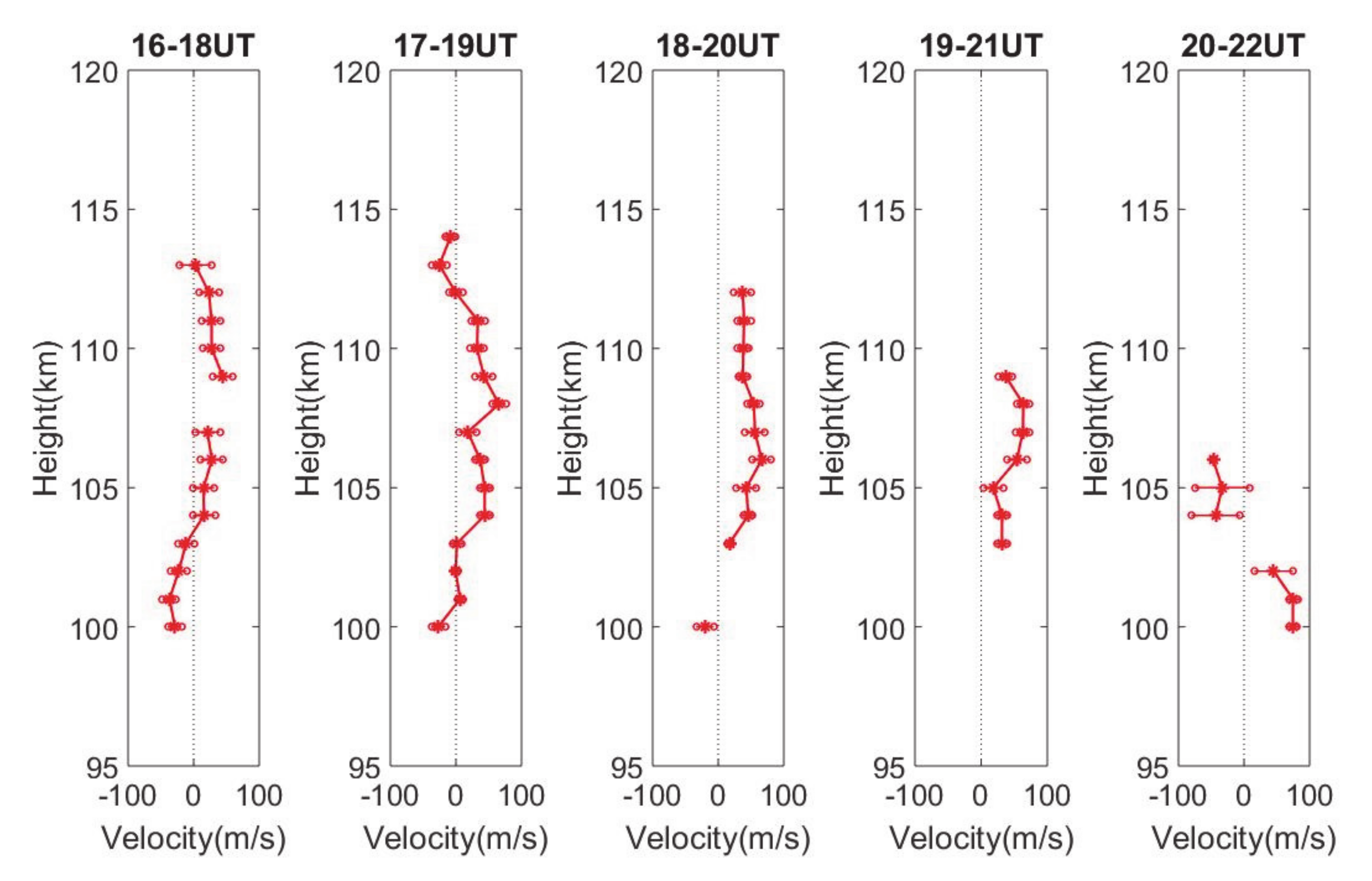
6. Horizontal Wind Estimation and Comparison
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (1)
- The Fresnel integral
- (2)
- Radar equation variant
- (3)
- Directional cosines
- (4)
- Normalized Phase Discrepancy (NPD)
- (5)
- Calculation formulas of horizontal wind [29]
References
- Reid, I.M.; Vandepeer, B.G.W.; Dillon, S.C. The new Adelaide medium frequency Doppler radar. Radio Sci. 1995, 30. [Google Scholar] [CrossRef]
- Baumgaertner, A.J.G.; McDonald, A.J.; Fraser, G.J.; Plank, G.E. Long-term observations of mean winds and tides in the upper mesosphere and lower thermosphere above Scott Base, Antarctica. J. Atmos. Sol. Terr. Phys. 2005, 67, 1480–1496. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Vandepeer, B.; Reid, I.M.; Vincent, R.A. Differential absorption measurements of mesospheric and lower thermospheric electron densities using the Buckland Park MF radar. J. Atmos. Sol. Terr. Phys. 2002, 64, 2029–2042. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Holdsworth, D.; Nakamura, T.; Reid, I. Meteor observations with an MF radar. Earth Planets Space 1999, 51, 691–699. [Google Scholar] [CrossRef]
- Holdsworth, D.A. Influence of instrumental effects upon the full correlation analysis. Radio Sci. 1999, 34, 643–655. [Google Scholar] [CrossRef]
- Cervera, M. Meteor Observations with a Narrow Beam VHF Radar; University of Adelaide: Adelaide, Australia, 1996. [Google Scholar]
- Fahrutdinova, A.N.; Ganin, V.A.; Berdunov, N.V.; Ishmuratov, R.A.; Hutorova, O.G. Long-term variations of circulation in the mid-latitude upper mesosphere-lower thermosphere. Adv. Space Res. 1997, 20, 1161–1164. [Google Scholar] [CrossRef]
- Olsson-Steel, D.; Elford, W.G. The height distribution of radio meteors observations at 2 MHz. J. Atmos. Sol. Terr. Phys. 1987, 49, 243–258. [Google Scholar] [CrossRef]
- Meek, C.E.; Manson, A.H. MF radar interferometer measurements of meteor trail motions. Radio Sci. 1990, 25, 649–655. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Aso, T. MF radar observations of meteors and meteor-derived winds at Syowa (69°S, 39°E), Antarctica: A comparison with simultaneous spaced antenna winds. J. Geophys. Res. Atmos. 2005, 110, D24111. [Google Scholar] [CrossRef]
- Stephen, I.G. Medium Frequency Radar Studies of Meteors; University of Adelaide: Adelaide, Australia, 2003. [Google Scholar]
- Ceplecha, Z.; Borovička, J.; Elford, W.G.; Revelle, D.O.; Hawkes, R.L.; Porubčan, V.; Šimek, M. Meteor phenomena and bodies. Space Sci. Rev. 1998, 84, 327–471. [Google Scholar] [CrossRef]
- Rogers, L.A.; Hill, K.A.; Hawkes, R.L. Mass loss due to sputtering and thermal processes in meteoroid ablation. Planet. Space Sci. 2005, 53, 1341–1354. [Google Scholar] [CrossRef]
- Mckinley, D.W.R. Meteor Science and Engineering; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Herlofson, N. The theory of meteor ionization. Rep. Prog. Phys. 1947, 11, 444–454. [Google Scholar]
- Nakamura, T.; Tsutsumi, M.; Uehara, T.; Fukao, S.; Kato, S. Meteor wind observations with the MU radar. Radio Sci. 1991, 26, 857–869. [Google Scholar] [CrossRef]
- Cervera, M.A.; Reid, I.M. Comparison of simultaneous wind measurements using colocated VHF meteor radar and MF spaced antenna radar systems. Radio Sci. 1995, 30, 1245–1261. [Google Scholar] [CrossRef]
- Thorsen, D.; Franke, S.J.; Kudeki, E. A new approach to MF radar interferometry for estimating mean winds and momentum flux. Radio Sci. 1997, 32, 707–726. [Google Scholar] [CrossRef]
- Cunying, X.; Xiong, H.; Qingchen, X.; Xuxing, C.; Mingliang, Z. First MF radar observations of winds and tides in the mesosphere and lower thermosphere over Langfang, China. In Proceedings of the Chinese Geophysical Society, Changsha, China, 17 November 2011. [Google Scholar]
- Guanglin, M.; Xiong, H.; Qingchen, X.; Cunying, X. Investigation and application of FCA method for Langfang MF radar wind retrievals. Chin. J. Space Sci. 2011, 31, 618–626. [Google Scholar]
- Meek, C.E. Triangle size effect in spaced antenna wind measurements. Radio Sci. 1990, 25, 641–648. [Google Scholar] [CrossRef]
- Junfeng, Y.; Cunying, X.; Xiong, H.; Qingchen, X. Observations and sumulations of the mean winds in mesosphere and lower thermosphere over Langfang of China. Chin. J. Space Sci. 2017, 37, 284–290. [Google Scholar]
- Junfeng, Y.; Cunying, X.; Xiong, H.; Qingchen, X. Seasonal variations of wind tides in mesosphere and lower thermosphere over Langfang, China (39.4°N, 116.7°E). Prog. Geophys. 2017, 32, 1501–1509. [Google Scholar]
- Holdsworth, D.A. Signal Analysis with Applications to Atmospheric Radars; University of Adelaide: Adelaide, Australia, 1995. [Google Scholar]
- Hocking, W.K.; Fuller, B.; Vandepeer, B. Real-time determination of meteor-related parameters utilizing modern digital technology. J. Atmos. Sol. Terr. Phys. 2001, 63, 155–169. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Reid, I.M.; Cervera, M.A. Buckland Park all-sky interferometric meteor radar. Radio Sci. 2004, 39, RS5009. [Google Scholar] [CrossRef]
- Vandepeer, B.W.; Reid, I.M. Some preliminary results obtained with the new Adelaide MF Doppler radar. Radio Sci. 1995, 30, 1191–1203. [Google Scholar] [CrossRef]
- Vandepeer, B. A New MF Doppler Radar for Upper Atmospheric Research; University of Adelaide: Adelaide, Australia, 1993. [Google Scholar]
- Sato, T. Radar Principles. Handb. MAP 1989, 30, 19–53. [Google Scholar]



| Parameter | MF Radar | VHF Meteor Radar |
|---|---|---|
| Frequency | 1.99 MHz | 35 MHz |
| Transmitting Power | 64 kW | 20 kW |
| Pulse Repetition Frequency | 80 Hz | 440 Hz |
| Height Resolution | 2 km | 2 km |
| Time Resolution (the length of individual time series) | 2 min | 1 h |
| Number of Coherent Integrations | 2 | 16 |
| Sampling Range | 78–150 km | 70–110 km |
| Polarization | O Mode | O Mode |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, B.; Xu, Q.; Hu, X.; Yang, J. Initial Results of Meteor Wind with Langfang Medium Frequency Radar. Atmosphere 2020, 11, 507. https://doi.org/10.3390/atmos11050507
Cai B, Xu Q, Hu X, Yang J. Initial Results of Meteor Wind with Langfang Medium Frequency Radar. Atmosphere. 2020; 11(5):507. https://doi.org/10.3390/atmos11050507
Chicago/Turabian StyleCai, Bing, Qingchen Xu, Xiong Hu, and Junfeng Yang. 2020. "Initial Results of Meteor Wind with Langfang Medium Frequency Radar" Atmosphere 11, no. 5: 507. https://doi.org/10.3390/atmos11050507
APA StyleCai, B., Xu, Q., Hu, X., & Yang, J. (2020). Initial Results of Meteor Wind with Langfang Medium Frequency Radar. Atmosphere, 11(5), 507. https://doi.org/10.3390/atmos11050507





