Abstract
Estimates of the global warming potential (GWP) of methane rely on the predictions from global chemistry-transport models. These models employ many uncertain input parameters representing the sources and sinks for methane and those for the tropospheric ozone, which is formed as a by-product of the methane sink process. Five thousand quasi-randomly Monte Carlo sampled model runs employing a zonally averaged global model were completed, each with a base case and a pulse case that differed from the base case only in having an additional 149 Tg (1Tg = 109 kg) emission pulse of methane. Each of the five thousand pulse case experiments had a small excess of methane that decayed away throughout the twenty-year model experiment. The radiative forcing consequences of this excess methane, and the excess tropospheric ozone formed from it, were integrated over a 100-year time horizon. The GWP was calculated in each of the five thousand model experiments from the sum of the radiative forcing consequences of methane and tropospheric ozone, by expressing them relative to the radiative forcing consequences of an identical emission pulse of carbon dioxide. The 2-sigma confidence range surrounding the methane atmospheric lifetime estimated in the Monte Carlo analysis was considerably wider than that derived from observations, suggesting that some of the input parameter combinations may have been unrealistic. The rejection of the unrealistic Monte Carlo replicates increased the mean methane GWP and narrowed its 2-sigma confidence interval to 37 ± 10 over a 100-year time horizon for emission pulses of the order of 1 Tg. Multiple linear regression was used to attribute the uncertainty in the output GWPs to each of the 183 uncertain input parameters, which represented emission source sectors, chemical kinetic rate coefficients, dry deposition velocities and biases in temperature and water vapour concentrations. Overall, the only significant contributions to the uncertainty in the methane GWP came from the chemical kinetic parameters representing the CH4 + OH, CH3O2 + HO2, CH3O2 + NO and the terpene + O3 reaction rate coefficients.
1. Introduction
It has long been recognised that methane (CH4) is the second most important anthropogenic greenhouse gas after carbon dioxide (CO2) [1]. CH4 has significant anthropogenic and natural sources and features in the basket of trace gases that come under the control of the United Nations Framework Convention on Climate Change (UN FCCC) [2]. CH4 sources have elevated pre-industrial levels [3] from 720–740 ppb (where 1 ppb = 1 nmol CH4 mol−1 air when expressed as mole fraction or mixing ratio) to present day levels of 1800 ppb. These man-made sources include oil and gas operations, coal mining, natural gas leakage, landfills and enteric fermentation in livestock [4]. The main atmospheric removal processes for CH4 is its oxidation by hydroxyl (OH) radicals [5,6]. This chemical reaction has a significant temperature coefficient, which means that the sink is concentrated in the warmer, more moist, lower troposphere. The atmospheric lifetime from this oxidation process is of the order of ten years. There are weaker sinks from soil uptake (160 years) and stratospheric OH oxidation (120 years) [4]. The CH4 oxidation sink also acts as a source of tropospheric ozone (O3), another important greenhouse gas [1].
The CH4 oxidation sink involving OH radicals not only controls the CH4 atmospheric lifetime and hence the CH4 burden but is also an important process controlling the fast, photochemical balance of the troposphere. In fact, it is so important that increasing CH4 burdens reduce the OH radical steady state concentration and extend the atmospheric lifetime. Increasing CH4 burdens therefore effectively reduces their own sink strength, leading to a positive feedback or amplification [4]. Consequently, CH4 is a direct greenhouse gas by virtue of its infrared absorption spectrum and an indirect greenhouse gas because it is able to perturb its own tropospheric distribution and that of tropospheric O3, the third most important anthropogenic greenhouse gas after CO2 and CH4 [1].
There have been a number of studies on the direct and radiative forcing consequences of CH4 emissions and these have been kept under review by the Intergovernmental Panel on Climate Change. A convenient metric defining and quantifying these radiative forcing consequences is the Global Warming Potential (GWP) [7]. Over a 100-year time horizon, CH4 has a GWP of about 30 [1], that is to say, the time-integrated radiative forcing consequences of an emission of 1 Tg of CH4 is equivalent to the emission of 30 Tg of CO2. The GWP concept has, however, been criticised because it does not represent climate policy temperature goals [8] and other metrics have been proposed [9]. However, the aim of this study is to address the radiative forcing consequences of CH4 emissions and so the GWP metric will suffice as an endpoint in our analyses.
Studies on the radiative forcing consequences of anthropogenic CH4 emissions with global chemistry-transport models employed in the estimation of global warming potentials (GWPs) are not without some singular difficulties that are relevant solely to CH4. Because of its ten-year atmospheric lifetime, the global CH4 distribution is not always in steady state with its sources and sinks either in the real atmosphere or within the global chemistry-transport models. The difficulties are such that some global chemistry-transport models use prescribed CH4 levels, and, in others, relatively short run times are employed. This means that the quantification of CH4 amplification factors and indirect radiative forcing contributions are surrounded by uncertainties.
This is the third of a three-part study. In the first part [10], a methodology was laid out for a Monte Carlo (MC) analysis of the uncertainties in tropospheric O3 sources and sinks in a global Lagrangian chemistry-transport model. In the second part [11], this same MC methodology was applied within a zonally averaged coarse resolution global tropospheric O3 model to investigate the uncertainties in the global burdens and turnovers of CH4, carbon monoxide (CO) and tropospheric O3. Here, in the third part, the MC methodology is applied to the investigation of the uncertainties surrounding model estimates of the CH4 GWP. In this study, the methodological uncertainties surrounding the presence or absence of any steady state between CH4 sources and sinks have been removed by employing 20-year long model experiments. A Monte Carlo uncertainty analysis has then been completed to investigate where the main uncertainties lie, whether in the atmospheric life cycle of CH4, in the fast, photochemical balance of the troposphere or in the radiative forcing consequences of atmospheric releases of CH4. To reduce the computational burden of these global chemistry-transport model experiments, sacrifices have had to be made with the spatial resolution of the modelling tool employed, through the use of a zonally-averaged (latitude-altitude) model. The aim has been to identify where model input uncertainties are likely to be the most significant so that future research efforts can be focused on them to reduce uncertainties in the GWP for CH4.
2. Monte Carlo Uncertainty Analysis and Its Methodology
2.1. The Pulse Behaviour of Methane
For a trace gas with a spatially and temporally independent first-order loss process, for example, radioactive decay, integrating over the globe gives the loss rate (L in Tg year−1), which, when divided into the global burden, (B in Tg), gives the atmospheric lifetime or residence time (LT) [12]. If the trace gas is in a steady state, then an instantaneous pulse of the trace gas, A0, will decay with time, t, according to A = A0 exp(−k1t), with an e-folding time constant of the reciprocal of k1, which is equal to the lifetime, LT.
For CH4, where the first order loss process is controlled largely by OH radicals and where the OH radical steady state is depleted by increasing CH4 burdens, a different response is seen to CH4 perturbations. CH4 pulses reduce tropospheric OH, which increases the lifetime of the CH4 pulse and hence amplifies the response [13]. The decay of a CH4 pulse is thus no longer controlled by the atmospheric lifetime but by a longer time constant, the adjustment time, AT. Therefore, a CH4 pulse, [CH4]0, decays according to: [CH4] = [CH4]0 exp(−k2t), with an e-folding time constant of AT, which is equal to the reciprocal of k2. The ratio of the adjustment time to the lifetime depends on the exact formulation of the atmospheric chemistry of CH4, CO and OH, with values varying between 1.23 and 1.62 [4]. CH4 has an important chemical feedback that amplifies the impacts of CH4 perturbations [14]. This feedback or amplification was characterised using a feedback factor (FF), which represents the percentage change in CH4 loss frequency for a one percent increase in CH4 burden. Feedback factors have been reported in the range −0.17% to −0.35% [4] and these FF values are related to AT and LT using: AT/LT = 1/(1 + FF). Apparently, the feedback factors are not correlated with the CH4 lifetimes, suggesting that they do not depend on it, but depend rather on the CH4, CO and OH chemistry [12].
Pulses of CH4 lead to an increase in the already existing CH4 burden, which cannot be distinguished from the pulse itself. Accordingly, the ‘excess’ CH4 decays away with the adjustment time constant, that is to say: [CH4]excess = [CH4]0 exp(−k2t). If the pulse itself had been tagged, then it would be found to decay with the e-folding time of the atmospheric lifetime, that is to say: [CH4]pulse = [CH4]0.exp(−k1t). The difference between these two decays is the ‘new’ CH4, which has been produced by the depletion in the OH radical steady state by CH4. Accordingly, we can then write: [CH4]new = [CH4]0.exp(−k2t) − [CH4]0.exp(−k1t). This ‘new’ CH4 starts from zero, reaches a maximum and then declines towards zero. The fraction of the time-integrated ‘excess’ CH4 that is ‘new’ is found to be: 1 − k2/k1.
Over the years since the publication of the first Intergovernmental Panel on Climate Change (IPCC) report [7], these definitions have remained largely unchanged, as have the atmospheric lifetimes, adjustment times and feedback factors for CH4. A formal description of the delayed recovery of a CH4 perturbation in terms of the eigenvalues and eigenvectors of the coupled tropospheric CH4, CO and OH atmospheric chemistry system has been provided, together with a formal quantification of the CH4 adjustment time [15]. CH4 perturbations have been tracked by following CH4 perturbation runs minus control runs for up to a decade [16,17]. However, these decadal long chemistry-transport model studies are relatively rare with many global chemistry-transport model studies using fixed CH4 and CO levels to avoid the need for long model runs. For example, in the Atmospheric Chemistry Coupled Climate Model Intercomparison Project (ACCMIP) study, thirteen out of the fifteen models used fixed CH4 levels [10].
2.2. TROPOS Model
In the first part of this study [10], the MC methodology was applied within a global Lagrangian chemistry-transport model (CTM), but, because of limited computer resources, a sufficiently large enough number of MC replicates could not be completed. There was not enough statistical power to complete a regression analysis linking model output uncertainty to model input parameter uncertainty. In the second part [11], the MC methodology was applied within the cut-down and fast for the running of the CTM TROPOSpheric O3 model, and up to 10,000 MC replicates were performed, allowing regression analyses to be performed, linking uncertainties in global burdens and turnovers to TROPOS input uncertainties. Here, the MC methodology is again applied within TROPOS but this time to investigate the uncertainties in the model estimated CH4 GWP. We begin with a brief description of the TROPOS model to which the MC uncertainty analysis techniques are applied.
TROPOS uses a zonally averaged (altitude–latitude) and coarse resolution approach by averaging along latitude circles and dividing the atmosphere from the Earth’s surface to an altitude of 24 km into 12 km × 2 km layers and 24 latitude bands. A full description of the off-line advection and dispersion processes in TROPOS is available elsewhere [18]. The chemical mechanism in the original TROPOS model was replaced with an extended chemistry scheme (Common Representative Intermediates CRI v2-R5) [19,20]. This chemical scheme implemented here included 51 species that take part in 157 thermal and photochemical reactions. Emissions for a wide-range of trace gases, including 11 organic compounds, arising from anthropogenic, vegetation, biomass burning, lightning, soils and ocean sources, were set up using the global totals from our previous uncertainty study [8]. The TROPOS model equations were integrated using an automatic, accurate numerical integrator (FACSIMILE; [21]). Trace gases were removed from the lowest TROPOS model layer by dry deposition using the same deposition velocity approach as in STOCHEM-MC.
The surface distribution of O3 in TROPOS was compared with the observations for the year 2000 taken from the International Global Atmospheric Chemistry (IGAC) Tropospheric Ozone Assessment Report (TOAR) review [22]. TROPOS was able to reproduce the relatively constant observed levels found in the Southern Hemisphere, the rise in the mid-latitudes of the Northern Hemisphere peaking around 40–50° N and the fall towards high latitudes. All of the observations fell within the 2-sigma confidence interval calculated from the 5000 MC replicates, except for two sets of observations from the US Pacific marine boundary layer and Cape Matutula, Samoa. This level of agreement between the surface observations and TROPOS was considered satisfactory for the present purpose of studying the uncertainties in the TROPOS estimates of the CH4 GWP.
2.3. Monte Carlo Uncertainty Analysis
As in the first two parts of this study [10,11], there were three steps in our Monte Carlo assessment of uncertainties. In the first step, the TROPOS model code was altered to accept a multiplier for each model input parameter, scaling the fixed ‘Best Estimate’ value. In the second step, the uncertain input range for each parameter was sampled quasi-randomly and input values were set for the initialisation of a given TROPOS run. In the third step, TROPOS was run repeatedly a large number, typically 5000, of times, with each run having a different quasi-random selection of input parameters. Each TROPOS run returned the tropospheric CH4 and O3 burdens, together with the tropospheric CH4 and O3 distributions.
A total of 183 TROPOS input parameters were selected for Monte Carlo uncertainty analysis. Of these, 5 represented physical parameters, 34 represented parameters controlling emissions processing, 116 represented thermal chemical kinetic parameters and the remaining 28, photochemical kinetic parameters. Details of these parameters are provided in our previous study [10,11].
For each input parameter, a 3-sigma confidence range was established based on multiplicative scaling by a factor of between 0.65 and 1.35. The probability distribution within that range was taken to be uniformly distributed on either side of the ‘Best Estimate’, that is to say, ‘top hat’ in shape. For temperature, the probability distribution was assumed to be Gaussian, and additive scaling of between −5 K and +5 K was employed. The details of the Monte Carlo methodology are laid out in some detail elsewhere [10,11].
Having set the TROPOS parameter values for the 183 input parameters that control the life cycle of CH4, O3 precursor emissions, O3 formation and sinks, each uncertainty range was sampled quasi-randomly for each TROPOS run. TROPOS was then run many thousands of times, with each particular set of inputs, and the output results were stored. Each different set of inputs generated different CH4 and O3 burdens, and tropospheric CH4 and O3 distributions. Because the meteorological data were the same in each of the Monte Carlo replicates, small differences in model results could be accurately discerned between the replicates. Each of the 5000 Monte Carlo replicates required two runs of TROPOS. In one run, the ‘base case’ run, the input data were chosen by Monte Carlo sampling. The input data for the second run, the ‘pulse case’ run, differed only from the ‘base case’ in having and emission of 149 Tg of CH4 during the first month of the twenty-year model experiment. The choice of the 149 Tg CH4 pulse size, representing a 3% increase in the CH4 burden, was arbitrary, being small enough to keep the system in its linear range but large enough to produce discernible differences. We demonstrate linearity in Section 3 below and discuss the choice of the number of Monte Carlo replicates below. The Monte Carlo methodology aimed at replacing a single ‘Best Estimate’ TROPOS model run with a set of many thousand TROPOS Monte Carlo replicates, each with slightly different quasi-randomly sampled input data.
Table 1 summarises the results of the Monte Carlo analysis of the uncertainties in the global burdens and atmospheric lifetimes of tropospheric O3, CO and CH4 in the ‘base case’ scenarios of the 5000 Monte Carlo replicates in this study. The TROPOS and STOCHEM-MC estimates are based on 10,000 and 98 Monte Carlo replicates, respectively, and are presented in Table 1 for comparison with our previous studies [10,11]. Also presented are the corresponding estimates from the 14 Atmospheric Chemistry Coupled Climate Model Intercomparison Project (ACCMIP) chemistry-climate models [23,24]. Within the 2-sigma confidence limits, none of the differences between this study and the TROPOS and STOCHEM-MC models were found to be statistically significant. The observed estimate [24] of the 1998 atmospheric CH4 burden of 4950 Tg is close to the present estimate of 4842 ± 2230 Tg, see Table 1. In the present study, the TROPOS and STOCHEM-MC estimates of the CH4 lifetime are in agreement with that of 11.2 ± 1.3 years based on observations [23]. The observed tropospheric O3 burden for 2004–2010 is 328 Tg based on the Aura Ozone Monitoring Instrument (OMI) and the Microwave Limb Sounder (MLS) measurements [25]. This value is close to that from the present and previous studies and is well within the two-sigma confidence intervals from STOCHEM-MC. The O3 turnovers from the present and previous studies were also in close agreement with that of 15.1 ± 3 Tg day−1 from the ACCMIP models [24].

Table 1.
Monte Carlo uncertainties estimated in this work and in the literature for the burdens and atmospheric lifetimes of tropospheric O3, CO and CH4.
This level of agreement between this study and the other sources quantifying the tropospheric burdens and lifetimes was considered satisfactory for the present purposes of estimating likely uncertainty bounds in the GWP for CH4. However, an interesting difference was noted between the present study and the TROPOS results in Table 1. It was noted that the two-sigma confidence interval was significantly wider for the present study than for our previous TROPOS and STOCHEM-MC results. This is surprising since both studies used the same model and the same methodology and assumptions for their respective Monte Carlo analyses. The only difference between the studies was the lengths of the model experiments, twenty years in the present case and only three years in TROPOS. Here, the extra length of the model experiments ensured that CH4 always came into steady state with the model inputs, a situation that was not realised in TROPOS or the other models in Table 1. The extra length of the model experiments meant that CH4 burdens came into a steady state, with even the least and greatest atmospheric lifetimes, widening the range of the CH4 burdens to a considerable degree beyond that achieved in TROPOS or the other models. Indeed, the range achieved in the CH4 burden is considerably beyond that observed, calling into question its validity. We will return to the significance of this unduly wide uncertainty range in the Discussion and Conclusions section, below.
To understand how the uncertainties in each of the 183 model input parameters contributed to the uncertainty in a particular model output, multiple linear regression techniques were applied to the output results from the Monte Carlo replicates. The basic data employed in these regression analyses were the outputs calculated in the TROPOS runs, for example, the GWP for CH4, and the values of the 183 input scaling parameters, p1–183, employed in each TROPOS run. Multiple linear regression was then used to express the outputs as functions of the input parameters using Equation (1) of the form:
where a1–a183 represent the slopes of the regression. The software package (PV-WAVE, Visual Numerics, Boulder, CO, USA) also returned the fraction of the variance in the GWP that was accounted for by all the p1–p183 taken together and by the parameters individually. Much of the analysis presented here uses the partial correlation coefficients, R1–183, of the GWP on the individual parameters, p1–p183.
GWP = a1p1 + a2p2 + a3p3+ … + a183p183
Multiple linear regression assumes that parameters are normally distributed and independent, and there are some issues with this approach when these assumptions are not always found to be the case. However, in this application, multiple regression is used merely as a screening tool to indicate in which broad area the main uncertainties in the CH4 GWP arise, whether in the emissions, atmospheric chemistry, meteorology or physical parameterisations. Multiple regression is a widely used approach in the literature to understand the uncertainties in chemistry-transport models [26,27,28].
An important issue to establish from the outset is the number of Monte Carlo replicates to be performed. Because the aim of the study is to attribute the uncertainties in TROPOS model outputs to model inputs, an adequate number of replicates is required to be able to conduct multiple linear regression. Since we have identified 183 uncertain model inputs, this fixes the minimum number of replicates. The more replicates we have over and above this minimum, the greater the statistical power in the multiple linear regression. A multiple linear regression was conducted using the tropospheric O3 burden as output, beginning with 500 Monte Carlo replicates and then moving up in stages. We found that up to 5000 replicates were required before partial correlation coefficients settled down to within ± 10% and ceased changing with increasing numbers of replicates. On this basis, the number of 5000 replicates was chosen in subsequent Monte Carlo analyses.
3. CH4 Pulse Experiments under Uncertainty
TROPOS was set up with the ‘Best Estimate’ (BE) model input parameters and two model experiments were initiated. The first had the BE model inputs and the second differed from it in having an additional emission pulse of CH4 amounting to 149 Tg. All other model inputs were identical. Both the ‘base case’ and ‘pulse case’ experiments were integrated for 20 years, with model outputs taken at the end of each month and year. The emission pulse was restricted to the latitude range from 30–56.4° N, the most important latitude range for anthropogenic emissions, and was emitted over the period 1–31 January of the first model year. This same procedure was followed with each of the many thousands of Monte Carlo replicates, with each having a ‘base case’ and a ‘pulse case’ and each a CH4 emission pulse of 149 Tg.
At each time point, the CH4 mixing ratios differed slightly between the pair of model experiments because of the presence of the additional CH4 in the ‘pulse case’ experiment. Figure 1 presents the difference in the global mean CH4 mixing ratios between the pair of ‘Best Estimate’ model experiments over the 20-year experiment. The 149 Tg emission pulse initially caused an increase in the global mean CH4 mixing ratio of 60 ppb, as shown in Figure 1. This increase would be slightly different in each of the Monte Carlo replicates. This excess CH4 began to decay away and this decay persisted throughout the model experiment. The decay could be accurately quantified and was found initially to be about 10% per year, dropping to about 6% per year after about 20 months. By the end of the 20-year model experiment, the excess CH4 had decayed to 16 ppb, as shown in Figure 1. Averaged over the 3rd and subsequent years, the excess CH4 decayed with an e-folding timescale of 15.7 years in the ‘Best Estimate’ run and 17.5 ± 9.7 years in the Monte Carlo replicates, where the quoted uncertainties are two-sigma confidence limits, here and elsewhere in this paper. This e-folding timescale is significantly longer than the atmospheric lifetime of CH4 in the ‘base case’ experiment, which was found to be 10.9 years in the BE run (9.5 ± 5.3 in the M C replicates). The e-folding time constant corresponds to the adjustment timescale for CH4 and is 1.45 in the BE (1.87 ± 0.6 in the MC) times longer than the atmospheric lifetime. On this basis, an FF of −0.31 (−0.45 ± 0.17 in the MC) was estimated, which partly overlapped but covered a much wider range than that reported previously [4]. The reason for the wider range is discussed later but it stems from the twenty-year model experimental time, which has allowed CH4 to come into a steady state with each set of input data and thus extending the range of CH4 burdens and lifetimes achieved.
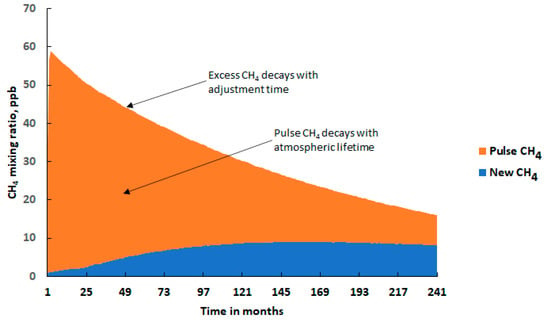
Figure 1.
Time development of the excess global mean CH4 mixing ratio following the addition of a 149 Tg CH4 emission pulse, showing the ‘excess’ CH4 = ‘pulse’ CH4 + ‘new’ CH4 as the upper curve, the pulse CH4 (red area) and new CH4 (blue area), based on a similar figure taken from ref. [13].
The excess CH4 decayed with an apparently longer timescale than the atmospheric lifetime because the emission pulse had caused a slight depletion in the tropospheric hydroxyl radical (OH) distribution, leading to a reduction in the OH + CH4 reaction flux. As a result of the diminution in the CH4 removal rate, additional CH4 accumulated in the model troposphere. This additional CH4 is shown as ‘new CH4’ in blue in Figure 1. It grew steadily during the first few years, then reached a maximum after 11 years or so and then begun to decline throughout the remainder of the experiment. The ‘pulse CH4’ decayed with the atmospheric lifetime, LT, and is shown in red in Figure 1, whereas the ‘excess CH4’ = ‘pulse CH4’ + ‘new CH4’, decayed more slowly with the adjustment timescale, AT. The fraction of the ‘excess’ CH4 that was ‘new’ was found to be 0.31 (0.45 ± 0.17).
The behaviour of CH4 in each CH4 ‘pulse case’ experiment was thus defined by three quantities:
- The time-integrated excess CH4 mixing ratio in ppb years over the 20-year model experiment: 649 ppb year (668 ± 162 ppb year);
- The excess CH4 mixing ratio at the end of the 20-year model experiment: 16 ppb (17.6 ± 11 ppb);
- The CH4 adjustment time: 15.7 years (17.5 ± 9.7 years).
To demonstrate linearity, the ‘Best Estimate’ ‘pulse case’ experiment was repeated with emission pulses decreasing in 10% steps, down to 10% of the original 149 Tg, see Table 2. Time-integrated excess CH4 mixing ratios and excess CH4 mixing ratios at the end of the 20-year model experiments, decreased exactly in 10% steps, down to levels that were one tenth of their original values. However, the adjustment times did not change and remained exactly the same as in the original experiment. Whereas the excess CH4 mixing ratios demonstrated accurate linearity, the CH4 adjustment times were completely independent of pulse size.

Table 2.
Time-integrated radiative forcing (rf) over a 100-year time horizon for different-sized CH4 emission pulses, together with the estimated global warming potential (GWP) with the ‘Best Estimate’ model input.
The additional CH4 in the ‘pulse case’ experiment also drove an increase in tropospheric O3 production relative to the base case. This increase in O3 production led to the build-up of an excess in tropospheric O3 as measured as an excess in the global mean O3 columns between the ‘pulse case’ and ‘base case’ in Dobson Units (DU). The time behaviour of excess O3 in the ‘Best Estimate’ pulse case with 149 Tg of CH4 is illustrated in Figure 2. The presence of a distinct seasonal cycle was evident in the excess O3, with a summertime maximum and a wintertime minimum. This figure also presents the excess CH4 for the same 149 Tg CH4 pulse from Figure 1. After an initial sharp rise, excess O3 levels decayed away with almost the same e-folding time constant as CH4 and hence the two traces in Figure 2 almost superimposed over one another. In fact, the O3 adjustment timescale was found to be 15.3 years, which was slightly shorter than the CH4 adjustment time of 15.7 years in this experiment.
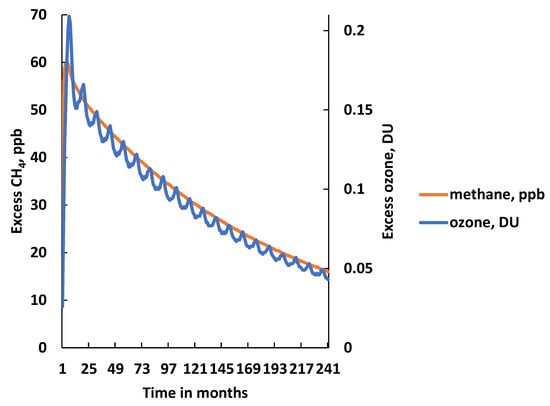
Figure 2.
Time development of the excess global mean CH4 mixing ratio and the excess global mean O3 column in Dobson Units following the addition of a 149 Tg CH4 emission pulse.
As with the CH4 response, the O3 response to the CH4 pulse could be characterised with three quantities:
- The time-integrated excess O3 in DU years over the 20-year model experiment: 1.85 DU year in the BE run (1.90 ± 0.75 DU year in the MC replicates);
- The excess O3 in DU at the end of the 20-year model experiment: 0.043 DU in the BE run (0.045 ± 0.019 DU in the MC replicates);
- The O3 adjustment time: 15.3 year in the BE run (15.7 ± 4.6 year in the MC replicates).
The time-integrated excess O3 and the excess O3 at the end of the 20-year model experiment were exactly linear in CH4 pulse size in the ‘Best estimate’ experiment over the range from 149 to 14.9 Tg, see Table 2. The O3 adjustment timescales were, however, completely independent of the CH4 pulse size, remaining constant at 15.25 years, with deviations inside ± 1%.
4. Estimation of the Global Warming Potential for CH4 under Uncertainty
CH4 acts as a radiatively active trace gas by virtue of its infrared absorption spectrum. However, it also reacts in the troposphere to produce O3, another important radiatively active trace gas, and so it is also an indirect radiatively active trace gas. In this section, an estimate is made of the global warming potential (GWP) of CH4 based on the direct and indirect radiative forcing (rf) contributions.
The GWP of CH4 is defined here as the ratio of the time-integrated radiative forcing resulting from the emission of 1 kg of the trace gas relative to that of 1 kg of CO2 over a time horizon that is taken here to be 100 years [7]. That is to say:
where ai is the instantaneous radiative forcing due to a unit increase in the mixing ratio of trace gas, i, and ci is the mixing ratio of the trace gas, i, remaining after time t after its release and T is the number of years over which the calculation is performed. For CH4, the numerator has to be calculated from the sum of the impacts of CH4 pulses on its direct radiative forcing and on its indirect radiative forcing from tropospheric O3.
To complete the calculation of the GWP of CH4, we use the time development of CH4 and tropospheric O3 from each of the 5000 MC replicates, the formula for the GWP in expression (2) and the radiative efficiency parameters aCH4 and aO3. We took aCH4 as 3.63 × 10−4 Wm−2 ppb−1 as the best estimate literature value from Appendix 8.A in [1], which gave a peak radiative forcing of 21.8 mWm–2 in the ‘Best Estimate’ (BE) model experiment for a CH4 emission pulse of 149 Tg. The time-integrated CH4 radiative forcing in the 20-year model experiment was found to be 235 mWm−2 year in the BE run (242 ± 59 mWm−2 year in the MC replicates). To complete the GWP calculation, the time-integrated CH4 radiative forcing is required over the complete 100-year time horizon so the plot in Figure 1 needed extending over the remaining 80 years. This time extension was not possible with TROPOS because of the long run times involved. However, the CH4 response could be extended to the end of the time horizon using the concept of trace gas adjustment timescales. That is to say, it was assumed that the excess CH4 continued to decay exponentially with the CH4 adjustment timescale throughout year 21 and subsequently through to the end of year 99. Both the excess CH4 at the end of the 20-year model experiment, hence its radiative forcing, and the CH4 adjustment time were well defined quantities. The time extension added a further time-integrated excess CH4 of 250 ppb year in the BE run (333 ± 376 ppb year in the MC replicates) and 90.9 mWm−2 year in the BE run (121 ± 136 mWm−2 year in the MC replicates) of radiative forcing for a 149 Tg CH4 pulse. Altogether, the time-integrated radiative forcing from CH4 over the entire 100-year time horizon amounted to 327 mWm−2 year in the BE run (363 ± 195 mWm−2 year in the MC replicates).
The estimation of the radiative forcing consequences of changes in the tropospheric distribution of O3 is not straightforward [29]. A description of a methodology is available that starts by characterising O3 column amounts on a 5° latitude × 5° longitude grid in Dobson Units (DU) and uses a complex radiation code to relate these column amounts to radiative forcing [29]. Using this approach [29], gridded estimates of radiative forcing per DU were employed to estimate the radiative forcing consequences of the changes in tropospheric O3 column amounts resulting from the CH4 emission pulses. In response to a 149 Tg CH4 emission pulse, the excess O3 response increased to a maximum of 0.21 DU in the ‘Best Estimate’ model experiment before decaying away with the O3 adjustment timescale. The time-integrated excess O3 over the 20-year model experiment amounted to 1.85 DU year in the BE run (1.90 ± 0.75 DU year in the MC replicates) or 62.5 mWm−2 year in the BE (64 ± 25 mWm−2 year in the MC replicates). Extension to the 100-year time horizon using the O3 adjustment timescale amounted to an additional 22.2 mWm−2 year in the BE run (24.0 ± 14 mWm−2 year in the MC replicates). The total radiative forcing from the excess O3 was therefore 84.7 mWm−2 year in the BE run (88.2 ± 34 mWm−2 year in the MC replicates) for a 149 Tg CH4 emission pulse.
To calculate the CH4 GWP, the numerator of expression (2) was formed by adding together the CH4 and tropospheric O3 forcing terms to make 411 mWm−2 year in the ‘Best Estimate’ model experiment, see Table 2, and 451 ± 190 mWm−2 year in the Monte Carlo replicates. Dividing this total radiative forcing by the pulse size of 149 Tg and dividing by the denominator of Equation (2), which was taken to be 0.0917 mWm−2 year from Appendix A.8 in [1], gave 30.1 in the BE run (33 ± 14 in the MC replicates) over a 100-year time horizon for 1 Tg emission pulses.
5. Origins of the Uncertainty in the GWP for CH4
Having quantified the GWP for CH4 and its 2-sigma confidence limits, the next step is to ascertain which are the most important input uncertainties that drive the uncertainties in the GWP. In Figure 3, the partial correlation coefficients are presented for those parameters that gave R values in the range −0.1 > R > +0.1. Also shown are analogous plots for additional outputs that influenced strongly the estimated GWPs, including the burdens of CH4 and O3 and the adjustment timescales for CH4 and O3. Altogether 22 input parameters contributed most to output uncertainty and these comprised 12 chemical kinetic rate coefficients, six emission sources and four meteorological and physical input parameters. These most important parameters are listed in Table 3.
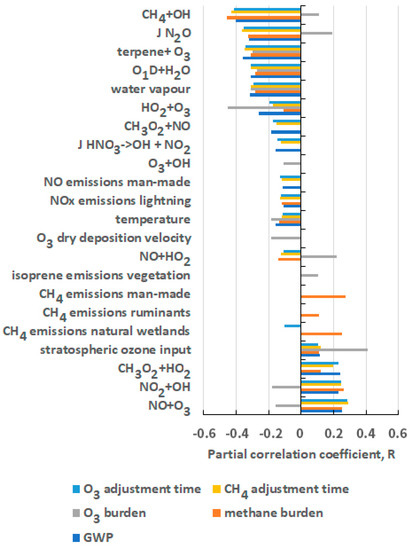
Figure 3.
Partial correlation coefficients from the multiple linear regression analyses of the adjustment times, burdens and the resulting GWP for CH4 on the 183 uncertain model input parameters.

Table 3.
Details of the most important input parameters contributing to the uncertainty in the burdens of O3 and CH4, the adjustment times for CH4 and O3 and the GWP for CH4.
The twelve most important chemical kinetic rate coefficients include several chemical processes that play a crucial role in establishing the fast, photochemical balance of the troposphere. These processes include CH4 + OH, O1D + H2O, HO2 + O3, CH3O2 + NO, O3 + OH, HO2 + O3, NO + HO2, NO2 + OH and CH3O2 + HO2. In addition, the NO + O3 reaction controls the ratio of NO to NO2, which in turn controls the relative rates of HO2 to OH recycling versus the loss of OH. The terpene + O3 reaction, together with the O3 deposition velocity, controls the lifetime of O3 close to the surface over forested areas. Two photolysis processes are listed in Table 3: the photolysis rate coefficient (J) for nitric acid and that for N2O in the stratosphere. The former controls the long-range transport of nitric acid and its renoxification back to NOx and the former controls the altitude profile of NOx in the lower stratosphere, the NOx-catalysed destruction of O3 there and hence the stratosphere–troposphere exchange flux of O3 into the troposphere.
Of all of the twelve chemical processes in Figure 3 and Table 3, the OH + CH4 reaction clearly dominates as a source of uncertainty in the CH4 GWP and its drivers. An important contribution to the overall uncertainty in this rate coefficient comes from the uncertainty in its temperature coefficient, which is one of the largest of all the processes in the fast, photochemical balance of the troposphere.
The six emission sources and sectors listed in Table 3 involve three trace gases: NOx, CH4 and isoprene. Emissions of NOx and CH4 provide important drivers of the fast photochemistry of the troposphere through the formation of CH4 oxidation products (CO, formaldehyde and methyl peroxy radicals) and the control they influence on the tropospheric distribution of CH4. Isoprene emissions from vegetation act as an important source of CO, HO2 and formaldehyde.
Uncertainty due to meteorological and physical parameters is strongly influenced by the uncertainties due to water vapour and temperature biases and to the parameters that control stratosphere–troposphere exchange and the deposition of O3, as shown in Table 3.
6. Discussion and Conclusions
In Section 2.2, above, it was noted that the atmospheric lifetime of CH4 from the 5000 MC replicates (9.5 ± 5.4 years) had a two-sigma confidence range that was significantly wider than that reported in the observations [23] (11.2 ± 1.3 years). That is to say, the two-sigma confidence range of the MC replicates was over four-fold wider than that in the observations. It was concluded that the two-sigma confidence range in the MC analysis was unrealistically wide and hence some of the 5000 input parameter combinations in the MC analysis may have been unrealistic. Further work is planned to investigate the reasons why some input parameter combinations appeared unrealistic and whether it would be possible to reduce their assumed uncertainty ranges accordingly.
If the MC analysis was constrained by the observed atmospheric lifetime for CH4, then 1249 MC replicates (about one quarter of the total) would be retained and 3751 (about three quarters of the total) would be rejected. The GWP for CH4 calculated with only the retained replicates would then be 37 ± 10, compared with 33 ± 14 based on all 5000 MC replicates. The rejection of the replicates with infeasible CH4 lifetimes caused a 12% or so increase in the GWP and a somewhat larger 30% decrease in the 95% confidence interval. This value of 37 ± 10 is outside the range of 28–34 given by Table 8.7 in [1], where the range addresses the issue of the non-inclusion (28) or inclusion (34) of climate-carbon feedbacks. For the purposes of this comparison, we take the non-inclusion value and conclude that our value obtained with the feasible MC input data overestimates the IPCC literature value [1] by about 24% and is considerably higher than our previously reported 23.2 [17] from nearly 20 years ago.
The atmospheric lifetime constraint was then used to adjust the weightings of the replicates in the multiple linear regression analysis of the uncertainties in the CH4 GWP. Those MC replicates that gave plausible CH4 lifetimes in their base runs were given a weighting of unity and those that did not were given a weighting factor that was several orders of magnitude smaller. With the constraint applied and the weightings adjusted, the partial correlation coefficients for the 183 input parameters shifted significantly relative to those without the constraint, see Figure 4. A significant increase was found in the partial correlation coefficient due to the CH4 + OH rate coefficient. With the constraint applied, the fraction of the uncertainty in the GWP for CH4 due to the CH4 + OH rate coefficient increased from 16% to 67%. There was a compensating decrease in the fraction of the uncertainty due to the rate coefficients for terpene + O3, O1D + H2O, NO2 + OH and the NO + O3 reactions. Uncertainties due to the photolysis rate of N2O in the stratosphere, temperature and water vapour biases and stratospheric O3 input also reduced dramatically. Overall uncertainty was reduced significantly by the application of the CH4 lifetime constraint and the only significant contributions remaining were from the CH4 + OH, CH3O2 + HO2, CH3O2 + NO and the terpene + O3 rate coefficients, see Figure 4.
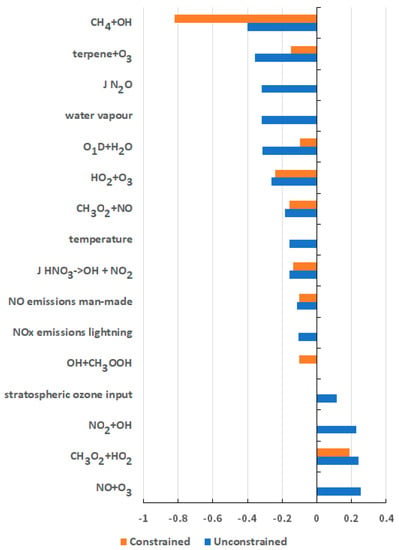
Figure 4.
Partial correlation coefficients from the multiple linear regression analyses of the GWP for CH4 on the 183 uncertain model input parameters in the unconstrained Monte Carlo replicates (blue bars) and those with CH4 lifetimes constrained in the range 11.2 ± 1.3 years (red bars).
Our recommendation for the CH4 GWP is therefore 37 ± 10 over a 100-year time horizon and means that the time-integrated radiative forcing from the release of 1 Tg of CH4 over a 100-year time horizon is equivalent to that from 37 ± 10 Tg of CO2. We also conclude that the principal area of uncertainty in this recommended GWP arises in the chemical kinetic rate coefficient input data for the five highlighted chemical processes. Additional research efforts focused on reducing the uncertainties in these rate coefficients may potentially reduce the uncertainties in the estimated CH4 GWP.
Funding
This Monte Carlo uncertainty analysis received no external funding.
Acknowledgments
R.G.D. thanks Professor David Stevenson, University of Edinburgh for help with the estimation of the radiative forcing consequences of the changes in the distribution of tropospheric ozone.
Conflicts of Interest
The author declares no conflict of interest.
References
- IPCC. Climate Change 2018: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- United Nations Framework Convention on Climate Change. United Nations Framework Convention on Climate Change; UNFCCC: New York, NY, USA, 1992. [Google Scholar]
- Etheridge, D.M.; Pearman, G.I.; Fraser, P.J. Changes in tropospheric methane between 1841 and 1978 from a high accumulation-rate Antarctic ice core. Tellus B 1992, 44, 282–294. [Google Scholar] [CrossRef]
- IPCC. Climate Change 1994. In Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Turner, A.J.; Frankenburg, C.; Wennberg, P.O.; Jacob, D.J. Ambiguity in the causes for decadal trends in atmospheric methane and hydroxyl. Proc. Natl. Acad. Sci. USA 2017, 114, 5367–5372. [Google Scholar] [CrossRef] [PubMed]
- Rigby, M.; Montzka, S.A.; Prinn, R.G.; White, J.W.; Young, D.; O’Doherty, S.; Lunt, M.F.; Ganesan, A.L.; Manning, A.J.; Simmonds, P.G.; et al. Role of atmospheric oxidation in recent methane growth. Proc. Natl. Acad. Sci. USA 2017, 114, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change: The IPCC Scientific Assessment; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Shine, K.P. The global warming potential—The need for an interdisciplinary retrial. Clim. Chang. 2009, 96, 467–472. [Google Scholar] [CrossRef]
- Shine, K.P.; Fuglestvedt, J.S.; Hailemariam, K.; Stuber, N. Alternatives to the global warming potential for comparing climate impacts of emissions of greenhouse gases. Clim. Chang. 2005, 68, 281–302. [Google Scholar] [CrossRef]
- Derwent, R.G.; Parrish, D.D.; Galbally, I.E.; Stevenson, D.S.; Doherty, R.M.; Naik, V.; Young, P.J. Uncertainties in models of tropospheric ozone based on Monte Carlo analysis: Tropospheric ozone burdens, atmospheric lifetimes and surface distributions. Atmos. Environ. 2018, 180, 93–102. [Google Scholar] [CrossRef]
- Derwent, R.G. Monte Carlo analyses of the uncertainties in the predictions from global tropospheric ozone models: Tropospheric burdens and seasonal cycles. Atmos. Environ. 2020, 213, 117545. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. Note on concepts of age and transit-time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Prather, M.J. Lifetimes and eigenstates in atmospheric chemistry. Geophys. Res. Lett. 1994, 21, 801–804. [Google Scholar] [CrossRef]
- Isaksen, I.S.A.; Hov, O. Calculation of trends in tropospheric O3, OH, CH4 and NOx. Tellus B 1987, 39, 271–285. [Google Scholar] [CrossRef][Green Version]
- Prather, M.J. Lifetimes and time scales in atmospheric chemistry. Phil. Trans. R. Soc. A 2007, 365, 1705–1726. [Google Scholar] [CrossRef] [PubMed]
- Wild, O.; Prather, M.J. Excitation of the primary tropospheric chemical mode in a global three-dimensional model. J. Geophys. Res. 2000, 105, 24647–24660. [Google Scholar] [CrossRef]
- Derwent, R.G.; Collins, W.J.; Johnson, C.E.; Stevenson, D.S. Transient behaviour of tropospheric ozone precursors in a global 3-D CTM and their indirect greenhouse effects. Clim. Chang. 2001, 49, 463–487. [Google Scholar] [CrossRef]
- Hough, A.M.; Derwent, R.G. Changes in the global concentration of tropospheric ozone due to human activities. Nature 1990, 344, 645–648. [Google Scholar] [CrossRef]
- Utembe, S.R.; Watson, L.A.; Shallcross, D.E.; Jenkin, M.E. A Common Representative Intermediates (CRI) mechanism for VOC degradation. Part 3: Development of a secondary organic aerosol module. Atmos. Environ. 2009, 43, 1982–1990. [Google Scholar] [CrossRef]
- Utembe, S.R.; Cooke, M.C.; Archibald, A.T.; Shallcross, D.E.; Derwent, R.G.; Jenkin, M.E. Simulating secondary organic aerosol in a 3-D Lagrangian chemistry transport model using the reduced Common Representative Intermediates mechanism (CRI v2-R5). Atmos. Environ. 2011, 45, 1604–1614. [Google Scholar] [CrossRef]
- Curtis, A.R.; Sweetenham, W.P. FACSIMILE Release H User’s Manual; AERE Report R11771; H.M. Stationery Office: London, UK, 1987. [Google Scholar]
- Cooper, O.R.; Parrish, D.D.; Ziemke, J.; Balashov, N.V.; Cupeiro, M.; Galbally, I.E.; Gilge, S.; Horowitz, L.; Jensen, N.R.; Lamarque, J.-F.; et al. Global distribution and trends of tropospheric ozone: An observation-based review. Elem. Sci. Anthr. 2014, 2, 000029. [Google Scholar] [CrossRef]
- Naik, V.; Voulgarakis, A.; Fiore, A.M.; Horowitz, L.W.; Lamarque, J.F.; Lin, M.; Prather, M.J.; Young, P.J.; Bergmann, D.; Cameron-Smith, P.J.; et al. Pre-industrial to present-day changes in tropospheric hydroxyl and methane lifetime from the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP). Atmos. Chem. Phys. 2013, 13, 5277–5298. [Google Scholar] [CrossRef]
- Young, P.J.; Archibald, A.T.; Bowman, K.W.; Lamarque, J.F.; Naik, V.; Stevenson, D.S.; Tilmes, S.; Voulgarakis, A.; Wild, O.; Bergmann, D.; et al. Pre-industrial to end 21st century projections of tropospheric ozone from the Atmospheric Chemistry and Climate Model Intercomparison Project. Atmos. Chem. Phys. 2013, 13, 2063–2090. [Google Scholar] [CrossRef]
- Ziemke, J.R.; Chandra, S.; Labow, G.J.; Bhartia, P.K.; Froidevaux, L.; Witte, J.C. A global climatology of tropospheric and stratospheric ozone derived from Aura OMI and MLS measurements. Atmos. Chem. Phys. 2011, 11, 9237–9251. [Google Scholar] [CrossRef]
- Revell, L.E.; Stenke, A.; Tummon, F.; Feinberg, A.; Rozanov, E.; Peter, T.; Abraham, N.L.; Akiyoshi, H.; Archibald, A.T.; Butchart, N.; et al. Tropospheric ozone in CCMI models and Gaussian process emulation to understand biases in the SOCLv3 chemistry-climate model. Atmos. Chem. Phys. 2018, 18, 16155–16172. [Google Scholar] [CrossRef]
- Newsome, B.; Evans, M. Impact of uncertainties in inorganic chemical rate constants on tropospheric composition and ozone radiative forcing. Atmos. Chem. Phys. 2017, 17, 14333–14352. [Google Scholar] [CrossRef]
- Wild, O.; Voulgarakis, A.; O’Connor, F.; Lamarque, J.F.; Ryan, E.; Lee, L. Global sensitivity analysis of chemistry-climate model budgets of tropospheric ozone and OH: Exploring model diversity. Atmos. Chem. Phys. 2020. [Google Scholar] [CrossRef]
- Stevenson, D.S.; Young, P.J.; Naik, V.; Lamarque, J.F.; Shindell, D.T.; Voulgarakis, A.; Skeie, R.B.; Dalsoren, S.B.; Myhre, G.; Berntsen, T.K.; et al. Tropospheric ozone changes, radiative forcing and attribution to emissions in the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP). Atmos. Chem. Phys. 2013, 13, 3063–3085. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).