Abstract
The measurement of deposited aerosol particles in the respiratory tract via in vivo and in vitro approaches is difficult due to those approaches’ many limitations. In order to overcome these obstacles, different computational models have been developed to predict the deposition of aerosol particles inside the lung. Recently, some remarkable models have been developed based on conventional semi-empirical models, one-dimensional whole-lung models, three-dimensional computational fluid dynamics models, and artificial neural networks for the prediction of aerosol-particle deposition with a high accuracy relative to experimental data. However, these models still have some disadvantages that should be overcome shortly. In this paper, we take a closer look at the current research trends as well as the future directions of this research area.
1. Introduction
The lung is an organ that is continuously exposed to environmental agents [1]. As such, it can be negatively affected by toxic agents that are prevalent in the atmosphere [2]. Millions of people around the world suffer from related diseases such as chronic obstructive pulmonary disease (COPD) and asthma [3].
An aerosol is solid or particulate matter suspension in air. Aerosols are derived from nature (volcanos, dust storms, and forest fires) or human activities (cooking and fuel-burning) [4]. Particulate matter (PM) is one of the major pollutants that has harmful effects on human health [5]. The International Agency for Research on Cancer (IARC), to take one example, has classified PM as carcinogenic to humans (Group 1, IARC) [6,7]. Pope and Dockery (2006) indicated that an increase of PM2.5 of around 10 μg/m3 could lead to a 1% mortality increase [8]. According to the WHO (2013), daily mortality is expected to increase to about 0.2%–0.6% per 10 µg/m3 of PM10, while the exposure of PM2.5 could lead to an increase of cardiopulmonary mortality by 6%–13% per 10 μg/m3. According to the European air quality standards for PM concentrations (Directives 1999/30/EC and 2008/50/EC; EC: European Commission), the annual limit values are 25 μg/m3 for PM2.5 and 40 μg/m3 for PM10. The 24-h limit for PM is set as 50 μg/m3 [9]. For the level of arsenic, cadmium, and lead in particulate matter (PMAs, PMCd, and PMPb), the annual limit values are 6, 5, and 500 ng/m3, respectively (Directives 1999/30/EC and 2008/50/EC) [9]. Inhaled drug therapy can be a useful option against many lung diseases such as asthma or COPD. The efficiency of pharmaceutical aerosols depends on their deposition in the airways, especially the upper generations [10]. The estimation of aerosol transportation and deposition in the human lung can therefore indicate strategies for the prevention or alleviation of health effects from inhaled toxic particles or new drug-aerosol delivery approaches that can overcome the limitations of inhalers [11]. Atmospheric-aerosol deposition in the human respiratory tract (RT) can be directly measured by monitoring and comparing inhaled and exhaled particle concentrations. However, due to experimental limitations, the regional dose in the respiratory system is hard to measure experimentally but can be predicted by the application of different mathematical models. Suitable mathematical models are those that show a reasonable correlation between results obtained from modeling and empirical measurements [12]. Computational models generally consist of three elements: (1) a mathematical formulation that describes the relevant physical and chemical processes, (2) the setting of specific initial and boundary conditions, and (3) the solving of equations for the specified geometry. The accuracy of a computational model depends on the extent to which these elements are realistic. Additionally, regardless of the computational model that is applied, four types of input data are required: (1) lung morphometry, (2) breathing pattern, (3) particle properties, and (4) gas/vapor properties (Figure 1) [4]. The effects of these input data to the computational models were introduced in the review of Rostami (2009) and Hussain et al. (2011) [4,13]. In this review, we only present the advances of lung geometry models due to their strong relations to the accuracies of the computational models [4,13].
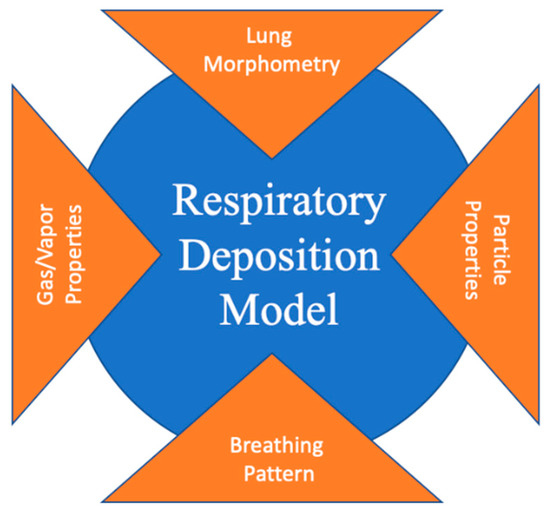
Figure 1.
Four types of input data required for a computational aerosol deposition model [4].
The conventional models in the literature for the prediction of aerosol particles in the human respiratory tract are semi-empirical, one-dimensional whole-lung, and three-dimensional computational fluid dynamics (CFD) models. Novel approaches, such as those based on artificial neural networks, also have been tried. Each of these models has both advantages and disadvantages that are discussed in this review paper. The recent trends of this research area are also addressed.
2. Aerosol Deposition Mechanisms
According to Hinds (1999), aerosol particles can be deposited on the surface of the lung via six directed mechanisms: (1) impaction, (2) sedimentation, (3) interception, (4) diffusion, (5) electrostatic precipitation, and (6) convection (Figure 2) [14]. These mechanisms were well-described in a review paper of Rostami (2009) [4]. Aerosol particles also can be deposited on the lung via an indirect mechanism by which aerosol particles are transferred from the tidal air to the residential air and consequently deposited on the lung via intrinsic particle motion [4]. Overall, as particle size increases, impaction, sedimentation, and interception become prominent while diffusion and convection become less significant [4].

Figure 2.
Deposition mechanisms in the respiratory tract (RT) [4].
The Stokes number (Skt) is a dimensionless number that is used to characterize the behavior of particles in a fluid flow. The following equation generates the Stokes number:
or
where τ is the relaxation time, Uo is the mean velocity of the fluid in the lung airway the particle is in, R is the diameter of the lung airway the particle is in, and Sp is the stopping distance. The relaxation time and stopping distance are known to be related to the Stokes number. The influence of the Stokes number on the aerosol deposition mechanisms was discussed in the recently published book chapter that was written by Finley (2019) [15].
2.1. Impaction
For impaction, the stopping distance is the distance traveled by a particle before a considerable change in direction:
where Vp is the particle initial velocity and τ is the relaxation time, which is calculated as:
where ρp is the particle density, d is the particle diameter, Cc is the slip correction factor, and η is the air viscosity.
The stopping distance becomes the Stokes number when it is divided into airway diameter [13]:
where R is the airway diameter.
2.2. Sedimentation
For sedimentation, the settling distance is defined as:
with the terminal velocity (Vt) given by:
where g is the gravitational acceleration and τ is the relaxation time.
The deposition probability of aerosol particles via the sedimentation mechanism can be calculated as:
where R is the airway diameter.
2.3. Diffusion
Diffusion length is applied to the diffusion mechanism as follows:
where t is the residence time and D is the diffusion coefficient of the aerosol particles that is given by the Stokes–Einstein equation:
where k and T are the Boltzmann constant and absolute temperature, respectively.
The deposition probability of aerosol particles via the diffusion mechanism can be calculated as:
where R is the airway diameter.
Based on the above equations, particle properties, and airway dimensions as given by Baron et al. (1993) and Weibel (1963) [16,17], the deposition probability of aerosol particles via impaction, sedimentation, and diffusion for each airway generation can easily be calculated (Table S1) [4].
Additionally, the PM deposited in the human respiratory tract depends on different factors such as PM exposure concentration, PM physicochemical characteristics, exposure duration, and exposed-subject characteristics (age, gender, state of health, lung morphology, and breathing parameters) [12].
The deposition of PM in the RT is strongly dependent on particle size and chemical composition. For example, coarse particles (PM2.5–10) are mainly deposited in the extrathoracic (ET) region, while fine particles (PM2.5) are deposited more in-depth in the alveolar (AL) region [13,18,19]. The particles that are deposited in the ET region might be swallowed and transferred to the gastrointestinal (GI) tract, while those deposited in the AL region might remain in the lungs [9]. Regarding chemical composition, PMPb can lead to renal damage, neurological dysfunction, and anemia [20]; PMAs and PMCd can lead to carcinogenic effects [21]; and PMMn can induce severe neurotoxic impairments [22].
3. Lung-Geometry Models
The lung airway structure begins with the ET region, followed by the larynx, trachea, main bronchi, then down to the gas-exchange tissue, and it ends with the alveoli. From the upper down to the lower airways, the number of airways is mainly multiplied via dichotomous branching patterns [23]. The dimensions of airways are reduced with each bifurcation [13].
Understanding lung geometry helps clinicians to prescribe pharmaceutical aerosols and optimize inhaler devices. Weibel (1963) numbered the airways of the RT from trachea as 0 to the terminal alveoli as 23 (Figure S1) [16]. The portion between the two bifurcations of the airways is defined as one generation. More realistic lung-geometry models can be developed from real images of airway bifurcations [24,25,26,27]. Magnetic resonance imaging (MRI) [28] and positron emission tomography (PET) [29] are two standard techniques for the three-dimensional imaging of the lung. Though these techniques allow for the identification of the real dimensions, their main limitations, arising from insufficient spatial and temporal resolutions, necessitate the introduction of contrast agents [30].
There has been some progress in lung model reconstruction. Recently, Shang et al. (2019) developed a realistic lung airway model from computed tomography (CT) images [2]. This model covers both subject-specific upper and lower airways, starts from the nasal and oral openings, and ends at the terminal bronchioles (15th generation) (Figure 3). It consists of 128 outlets within the respiratory conducting zone. Based on subject-specific airways, topological information is extracted, and a digital signal reference model that has strong asymmetry and multifractal properties can be obtained. Inhalation flow rates of 18 and 50 L/min, as resting and light exercise inhalation modes, respectively, were applied to evaluate the model. The regional airflow with axial velocity and secondary flow vortices were extracted. The results showed that while the secondary flow currents could be observed in the larynx–trachea segment as well as the left main bronchus, a smoother airflow with no secondary flow currents could be obtained for the terminal conducting airway in the right lower lobe [2]. Understanding of secondary flows could help elucidate the toxicology of PM and, thereby, help researchers to optimize pharmaceutical aerosol drug delivery [2]. Another remarkable piece of research about lung morphology generation could be found in a study by Kikaota et al. (2013) [31]. They introduced free software (including Lung4Cer, PL4cer, and CFD4cer) to generate 4D lung models (3D + time). The models generated from their software are beneficial for the study of lung anatomy, physiology, and pathophysiology [31]. Some progress in lung model generation can also be found in the works of Wall et al. [32,33]. For example, they generated lung morphology from computed tomography data composed of 60,143 conducting airways, 30,072 acini, and 140,135 inter-acinar linkers. The 0D inter-acinar linker elements were used to describe the relationship between neighboring alveoli. This model could be used to present both healthy and diseased lung geometries [32].

Figure 3.
Human lung airway model from Shang et al. (2019). Reprinted with permission from [2]. Copyright 2019, Elsevier.
Different lung-geometry models might return different predicted results. For example, Kim et al. (2019) compared different airway models based on CFD for air flows and particle deposition under various inspiratory conditions [34]. The investigated models included classic Weibei airways (WA) and two Kitaoka models that go down from the trachea to the 7th (KG7) and 11th generations (KG11) (Figure S2). The WA model of generation 3 to generation 6 was formulated to describe the detailed upper tracheobronchial (TB) regions of the RT. It consists of 8 outlets with a 30o airway bending angle [35,36]. In contrast, the realistic lung airway model of Kitaoka et al. (2011) applied four algorithms to build a 3D airway tree, a 3D pulmonary acinus, a 4D alveolar system, and 4D lung shape [37]. Both similarities and differences were shown between these models. An inspiratory airflow was symmetric in the WA model, while it was non-symmetric in the Kikaota model. The Kikaota model exhibited a more complicated particle deposition pattern with higher efficiency of particle deposition compared with the WA model. In contrast, the effects of the flow rate for both models were found to be the same. Additionally, there were small differences between KG7 and KG11 in the cases of inspiratory air velocity and particle deposition efficiency. Kim et al. (2019) suggested that KG7 is a sufficient model for the derivation of particle deposition patterns that closely match reality [34].
4. Semi-Empirical Models
4.1. ICRP Model
4.1.1. Introduction
In 1996, the International Commission on Radiological Protection (ICRP) introduced the ICRP66 model for dust deposition prediction and clearance in the RT. In this model, the human respiratory tract was represented as a series of anatomical compartments through which aerosols pass during the inhalation and exhalation processes [13]. Each compartment of the RT is considered as a filter for which deposition is calculated by semi-empirical equations that are obtained from the fitting of experimental data as a function of particle size and flow rate (Figure 4).
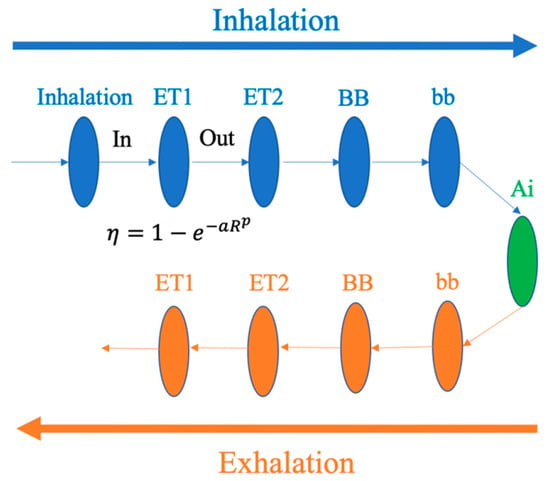
Figure 4.
Lung compartments treated as filters in the International Commission on Radiological Protection 66 (ICRP66) lung model [4].
The filter efficiency was calculated as:
where a, R, P are the constants that are given in ICRP66.
The deposition in each section of the lung (DEi) can be calculated via the following equation [38]:
where DEi is a dimensionless quantity that is used to present the total of aerosol particles that are deposited in the ith compartments, εi is used to display the varying volumes in the respective lung sections, and i − 1 means the number of particles deposited on the ith section is dependent on the number of particles that have passed through the section (i − 1)th.
The advantages of the ICRP model come from its ease of use and lesser computational resource requirements [13]. However, as a semi-empirical model, it is limited when applied to non-standard cases that are not mentioned in the database. Additionally, its accuracy of the prediction of particle deposition in cases where particle composition and size are not preserved throughout the inhalation and exhalation processes is poor [39].
4.1.2. Applications
A critical benefit of the ICRP model is owed to its open sources, thanks to which users can modify it for adaptation to their specific requirements [38]. For example, Guha et al. (2014) modified the ICRP model to investigate the effects of pathogenic bioaerosols such as botulinum toxin (BTX), influenza virus, and Bacillus anthracis on human health [38]. There are some differences between their model and the original one: 1) The modified ICRP model could automatically calculate the shape factor of nonspherical particles, 2) it could implement the normal size distributions of the purified monomers of bioaerosols, and 3) it could convert the lung deposition estimation from a function of age to a function of height due to the relations between these two factors. The differences between the modified ICRP and the original ICRP and Lung Dose Evaluation Program (LUDEP) model can be seen in Figure S3. According to that data, for adults, the order of toxicological effects was BTX > influenza virus > B. anthracis, whereas the order for infants was BTX > B. anthracis > influenza virus. Due to infants’ lower breathing flow rates, the doses of most biological matter in the ET, TB, and AL regions, as well as the total dose, were lower for them than for adults. However, the deposition per unit surface area was higher for infants, due to their smaller lung and lung area. Therefore, infants are more susceptible to biological aerosols, especially B. anthracis, due to their weaker immunity [38,40].
4.2. Exposure Dose Model (ExDoM)
4.2.1. Introduction
The Exposure Dose Model (ExDoM) was extended from ICRP66 to study both particle exposure and dose for different size distributions. According to the experimental data, the ExDoM can calculate the particle-size characteristics, the deposition fraction, and the particle dose in the RT regions. It can also estimate the clearance, the retention (in the RT, GI tract, lymph nodes), and the absorption of aerosol particles into blood capillaries during and after exposure. The workflow and input/output data for the model are shown in Figure 5. In the ExDoM, the aerosol size distribution, the individual dose rate, the clearance of deposited particles, and the particle mass in each region of the lung during and after particle exposure and their transfer to the GI tract, lymph nodes, and blood can be calculated by Equations (1)–(4) in the Supplementary Information.
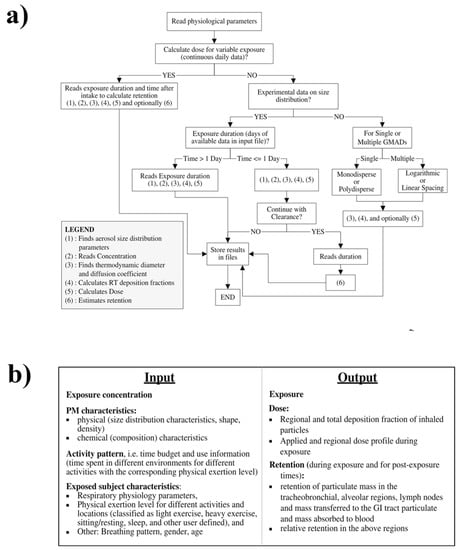
Figure 5.
The workflow (a) and input/output data (b) for the Exposure Dose Model (ExDoM) [39]. Reprinted with permission from [39]. Copyright 2013, Springer.
In the ExDoM, the input files should contain information on human lung geometry (total lung capacity, functional residual capacity, diameters of the trachea, bronchi, ET, and thoracic dead spaces) and the default breathing values (volumetric flow rate, breathing frequency, and tidal volume). The model has already included the breathing patterns of adult Caucasians, adolescents, children, and infants (three months old) under different activity levels such as sitting and sleep, as well as light and heavy exercise as default values. The exposure conditions (concentration and particle characteristics) can be constant or variable. Outdoor and indoor reference activity patterns for Caucasian males also are incorporated into the model.
The deposition results from the ExDoM are compared with those from LUDEP and Multiple-Path Particle Dosimetry (MPPD) (Price et al., 2002 [41]) below in Table 1. The details of the MPPD models are discussed in Section 5.2.

Table 1.
Local deposition fraction (%) of 5 μm monodisperse and polydisperse (σg = 2.5) aerosol from the ExDoM compared with the Lung Dose Evaluation Program (LUDEP) and Multiple-Path Particle Dosimetry (MPPD) models. Reprinted with permission from [39]. Copyright 2013, Springer.
Compared with the ICRP model, the ExDOM could predict data more closely to the experimental data. This advantage explains the difference in the inhalability calculations.
4.2.2. Applications
Aleksandropoulou (2013) applied the ExDoM to investigate particle exposure and dose in the human respiratory tract at a Finokalia coastal site (Greece) and a suburban site in Oslo (Norway) [39]. In Finokalia, the fine-particle concentration was 8.6–20.1 μg/m3, whereas that for coarse particles was 8.0–20.9 μg/m3. By using the ExDoM for an adult Caucasian male, the cumulative daily dose was estimated to be from 345 to 761 μg total particles. The fine- and coarse-particle doses were associated with their relative concentrations on each observation day. The results indicated that ~50% of the exposed particulate mass was finally delivered and deposited into the RT surfaces. In general, most fine particles are absorbed in the blood, while most of coarse particles are delivered to the trachea region by the mucociliary escalator and then swallowed. Particle retention is determined by the particles’ delivered dose and size distribution, especially in areas such as the bronchiolar (bb), airway walls, and the AL region. A total of 3286 of the 4873 μg particles deposited to the RT (except for ET1) were transferred to the GI tract (~67.4%), and 375 μg (~7.7%) continued to the blood. About 24.9% of the deposited particles remained in the RT (mainly in the alveolar-interstitial (AI region) at the end of the exposure. In Oslo, the average PM10 concentration ranged from 4 to 20 μg/m3 per hour, the exposure concentration ranged from 7.60 to 12.37 μg/m3 per hour, and the cumulative dose ranged from 133 to 212 μg/m3 per day. A total of 56 of the 197 μg of particles deposited to the RT (except for ET1) were transferred to the GI tract (~29%), and 139 μg continued to the blood (~71%). Approximately 0.2% of the deposited particles remained in the RT at the end of the exposure. The mean of fine-particle diameter was 0.15~0.35 μm, whereas for the coarse mode, it was more significant, with values varying from 1.15 to 3.89 μm. It was found that the fine-particle dose was higher in the AL region, whereas the coarse-particle dose was deposited mainly in the ET region. The elemental and organic carbon (EC and OC, respectively) were collected mostly in the ET region at doses four times larger than the inorganic ion dose [39].
Because commuters face different mobile emission sources, high PM exposure levels have been found for all transportation modes (car, bus, subway, motorbike, cycling, and pedestrian). In the case of subway systems, PM concentration levels are higher than in the outdoor ambient air [12]. The movement of trains, passengers, and also outside air flows through ventilation systems can contribute to the generation of PM [42]. Martin et al. (2015) also used the ExDoM to predict PM deposition in the human respiratory tract, explicitly using the published PM2.5 concentrations of the Barcelona metro system [12]. They found that, although the PM2.5 level inside the train was lower than those on the station platforms, the highest dose was found inside the trains due to the longer duration of exposure. Therefore, the particle dose was determined to be closely related to the exposure period. During a commute by subway, ~80% of the inhaled subway PM2.5 mass was deposited in the RT. PM2.5 particles were deposited mostly in the ET region (68%), followed by the AL region (4%). An individual’s daily PM2.5 exposure and dose also were predicted by utilizing a time–activity pattern of an adult male who lived and commuted by subway in Barcelona. The results showed that although the subject spent only ~3% of the day in the subway system, the PM2.5 dose in this microenvironment accounted for ~47% of the total daily dose [12].
4.3. Exposure Dose Model 2 (ExDoM2)
4.3.1. Introduction
The Exposure Dose Model 2 (ExDoM2) was developed from the ExDoM with a physiologically-based pharmacokinetics (PBPK) model also by Chalvalzaki et al. (2015) [43]. PBPK has been used to examine metal (As, Pb, Cd, Cr, and Mn) distributions from the blood circulation system to different organs such as the kidneys, heart, brain, muscle, and bone [43].
The PBPK model also can be used to estimate the absorption, distribution, metabolism, and clearance of chemicals that are inhaled into the body. Different equations in the PBPK model quantitatively represent actual physiological processes to simulate the behavior of compounds in the body [44,45]. They can also be specifically used for prediction of the behavior of As, Pb, Cd, Cr, and Mn in RT [43]. The PBPK model’s structures for As, Pb, Cd, and Mn are presented in Figure S4. The fate of these elements was estimated with Equations (5) and (6), as shown in the Supplementary Information [44,46].
4.3.2. Applications
Chalvatzaki and Lazaridis (2015) applied the ExDoM2 to estimate the internal human dose for an adult Caucasian male who was exposed to PMPb, PMCd, PMMn, and PMCr in an urban area of Athens (Greece) under a one-day exposure scenario [43]. The results showed that PMPb was accumulated mainly in the bone (2.29 × 10−1 µg), blood (7.50 × 10−2 µg), and muscle (4.84 × 10−2 µg); PMCd was mainly accumulated in the lungs (2.68 × 10−3 µg) and intestines (4.75 × 10−4 µg); PMMn was mainly accumulated in the lungs (8.72 × 10−2 µg) and other tissues (1.17 × 10−1 µg); and PMCr was mainly accumulated in the gastrointestinal (GI) tract (9.17 × 10−2 µg) and lungs (5.29 × 10−2 µg) [43]. For PM8.8, 158 µg was deposited to the RT, 72 µg to the ET1 region, and 86 µg to the ET2, trachea, bronchi (BB), bb, and AL. Of the PM8.8 deposited in the ET1, 13 µg was cleared by nose blowing, while 31 µg was transferred to the ET2 region. Therefore, the PM8.8 deposition concentration in the ET2 was increased to 117 µg. Of this 117 µg, 73 µg (~62%) was transferred to the esophagus, while 7 µg (~6%) was absorbed into the blood. At the end of the exposure, ~32% of the particles deposited in the four regions of the RT (ET2, BB, bb, and AL) remained [43]. Chalvatzaki and Lazaridis (2015) compared these results from the ExDoM2 with the original ExDoM. In the ExDoM, of the 109 µg that was deposited in ET2, ~57% of particles that were deposited in the four regions of the RT were transferred to the GI tract, ~7% were transferred to the blood, and ~36% remained after the exposure time. The differences between the ExDoM and the ExDoM2 arose from the differences in the clearance rates from the respective compartments of the lung, the default adsorption parameters, and the changes in the treatment of ET due to the transfer from ET1 to ET2 and, therefore, the higher systemic uptake in the GI tract [43].
Chalvatzaki et al. (2018) continued to apply the ExDoM2 to predict PM deposition by using data from three different cities, including Athens, Kuopio, and Lisbon [9]. The results showed that the deposited dose in the RT was the highest for Lisbon, which also had the highest PM concentration among the three cities. They also found that the activity profile and individual physical characteristics of the subject had strong influences on the predicted deposited dose. For example, a subject with light activity had a higher deposited dose than did a subject with no activity, while an adult male was exposed to higher doses. Both findings were found to be related to a higher inhalation rate. Most of the PM was deposited in the lungs, followed by the muscle for PMAs, the GI tract for PMCr, other tissues for PMMn, the intestines for PMCd, and bone and blood for PMPb [9].
With a confined underground space, a weak ventilation system, and indoor emission sources, the metro-environment has been characterized by high concentrations of PM and chemical elements that have adverse effects on human health [47]. The PM comes mainly from wheels, rail tracks, and brake pads [48]. Moreno et al. (2005) found that most PM in the metro system of Barcelona was Fe-oxide, mostly Fe2O3, from the rapid oxidation of Fe3O4 [49]. Karlsson et al. (2005) found that the genotoxicity of PM in a metro microenvironment was eight times higher than for outdoor particles, and that the potential to cause oxidative stress was four times higher for lung cancer cells [50]. Recently, Mammi-Galani et al. (2017) used the ExDoM2 to calculate the deposition, dose, and retention of PM inside the subway system of Athens (Greece) [51]. The model was applied to three different subjects: a commuter who used the metro for 1 hour/day; a metro worker with a sedentary occupation, and a metro worker with a light-exercise occupation. The highest dose was found in the ET region. Figure S5 shows that PM was deposited mostly in the ET1 of the RT, followed by the ET2 and the AL. In the case of the commuter, 46.4% of the deposited particles remained in the RT. This rate for the metro worker with the sedentary occupation and the metro worker with the light-exercise occupation was 44.5% and 36.9%, respectively. The deposited dose after 1 h of traveling by metro was 125.4 μg, which amount contributed 36.3% of the total individual daily dose [51].
In general, existing semi-empirical models can predict the whole-lung depositions of aerosol particles with a high accuracy. However, local depositions require more advanced modeling techniques [52,53].
5. One-Dimensional (1D) Whole-Lung Deposition Models
The advantages of 1D whole-lung models come from their ease of use and potential for entire RT prediction. However, these models also have many disadvantages. For example, they cannot cover all deposition mechanisms that are related to pharmaceutical aerosols that are delivered from multiple platforms. Another common disadvantage of these models is that the deposition location is not precise: The prediction results indicate only general regions such as the mouth–throat or TB airways. Importantly, the geometric complexity of the airways and the many factors that influence particle deposition are neglected [52,54]. Some remarkable models based on the 1D whole-lung model are trumpet models, single-path models, multiple-path models, and stochastic models.
5.1. Trumpet Model
5.1.1. Introduction
The trumpet model was developed by Yu (1978) [55]. The human lung morphometry from Weibel [16] was applied, and airways were considered as a one-dimensional system wherein the flow cross-section area differs with airway depth [13]. In this type of model, the cross-sectional area of each generation is plotted as one parameter, thus yielding a trumpet shape (Figure 6).

Figure 6.
Example of a trumpet-shaped lung model [13].
The trumpet model is suitable for stable or monodisperse particles. According to this model, inhaled particles are transported via convective and diffusive mechanisms, while their deposition along the trumpet axis occurs via a mixture of tidal air and reverse air volume, as described by a mass balance equation that incorporates different deposition mechanisms. The aerosol concentration that is inhaled by breathing is a function of airway depth and time. If one knows the concentration, one can easily calculate the deposition in each region [13].
There have been some efforts to improve the accuracy of the prediction of aerosol deposition in the AL region. In this region, sedimentation and diffusion are the two main mechanisms that lead to the deposition of aerosol particles. These mechanisms are affected mainly by wall motion, which is essential in the AL airways during respiration [52]. In the study of Choi and Kim (2007), the AL deposition of aerosol particles was divided into the alveolar duct and alveoli deposition fractions. There are two separate but related transport processes in the AL region: axial transport in the alveolar duct and lateral transport in the extracting or contracting alveoli. Both axial convective dispersion and Brownian diffusion can be implemented to predict nanoparticle deposition. For particles in the range of 0.001–100 μm, the prediction results have been highly consistent with experimental data [56].
5.1.2. Applications
Deng et al. (2019) recently used a one-dimensional lumped “trumpet” model with a variable cross-sectional area to predict PM deposition inside the human lung [57]. The following equation described the particles transport and deposition:
where A is the cross-section area of airways, is the alveolar volume per unit length of the airway, C is particle concentration, Q is the airflow rate, D is the diffusion coefficient due to convection, and L is the particle loss.
The transportation and deposition of PM in their study were determined by applying a finite difference method. A first-order forward scheme was utilized for time, a central difference scheme was utilized for diffusion, and an upwind scheme was applied for the convective term. The following boundary conditions were applied: The particle concentration was 10−6 particles/cm3 in the G0 generation of the lung (first generation) during inhalation, and the concentration gradient was zero (∂C/∂x = 0). In the last generation, the ∂C/∂x was also set to zero, i.e., as no mass flux was assumed [58]. In all generations, the initial particle concentration was set to zero with the establishment of steady-state after several cycles of breathing. After this numerical modeling, the deposition fraction (DF) in different airways of the human lungs could be achieved [57].
They found that, while impaction was the primary mechanism for the deposition of coarse particles (> 2.5 μm) in the TB, sedimentation and diffusion were the main mechanisms for the deposition of fine particles (< 2.5 μm) in the pulmonary (P) region. However, they also found that, if coarse particles have a low density, they also can be deposited in the pulmonary area. Additionally, they found some differences between the deposition of soil-dust particles and traffic particles. Whereas traffic particles were deposited mainly via diffusion and sedimentation, soil-dust particle deposition was driven by sedimentation only [57]. Deng et al. (2019) also indicated, as a limitation of their study, the fact that particle dynamics during transport in the RT, such as collision, growth, and aggregation, are not considered in their model. Additionally, because the lumped “trumpet” model was used, they could not consider the heterogeneity of the lung’s structure. One further limitation is that they only evaluated the effect of deposition location on health, and they did not consider the toxicity of chemical compositions [57]. It is a common limitation that is seen in many studies that have applied the 1-D model for the prediction of aerosol particle deposition.
5.2. Multiple-Path Particle Dosimetry Model (MPPD)
5.2.1. Introduction
The multiple-path model was created by the Center for Health Research (currently the Hamner Institutes for Health Sciences, Research Triangle Park, USA). This model closely matches reality due to its application of actual airways measurements and the asymmetry of lung morphology. The theory behind the MPPD model can be found in a study by Anjilvel and Asgharian (1995) [59]. The deposited concentration in each airway is calculated as a function of time for the proximal and distal ends. If one knows the particle concentration at the proximal end of an airway, the particle concentration at its distal end can be calculated for different deposition mechanisms [13].
5.2.2. Applications
Manigrasso et al. (2015) utilized an MPPD model to investigate the deposition of aerosol from electronic cigarettes with different nicotine levels and flavoring [60]. The particle concentrations were 3.26 × 109–4.09 × 109 particles/cm3 for e-liquids without nicotine and 5.08 × 109–5.29 × 109 particles/cm3 for liquid with nicotine. They found that flavoring did not affect particle concentrations. After a single 2-s puff, 6.25 × 1010 particles were deposited in the RT, with the highest deposition densities in the lobar bronchi, correlating to ~30% of the daily dose of a non-smoker [60].
Recently, Manojkumar et al. (2018) applied an MPPD model to investigate the effects of age on the deposition of PM in the human respiratory tract [61]. The lung geometries of infants (3 and 28 months), children (3, 8, 9, and 14 years), and adults (18 and 21 years) were applied along with factors such as PM concentration, body orientation, breathing scenario, tidal volume, pause fraction, inspiration fraction, and breathing frequency. The protocol of the study is presented in Figure S6. They found that groups of 8-year-old children and 28-months-old infants had the maximum and minimum size-segregated PM depositions, respectively. While PM10 was deposited mainly in the regions of the head (55%–95%) and TB (3%–44%), PM2.5 and PM1 were deposited mostly in the head (36%–63%) and pulmonary (28.2%–52.7%) regions. Except for the adult groups, PM2.5 was deposited primarily in the TB and pulmonary areas. In the case of lobar depositions, the lower lobes received the maximum deposition (66.4%) relative to the upper (27.2%) and middle (6.4%) ones. PM2.5 was found predominantly in all five lobes of infants, children, and adults. Additionally, it was found that the clearance rate in the TB region was high, whereas it was low in the pulmonary part. It was suggested that, for lung deposition, PM2.5 is the most critical size fraction [61].
5.3. Stochastic Model
5.3.1. Introduction
The stochastic nature of the lung means that the differences in morphometric, physiologic, and histologic parameters can lead to dose differences at the cellular level. These parameters can be solved by a stochastic model in which they are randomly selected via Monte Carlo methods based on their probability distributions. Inhaled particles are passed through this stochastic airway structure via the random selection of airway sequences for each particle until the occurrence of deposition. A fully stochastic deposition model (IDEAL) was developed and introduced by Koblinger, Hofmann et al. [62,63,64,65,66]. This model could be used to calculate the total, regional, and generation-by-generation deposition of inhaled particles [13].
5.3.2. Applications
Though many nanoparticles have been classified as hazardous materials, their behavior in the human lung still needs to be better represented [67]. Sturm (2016) studied the deposition of carbon nanotubes (CNTs) in the human lung by using the stochastic model [67]. The deposition mechanism of CNTs inside the lung is shown in Figure S7. The fluid-dynamic characteristics of the particles were simulated by the implementation of a rigid fiber model that accounted for diverse forces and torques acting on the particles during their translocation within the inhalation process. The deposition of CNTs in the entire RT was estimated via the application of the aerodynamic/thermodynamic diameters concepts as well as related empirical deposition formulae. According to the results, CNT deposition depends on their size and conditions. It was found that particles of ~1 nm diameter were deposited mainly in the AT airway, whereas particles of ~10 nm size were deposited primarily in the alveoli. CNTs of large size (~100 nm) seem not to be deposited in the RT [67].
Sturm (2012) also used a stochastic model to investigate the deposition of PM ranging from 1 to 10 μm inside the lungs of children [68]. He found that most PM was deposited in the ET and upper bronchi regions for infants and children, while for adolescents and adults, PM was deposited mainly in lower regions such as the lower bronchi and alveoli. He also found that even though mucus viscosities are lower in young subjects, the clearance rate is faster in small lungs because of the shorter clearance paths. However, PM is still considered to be a hazardous material for young subjects due to the fact that the particle concentrations per area of lung tissue can reach alarming values within a short inhalation period [68].
6. Three-Dimensional (3D) Computational Fluid Dynamics (CFD) Models
6.1. Introduction
The realistic simulation of lung-aerosol dynamics can provide important information on how toxic particles can be deposited and related to the treatment of pulmonary diseases such as asthma, cystic fibrosis, COPD, respiratory distress syndrome (ARDS), and pulmonary fibrosis [69,70,71,72]. However, due to the limitations of current computational resources, it is challenging to simulate the transportation of aerosol dynamics in all generations of the human respiratory tract. Thus, it is necessary to simplify lung configurations to adapt to specific modeling requirements [72]. There are different simplified lung configurations in the literature, such as the earlier-noted semi-empirical models (such as the ICRP model), the trumpet model, the multiple-path model, and the stochastic multi-path lung model. These models are popular due to their ease of use and low computational resource requirement [73]. However, due to their simple inlet conditions and semi-analytical correlations for mechanisms of deposition, the accuracies of these computed deposition models are still questionable [74].
For the development of CFD models, detailed three-dimensional fluid flow and equations that represent particle transport are used. The airways in these models can be divided into small volumetric elements; thus, it is possible to calculate the regional deposition for each airway’s surface element. However, most CFD-based models require very long computational processing times. Morphological variations of airway geometry, including axial and lateral airway surface, can be accounted for in a CFD model. Geometric differences due to subjects’ age and gender can also be covered [4].
CFD models have some benefits compared with semi-empirical and 1D whole-lung models. In CFD models, factors such as transient flow, turbulence, and turbulent particle dispersion, hygroscopic particle-size change, and fluid–wall interactions in complex geometries can be directly accounted for in simulations. With the employment of realistic geometries, the deposition of aerosol particles in complex structures such as the larynx, bifurcations, and constricted airways can be predicted. Notably, the influence of jet and spray momentum from an inhaler on pharmaceutical aerosols that pass the mouth–throat (MT) region and upper TB airways can be directly predicted [54].
The limitation of CFD models is their estimation of an aerosol deposition only in the oronasal region and the upper RT. Because there are no reliable morphometric data on the lower generations, there are no CFD models for the whole lung. Additionally, because the deposition mechanisms in the lower airway are mainly gravitational, diffusional and are not affected by air-flow conditions, high computational resources are required for processing [4].
The fundamentals of computational fluid dynamics can be found in the review paper of Kleven and Mellaen (2012) [75]. The basic steps of CFD are presented in Figure 7.

Figure 7.
Basic steps of computational fluid dynamics (CFD).
The Navier–Stokes equation is a partial differential equation that presents the flows of incompressible fluids. In the case of upper airways, the flow is considered incompressible due to the low Mach number. Therefore, the governing equation is presented by the following equation [76]:
Continuity equation:
Momentum equation:
where u is the velocity vector, is the mass density, p is the pressure, and ν is the kinematic viscosity.
For flow rate, the Reynolds number can be used to determine the state of the flows. Based on the Reynolds number, suitable laminar, transitional, and fully turbulent solutions were chosen to resolve the flow field and evaluate the associated aerosol dynamics [25]. The Reynolds (Re) number is defined by Equation (7) in the Supplementary Information.
In CFD models, the Navier–Stokes equation is numerically solved to model the airflow in the upper airways of the human lung. Different discretization techniques such as finite element methods, finite volume methods, finite different methods, spectral element methods, and boundary element methods can be used to numerically solve the Navier–Stokes equation. Finite different methods are the oldest methods, while finite element methods are better used in computational solid-mechanics than in fluids mechanics. In comparison to these discretization techniques, finite volume methods are a better choice. However, the finite volume methods are mostly applied for internal grid-points, while finite difference methods are frequently applied for boundary grid points [77]. On the other hand, finite element methods are still applied for fluids mechanics due to their higher stability compared to finite volume methods [78]. However, finite element methods cost more memory and have slower solution times compared to finite volume methods [79].
For fluid turbulence, the Reynolds-averaged Navier–Stokes equations (RANS) are time-averaged equations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity (velocity u) is decomposed into its time-averaged ( and fluctuating quantities (u’):
These equations can be used with approximations based on knowledge of the properties of flow turbulence to give approximate time-averaged to the Navier–Stokes Equations. For laminar and turbulent flow models, the RANS equations can be used to present the conversion of mass and momentum [73]:
where is the time-averaged velocity in three coordinate directions, i.e., i = 1, 2, and 3; and is turbulent viscosity. For laminar flow, is zero [25].
Other methods, such as large eddy simulation (LES) and direct numerical simulation (DNS), could also be used. DNS can numerically solve the Navier–Stokes equation for all significant spatial and temporal scales, while they do not require any additional turbulence modeling. However, the computational cost increases with Reynolds number as Re3 [80].
On the other hand, LES requires the explicit representation of large-scale turbulent eddies, including anisotropic energy, while more isotropic turbulent motions are modeled in the smaller case. This method is far less computationally expensive than the DNS method, but it is still higher than RANS. Compared to these methods, RANS is still the most popular due to its lesser computer demands [76]. However, because RANS was mainly developed for turbulent flows, it is the least accurate method when applied to complex structures such as the human lung. Even for upper human airways, where the flow is mainly turbulent, Zang and Kleinstreuer (2011) showed that the RANS method, when using the standard k-ω turbulent model, could not compete with the LES computational method in general. However, the results from the low-Reynolds number (LRN) k-ω and the shear-stress transport (SST) are similar to those of the LES method [81]. Though LES and DNS are more computationally expensive than RANS, the time for the simulation of aerosol deposition by LES and DNS could be reduced due to the availability of high-performance computing [82,83].
In CFD models, particle transport and deposition could be described via the Lagrangian or Eulerian approaches. The Lagrangian and Eulerian approaches were deeply discussed in the review papers of Rostami et al. (2009) and Tang and Guo (2011) [4,80]. The Lagrangian approach is suitable for larger particles (> 0.3 μm) [4]. For ultrafine particles, the Eulerian approach is more suitable [80]. The particle motion in the Lagrangian and Eulerian description methods re presented by Equations (8)–(11) in the Supplementary Information.
6.2. Applications
In contrast with comparisons of prediction data from CFD models with in vitro data, comparisons of prediction data from CFD models with in vivo data for pharmaceutical aerosols are still rare [84]. Kleinstreuer et al. (2007) and Vinchurkar et al. (2012) compared the predictions of MT deposition and lung delivery by CFD models with in vivo data sets for metered dose inhalers (MDIs). However, these models are usable only for the MT region and upper TB airways [85,86]. Tian et al. (2015) compared the CFD prediction results with in vivo data for pharmaceutical aerosol deposition [54]. The CFD model includes a dry powder inhaler (DPI), a soft mist inhaler (SMI), a characteristics model for the MT region and upper TB airways, stochastic individual pathways (SIPs) for the remaining TB regions, and CFD-based models to estimate the deposition of pharmaceutical aerosols in the AL region. For generations are turbulent flows were expected, the LRN k-ω model has been used for simulation due to its high accuracy in the prediction of pressure drop, velocity profiles and shear stress for transitional and turbulent flows. In lower generations where turbulence does not occur, laminar simulations have been applied. For particle transport, the Lagrangian tracking method has been applied. The random walk model has been used to model the effect of turbulent fluctuations on the trajectories of aerosol particles. The anisotropic turbulence correction has been used to improve the simulation of turbulent effects on particles. In order to improve the accuracy of the prediction of particle deposition in the turbulent flow fields, the near-wall interpolation has been included. The predicted total lung deposition for the monodisperse aerosol of 1–7 µm size has been found to be close to the in vivo data, with a relative error of 6%. For the MT region, specifically the central airways (bifurcations B1–B7), and airways from B8 through the alveoli, the CFD predictions have been found to have a <10% average relative error for both the DPI and SMI inhalers [54].
Longest et al. (2016) validated the use of whole-airway CFD with in vivo data to predict the deposition of DPI aerosols at multiple flow rates [84]. This approach is flexible enough to directly involve aerosol physics for the development of new drug delivery and inhaler strategies. A Novolizer DPI with a budesonide formulation was chosen based on the two-dimensional (2D) gamma scintigraphy data available for humans and three different inhalation waveforms. To characterize the particle-size distribution (PSD), in vitro cascade impaction experiments were initially conducted at multiple constant (square-wave) particle-size flow rates. At the point that aerosols were formed in the inhaler, a CFD model was applied to determine the PSDs. The whole-lung airway geometries were characterized by combining CFD with SIPs. For each inhalation waveform, the PSD was determined based on a constant particle-size flow rate that was equal to the average peak inspiratory flow rate (PIFR) and mean flow rate (AVG (PIFR, Mean)). After applying this technique, the prediction results agreed with the in vivo data, with <15% acceptable differences across the three different regions for all of the inhalation waveforms. Large flow-rate-dependent differences were found via defining the ratio between peripheral and central deposition (P/C) based on the AL and TB compartments, which were not indicated in the original 2D in vivo data. The agreement between the estimation from the CFD and in vivo data was dependent on the accuracy of the PSD initial estimation; thus, the combination of the in vitro and in silico approaches was emphasized. Besides, the AVG (PIFR, Mean) value was proven as a potential method for the characterization of DPI aerosols at a constant flow rate. The approach from Longest et al. (2016) remains disadvantageous given the complexity of the underlying physics [84].
Augusto et al. (2016) applied the CFD model to evaluate the effects of physical mechanisms, particle size, and breathing conditions on particulate deposition in a triple-bifurcation airway [35]. In their study, four breathing conditions, including sleep, resting, moderate, and intense activity, were employed with particle diameters ranging from 1 to 10 μm. A 3D triple-bifurcation model (four generations) was applied for the simulation. In the results, the deposition of aerosol particles in each of the three bifurcations was not uniform and was dependent on particle diameter. The effects of the gravitational settling and Brownian diffusion mechanisms on particle deposition were also evaluated. In the results, the pathways of the larger particles were strongly influenced by gravitational settling, especially when for low velocity. With a particle diameter of 10 μm, the difference between the simulations with and without gravity could reach ~172%. Brownian diffusion also influenced the deposition of particles when the velocity was lower, but this mechanism was more significant for the particles of smaller size. However, this effect was small, showing a maximum value of 11% for particles of 1 μm diameter. Additionally, the increase in air-flow velocity and particle size were able to affect the deposition pattern. For example, for sleep and resting activities, particles of <6 μm diameter were mostly deposited in the first bifurcation, whereas larger particles were mostly deposited in the third bifurcation. For the moderate and intense conditions, inhaled particles were deposited predominantly in the first bifurcation for all of the particle diameters that were accounted for in the study. The authors also concluded that the particle deposition in the human RT was significantly higher with more vigorous activity, such as exercise [35]. Lintermann et al. (2017) used the one-way coupled Euler–Lagrange approach for the flow in the lung to investigate the deposition of particles in the upper human tracheobronchial tract [87]. The lattice-Boltzmann method was used to stimulate the flows, while a practical solver was used to tract the aerosol. They found that 32% of more massive and large particles with a diameter of 100 μm were deposited in the deep airways of the lung, and a particle mixture of 2.5–10 μm was deposited in the primary, lobar, and segmental bronchi. The deposition of particulate matters below the sixth generation and could lead to bronchi damage [87].
In order to reduce simulation time, high-performance computers can be used. Calmet et al. (2019) recently applied LES coupled with a Lagrangian method to model the transport of aerosol medicine during exhalation [88]. They found that deposition increased with the exercise breathing condition. In their study, a MareNostrum supercomputer (Barcelona Supercomputing Center) was used for the simulation. In order to carry out the simulation, 110,000 time-steps were required on 480 cores that required ~20 hours, and 20,000–30,000 mesh elements were used on each core to maintain a good parallel efficiency [88]. Calmet et al. (2016) conducted the large-scale CFD stimulation of the transitional and turbulent flow by using two supercomputers to solve the transient Navier–Strokes equation [89]. The lung geometry in the study composed of an exterior face and the airways from the nasal cavity to the third lung bifurcation. They found that the complex flows were produced from the transient flow over a wide range of Reynolds numbers. From their study, it was found that the turbulent level is higher in the throat than in the nose [89].
Aerosol deposition, as predicted through CFD approaches, remains challenging and should be further simplified [84]. There have been some efforts to reduce the complexity of CFD [90,91,92,93]. One strategy is the combination of CFD models with other techniques. Kolanjiyil and Kleinstreuer (2016) introduced a new whole-lung-airway model (WLAM) that tries to represent the actual lung geometry by combining a basic 3D configuration from mouth to trachea, subsequently lumping the remaining airways together as a 1D conduit [73]. In their models, the shear stress transport (SST) k-ω is used to stimulate the laminar, transitional, and fully turbulent flow regimes, while the Lagrangian method is used for particle transport. The WLAM could simplify the modeling strategy for the geometry of bifurcating airways as well as the related fluid-particle dynamics. In WLAM model, a wall-displacement boundary condition is applied for the fluid-particle dynamics in the AL region. Such models to track the trajectories of transient particles from the inhalation point to either deposition or exhalation during multiple breathing cycles [11].
WLAM can simulate different breathing conditions (Figure S8) [73]. The results from the steady-state simulation of the airways of the oral–tracheobronchial region have shown that the estimated effects are similar to the experimental data. The WLAM can capture the airflow and behavior of transient particles under realistic breathing conditions and provide both total and regional particle deposition results with a high accuracy relative to experimental data (Figure S9). The authors also expected that drugs of 10 μm size were mainly deposited in the upper TB, while drugs of 5 μm size were mainly deposited in the AL region [73].
Kolanjiyil et al. (2017) continued to apply the WLAM to understand the efficacy of drug-aerosols that are injected by using DPI [72]. Their total and regional particle deposition results returned by the WLAM were similar to the experimental data in the literature. By using curcumin aerosols as target drugs, they found that the current DPI could deposit ~50% of drugs in the oral cavity. They also highlighted the difference between curcumin drugs in their polydisperse and monodisperse forms. The percentage of polydisperse curcumin drugs that were deposited in the oral cavity was higher than that of monodisperse curcumin drugs due to the larger particle size [72].
However, the WLAM still has some limitations. One is that the model can estimate the inhomogeneity of regional deposition only in the extra-thoracic airways, whereas, for the remaining airways, it segmentally averages the deposited particle concentrations. Another limitation is that it does not yet account for subject-specific lung morphology. Furthermore, the asymmetrical nature of human lung airways is not yet covered either. However, the current WLAM can be combined with different lung data for subject-specific purposes. Additionally, the WLAM can estimate the deposition of aerosol particles of > 400 nm size. For nano drugs of < 100 nm diameter, additional models such as Brownian diffusion are required. Kolanjiyil et al. (2016) claimed that it is possible to upgrade the current WLAM with more realistic upper TB airways because particle transport is influenced mainly by the asymmetrical flow structures in this region [94]. Therefore, the updated model can increase the accuracy of the current model, but this would come at the cost of more computational time and resources [73].
7. Artificial Neural Networks
7.1. Introduction
Artificial neural networks (ANN) comprise a mathematical model based on a collection of artificial neurons that are connected or functionally-related to each other. Each of the nodes of ANN models behaves like neurons in a biological brain [95,96]. Overall, the neurons of ANN models are arranged within an input layer, hidden layers, and an output layer (Figure 8). Signals pass from the input layer to the output layer. All neurons in a layer are linked to all neurons in neighbor layers by synaptic weights playing the role of signaling coefficients to the corresponding connections [95,96,97]. These connecting signals are real numbers, and the output of each of the artificial neurons is analyzed by many linear or non-linear statistical techniques [95,98]. The multilayer Perceptron (MLP) neural network and the radial basis function (RBF) network are two of the most popular neural networks [98].

Figure 8.
Artificial neural network (ANN) structure.
7.2. Applications
Nazir et al. (2002) used experimental data to train MLP networks to predict the regional and total lung depositions of aerosols [99]. Particle sizes ranging from 0.05 to 15 μm, and three breathing patterns (from “quiet” breathing to “under physical work” conditions) from the data were used. Additionally, three different MLP networks were used to separately predict the depositions of aerosol particles in the laryngeal, bronchial, and AL regions. For a set of breathing conditions, the total deposition fraction was computationally predicted by the sum of the outputs that was obtained from the corresponding regional depositions. In the results, the developed ANN models could predict both the regional and total aerosol depositions with a high accuracy (with an averaged error of less than 0.04%) [99]. Nazir et al. (2005) continued to predict the fate of polydisperse aerosols in the human lung by using the ANN model [100]. ANN models have shown a high accuracy for the prediction of polydisperse aerosol deposition in all lung regions, with all particle sizes and breathing conditions (with averaged error less than 0.0025%). Further testing of the ANN, by using “unseen” in vitro and in vivo data, has yielded good agreement with lung dosages [100].
It may be possible to correlate some in vitro measures of quality with the pharmacokinetic profiles of active substances in human subjects [101]. De Matas et al. (2008) applied an ANN with a single hidden layer and three hidden nodes to evaluate the in vitro in vivo correlations (IVIVCs) for DPI delivery [102]. In 12 volunteers, the ANN model linked the in vitro aerodynamic characteristics of the emitted dose and the volunteer body surface area (input) with the urinary excretion of the drug and its metabolites in the 24 h period after inhalation (output). In 11 mild asthmatics, the ANN model linked in vitro data, baseline lung function, body surface area, and age (input) with bronchodilator response data (post-treatment improvements in forced expiratory volume in 1 s (FEV1, output). There was a close relationship between the prediction and observed data, with the squared correlation coefficients (R2) being 0.83 and 0.84 for urinary excretion and lung function data, respectively [102]. Though some efforts have been made to apply ANNs to the prediction of aerosols in the lung, they are still rare in the literature and should continue to be developed.
For pharmaceutical aerosols, the fine-particle fraction (FPF) prediction of dry powder inhalers (DPI) is also beneficial to the estimation of lung deposition and disease treatment. Muddle et al. (2017) evaluated the potential of 31 ANN architectures to estimate the FPF of salmeterol and salbutamol sulfate dry powder inhalers (237 experimental observations) [103]. The ANN models were designed by orthogonal arrays (OAs) and optimized by the Taguchi method. The optimized ANN model had a 9-4-1 architecture and average R2 values of 0.9 ± 0.02 that reflected the importance and interdependency of active pharmaceutical ingredients, formulations, and device inputs in the performance of dry powder inhalers. However, although the Taguchi method is useful for the optimization of ANN architectures, it requires more massive datasets and more variable inputs [103].
8. Conclusios
There are many computational models in the literature. The most common ones are semi-empirical models, 1D whole-lung models, and 3D computational fluid dynamics (CFD) models. Each of them has its advantages and disadvantages. While semi-empirical models can predict the total lung-deposited concentration with acceptable accuracy, they are limited in the prediction of the regional deposition of aerosol particles. On the other hand, while 1D whole-lung models can also predict aerosol deposition in the entire lung, they cannot cover all aerosol deposition mechanisms, and they neglect the complexity of geometry and various other factors that influence particle deposition. Other remarkable models in the literature are CFD models, which have many benefits compared to semi-empirical and 1D whole-lung models due to their use of realistic lung geometry and particle transport equations. However, most CFD models can predict the deposition of aerosol particles only in the oronasal and the upper RT. The major limitation of CFD-based models that prevents their full application is the requirement of high computational resources. Besides conventional models, which have been frequently used to simulate aerosol-particle deposition in the lungs, some reported ones use the advantages of artificial intelligence (AI) technologies. However, the major limitation of these models is their requirement of big data from experiments for model development and training. The advantages and disadvantages of the mentioned models, with some recent updates, are briefly summarized below (Table 2).

Table 2.
Advantages and disadvantages of different computational models for prediction of aerosol in the human respiratory tract.
The above-noted models share the same limitations. One limitation comes from the complexity of the airway geometries and the unavailability of morphometric data. Another limitation relates to the difficulty of simulating realistic physiological conditions of the RT environment, especially for the AL region. Additionally, the complex physical and chemical phenomena related to dense and multicomponent aerosols make the modeling tasks more challenging to predict the deposition of aerosol accuracy [4].
There have been some efforts to improve the accuracy of conventional computational models for aerosol deposition in the human lung. For semi-empirical models, the development of ExDoM and ExDOM2 has aided in the calculation of aerosol dose, deposition, and retention, as well as the behavior of specific elements in the human body. Though some limitations remain, 1-D whole-lung models are still popular today due to their ease of use (for example, the MPPD software (ARA Inc, United States) can be freely downloaded and has a friendly user interface). However, for both semi-empirical and 1-D whole-lung models, the accuracies of these models should be further clarified in future research. For CFD models, the advances of the high-performance computing with supercomputers and thousands of CPUs can be used to reduce simulation time. In the near future, the presence of a new generation of supercomputers will continue to reduce simulation time. For ANN models, they are only useful when big data exist. Therefore, it is necessary to develop big data about the lung deposition of aerosol. In general, lung morphology data and experimental data about aerosol deposition should continue to be upgraded to develop and optimize all mentioned computational models.
In order to overcome the limitations of the current models, one remarkable strategy is the combination of different models. For example, the CFD models and 1D whole lung model could be combined. In our opinion, the application of ANNs could also be used to reduce the complexity of conventional models or to improve their accuracies. For example, we can use 1D whole lung models or CFD models for the prediction of aerosol particles in the lung and then use ANN models to investigate the retention and the clearance of these particles inside the body. ANNs could also be used to support the deposition of aerosol pharmaceuticals by providing information about the fine-particle fraction of a DPI [103]. We believe these trends will be continued in the near future.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/2/137/s1, Supporting equations for ExDoM, ExDoM2, and CFD models; Table S1: Deposition probability of aerosol particles via impaction, sedimentation, and diffusion for each airway generation; Figure S1: Tracheobronchial region (generations 0–16) and pulmonary region (generation 17–23) of airway; Figure S2: Structures of Weibei airways (WA) (a), Kitaoka models that go down from the trachea to the 7th (KG7, b) and 11th generations (KG11, c); Figure S3: Schematic of modified International Commission on Radiological Protection (ICRP) model developed by Guha et al. (2014). The light-grey boxes are functions that were not included in the original ICRP model; the dark-grey boxes are functions that were not included in the Lung Dose Evaluation Program (LUDEP); Figure S4: Physiologically-based pharmacokinetics (PBPK) model’s structures for As, Pb, Cd, and Mn; Figure S5: (a) Regional Particulate matter (PM) dose in the human lung for 24 hours and (b) retention of particles in RT, dose of material transferred to GI tract and blood adsorption after 24-h exposure of commuter, metro worker with sedentary occupation and metro worker with light-exercise occupation; Figure S6: Example of Multiple-Path Particle Dosimetry MPPD model protocol; Figure S7: (a) The translational and rotational force applied to carbon nanotubes (CNT) during its transport. (b) Mechanisms of deposition of CNT in tracheobronchial tree: 1) inertial impaction; 2) interception; (3) diffusion; and (4) sedimentation; Figure S8: Velocity contours and secondary velocity vectors in mid-plane of oral-upper airway at different flow rates of steady inhalation: (a) 15 liters per minute (LPM), (b) 30 LPM, and (c) 60 LPM; Figure S9: Comparison of particle depositions predicted by whole-lung-airway model (WLAM) and experimental results for (a) 15 LPM of inhalation flow rate and 500 cm3 of tidal volume; (b) 15 LPM of inhalation flow rate and 1000 cm3 of tidal volume; (c) 15 LPM of inhalation flow rate and 1500 cm3 of tidal volume; (d) 30 LPM of inhalation flow rate and 1000 cm3 of tidal volume; and (e) 45 LPM of inhalation flow rate and 1500 cm3 of tidal volume.
Author Contributions
V.K.H.B., D.P., and Y.-C.L. planned and contributed the main ideas of the manuscript; V.K.H.B. collected references and mainly wrote the manuscript; J.-Y.M., M.C., D.P., and Y.-C.L. commented on and upgraded the manuscript before submission; D.P. and Y.-C.L. are the corresponding authors of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from the Subway Fine Dust Reduction Technology Development Project of the Ministry of Land Infrastructure and Transport (19QPPW-B152306-01) and the Ministry of Environment acting as the Korea Environmental Industry & Technology Institute (KEITI) (NO. 2018000120004). This work was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (NRF2017R1D1A1A09000642) and also by Biocell Korea Co., Ltd.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| 1D | One dimensional |
| 2D | Two dimensional |
| 3D | Three dimensional |
| AL | Alveolar |
| ANN | Artificial neural networks |
| BB | Trachea and bronchi |
| bb | Bronchiolar |
| CFD | Computational fluid dynamics |
| COPD | Chronic obstructive pulmonary disease |
| DPI | Dry Powder Inhaler |
| ET | Extrathoracic |
| GI | Gastrointestinal |
| ICRP | International Commission on Radiological Protection |
| LUDEP | Lung Dose Evaluation Program |
| MLP | Multilayer perceptron |
| PM | Particulate matter |
| RT | Respiratory tract |
| SIPs | Stochastic individual pathways |
| TB | Tracheobronchial |
| WLAM | Whole-lung-airway model |
References
- Olivieri, D.; Scoditti, E. Impact of environmental factors on lung defences. Eur. Respir. Rev. 2005, 14, 51 LP-56. [Google Scholar] [CrossRef]
- Shang, Y.; Dong, J.; Tian, L.; Inthavong, K.; Tu, J. Detailed computational analysis of flow dynamics in an extended respiratory airway model. Clin. Biomech. 2019, 61, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Barnes, P.J.; Blasi, F.; Ward, B.; Reeves, E.; Rabe, K.F. Respiratory diseases in the world: One voice “united for lung health”. Eur. Respir. J. 2014, 43, 3. [Google Scholar] [CrossRef] [PubMed]
- Rostami, A.A. Computational modeling of aerosol deposition in respiratory tract: A review. Inhal. Toxicol. 2009, 21, 262–290. [Google Scholar] [CrossRef] [PubMed]
- EPA, U.S. Air Quality Criteria for Particulate Matter (Final Report, 1996); Vol. EPA 600/P-95/001; U.S. Environmental Protection Agency: Washington, DC, USA, 1996. [Google Scholar]
- IARC. Outdoor Air Pollution a Leading Environmental Cause of Cancer Deaths; IARC Scientific Publication: Lyon, France, 2013. [Google Scholar]
- IARC. Outdoor air pollution. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; IARC: Lyon, France, 2016; Volume 109. [Google Scholar]
- Pope, C.A.; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef] [PubMed]
- Chalvatzaki, E.; Chatoutsidou, E.S.; Mammi-Galani, E.; Almeida, M.S.; Gini, I.M.; Eleftheriadis, K.; Diapouli, E.; Lazaridis, M. Estimation of the personal deposited dose of particulate matter and particle-bound metals using data from selected european cities. Atmosphere 2018, 9. [Google Scholar] [CrossRef]
- Patton, J.S.; Byron, P.R. Inhaling medicines: Delivering drugs to the body through the lungs. Nat. Rev. Drug Discov. 2007, 6, 67–74. [Google Scholar] [CrossRef]
- Kolanjivil, A.V.; Kleinstreuer, C. Computational analysis of aerosol-dynamics in a human whole-lung airway model. J. Aerosol Sci. 2017, 114, 301–316. [Google Scholar] [CrossRef]
- Martins, V.; Cruz Minguillón, M.; Moreno, T.; Querol, X.; de Miguel, E.; Capdevila, M.; Centelles, S.; Lazaridis, M. Deposition of aerosol particles from a subway microenvironment in the human respiratory tract. J. Aerosol Sci. 2015, 90, 103–113. [Google Scholar] [CrossRef]
- Hussain, M.; Madl, P.; Khan, A. Lung deposition predictions of airborne particles and the emergence of contemporary diseases - part I. theHealth 2011, 2, 51–59. [Google Scholar]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1999; p. 504. [Google Scholar]
- Finlay, W.H. Chapter 3 - Motion of a single aerosol particle in a fluid. In The Mechanics of Inhaled Pharmaceutical Aerosols (Second Edition); Finlay, W.H., Ed.; Academic Press: London, UK, 2019; pp. 21–52. [Google Scholar]
- Weibel, E.E. Morphometry of the Human Lung; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- Baron, P.A.; Willeke, K. Aerosol Measurement: Principles, Techniques, and Applications; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Bi, X.; Sheng, G.; Peng, P.a.; Chen, Y.; Fu, J. Size distribution of n-alkanes and polycyclic aromatic hydrocarbons (PAHs) in urban and rural atmospheres of Guangzhou, China. Atmos. Environ. 2005, 39, 477–487. [Google Scholar] [CrossRef]
- Oberdörster, G. Effects and fate of inhaled ultrafine particles. In Nanotechnology and the Environment; American Chemical Society: Washington, DC, USA, 2004; Volume 890, pp. 37–59. [Google Scholar]
- Flora, G.; Gupta, D.; Tiwari, A. Toxicity of lead: A review with recent updates. Interdiscip. Toxicol. 2012, 5, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Jaishankar, M.; Tseten, T.; Anbalagan, N.; Mathew, B.B.; Beeregowda, K.N. Toxicity, mechanism and health effects of some heavy metals. Interdiscip. Toxicol. 2014, 7, 60–72. [Google Scholar] [CrossRef]
- Di Vaio, P.; Magli, E.; Caliendo, G.; Corvino, A.; Fiorino, F.; Frecentese, F.; Saccone, I.; Santagada, V.; Severino, B.; Onorati, G.; et al. Heavy metals size distribution in PM10 and environmental-sanitary risk analysis in Acerra (Italy). Atmosphere 2018, 9. [Google Scholar] [CrossRef]
- Horsfield, K.; Cumming, G. Morphology of the bronchial tree in man. J. Appl. Physiol. 1968, 24, 373–383. [Google Scholar] [CrossRef]
- Takano, H.; Nishida, N.; Itoh, M.; Hyo, N.; Majima, Y. Inhaled particle deposition in unsteady-state respiratory flow at a numerically constructed model of the human larynx. J. Aerosol Med. 2006, 19, 314–328. [Google Scholar] [CrossRef]
- Xi, J.; Longest, P.W. Transport and deposition of micro-aerosols in realistic and simplified models of the oral airway. Ann. Biomed. Eng. 2007, 35, 560–581. [Google Scholar] [CrossRef]
- Luo, H.Y.; Liu, Y. Modeling the bifurcating flow in a CT-scanned human lung airway. J. Biomech. 2008, 41, 2681–2688. [Google Scholar] [CrossRef]
- Imai, Y.; Miki, T.; Ishikawa, T.; Aoki, T.; Yamaguchi, T. Deposition of micrometer particles in pulmonary airways during inhalation and breath holding. J. Biomech. 2012, 45, 1809–1815. [Google Scholar] [CrossRef]
- Ebert, M.; Grossmann, T.; Heil, W.; Otten, E.W.; Surkau, R.; Thelen, M.; Leduc, M.; Bachert, P.; Knopp, M.V.; Schad, L.R. Nuclear magnetic resonance imaging with hyperpolarised helium-3. The Lancet 1996, 347, 1297–1299. [Google Scholar] [CrossRef]
- Musch, G.; Layfield, J.D.H.; Harris, R.S.; Melo, M.F.V.; Winkler, T.; Callahan, R.J.; Fischman, A.J.; Venegas, J.G. Topographical distribution of pulmonary perfusion and ventilation, assessed by PET in supine and prone humans. J. Appl. Physiol. 2002, 93, 1841–1851. [Google Scholar] [CrossRef] [PubMed]
- Jannasch, K.; Missbach-Guentner, J.; Alves, F. Using in vivo imaging for asthma. Drug Discov. Today Dis. Models 2009, 6, 129–135. [Google Scholar] [CrossRef]
- Kitaoka, H.; Koc, S.; Tetsumoto, S.; Koumo, S.; Hirata, H.; Kijima, T. 4D model generator of the human lung, “Lung4Cer”. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 453–456. [Google Scholar]
- Roth, C.J.; Ismail, M.; Yoshihara, L.; Wall, W.A. A comprehensive computational human lung model incorporating inter-acinar dependencies: Application to spontaneous breathing and mechanical ventilation. Int. J. Numer. Meth. Bio. 2017, 33. [Google Scholar] [CrossRef] [PubMed]
- Roth, C.J.; Becher, T.; Frerichs, I.; Weiler, N.; Wall, W.A. Coupling of EIT with computational lung modeling for predicting patient-specific ventilatory responses. J. Appl. Physiol. 2016, 122, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Tong, Z.B.; Chan, H.K.; Yang, R.Y. CFD modelling of air and particle flows in different airway models. J. Aerosol Sci. 2019, 134, 14–28. [Google Scholar] [CrossRef]
- Augusto, L.L.X.; Goncalves, J.A.S.; Lopes, G.C. CFD evaluation of the influence of physical mechanisms, particle size, and breathing condition on the deposition of particulates in a triple bifurcation airway. Water Air Soil Poll. 2016, 227, 56. [Google Scholar] [CrossRef]
- Kim, C.S.; Fisher, D.M. Deposition characteristics of aerosol particles in sequentially bifurcating airway models. Aerosol Sci. Tech. 1999, 31, 198–220. [Google Scholar] [CrossRef]
- Kitaoka, H. A 4D model generator of the human lung. Forma 2011, 26, 19–24. [Google Scholar]
- Guha, S.; Hariharan, P.; Myers, M.R. Enhancement of ICRP’s lung deposition model for pathogenic bioaerosols. Aerosol Sci. Tech. 2014, 48, 1226–1235. [Google Scholar] [CrossRef]
- Aleksandropoulou, V.; Lazaridis, M. Development and application of a model (ExDoM) for calculating the respiratory tract dose and retention of particles under variable exposure conditions. Air Qual. Atmos. Hlth. 2013, 6, 13–26. [Google Scholar] [CrossRef]
- Watanabe, T.; Bartrand, T.A.; Weir, M.H.; Omura, T.; Haas, C.N. Development of a dose-response model for SARs coronavirus. Risk Anal. 2010, 30, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
- Price, P.S.; Koontz, M.; Wilkes, C.; Ryan, B.; Macintosh, D.; Georgopoulos, P. Construction of a Comprehensive Chemical Exposure Framework Using Person Oriented Modeling; American Chemistry Council: Washington, DC, USA, 2003; Contract Number 1338. [Google Scholar]
- Querol, X.; Moreno, T.; Karanasiou, A.; Reche, C.; Alastuey, A.; Viana, M.; Font, O.; Gil, J.; Miguel, E.d.; Capdevila, M. Variability of levels and composition of PM10 and PM2.5 in the Barcelona metro system. Atmos. Chem. Phys. 2012, 12, 5055–5076. [Google Scholar] [CrossRef]
- Chalvatzaki, E.; Lazaridis, M. Development and application of a dosimetry model (ExDoM2) for calculating internal dose of specific particle-bound metals in the human body. Inhal. Toxicol. 2015, 27, 308–320. [Google Scholar] [CrossRef] [PubMed]
- Chou, W.-C.; Chio, C.-P.; Liao, C.-M. Assessing airborne PM-bound arsenic exposure risk in semiconductor manufacturing facilities. J. Hazard. Mater. 2009, 167, 976–986. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Maheshwari, M.; Morisawa, S. Dietary and inhalation intake of lead and estimation of blood lead levels in adults and children in kanpur, india. Risk Anal. 2005, 25, 1573–1588. [Google Scholar] [CrossRef]
- O’Flaherty, E.J.; Kerger, B.D.; Hays, S.M.; Paustenbach, D.J. A physiologically based model for the ingestion of chromium(III) and chromium(VI) by humans. Toxicol. Sci. 2001, 60, 196–213. [Google Scholar] [CrossRef]
- Gali, N.K.; Jiang, S.Y.; Yang, F.; Sun, L.; Ning, Z. Redox characteristics of size-segregated PM from different public transport microenvironments inHong Kong. Air Qual. Atmos. Hlth. 2017, 10, 833–844. [Google Scholar] [CrossRef]
- Johansson, C.; Johansson, P.-Å. Particulate matter in the underground of Stockholm. Atmos. Environ. 2003, 37, 3–9. [Google Scholar] [CrossRef]
- Moreno, T.; Martins, V.; Querol, X.; Jones, T.; BéruBé, K.; Minguillón, M.C.; Amato, F.; Capdevila, M.; de Miguel, E.; Centelles, S.; et al. A new look at inhalable metalliferous airborne particles on rail subway platforms. Sci. Total Environ. 2015, 505, 367–375. [Google Scholar] [CrossRef]
- Karlsson, H.L.; Nilsson, L.; Möller, L. Subway particles are more genotoxic than street particles and induce oxidative stress in cultured human lung cells. Chem. Res. Toxicol. 2005, 18, 19–23. [Google Scholar] [CrossRef] [PubMed]
- Mammi-Galani, E.; Eleftheriadis, K.; Mendes, L.; Lazaridis, M. Exposure and dose to particulate matter inside the subway system of Athens, Greece. Air Qual. Atmos. Hlth. 2017, 10, 1015–1028. [Google Scholar] [CrossRef]
- Longest, P.W.; Holbrook, L.T. In silico models of aerosol delivery to the respiratory tract—Development and applications. Adv. Drug Deliver. Rev. 2012, 64, 296–311. [Google Scholar] [CrossRef] [PubMed]
- Byron, P.R.; Hindle, M.; Lange, C.F.; Longest, P.W.; McRobbie, D.; Oldham, M.J.; Olsson, B.; Thiel, C.G.; Wachtel, H.; Finlay, W.H. In vivo–in vitro correlations: Predicting pulmonary drug deposition from pharmaceutical aerosols. J. Aerosol Med. Pulm. D. 2010, 23, S-59–S-69. [Google Scholar] [CrossRef]
- Tian, G.; Hindle, M.; Lee, S.; Longest, P.W. Validating CFD predictions of pharmaceutical aerosol deposition with in vivo data. Pharm. Res. 2015, 32, 3170–3187. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.P. Exact analysis of aerosol deposition during steady breathing. Powder Technol. 1978, 21, 55–62. [Google Scholar] [CrossRef]
- Choi, J.-I.; Kim, C.S. Mathematical analysis of particle deposition in human lungs: An improved single path transport model. Inhal. Toxicol. 2007, 19, 925–939. [Google Scholar] [CrossRef]
- Deng, Q.; Deng, L.; Miao, Y.; Guo, X.; Li, Y. Particle deposition in the human lung: Health implications of particulate matter from different sources. Environ. Res. 2019, 169, 237–245. [Google Scholar] [CrossRef]
- Karthiga Devi, S.G.; Panchagnula, M.V.; Alladi, M. Designing aerosol size distribution to minimize inter-subject variability of alveolar deposition. J. Aerosol Sci. 2016, 101, 144–155. [Google Scholar] [CrossRef]
- Anjilvel, S.; Asgharian, B. A multiple-path model of particle deposition in the rat lung. Fund. Appl. Toxicol. 1995, 28, 41–50. [Google Scholar] [CrossRef]
- Manigrasso, M.; Buonanno, G.; Fuoco, F.C.; Stabile, L.; Avino, P. Aerosol deposition doses in the human respiratory tree of electronic cigarette smokers. Environ. Pollut. 2015, 196, 257–267. [Google Scholar] [CrossRef] [PubMed]
- Manojikumar, N.; Srimuruganandam, B.; Nagendra, S.M.S. Application of multiple-path particle dosimetry model for quantifying age specified deposition of particulate matter in human airway. Ecotox. Environ. Safe. 2019, 168, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, W.; Koblinger, L. Monte carlo modeling of aerosol deposition in human lungs. Part II: Deposition fractions and their sensitivity to parameter variations. J. Aerosol Sci. 1990, 21, 675–688. [Google Scholar] [CrossRef]
- Hofmann, W.; Asgharian, B.; Winkler-Heil, R. Modeling intersubject variability of particle deposition in human lungs. J. Aerosol Sci. 2002, 33, 219–235. [Google Scholar] [CrossRef]
- Hofmann, W.; Bergmann, R.; Koblinger, L. Characterization of local particle deposition patterns in human and rat lungs by different morphometric parameters. J. Aerosol Sci. 1999, 30, 651–667. [Google Scholar] [CrossRef]
- Hofmann, W.; Bolt, L.; Sturm, R.; Fleming, J.S.; Conway, J.H. Simulation of three-dimensional particle deposition patterns in human lungs and comparison with experimental spect data. Aerosol Sci. Tech. 2005, 39, 771–781. [Google Scholar] [CrossRef]
- Hofmann, W.; Winkler-Heil, R.; Balásházy, I. The effect of morphological variability on surface deposition densities of inhaled particles in human bronchial and acinar airways. Inhal. Toxicol. 2006, 18, 809–819. [Google Scholar] [CrossRef]
- Sturm, R. A stochastic model of carbon nanotube deposition in the airways and alveoli of the human respiratory tract. Inhal. Toxicol. 2016, 28, 49–60. [Google Scholar] [CrossRef]
- Sturm, R. Theoretical models of carcinogenic particle deposition and clearence in children’s lung. J. Thorac. Dis. 2012, 4, 368–376. [Google Scholar]
- Kolanjiyil, A.V.; Kleinstreuer, C. Nanoparticle mass transfer from lung airways to systemic regions—part I: Whole-lung aerosol dynamics. J. Biomech. Eng. 2013, 135. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. Airflow and particle transport in the human respiratory system. Annu. Rev. Fluid Mech. 2009, 42, 301–334. [Google Scholar] [CrossRef]
- Kolanjiyil, A.V.; Kleinstreuer, C. Nanoparticle mass transfer from lung airways to systemic regions—part II: Multi-compartmental modeling. J. Biomech. Eng. 2013, 135. [Google Scholar] [CrossRef] [PubMed]
- Kolanjiyil, A.V.; Kleinstreuer, C.; Sadikot, R.T. Computationally efficient analysis of particle transport and deposition in a human whole-lung-airway model. Part II: Dry powder inhaler application. Comput. Biol. Med. 2017, 84, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Kolanjiyil, A.V.; Kleinstreuer, C. Computationally efficient analysis of particle transport and deposition in a human whole-lung-airway model. Part I: Theory and model validation. Comput. Biol. Med. 2016, 79, 193–204. [Google Scholar] [CrossRef]
- Hofmann, W. Modelling inhaled particle deposition in the human lung—a review. J. Aerosol Sci. 2011, 42, 693–724. [Google Scholar] [CrossRef]
- Kleven, M.; Melaaen, M.C.; Djupesland, P.E.R.G. Computational fluid dynamics (CFD) applied in the drug delivery design process to the nasal passages: A review. J. Mech. Med. Biol. 2012, 12, 1230002. [Google Scholar] [CrossRef]
- Aasgrav, E.; Johnsen, S.G.; Simonsen, A.J.; Muller, B. CFD simulations of turbulent flow in the human upper airways. In Proceedings of the 12th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 2017. [Google Scholar]
- Sharma, A. Introduction to Computational Fluid Dynamics: Development, Application, and Analysis; Wiley: West Sussex, UK, 2017. [Google Scholar]
- Surana, K.S.; Allu, S.; Tenpas, P.W.; Reddy, J.N. K-version of finite element method in gas dynamics: Higher-order global differentiability numerical solutions. Int. J. Numer. Meth. Eng. 2007, 69, 1109–1157. [Google Scholar] [CrossRef]
- Huebner, K.H.; Dewhrist, D.L.; Smith, D.E.; Byrom, T.G. The Finite Element Method for Engineers, 4th ed.; Wiley: West Sussex, UK, 2001; p. 720. [Google Scholar]
- Tang, Y.; Guo, B. Computational fluid dynamics simulation of aerosol transport and deposition. Front. Env. Sci. Eng. China 2011, 5, 362–377. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C. Laminar-to-turbulent fluid–nanoparticle dynamics simulations: Model comparisons and nanoparticle-deposition applications. Int. J. Numer. Meth. Bio. 2011, 27, 1930–1950. [Google Scholar] [CrossRef]
- Houzeaux, G.; Borrell, R.; Fournier, Y.; Garcia-Gasulla, M.; Gobbert, J.H.; Hachem, E.; Mehta, V.; Mesri, Y.; Owen, H.; Vazquez, M. High-Performance Computing: Dos and Don’ts; Ionescu, A., Ed.; IntechOpen: London, UK, 2018. [Google Scholar]
- Lintermann, A. Efficient parallel geometry distribution for the simulation of complex flows. In ECCOMAS Congress; ECCOMAS: Crete, Greece, 2016. [Google Scholar]
- Longest, P.W.; Tian, G.; Khajeh-Hosseini-Dalasm, N.; Hindle, M. Validating whole-airway CFD predictions of DPI aerosol deposition at multiple flow rates. J. Aerosol Med. Pulm. D. 2016, 29, 461–481. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, C.; Shi, H.; Zhang, Z. Computational analyses of a pressurized metered dose inhaler and a new drug–aerosol targeting methodology. J. Aerosol Med. 2007, 20, 294–309. [Google Scholar] [CrossRef] [PubMed]
- Vinchurkar, S.; De Backer, L.; Vos, W.; Van Holsbeke, C.; De Backer, J.; De Backer, W. A case series on lung deposition analysis of inhaled medication using functional imaging based computational fluid dynamics in asthmatic patients: Effect of upper airway morphology and comparison with in vivo data. Inhal. Toxicol. 2012, 24, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Lintermann, A.; Schröder, W. Simulation of aerosol particle deposition in the upper human tracheobronchial tract. Eur. J. Mech. B-Fluid. 2017, 63, 73–89. [Google Scholar] [CrossRef]
- Calmet, H.; Yamamoto, T.; Eguzkitza, B.; Lehmkuhl, O.; Olivares, E.; Kobayashi, Y.; Tomoda, K.; Houzeaux, G.; Vázquez, M. Numerical evaluation of aerosol exhalation through nose treatment. J. Aerosol Sci. 2019, 128, 1–13. [Google Scholar] [CrossRef]
- Calmet, H.; Gambaruto, A.M.; Bates, A.J.; Vázquez, M.; Houzeaux, G.; Doorly, D.J. Large-scale CFD simulations of the transitional and turbulent regime for the large human airways during rapid inhalation. Comput. Biol. Med. 2016, 69, 166–180. [Google Scholar] [CrossRef]
- Lin, C.-L.; Tawhai, M.H.; McLennan, G.; Hoffman, E.A. Multiscale simulation of gas flow in subject-specific models of the human lung. IEEE Eng. Med. Biol. 2009, 28, 25–33. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. An adjustable triple-bifurcation unit model for air-particle flow simulations in human tracheobronchial airways. J. Biomech. Eng. 2008, 131. [Google Scholar] [CrossRef]
- Walters, D.K.; Luke, W.H. A method for three-dimensional Navier–Stokes simulations of large-scale regions of the human lung airway. J. Fluid. Eng. 2010, 132. [Google Scholar] [CrossRef]
- Walters, D.K.; Luke, W.H. Computational fluid dynamics simulations of particle deposition in large-scale, multigenerational lung models. J. Biomech. Eng. 2010, 133. [Google Scholar] [CrossRef]
- Paiva, M.; Engel, L.A. Pulmonary interdependence of gas transport. J. Appl. Physiol. 1979, 47, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Grivas, G.; Chaloulakou, A. Artificial neural network models for prediction of PM10 hourly concentrations, in the greater area of Athens, Greece. Atmos. Environ. 2006, 40, 1216–1229. [Google Scholar] [CrossRef]
- Perez, P.; Reyes, J. An integrated neural network model for PM10 forecasting. Atmos. Environ. 2006, 40, 2845–2851. [Google Scholar] [CrossRef]
- Ngoc, L.T.N.; Kim, M.; Bui, V.K.H.; Park, D.; Lee, Y.-C. Particulate matter exposure of passengers at bus stations: A review. Int. J. Environ. Res. Public Health 2018, 15. [Google Scholar] [CrossRef]
- Nazir, J.; Barlow, D.J.; Lawrence, M.J.; Richardson, C.J.; Shrubb, I. Artificial neural network prediction of aerosol deposition in human lungs. Pharm. Res. 2002, 19, 1130–1136. [Google Scholar] [CrossRef]
- Nazir, J.; Barlow, D.J.; Lawrence, M.J.; Shrubb, I. Artificial neural network prediction of the patterns of deposition of polydisperse aerosols within human lungs. J. Pharm. Sci. 2005, 94, 1986–1997. [Google Scholar] [CrossRef]
- Emami, J. In vitro - in vivo Correlation: From Theory to Applications. J. Pharm. Pharm. Sci. 2006; Volume 9, 169–189. [Google Scholar]
- Matas, M.d.; Shao, Q.; Richardson, C.H.; Chrystyn, H. Evaluation of in vitro in vivo correlations for dry powder inhaler delivery using artificial neural networks. Eur. J. Pharm. Sci. 2008, 33, 80–90. [Google Scholar] [CrossRef]
- Muddle, J.; Kirton, S.B.; Muddle, I.P.A.; Murnane, D.; Ali, J.; Brown, M.; Page, C.; Forbes, B. Predicting the fine particle fraction of dry powder inhalers using artificial neural networks. J. Pharm. Sci. 2017, 106, 313–321. [Google Scholar] [CrossRef][Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).