Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes
Abstract
1. Introduction
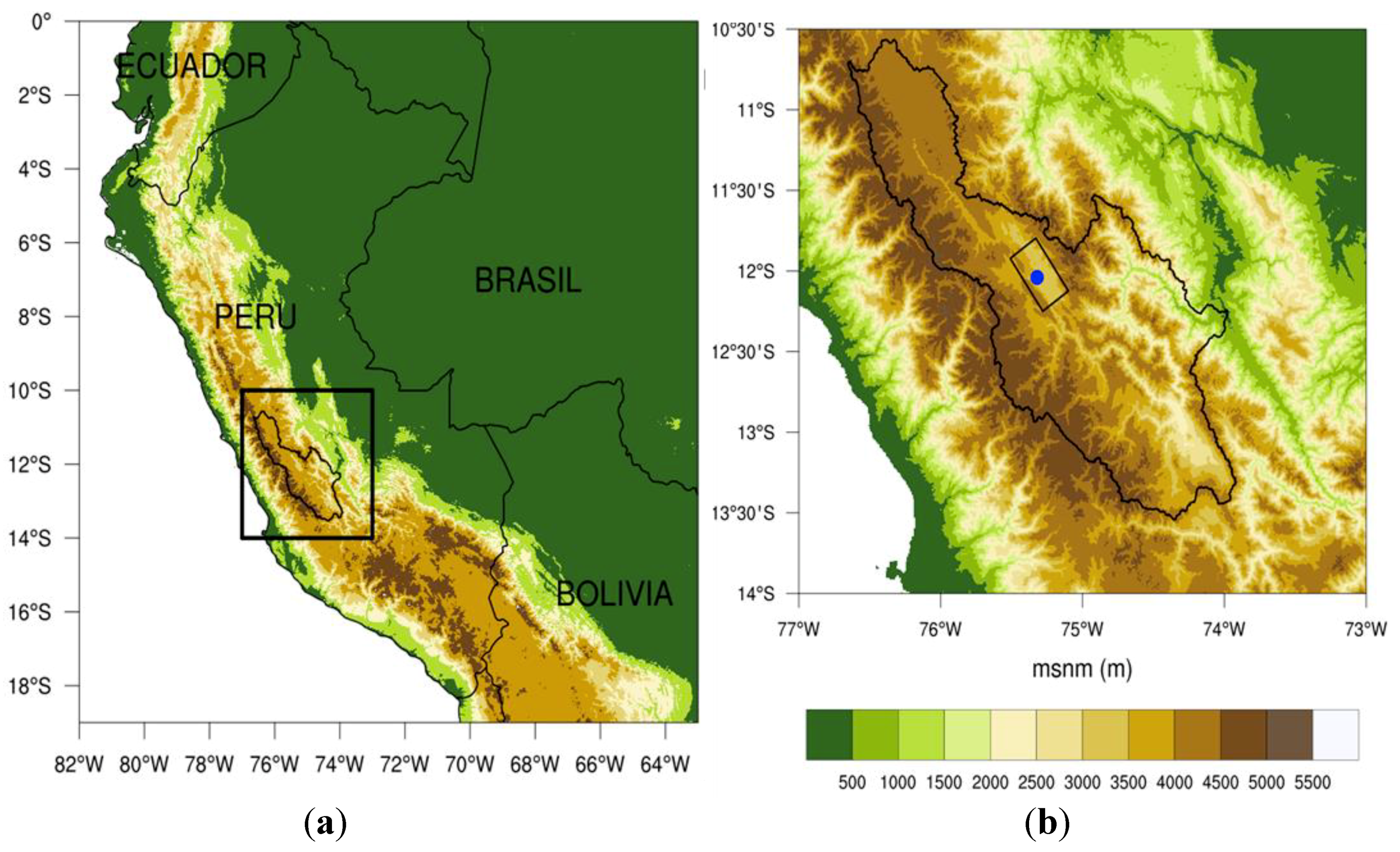
2. Instrumentation and Methodology
2.1. Parsivel Disdrometer
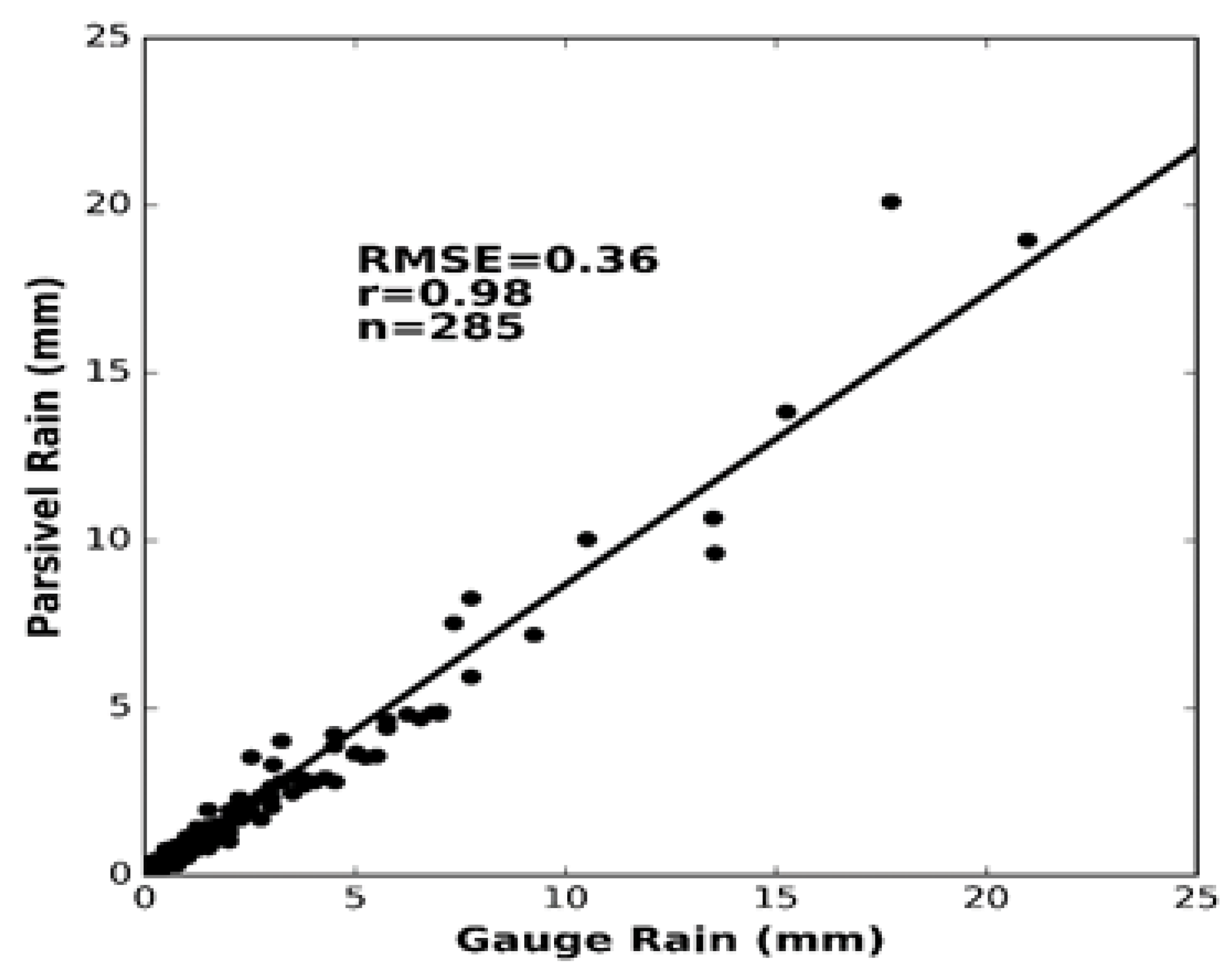
2.2. Methodology
3. Results and Discussion
3.1. Raindrop Size Distribution
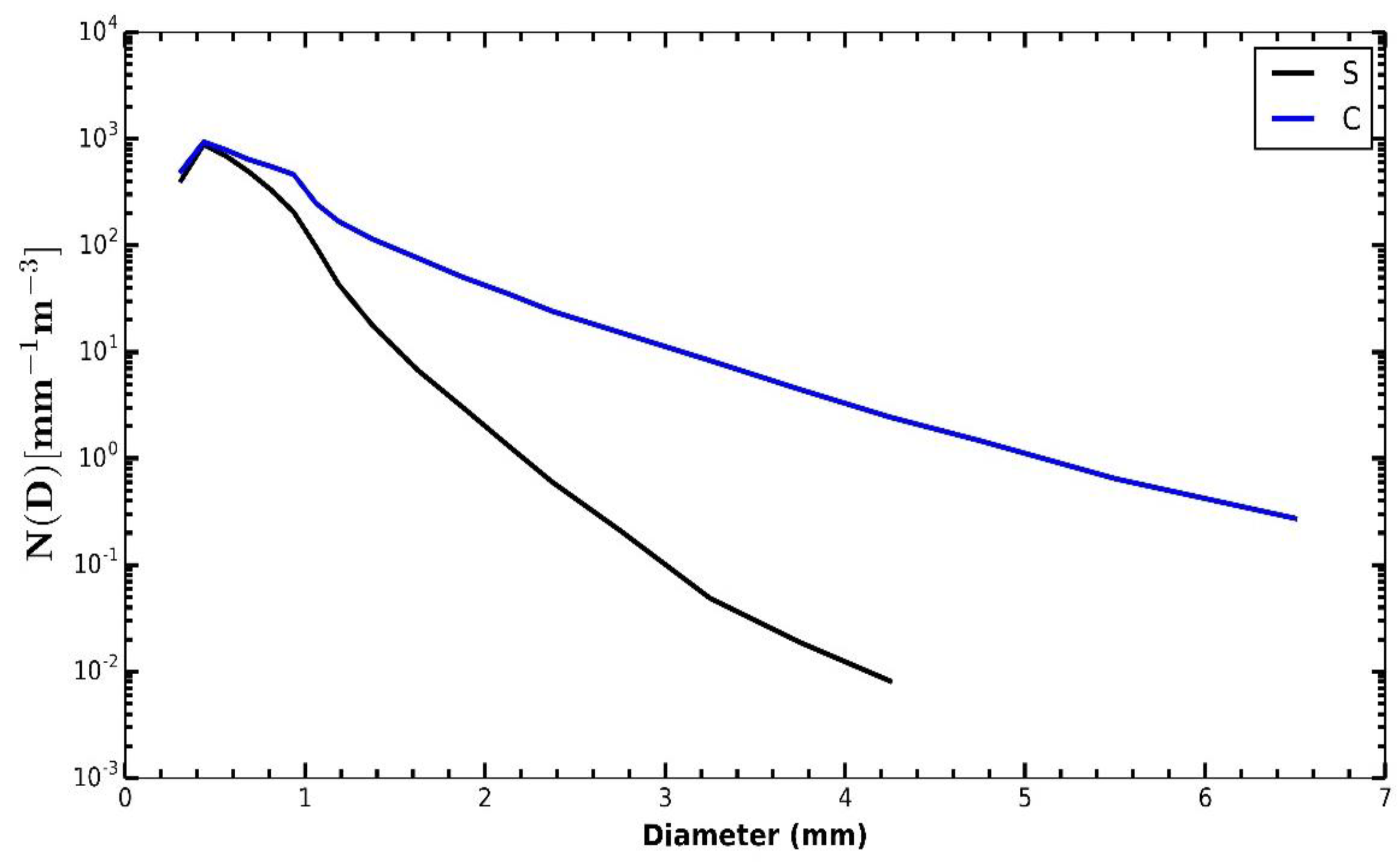
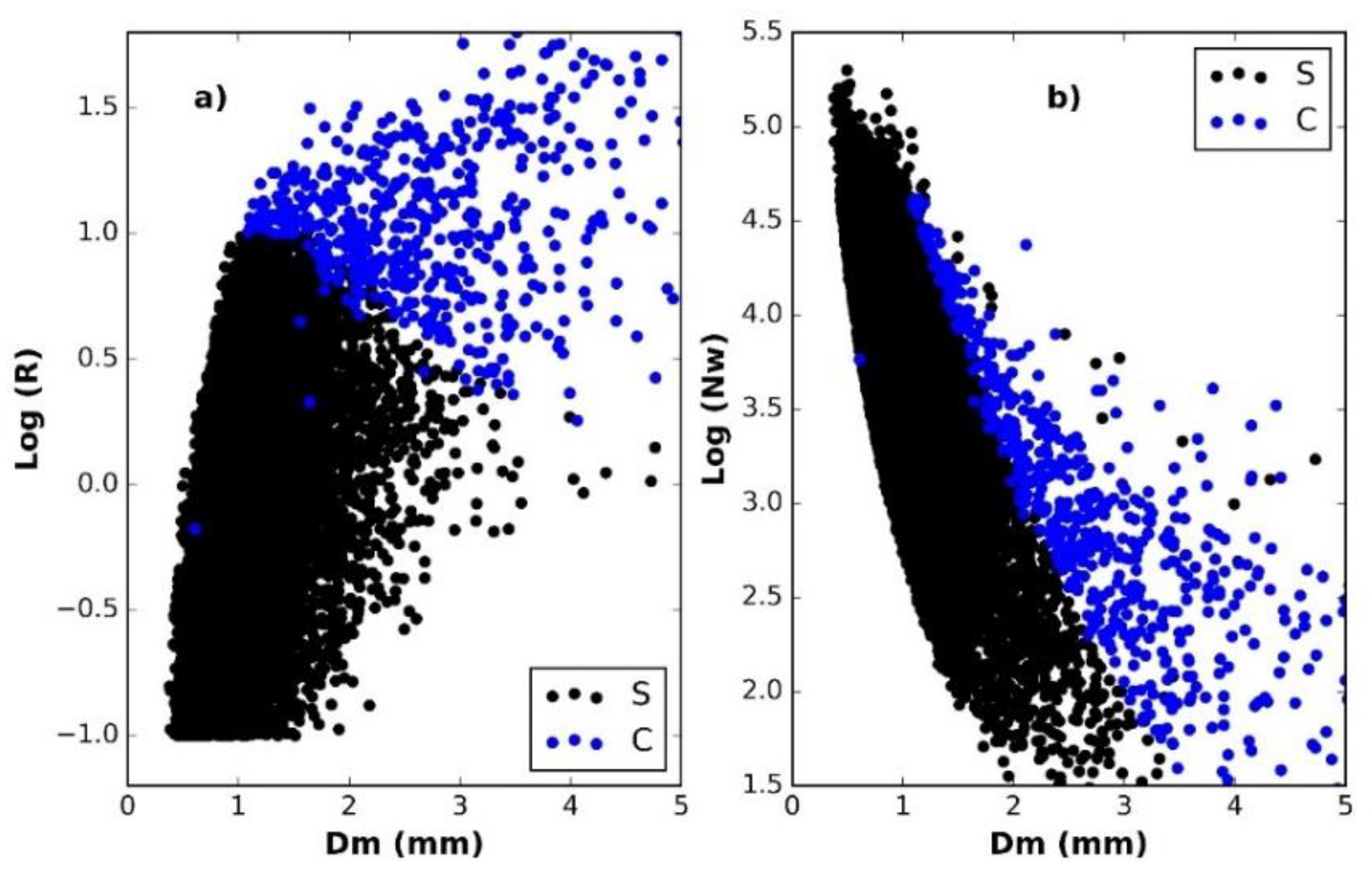
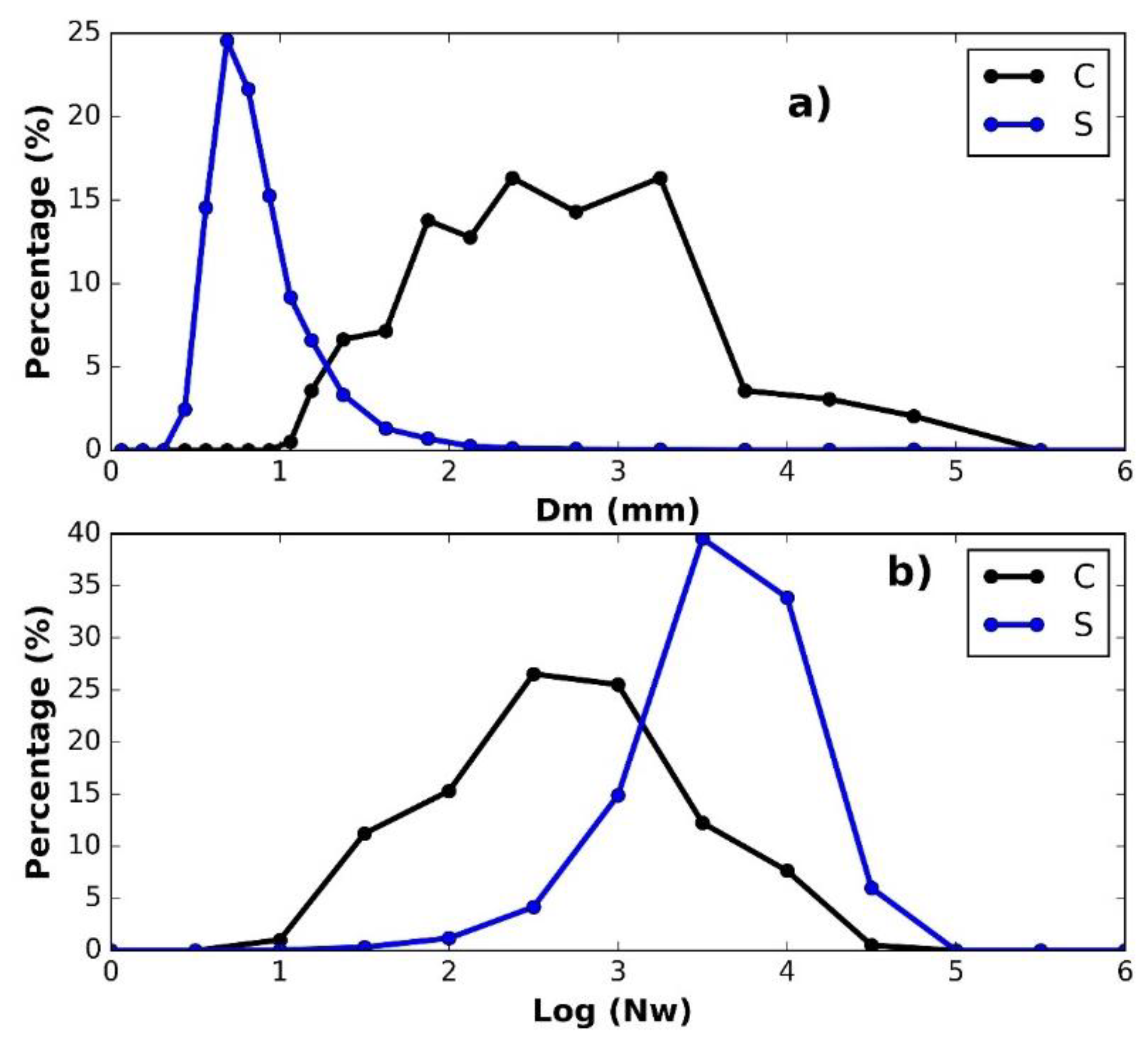
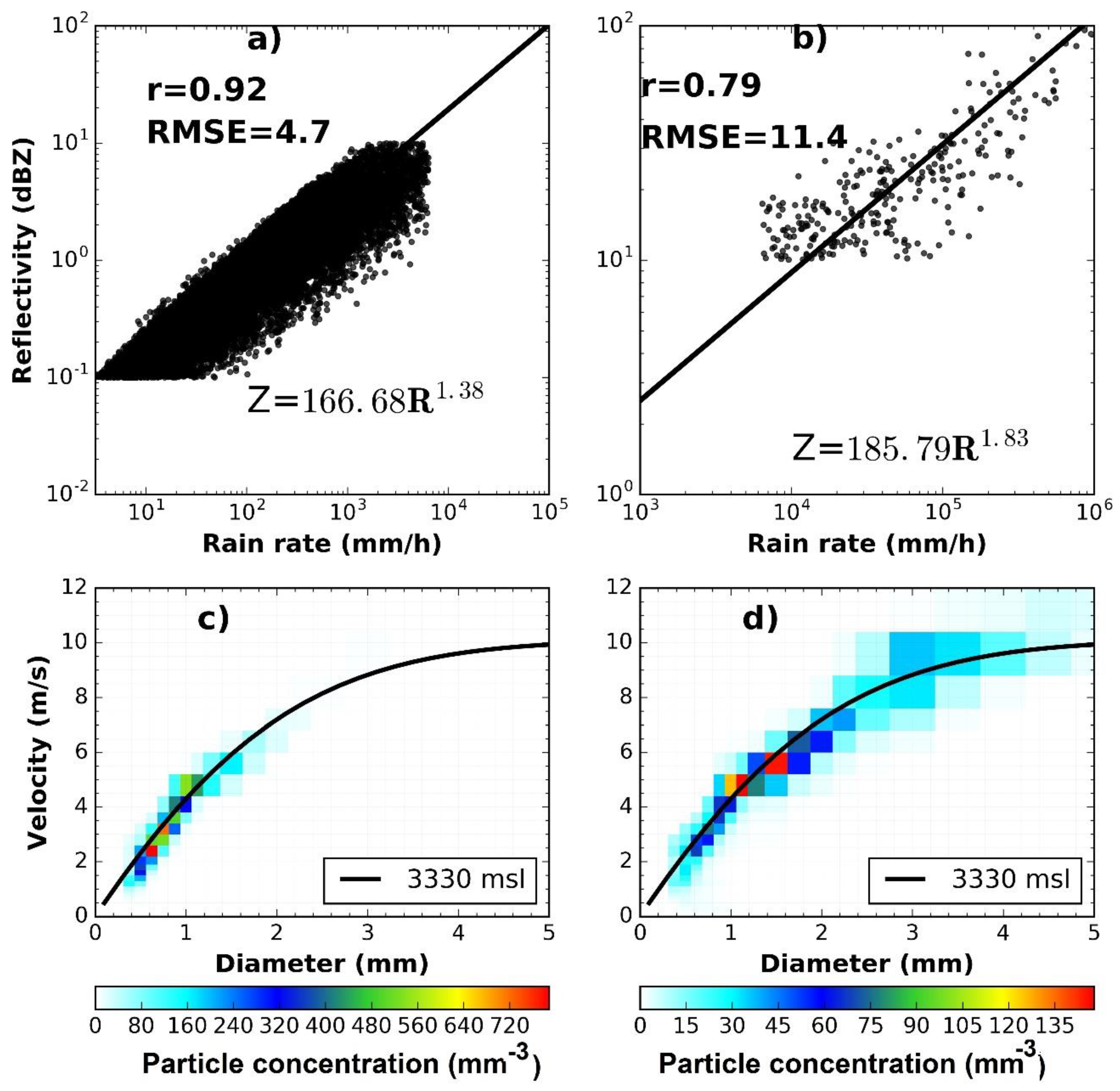
3.2. Convective and Stratiform Rainfall
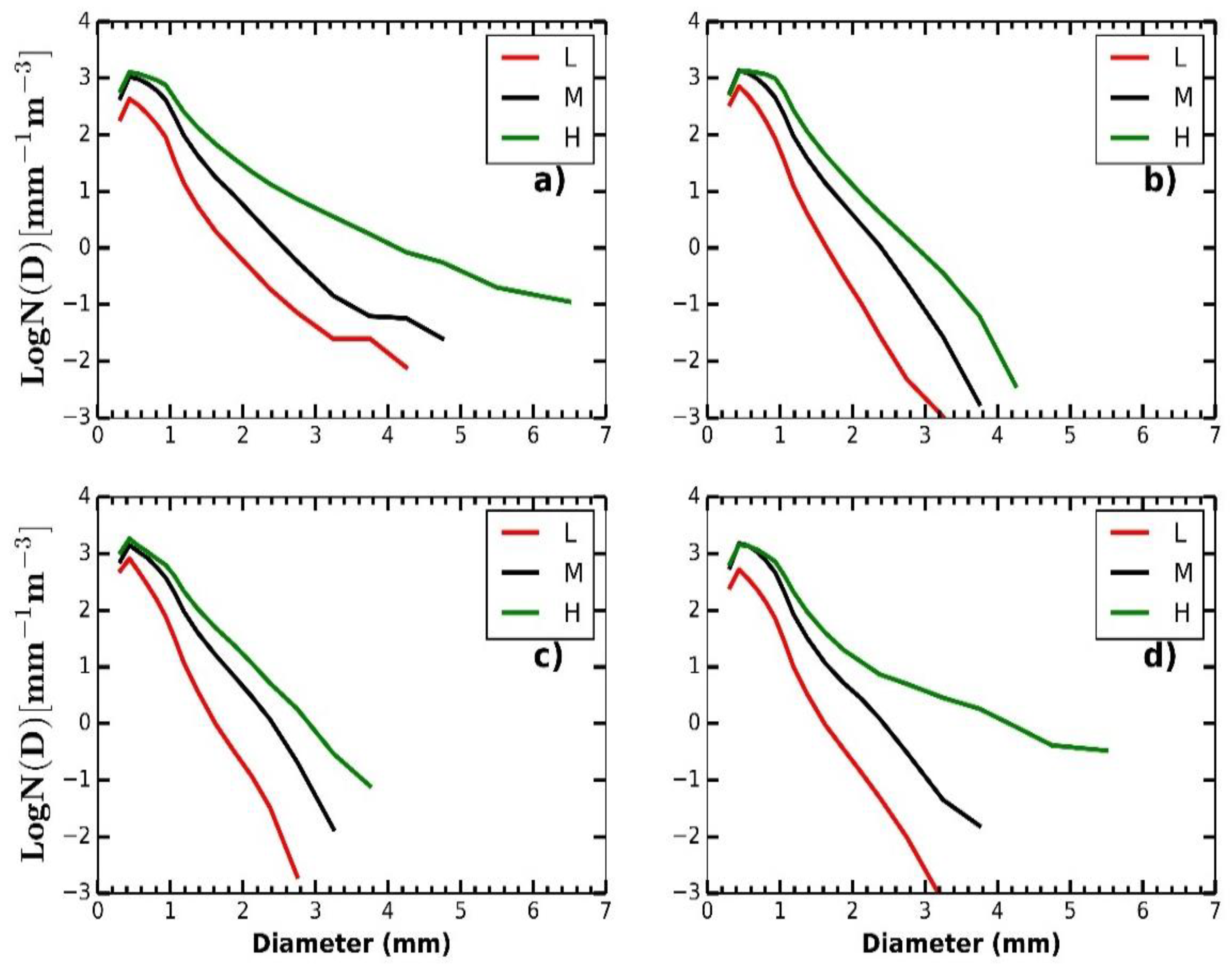
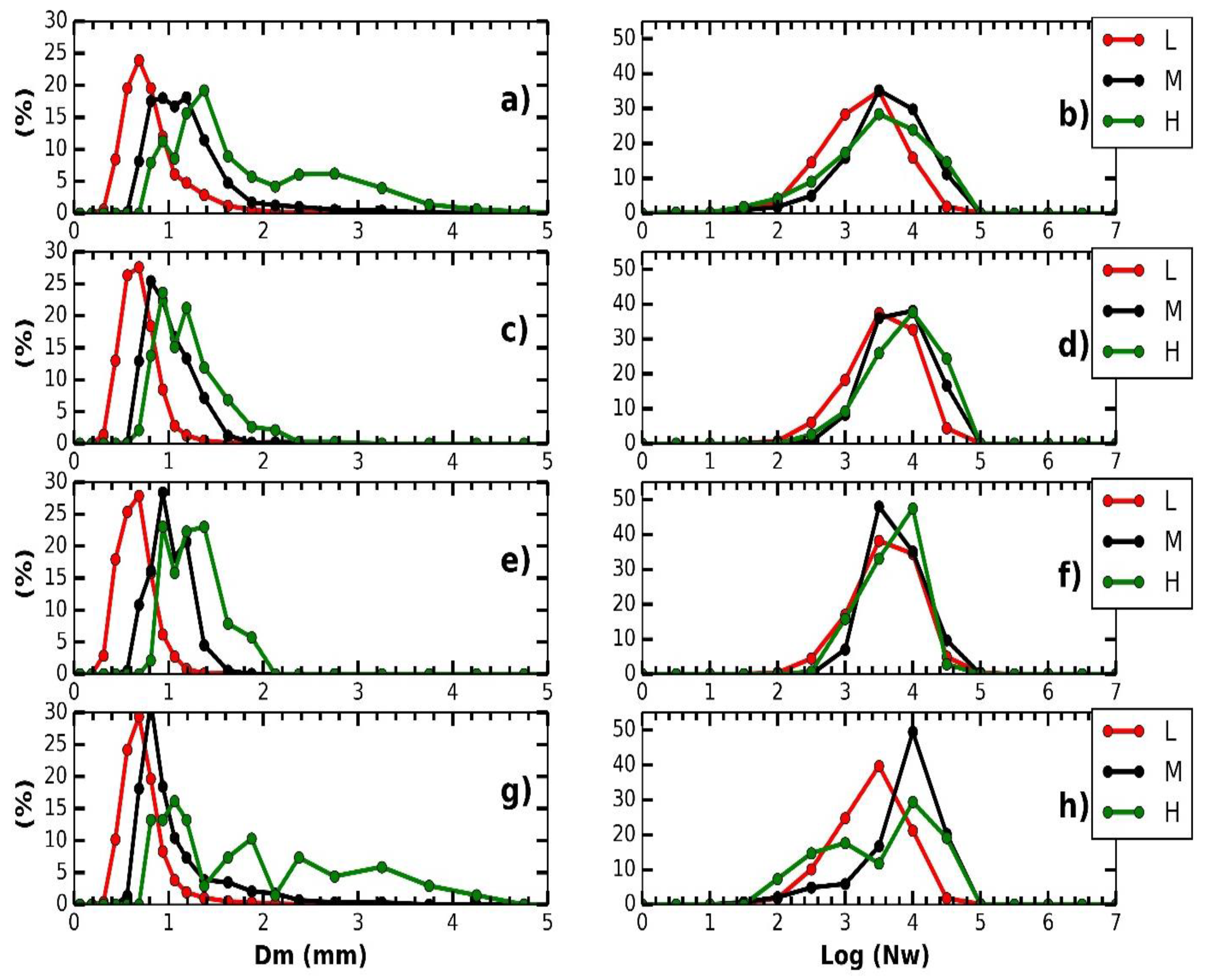
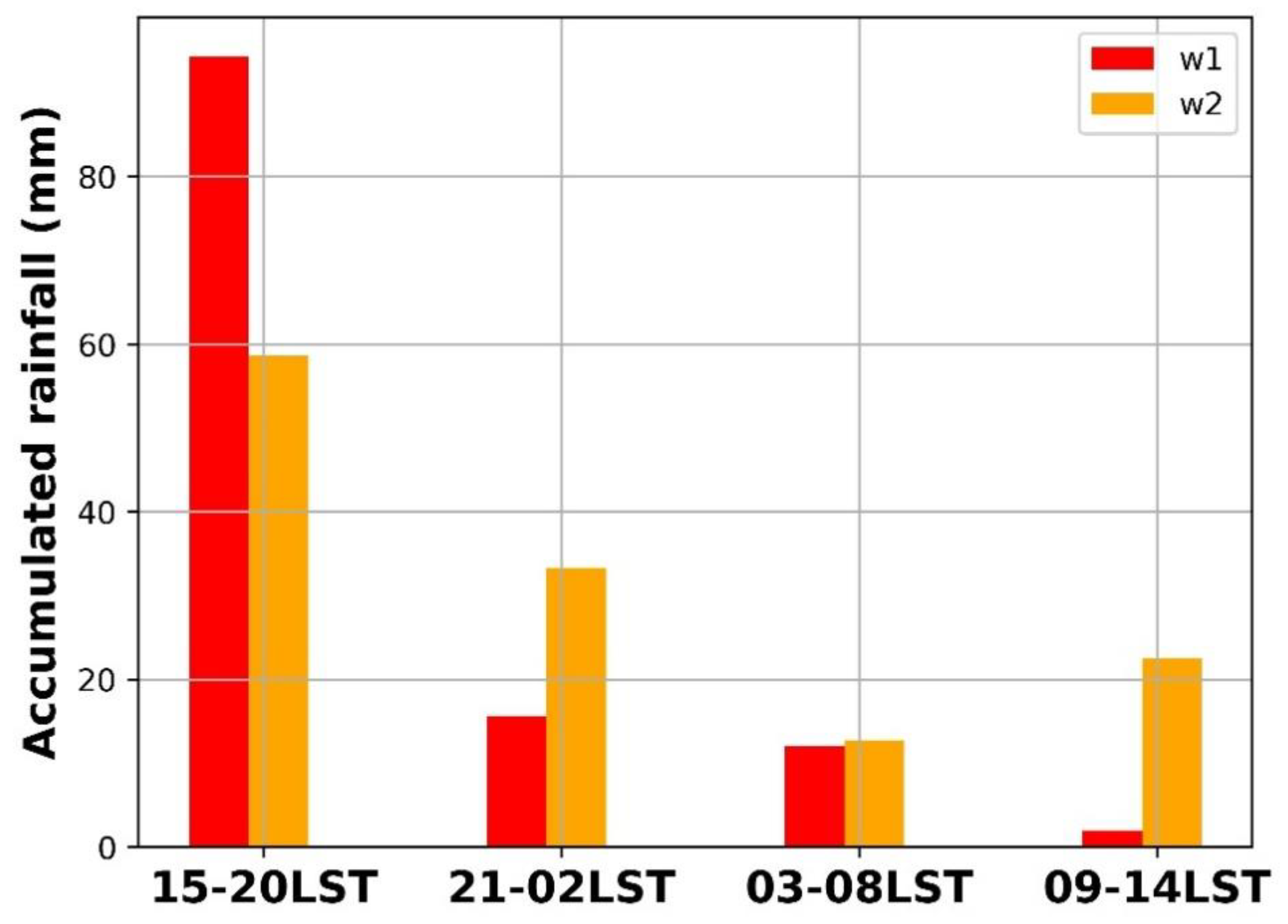
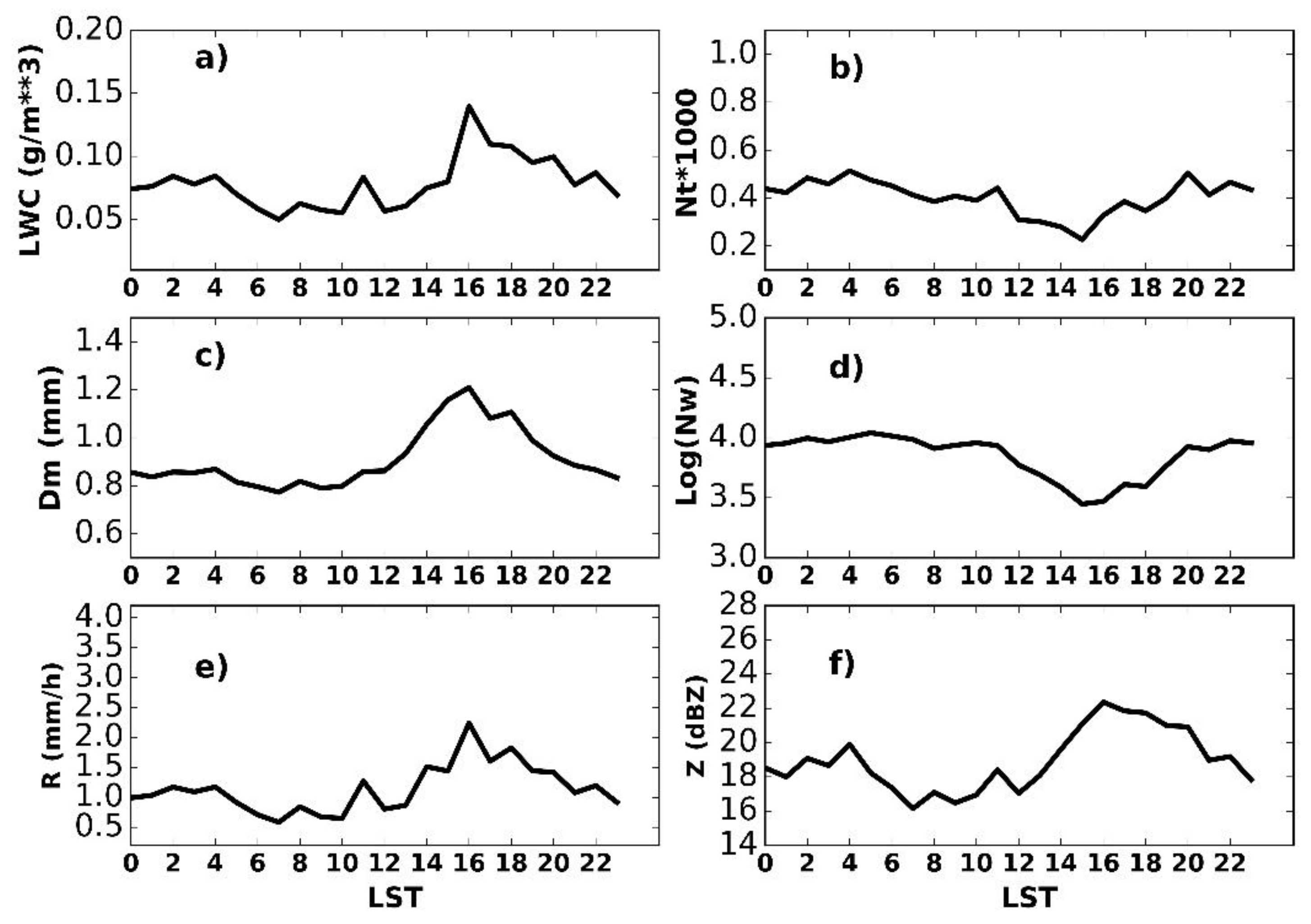
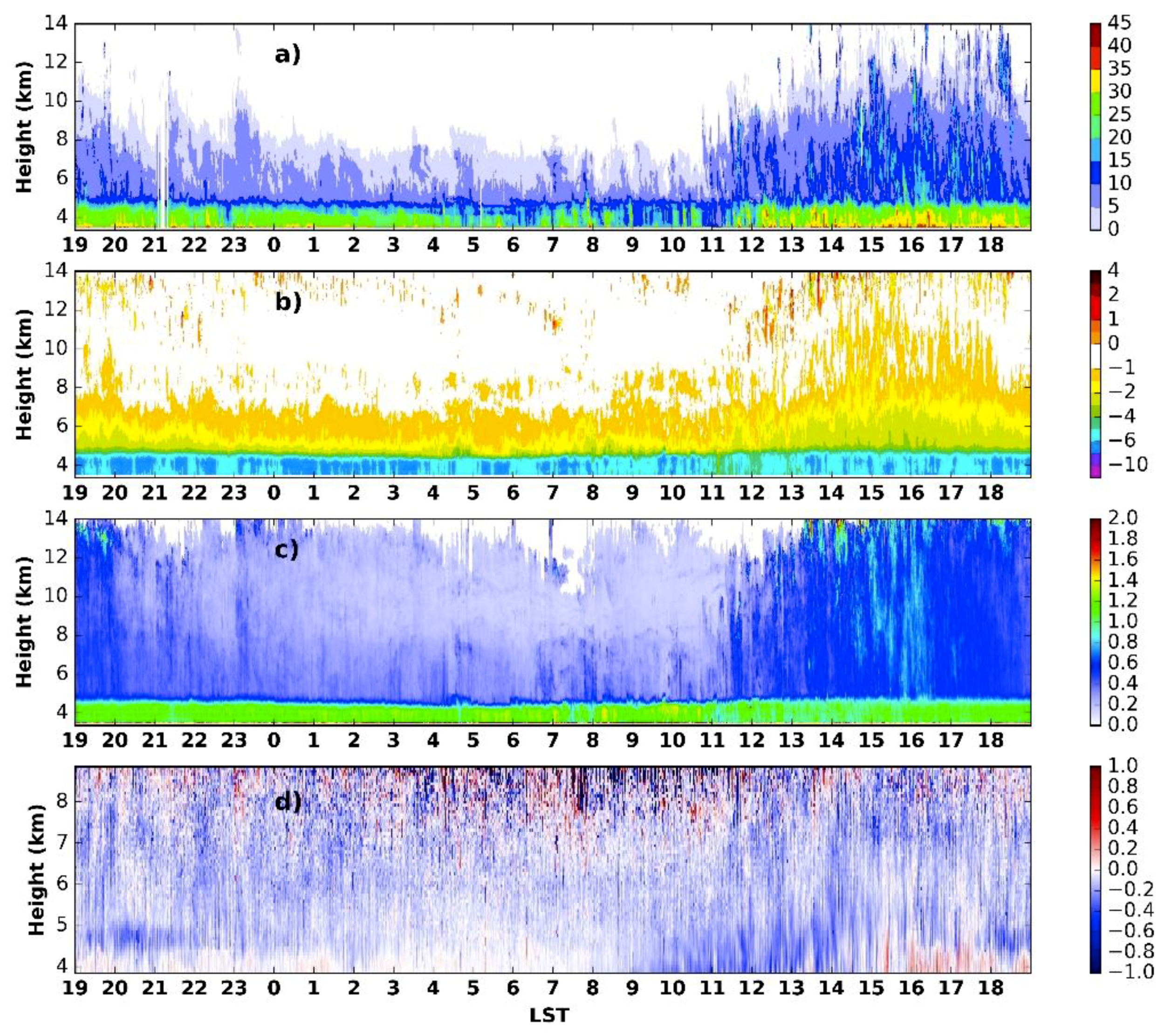
3.3. Diurnal Cycle
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jensen, A.A.; Harrington, J.Y.; Morrison, H. Microphysical characteristics of squall-line stratiform precipitation and transition zones simulated using an ice particle property-evolving model. Mon. Weather Rev. 2018, 146, 723–743. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The Distribution of Raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Prat, O.P.; Barros, A.P. Exploring the transient behavior of Z-R relationships: Implications for radar rainfall estimation. J. Appl. Meteorol. Climatol. 2009, 48, 2127–2143. [Google Scholar] [CrossRef]
- Ghada, W.; Buras, A.; Lüpke, M.; Schunk, C.; Menzel, A. Rain microstructure parameters vary with large-scale weather conditions in Lausanne, Switzerland. Remote Sens. 2018, 10, 811. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- You, C.H.; Kang, M.Y.; Hwang, Y.; Yee, J.J.; Jang, M.; Lee, D.I. A statistical approach to radar rainfall estimates using polarimetric variables. Atmos. Res. 2018, 209, 65–75. [Google Scholar] [CrossRef]
- Nzeukou, A.; Sauvageot, H.; Ochou, A.D.; Kebe, C.M.F. Raindrop size distribution and radar parameters at Cape Verde. J. Appl. Meteorol. 2004, 43, 90–105. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Thurai, M.; Han, D. Characteristics of raindrop spectra as normalized gamma distribution from a Joss-Waldvogel disdrometer. Atmos. Res. 2012, 108, 57–73. [Google Scholar] [CrossRef]
- Houze, R.A. Stratiform Precipitation in regions of convection: A meteorological paradox? Bull. Am. Meteorol. Soc. 1997, 78, 2179–2196. [Google Scholar] [CrossRef]
- Martinez, D.; Gori, E.G. Raindrop size distributions in convective clouds over Cuba. Atmos. Res. 1999, 52, 221–239. [Google Scholar] [CrossRef]
- Villalobos-Puma, E.; Martinez-Castro, D.; Kumar, S.; Silva, Y.; Fashe, O. Estudio de tormentas convectivas sobre los Andes Centrales del Perú usando los radares PR-TRMM y KuPR-GPM. Rev. Cub. Meteor. 2019, 25, 59–75. [Google Scholar]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uijlenhoet, R. A general approach to double-moment normalization of drop size distributions. J. Appl. Meteorol. 2004, 43, 264–281. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteor. 1969, 35, 355–371. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using dual-polarized radar and dual-frequency profiler for DSD characterization: A case study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- Thompson, E.J.; Rutledge, S.A.; Dolan, B.; Thurai, M. Drop size distributions and radar observations of convective and stratiform rain over the equatorial Indian and West Pacific Oceans. J. Atmos. Sci. 2015, 72, 4091–4125. [Google Scholar] [CrossRef]
- Instituto Geofisico del Peru. Vulnerabilidad Actual y Futura Ante el Cambio Climático Y Medidas de Adaptación en la Cuenca del Rio Mantaro: Volumen III. 2005. Available online: https://repositorio.igp.gob.pe/handle/IGP/742 (accessed on 27 December 2019).
- Silva, Y.; Takahashi, K.; Chávez, R. Dry and wet rainy seasons in the Mantaro river basin (Central Peruvian Andes). Adv. Geosci. 2008, 14, 261–264. [Google Scholar] [CrossRef]
- Saavedra, M.; Takahashi, K. Physical controls on frost events in the central Andes of Peru using in situ observations and energy flux models. Agric. For. Meteorol. 2017, 239, 58–70. [Google Scholar] [CrossRef]
- Zubieta, R.; Saavedra, M.; Silva, Y.; Giráldez, L. Erratum to: Spatial analysis and temporal trends of daily precipitation concentration in the Mantaro River basin: Central Andes of Peru. Stoch. Environ. Res. Risk Assess. 2017, 31. [Google Scholar] [CrossRef]
- Flores-Rojas, J.L.; Moya-Alvarez, A.S.; Kumar, S.; Martinez-Castro, D.; Villalobos-Puma, E.; Silva-Vidal, Y. Analysis of possible triggering mechanisms of severe thunderstorms in the tropical central Andes of Peru, Mantaro Valley. Atmosphere 2019, 10, 301. [Google Scholar] [CrossRef]
- Giovannettone, J.P.; Barros, A.P. Probing regional orographic controls of precipitation and cloudiness in the Central Andes using satellite data. J. Hydrometeorol. 2009, 10, 167–182. [Google Scholar] [CrossRef]
- Kirshbaum, D.J.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist orographic convection: Physical mechanisms and links to surface-exchange processes. Atmosphere 2018, 9, 80. [Google Scholar] [CrossRef]
- Martínez-Castro, D.; Kumar, S.; Flores Rojas, J.L.; Moya-Álvarez, A.; Valdivia-Prado, J.M.; Villalobos-Puma, E.; Del Castillo-Velarde, C.; Silva-Vidal, Y. The impact of microphysics parameterization in the simulation of two convective rainfall events over the central andes of peru using WRF-ARW. Atmosphere 2019, 10, 442. [Google Scholar] [CrossRef]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the new version of the laser-optical disdrometer, OTT parsivel. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL snow observations: A critical assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Sokol, Z.; Minářová, J.; Novák, P. Classification of hydrometeors using measurements of the ka-band cloud radar installed at the Milešovka Mountain (Central Europe). Remote Sens. 2018, 10, 1674. [Google Scholar] [CrossRef]
- Willis, P.T. Functional fits to some observed drop size distributions and parameterization of rain. J. Atmos. Sci. 1984, 41, 1648–1661. [Google Scholar] [CrossRef]
- Dou, X.; Testud, J.; Amayenc, P.; Black, R. The parameterization of rain for a weather radar. Comptes Rendus l’Academie Sci.-Ser. IIA Sci. la Terre des. Planetes 1999, 328, 577–582. [Google Scholar] [CrossRef]
- Beard, K.V. Simple altitude adjustments to raindrop velocities for Doppler radar analysis. J. Atmos. Ocean. Technol. 1985, 2, 468–471. [Google Scholar] [CrossRef][Green Version]
- Lhermitte, R. Attenuation and scattering of millimeter wavelength radiation by clouds and precipitation. J. Atmos. Ocean. Technol. 1990, 7, 464–479. [Google Scholar] [CrossRef]
- Houghton, H.G. On precipitation mechanisms and their artificial modification. J. Appl. Meteorol. 1968, 7, 851–859. [Google Scholar] [CrossRef]
- Gamache, J.F.; Houze, R.A. Mesoscale air motions associated with a tropical squall line. Mon. Weather Rev. 1982, 110, 118–135. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A.; Williams, C.R.; Ecklund, W.L.; Gage, K.S. Tropical rainfall associated with convective and stratiform clouds: Intercomparison of disdrometer and profiler measurements. J. Appl. Meteorol. 1999, 38, 302–320. [Google Scholar] [CrossRef]
- Suh, S.H.; You, C.H.; Lee, D.I. Climatological characteristics of raindrop size distributions in Busan, Republic of Korea. Hydrol. Earth Syst. Sci. 2016, 20, 193–207. [Google Scholar] [CrossRef]
- Caracciolo, C.; Porcù, F.; Prodi, F. Precipitation classification at mid-latitudes in terms of drop size distribution parameters. Adv. Geosci. 2008, 16, 11–17. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Chavez, S.; Ronchail, J.; Junquas, C.; Takahashi, K.; Lavado, W. Rainfall hotspots over the southern tropical Andes: Spatial distribution, rainfall intensity, and relations with large-scale atmospheric circulation. Water Resour. Res. 2015, 51, 3459–3475. [Google Scholar] [CrossRef]
- Junquas, C.; Li, L.; Vera, C.S.; Le Treut, H.; Takahashi, K. Influence of south america orography on summertime precipitation in Southeastern South America. Clim. Dyn. 2016, 46, 3941–3963. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of raindrop sizes and fall velocities in a semiarid plateau climate: Convective versus stratiform rains. J. Appl. Meteorol. Climatol. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Lagos, P.; Silva, Y.; Nickl, E.; Mosquera, K. El Niño-Related precipitation variability in Perú. Adv. Geosci. 2008, 14, 231–237. [Google Scholar] [CrossRef]
- Moya-Álvarez, A.S.; Gálvez, J.; Holguín, A.; Estevan, R.; Kumar, S.; Villalobos, E.; Martínez-Castro, D.; Silva, Y. Extreme rainfall forecast with the WRF-ARW model in the Central Andes of Peru. Atmosphere 2018, 9, 362. [Google Scholar] [CrossRef]
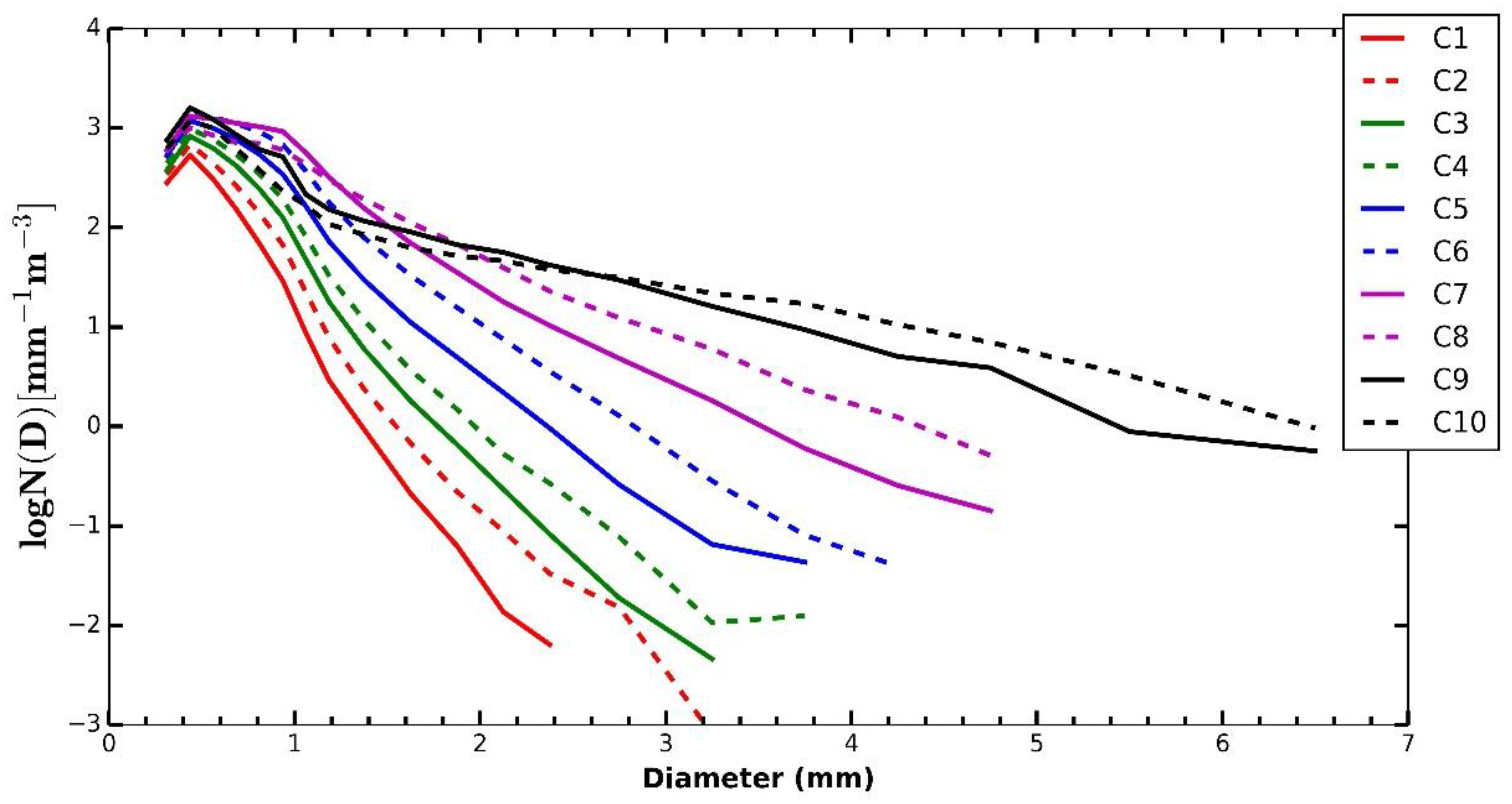
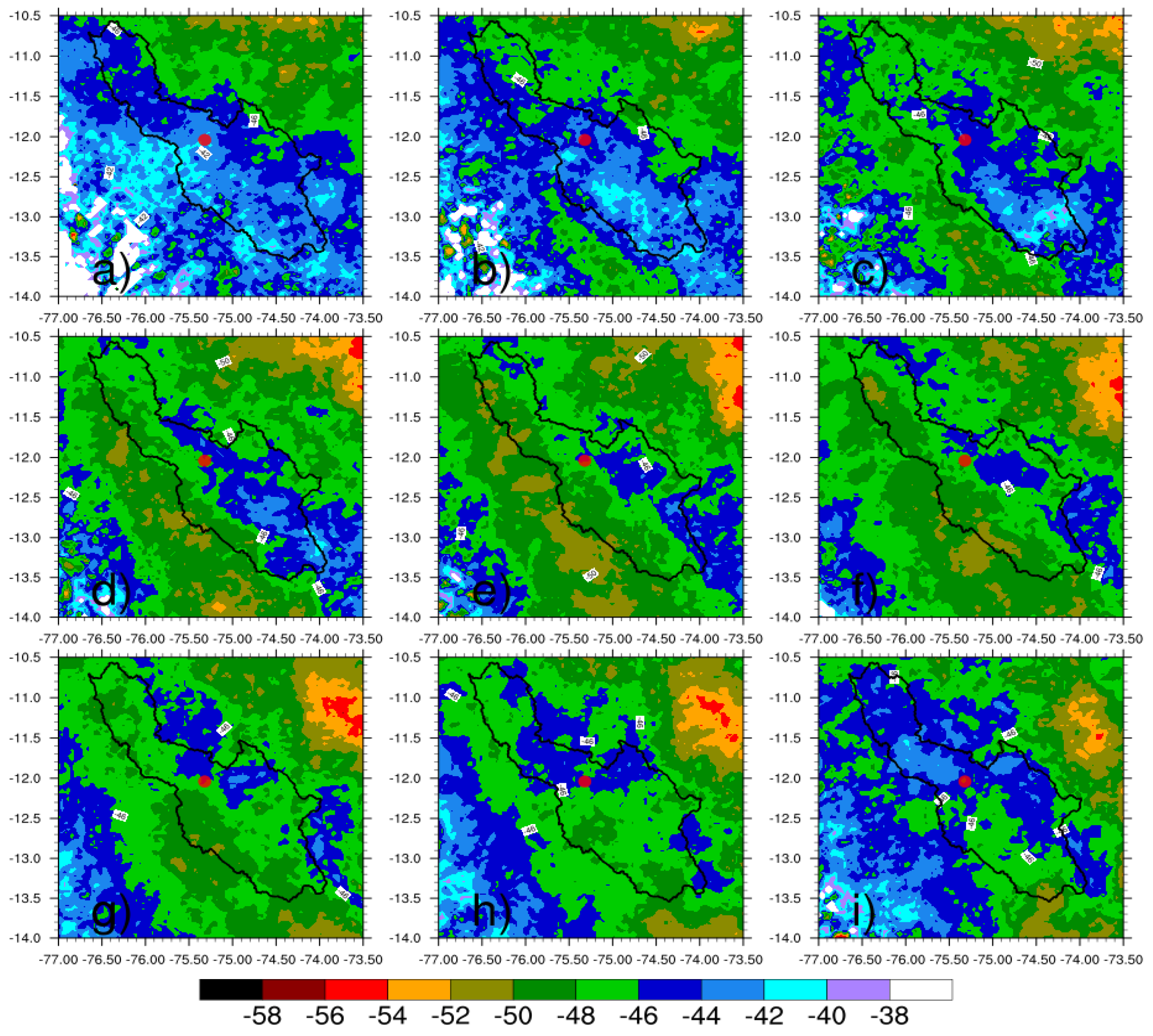
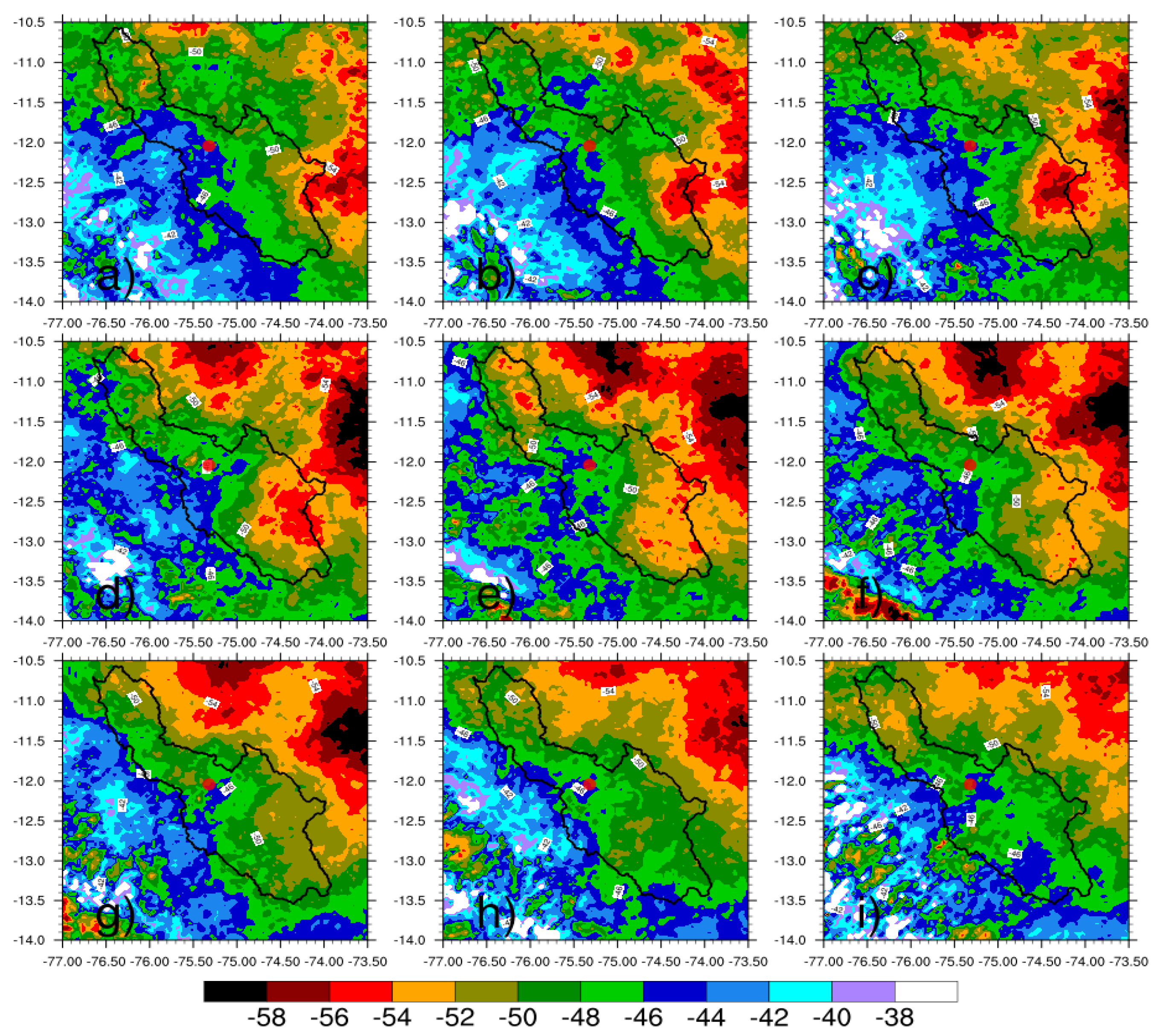
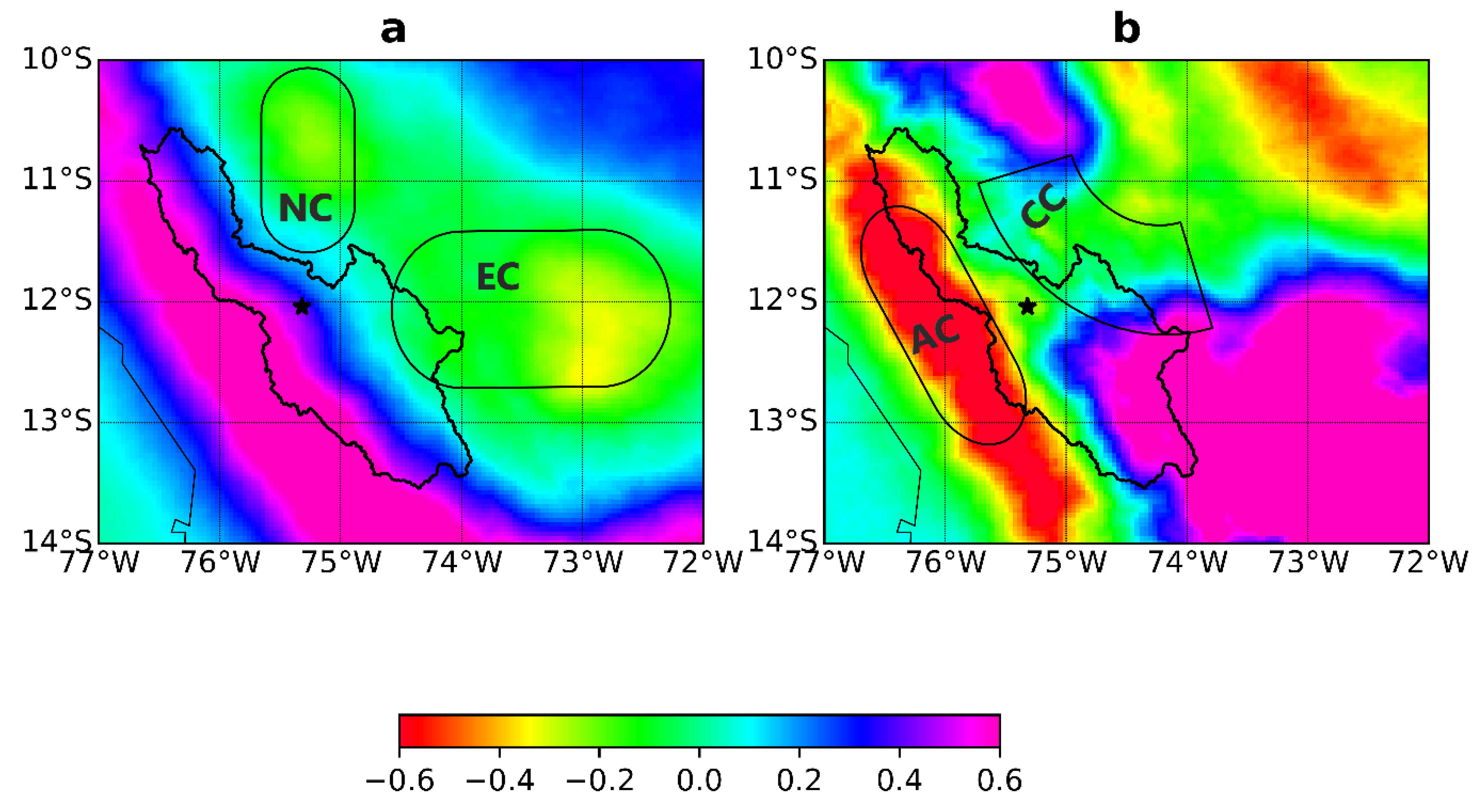
| Class | n | R | LWC | Nt | Dm | Nw |
|---|---|---|---|---|---|---|
| C1(0.1–0.2) | 3912 | 0.1 | 0.02 | 173 | 0.70 | 3.73 |
| C2(0.2–0.4) | 6203 | 0.3 | 0.03 | 247 | 0.77 | 3.81 |
| C3(0.4–0.7) | 5503 | 0.5 | 0.05 | 337 | 0.84 | 3.89 |
| C4(0.7–1.0) | 3383 | 0.8 | 0.07 | 428 | 0.91 | 3.91 |
| C5(1.0–3.0) | 8037 | 1.5 | 0.12 | 587 | 1.05 | 3.92 |
| C6(3.0–6.0) | 2070 | 3.6 | 0.25 | 851 | 1.22 | 3.97 |
| C7(6.0–10) | 452 | 6.9 | 0.44 | 968 | 1.55 | 3.79 |
| C8(10–20) | 206 | 11.6 | 0.63 | 772 | 2.10 | 3.43 |
| C9(20–40) | 87 | 28.4 | 1.24 | 867 | 3.27 | 2.95 |
| C10(40–120) | 36 | 51.7 | 1.76 | 658 | 3.89 | 2.80 |
| Hours during the Day | 15–20 LST | 21–02 LST | 03–08 LST | 09–14 LST | ||||
|---|---|---|---|---|---|---|---|---|
| Contribution to rainfall (mm) | 334.6 (49%) | 201.8 (29%) | 88.2(13%) | 60.8(9%) | ||||
| Time of duration (minutes) | 17952 | 13594 | 8340 | 5268 | ||||
| Classes of events | M | H | M | H | M | H | M | H |
| Contribution (%) | 29 | 46 | 42 | 22 | 36 | 15 | 24 | 35 |
| N° | Date | C | S | ||
|---|---|---|---|---|---|
| 1 | 20171015 12:38 | 10 | 48 | 2.3 | 24.4 |
| 2 | 20171223 16:09 | 22 | 29 | 4.6 | 46.8 |
| 3 | 20180111 17:50 | 37 | 94 | 4.0 | 76.2 |
| 4 | 20180113 15:53 | 10 | 4 | 5.4 | 23.5 |
| 5 | 20180117 19:47 | 15 | 63 | 1.7 | 31.5 |
| 6 | 20180118 18:31 | 14 | 16 | 2.3 | 32.1 |
| 7 | 20180209 15:40 | 10 | 55 | 3.1 | 21.5 |
| 8 | 20180217 19:29 | 15 | 18 | 3.0 | 30.8 |
| 9 | 20180221 15:40 | 10 | 13 | 5.3 | 32.2 |
| 10 | 20180221 16:04 | 10 | 148 | 1.6 | 11.5 |
| 11 | 20180226 18:52 | 16 | 36 | 5.5 | 16.6 |
| 12 | 20180807 14:50 | 16 | 30 | 5.8 | 52.6 |
| 13 | 20180915 16:20 | 33 | 22 | 5.3 | 96.0 |
| 14 | 20181115 17:58 | 15 | 135 | 3.9 | 90.6 |
| 15 | 20190307 14:26 | 18 | 15 | 4.6 | 43.3 |
| 16 | 20190402 11:14 | 10 | 88 | 2.6 | 32.8 |
| 17 | 20190403 14:53 | 10 | 15 | 3.7 | 37.6 |
| 18 | 20190410 14:36 | 13 | 23 | 5.4 | 58.1 |
| Class | n | R | LWC | Nt | Dm | Nw |
|---|---|---|---|---|---|---|
| C | 565 | 13.6 | 0.7 | 630 | 2.98 | 3.73 |
| S | 31649 | 0.8 | 0.08 | 402 | 1.04 | 2.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalobos-Puma, E.; Martinez-Castro, D.; Flores-Rojas, J.L.; Saavedra-Huanca, M.; Silva-Vidal, Y. Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes. Atmosphere 2020, 11, 38. https://doi.org/10.3390/atmos11010038
Villalobos-Puma E, Martinez-Castro D, Flores-Rojas JL, Saavedra-Huanca M, Silva-Vidal Y. Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes. Atmosphere. 2020; 11(1):38. https://doi.org/10.3390/atmos11010038
Chicago/Turabian StyleVillalobos-Puma, Elver, Daniel Martinez-Castro, Jose Luis Flores-Rojas, Miguel Saavedra-Huanca, and Yamina Silva-Vidal. 2020. "Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes" Atmosphere 11, no. 1: 38. https://doi.org/10.3390/atmos11010038
APA StyleVillalobos-Puma, E., Martinez-Castro, D., Flores-Rojas, J. L., Saavedra-Huanca, M., & Silva-Vidal, Y. (2020). Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes. Atmosphere, 11(1), 38. https://doi.org/10.3390/atmos11010038






