Low Polluting Building Materials and Ventilation for Good Air Quality in Residential Buildings: A Cost–Benefit Study
Abstract
1. Introduction
2. Methodology
2.1. Analytical Modelling of the Contaminants and Ventilation Rates
2.1.1. Contaminants Emission Rates
2.1.2. Ventilation Rates
- Well-mixed internal air;
- Constant external CO2 concentration (400 ppm); and
- Zero external formaldehyde concentration.
2.2. Dynamic Thermal Modelling
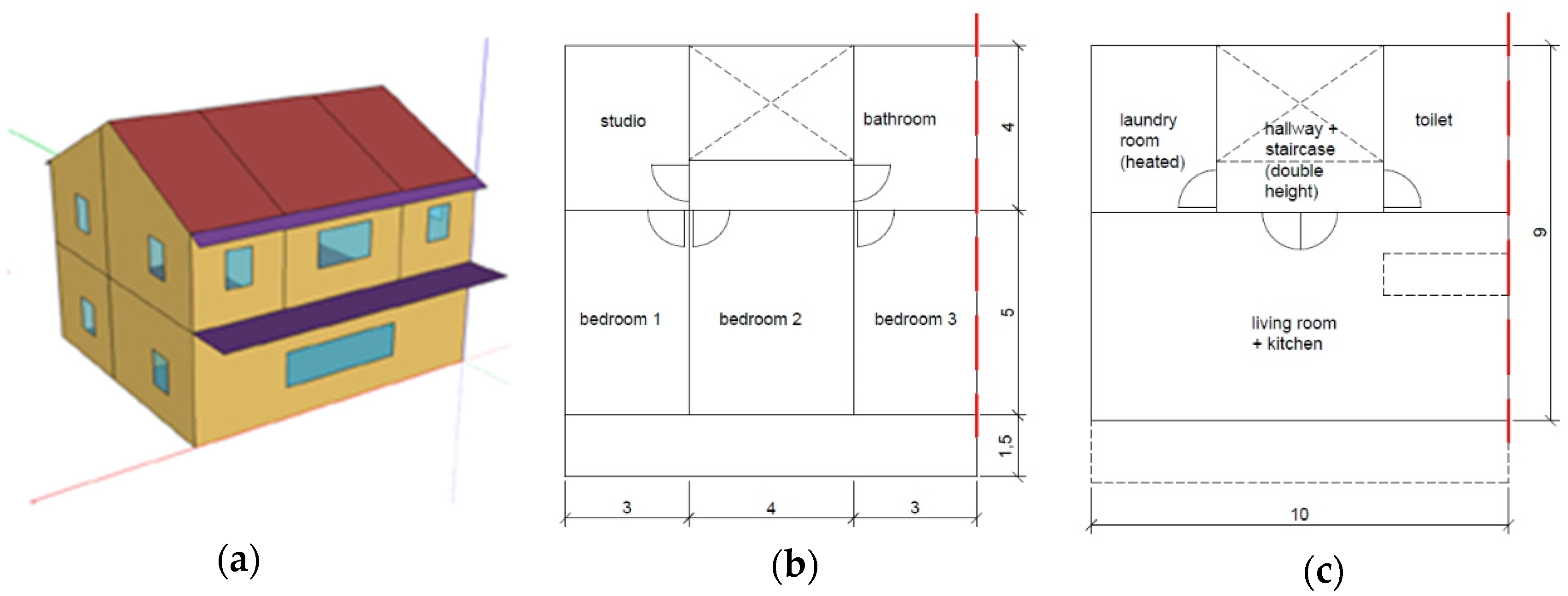
2.2.1. Geometry and Construction Type
2.2.2. Internal Gains
2.2.3. Solar Shading
2.2.4. Ventilation
2.2.5. Heating System
2.3. Economic Evaluation
2.3.1. From Heating Energy Demand to Heating Final Energy
2.3.2. Specific Fan Power
2.3.3. Energy Prices
2.3.4. Economic Parameters
2.3.5. Scenarios and Calculations
3. Results
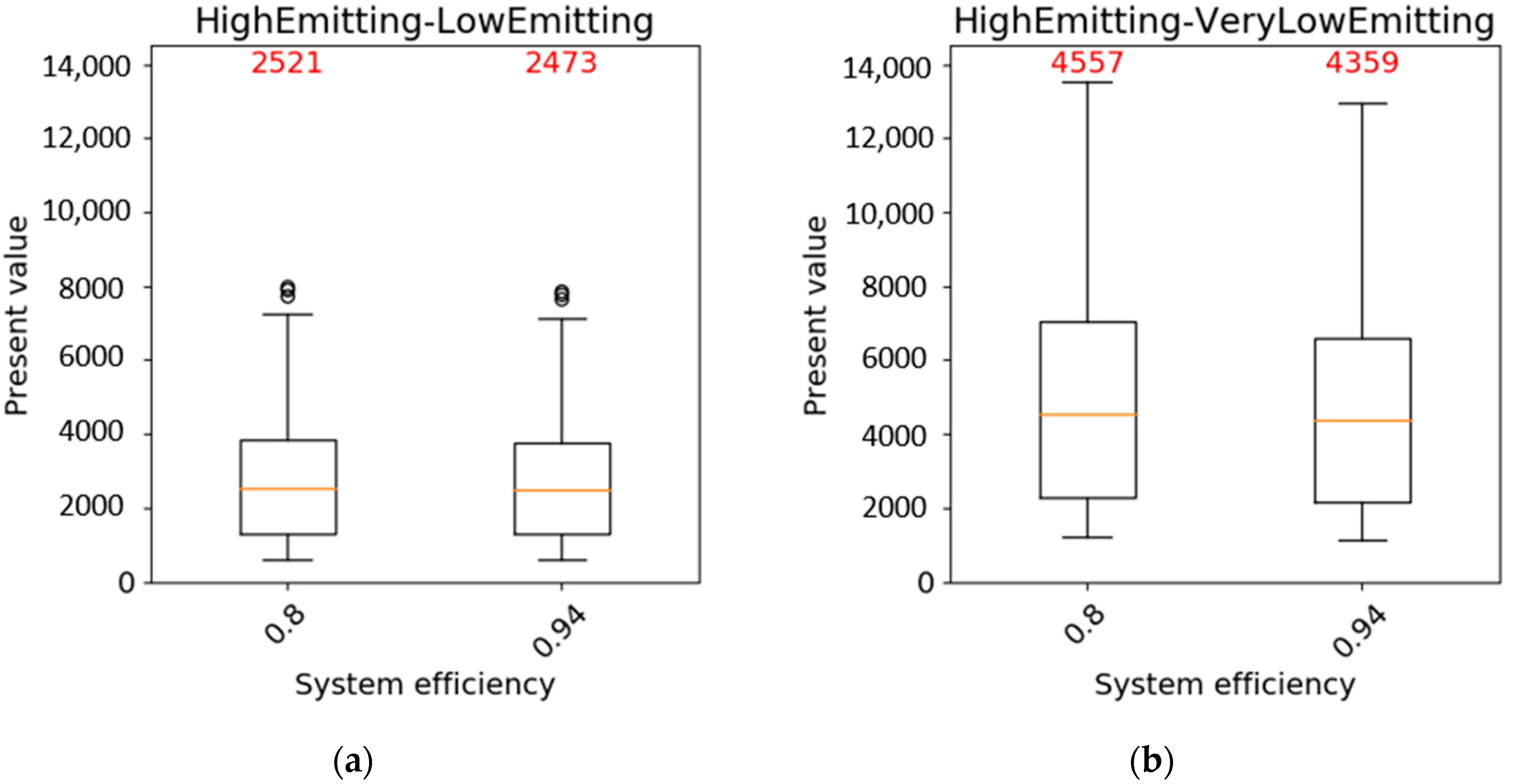
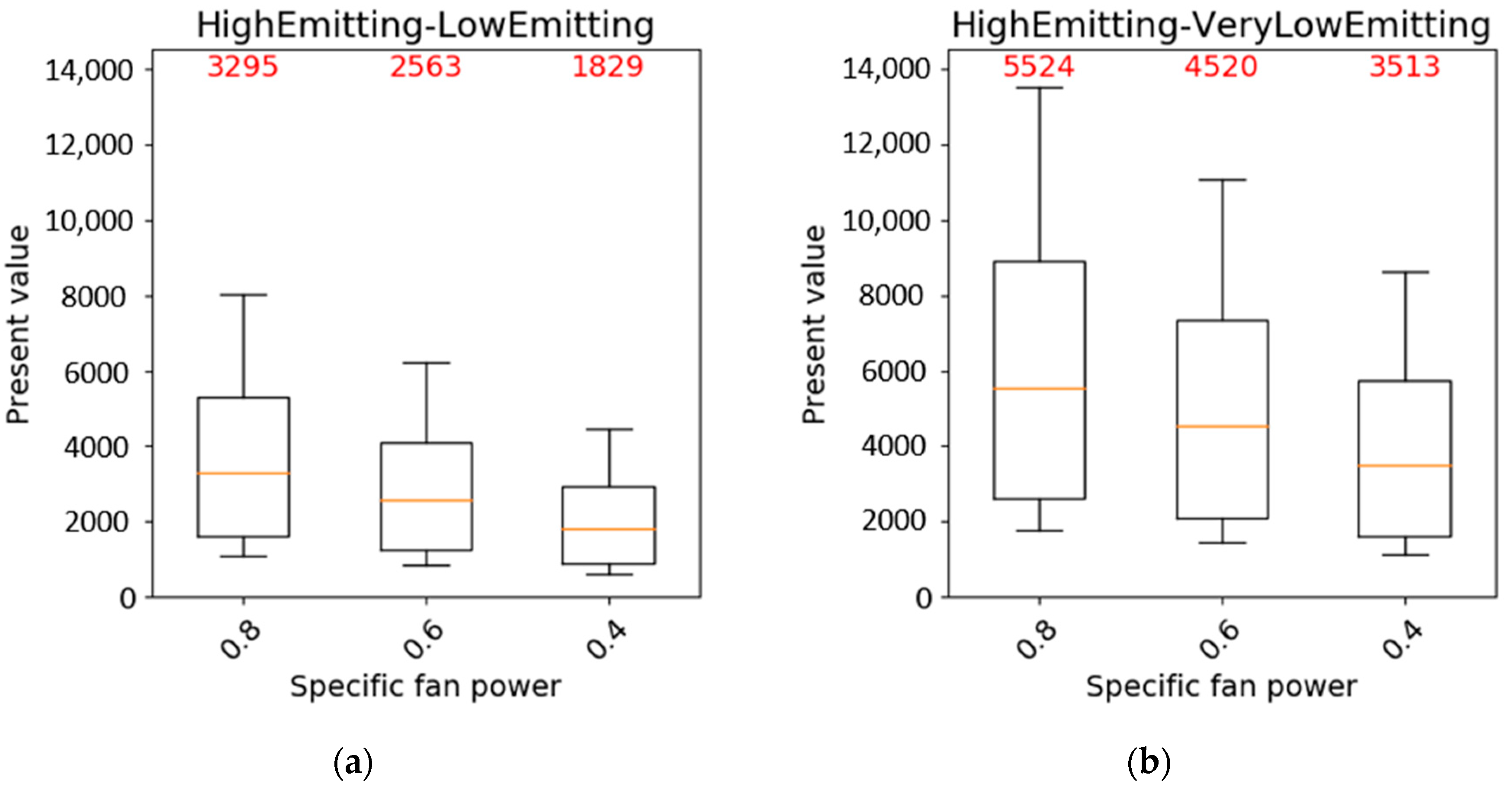
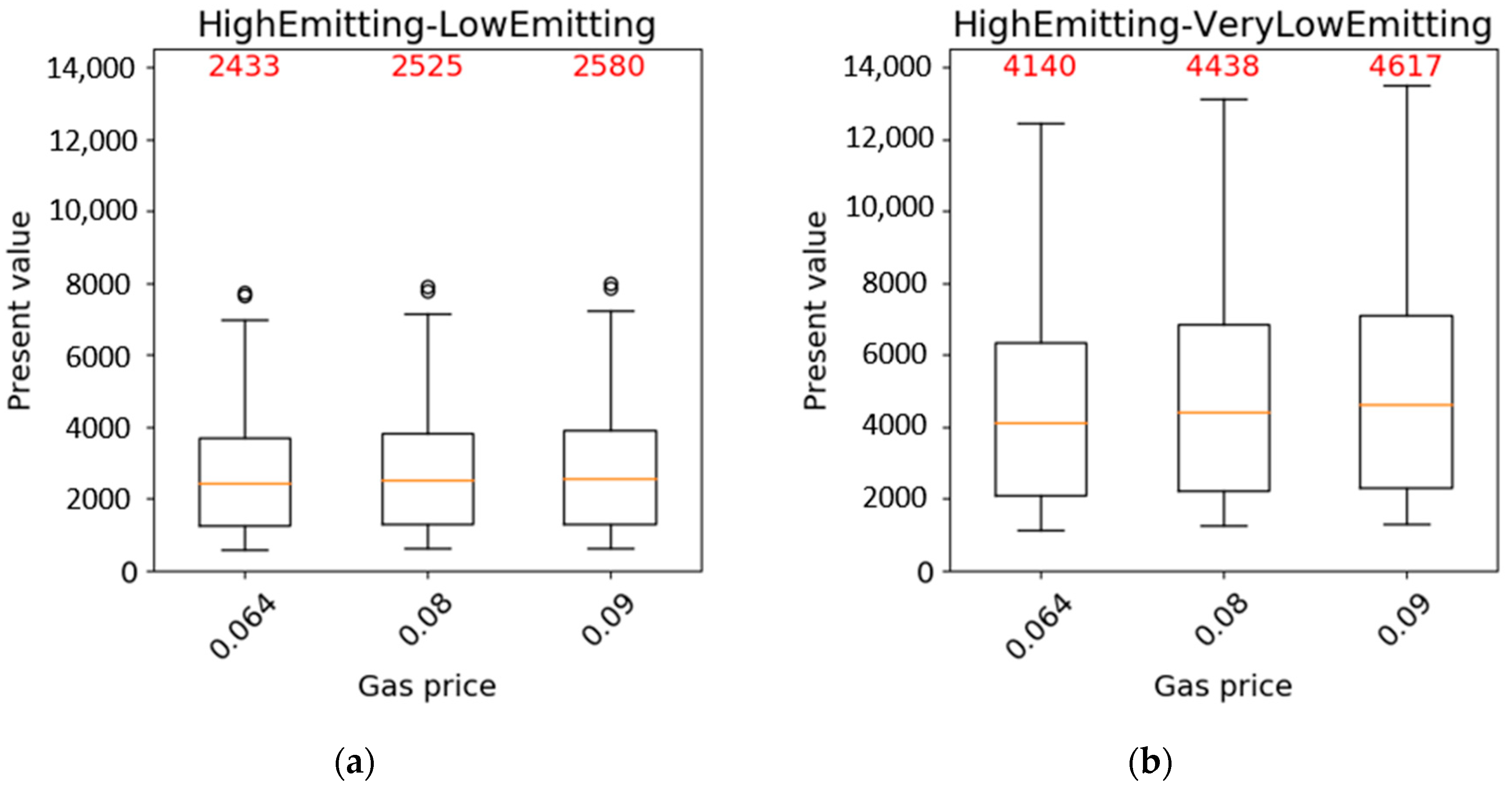
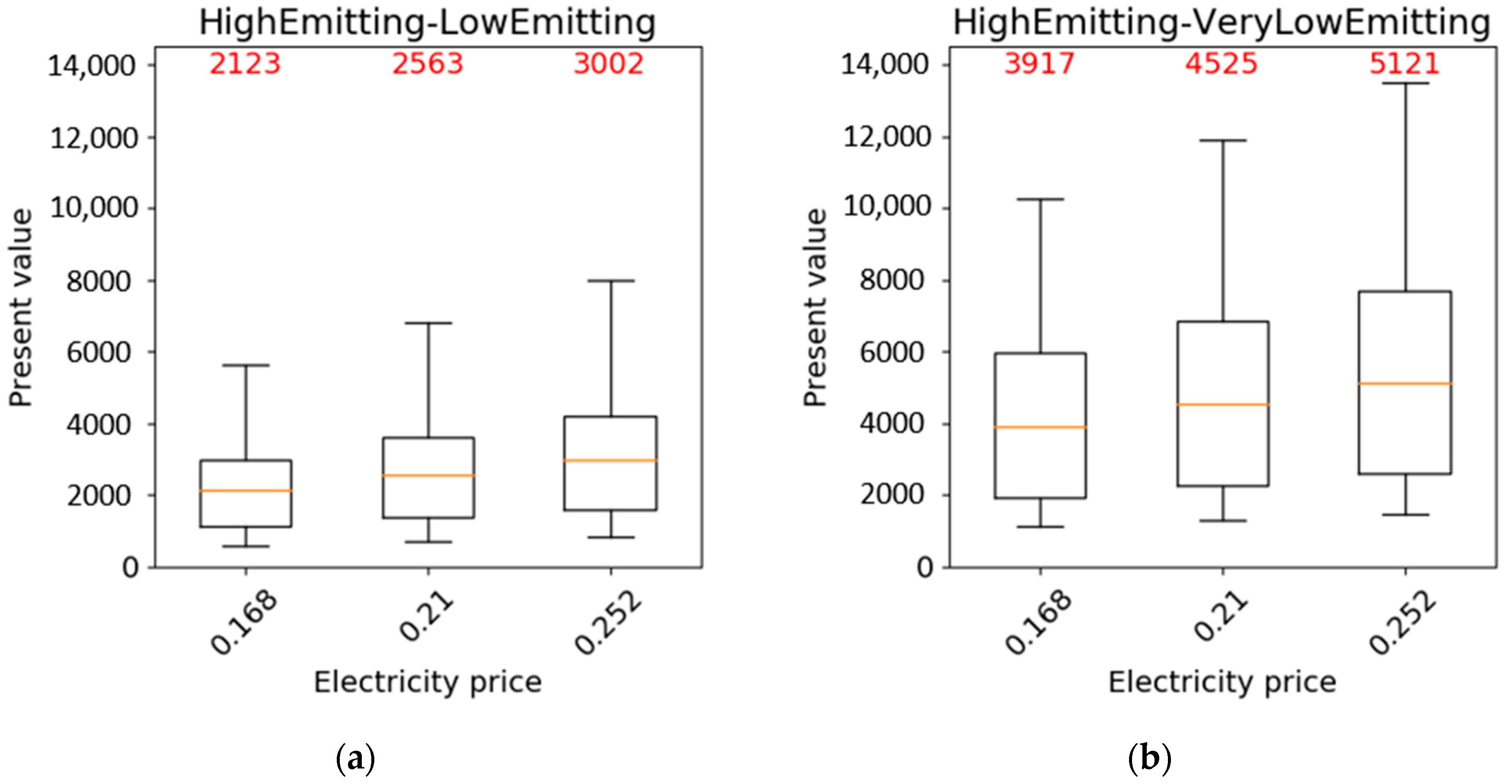
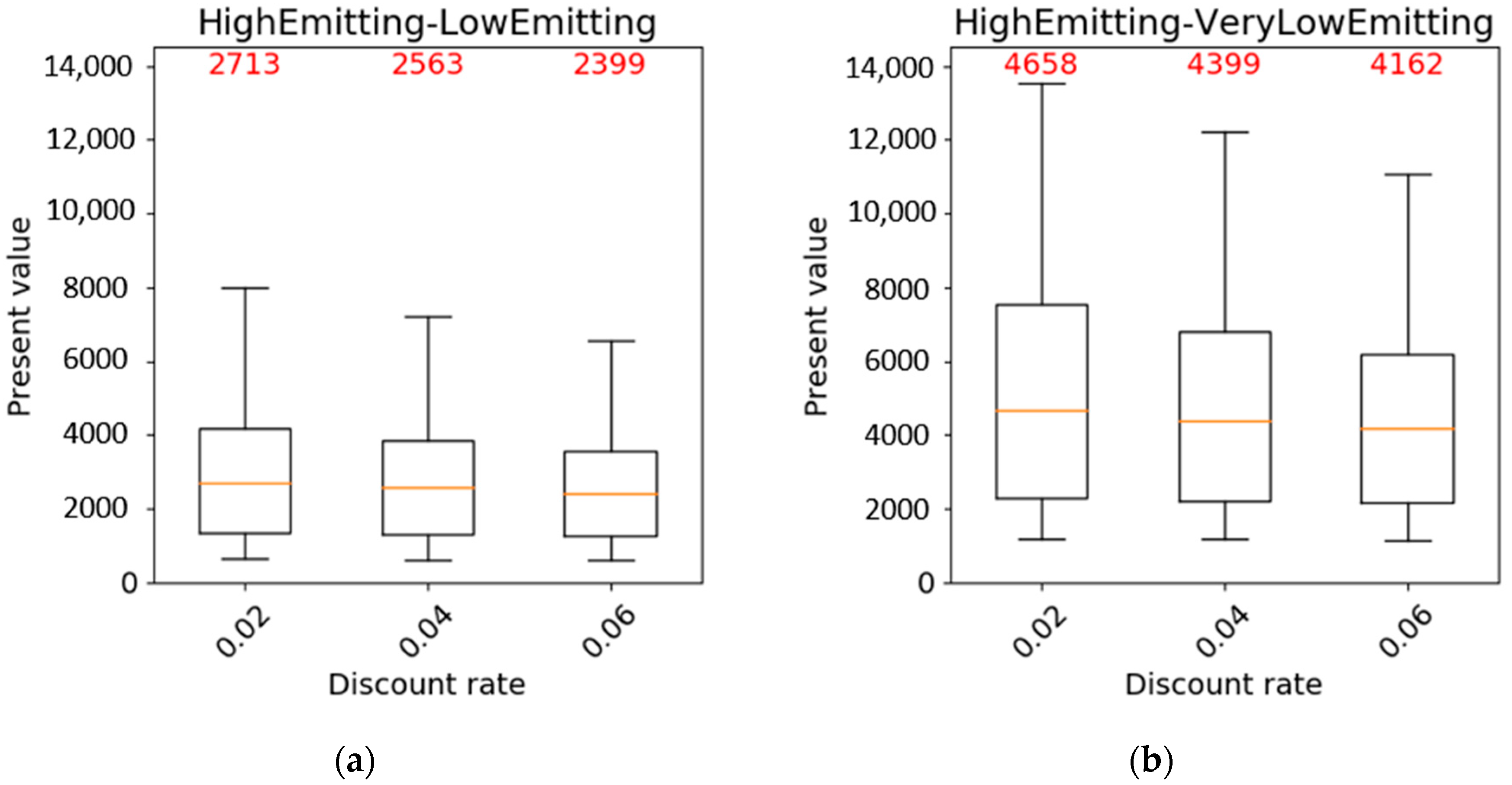
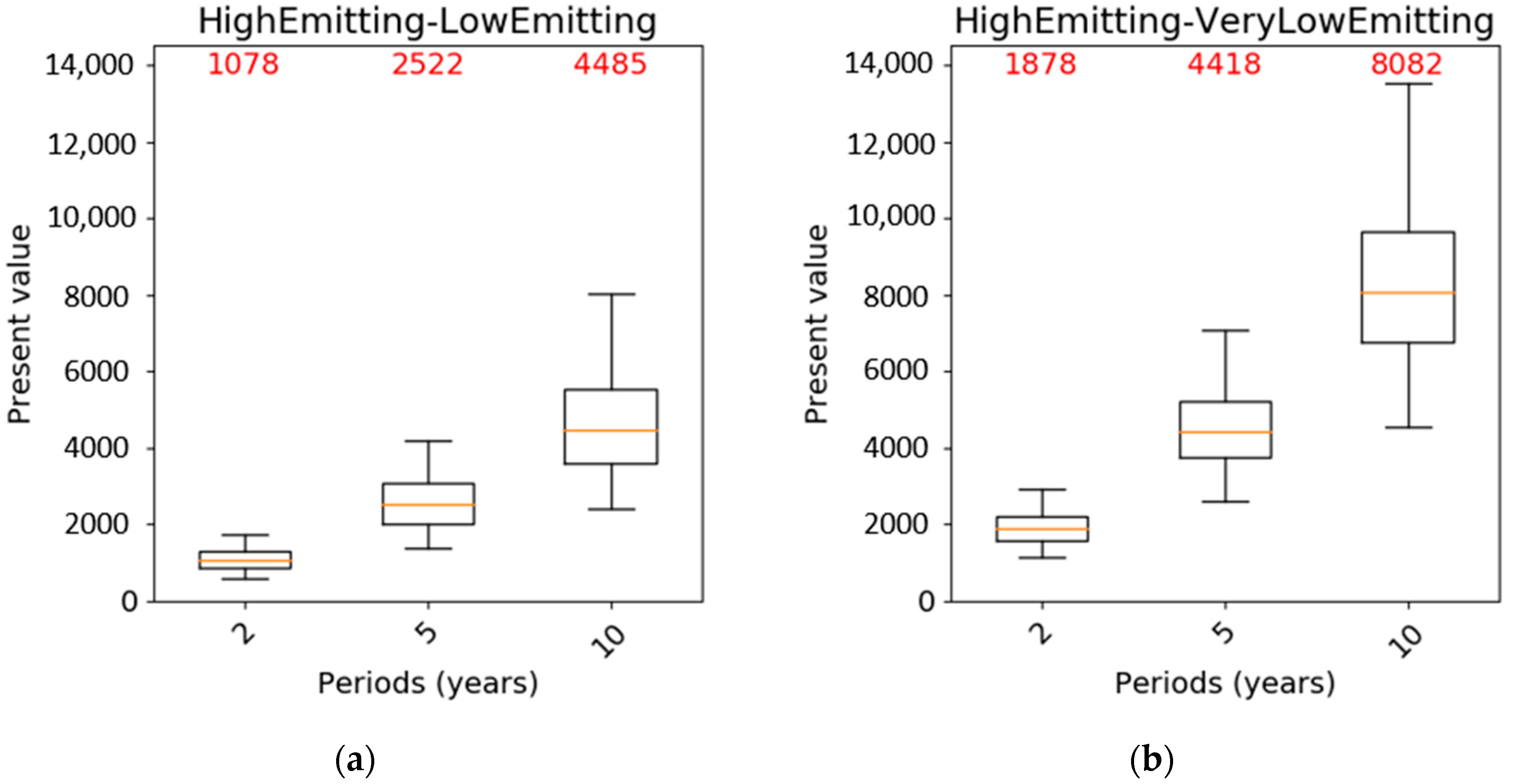
3.1. Results of the Cost–Benefit Analysis
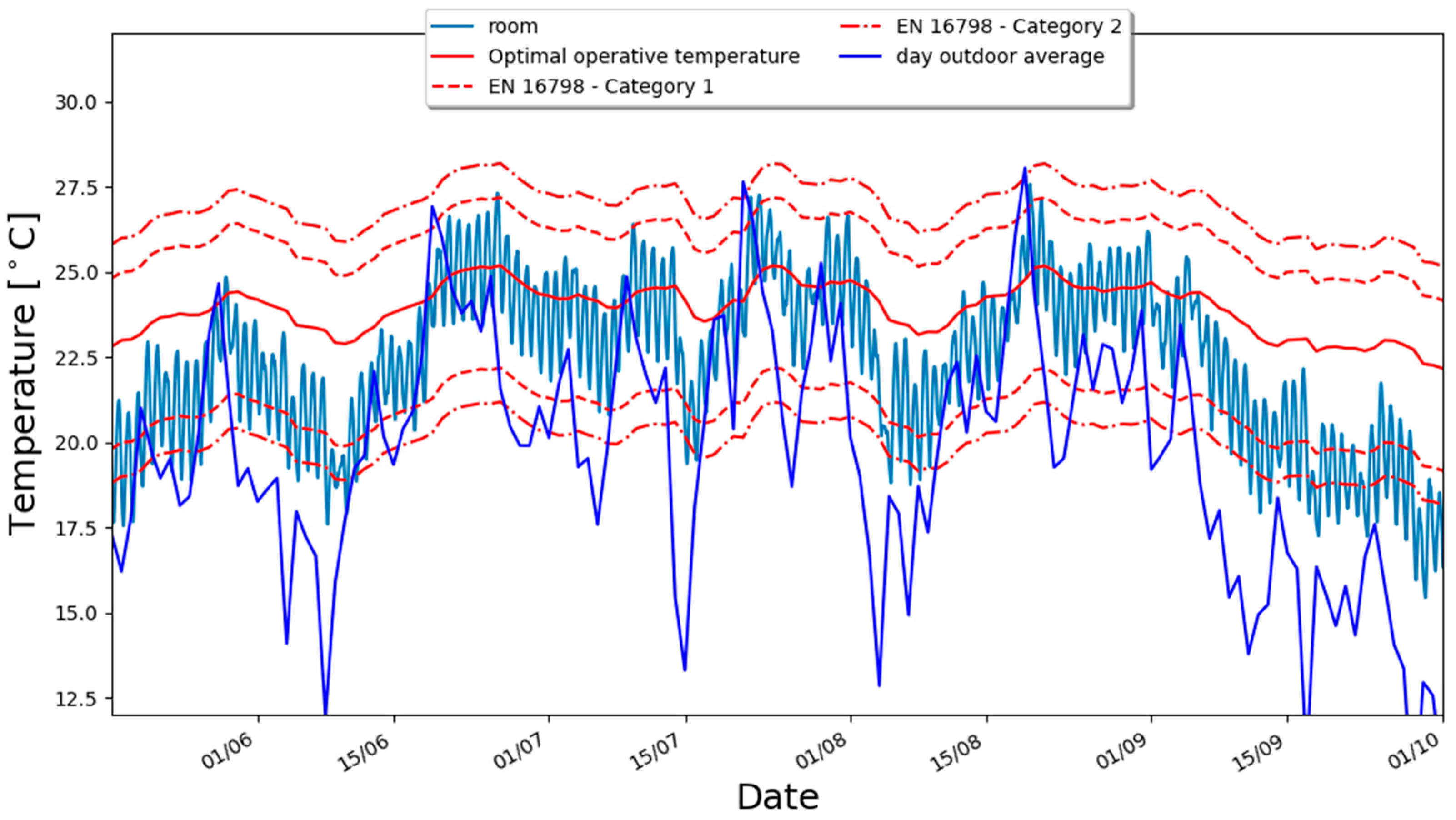
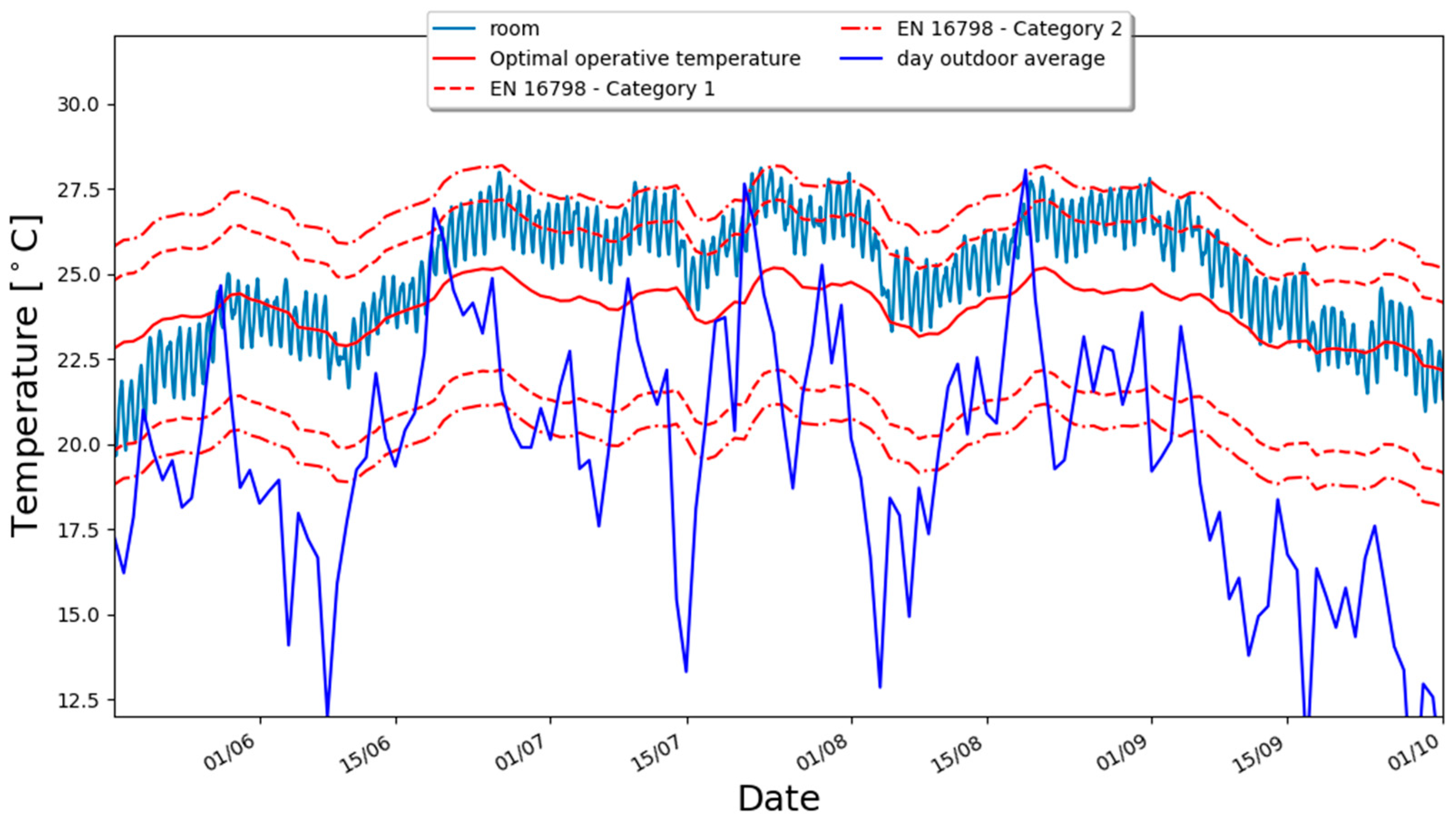
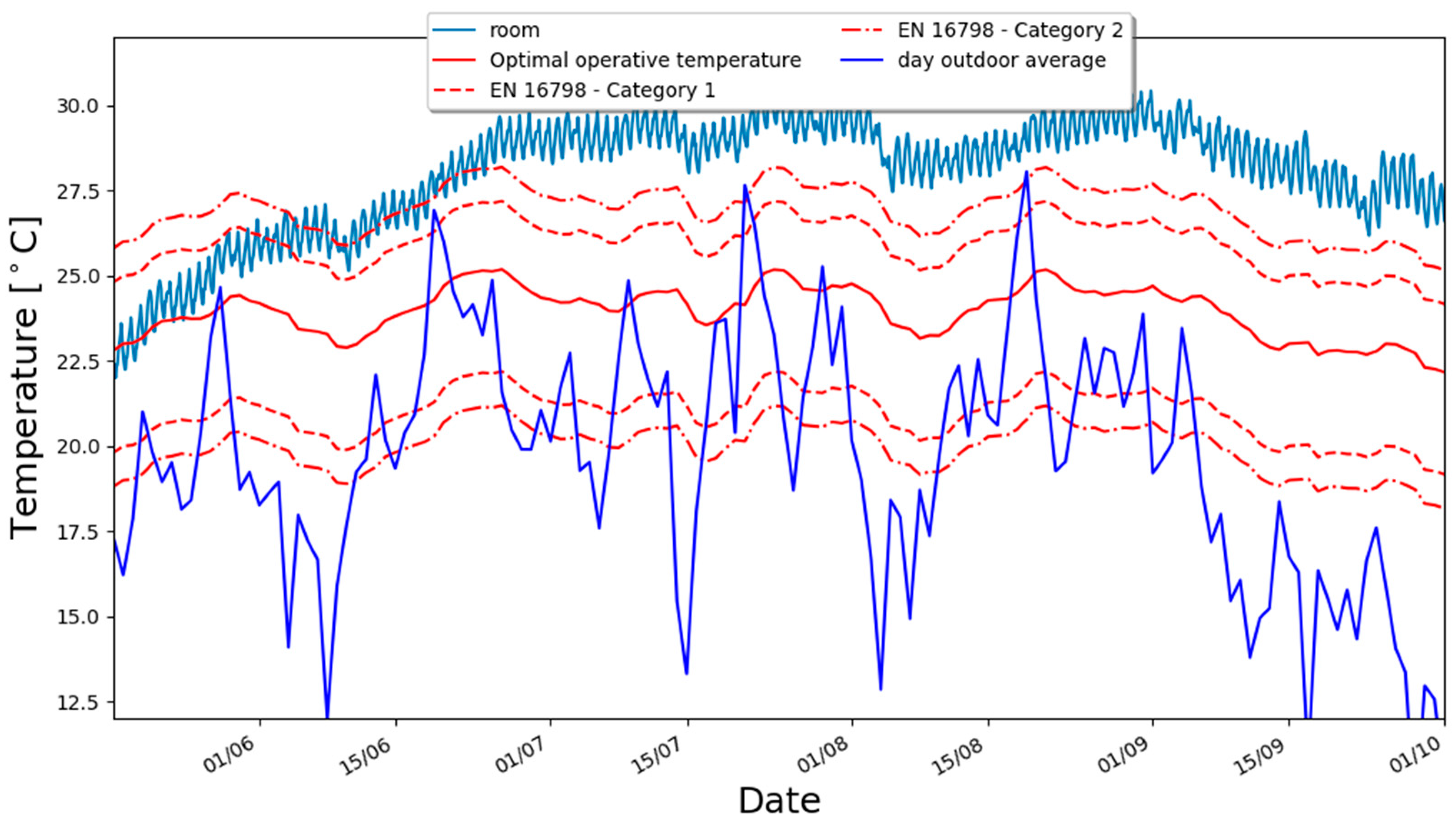
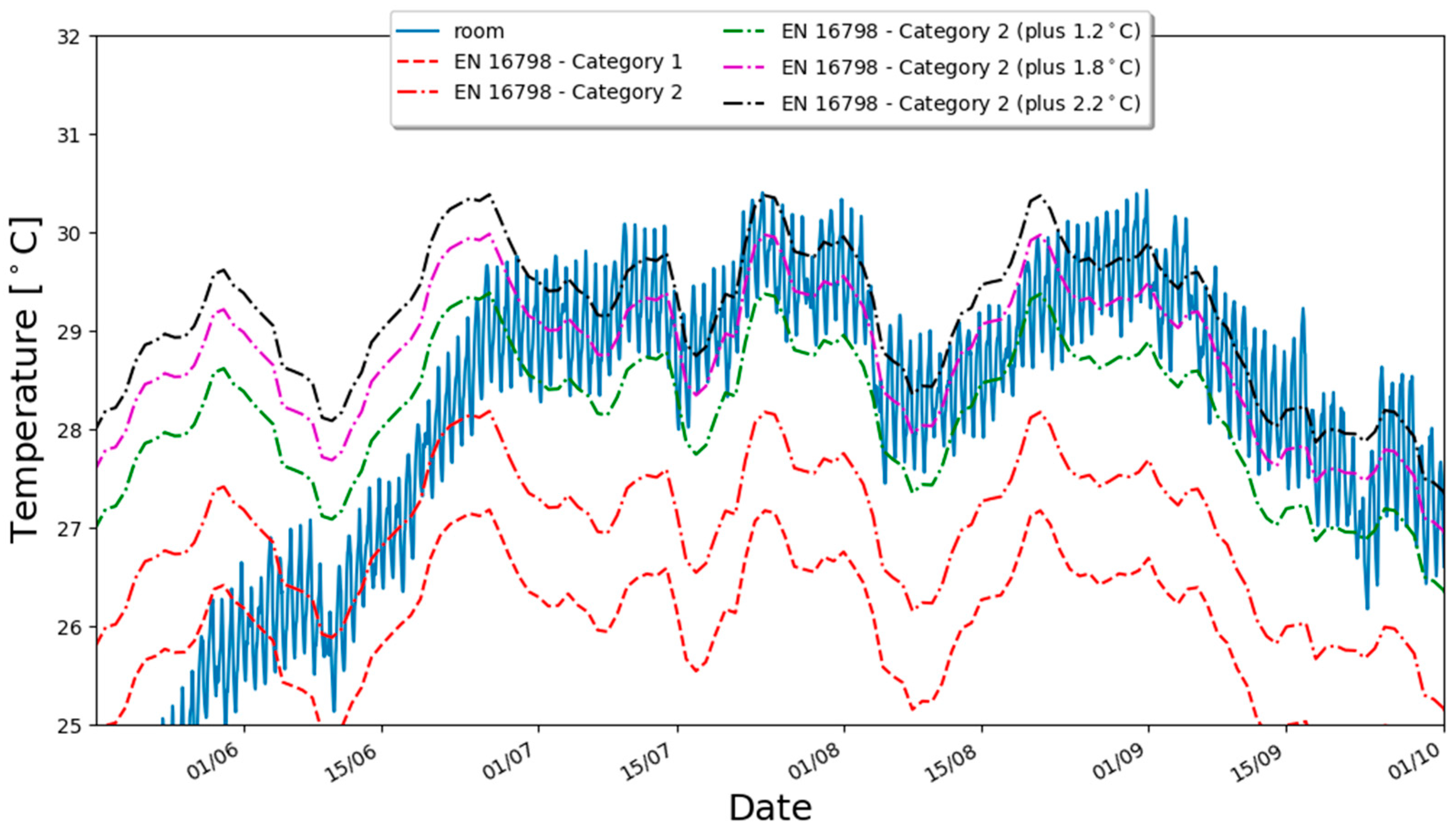
3.2. Thermal Comfort Analysis
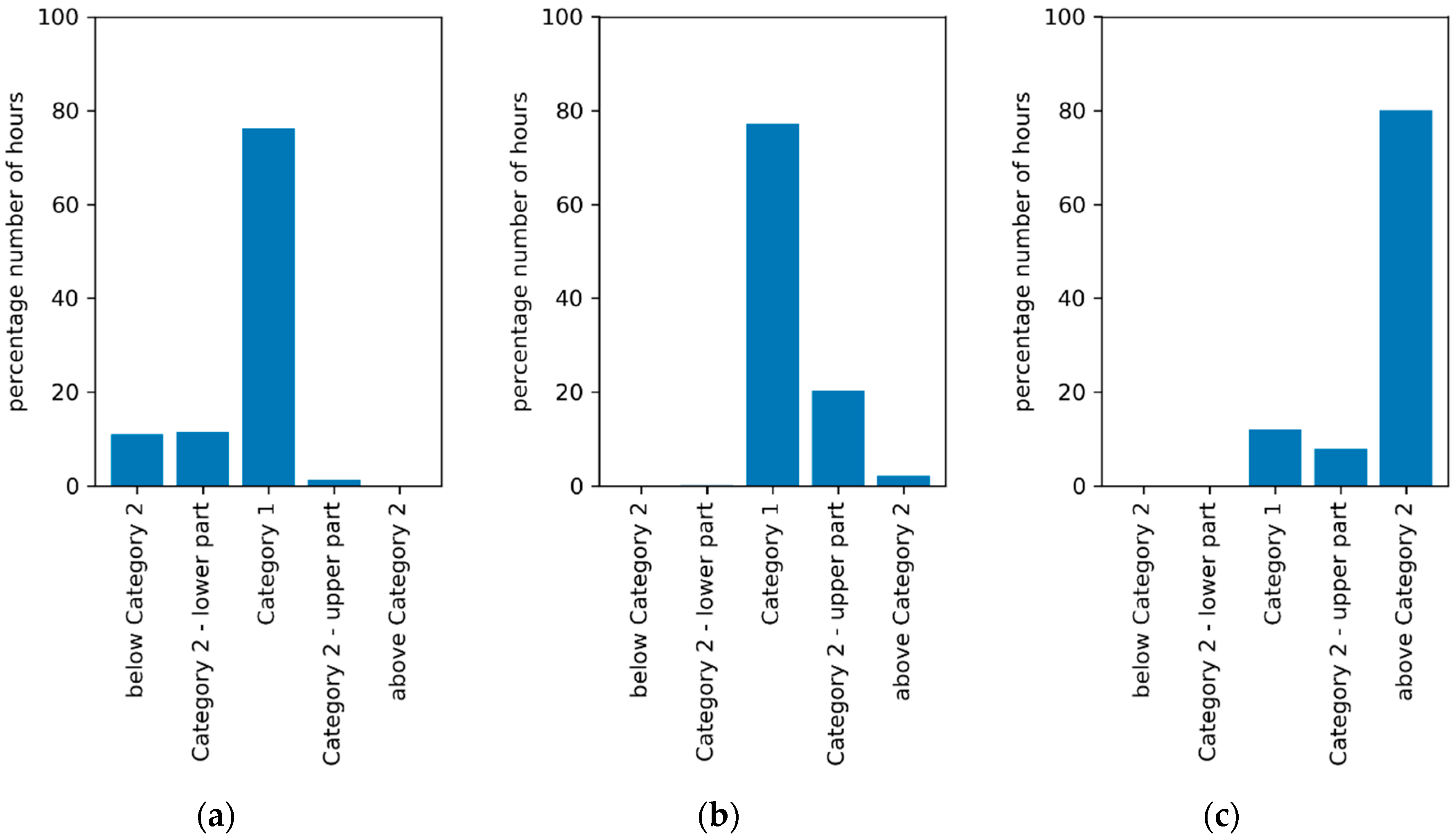
3.3. Comparison of the Required Ventilation Rates to Control Different Pollutants within the Room
4. Discussion
5. Conclusions
- Depending on the scenario, the use of low- and very low-emitting materials enables an up to 13,500€ running cost reduction over a 10-year period, which results in extra in the budget that could be used to purchase these higher quality materials.
- In the cost–benefit analysis, the variables that have the largest effect on the present value are the number of periods (i.e., years) and those related to electricity (cost and efficiency).
- In Bolzano climatic conditions, the use of a ventilation strategy based only on IAQ does not ensure the thermal comfort requirements are met during summer unless some cooling strategies are adopted.
- An analysis of the co-benefits is essential to fully understand why and the extent to which people are willing to accept extra costs to have a better indoor and outdoor environment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klepeis, N.; Nelson, W.C.; Ott, W.R.; Robinson, J.P.; Tsang, A.M.; Switzer, P.; Behar, J.V.; Hern, S.C.; Engelmann, W.H. The National Human Activity Pattern Survey (NHAPS): A Resource for Assessing Exposure to Environmental Pollutants. J. Expo. Sci. Environ. Epidemiol. 2001, 11, 231–252. [Google Scholar] [CrossRef] [PubMed]
- Eurostat. Manual for Statistics on Energy Consumption in Households; Publications office of the European Union: Luxembourg, 2013.
- ASHRAE. Standard 62.1—Ventilation for Acceptable Indoor Air Quality; ASHRAE: Atlanta, GA, USA, 2016. [Google Scholar]
- WHO Global Health Observatory (GHO) Data. Available online: https://www.who.int/gho/phe/en/ (accessed on 5 November 2019).
- Abadie, M.; Wargocki, P.; Rode, C.; Zhang, J. General rights Proposed metrics for IAQ in low-energy residential buildings. ASHRAE J. 2019, 61, 62–65. [Google Scholar]
- Abadie, M.O.; Wargocki, P.; Rode, C.; Rojas-Kopeinig, G.; Kolarik, J.; Laverge, J.; Cony, L.; Qin, M.; Blondeau, P. Indoor Air Quality Design and Control in Low-Energy Residential Buildings-Annex 68 | Subtask 1: Defining the Metrics in the Search of Indices to Evaluate the Indoor Air Quality of Low-Energy Residential Buildings; IEA-EBC: Birmingham, UK, 2017. [Google Scholar]
- Gibson, G.J.; Loddenkemper, R.; Lundbäck, B.; Sibille, Y. Respiratory health and disease in Europe: the new European Lung White Book. Eur. Respir. J. 2013, 42, 59–563. [Google Scholar] [CrossRef] [PubMed]
- Salthammer, T. Data on formaldehyde sources, formaldehyde concentrations and air exchange rates in European housings. Data Br. 2019, 22, 400–435. [Google Scholar] [CrossRef] [PubMed]
- WHO. WHO Guidelines for Indoor Air Quality: Selected Pollutants; Regional Office for Europe: Copenhagen, Denmark, 2010. [Google Scholar]
- Walker, I.; Sherman, M.; Jones, B. Economics of Indoor Air Quality. In Proceedings of the 39th AIVC Conference “Smart Ventilation for Buildings”, Antibes Juan-Les-Pins, France, 18–19 September 2018; pp. 1–9. [Google Scholar]
- Guyot, G.; Sherman, M.H.; Walker, I.S. Smart ventilation energy and indoor air quality performance in residential buildings: A review. Energy Build. 2018, 165, 416–430. [Google Scholar] [CrossRef]
- Rakennustietosäätiö RTS sr. M1 Emission Classification of Building Materials: Protocol for Chemical and Sensory Testing of Building Materials; Finnish Building Information Foundation RTS sr: Helsinki, Finland, 2017. [Google Scholar]
- NIST ContamLink | NIST. Available online: https://www.nist.gov/el/energy-and-environment-division-73200/nist-multizone-modeling/software-tools/contamlink (accessed on 10 October 2019).
- Brown, S.K. Chamber Assessment of Formaldehyde and VOC Emissions from Wood-Based Panels. Indoor Air 1999, 9, 209–215. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE. Standard 55 - Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- ASHRAE. Handbook of Fundamentals; ASHRAE: Atlanta, GA, USA, 2013. [Google Scholar]
- CEN. EN 16798-1 - Energy Performance of Buildings - Ventilation for Buildings - Part 1: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustic; European Standard: Bruxelles, Belgium, 2019. [Google Scholar]
- CEN. CEN/TR 16798-2 - Energy Performance of Buildings - Ventilation for Buildings - Part 2: Interpretation of the Requirements in EN 16798-1; European Standard: Bruxelles, Belgium, 2019. [Google Scholar]
- IEE TABULA - Typology Approach for Building Stock Energy Assessment. Available online: https://ec.europa.eu/energy/intelligent/projects/en/projects/tabula (accessed on 1 September 2019).
- Wilson, E.; Engebrecht-Metzger, C.; Horowitz, S.; Hendron, R. 2014 Building America House Simulation Protocols; National Renewable Energy Lab (NREL): Denver, CO, USA, 2014.
- UNI UNI/TS 11300-2 - Prestazioni energetiche degli edifici - Parte 2: Determinazione del fabbisogno di energia primaria e dei rendimenti per la climatizzazione invernale, per la produzione di acqua calda sanitaria, per la ventilazione e per l’illuminazione in; UNI: Milano, Italy, 2019.
- Merzkirch, A.; Maas, S.; Scholzen, F.; Waldmann, D. Field tests of centralized and decentralized ventilation units in residential buildings – Specific fan power, heat recovery efficiency, shortcuts and volume flow unbalances. Energy Build. 2016, 116, 376–383. [Google Scholar] [CrossRef]
- Eurostat Natural Gas Price Statistics - Statistics Explained. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Natural_gas_price_statistics (accessed on 31 October 2019).
- Eurostat Electricity Price Statistics - Statistics Explained. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics (accessed on 31 October 2019).
- Heiselberg, P.; O’Donnavan, A.; Belleri, A.; Flourentzou, F.; Zhang, G.-Q.; Carrilho da Graca, G.; Breesch, H.; Justo-Alonso, M.; Kolokotroni, M.; Pomianowski, M.; et al. Ventilative Cooling Design Guide - IEA Annex 62 Report; IEA-EBC: Birmingham, UK, 2018. [Google Scholar]
- Babich, F.; Cook, M.J.; Loveday, D.L.; Rawal, R.; Shukla, Y. A new methodological approach for estimating energy savings due to air movement in mixed mode buildings. In Proceedings of the IBPSA, San Francisco, CA, USA, 7–9 August 2017. [Google Scholar]
- Manu, S.; Shukla, Y.; Rawal, R.; Thomas, L.E.; De Dear, R. Field studies of thermal comfort across multiple climate zones for the subcontinent: India Model for Adaptive Comfort (IMAC). Build. Environ. 2016, 98, 55–70. [Google Scholar] [CrossRef]
| Building Material Emission Class | Formaldehyde Emission | Units |
|---|---|---|
| HE building | 320 | µg/(m2h) |
| LE building | 125 | µg/(m2h) |
| VLE building | 50 | µg/(m2h) |
| Elements | Description | Thickness (m) | U-Value (W/m2K) |
|---|---|---|---|
| exterior wall | massive wall with external insulation | 0.49 | 0.18 |
| roof | wooden roof isolated with wood fiber | 0.33 | 0.14 |
| ground floor | concrete slab with insulation | 0.165 | 0.165 |
| window | triple glazing window with argon and wooden frame | 0.084 | 0.49 (Ug = 0.6 Uf = 1.2) |
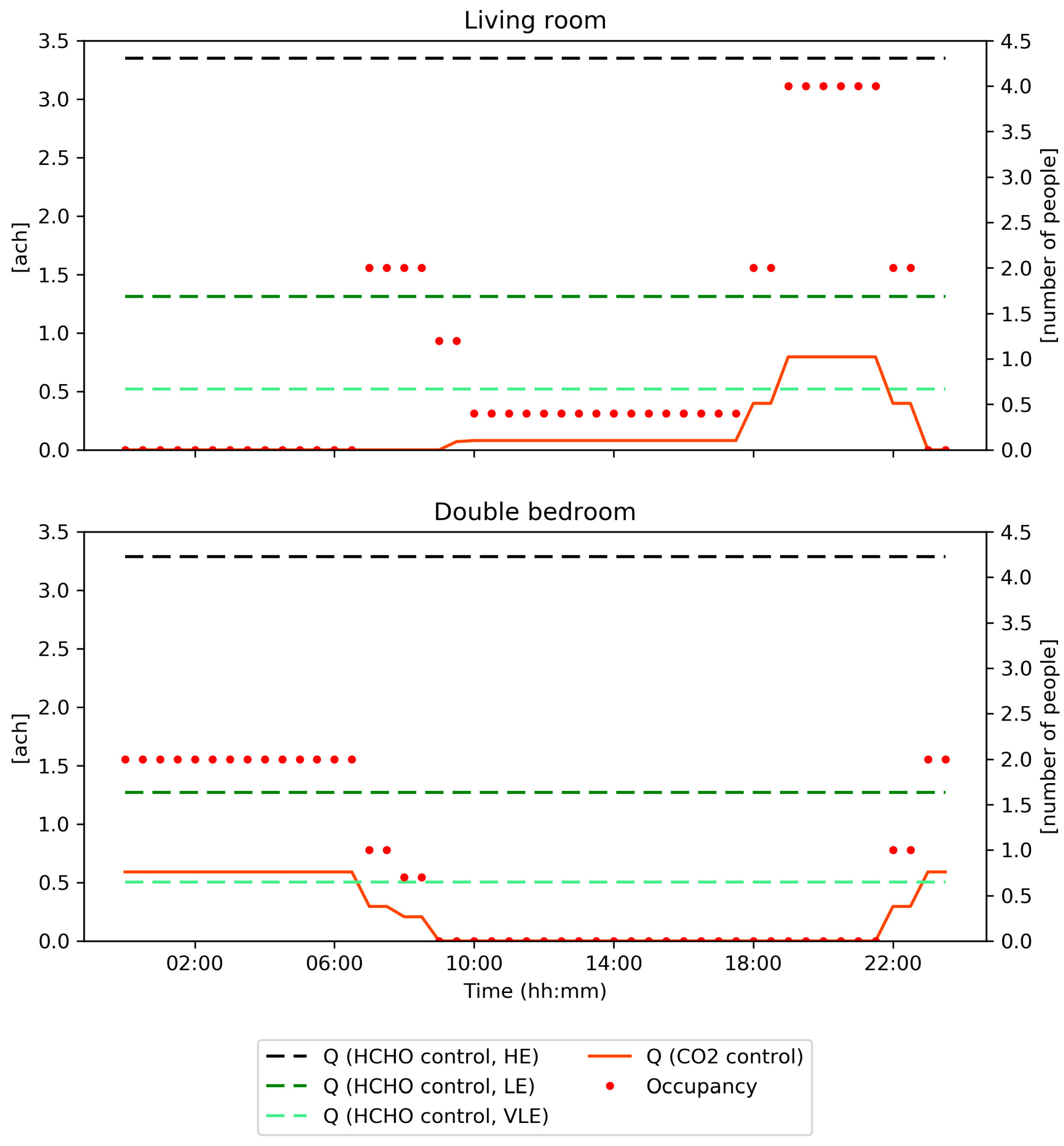
| Case-Study Building | Living Room | Double Bedroom | ||||
|---|---|---|---|---|---|---|
| Air Change Rate (1/h) | Max CO2 Concentration (ppm) | Max HCHO Concentration (µg/m3) | Air Change Rate (1/h) | Max CO2 Concentration (ppm) | Max HCHO Concentration (µg/m3) | |
| HE | 3.4 | 573 | 28 | 3.3 | 531 | 28 |
| LE | 1.3 | 822 | 28 | 1.3 | 739 | 28 |
| VLE | 0.5–0.8 | 1126 | 28 | 0.5–0.6 | 1174 | 29 |
| Parameters | Values | Units |
|---|---|---|
| Heating system efficiency | 80, 94 | % |
| Specific fan power | 0.40, 0.60, 0.80 | Wh/m3 |
| Electricity price | 0.17, 0.21, 0.25 | €/kWh |
| Gas price | 0.06, 0.08, 0.10 | €/kWh |
| Discount rate | 2, 4, 6 | % |
| Years | 2, 5, 10 | years |
| Variable | Scenario HE − LE | Scenario HE − VLE | Units |
|---|---|---|---|
| Heating demand | 913 | 3738 | kWh/year |
| Electricity demand | 3916 | 5392 | kWh/year |
| Present Value | Scenario HE − LE | Scenario HE − VLE | Units |
|---|---|---|---|
| Median | 2493 | 4418 | € |
| Mean | 2781 | 4910 | € |
| Maximum | 8009 | 13,524 | € |
| Minimum | 596 | 1130 | € |
| EN16798 Category | High Emitting | Low Emitting | Very Low Emitting |
|---|---|---|---|
| Below category 2 | 359 (10.9%) | 0 (0.0%) | 0 (0.0%) |
| Category 2-lower part | 381 (11.6%) | 7 (0.2%) | 0 (0.0%) |
| Category 1 | 2507 (76.2%) | 2543 (77.3%) | 395 (12.0%) |
| Category 2-upper part | 40 (1.2%) | 668 (20.3%) | 257 (7.8%) |
| Above Category 2 | 2 (0.1%) | 71 (2.2%) | 2637 (80.2%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babich, F.; Demanega, I.; Avella, F.; Belleri, A. Low Polluting Building Materials and Ventilation for Good Air Quality in Residential Buildings: A Cost–Benefit Study. Atmosphere 2020, 11, 102. https://doi.org/10.3390/atmos11010102
Babich F, Demanega I, Avella F, Belleri A. Low Polluting Building Materials and Ventilation for Good Air Quality in Residential Buildings: A Cost–Benefit Study. Atmosphere. 2020; 11(1):102. https://doi.org/10.3390/atmos11010102
Chicago/Turabian StyleBabich, Francesco, Ingrid Demanega, Francesca Avella, and Annamaria Belleri. 2020. "Low Polluting Building Materials and Ventilation for Good Air Quality in Residential Buildings: A Cost–Benefit Study" Atmosphere 11, no. 1: 102. https://doi.org/10.3390/atmos11010102
APA StyleBabich, F., Demanega, I., Avella, F., & Belleri, A. (2020). Low Polluting Building Materials and Ventilation for Good Air Quality in Residential Buildings: A Cost–Benefit Study. Atmosphere, 11(1), 102. https://doi.org/10.3390/atmos11010102






