Stepwise Assessment of Different Saltation Theories in Comparison with Field Observation Data
Abstract
1. Introduction
2. Data and Method
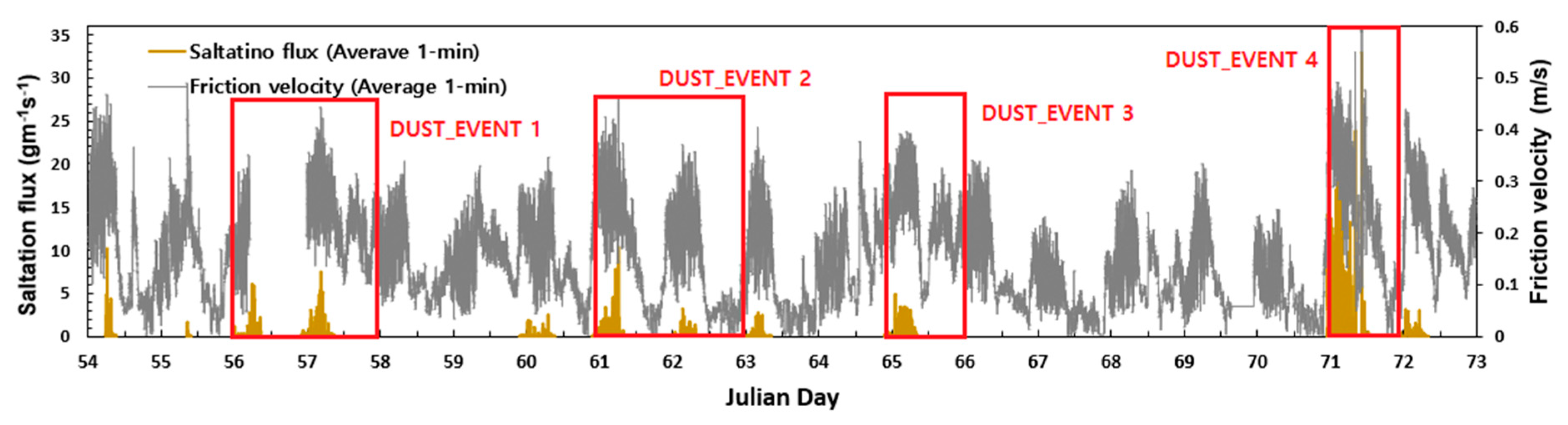
2.1. Observational Data
2.2. Wind-Blown Dust Model
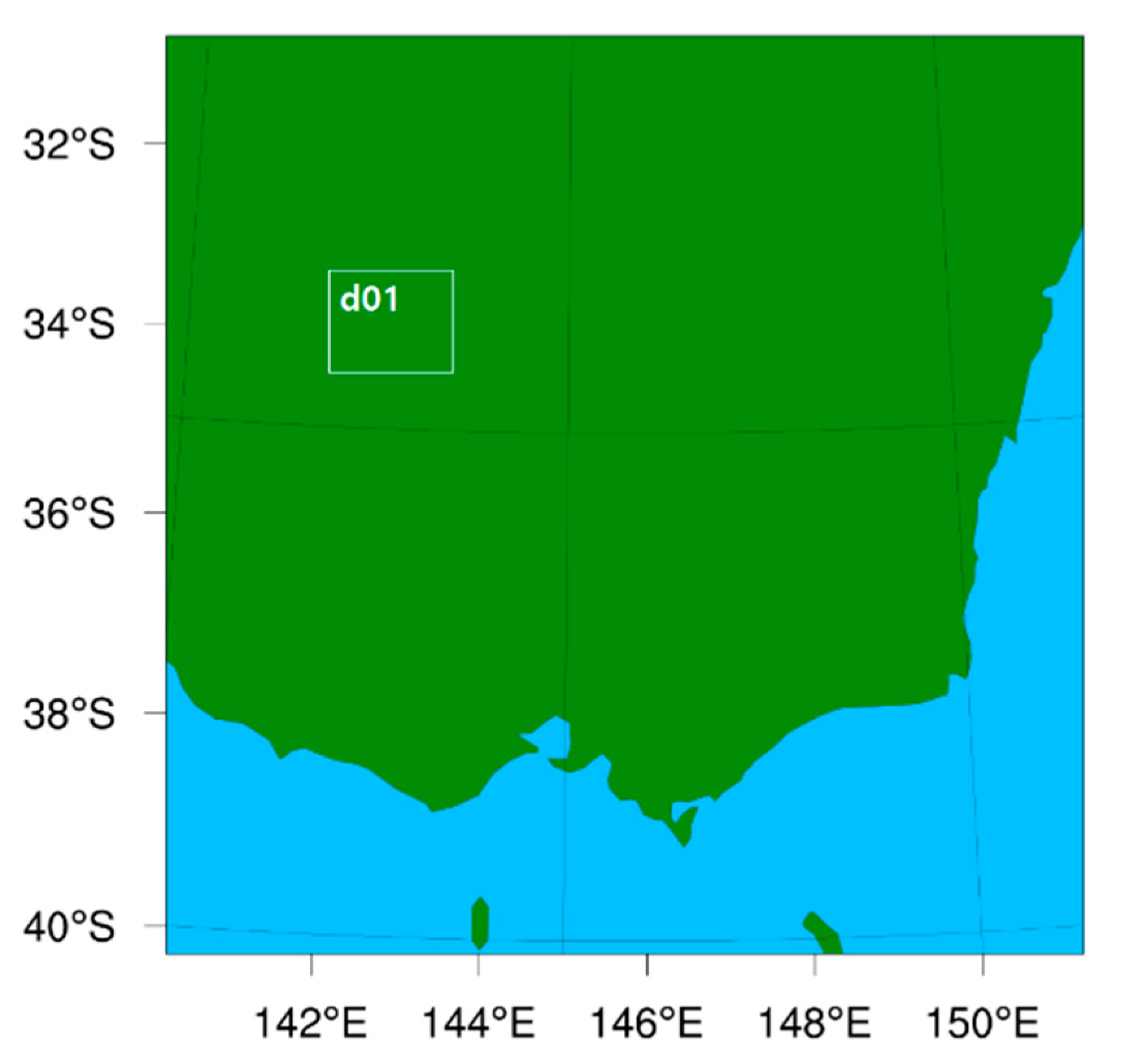
2.2.1. Domain and Configuration of Meteorological Model
2.2.2. Friction Velocity
2.2.3. Roughness Length
2.2.4. Threshold Friction Velocity of Dry Bare Soil
2.2.5. Drag Partitioning Effect
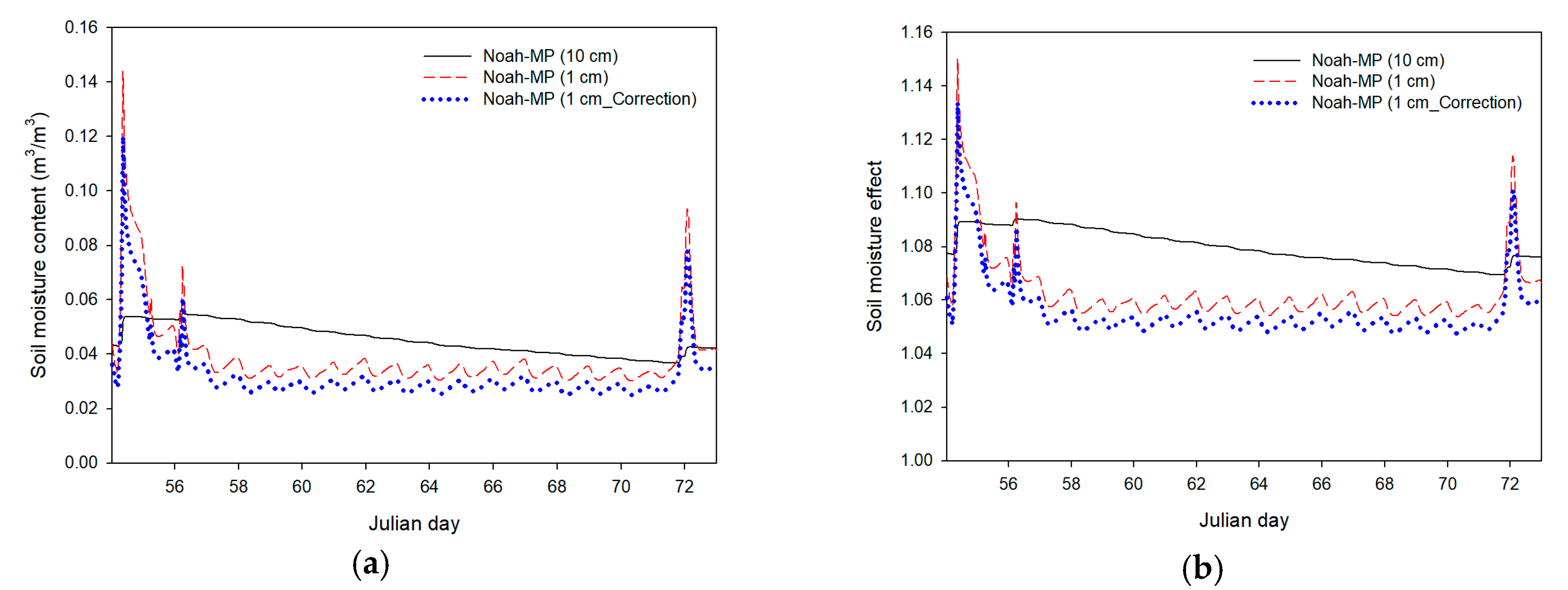
2.2.6. Soil Moisture Effect
- Modify the soil layer-related pretreatment part of the WRF code to construct a 1 cm top soil layer in Noah’s scheme [58].
2.2.7. Saltation Flux
3. Results and Discussion
3.1. Effect of the Roughness Length on the Friction Velocity
3.2. Drag Partitioning Effect
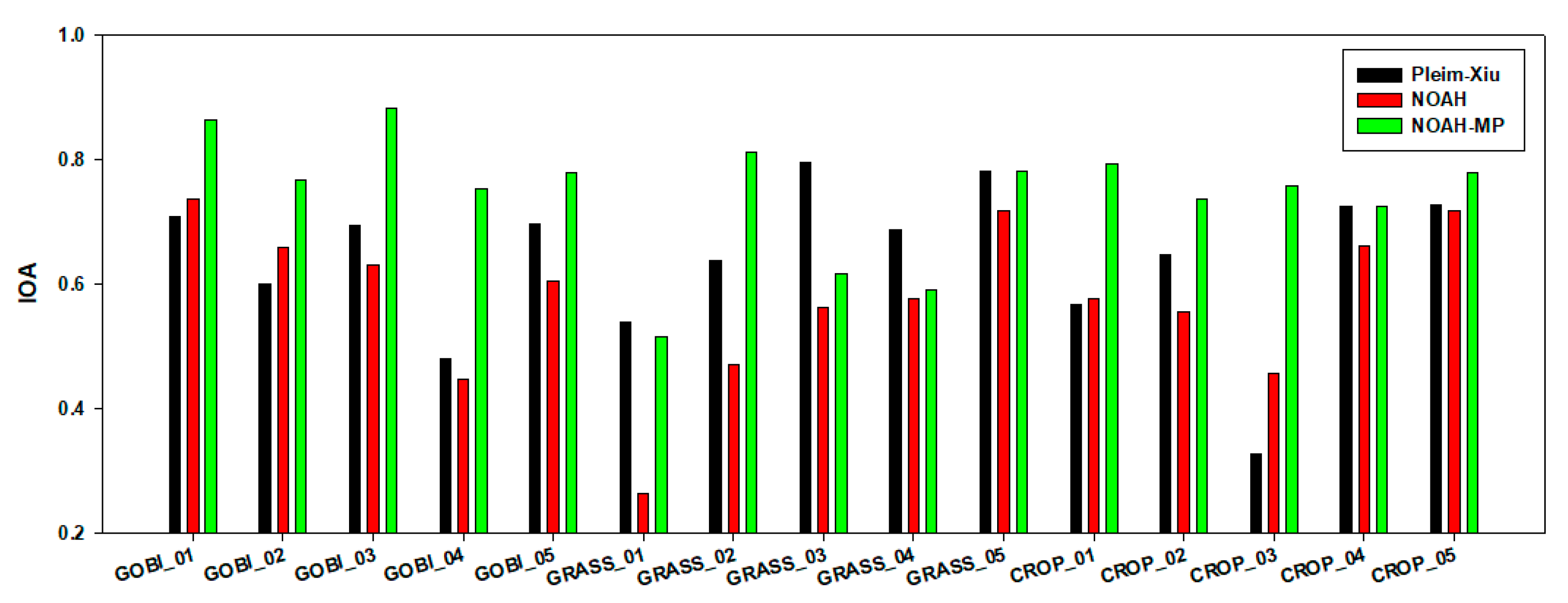
3.3. Effect of Land Surface Scheme on Soil Moisture
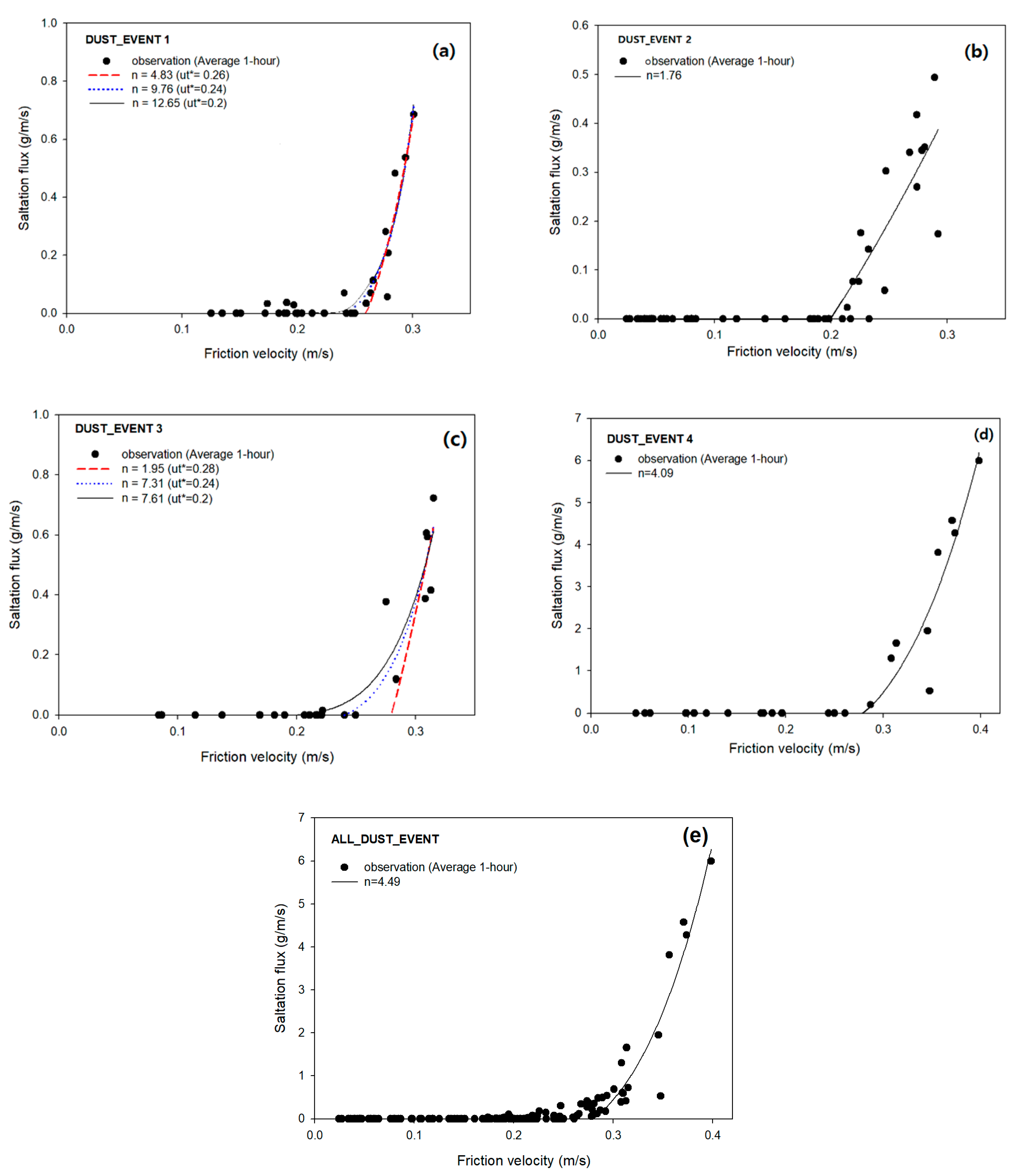
3.4. Estimation of the Threshold Friction Velocity
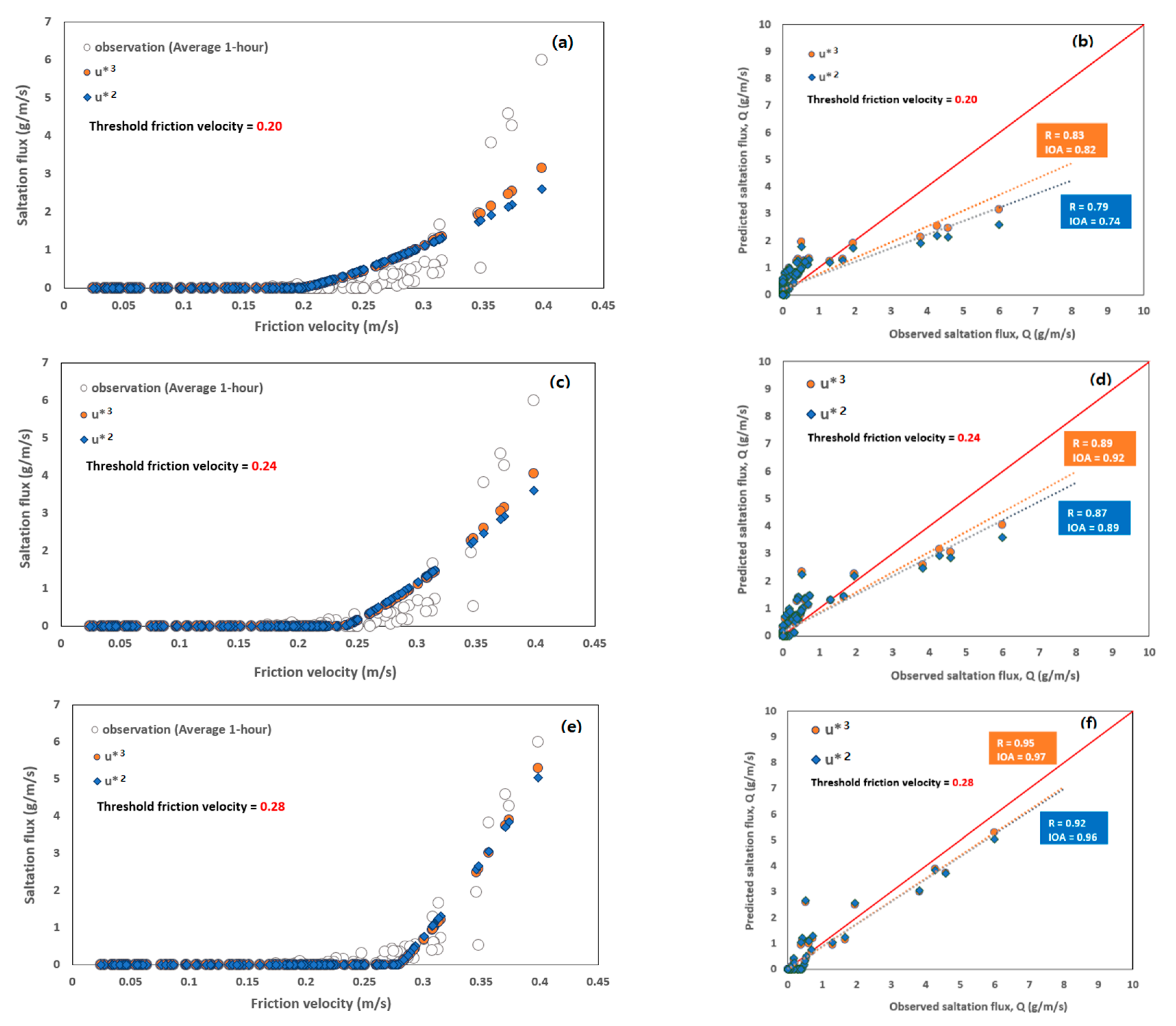
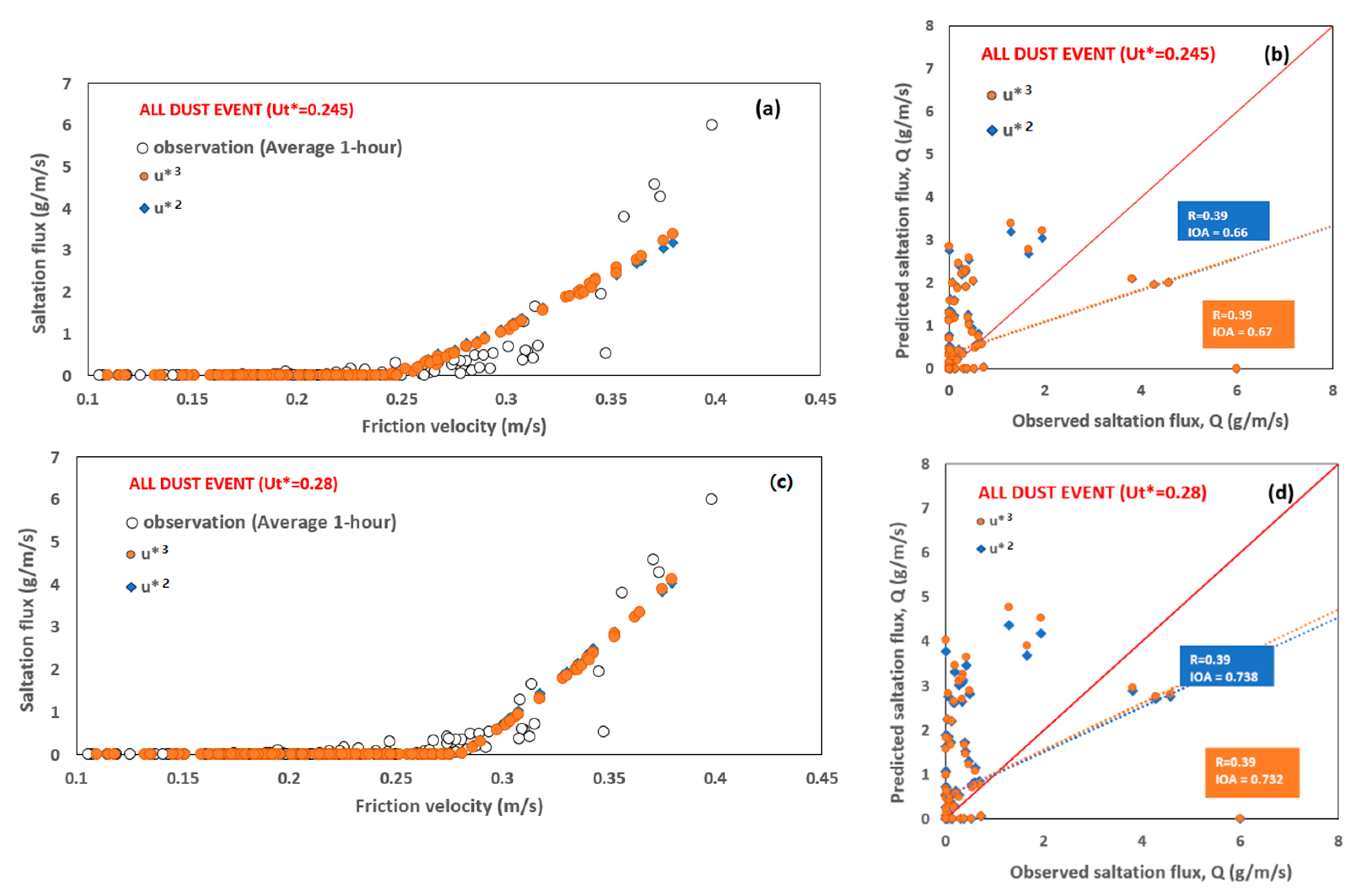
3.5. Saltation Flux
3.5.1. Determination of the Exponent of the Saltation Scheme
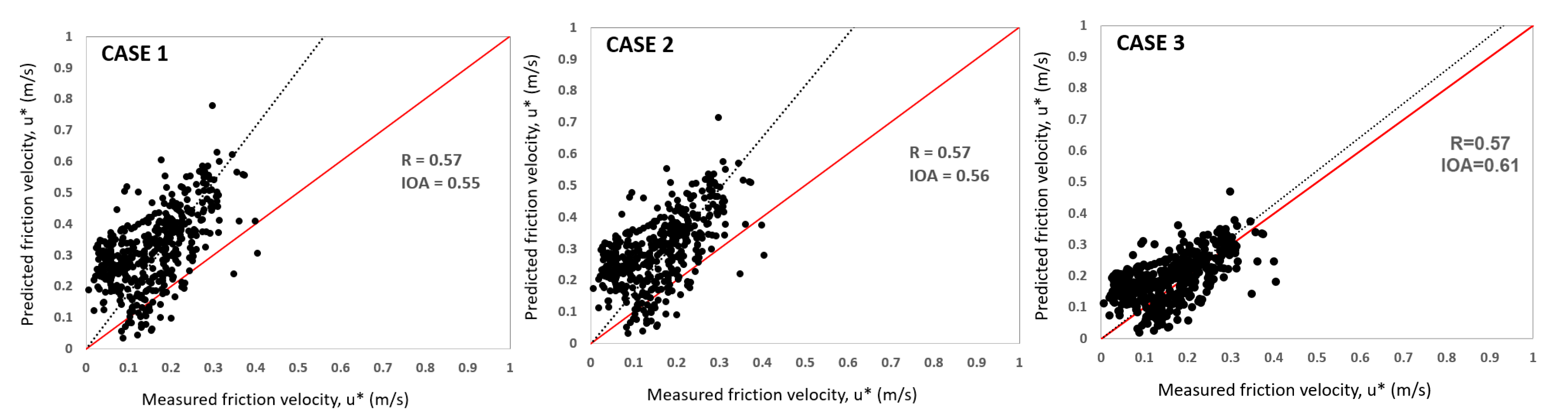
3.5.2. Comparison of Two Saltation Schemes with the Measured Friction Velocity
3.5.3. Comparison of Two Saltation Schemes with the Model-Predicted Friction Velocity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Uno, I.; Eguchi, K.; Yumimoto, K.; Takemura, T.; Shimizu, A.; Uematsu, M.; Liu, Z.; Wang, Z.; Hara, Y.; Sugimoto, N. Asian Dust Transported One Full Circuit Around the Globe. Nat. Geosci. 2009, 2, 557–560. [Google Scholar] [CrossRef]
- Sun, J.M.; Zhang, M.Y.; Liu, T.S. Spatial and Temporal Characteristics of Dust Storms in China and its Surrounding Regions, 1960–1999: Relations to Source Area and Climate. J. Geophys. Res. 2001, 106, 10325–10333. [Google Scholar] [CrossRef]
- Wang, X.; Dong, Z.; Zhang, J.; Liu, L. Modern Dust Storms in China: An Overview. J. Arid Environ. 2004, 58, 559–574. [Google Scholar] [CrossRef]
- Kimura, R.; Shinoda, M. Spatial Distribution of Threshold Wind Speeds for Dust Outbreaks in Northeast Asia. Geomorphology 2010, 114, 319–325. [Google Scholar] [CrossRef]
- Jung, M.; Son, S.; Kim, H.C.; Kim, S.; Park, R.J.; Chen, D. Contrasting Synoptic Weather Patterns between Non-Dust High Particulate Matter Events and Asian Dust Events in Seoul, South Korea. Atmos. Environ. 2019, 214. [Google Scholar] [CrossRef]
- Tsedendamba, P.; Dulam, J.; Baba, K.; Hagiwara, K.; Noda, J.; Kawai, K.; Sumiya, G.; McCarthy, C.; Kai, K.; Hoshino, B. Northeast Asian Dust Transport: A Case Study of a Dust Storm Event from 28 March to 2 April 2012. Atmosphere 2019, 10, 69. [Google Scholar] [CrossRef]
- Uno, I.; Amano, H.; Emori, S.; Kinoshita, N.; Matsu., I.; Sugimoto, N. Trans-Pacific Yellow Sand Transport Observed in April 1998: Numerical Simulation. J. Geophys. Res. 2001, 106, 331–344. [Google Scholar] [CrossRef]
- Ravi, S.; Zobeck, T.M.; Oer, T.M.; Okin, G.S.; D’odorico, P. On the Effect of Moisture Bonding Forces in Air-Dry Soils on Threshold Friction Velocity of Wind Erosion. Sedimentology 2006, 53, 597–609. [Google Scholar] [CrossRef]
- Webb, N.P.; Strong, C.L. Soil Erodibility Dynamics and its Representation for Wind Erosion and Dust Emission Models. Aeolian Res. 2011, 3, 165–179. [Google Scholar] [CrossRef]
- Yin, D.; Nickovic, S.; Sprigg, W.A. The Impact of using Different Land Cover Data on Wind-Blown Desert Dust Modeling Results in the Southwestern United States. Atmos. Environ. 2007, 41, 2214–2224. [Google Scholar] [CrossRef]
- Darmenova, K.; Sokolik, I.N.; Shao, Y.; Marticorena, B.; Bergametti, G. Development of a Physically Based Dust Emission Module within the Weather Research and Forecasting (WRF) Model: Assessment of Dust Emission Parameterizations and Input Parameters for Source Regions in Central and East Asia. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Raupach, M.R. Drag and Drag Partition on Rough Surfaces. Bound.-Layer Meteorol. 1992, 60, 375–395. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, Y. A Scheme for Drag Partition Over Rough Surfaces. Atmos. Environ. 2005, 39, 7351–7361. [Google Scholar] [CrossRef]
- Fecan, F.; Marticorena, B.; Bergametti, G. Parametrization of the Increase of the Aeolian Erosion Threshold Wind Friction Velocity due to Soil Moisture for Arid and Semi-Arid Areas. Ann. Geophys. 1999, 17, 149–157. [Google Scholar] [CrossRef]
- Shao, Y.; Lu, H. A Simple Expression for Wind Erosion Threshold Friction Velocity. J. Geophys. Res. 2000, 105, 437–443. [Google Scholar] [CrossRef]
- Bagnold, R.A. The Physics of Blown Sand and Desert Dunes; Courier Corporation: Morrow, NY, USA, 1941; p. 265. [Google Scholar]
- Marticorena, B.; Bergametti, G. Modeling the Atmospheric Dust Cycle. Part 1: Design of a Soil-Derived Dust Emission Scheme. J. Geophys. Res. 1995, 100, 16415–16430. [Google Scholar] [CrossRef]
- Alfaro, S.C.; Gaudichet, A.; Gomes, L.; Maille, M. Modeling the Size Distribution of a Soil Aerosol Produced by Sandblasting. J. Geophys. Res. 1997, 102, 11239–11249. [Google Scholar] [CrossRef]
- Gillette, D. A Wind Tunnel Simulation of the Erosion of Soil: Effect of Soil Texture, Sandblasting, Wind Speed, and Soil Consolidation on Dust Production. Atmos. Environ. 1978, 12, 1735–1743. [Google Scholar] [CrossRef]
- Uno, I.; Wang, Z.; Chiba, M.; Chun, Y.S.; Gong, S.L.; Hara, Y.; Jung, E.; Lee, S.; Liu, M.; Mikami, M.; et al. Dust Model Intercomparison (DMIP) Study Over Asia: Overview. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Kang, J.; Yoon, S.; Shao, Y.; Kim, S. Comparison of Vertical Dust Flux by Implementing Three Dust Emission Schemes in WRF/Chem. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Lu, H.; Shao, Y. A New Model for Dust Emission by Saltation Bombardment. J. Geophys. Res. 1999, 104, 827–842. [Google Scholar] [CrossRef]
- Liu, M.; Westphal, D.L.; Wang, S.; Shimizu, A.; Sugimoto, N.; Zhou, J.; Chen, Y. A High-Resolution Numerical Study of the Asian Dust Storms of April 2001. J. Geophys. Res. 2003, 108, 8653. [Google Scholar] [CrossRef]
- In, H.; Park, S. A Simulation of Long-Range Transport of Yellow Sand Observed in April 1998 in Korea. Atmos. Environ. 2002, 36, 4173–4187. [Google Scholar] [CrossRef]
- Park, S.U.; In, H.J. Parameterization of Dust Emission for the Simulation of the Yellow Sand (Asian Dust) Event Observed in March 2002 in Korea. J. Geophys. Res. 2003, 108, 4618. [Google Scholar] [CrossRef]
- Gong, S.L.; Zhang, X.Y.; Zhao, T.L.; McKendry, I.G.; Jaffe, D.A.; Lu, N.M. Characterization of Soil Dust Distributions in China and its Transport during ACE-ASIA: 2. Model Simulation and Validation. J. Geophys. Res. 2003, 108, 4262. [Google Scholar]
- Nickovic, S.; Kallos, G.; Papadopoulos, A.; Kakaliagou, O. A Model for Prediction of Desert Dust Cycle in the Atmosphere. J. Geophys. Res. 2001, 106, 113–129. [Google Scholar] [CrossRef]
- Shao, Y.; Raupach, M.R.; Findlater, P.A. Effect of Saltation Bombardment on the Entrainment of Dust by Wind. J. Geophys. Res. 1993, 98, 12719–12726. [Google Scholar] [CrossRef]
- Shao, Y.; Raupach, M.R.; Leys, J.F. A Model for Predicting Aeolian Sand Drift and Dust Entrainment on Scales from Paddock to Region. Aust. J. Soil Res. 1996, 34, 309–342. [Google Scholar] [CrossRef]
- Shao, Y. A Model for Mineral Dust Emission. J. Geophys. Res. 2001, 106, 20239–20254. [Google Scholar] [CrossRef]
- Uno, I.; Carmichael, G.; Streets, D.; Satake, S.; Takemura, T.; Woo, J.; Uematsu, M.; Ohta, S. Analysis of Surface Black Carbon Distributions during ACE-Asia using a Regional-Scale Aerosol Model. J. Geophys. Res. 2003, 108, 8636. [Google Scholar] [CrossRef]
- Christensen, J.H. The Danish Eulerian Hemispheric ModelAa Three-Dimensional Air Pollution Model used for the Arctic. Atmos. Environ. 1997, 31, 4169–4191. [Google Scholar] [CrossRef]
- Tanaka, T.Y.; Chiba, M. Global Simulation of Dust Aerosol with a Chemical Transport Model, MASINGAR. J. Meteorol. Soc. Jpn. Ser. II 2005, 83, 255–278. [Google Scholar] [CrossRef]
- Luo, C.; Mahowald, N.; Jones, C. Temporal Variability of Dust Mobilization and Concentration in Source Regions. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Darmenova, K.; Sokolik, I.; Shao, Y.; Bergametti, G.; Marticorena, B.; Uno, I. Development of a Regional Dust Modeling System for Central and East Asia Under the NEESPI Initiative; American Geophysical Union: San Francisco, CA, USA, 2006. [Google Scholar]
- White, B.R. Soil Transport by Wind on Mars. J. Geophys. Res. Solid Earth 1979, 84, 4643–4651. [Google Scholar] [CrossRef]
- Owen, P.R. Saltation of Uniform Grains in Air. J. Fluid Mech. 1964, 20, 225–242. [Google Scholar] [CrossRef]
- Mikami, M.; Yamada, Y.; Ishizuka, M.; Ishimaru, T.; Gao, W.; Zeng, F. Measurement of Saltation Process Over Gobi and Sand Dunes in the Taklimakan Desert, China, with Newly Developed Sand Particle Counter. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Ishizuka, M. JADE Data, Mendeley Data v1; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Liu, D.; Ishizuka, M.; Mikami, M.; Shao, Y. Turbulent Characteristics of Saltation and Uncertainty of Saltation Model Parameters. Atmos. Chem. Phys. 2018, 18, 7595–7606. [Google Scholar] [CrossRef]
- Xi, X.; Sokolik, I.N. Seasonal Dynamics of Threshold Friction Velocity and Dust Emission in Central Asia. J. Geophys. Res. Atmos. 2015, 120, 1536–1564. [Google Scholar] [CrossRef]
- Laurent, B.; Marticorena, B.; Bergametti, G.; Chazette, P.; Maignan, F.; Schmechtig, C. Simulation of the Mineral Dust Emission Frequencies from Desert Areas of China and Mongolia using an Aerodynamic Roughness Length Map Derived from the POLDER/ADEOS 1 Surface Products. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Shao, Y.; Ishizuka, M.; Mikami, M.; Leys, J.F. Parameterization of Size-resolved Dust Emission and Validation with Measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Ishizuka, M.; Mikami, M.; Leys, J.; Yamada, Y.; Heidenreich, S.; Shao, Y.; McTainsh, G.H. Effects of Soil Moisture and Dried Raindroplet Crust on Saltation and Dust Emission. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Ishizuka, M.; Mikami, M.; Leys, J.F.; Shao, Y.; Yamada, Y.; Heidenreich, S. Power Law Relation between Size-Resolved Vertical Dust Flux and Friction Velocity Measured in a Fallow Wheat Field. Aeolian Res. 2014, 12, 87–99. [Google Scholar] [CrossRef]
- Sugita, F.; Kishii, T.; Kuzuha, Y.; Yamanaka, T. A Wind Tunnel Investigation of Roughness Properties over Non-Homogeneous Rough Surfaces. Hydrol. Process. 1998, 12, 2149–2161. [Google Scholar] [CrossRef]
- Marticorena, B.; Kardous, M.; Bergametti, G.; Callot, Y.; Chazette, P.; Khatteli, H.; Le Hégarat-Mascle, S.; Maillé, M.; Rajot, J.; Vidal-Madjar, D.; et al. Surface and Aerodynamic Roughness in Arid and Semiarid Areas and their Relation to Radar Backscatter Coefficient. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Hébrard, E.; Listowski, C.; Coll, P.; Marticorena, B.; Bergametti, G.; Määttänen, A.; Montmessin, F.; Forget, F. An Aerodynamic Roughness Length Map Derived from Extended Martian Rock Abundance Data. J. Geophys. Res. 2012, 117, E04008. [Google Scholar] [CrossRef]
- Foroutan, H.; Young, J.; Napelenok, S.; Ran, L.; Appel, K.W.; Gilliam, R.C.; Pleim, J.E. Development and Evaluation of a Physics-Based Windblown Dust Emission Scheme Implemented in the CMAQ Modeling System. J. Adv. Model. Earth Syst. 2017, 9, 585–608. [Google Scholar] [CrossRef]
- King, J.; Nickling, W.G.; Gillies, J.A. Representation of Vegetation and Other Nonerodible Elements in Aeolian Shear Stress Partitioning Models for Predicting Transport Threshold. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Zhao, T.L.; Gong, S.L.; Zhang, X.Y.; Abdel-Mawgoud, A.; Shao, Y.P. An Assessment of Dust Emission Schemes in Modeling East Asian Dust Storms. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Park, Y.; Park, S.H. Development of a New Wind-Blown-Dust Emission Module using Comparative Assessment of Existing Dust Models. Part. Sci. Technol. 2010, 28, 267–286. [Google Scholar] [CrossRef]
- Park, Y.; Park, S.H. Estimation of Threshold Friction Velocity using a Physical Parameterization Over the Asian Dust Source Region. Particul. Sci. Technol. 2013, 31, 119–127. [Google Scholar] [CrossRef]
- Kok, J.F.; Mahowald, N.M.; Fratini, G.; Gillies, J.A.; Ishizuka, M.; Leys, J.F.; Mikami, M.; Park, M.; Park, S.; Van Pelt, R.S. An Improved Dust Emission model–Part 1: Model Description and Comparison against Measurements. Atmos. Chem. Phys. 2014, 14, 13023–13041. [Google Scholar] [CrossRef]
- Kok, J.F.; Albani, S.; Mahowald, N.M.; Ward, D.S. An Improved Dust Emission model–Part 2: Evaluation in the Community Earth System Model, with Implications for the use of Dust Source Functions. Atmos. Chem. Phys. 2014, 14, 13043–13061. [Google Scholar] [CrossRef]
- Pérez, C.; Haustein, K.; Janjic, Z.; Jorba, O.; Huneeus, N.; Baldasano, J.M.; Black, T.; Basart, S.; Nickovic, S.; Miller, R.L.; et al. Atmospheric Dust Modeling from Meso to Global Scales with the Online NMMB/BSC-Dust Model—Part 1: Model Description, Annual Simulations and Evaluation. Atmos. Chem. Phys. 2011, 11, 13001–13027. [Google Scholar] [CrossRef]
- Wyatt, V.E.; Nickiing, W.G. Drag and Shear Stress Partitioning in Sparse Desert Creosote Communities. Can. J. Earth Sci. 1997, 34, 1486–1498. [Google Scholar] [CrossRef]
- Campbell, P.C.; Bash, J.O.; Spero, T.L. Updates to the Noah Land Surface Model in WRF-CMAQ to Improve Simulated Meteorology, Air Quality, and Deposition. J. Adv. Model. Earth Syst. 2019, 11, 231–256. [Google Scholar] [CrossRef]
- Pan, H.-L.; Mahrt, L. Interaction between Soil Hydrology and Boundary-Layer Development. Bound.-Layer Meteorol. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of Land Surface Evaporation by Four Schemes and Comparison with FIFE Observations. J. Geophys. Res. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Wea. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah Land Surface Model Advances in the National Centers for Environmental Prediction Operational Mesoscale Eta Model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Pleim, J.E.; Chang, J.S. A Non-Local Closure Model for Vertical Mixing in the Convective Boundary Layer. Atmos. Environ. 1992, 26, 965–981. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-Scale Measurements. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Yang, Z.; Niu, G.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 2. Evaluation Over Global River Basins. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; Xia, Y.; Huang, M.; Wei, H.; Leung, L.R.; Ek, M.B. Assessment of Simulated Water Balance from Noah, Noah-MP, CLM, and VIC Over CONUS using the NLDAS Test Bed. J. Geophys. Res. Atmos. 2014, 119, 751–770. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; David, C.; Niu, G.; Rodell, M. Hydrological Evaluation of the Noah-MP Land Surface Model for the Mississippi River Basin. J. Geophys. Res. Atmos. 2014, 119, 23–38. [Google Scholar] [CrossRef]
- Hong, S.; Park, S.K.; Yu, X. Scheme-Based Optimization of Land Surface Model using a Micro-Genetic Algorithm: Assessment of its Performance and Usability for Regional Applications. SOLA 2015, 11, 129–133. [Google Scholar] [CrossRef]
- Mckenna Neuman, C. Effects of Temperature and Humidity upon the Entrainment of Sedimentary Particles by Wind. Bound.-Layer Meteorol. 2003, 108, 61–89. [Google Scholar] [CrossRef]
- Gillett, D.A. Environmental factors affecting dust emission by wind erosion. In Saharan Dust; Morales, C., Ed.; Wiley: New York, NY, USA, 1979; pp. 71–94. [Google Scholar]
- Kawamura, R. Study of Sand Movement by Wind Translated. In Hydraulics Engineering Laboratory Report HEL 2.8; University of California: Berkeley, CA, USA, 1951. [Google Scholar]
- Kok, J.F.; Parteli, E.J.R.; Michaels, T.I.; Karam, D.B. The Physics of Wind-Blown Sand and Dust. Rep. Prog. Phys. 2012, 75, 106901. [Google Scholar] [CrossRef]
- Martin, R.L.; Kok, J.F. Wind-Invariant Saltation Heights Imply Linear Scaling of Aeolian Saltation Flux with Shear Stress. Sci. Adv. 2017, 3, e1602569. [Google Scholar] [CrossRef]
| Model Attribute | WRFV3.8.1 |
|---|---|
| Domain (Horizontal grid) | Australia (74 61) |
| Horizontal resolution | 5 km |
| Land-use data | IGBP (International Geosphere-Biosphere Programme)-Modified MODIS (Modarate Resolution Imaging Spectroradiometer) 20-category |
| Microphysics | WRF Single-Moment 6-class |
| Longwave radiation | RRTMG (The Rapid Radiative Transfer Model for GCMs) |
| Shortwave radiation | RRTMG |
| Land surface | Modified Noah-MP |
| Planetary Boundary layer | Yonsei University (YSU) |
| Cumulus parameterization | Grell-Devenyi |
| Initial data | NCEP FNL Operational Model Global Tropospheric Analyses (ds083.2) |
| Simulation period (Spin-up) | 15 February to 16 March 2006 (8-day) |
| CASE | Land-use Type | Vegetation Fraction (%) | Roughness Length (mm) | Friction Velocity IOA |
|---|---|---|---|---|
| CASE 1 | Shrub land | 25.25 | 13.61 | 0.55 |
| CASE 2 | Barren land | 25.25 | 8.59 | 0.56 |
| CASE 3 | Barren land | 2.00 | 0.48 | 0.61 |
| Contents | ||
|---|---|---|
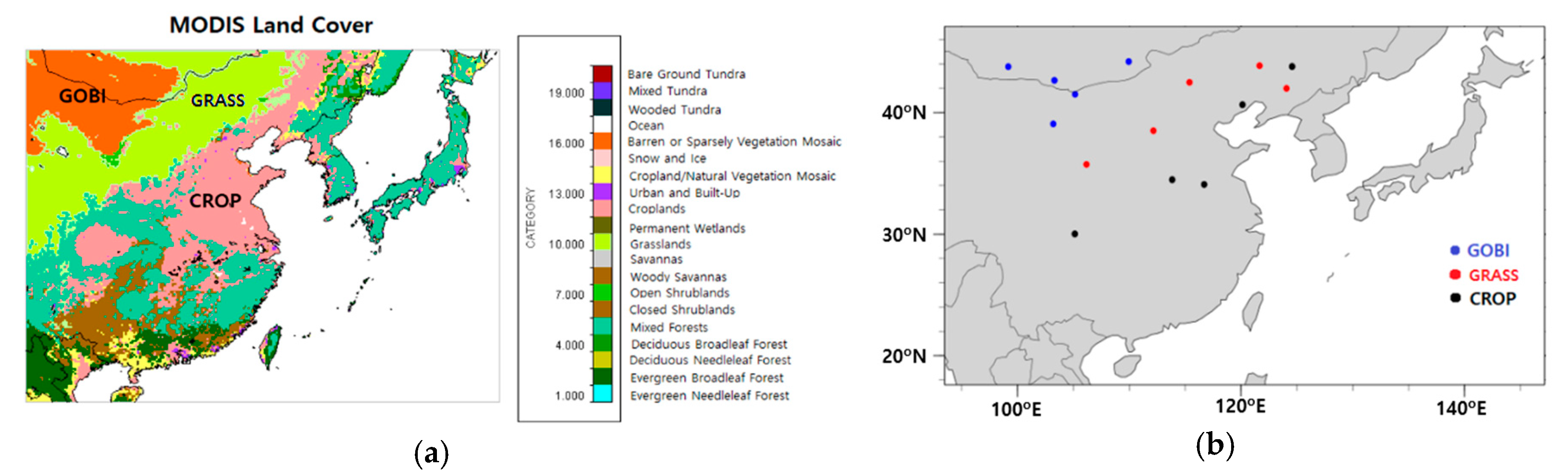
| Analysis Site | East Asia | Australia |
| Observation data | Satellite data | Measured field data |
| (SMAP L4 Global 9 km Surface and Rootzone Soil Moisture, topmost layer 5 cm) | (Soil moisture content (topmost layer 0.2~2 cm) reported by Liu et al. (2018) and Shao et al. (2011)) | |
| Land surface scheme | Noah, Noah-MP, Pleim-Xiu | Noah-MP |
| Period | 2016 (1-year) | JADE project (2006.2.23~3.12, 18-day) |
| Scheme | Gobi_1 | Gobi_2 | Gobi_3 | Gobi_4 | Gobi_5 | |||||
| IOA | R | IOA | R | IOA | R | IOA | R | IOA | R | |
| Pleim-Xiu | 0.82 | 0.58 | 0.74 | 0.35 | 0.82 | 0.57 | 0.69 | 0.50 | 0.80 | 0.52 |
| Noah | 0.55 | 0.49 | 0.53 | 0.25 | 0.54 | 0.64 | 0.51 | 0.52 | 0.49 | 0.19 |
| Noah-MP | 0.78 | 0.68 | 0.81 | 0.52 | 0.85 | 0.75 | 0.81 | 0.48 | 0.72 | 0.38 |
| Scheme | Grass_1 | Grass_2 | Grass_3 | Grass _4 | Grass _5 | |||||
| IOA | R | IOA | R | IOA | R | IOA | R | IOA | R | |
| Pleim-Xiu | 0.73 | 0.39 | 0.78 | 0.43 | 0.67 | 0.50 | 0.49 | 0.61 | 0.65 | 0.62 |
| Noah | 0.32 | 0.61 | 0.72 | 0.53 | 0.73 | 0.46 | 0.69 | 0.64 | 0.65 | 0.49 |
| Noah-MP | 0.50 | 0.73 | 0.83 | 0.77 | 0.70 | 0.42 | 0.53 | 0.70 | 0.64 | 0.60 |
| Scheme | Crop_1 | Crop_2 | Crop_3 | Crop_4 | Crop_5 | |||||
| IOA | R | IOA | R | IOA | R | IOA | R | IOA | R | |
| Pleim-Xiu | 0.42 | 0.54 | 0.56 | 0.39 | 0.24 | 0.27 | 0.68 | 0.34 | 0.63 | 0.50 |
| Noah | 0.63 | 0.59 | 0.45 | 0.39 | 0.48 | 0.31 | 0.52 | 0.59 | 0.58 | 0.46 |
| Noah-MP | 0.69 | 0.61 | 0.64 | 0.42 | 0.62 | 0.36 | 0.63 | 0.59 | 0.70 | 0.45 |
| CASE | Land-Use Type | Vegetation Fraction (%) | Drag Partitioning Effect Factor | Soil Moisture Effect Factor | Threshold Friction Velocity (m/s) |
|---|---|---|---|---|---|
| CASE 1 | Shrub land | 25.25 | 3.438 | 10 cm: 1.079 | 0.781 |
| 1 cm: 1.063 | 0.769 | ||||
| Correction 1 cm: 1.056 | 0.764 | ||||
| CASE 2 | Barren land | 25.25 | 2.074 | 10 cm: 1.079 | 0.471 |
| 1 cm: 1.063 | 0.464 | ||||
| Correction 1 cm: 1.056 | 0.461 | ||||
| CASE 3 | Barren land | 2.00 | 1.110 | 10 cm: 1.079 | 0.250 |
| 1 cm: 1.063 | 0.247 | ||||
| Correction 1 cm: 1.056 | 0.245 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Park, S.H. Stepwise Assessment of Different Saltation Theories in Comparison with Field Observation Data. Atmosphere 2020, 11, 10. https://doi.org/10.3390/atmos11010010
Lee H, Park SH. Stepwise Assessment of Different Saltation Theories in Comparison with Field Observation Data. Atmosphere. 2020; 11(1):10. https://doi.org/10.3390/atmos11010010
Chicago/Turabian StyleLee, Haeju, and Sung Hoon Park. 2020. "Stepwise Assessment of Different Saltation Theories in Comparison with Field Observation Data" Atmosphere 11, no. 1: 10. https://doi.org/10.3390/atmos11010010
APA StyleLee, H., & Park, S. H. (2020). Stepwise Assessment of Different Saltation Theories in Comparison with Field Observation Data. Atmosphere, 11(1), 10. https://doi.org/10.3390/atmos11010010




