Atmospheric Characterization Based on Relative Humidity Control at Optical Turbulence Generator
Abstract
:1. Introduction
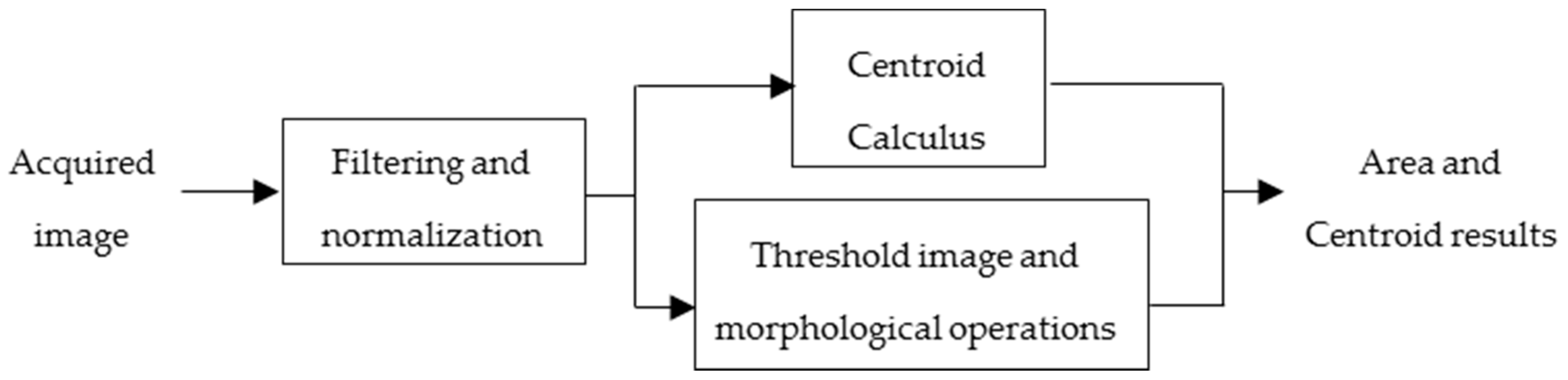
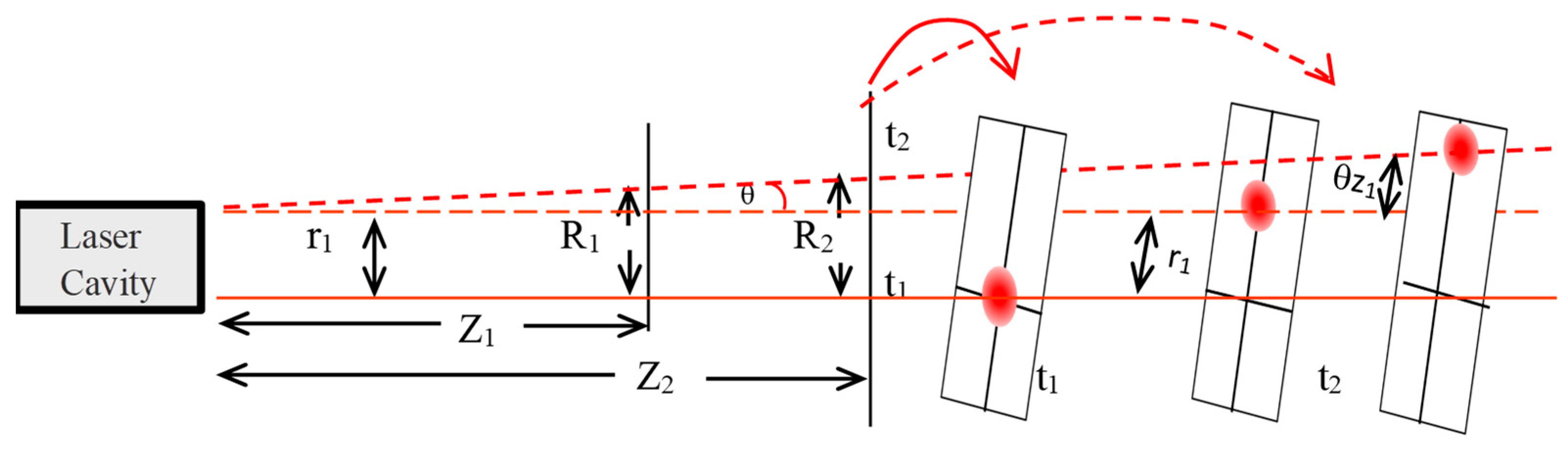
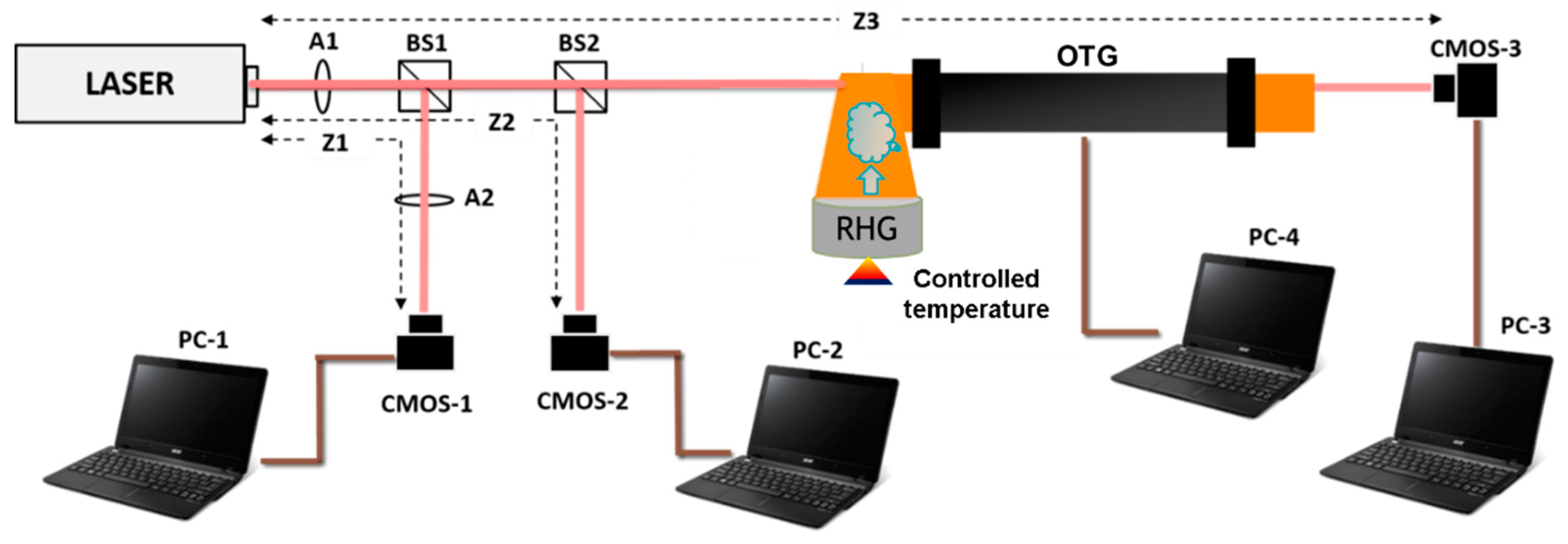
2. Proposed System Description and Methods
3. Results
3.1. Synchronization
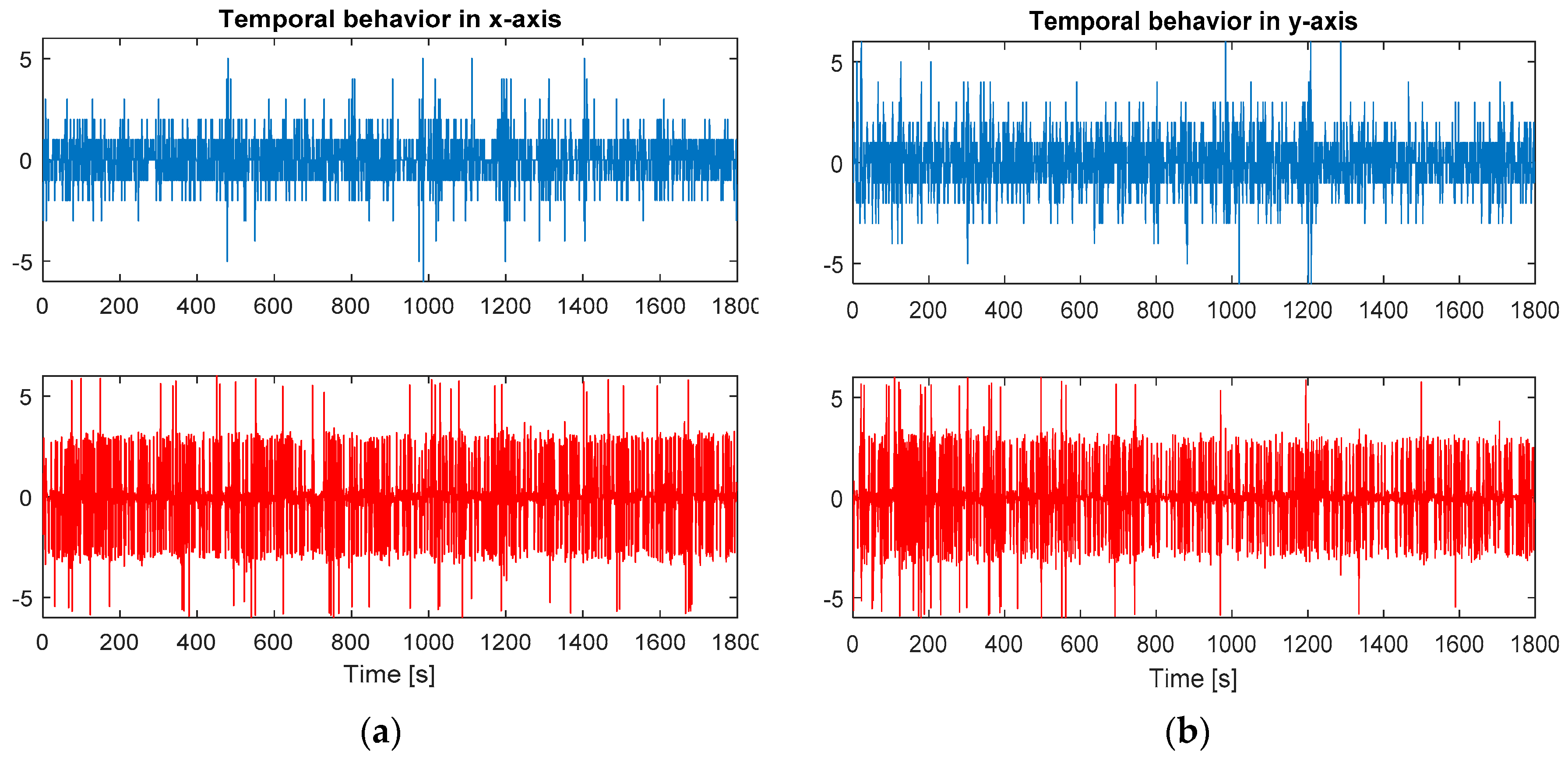
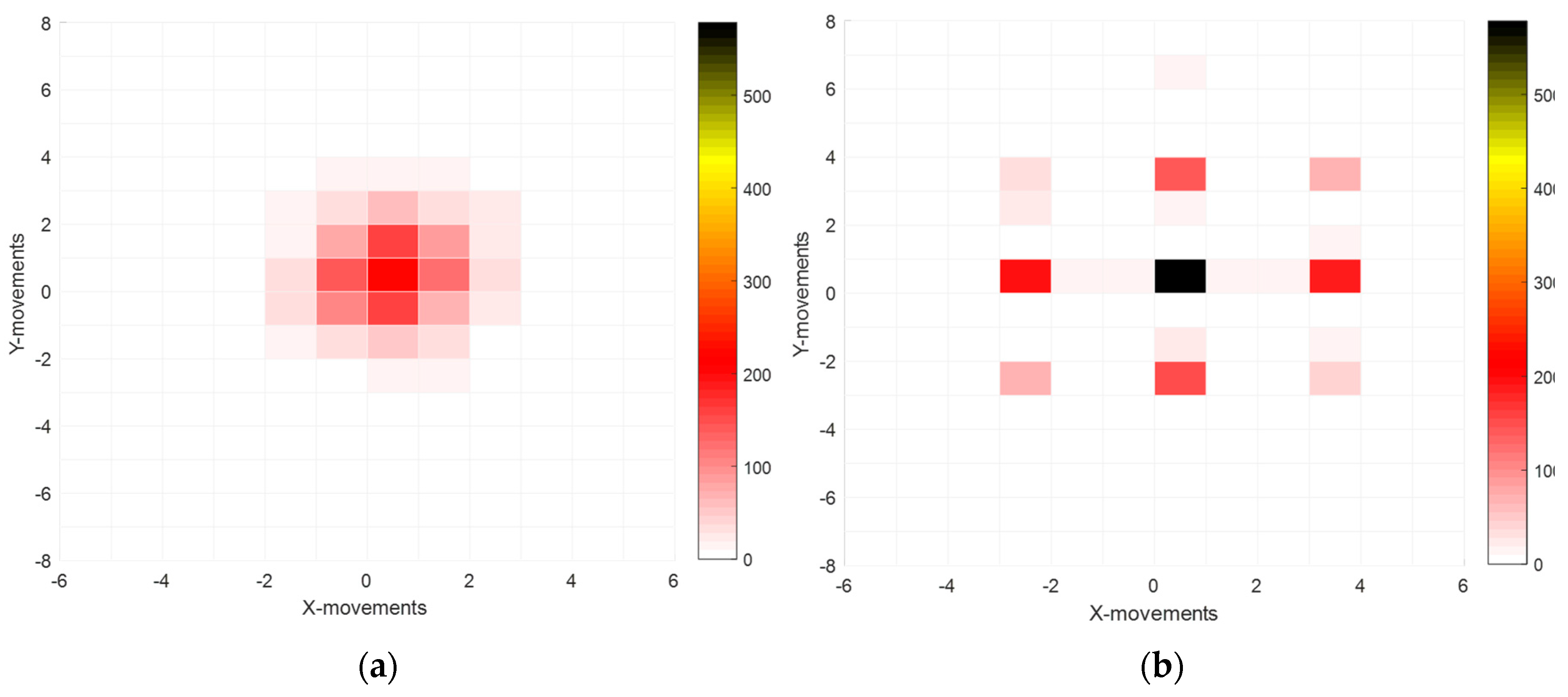
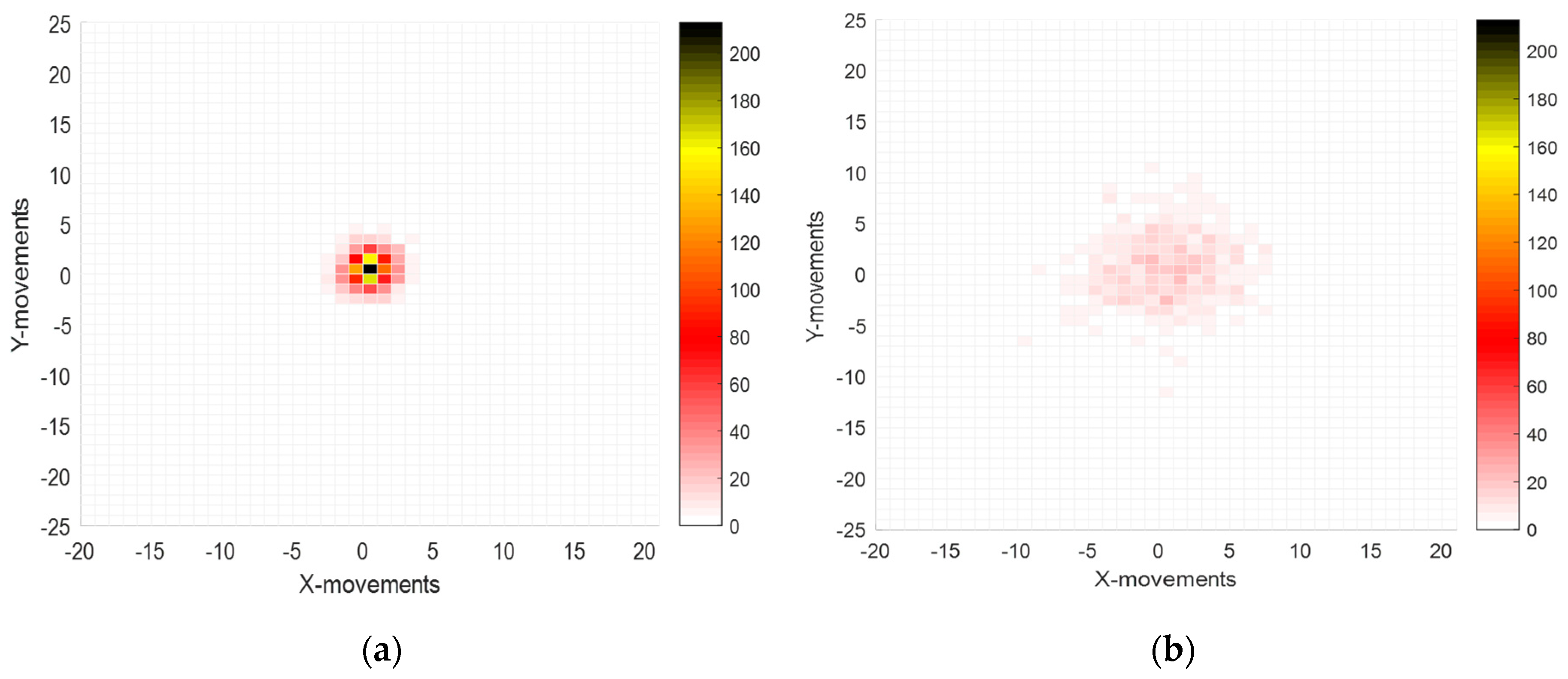
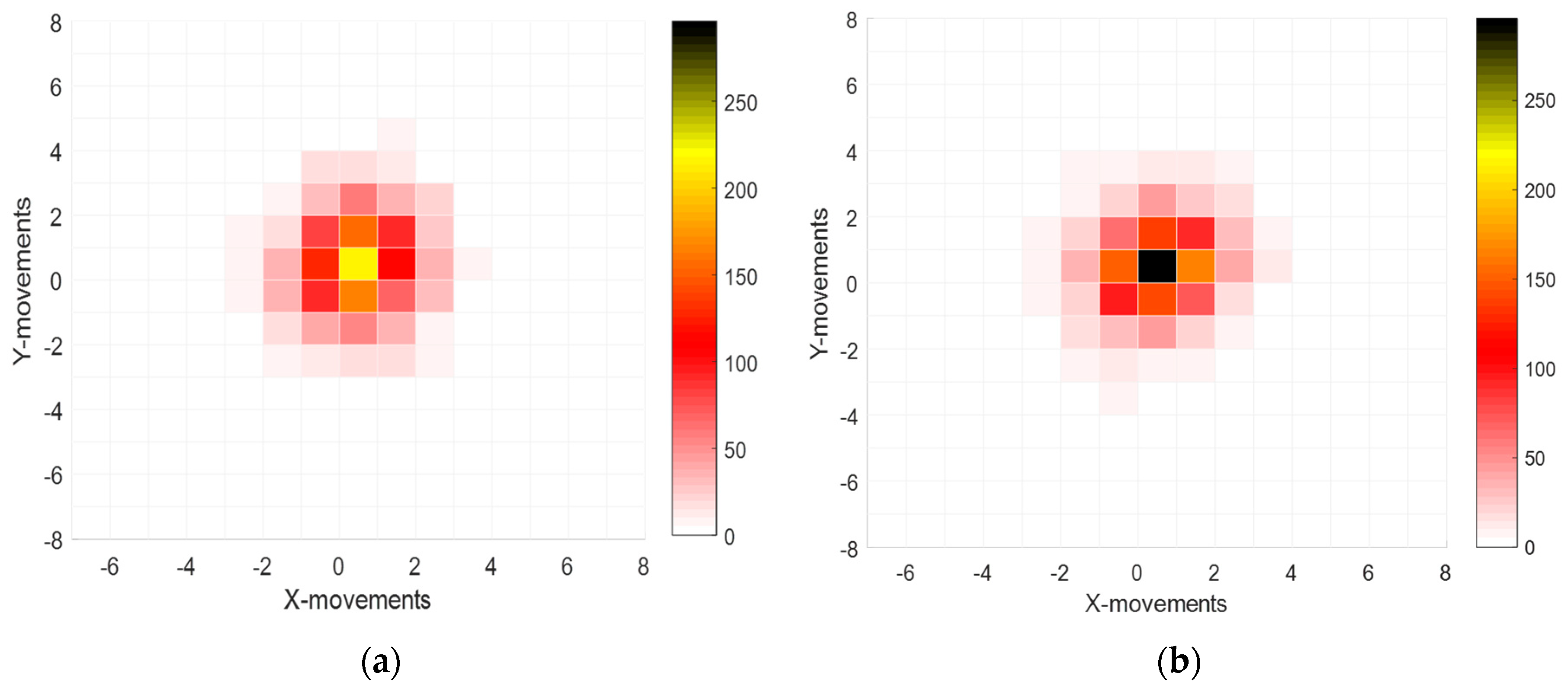
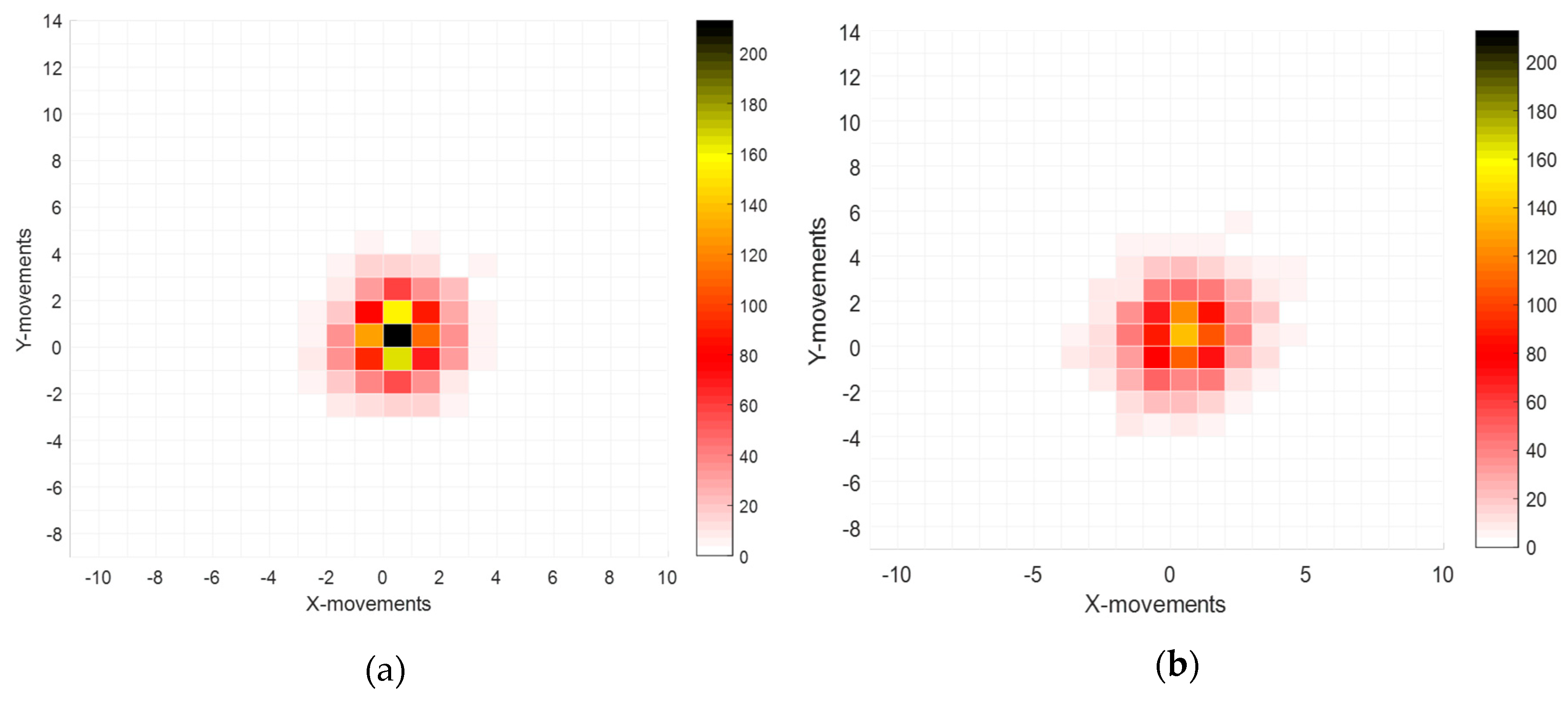
3.2. Centroids Fluctuations
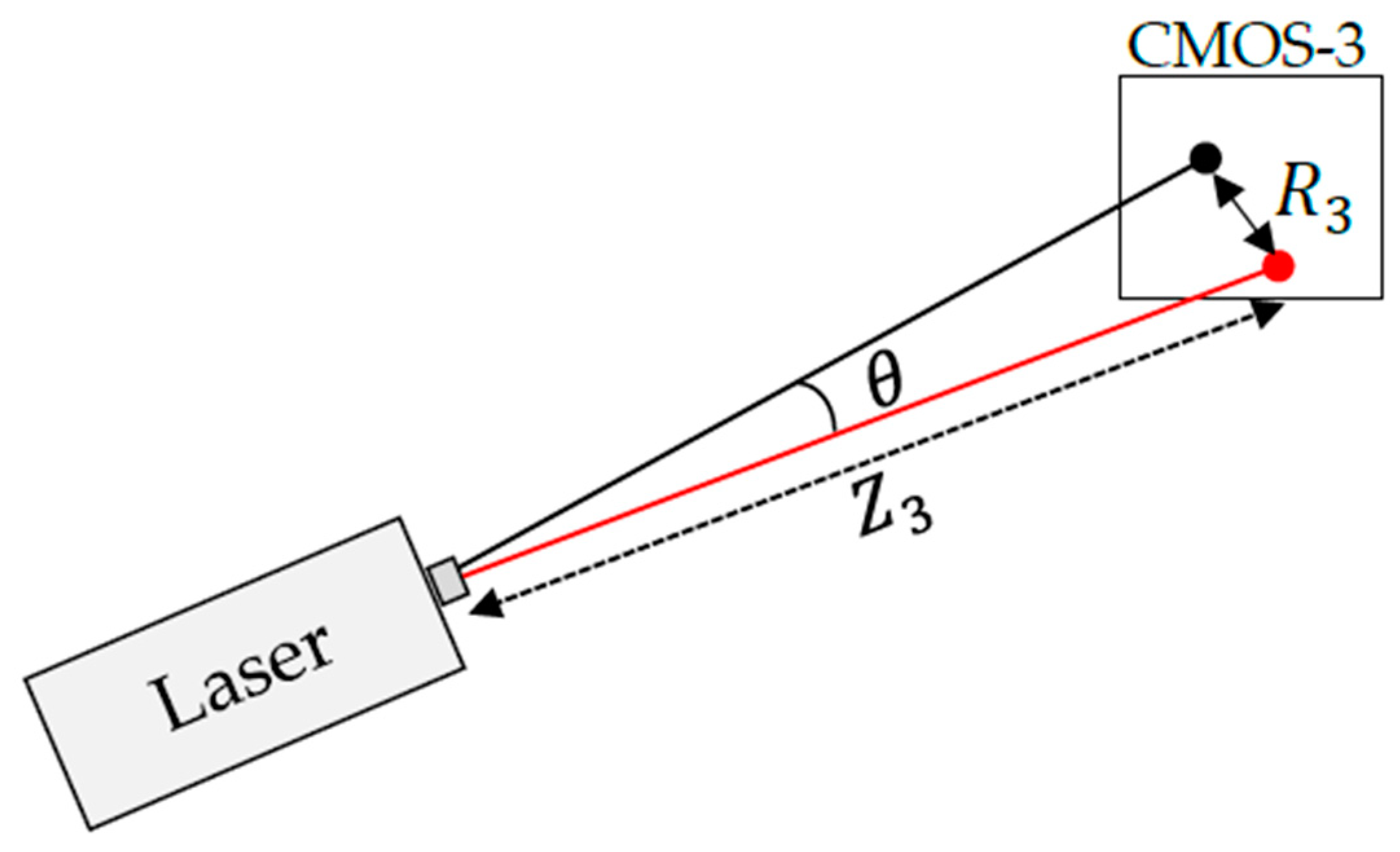
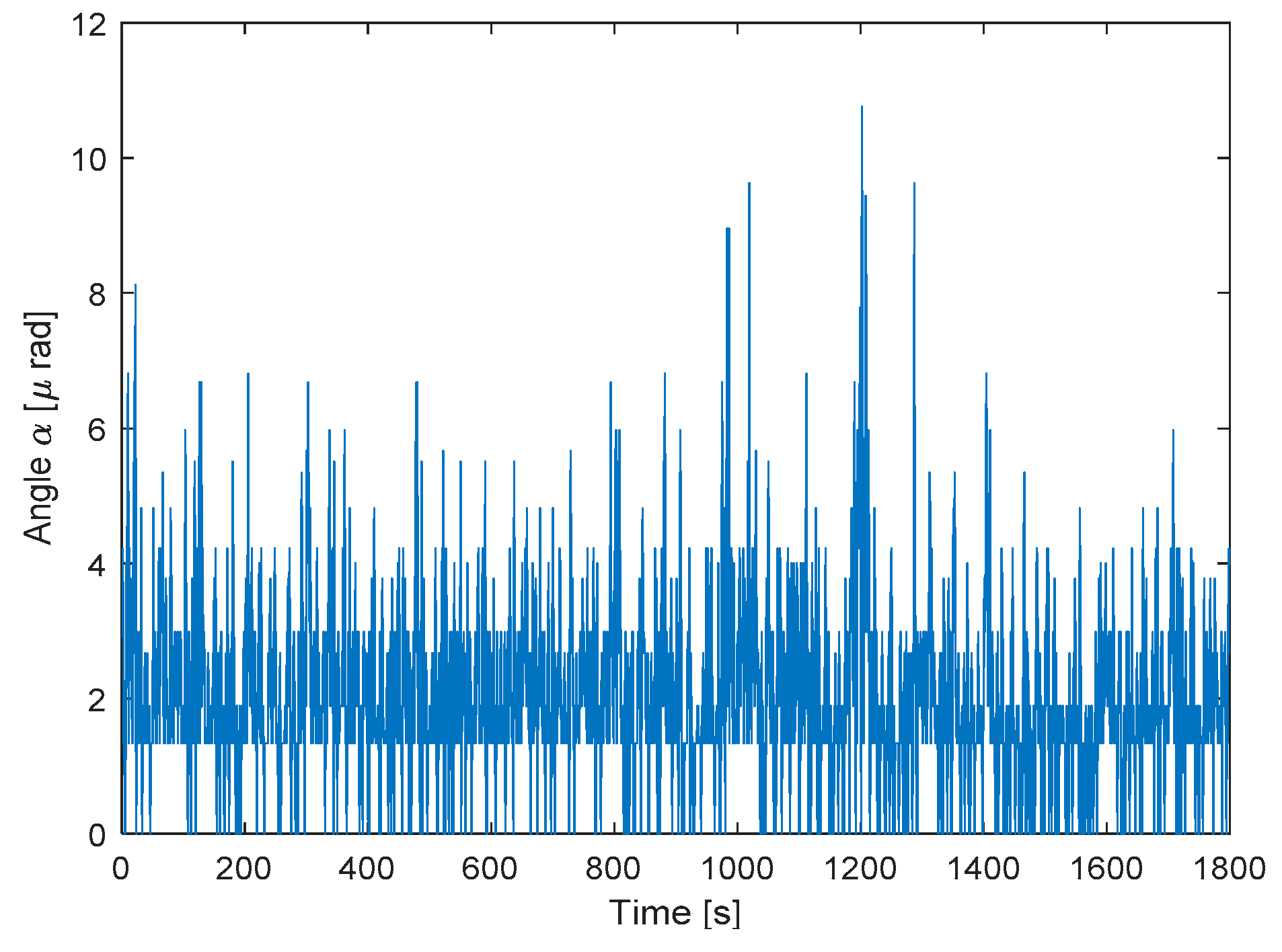
3.3. Angle Computation
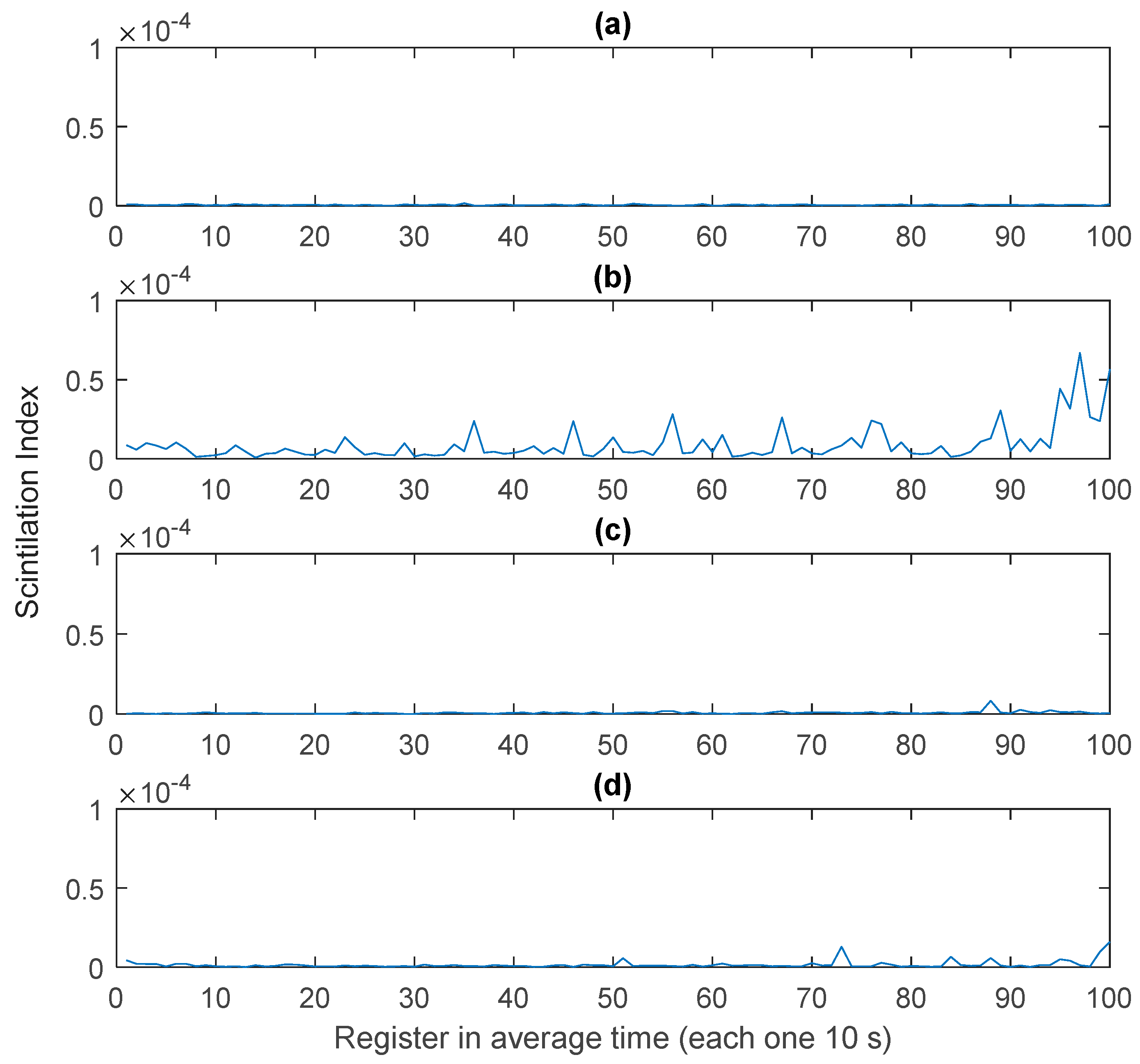
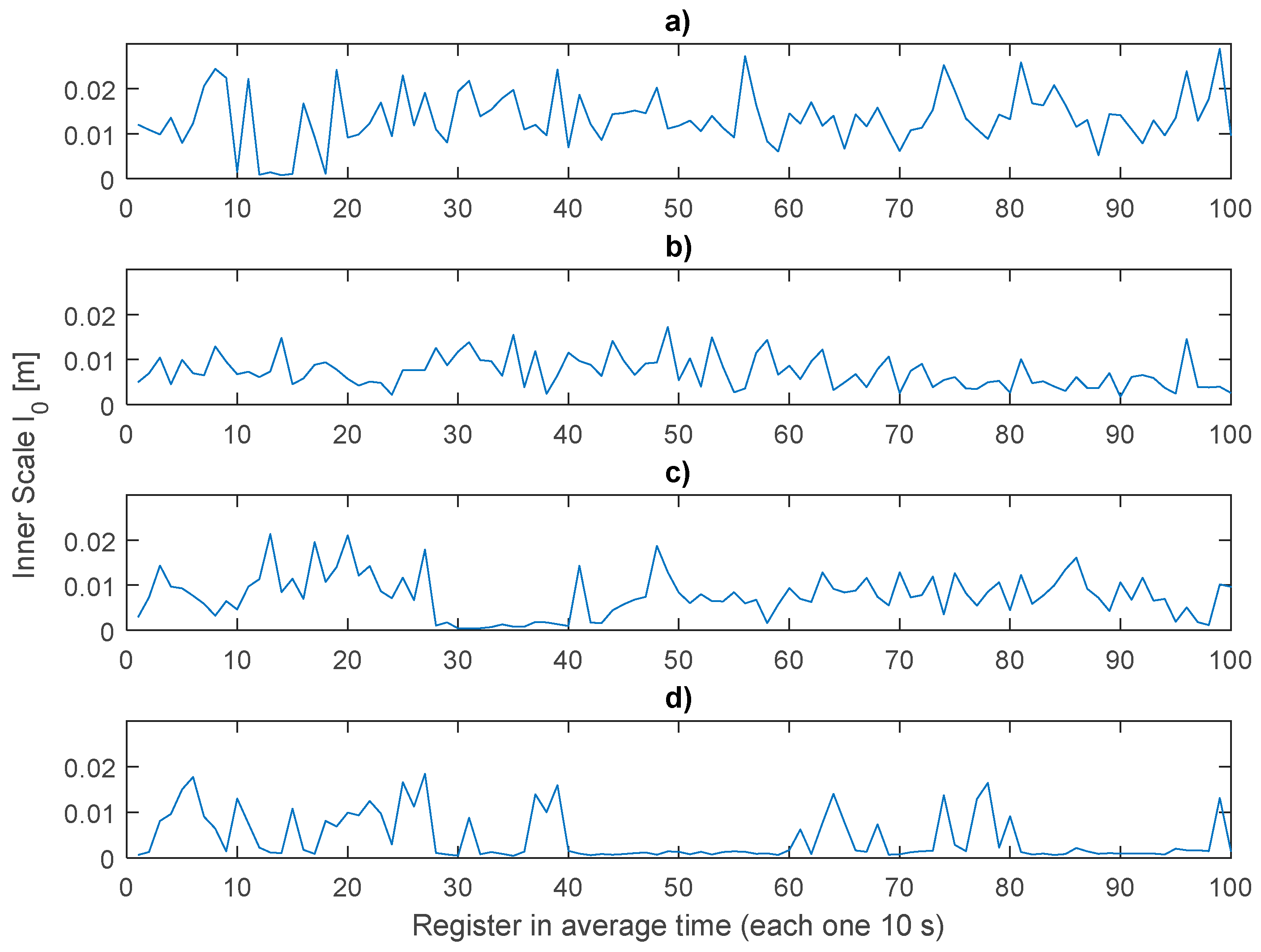
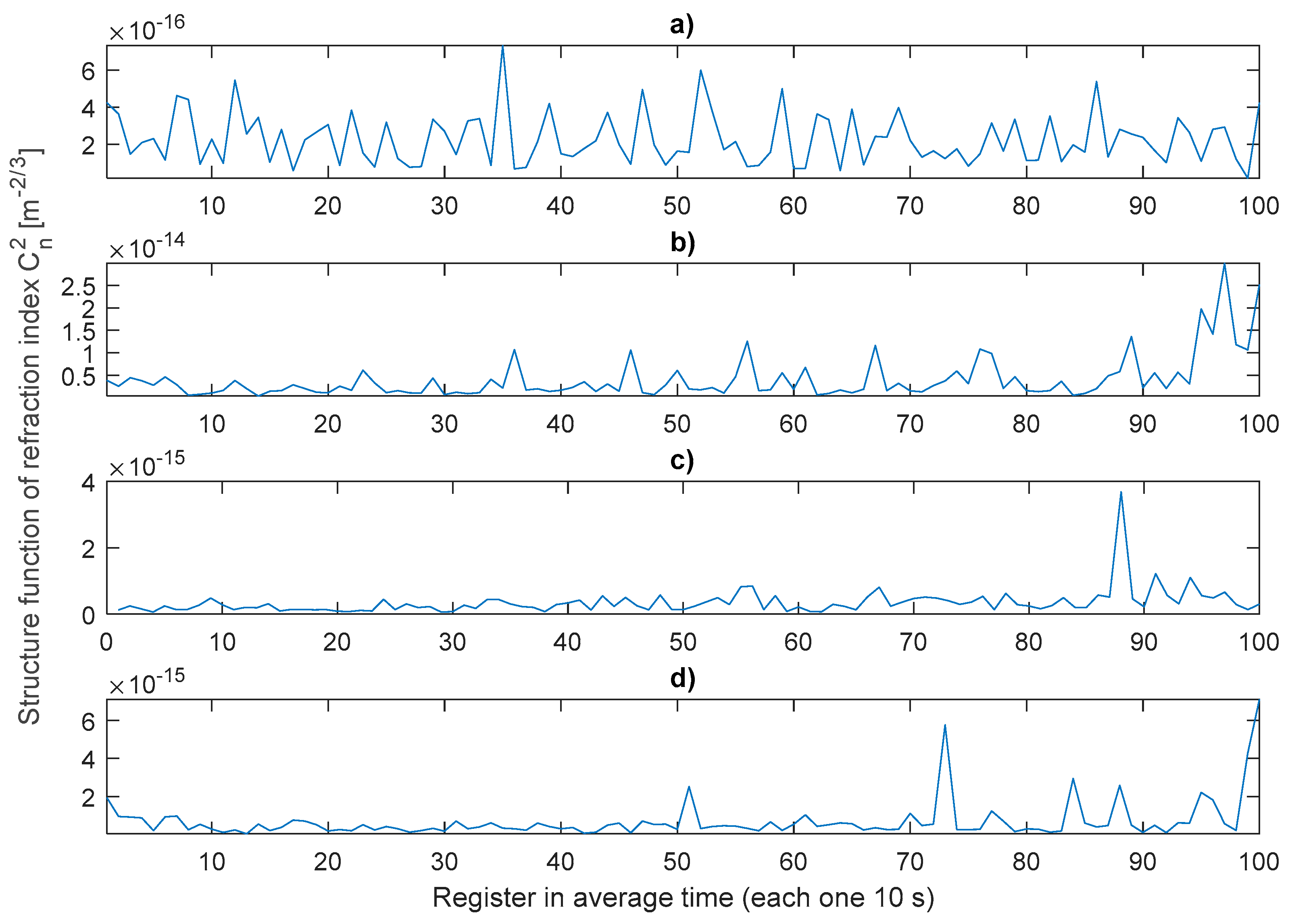
3.4. Structure Functions and Turbulence Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; Dover Publ.: Toronto, ON, Canada, 1961. [Google Scholar]
- Larry, L.C.; Philips, R.L. Laser Beam Propagation through Random Media; SPIE Optic.: Washington, DC, USA, 2005; Volume 2, ISBN 0819459488. [Google Scholar]
- Dashti, M.; Rasouli, S. Measurement and statistical analysis of the wavefront distortions induced by atmospheric turbulence using two-channel moire deflectometry. J. Opt. 2012, 14, 095704. [Google Scholar] [CrossRef]
- Rasouli, S.; Tavassoly, M.T. Application of moiré technique to the measurement of the atmospheric turbulence parameters related to the angle of arrival fluctuations. Opt. Lett. 2006, 31, 3276–3278. [Google Scholar] [CrossRef] [PubMed]
- Rasouli, S. Use of a moiré deflectometer on a telescope for atmospheric turbulence measurements. Opt. Lett. 2010, 35, 1470–1472. [Google Scholar] [CrossRef] [PubMed]
- Consortini, A.; Sun, Y.Y.; Innocenti, C.; Li, Z.P. Measuring inner scale of atmospheric turbulence by angle of arrival and scintillation. Opt. Commun. 2003, 216, 19–23. [Google Scholar] [CrossRef]
- Gustavo, F.; Garavaglia, M. Determinación de la Constantes de Estructura del Aire Turbulento Mediante Interferometría Young; Universidad Nacional de la Plata: Buenos Aires, Argentina, 2011. [Google Scholar]
- Jurado Navas, A.; Puerta Notario, A. Enlaces ópticos no Guiados con téCnicas de Diversidad en Canal AtmosféRico Afectado por Turbulencias; Universidad de Málaga: Malaga, Spain, 2010; Volume 43. [Google Scholar]
- Kwiecień, J. The effects of atmospheric turbulence on laser beam propagation in a closed space—An analytic and experimental approach. Opt. Commun. 2019, 433, 200–208. [Google Scholar] [CrossRef]
- Mckechnie, T.S. General Theory of Light Propagation and Imaging Through the Atmosphere; Rhodes, W.T., Ed.; Springer: Basel, Switzerland, 2016; ISBN 9783319182087. [Google Scholar]
- Herreño Vanegas, M.F.; Villamizar Conde, J. Estudio de los Efectos de la Humedad en la Caracterización de la Propagación de un haz láser a Través de la Turbulencia Atmosférica a Bajas Alturas en Trayectorias Horizontales; Universidad Industrial de Santander: Bucaramanga, Colombia, 2016; Volume 1. [Google Scholar]
- Hovis, J. What Causes Humidity? Available online: https://www.scientificamerican.com/article/what-causes-humidity/ (accessed on 13 December 2017).
- Tíjaro, O.; Galeano, Y.; Torres, Y. Method to measure effects of turbulence using CCD sensors and beam centroids. Laser Commun. Propag. through Atmos. Ocean. V 2016, 9979, 99790P. [Google Scholar] [CrossRef]
- Rhodes, W.T. Time-average Fourier telescopy: A scheme for high-resolution imaging through horizontal-path turbulence. Appl. Opt. 2012, 51, A11. [Google Scholar] [CrossRef] [PubMed]
- Meneses, J.; Gharbi, T.; Humbert, P. Phase-unwrapping algorithm for images with high noise content based on a local histogram. Appl. Opt. 2005, 44, 1207–1215. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.I. Consideration of atmospheric turbulence in laser systems design. Appl. Opt. 1966, 5, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Wilfert, O. Laser beam attenuation determined by the method of available optical power in turbulent atmosphere. J. Telecommun. Inf. Technol. 2009, 53–57. [Google Scholar]
- Spectra-Physics Model 107B/Model 127 (25 or 35 mW) Helium-Neon Lasers. 1996, pp. 1–4. Available online: http://www.asi-team.com/asi%20team/brookhaven/35mW-Laser.pdf (accessed on 1 September 2019).
- Optics, E. EO 1312C 1/1.8” CMOS Color USB Camera. 1992, 473. Available online: https://www.edmundoptics.com/p/eo-1312c-118-cmos-color-usb-camera/26850/ (accessed on 1 September 2019).
- Specialties, M. HTS2030SMD–Temperature and Relative Humidity Sensor. Available online: https://datasheet.octopart.com/HTS2030SMD-TE-Connectivity-datasheet-15992094.pdf (accessed on 1 September 2019).
- Arduino Platform. Available online: https://www.arduino.cc/ (accessed on 1 September 2019).
- Imaging Developem Systems, I. uEye ActiveX Control. Available online: https://en.ids-imaging.com/manuals-ueye-software.html (accessed on 3 September 2019).
- Holm, D.D. Taylor’s Hypothesis, Hamilton’s Principle, and the LANS-a Model for Computing Turbulence. Los Alamos Sci. 2005, 172–180. [Google Scholar]
- Labeyrie, A.; Lipson, S.G.; Nisenson, P. An Introduction to Optical Stellar Interferometry; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780521828727. [Google Scholar]



| Device | Characteristics |
|---|---|
| Laser | He-Ne Laser. Model 127-35. Power output: 35 mW. Wavelength: 632.8 nm [19]. |
| CMOS Camera | Model: 1312C. Pixel Size: 5.3 μm. Pixels (H × V): 1280 × 1024. Area (H × V) (mm): 6.79 × 5.43 [20]. |
| Relative Humidity Sensor | HST2030SMD – Temperature and Humidity Sensor by Measurement specialties [21] |
| Laptop | Intel processor, Core i3–i5. RAM Memory: 4GB. |
| Software | MATLAB ®, Arduino Platform [22], IDS uEye [23]. |
| RHG | Metal pot with an electronic temperature control. |
| Test Name | Relative Humidity (RH) Average (%) | RH Standard Deviation (%) | Temperature Average (°C) | T Standard Deviation (°C) |
|---|---|---|---|---|
| Pattern | 64.05 | ±0.49 | 30.12 | ±0.32 |
| Test 1 | 99.13 | ±0.26 | 31.13 | ±0.20 |
| Test 2 | 57.88 | ±1.18 | 34.23 | ±0.08 |
| Test 3 | 84.61 | ±1.49 | 29.8 | ±0.27 |
| Test Name | PC1 vs PC2 (ms) | PC1 vs PC3 (ms) | PC1 vs PC4 (ms) | |||
|---|---|---|---|---|---|---|
| Time | Stand. Dev. | Time | Stand. Dev. | Time | Stand. Dev. | |
| Pattern | 26,45 | 16,57 | 40,3 | 18,8 | 13,84 | 8,10 |
| Test 1 | 12,16 | 11,57 | 19,18 | 10,69 | 7,01 | 7,23 |
| Test 2 | 39,27 | 30,61 | 34,77 | 19,19 | 4,49 | 8,13 |
| Test 3 | 45,21 | 20,63 | 38,05 | 19,19 | 7,16 | 7,85 |
| Test Name | Average Angle (prad) | Stand. Dev. Angle (prad) | Average (10−6) | Stand. Dev. (10−6) | Average (mm) | Stand. Dev. (mm) |
|---|---|---|---|---|---|---|
| Pattern | 2.02 | 2.15 | 0.58 | 0.71 | 16.31 | 6.98 |
| Test 1 | 34.8 | 34.2 | 243.4 | 133.1 | 6.02 | 4.16 |
| Test 2 | 2.39 | 2.66 | 1.14 | 2. 08 | 7.37 | 4.17 |
| Test3 | 3.64 | 5.15 | 5.89 | 0.55 | 6.97 | 3.70 |
| Test Name | Average () | Stand. Dev. () |
|---|---|---|
| Pattern | 2.28 × 10−16 | 1.4 × 10−16 |
| Test #1 | 4.05 × 10−15 | 4.91 × 10−15 |
| Test #2 | 3.45 × 10−16 | 4.01 × 10−16 |
| Test #3 | 6.95 × 10−16 | 1.01 × 10−15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villamizar, J.; Herreño, M.; Tíjaro, O.; Torres, Y. Atmospheric Characterization Based on Relative Humidity Control at Optical Turbulence Generator. Atmosphere 2019, 10, 550. https://doi.org/10.3390/atmos10090550
Villamizar J, Herreño M, Tíjaro O, Torres Y. Atmospheric Characterization Based on Relative Humidity Control at Optical Turbulence Generator. Atmosphere. 2019; 10(9):550. https://doi.org/10.3390/atmos10090550
Chicago/Turabian StyleVillamizar, Jhonny, Manuel Herreño, Omar Tíjaro, and Yezid Torres. 2019. "Atmospheric Characterization Based on Relative Humidity Control at Optical Turbulence Generator" Atmosphere 10, no. 9: 550. https://doi.org/10.3390/atmos10090550
APA StyleVillamizar, J., Herreño, M., Tíjaro, O., & Torres, Y. (2019). Atmospheric Characterization Based on Relative Humidity Control at Optical Turbulence Generator. Atmosphere, 10(9), 550. https://doi.org/10.3390/atmos10090550





