Relationship between Rainfall Variability and the Predictability of Radar Rainfall Nowcasting Models
Abstract
1. Introduction
2. Data Sources and Methods
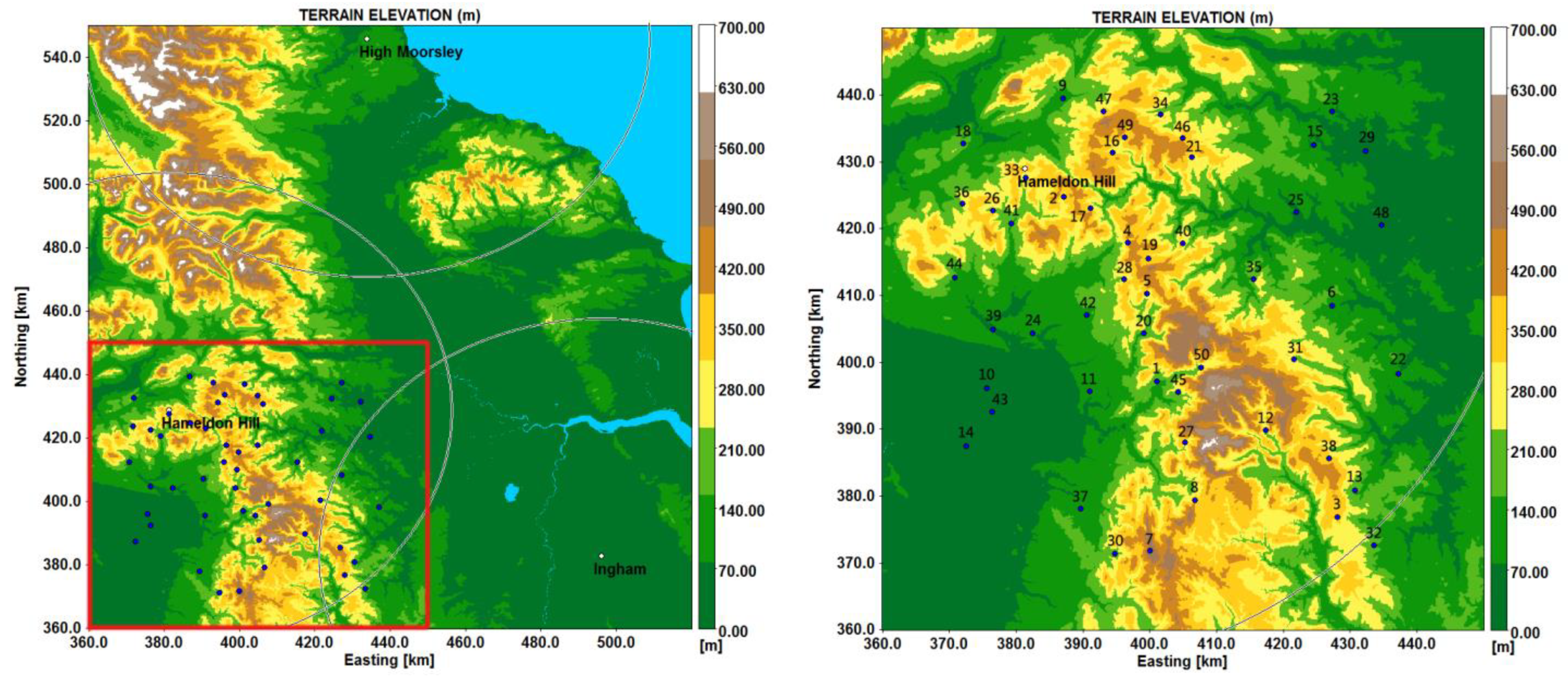
2.1. Study Area and Data Sources
2.2. Short-Term Ensemble Prediction System Model
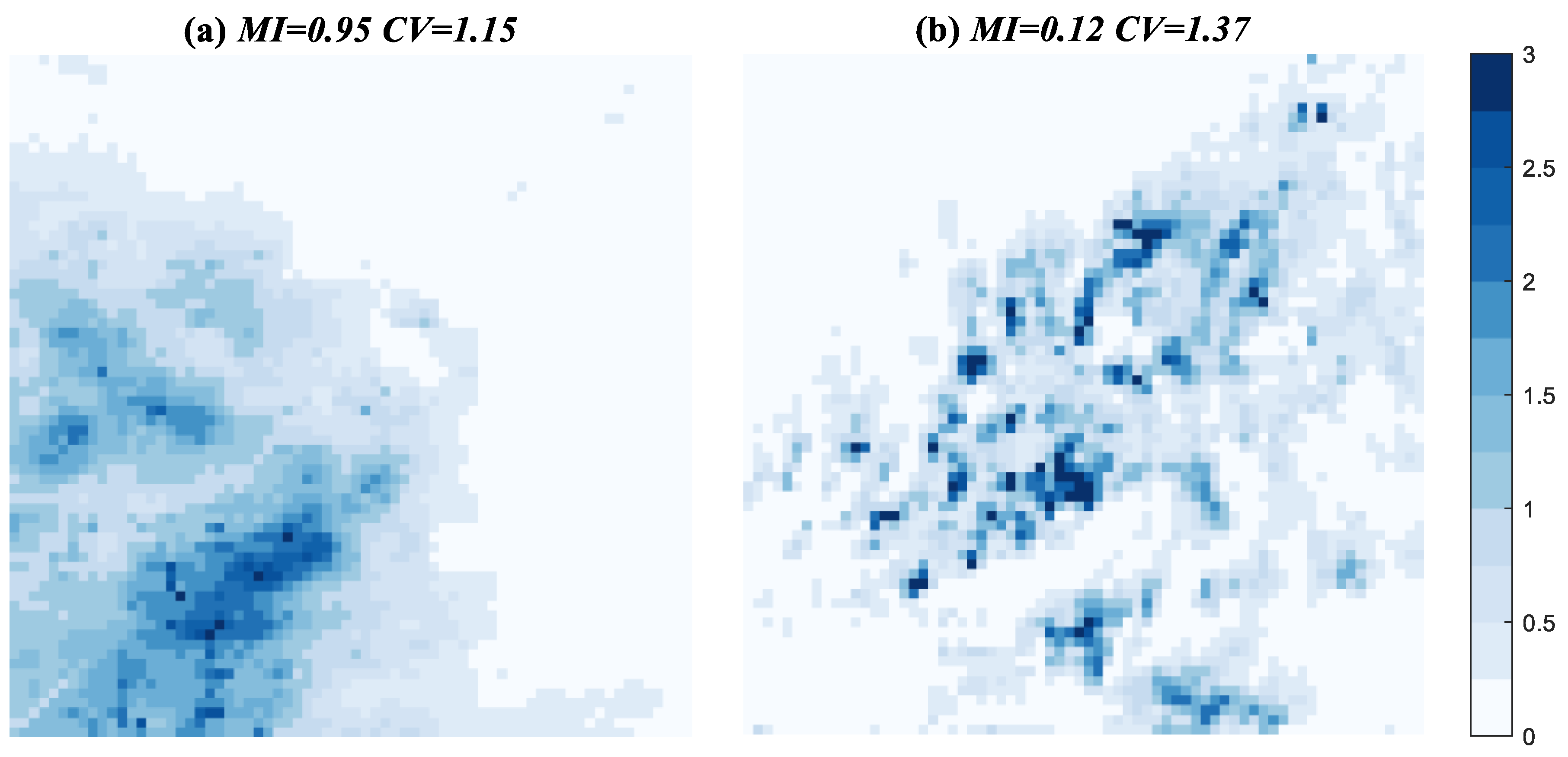
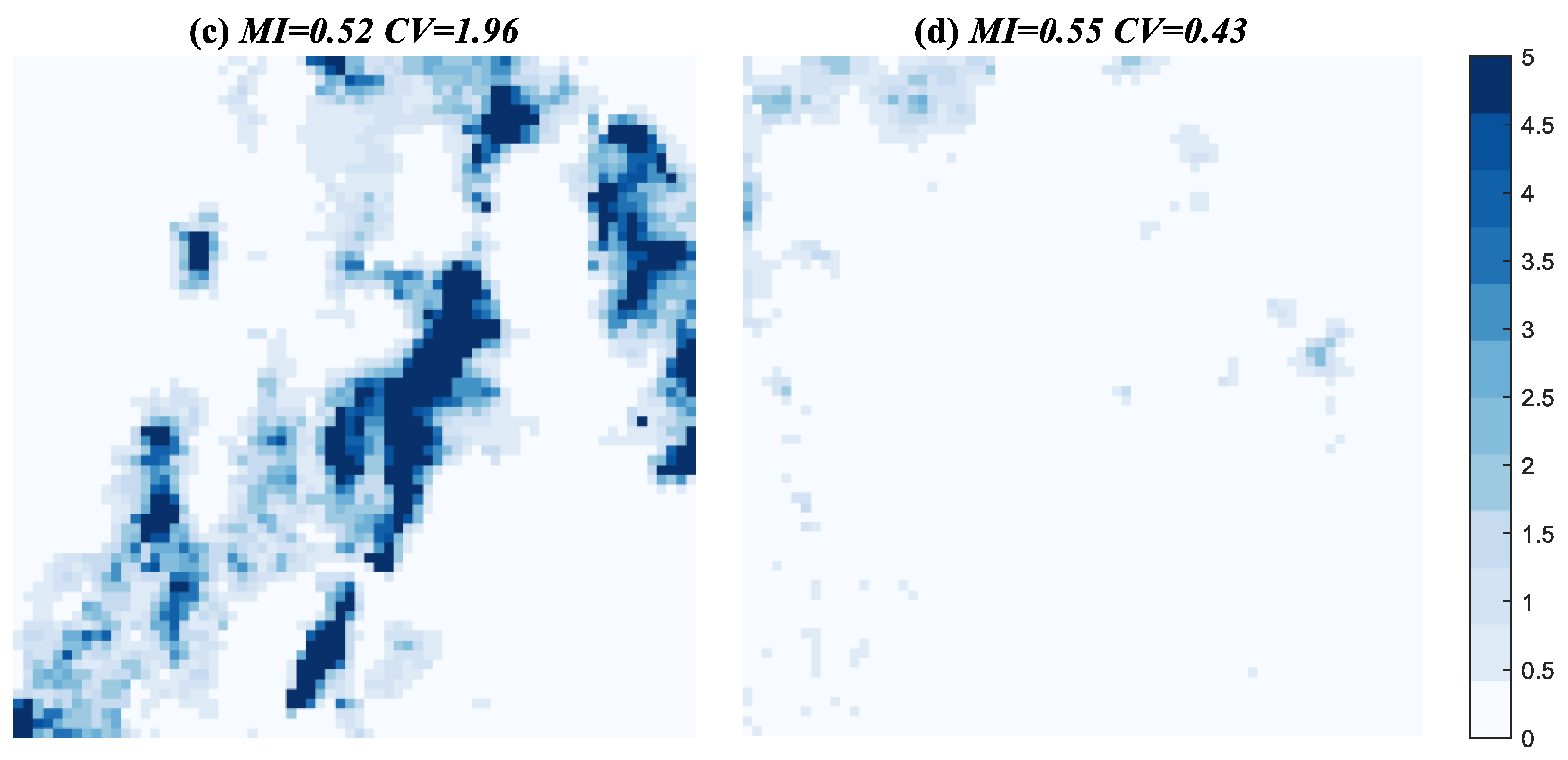
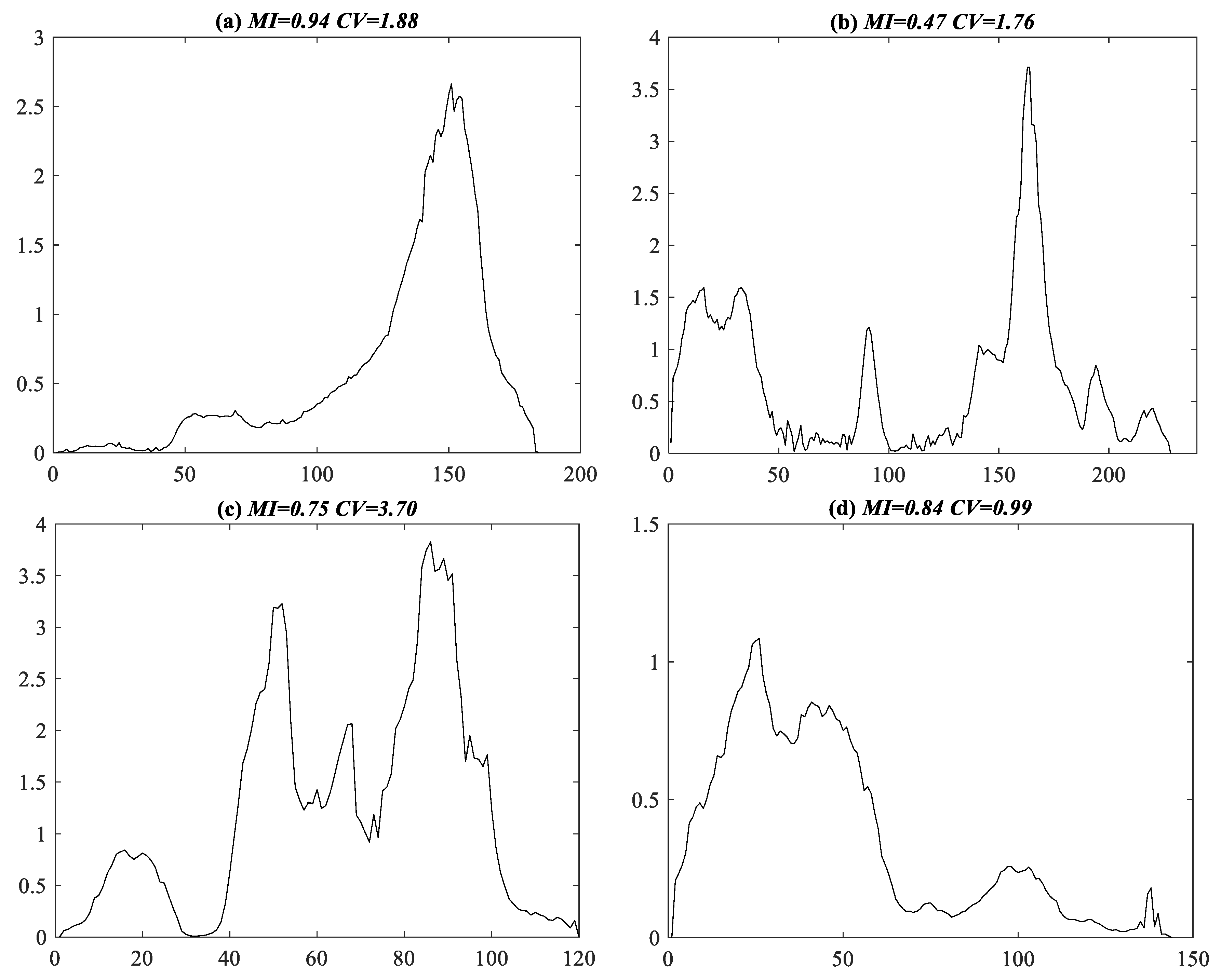
2.3. Spatial and Temporal Variability of a Storm
2.4. Rainfall Nowcasting Skills
3. Results
3.1. Radar Rainfall Nowcasts
3.2. Spatial and Temporal Rainfall Variability Calculation
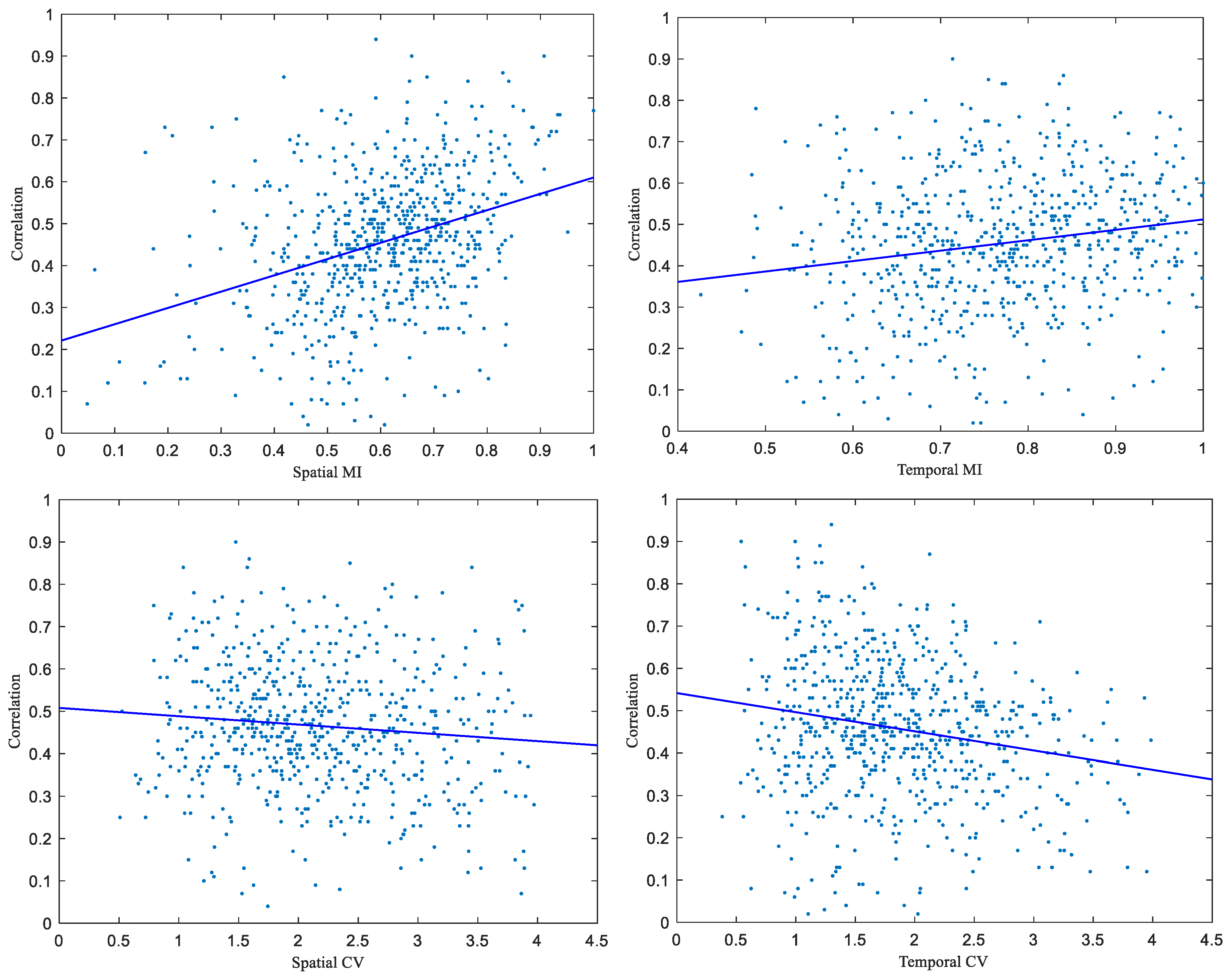
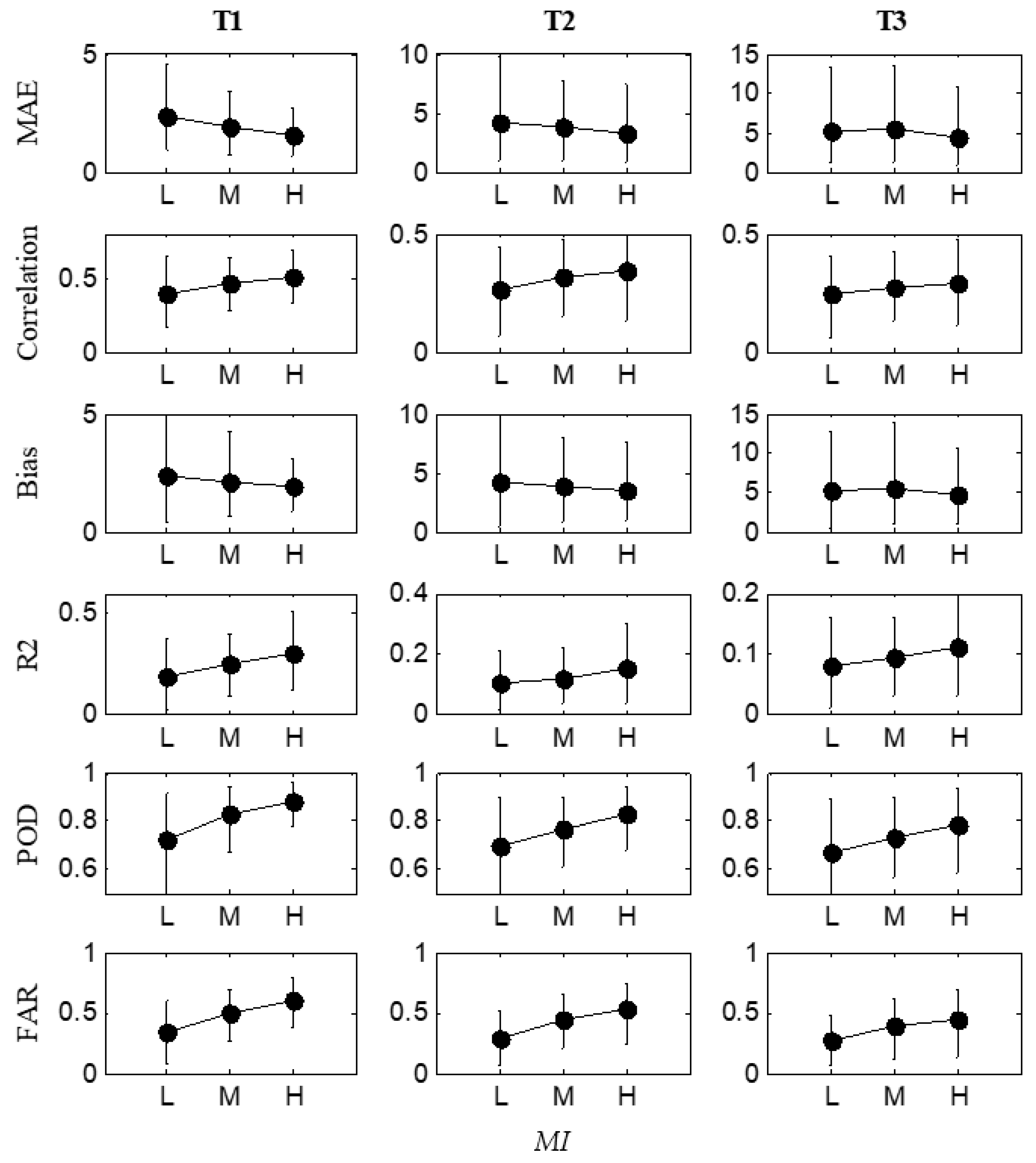
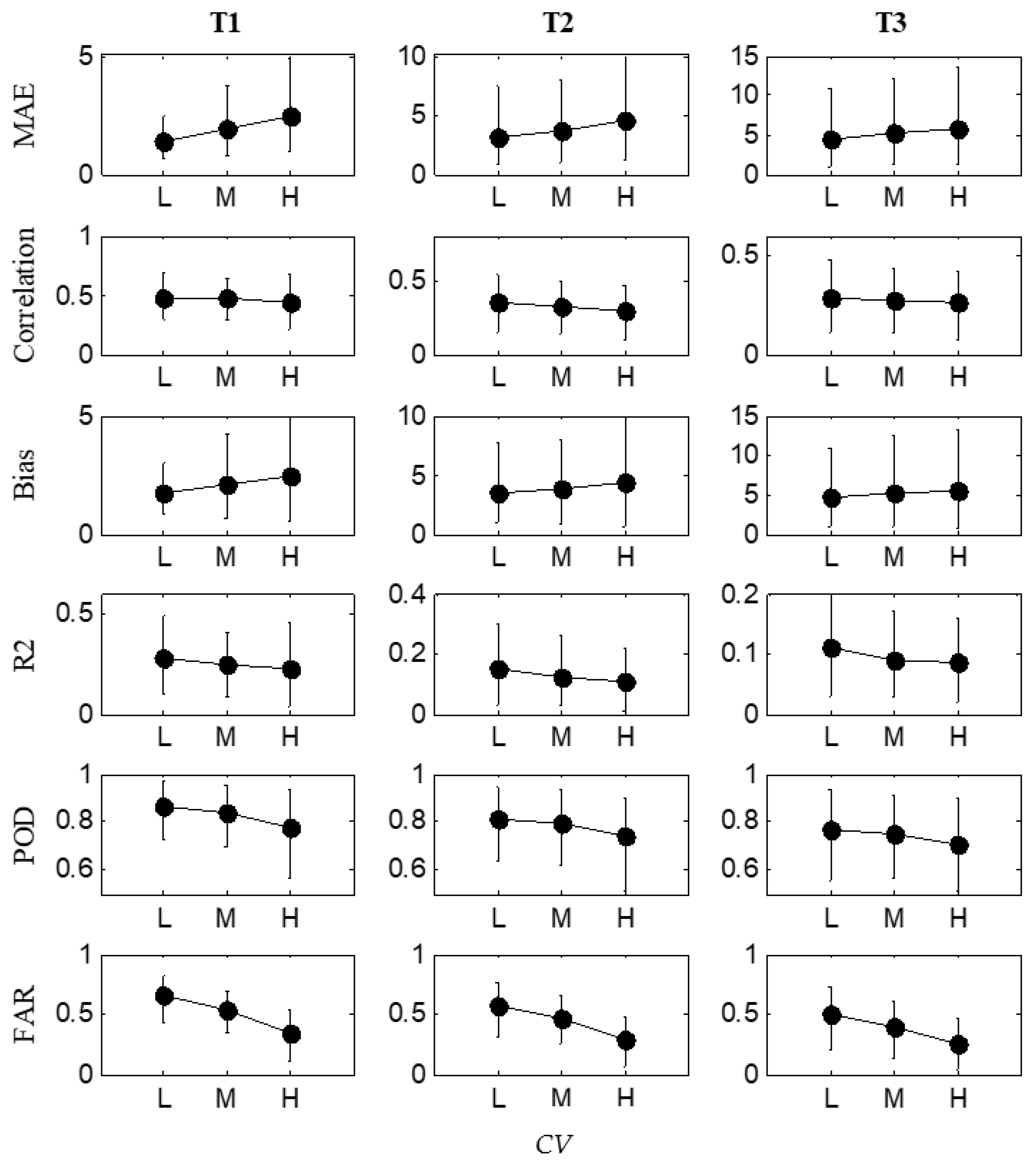
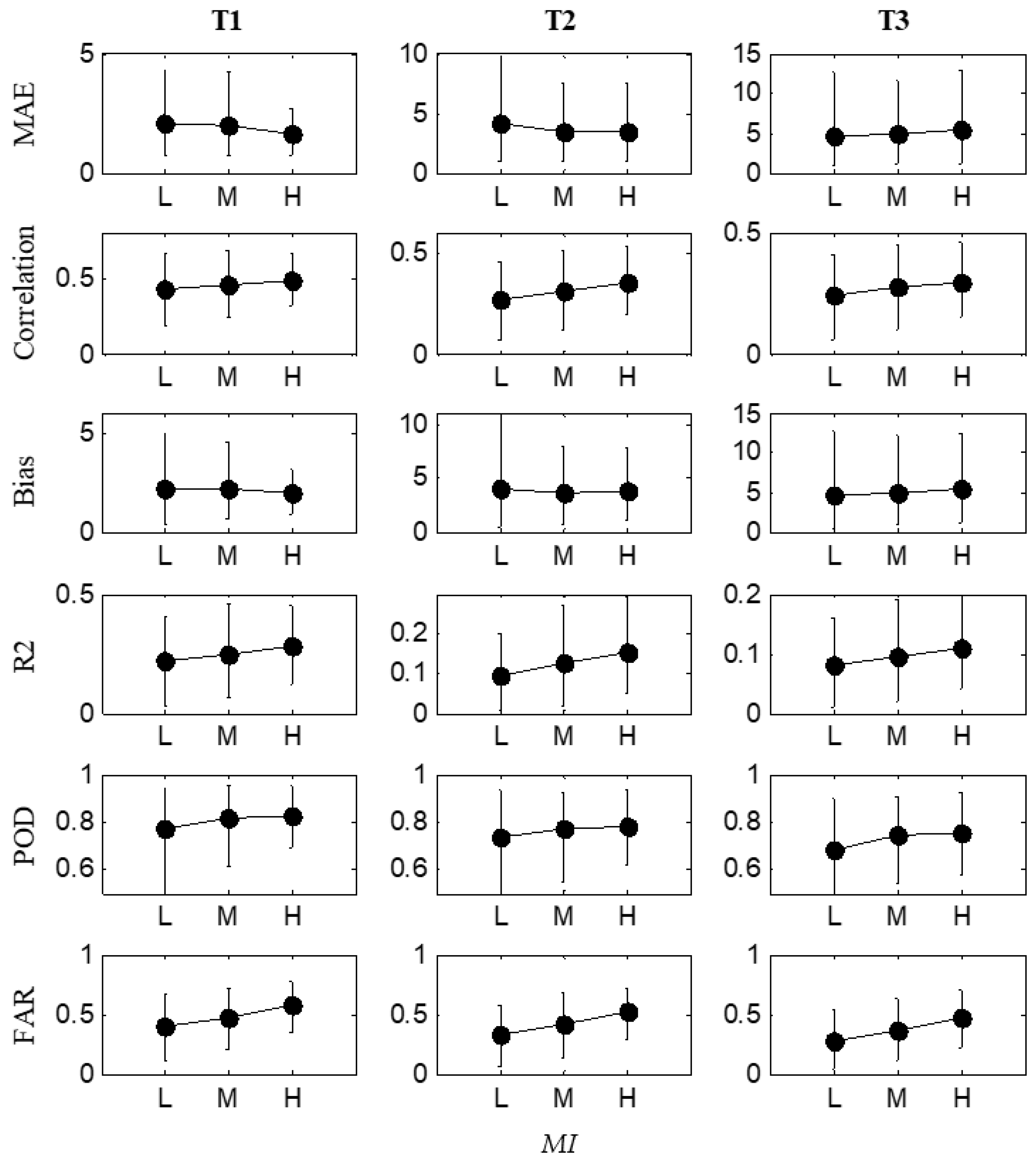
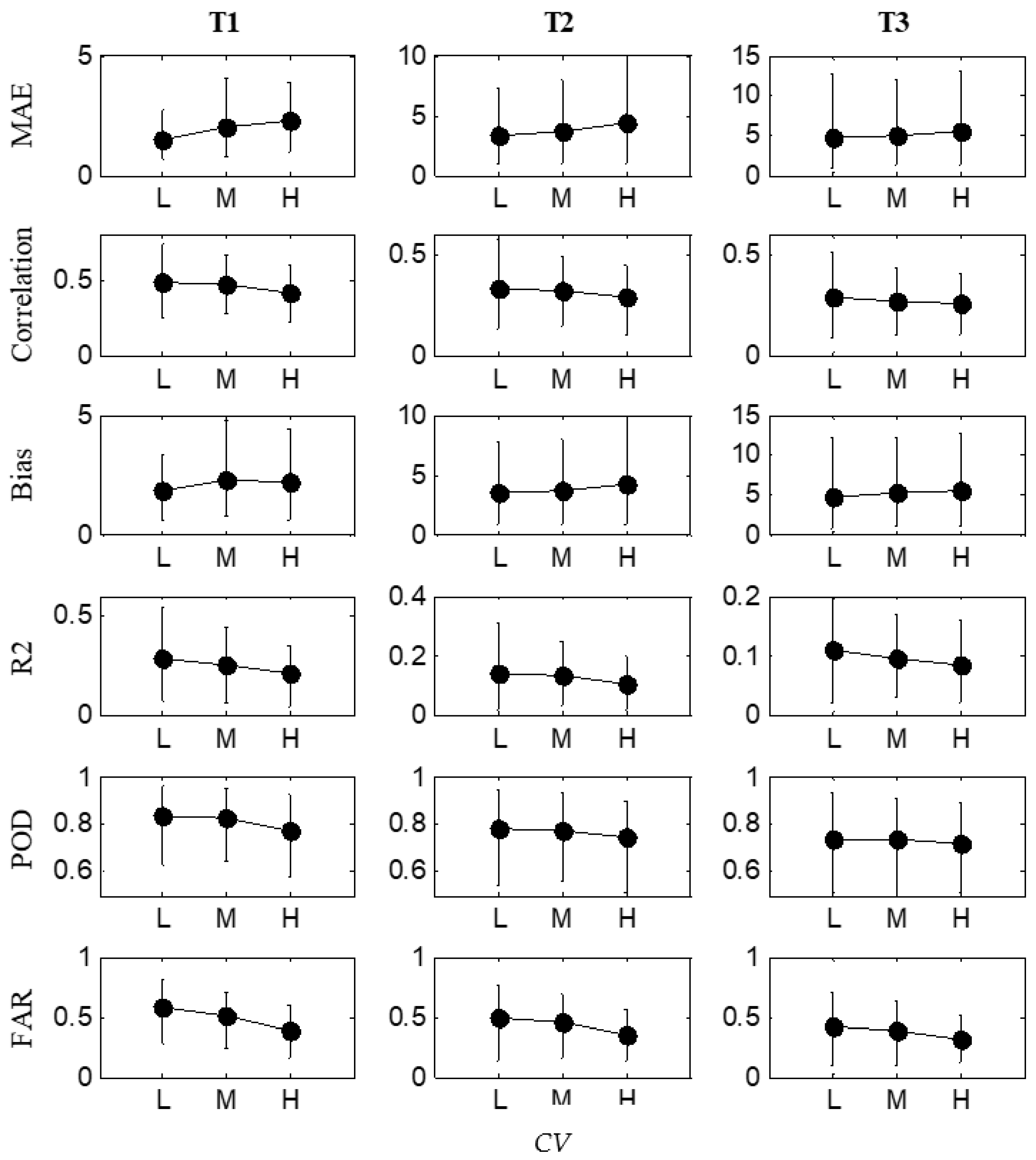
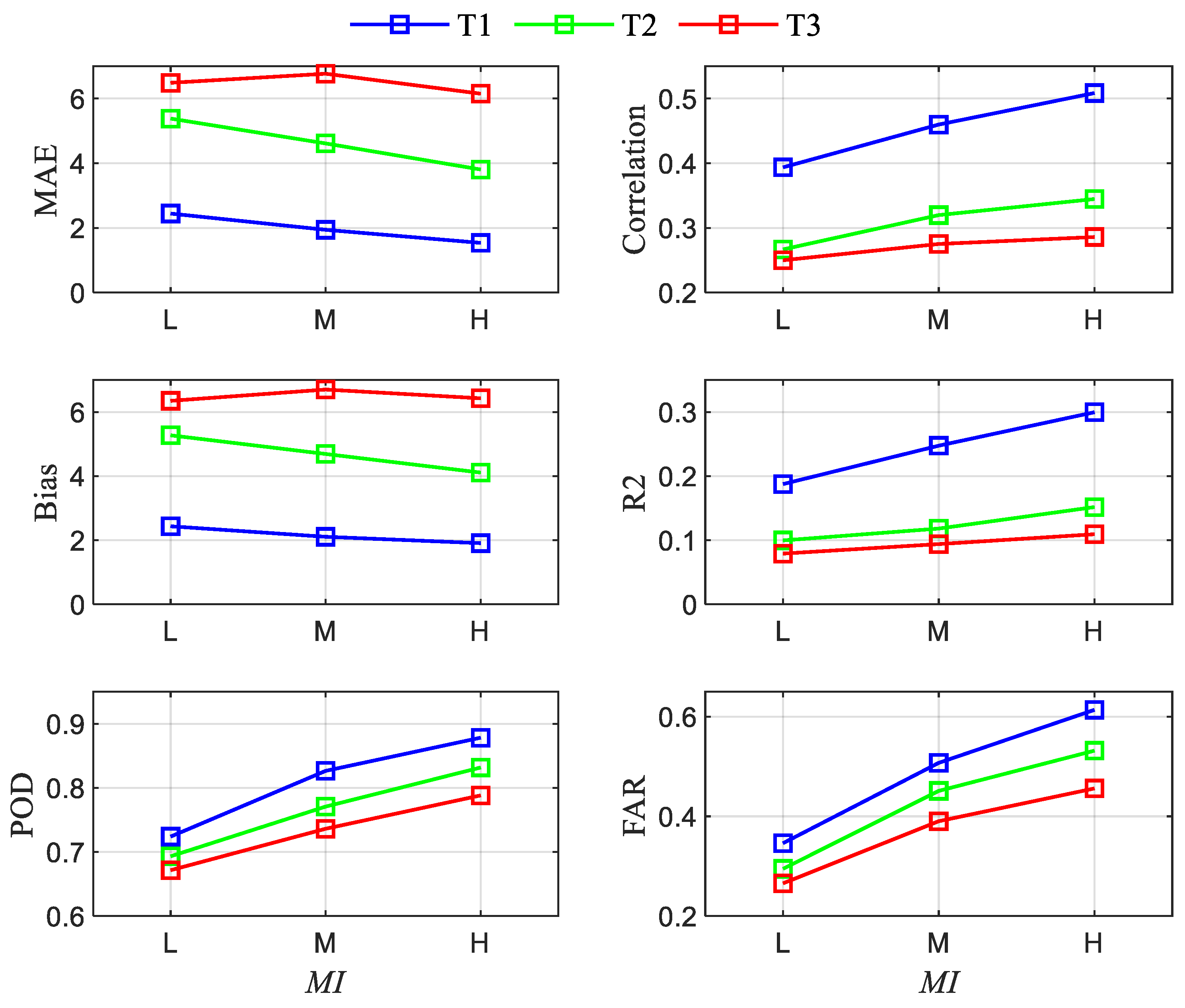
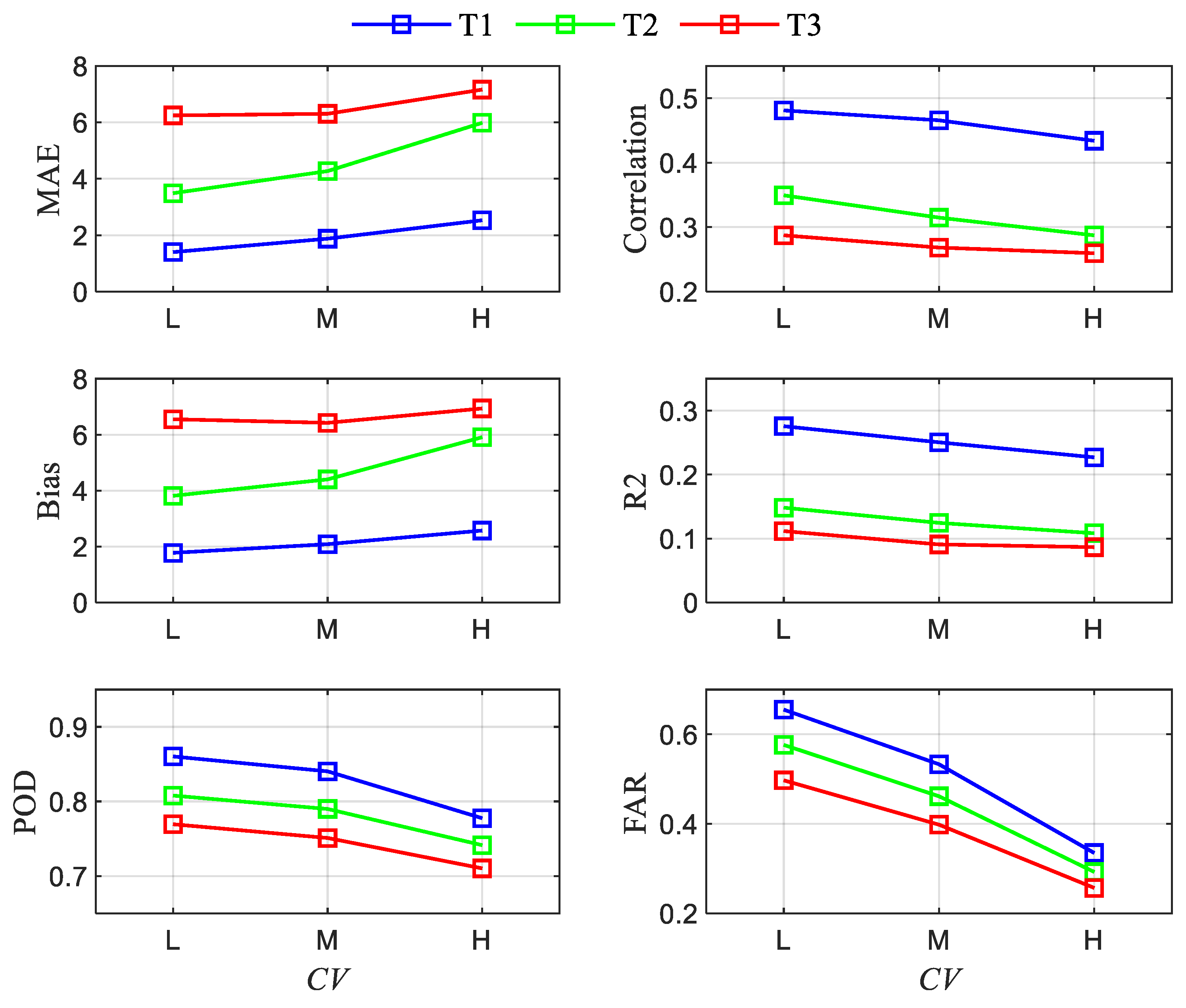
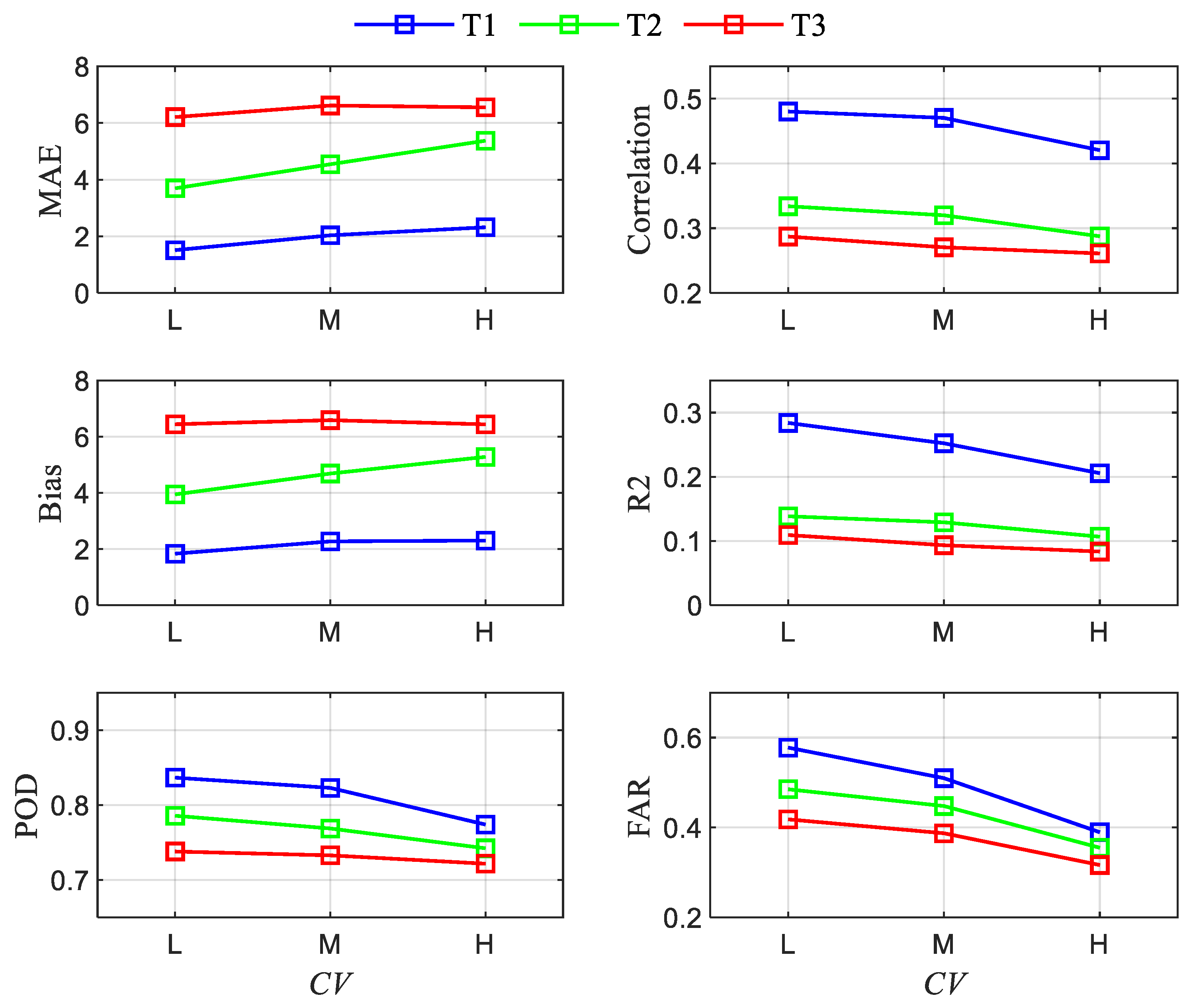
3.3. Relationship between Storm Variability and Rainfall Nowcasting Skill
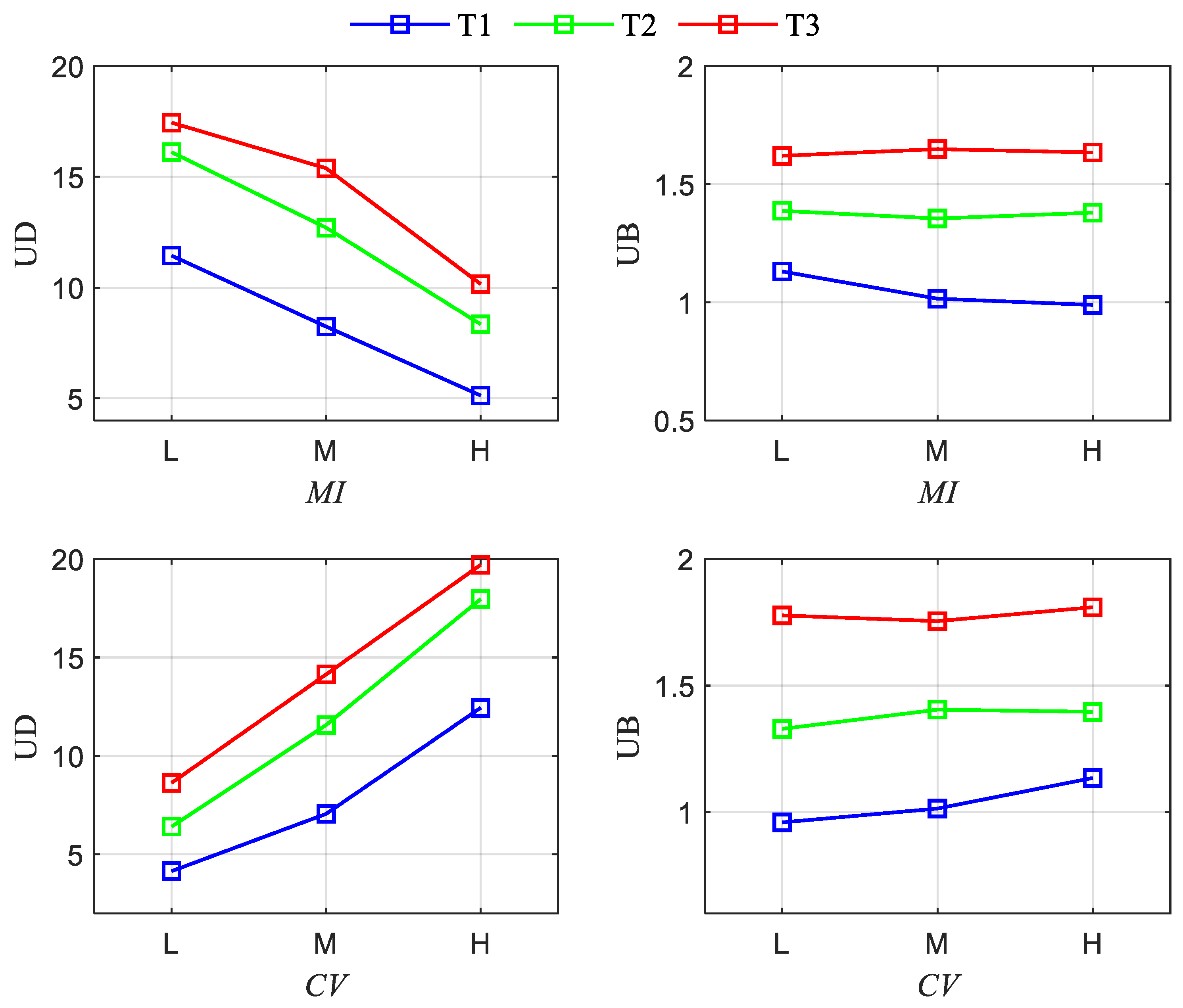
3.4. Relationship between Storm Variability and Rainfall Uncertainty Band
3.5. Rainfall Predictability under Different Storm Variability Scenarios
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wilson, J.W.; Ebert, E.E.; Saxen, T.R.; Roberts, R.D.; Mueller, C.K.; Sleigh, M.; Pierce, C.E.; Seed, A. Sydney 2000 forecast demonstration project: Convective storm nowcasting. Weather Forecast. 2004, 19, 131–150. [Google Scholar] [CrossRef]
- Browning, K. Review Lecture: Local Weather Forecasting. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1980, 371, 179–211. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A. Quantitative assessment of short-term rainfall forecasts from radar nowcasts and MM5 forecasts. Hydrol. Process. 2012, 26, 3842–3857. [Google Scholar] [CrossRef]
- Tuttle, J.D.; Foote, G.B. Determination of the boundary layer airflow from a single Doppler radar. J. Atmos. Ocean. Technol. 1990, 7, 218–232. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm identification, tracking, analysis, and nowcasting-A radar-based methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Johnson, J.; MacKeen, P.L.; Witt, A.; Mitchell, E.D.W.; Stumpf, G.J.; Eilts, M.D.; Thomas, K.W. The storm cell identification and tracking algorithm: An enhanced WSR-88D algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Handwerker, J. Cell tracking with TRACE3D—A new algorithm. Atmos. Res. 2002, 61, 15–34. [Google Scholar] [CrossRef]
- Grecu, M.; Krajewski, W. A large-sample investigation of statistical procedures for radar-based short-term quantitative precipitation forecasting. J. Hydrol. 2000, 239, 69–84. [Google Scholar] [CrossRef]
- Montanari, L.; Montanari, A.; Toth, E. A comparison and uncertainty assessment of system analysis techniques for short-term quantitative precipitation nowcasting based on radar images. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Steinheimer, M.; Haiden, T. Improved nowcasting of precipitation based on convective analysis fields. Adv. Geosci. 2007, 10, 125–131. [Google Scholar] [CrossRef][Green Version]
- Dai, Q.; Rico-Ramirez, M.A.; Han, D.; Islam, T.; Liguori, S. Probabilistic radar rainfall nowcasts using empirical and theoretical uncertainty models. Hydrol. Process. 2015, 29, 66–79. [Google Scholar] [CrossRef]
- He, S.; Raghavan, S.V.; Nguyen, N.S.; Liong, S.Y. Ensemble rainfall forecasting with numerical weather prediction and radar-based nowcasting models. Hydrol. Process. 2013, 27, 1560–1571. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.l.; Sorooshian, S.; Gourley, J.; Lakshmanan, V.; Hong, Y.; Bellerby, T. Quantitative precipitation nowcasting: A Lagrangian pixel-based approach. Atmos. Res. 2012, 118, 418–434. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Chen, S.Y.; Kuo, C.M.; Tseng, H.W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Seed, A. A dynamic and spatial scaling approach to advection forecasting. J. Appl. Meteorol. 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Dai, Q.; Han, D.; Rico-Ramirez, M.A.; Islam, T. The impact of raindrop drift in a three-dimensional wind field on a radar–gauge rainfall comparison. Int. J. Remote Sens. 2013, 34, 7739–7760. [Google Scholar] [CrossRef]
- Cecinati, F.; Rico-Ramirez, M.A.; Heuvelink, G.B.; Han, D. Representing radar rainfall uncertainty with ensembles based on a time-variant geostatistical error modelling approach. J. Hydrol. 2017, 548, 391–405. [Google Scholar] [CrossRef]
- Dai, Q.; Han, D.; Rico-Ramirez, M.; Srivastava, P.K. Multivariate distributed ensemble generator: A new scheme for ensemble radar precipitation estimation over temperate maritime climate. J. Hydrol. 2014, 511, 17–27. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale-dependence of the predictability of precipitation from continental radar images. Part I: Description of the methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.E.; Seed, A.W. STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP. Q. J. R. Meteorol. Soc. 2006, 132, 2127–2155. [Google Scholar] [CrossRef]
- Dai, Q.; Han, D.; Zhuo, L.; Zhang, J.; Islam, T.; Srivastava, P.K. Seasonal ensemble generator for radar rainfall using copula and autoregressive model. Stoch. Environ. Res. Risk Assess. 2016, 30, 27–38. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the different sources of uncertainty in single polarization radar-based estimates of rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Villarini, G.; Seo, B.C.; Serinaldi, F.; Krajewski, W.F. Spatial and temporal modeling of radar rainfall uncertainties. Atmos. Res. 2014, 135, 91–101. [Google Scholar] [CrossRef]
- Harrison, D.L.; Scovell, R.W.; Kitchen, M. High-resolution precipitation estimates for hydrological uses. In Proceedings of the Institution of Civil Engineers-Water Management; ICE: Washington, DC, USA, 2009; pp. 125–135. [Google Scholar]
- Berenguer, M.; Sempere-Torres, D.; Pegram, G.G. SBMcast—An ensemble nowcasting technique to assess the uncertainty in rainfall forecasts by Lagrangian extrapolation. J. Hydrol. 2011, 404, 226–240. [Google Scholar] [CrossRef]
- Seed, A.W.; Pierce, C.E.; Norman, K. Formulation and evaluation of a scale decomposition-based stochastic precipitation nowcast scheme. Water Resour. Res. 2013, 49, 6624–6641. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.E.; Seed, A. Development of a precipitation nowcasting algorithm based upon optical flow techniques. J. Hydrol. 2004, 288, 74–91. [Google Scholar] [CrossRef]
- Foresti, L.; Seed, A. The effect of flow and orography on the spatial distribution of the very short-term predictability of rainfall from composite radar images. Hydrol. Earth Syst. Sci. 2014, 18, 4671–4686. [Google Scholar] [CrossRef]
- Faurès, J.M.; Goodrich, D.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bievre, B.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Tucker, G.E.; Bras, R.L. A stochastic approach to modeling the role of rainfall variability in drainage basin evolution. Water Resour. Res. 2000, 36, 1953–1964. [Google Scholar] [CrossRef]
- Zhang, J.; Han, D. Assessment of rainfall spatial variability and its influence on runoff modelling: A case study in the Brue catchment, UK. Hydrol. Process. 2017, 31, 2972–2981. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I. Exploring complexity in the structure of rainfall. Adv. Water Resour. 1991, 14, 162–167. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Dai, Q.; Yang, Q.; Zhang, J.; Zhang, S. Impact of Gauge Representative Error on a Radar Rainfall Uncertainty Model. J. Appl. Meteorol. Clim. 2018, 57, 2769–2787. [Google Scholar] [CrossRef]
- Bringi, V.; Rico-Ramirez, M.; Thurai, M. Rainfall estimation with an operational polarimetric C band radar in the United Kingdom: Comparison with a gauge network and error analysis. J. Hydrometeorol. 2011, 12, 935–954. [Google Scholar] [CrossRef]


| Event | Start Date | End Date | Mean Rainfall (cm) |
|---|---|---|---|
| 1 | 28 April 2009 1:00 | 29 April 2009 02:00 | 0.59 |
| 2 | 5 December 2009 17:00 | 6 December 2009 12:00 | 0.70 |
| 3 | 14 July 2010 13:00 | 14 July 2010 23:00 | 1.20 |
| 4 | 13 July 2010 16:00 | 14 July 2010 04:00 | 0.36 |
| Variability Indicator | Spatial | Temporal |
|---|---|---|
| MI | 0.38 | 0.21 |
| CV | −0.12 | −0.25 |
| Variability Type | Spatial | Temporal | ||
|---|---|---|---|---|
| MI | CV | MI | CV | |
| L | 0.0–0.5 | 0.0–1.7 | 0.0–0.7 | 0.0–1.5 |
| M | 0.5–0.7 | 1.7–2.5 | 0.7–0.8 | 1.5–2.1 |
| H | 0.7–1.0 | 2.5–5.0 | 0.8–1.0 | 2.1–5.0 |
| Scenario | MAE | COR | BIAS | R2 | POD | FAR |
|---|---|---|---|---|---|---|
| LL | 1.96 | 0.22 | 2.38 | 0.08 | 0.90 | 0.52 |
| LM | 1.66 | 0.39 | 1.74 | 0.19 | 0.82 | 0.46 |
| LH | 2.62 | 0.40 | 2.58 | 0.19 | 0.69 | 0.30 |
| ML | 1.42 | 0.42 | 1.69 | 0.21 | 0.89 | 0.62 |
| MM | 2.13 | 0.46 | 2.27 | 0.25 | 0.83 | 0.49 |
| MH | 2.00 | 0.49 | 2.12 | 0.28 | 0.77 | 0.43 |
| HL | 1.38 | 0.50 | 1.77 | 0.30 | 0.89 | 0.64 |
| HM | 2.02 | 0.53 | 2.32 | 0.31 | 0.85 | 0.51 |
| HH | 1.99 | 0.58 | 2.27 | 0.31 | 0.82 | 0.56 |
| Lead | MAE | COR | BIAS | R2 | POD | FAR |
|---|---|---|---|---|---|---|
| LL | 1.76 | 0.49 | 1.91 | 0.30 | 0.77 | 0.43 |
| LM | 1.99 | 0.45 | 2.23 | 0.22 | 0.82 | 0.47 |
| LH | 2.38 | 0.39 | 2.30 | 0.17 | 0.75 | 0.36 |
| ML | 1.56 | 0.49 | 1.88 | 0.28 | 0.87 | 0.56 |
| MM | 2.27 | 0.46 | 2.48 | 0.25 | 0.82 | 0.50 |
| MH | 2.12 | 0.43 | 2.12 | 0.22 | 0.79 | 0.42 |
| HL | 1.37 | 0.48 | 1.78 | 0.28 | 0.85 | 0.66 |
| HM | 1.86 | 0.50 | 2.11 | 0.29 | 0.83 | 0.55 |
| HH | 2.22 | 0.49 | 2.30 | 0.27 | 0.78 | 0.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Dai, Q.; Zhuo, L. Relationship between Rainfall Variability and the Predictability of Radar Rainfall Nowcasting Models. Atmosphere 2019, 10, 458. https://doi.org/10.3390/atmos10080458
Liu Z, Dai Q, Zhuo L. Relationship between Rainfall Variability and the Predictability of Radar Rainfall Nowcasting Models. Atmosphere. 2019; 10(8):458. https://doi.org/10.3390/atmos10080458
Chicago/Turabian StyleLiu, Zhenzhen, Qiang Dai, and Lu Zhuo. 2019. "Relationship between Rainfall Variability and the Predictability of Radar Rainfall Nowcasting Models" Atmosphere 10, no. 8: 458. https://doi.org/10.3390/atmos10080458
APA StyleLiu, Z., Dai, Q., & Zhuo, L. (2019). Relationship between Rainfall Variability and the Predictability of Radar Rainfall Nowcasting Models. Atmosphere, 10(8), 458. https://doi.org/10.3390/atmos10080458







