Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band
Abstract
1. Introduction
2. Methods of Simulation
2.1. Forward Model and Simulator
2.2. Basic Microphysical Parameters
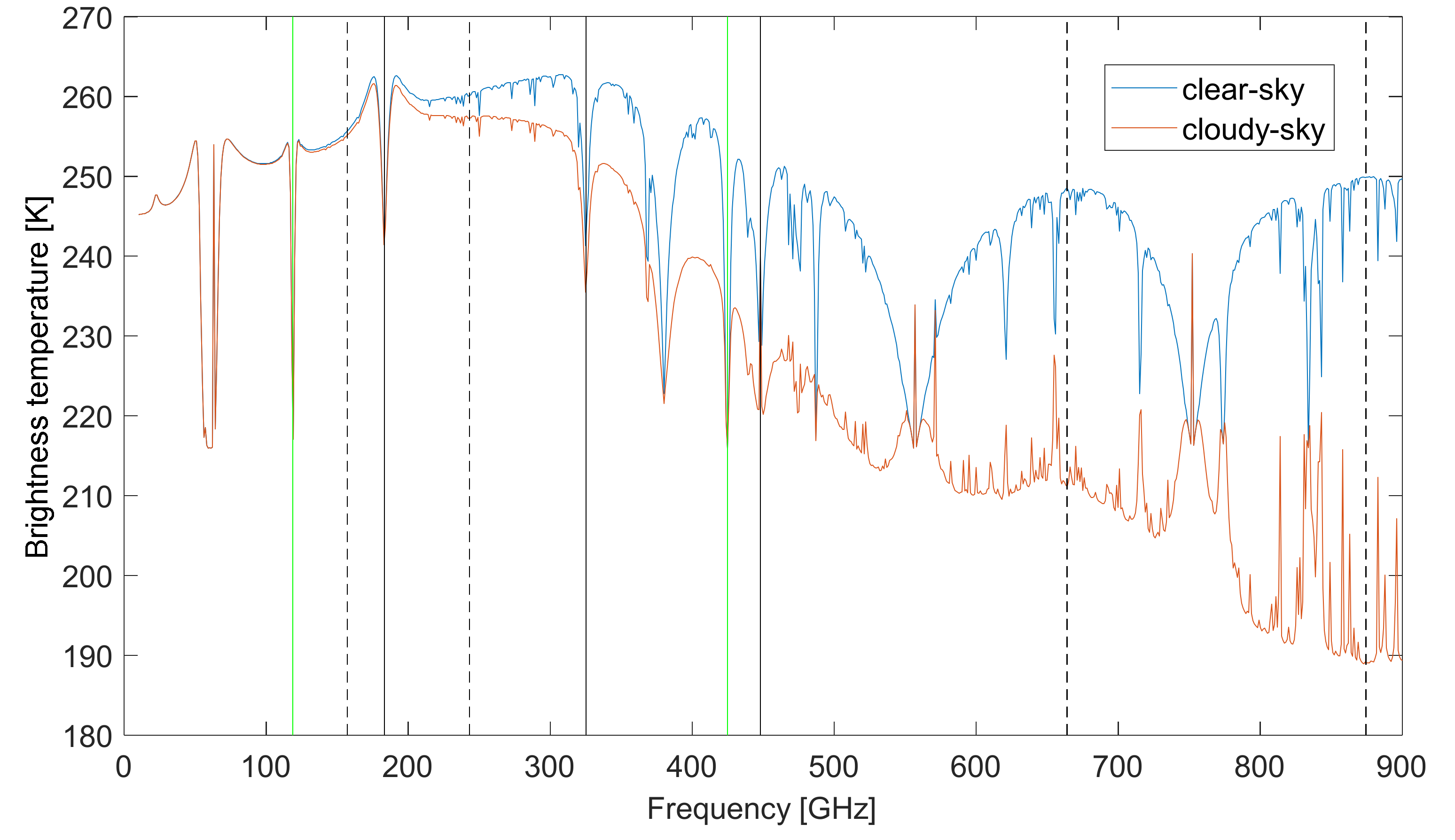
2.3. Selection of Channels
3. Influence of Ice Cloud on Terahertz Radiation
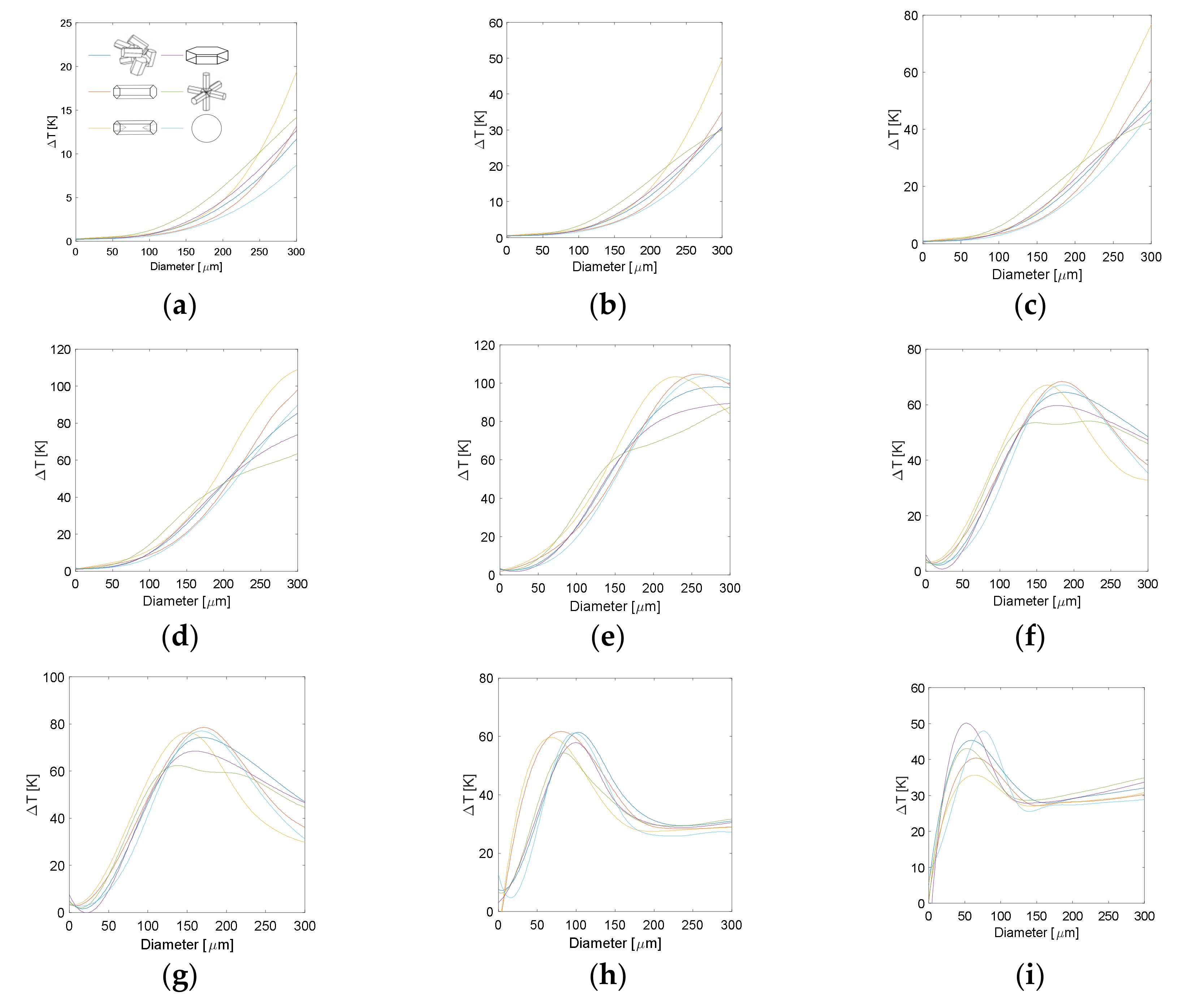
3.1. Effect of Particle Shape
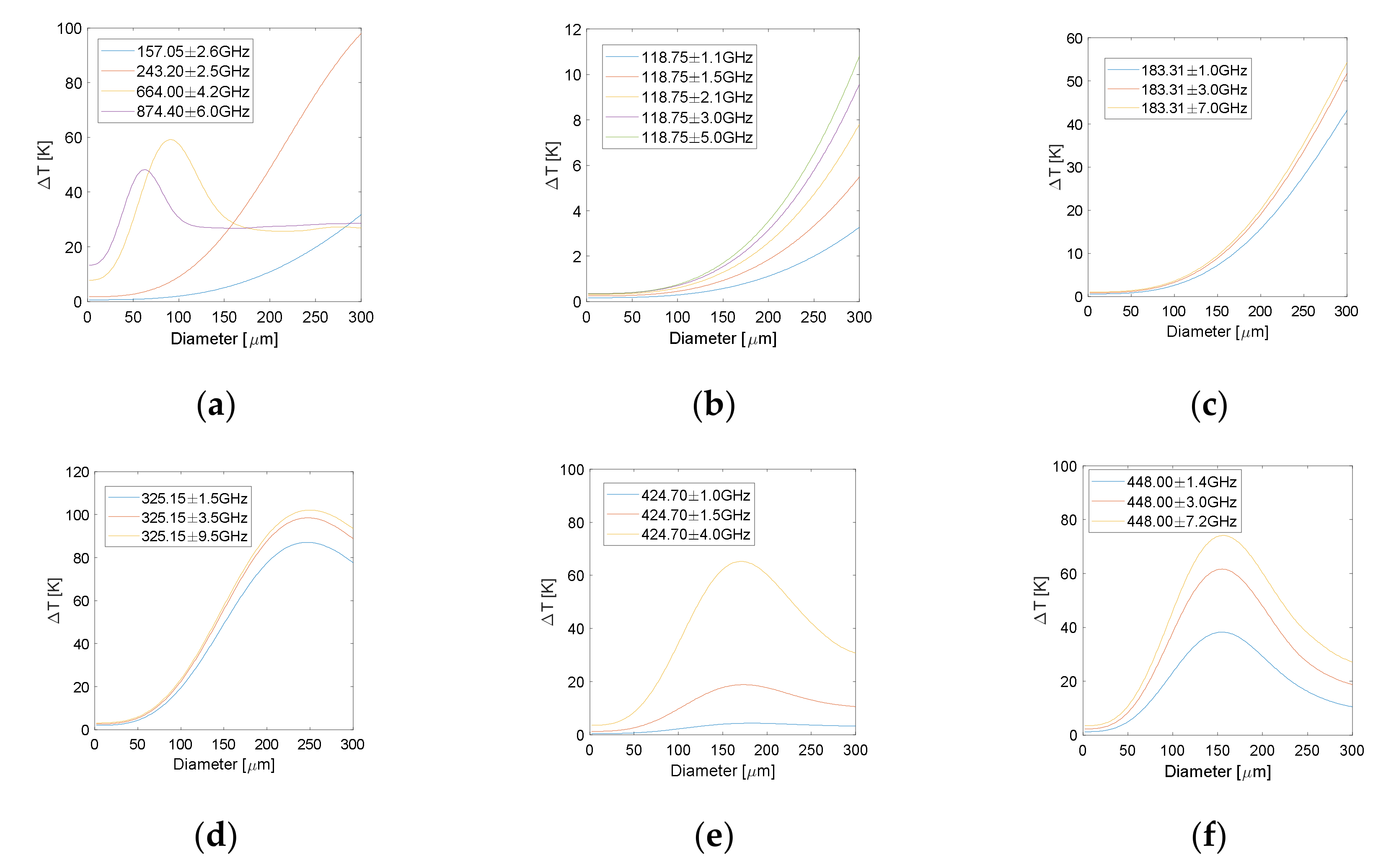
3.2. Effect of Effective Particle Size
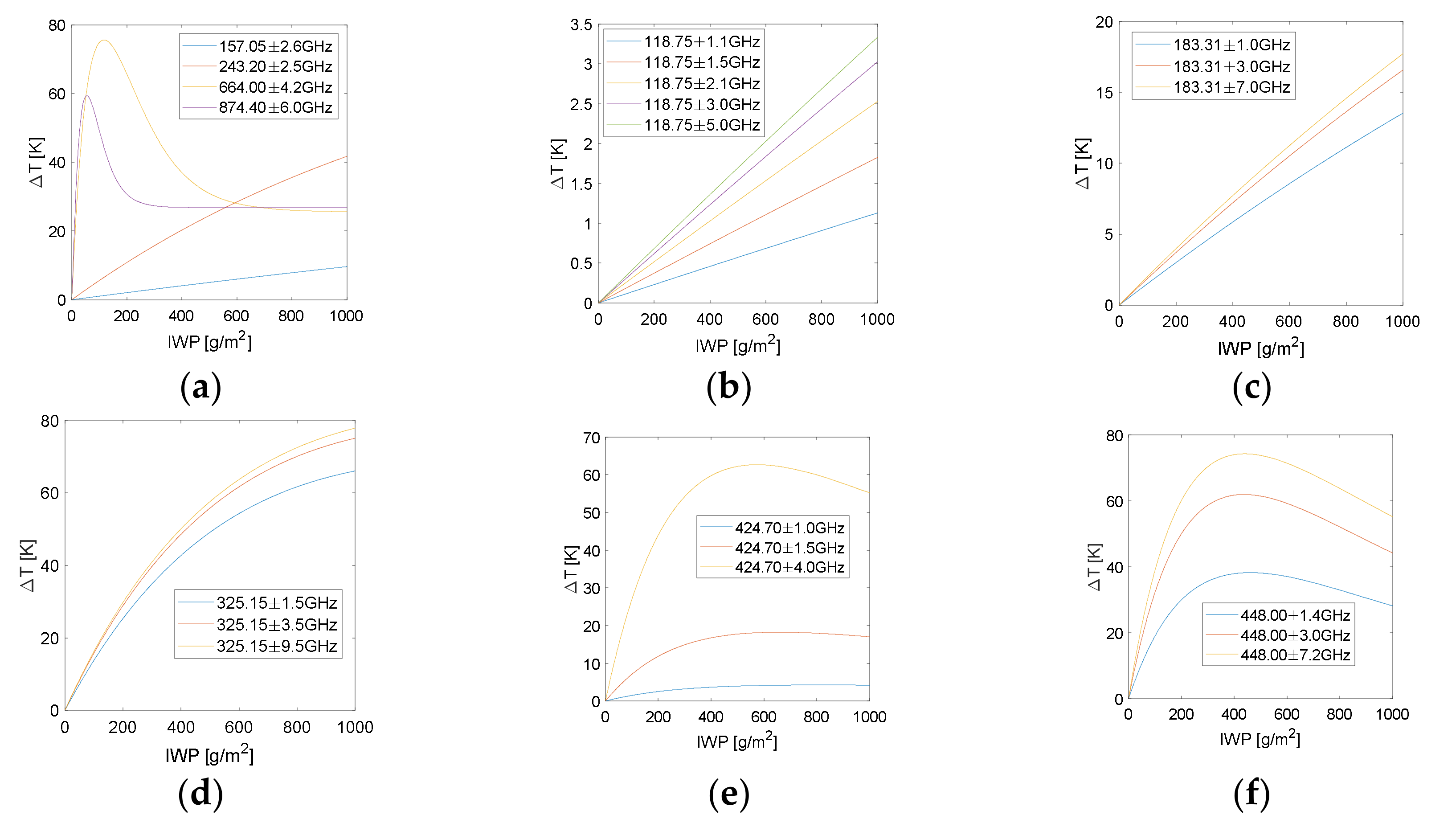
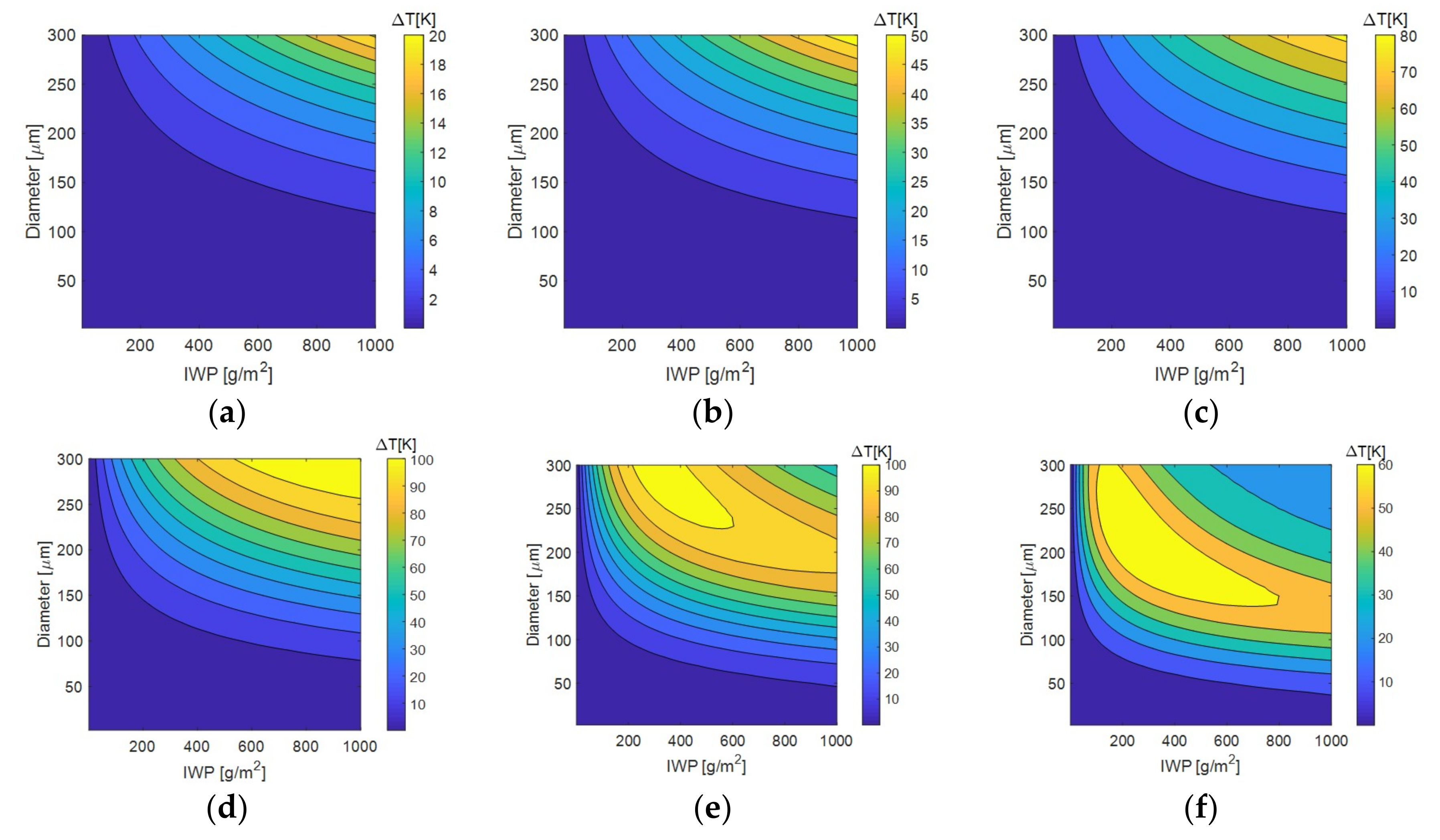
3.3. Effect of Ice Water Path
4. Multi-Channel Regression Inversion
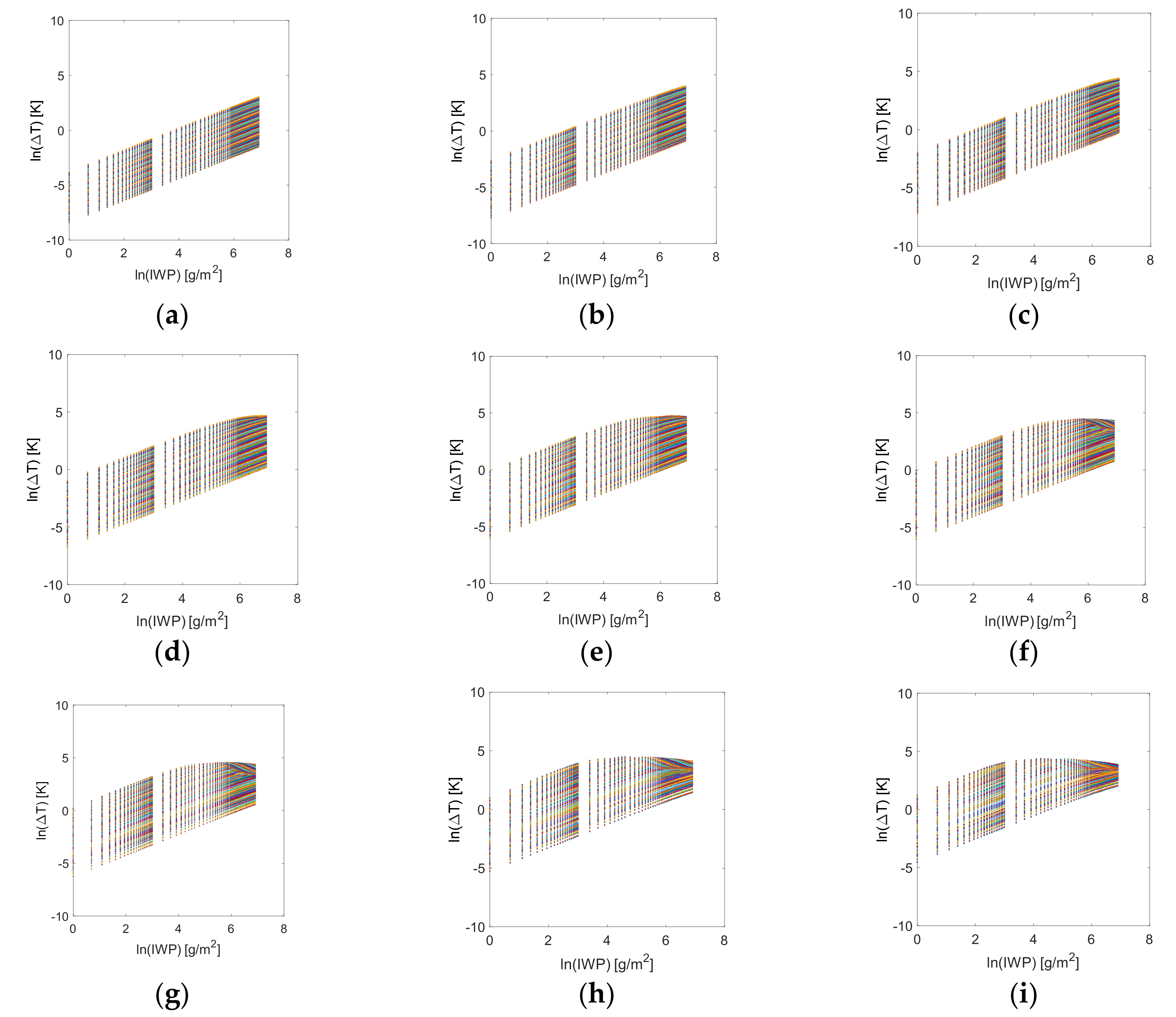
4.1. Multi-Channel Regression Method
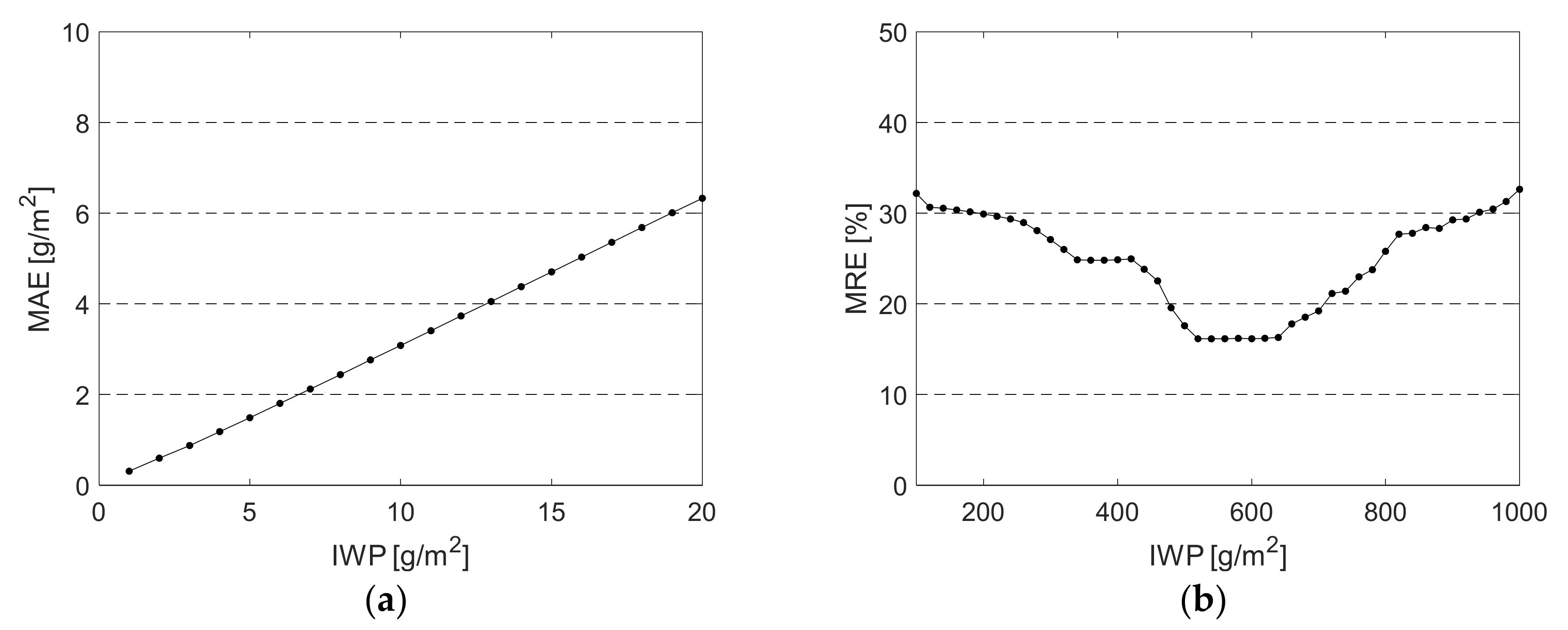
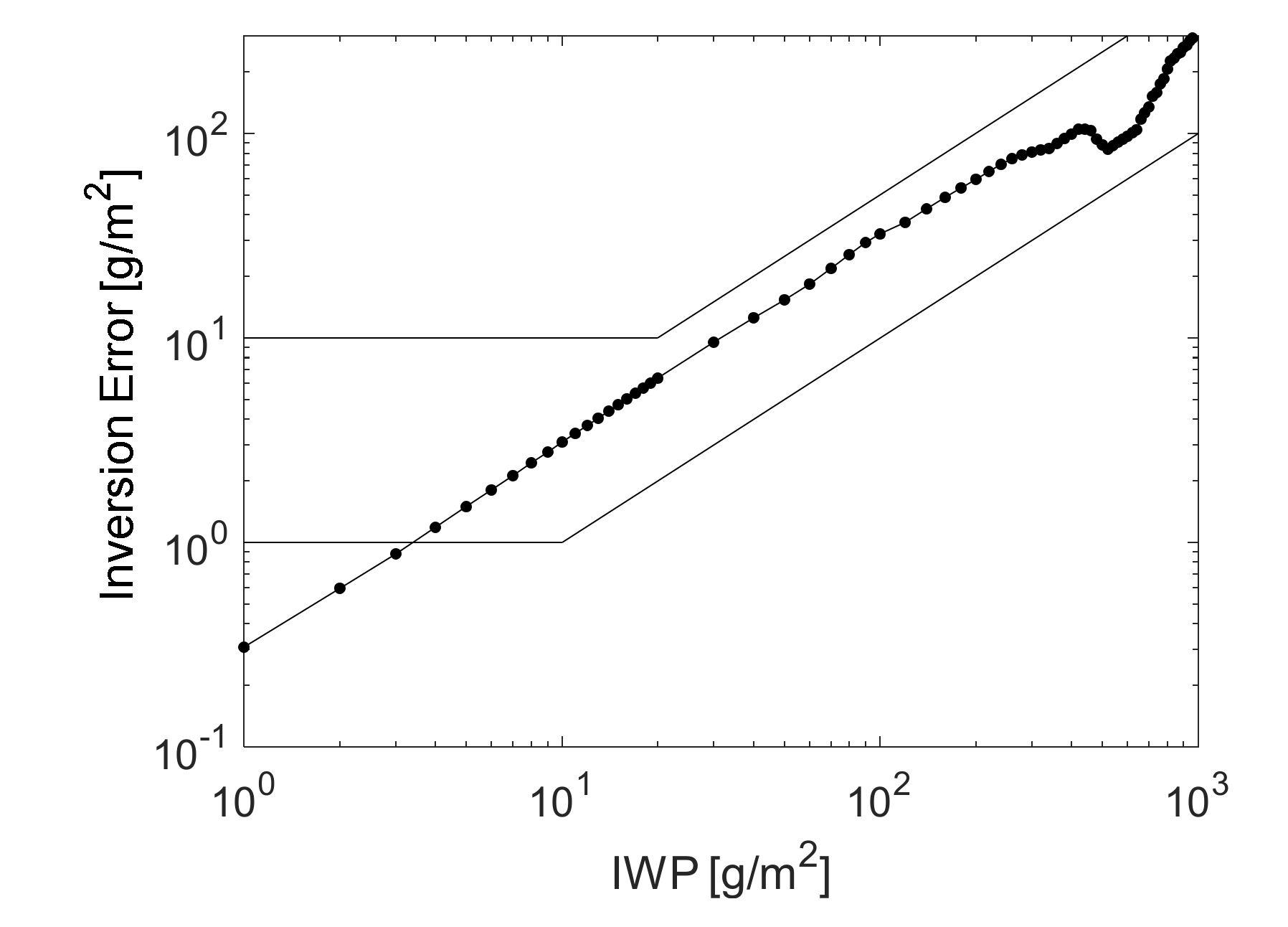
4.2. Inversion Error Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guerbette, J.; Mahfouf, J.-F.; Plu, M. Towards the assimilation of all-sky microwave radiances from the SAPHIR humidity sounder in a limited area NWP model over tropical regions. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 28620. [Google Scholar] [CrossRef]
- Geer, A.J.; Baordo, F.; Bormann, N.; Chambon, P.; English, S.J.; Kazumori, M.; Lawrence, H.; Lean, P.; Lonitz, K.; Lupu, C. The growing impact of satellite observations sensitive to humidity, cloud and precipitation. Q. J. R. Meteorol. Soc. 2017, 143, 3189–3206. [Google Scholar] [CrossRef]
- Brath, M.; Fox, S.; Eriksson, P.; Harlow, R.C.; Burgdorf, M.; Buehler, S.A. Retrieval of an ice water path over the ocean from ISMAR and MARSS millimeter and submillimeter brightness temperatures. Atmos. Meas. Tech. 2018, 11, 611–632. [Google Scholar] [CrossRef]
- Wang, X.; Liou, K.N.; Ou, S.S.C.; Mace, G.G.; Deng, M. Remote sensing of cirrus cloud vertical size profile using MODIS data. J. Geophys. Res 2009, 114. [Google Scholar] [CrossRef]
- Holl, G.; Eliasson, S.; Mendrok, J.; Buehler, S.A. SPARE-ICE: Synergistic ice water path from passive operational sensors. J. Geophys. Res. Atmos 2014, 119, 1504–1523. [Google Scholar] [CrossRef]
- Evans, K.F.; Wang, J.R.C.; Starr, D.; Heymsfield, G.; Li, L.; Tian, L.; Lawson, R.P.; Heymsfield, A.J.; Bansemer, A. Ice hydrometeor profile retrieval algorithm for high-frequency microwave radiometers: application to the CoSSIR instrument during TC4. Atmos. Meas. Tech. 2012, 5, 2277–2306. [Google Scholar] [CrossRef]
- Fox, S.; Lee, C.; Moyna, B.; Philipp, M.; Rule, I.; Rogers, S.; King, R.; Oldfield, M.; Rea, S.; Henry, M.; et al. ISMAR: An airborne submillimetre radiometer. Atmos. Meas. Tech. 2017, 10, 477–490. [Google Scholar] [CrossRef]
- Evans, K.F.; Walter, S.J.; Heymsfield, A.J.; Mcfarquhar, G.M. Submillimeter-wave cloud ice radiometer: Simulations of retrieval algorithm performance. J. Geophys. Res. Atmos. 2002, 107, AAC 2-1–AAC 2-21. [Google Scholar] [CrossRef]
- Evans, K.F.; Wang, J.R.; Racette, P.E.; Heymsfield, G.; Li, L. Ice Cloud Retrievals and Analysis with the Compact Scanning Submillimeter Imaging Radiometer and the Cloud Radar System during CRYSTAL FACE. J. Appl. Meteorol. 2005, 44, 839–859. [Google Scholar] [CrossRef][Green Version]
- Jiménez, C.; Eriksson, P.; Murtagh, D. First inversions of observed submillimeter limb sounding radiances by neural networks. J. Geophys. Res. Atmos. 2003, 108, D24. [Google Scholar] [CrossRef]
- Jiménez, C.; Buehler, S.A.; Rydberg, B.; Eriksson, P.; Evans, K.F. Performance simulations for a submillimetre-wave satellite instrument to measure cloud ice. Q. J. R. Meteorol. Soc. 2007, 133, 129–149. [Google Scholar] [CrossRef]
- Rydberg, B.; Eriksson, P.; Buehler, S.A. Prediction of cloud ice signatures in submillimetre emission spectra by means of ground-based radar and in situ microphysical data. Q. J. R. Meteorol. Soc. 2007, 133, 151–162. [Google Scholar] [CrossRef]
- Li, S.; Liu, L.; Gao, T.; Shi, L.; Qiu, S.; Hu, S. Radiation characteristics of the selected channels for cirrus remote sensing in terahertz waveband and the influence factors for the retrieval method. J. Infrared Millim. Waves 2018, 37, 60–65. [Google Scholar]
- Li, S.; Liu, L.; Gao, T.; Hu, S.; Huang, W. Retrieval method of cirrus microphysical parameters at terahertz wave based on multiple lookup tables. Acta Phys. Sin. 2017, 66, 78–87. [Google Scholar] [CrossRef]
- Li, S.; Liu, L.; Gao, T.; Huang, W.; Hu, S. Sensitivity analysis of terahertz wave passive remote sensing of cirrus microphysical parameters. Acta Phys. Sin. 2016, 65, 100–110. [Google Scholar] [CrossRef]
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the Atmospheric Radiative Transfer Simulator—Version 2.2, the planetary toolbox edition. Geosci. Model Dev. 2018, 11, 1537–1556. [Google Scholar] [CrossRef]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.X.; Chetwynd, J.H.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0–120 km); Optical Physics Division, Air Force Geophysics Laboratory: Lexington, MA, USA, 1986. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Hong, G.; Yang, P.; Baum, B.A.; Heymsfield, A.J.; Weng, F.; Liu, Q.; Heygster, G.; Buehler, S.A. Scattering database in the millimeter and submillimeter wave range of 100–1000 GHz for nonspherical ice particles. J. Geophys. Res. 2009, 114, D06201. [Google Scholar] [CrossRef]
- Yang, P.; Liou, K.N.; Wyser, K.; Mitchell, D. Parameterization of the scattering and absorption properties of individual ice crystals. J. Geophys. Res.Atmos. 2000, 105, 4699–4718. [Google Scholar] [CrossRef]
- Geer, A.J.; Baordo, F. Improved scattering radiative transfer for frozen hydrometeors at microwave frequencies. Atmos. Meas. Tech. 2014, 7, 1839–1860. [Google Scholar] [CrossRef]
- John, V.O.; Buehler, S.A. The impact of ozone lines on AMSU-B radiances. Geophys. Res. Lett. 2004, 31, L21108. [Google Scholar] [CrossRef]
- Eriksson, P.; Ekström, M.; Rydberg, B.; Murtagh, D.P. First Odin sub-mm retrievals in the tropical upper troposphere: ice cloud properties. Atmos. Chem. Phys. 2007, 7, 471–483. [Google Scholar] [CrossRef]
- Buehler, S. Cloud Ice Water Submillimeter Imaging Radiometer (CIWSIR): ESA Earth Explorer Mission Proposal; University of Bremen: Bremen, Germany, 2005. [Google Scholar]
- Buehler, S.A.; Jiménez, C.; Evans, K.F.; Eriksson, P.; Rydberg, B.; Heymsfield, A.J.; Stubenrauch, C.J.; Lohmann, U.; Emde, C.; John, V.O.; et al. A concept for a satellite mission to measure cloud ice water path, ice particle size, and cloud altitude. Q. J. R. Meteorol. Soc. 2007, 133, 109–128. [Google Scholar] [CrossRef]

| Center Frequency (GHz) | Frequency Offset (GHz) | Channel Characteristics | Channel Number |
|---|---|---|---|
| 118.75 | ±1.1, ±1.5, ±2.1, ±3.0, ±5.0 | oxygen | (1.1), (1.2), (1.3), (1.4), (1.5) |
| 157.05 | ±2.6 | window | (2) |
| 183.31 | ±1.0, ±3.0, ±7.0 | water vapor | (3.1), (3.2), (3.3) |
| 243.20 | ±2.5 | window | (4) |
| 325.15 | ±1.5, ±3.5, ±9.5 | water vapor | (5.1), (5.2), (5.3) |
| 424.70 | ±1.0, ±1.5, ±4.0 | oxygen | (6.1), (6.2), (6.3) |
| 448.0 | ±1.4, ±3.0, ±7.2 | water vapor | (7.1), (7.2), (7.3) |
| 664.0 | ±4.2 | window | (8) |
| 874.4 | ±6.0 | window | (9) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, C.; Liu, L.; Gao, T.; Hu, S.; Li, S.; Dou, F.; Shang, J. Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band. Atmosphere 2019, 10, 437. https://doi.org/10.3390/atmos10080437
Weng C, Liu L, Gao T, Hu S, Li S, Dou F, Shang J. Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band. Atmosphere. 2019; 10(8):437. https://doi.org/10.3390/atmos10080437
Chicago/Turabian StyleWeng, Chensi, Lei Liu, Taichang Gao, Shuai Hu, Shulei Li, Fangli Dou, and Jian Shang. 2019. "Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band" Atmosphere 10, no. 8: 437. https://doi.org/10.3390/atmos10080437
APA StyleWeng, C., Liu, L., Gao, T., Hu, S., Li, S., Dou, F., & Shang, J. (2019). Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band. Atmosphere, 10(8), 437. https://doi.org/10.3390/atmos10080437





