Impact of Along-Valley Orographic Variations on the Dispersion of Passive Tracers in a Stable Atmosphere
Abstract
1. Introduction
2. Methods
2.1. Numerical Model
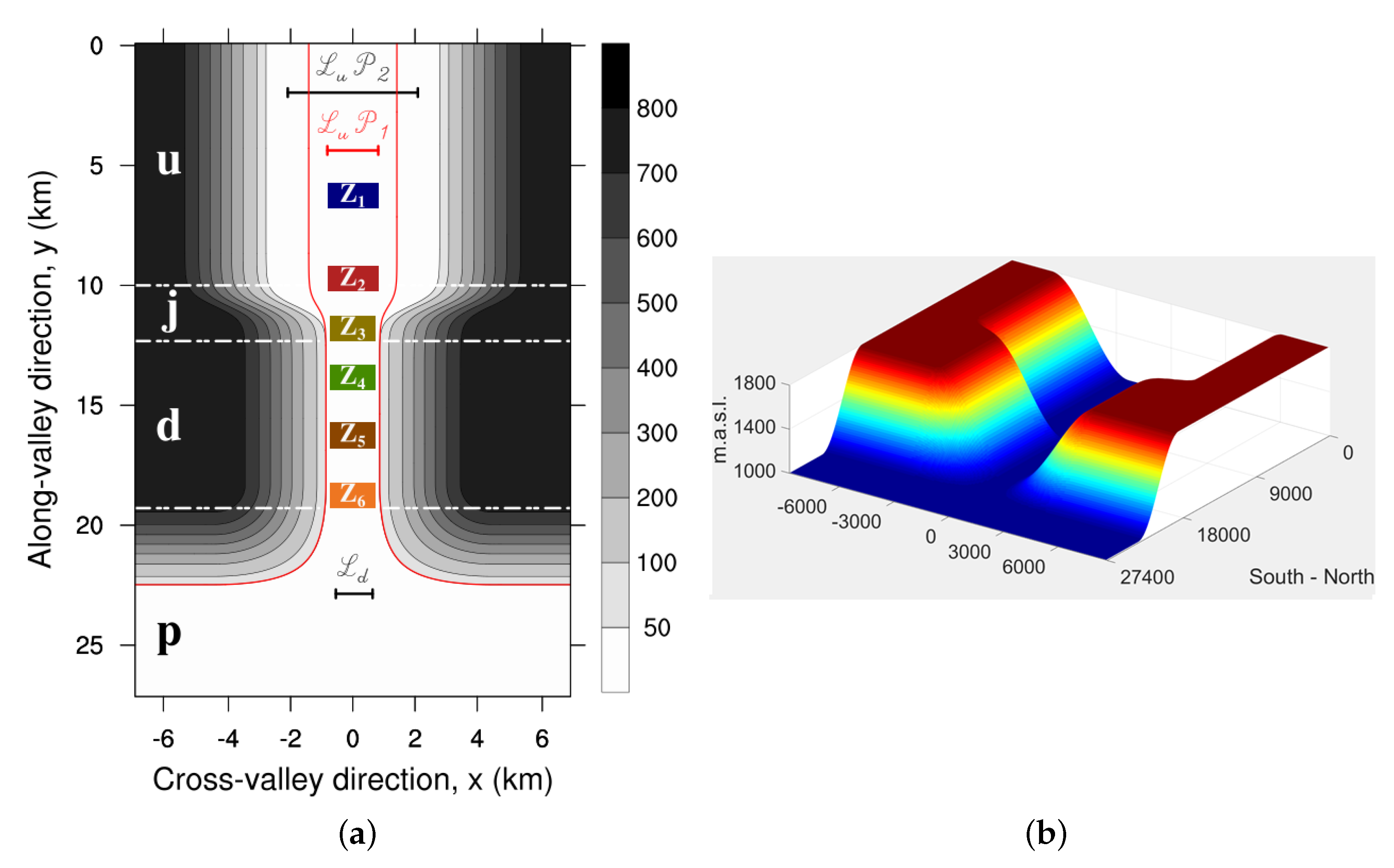
2.2. Topography
2.3. Numerical Setup
2.4. Passive Tracer Emission
3. Low Atmosphere Structure
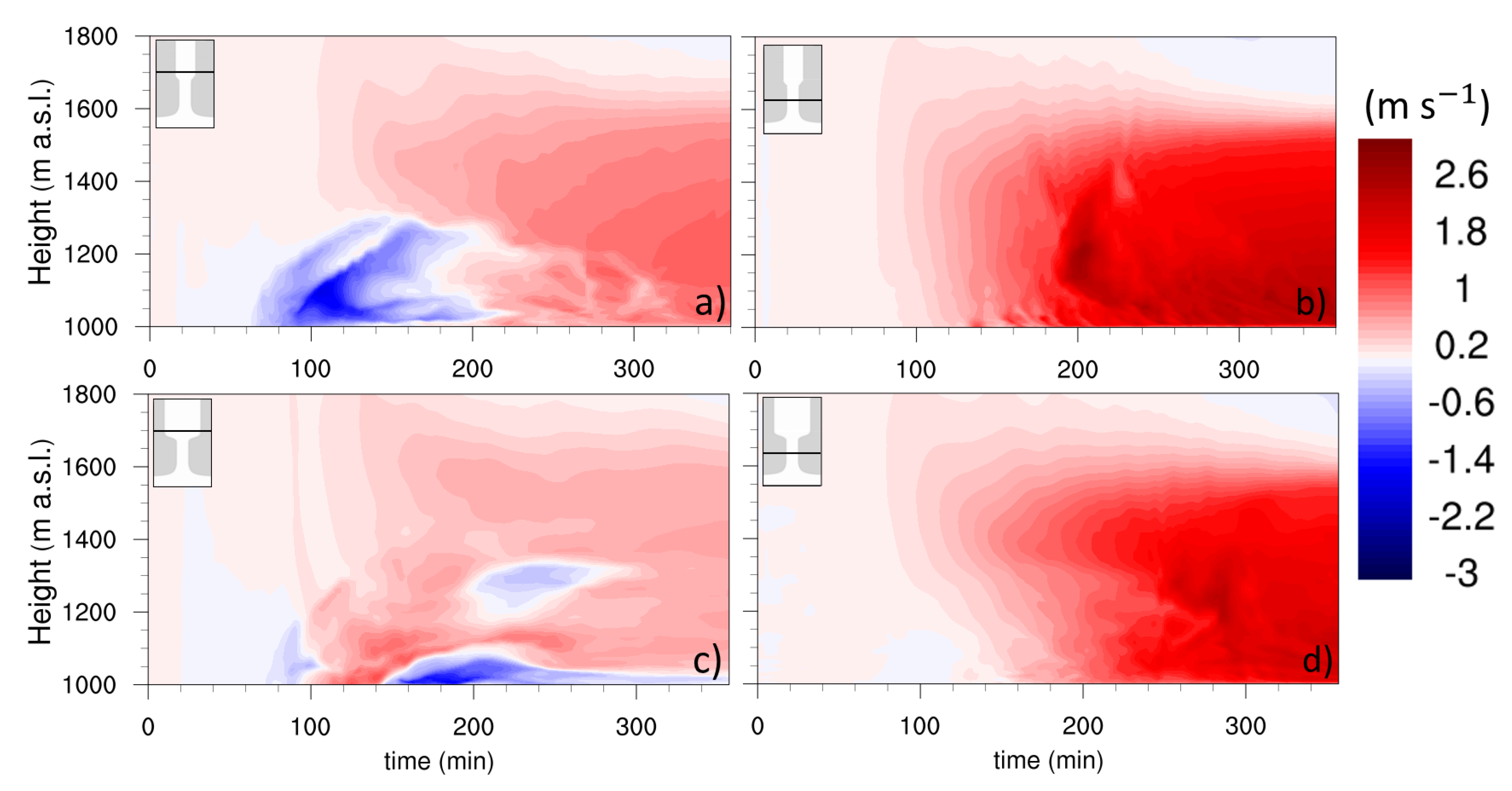
3.1. Along-Valley Flow
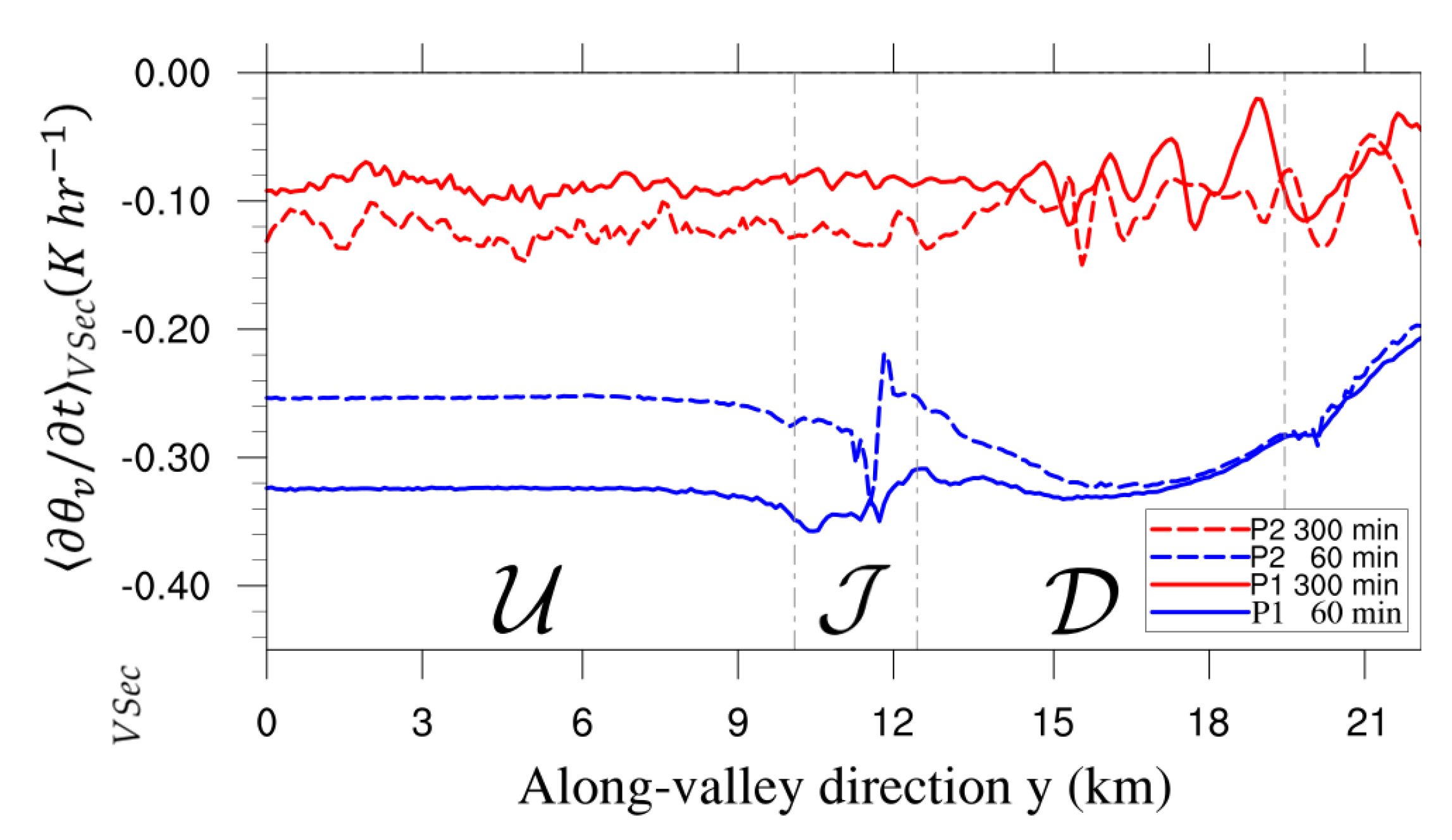
3.2. Thermal Structure
4. Stagnation and Ventilation Zones
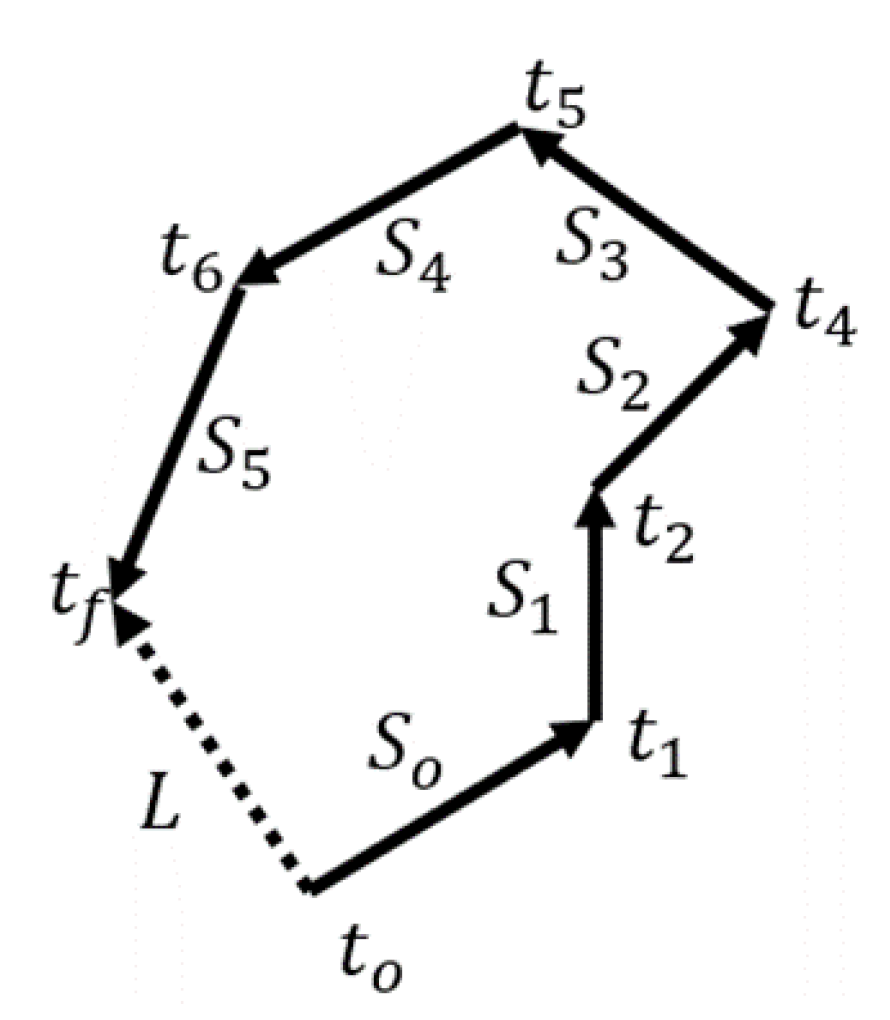
4.1. Summary of the Methodology Proposed by Allwine & Whiteman (1994)
- the time series , where is the virtual distance that an air parcel would travel during the time period T, assuming the air parcel does not experience any change in speed or direction during this time period, that is . Over the time , the parcel has travelled the virtual distance , where S is the wind run. The effective distance travelled by the fluid particle over time is denoted by L (see Figure 6).
- the recirculation index R defined by:R quantifies the recirculation character of the flow: when R tends to 1, an air parcel following the flow may have travelled some distance, but its final position remains close to the initial position, meaning that it has experienced recirculation. Conversely, if R tends to 0, an air parcel is continuously moving away from its initial position; i.e., it has experienced ventilation (if S is large enough).
- if in a given zone, this zone is defined as a stagnation zone;
- if in a given zone, this zone is defined as a recirculation zone.
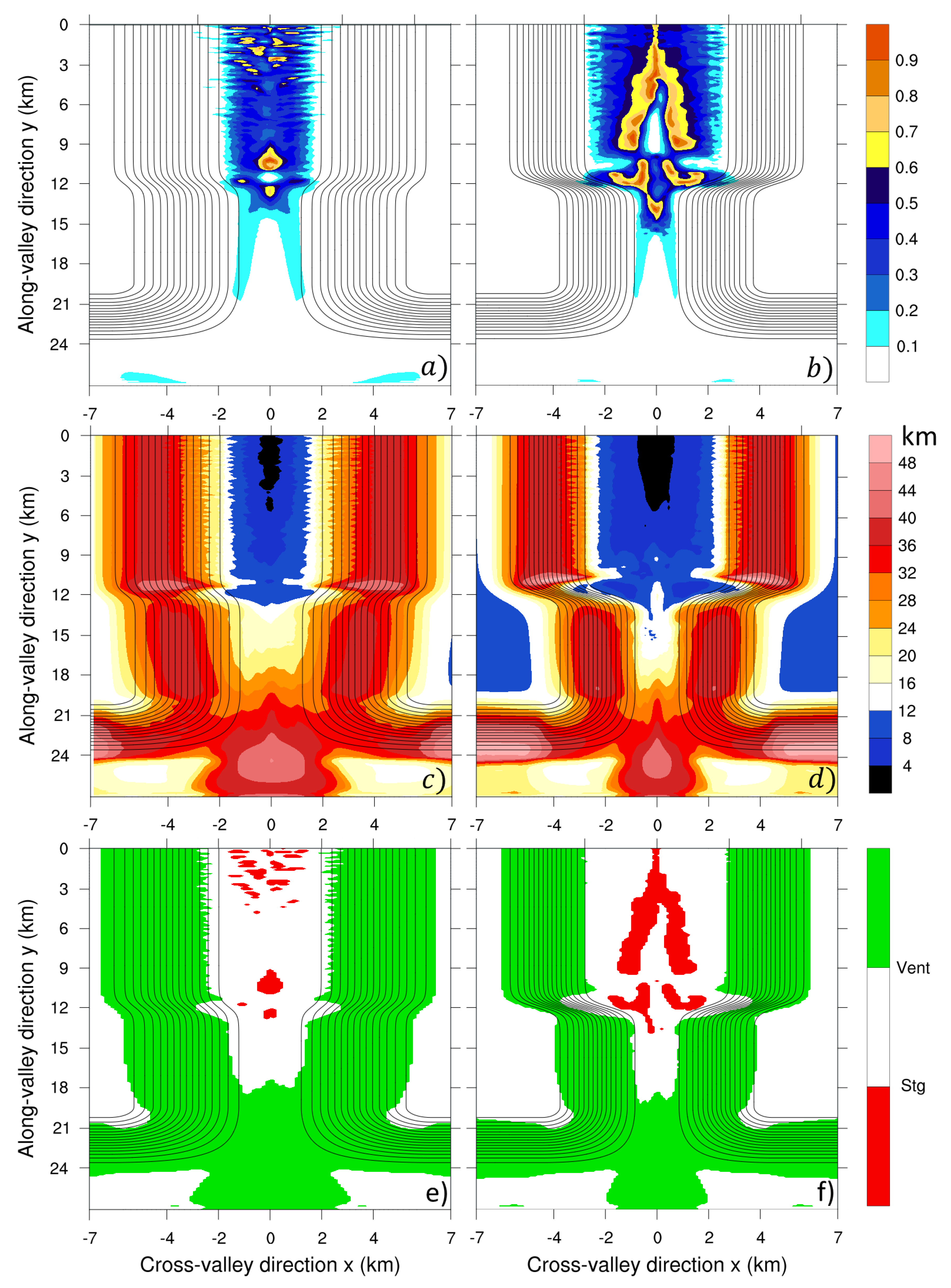
- if and in a given zone, this zone is defined as a ventilation zone (green color in Figure 7e,f).
- if and , this zone is defined as a critical stagnation zone (red color in Figure 7e,f).
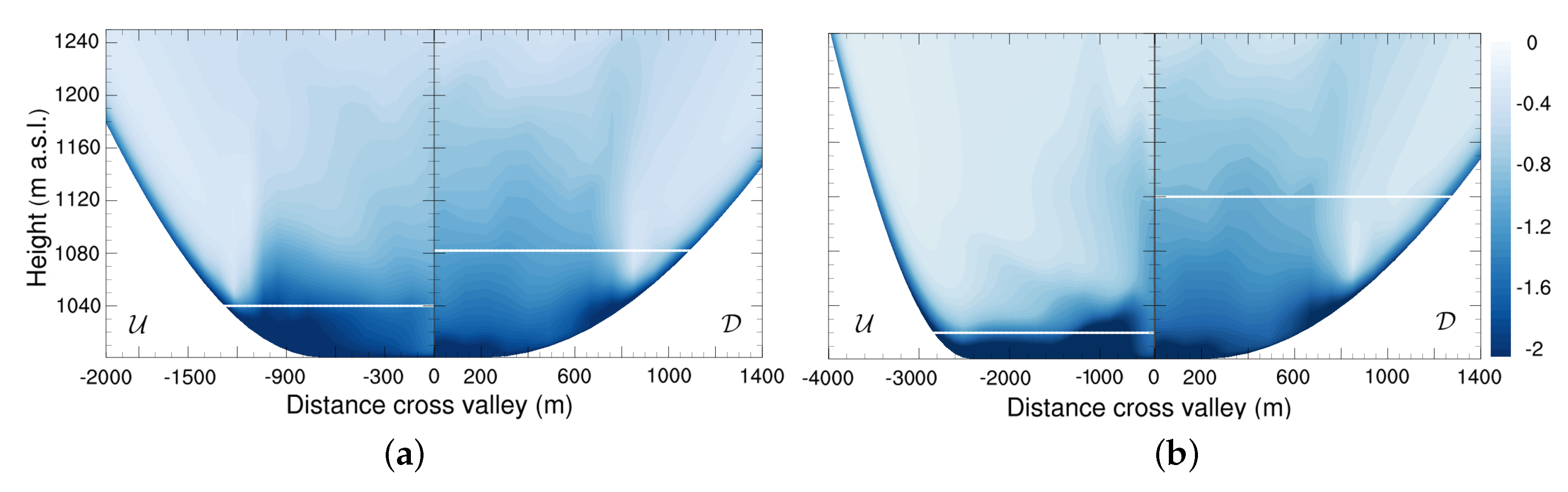
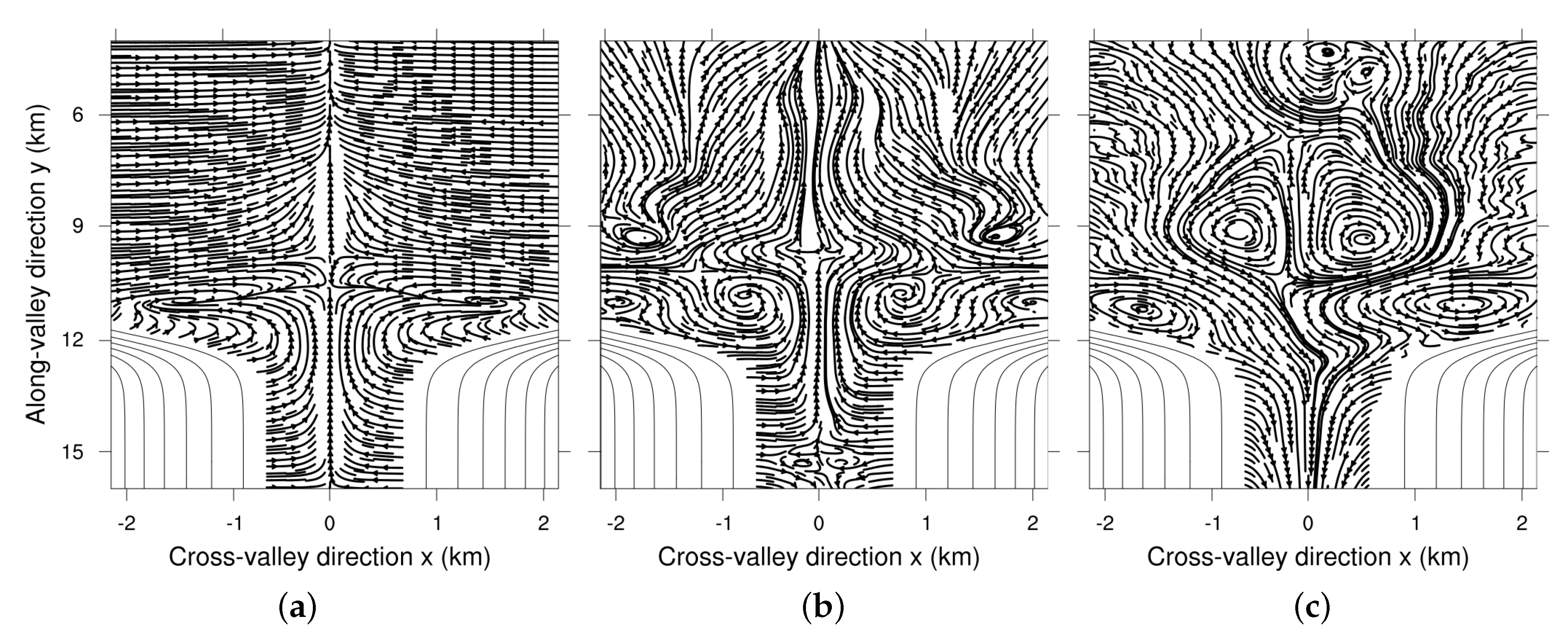
4.2. Recirculation, Stagnation and Ventilation Zones
5. Transport of Passive Tracers
5.1. Horizontal Distribution of Tracers in the Lower Atmosphere
5.2. Ventilation Efficiency
6. Summary and Conclusions
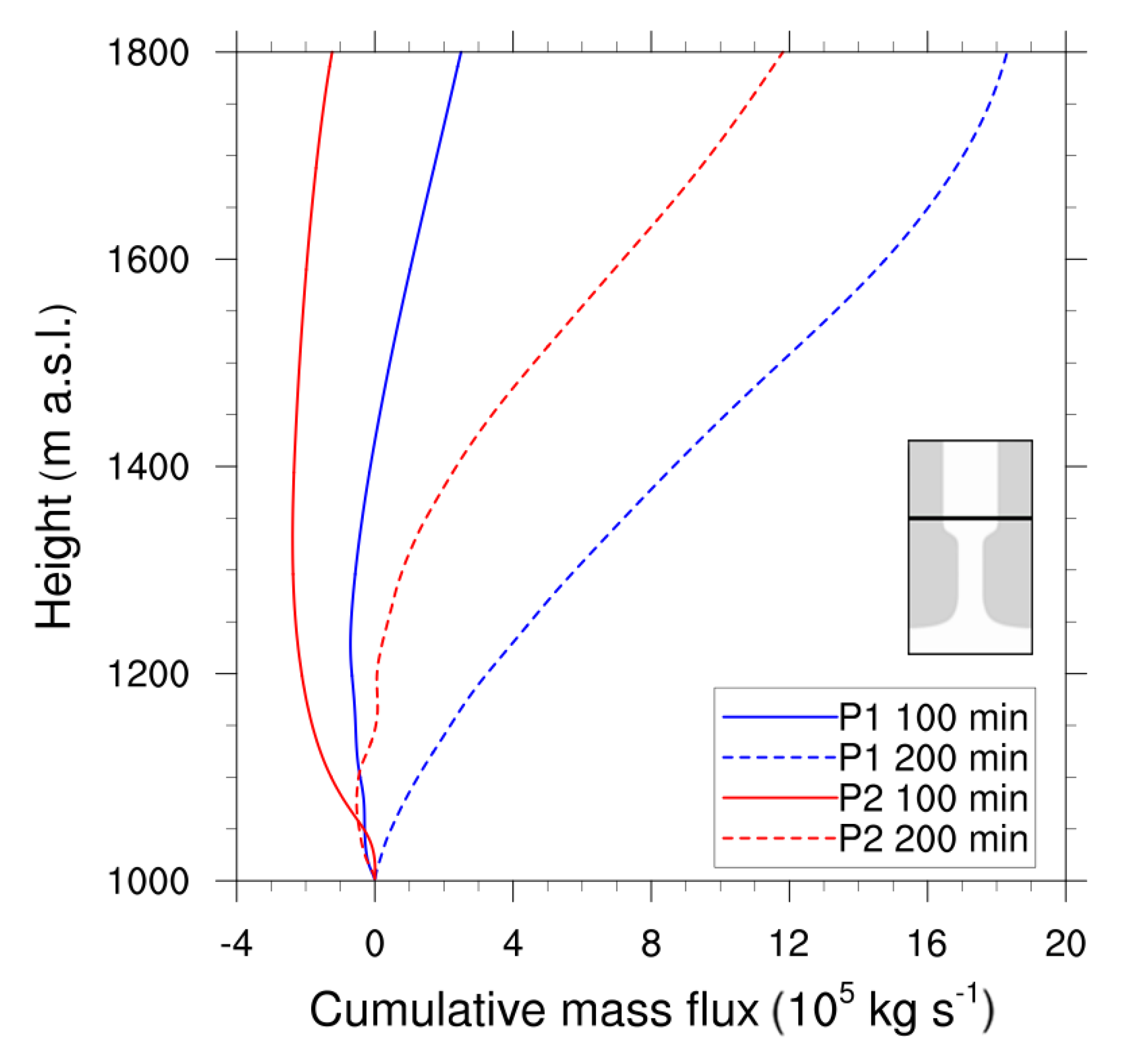
- The change in the thermal structure of the atmosphere within the different sections of the valley and the plain generates a horizontal pressure gradient that leads to the development of an along-valley flow. For P1 it is up-valley in the upstream-valley section during the first three hours of simulation and then reverses in the downstream direction for the rest of the simulated time period (six hours). For P2 a faster up-valley flow persists in the upstream-valley section until the end of the simulated period. These differences in the dynamics between P1 and P2 translate into differences in the horizontal mass flux in the upstream-valley section: after 3 h of simulation it is times larger for P1 than for P2 (see Figure 3).
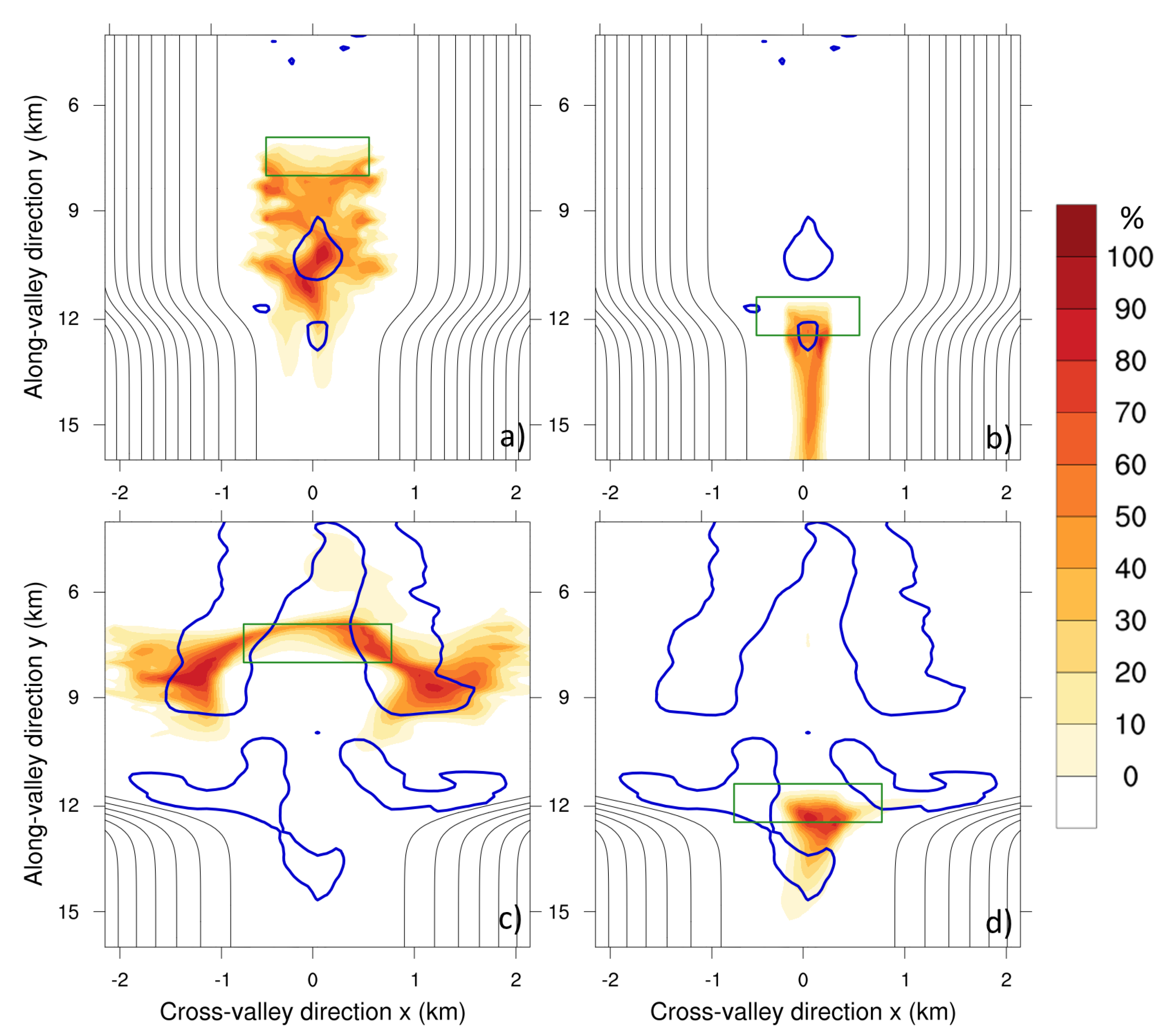
- The methodology proposed by Allwine and Whiteman (1994) [23] to predict locations prone to ventilation, stagnation and recirculation was evaluated and found to work well for predicting areas with high tracer concentration. Indeed, the zones where critical stagnation is detected agree well with zones of high tracer concentration (see Figure 9). However, the relationship between areas identified as prone to stagnation and the zones of high tracer concentration should be considered with caution since the variability in the concentration of air pollutants is not only a function of atmospheric dynamics but also of the emission location and rate, as shown in Figure 9d.
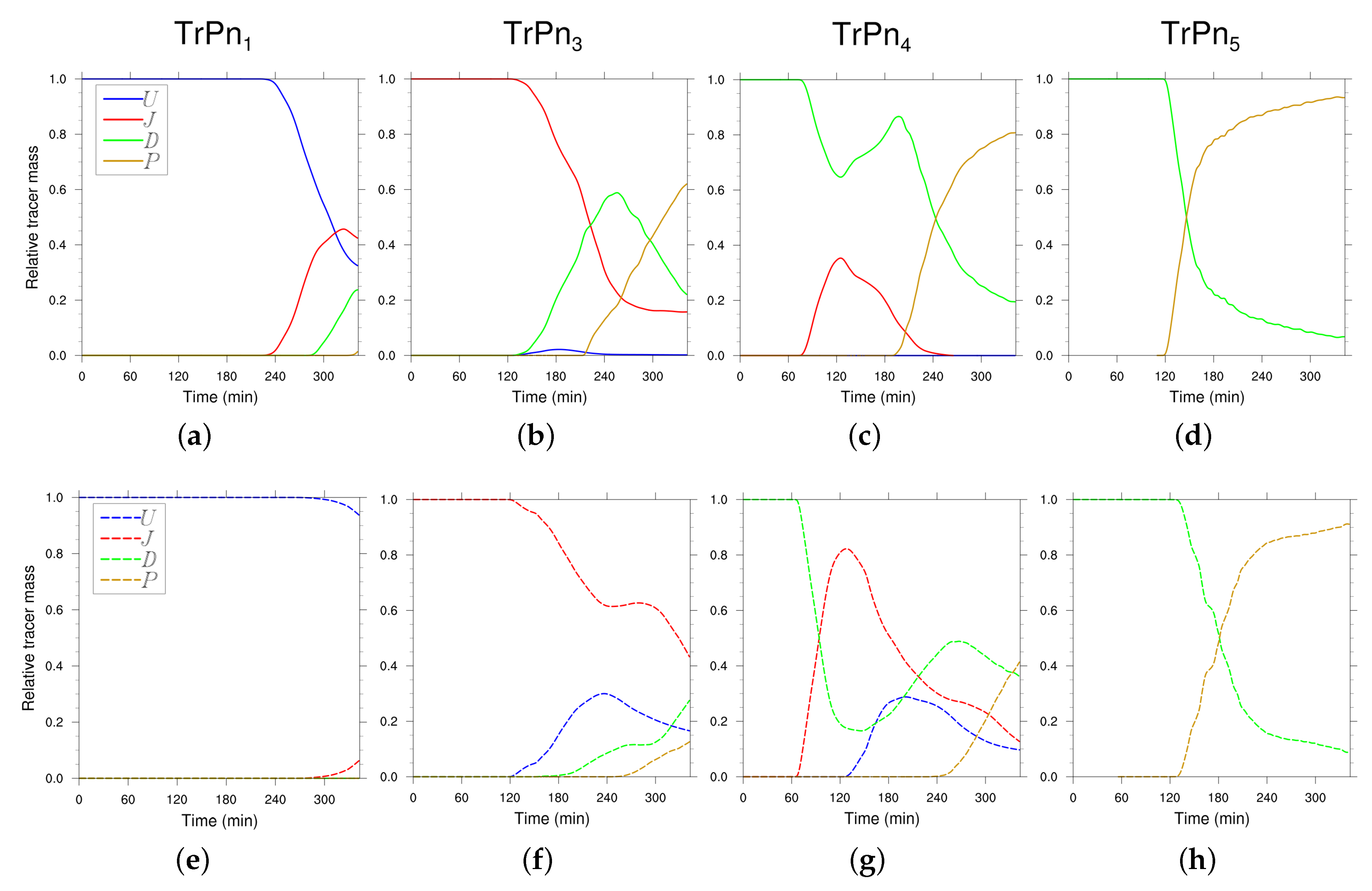
- The sizable change in the cross-sectional area between the upstream () and downstream () valleys affects atmospheric dynamics, and hence tracer transport across the domain. The export of tracers out of is reduced by about 50% for P2 compared to that for P1 (see Figure 10a,e). Intra-valley transport of tracers is also reduced in . By the end of the simulated period 80% of the total mass emitted for tracer (at the beginning of ) has been transported out of the valley section while for tracer (which is emitted at the same position but for P2) only 40% of the total mass emitted have left the valley section (see Figure 10c,g).
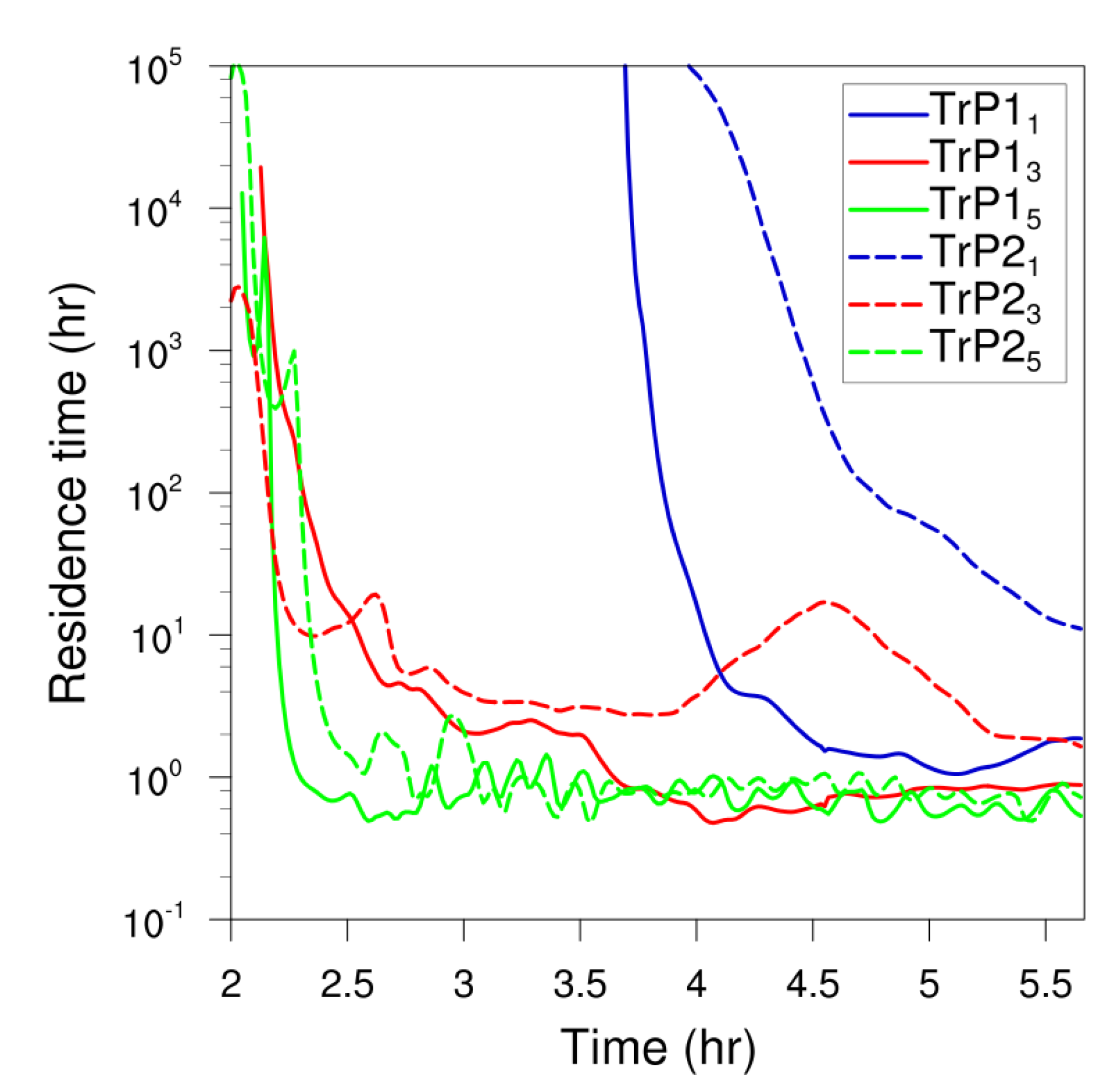
- The ventilation efficiency within the different sections of the valley system was quantified by a residence time. For P1 the residence time within (about two hours) is more than twice that within (about one hour) at the end of the simulated time period (Figure 11). On the other hand, this difference is more pronounced for P2, where the ventilation efficiency for (about 10 h) is reduced by more than a factor of ten when compared to that of (about one hour).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gohm, A.; Harnisch, F.; Vergeiner, J.; Obleitner, F.; Schnitzhofer, R.; Hansel, A.; Fix, A.; Neininger, B.; Emeis, S.; Schäfer, K. Air pollution transport in an Alpine valley: Results from airborne and ground-based observations. Bound.-Layer Meteorol. 2009, 131, 441–463. [Google Scholar] [CrossRef]
- Silcox, G.D.; Kelly, K.E.; Crosman, E.T.; Whiteman, C.D.; Allen, B.L. Wintertime PM 2.5 concentrations during persistent, multi-day cold-air pools in a mountain valley. Atmos. Environ. 2012, 46, 17–24. [Google Scholar]
- Chemel, C.; Burns, P. Pollutant dispersion in a developing valley cold-air pool. Bound.-Layer Meteorol. 2015, 154, 391–408. [Google Scholar] [CrossRef]
- Largeron, Y.; Staquet, C. Persistent inversion dynamics and wintertime PM 10 air pollution in Alpine valleys. Atmos. Environ. 2016, 135, 92–108. [Google Scholar] [CrossRef]
- Jaffrezo, J.L.; Aymoz, G.; Delaval, C.; Cozic, J. Seasonal variations of the water soluble organic carbon mass fraction of aerosol in two valleys of the French Alps. Atmos. Chem. Phys. 2005, 5, 2809–2821. [Google Scholar] [CrossRef]
- Whiteman, C.D. Observations of thermally developed wind systems in mountainous terrain. In Atmospheric Processes over Complex Terrain; American Meteorological Society: Boston, MA, USA, 1990; pp. 5–42. [Google Scholar]
- Whiteman, C.D.; Hoch, S.W.; Horel, J.D.; Charland, A. Relationship between particulate air pollution and meteorological variables in Utah’s Salt Lake Valley. Atmos. Environ. 2014, 94, 742–753. [Google Scholar] [CrossRef]
- Chemel, C.; Arduini, G.; Staquet, C.; Largeron, Y.; Legain, D.; Tzanos, D.; Paci, A. Valley heat deficit as a bulk measure of wintertime particulate air pollution in the Arve River Valley. Atmos. Environ. 2016, 128, 208–215. [Google Scholar] [CrossRef]
- Allwine, K.J.; Whiteman, C.D. Ventilation of pollutants trapped in valleys: A simple parameterization for regional-scale dispersion models. Atmos. Environ. 1988, 22, 1839–1845. [Google Scholar] [CrossRef]
- Regmi, R.P.; Kitada, T.; Kurata, G. Numerical simulation of late wintertime local flows in Kathmandu valley, Nepal: Implication for air pollution transport. J. Appl. Meteorol. 2003, 42, 389–403. [Google Scholar] [CrossRef]
- Maurizi, A.; Russo, F.; Tampieri, F. Local vs. external contribution to the budget of pollutants in the Po Valley (Italy) hot spot. Sci. Total Environ. 2013, 458, 459–465. [Google Scholar] [CrossRef]
- Rotach, M.W.; Wohlfahrt, G.; Hansel, A.; Reif, M.; Wagner, J.; Gohm, A. The world is not flat: Implications for the global carbon balance. Bull. Am. Meteorol. Soc. 2014, 95, 1021–1028. [Google Scholar] [CrossRef]
- Serafin, S.; Zardi, D. Daytime heat transfer processes related to slope flows and turbulent convection in an idealized mountain valley. J. Atmos. Sci. 2010, 67, 3739–3756. [Google Scholar] [CrossRef]
- Colette, A.; Chow, F.K.; Street, R.L. A numerical study of inversion-layer breakup and the effects of topographic shading in idealized valleys. J. Appl. Meteorol. 2003, 42, 1255–1272. [Google Scholar] [CrossRef]
- Lehner, M.; Gohm, A. Idealised simulations of daytime pollution transport in a steep valley and its sensitivity to thermal stratification and surface albedo. Bound.-Layer Meteorol. 2010, 134, 327–351. [Google Scholar] [CrossRef]
- Quimbayo-Duarte, J.; Staquet, C.; Chemel, C.; Arduini, G. Dispersion of Tracers in the Stable Atmosphere of a Valley Opening onto a Plain. Bound.-Layer Meteorol. 2019. under review. [Google Scholar] [CrossRef]
- Wagner, A. Theorie und beobachtung der periodischen Gebirgswinde. Gerlands Beitr. Geophys. 1938, 52, 408–449. [Google Scholar]
- Steinacker, R. Area-height distribution of a valley and its relation to the valley wind. Contrib. Atmos. Phys. 1984, 57, 64–71. [Google Scholar]
- Vergeiner, I.; Dreiseitl, E. Valley winds and slope winds—Observations and elementary thoughtsBerg-und Tal-bzw. Hangwinde—Beobachtungen und grundsätzliche Überlegungen. Meteorol. Atmos. Phys. 1987, 36, 264–286. [Google Scholar] [CrossRef]
- McKee, T.B.; O’Neal, R.D. The role of valley geometry and energy budget in the formation of nocturnal valley winds. J. Appl. Meteorol. 1989, 28, 445–456. [Google Scholar] [CrossRef]
- Arduini, G.; Chemel, C.; Staquet, C. Energetics of deep alpine valleys in pooling and draining configurations. J. Atmos. Sci. 2017, 74, 2105–2124. [Google Scholar] [CrossRef]
- Li, J.; Atkinson, B. Transition regimes in valley airflows. Bound.-Layer Meteorol. 1999, 91, 385–411. [Google Scholar] [CrossRef]
- Allwine, K.J.; Whiteman, C.D. Single-station integral measures of atmospheric stagnation, recirculation and ventilation. Atmos. Environ. 1994, 28, 713–721. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF, Version 3; Technical Report; Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research: Boulder, CO, USA, 2005. [Google Scholar]
- Catalano, F.; Cenedese, A. High-resolution numerical modeling of thermally driven slope winds in a valley with strong capping. J. Appl. Meteorol. Climatol. 2010, 49, 1859–1880. [Google Scholar] [CrossRef]
- Wagner, J.S.; Gohm, A.; Rotach, M.W. The impact of horizontal model grid resolution on the boundary layer structure over an idealized valley. Mon. Weather Rev. 2014, 142, 3446–3465. [Google Scholar] [CrossRef]
- Burns, P.; Chemel, C. Interactions between downslope flows and a developing cold-air pool. Bound.-Layer Meteorol. 2015, 154, 57–80. [Google Scholar] [CrossRef][Green Version]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Scotti, A.; Meneveau, C.; Lilly, D.K. Generalized Smagorinsky model for anisotropic grids. Phys. Fluids A Fluid Dyn. 1993, 5, 2306–2308. [Google Scholar] [CrossRef]
- Largeron, Y.; Staquet, C. The atmospheric boundary layer during wintertime persistent inversions in the Grenoble valleys. Front. Earth Sci. 2016, 4, 70. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Toward Numerical Modeling in the Terra Incognita. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 663–682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Zardi, D.; Whiteman, C.D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting; Springer: Dordrecht, The Netherlands, 2013; pp. 35–119. [Google Scholar]
- Largeron, Y. Dynamique de la Couche Limite Atmosphérique Stable en Relief Complexe. Application aux épisodes de Pollution Particulaire des Vallées Alpines. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2010. [Google Scholar]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Whiteman, C.D.; McKee, T.B.; Doran, J. Boundary layer evolution within a canyonland basin. Part I: Mass, heat, and moisture budgets from observations. J. Appl. Meteorol. 1996, 35, 2145–2161. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quimbayo-Duarte, J.; Staquet, C.; Chemel, C.; Arduini, G. Impact of Along-Valley Orographic Variations on the Dispersion of Passive Tracers in a Stable Atmosphere. Atmosphere 2019, 10, 225. https://doi.org/10.3390/atmos10040225
Quimbayo-Duarte J, Staquet C, Chemel C, Arduini G. Impact of Along-Valley Orographic Variations on the Dispersion of Passive Tracers in a Stable Atmosphere. Atmosphere. 2019; 10(4):225. https://doi.org/10.3390/atmos10040225
Chicago/Turabian StyleQuimbayo-Duarte, Julian, Chantal Staquet, Charles Chemel, and Gabriele Arduini. 2019. "Impact of Along-Valley Orographic Variations on the Dispersion of Passive Tracers in a Stable Atmosphere" Atmosphere 10, no. 4: 225. https://doi.org/10.3390/atmos10040225
APA StyleQuimbayo-Duarte, J., Staquet, C., Chemel, C., & Arduini, G. (2019). Impact of Along-Valley Orographic Variations on the Dispersion of Passive Tracers in a Stable Atmosphere. Atmosphere, 10(4), 225. https://doi.org/10.3390/atmos10040225




