A New Clear-Sky Method for Assessing Photosynthetically Active Radiation at the Surface Level
Abstract
1. Introduction
2. Ground–Based Measurements Used
3. Method
3.1. Inputs to Libradtran
3.2. Description of the Spectral Resampling and the Proposed Method
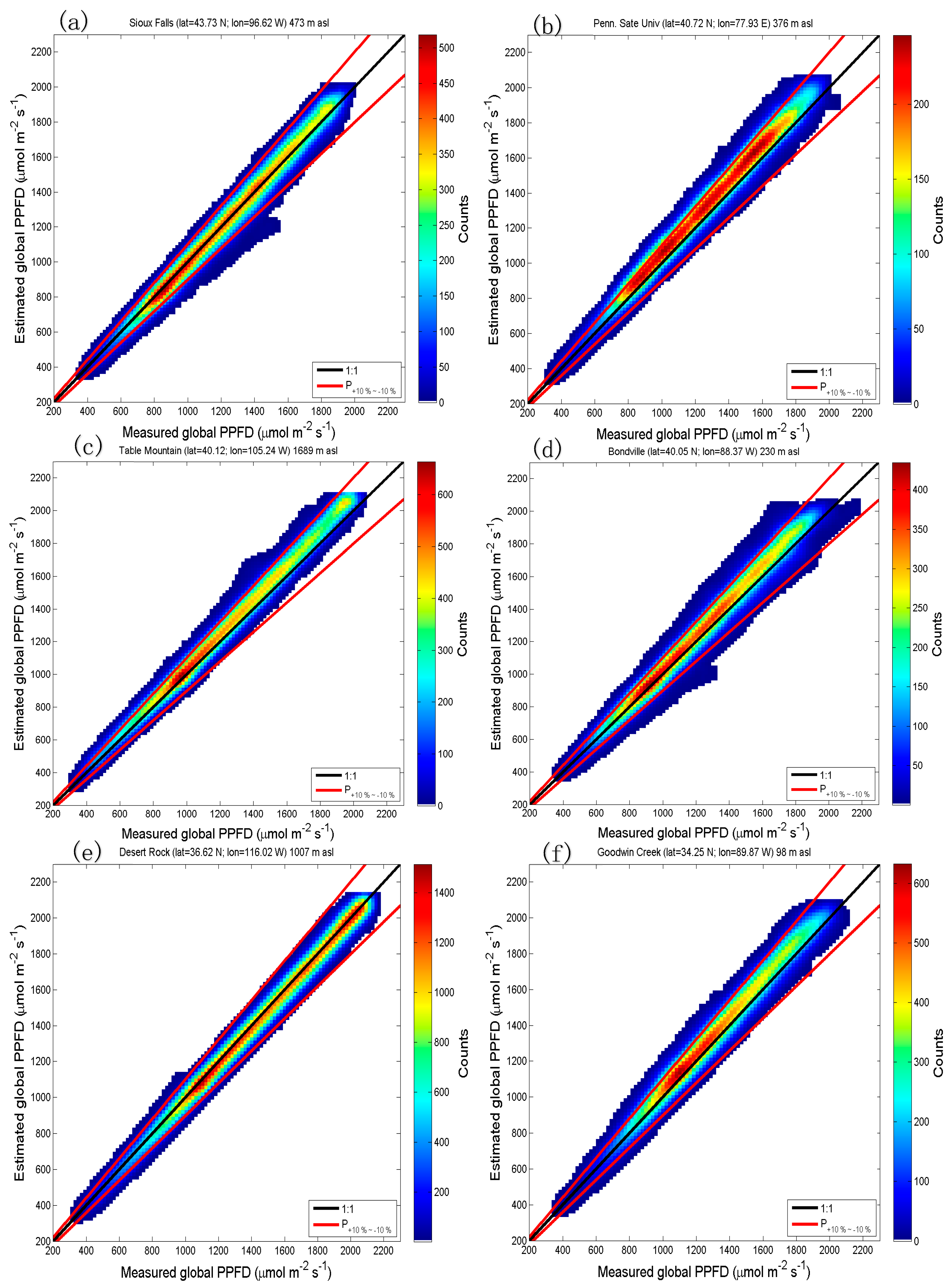
4. Results of the Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- McCree, K.J. Photosynthetically active radiation. In Physiology Plant Ecology I; Springer: Berlin/Heidelberg, Germany, 1981; pp. 41–55. [Google Scholar]
- Frolking, S.E.; Bubier, J.L.; Moore, T.R.; Ball, T.; Bellisario, L.M.; Bhardwaj, A.; Carroll, P.; Crill, P.M.; Lafleur, P.M.; McCaughey, J.H.; et al. Relationship between ecosystem productivity and photosynthetically active radiation for northern peatlands. Glob. Biogeochem. Cycles 1998, 12, 115–126. [Google Scholar] [CrossRef]
- Frouin, R.; Murakami, H. Estimating photosynthetically available radiation at the ocean surface from ADEOS-II global imager data. J. Oceanogr. 2007, 63, 493–503. [Google Scholar] [CrossRef]
- McCree, K.J. Test of current definitions of photosynthetically active radiation against leaf photosynthesis data. Agric. For. Meteorol. 1972, 10, 443–453. [Google Scholar] [CrossRef]
- Li, T.; Yang, Q. Advantages of diffuse light for horticultural production and perspectives for further research. Front. Plant Sci. 2015, 6, 704. [Google Scholar] [CrossRef] [PubMed]
- Light Measurement. Available online: https://www.licor.com/documents/3bjwy50xsb49jqof0wz4 (accessed on 14 April 2019).
- Jacovides, C.P.; Timvios, F.; Asimakopoulos, D.N.; Steven, M.D. Urban aerosol and clear skies spectra for global and diffuse photosynthetically active radiation. Agric. For. Meteorol. 1997, 97, 21–31. [Google Scholar] [CrossRef]
- Mottus, M.; Ross, J.; Sulev, M. Experimental study of ratio of PAR to direct integral solar radiation under cloudless conditions. Agric. For. Meteorol. 2001, 109, 161–170. [Google Scholar] [CrossRef]
- Gonzalez, J.A.; Calbo, J. Modelled and measured ratio of PAR to global radiation under cloudless skies. Agric. For. Meteorol. 2002, 110, 319–325. [Google Scholar] [CrossRef]
- Udo, S.O.; Aro, T.O. Global PAR related to global solar radiation for central Nigeria. Agric. For. Meteorol. 1999, 97, 21–31. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Timvios, F.S.; Papaioannou, G.; Asimakopoulos, D.N.; Theofilou, C.M. Ratio of PAR to broadband solar radiation measured in Cyprus. Agric. For. Meteorol. 2004, 121, 135–140. [Google Scholar] [CrossRef]
- Amillo, A.G.; Huld, T.; Müller, R. A new database of global and direct solar radiation using the Eastern Meteosat Satellite, models and validation. Remote Sens. 2014, 6, 8165–8189. [Google Scholar] [CrossRef]
- Blanc, P.; Gschwind, B.; Lefèvre, M.; Wald, L. The HelioClim project: Surface solar irradiance data for climate applications. Remote. Sens. 2011, 3, 343–361. [Google Scholar] [CrossRef]
- Chen, M.; Zhuang, Q.; He, Y. An efficient method of estimating downward solar radiation based on the MODIS observations for the use of land surface modeling. Remote Sens. 2014, 6, 7136–7157. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Bengulescu, M.; Blanc, P.; Boilley, A.; Wald, L. Do modelled or satellite-based estimates of surface solar irradiance accurately describe its temporal variability? Adv. Sci. Res. 2017, 14, 35–48. [Google Scholar] [CrossRef]
- Boilley, A.; Wald, L. Comparison between meteorological re-analyses from ERA-Interim and MERRA and measurements of daily solar irradiation at surface. Renew. Energy 2015, 75, 135–143. [Google Scholar] [CrossRef]
- Trolliet, M.; Walawender, J.P.; Bourlès, B.; Boilley, A.; Trentmann, J.; Blanc, P.; Lefèvre, M.; Wald, L. Estimating downwelling solar irradiance at the surface of the tropical Atlantic Ocean: A comparison of PIRATA measurements against several re-analyses and satellite-derived data sets. Ocean Sci. 2018, 14, 1021–1056. [Google Scholar] [CrossRef]
- Oumbe, A.; Qu, Z.; Blanc, P.; Lefèvre, M.; Wald, L.; Cros, S. Decoupling the effects of clear atmosphere and clouds to simplify calculations of the broadband solar irradiance at ground level. Geosci. Model Dev. 2014, 7, 1661–1669. [Google Scholar] [CrossRef]
- Su, W.; Charlock, T.P.; Rose, F.G.; Rutan, D. Photosynthetically active radiation from Clouds and the Earth’s Radiant Energy System (CERES) products. J. Geophys. Res. Biogeosci. 2007, 112. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD—A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Bosch, J.L.; López, G.; Batlles, F.J. Global and direct photosynthetically active radiation parameterizations for clear-sky conditions. Agric. For. Meteorol. 2009, 149, 146–158. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, H.; Liu, J.; Shi, G. Estimation of photosynthetically active radiation using solar radiation in the UV–visible spectral band. Sol. Energy 2017, 153, 611–622. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Kato, S.; Ackerman, T.; Mather, J.; Clothiaux, E. The k-distribution method and correlated-k approximation for shortwave radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Espinar, B.; Blanc, P.; Wald, L. How close to detailed spectral calculations is the k-distribution method and correlated-k approximation of Kato et al. (1999) in each spectral interval? Meteorol. Z. 2014, 23, 547–556. [Google Scholar] [CrossRef]
- Gschwind, B.; Ménard, L.; Albuisson, M.; Wald, L. Converting a successful research project into a sustainable service: The case of the SoDa Web service. Environ. Model. Softw. 2006, 21, 1555–1561. [Google Scholar] [CrossRef]
- Lefèvre, M.; Blanc, P.; Espinar, B.; Gschwind, B.; Ménard, L.; Ranchin, T.; Wald, L.; Saboret, L.; Thomas, C.; Wey, E. The HelioClim-1 database of daily solar radiation at Earth surface: An example of the benefits of GEOSS Data-CORE. IEEE J. STARS 2014, 7, 1745–1753. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Espinar, B.; Blanc, P.; Wald, L. Estimating the photosynthetically active radiation under clear skies by means of a new approach. Adv. Sci. Res. 2015, 12, 5–10. [Google Scholar] [CrossRef]
- Blanc, P.; Gschwind, B.; Lefèvre, M.; Wald, L. Twelve monthly maps of ground albedo parameters derived from MODIS data sets. In Proceedings of the IGARSS 2014, Quebec, QC, Canada, 13–18 July 2014; pp. 3270–3272. [Google Scholar] [CrossRef]
- SURFRAD FTP Server. Available online: ftp://aftp.cmdl.noaa.gov/data/radiation/surfrad/ (accessed on 14 April 2019).
- Ohmura, A.; Gilgen, H.; Hegner, H.; Müller, G.; Wild, M.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Philipona, R.; Heimo, A.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New precision radiometry for climate research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Pinker, R.T.; Laszlo, I. Global distribution of photosynthetically active radiation as observed from satellites. J. Clim. 1992, 5, 56–65. [Google Scholar] [CrossRef]
- Blanc, P.; Wald, L. The SG2 algorithm for a fast and accurate computation of the position of the Sun. Sol. Energy 2012, 86, 3072–3083. [Google Scholar] [CrossRef]
- Gschwind, B.; Wald, L.; Blanc, P.; Lefèvre, M.; Schroedter-Homscheidt, M.; Arola, A. Improving the McClear model estimating the downwelling solar radiation at ground level in cloud-free conditions—McClear-v3. Meteorol. Z. 2019. to be published. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Pitkänen, M.; Aoun, Y.; Blanc, P.; Heikkilä, A.; Lakkala, K.; Bernhard, G.; Koskela, T.; Lindfors, A.; Arola, A.; et al. A new method for estimating UV fluxes at ground level in cloud-free conditions. Atmos. Meas. Tech. 2017, 10, 4965–4978. [Google Scholar] [CrossRef]
- CAMS Radiation Service. Available online: https://atmosphere.copernicus.eu/solar-energy (accessed on 14 April 2019).
- Huang, G.H.; Ma, M.G.; Liang, S.L.; Liu, S.M.; Li, X. A LUT-based approach to estimate surface solar irradiance by combining MODIS and MTSAT data. J. Geophys. Res. Atmos. 2011, 116, D22201. [Google Scholar] [CrossRef]
- Calbó, J.; Pages, D.; González, J.A. Empirical studies of cloud effects on UV radiation: A review. Rev. Geophys. 2005, 43, RG2002. [Google Scholar] [CrossRef]
- den Outer, P.N.; Slaper, H.; Kaurola, J.; Lindfors, A.; Kazantzidis, A.; Bais, A.F.; Feister, U.; Junk, J.; Janouch, M.; Josefsson, W. Reconstructing of erythemal ultraviolet radiation levels in Europe for the past 4 decades. J. Geophys. Res. Atmos. 2010, 115, D10102. [Google Scholar] [CrossRef]
- Krotkov, N.A.; Herman, J.R.; Bhartia, P.K.; Fioletov, V.; Ahmad, Z. Satellite estimation of spectral surface UV irradiance: 2. Effects of homogeneous clouds and snow. J. Geophys. Res. Atmos. 2001, 106, 11743–11759. [Google Scholar] [CrossRef]
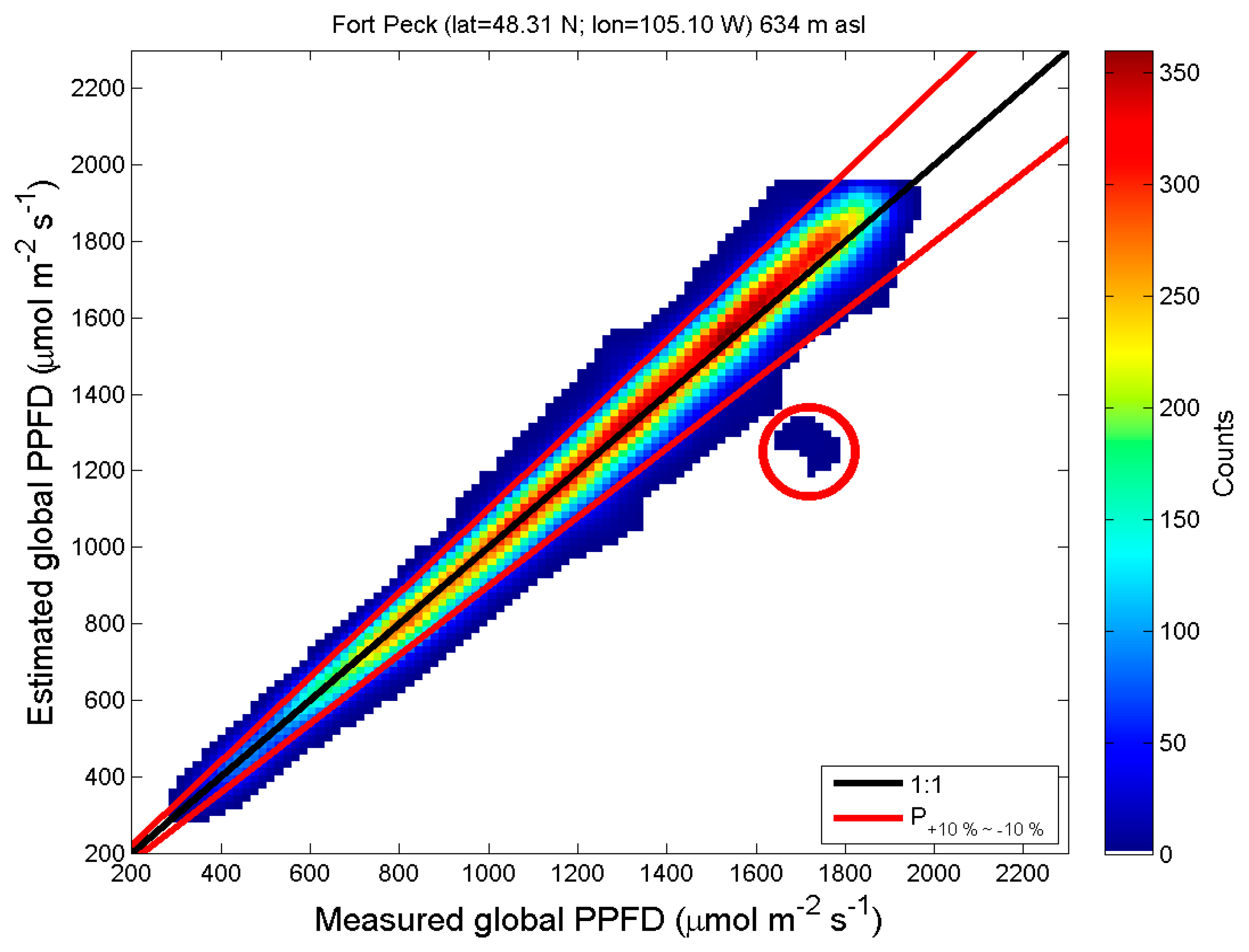
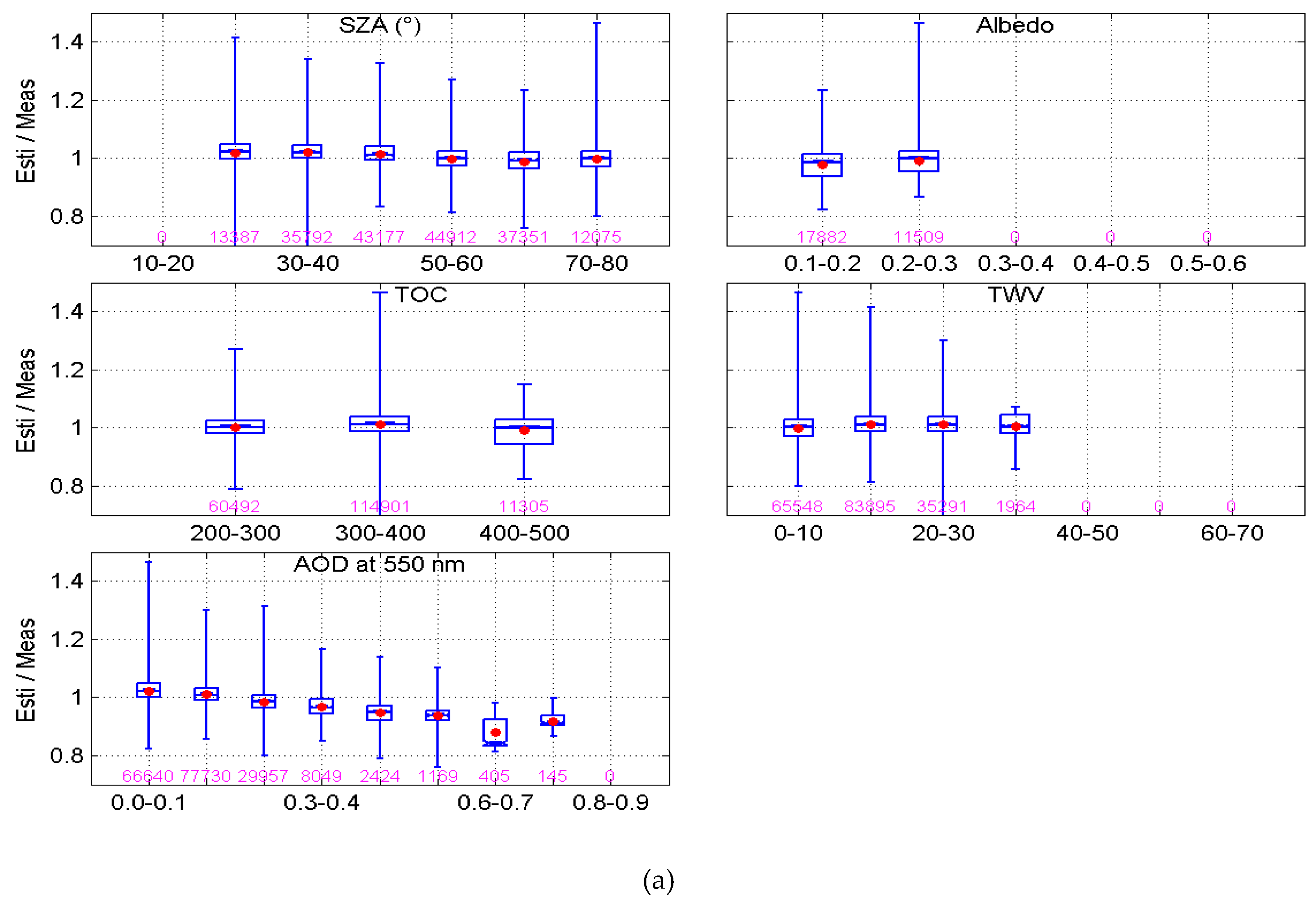
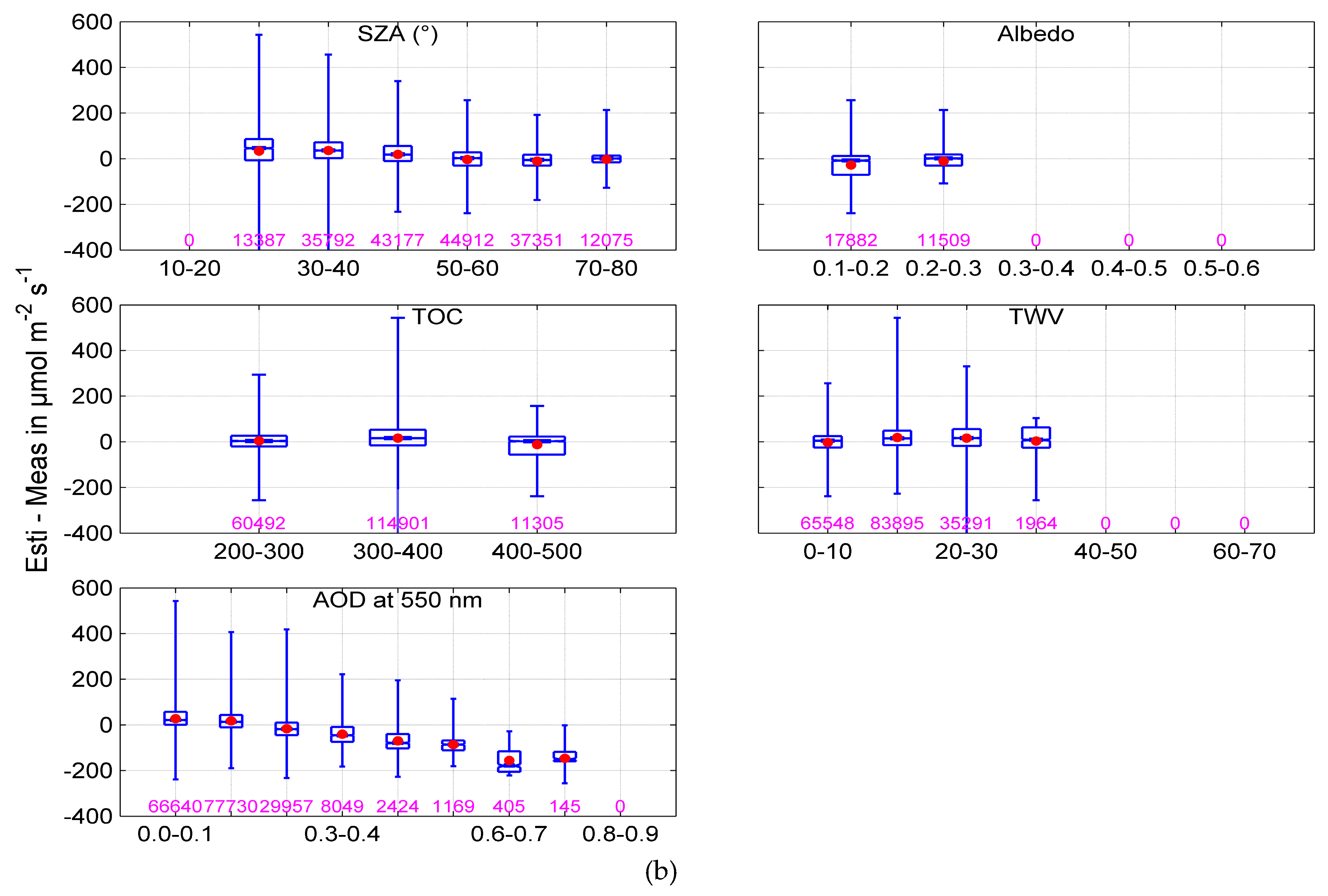
| Station | Fort Peck | Sioux Falls | Penn. Sate Univ | Table Mountain | Bondville | Desert Rock | Goodwin Creek |
|---|---|---|---|---|---|---|---|
| Code | FPK | SXF | PSU | TBL | BND | DRA | GCM |
| Latitude (°) | 48.31 | 43.73 | 40.72 | 40.12 | 40.05 | 36.62 | 34.25 |
| Longitude (°) | −105.10 | −96.62 | −77.93 | −105.24 | −88.37 | −116.02 | −89.87 |
| Elevation amsl * (m) | 634 | 473 | 376 | 1689 | 213 | 1007 | 98 |
| NCLP ** | 186,698 | 245,355 | 120,097 | 260,509 | 196,871 | 603,727 | 230,420 |
| KB | Interval Δλ, µm | Sub-Interval NBi, µm (#i) | Direct | Global | ||
|---|---|---|---|---|---|---|
| Slope | Intercept | Slope | Intercept | |||
| 6 | 0.363–0.408 | 0.385–0.386 (#1) | 0.9987 | −0.0023 | 1.0030 | −0.0032 |
| 7 | 0.408–0.452 | 0.430–0.431 (#2) | 1.0026 | −0.0004 | 0.9995 | 0.0013 |
| 8 | 0.452–0.518 | 0.484–0.485 (#3) | 1.0034 | 0.0005 | 0.9979 | 0.0000 |
| 9 | 0.518–0.540 | 0.528–0.529 (#4) | 0.9998 | −0.0005 | 1.0008 | −0.0013 |
| 10 | 0.540–0.550 | 0.545–0.546 (#5) | 1.0001 | 0.0003 | 1.0003 | −0.0003 |
| 11 | 0.550–0.567 | 0.558–0.559 (#6) | 1.0004 | 0.0004 | 0.9997 | 0.0012 |
| 0.569–0.570 (#7) | 0.9960 | −0.0119 | 1.0024 | −0.0100 | ||
| 12 | 0.567–0.605 | 0.586–0.587 (#8) | 1.0123 | 0.0064 | 0.9929 | 0.0267 |
| 0.589–0.590 (#9) | 0.9568 | −0.0109 | 0.9804 | −0.0434 | ||
| 0.602–0.603 (#10) | 1.0150 | 0.0167 | 1.0051 | 0.0212 | ||
| 13 | 0.605–0.625 | 0.615–0.616 (#11) | 1.0004 | 0.0009 | 0.9977 | 0.0033 |
| 0.625–0.626 (#12) | 1.0104 | −0.0174 | 1.0622 | −0.0551 | ||
| 14 | 0.625–0.667 | 0.644–0.645 (#13) | 1.0072 | 0.0029 | 0.9960 | 0.0154 |
| 0.656–0.657 (#14) | 0.9915 | 0.0068 | 0.9698 | 0.0205 | ||
| 15 | 0.667–0.684 | 0.675–0.676 (#15) | 1.0006 | 0.0007 | 0.9978 | 0.0036 |
| 0.685–0.686 (#16) | 1.0473 | 0.0212 | 0.9681 | 0.1036 | ||
| 16 | 0.684–0.704 | 0.687–0.688 (#17) | 0.9602 | −0.0130 | 1.0041 | −0.0531 |
| 0.694–0.695 (#18) | 0.9828 | −0.0153 | 1.0323 | −0.0642 | ||
| 17 | 0.704–0.743 | 0.715–0.716 (#19) | 1.0262 | 0.0121 | 0.9771 | 0.0596 |
| Station | N | Mean | Bias | RMSD | rBias (%) | rRMSD (%) | R2 |
|---|---|---|---|---|---|---|---|
| Fort Peck | 186,698 | 1262 | 11 | 58 | 1 | 5 | 0.98 |
| Sioux Falls | 245,355 | 1247 | 1 | 53 | 0 | 4 | 0.98 |
| Penn. State Univ | 120,097 | 1273 | 61 | 82 | 5 | 6 | 0.98 |
| Table Mountain | 260,509 | 1263 | 50 | 69 | 4 | 5 | 0.99 |
| Bondville | 196,871 | 1257 | 36 | 74 | 3 | 6 | 0.97 |
| Desert Rock | 603,727 | 1424 | −12 | 37 | −1 | 3 | 0.99 |
| Goodwin Creek | 230,420 | 1320 | 42 | 70 | 3 | 5 | 0.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wandji Nyamsi, W.; Blanc, P.; Augustine, J.A.; Arola, A.; Wald, L. A New Clear-Sky Method for Assessing Photosynthetically Active Radiation at the Surface Level. Atmosphere 2019, 10, 219. https://doi.org/10.3390/atmos10040219
Wandji Nyamsi W, Blanc P, Augustine JA, Arola A, Wald L. A New Clear-Sky Method for Assessing Photosynthetically Active Radiation at the Surface Level. Atmosphere. 2019; 10(4):219. https://doi.org/10.3390/atmos10040219
Chicago/Turabian StyleWandji Nyamsi, William, Philippe Blanc, John A. Augustine, Antti Arola, and Lucien Wald. 2019. "A New Clear-Sky Method for Assessing Photosynthetically Active Radiation at the Surface Level" Atmosphere 10, no. 4: 219. https://doi.org/10.3390/atmos10040219
APA StyleWandji Nyamsi, W., Blanc, P., Augustine, J. A., Arola, A., & Wald, L. (2019). A New Clear-Sky Method for Assessing Photosynthetically Active Radiation at the Surface Level. Atmosphere, 10(4), 219. https://doi.org/10.3390/atmos10040219





