Abstract
High frequency aircraft observations from the Government Flying Service of the Hong Kong Government, penetrating a tropical cyclone at low altitude over the South China Sea, were thinned by arithmetic means over different time intervals to identify structures of tropical cyclone at different scales. It is found that the thinning process can reduce serial correlation in observational errors and enhance the representation of aircraft observations. Assimilation experiments demonstrate that aircraft observations can improve the track and intensity forecasts of Typhoon Nida (2016). The changes in dynamic structures indicate that the imbalance generated from assimilating aircraft observations at the sub-grid scale can be alleviated by using longer time intervals of the arithmetic mean. Assimilating aircraft observations at the grid scale achieves optimal forecasts based on verifications against independent observations and investigations of environmental and ventilation flows. In addition, it is indicated that decreasing the quality control threshold and changing the observational error of aircraft observations in the data assimilation can reduce the representation errors.
1. Introduction
Although weather forecasts for tracks of tropical cyclones have improved over the last decades [1], predicting tropical cyclone intensity based on their inner core structures has improved more slowly [2], and forecasts of maximum surface wind and precipitation after landfall have limited predictability. Therefore, observations containing inner core structures of tropical cyclones should be assimilated to improve the initial conditions for numerical weather models.
By providing a mechanism to compare satellite and radar observations, the aircraft platform is effective for understanding intensity change and precipitation during the entire life of tropical cyclones [3]. Furthermore, the assimilation of targeted dropsonde observations deployed by Dropwindsonde Observations for Typhoon Surveillance near the Taiwan Region (DOTSTAR; [4]) has provided improved initial position and subsequent track forecast compared with experiments that only assimilate conventional observations [5]. In the western Atlantic Ocean, a number of studies [6,7,8,9] proved that assimilating observations penetrating tropical cyclones can result in better predictions of intensity due to improvements of their inner core structures. Averaged over all 102 applicable airborne Doppler missions for 22 Atlantic storms from 2008 to 2012, errors in forecast intensity for lead times of 2–4 days were 25–28% less than the corresponding official forecasts issued by the National Hurricane Center [10]. A total of 83 cases (20 individual tropical cyclones (TCs)) during 2008–2011 have shown statistically significant improvements in track and intensity forecasts by assimilating high density observations from an aircraft platform [11]. Unfortunately, to our knowledge, limited studies have been reported relating to assimilation of aircraft observations penetrating tropical cyclones over the South China Sea or western Pacific Ocean, locations of the most tropical cyclones worldwide. In fact, the west Pacific had access to aircraft observations penetrating tropical cyclones, but these observations stopped in 1987.
Recently, flight missions penetrating tropical cyclones over the South China Sea were launched by the Government Flying Service of the Hong Kong Government. A high sampling frequency instrument, Aircraft Integrated Meteorological Measuring System 20 Hz (AIMMS20), was equipped on a Jetstream 4100 (J41) fixed-wing aircraft. The records of AIMMS20 were used to compute and analyze the wind spectrum and turbulence intensity, such as eddy dissipation rate (EDR), at various locations from the center of tropical cyclones [12]. By analyzing vertical momentum diffusivity of four eye wall penetrations, Sparks et al. [13] found a super linear relationship between diffusivity and wind speed at the high wind speeds in the inner core of tropical cyclones, while the few existing boundary layer tropical cyclone observations in the North Atlantic suggest a more linear relationship. Furthermore, the data are also valuable for regional numerical weather prediction when tropical cyclones occur over the South China Sea, because the details of those inner core structures observed by J41 cannot be provided by any other observation platform or global forecast. Although AIMMS20 is a flight level probe, its quality control is much easier than remoting observations penetrating tropical cyclones, such as Tail Doppler Radar [14].
However, instruments with a high sampling frequency, such as AIMMS20, are likely to have serially correlated observation errors (red in time series). When the serial correlation in observational errors is ignored, the data assimilation scheme will degrade to a sub-optimal analysis [15,16]. Liu and Rabier [17] also revealed that using high density observations might produce false large increments and degrade the analysis in a practical four-dimensional variational data assimilation system. Thus, identifying ways to reduce serial correlation in observational errors and enhance representativeness of aircraft observations is an important step forward in assimilation of aircraft observations.
In this study, understandings of performing data thinning on aircraft observations and its impacts on data assimilation are based on the results of Typhoon Nida (2016), whose intensity forecasts issued officially by the China Meteorology Administration (CMA) displayed large biases in surface wind and precipitation. The remaining article is organized as follows. Section 2 describes the thinning process used on aircraft observations and the numerical weather prediction system, including the weather model and data assimilation method. The experiments are described in Section 3. Evaluations on the posterior ensemble mean and verifications against independent observations are provided in Section 4. Finally, the discussion and conclusions are given in Section 5 and Section 6, respectively.
2. Data and Methodology
2.1. Aircraft Observations
This flight mission for Typhoon Nida, penetrating an eye of tropical cyclone in the South China Sea, lasted approximately 2.5 h; the path is shown in Figure 1. Aircraft J41 departed from Hong Kong at around 0700 UTC and flew north of the center of Nida within the first hour. It then penetrated the center at about 1000 m altitude from 0750 UTC to 0822 UTC, while the eye was covered by clouds, as indicated by the brightness temperature observed by the Visible and Infrared Spin Scan Radiometer (VISSR) (10.3–11.3 μm) on the Fengyun satellite (FY2G) (Figure 1). The green wind barbs, illustrating Nida’s cyclonic circulation observed by J41, are supplementary observations of the inner core structures, because the infrared observations from the FY2G satellite cannot penetrate the clouds and ground-based radar stations were too distant. In addition to horizontal wind, low level pressure and temperature were also collected by AIMMS20; these observations can better discern Nida’s inner core structures in data assimilation, despite only one penetration across the tropical cyclone eye.
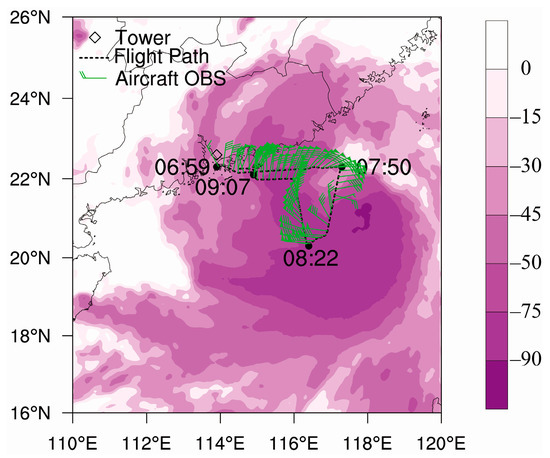
Figure 1.
The flight path of aircraft J41 (black dash line) with time stamps (dots), thinned aircraft observations (green wind barbs), and brightness temperature from FY2G (shaded, unit: K) at 0800 UTC on 1 August 2016. The diamond represents the position of tower observations.
Observations from J41 can describe tropical cyclone structures from synoptic scale to turbulence because of the high temporal resolution of AIMMS20. To illustrate multiscale structures in aircraft observations, we computed several diagnostics based on 30 s moving average. The mean value is computed by 30 s moving average, denoted by an overbar, and its fluctuating value is denoted by a superscript prime. Then, vertical turbulent flux of potential temperature, denoted by T, and turbulent kinetic energy, denoted by TKE, are computed by Equations (1) and (2), respectively.
where θ is potential temperature; and u, v, and w represent three components of wind velocity. The 30 s averaged horizontal wind speed shows inner core structures of Typhoon Nida, including maximum wind occurring in the eye wall and the rain band and minimum wind located at the eye (Figure 2a). In addition to the mesoscale features of tropical cyclones, the distribution of vertical turbulent flux of potential temperature in Figure 2b presents the dramatic vertical heat transports in the rain band where convection and turbulence are robust. The distribution of TKE in Figure 2c also demonstrates that turbulence is very active when J41 penetrated the rain band.
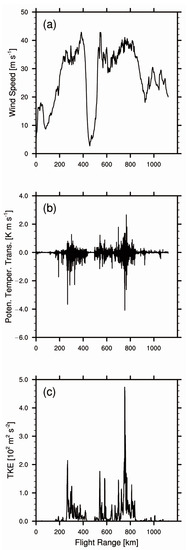
Figure 2.
(a) The mean horizontal wind speed (unit: m s−1), (b) the vertical turbulent flux of potential temperature (unit: K m s−1), and (c) the turbulent kinetic energy (unit: 102 m2 s−2) after 30 s moving average.
Data assimilation scheme leads to a sub-optimal analysis if it assimilates observations with correlated errors as if they were uncorrelated [18]. To describe the serial correlation in aircraft observations, we computed several time lagged autocorrelations of aircraft observations after 30, 60, 90, 120, and 150 s moving average in Figure 3. The autocorrelations of u wind, v wind, and potential temperature slowly decrease to approximately 0.65 when the lagged time increases to 600 s, which is rather larger than a threshold correlation value 0.15 between two adjacent observations [12]. Thus, the serial correlation in observation errors is robust in aircraft observations. In addition, there is no significant correlation in vertical wind unless the lagged time is shorter than 120 s. The long lagged time might reduce the features associated with robust vertical movements, such as convection and turbulence.
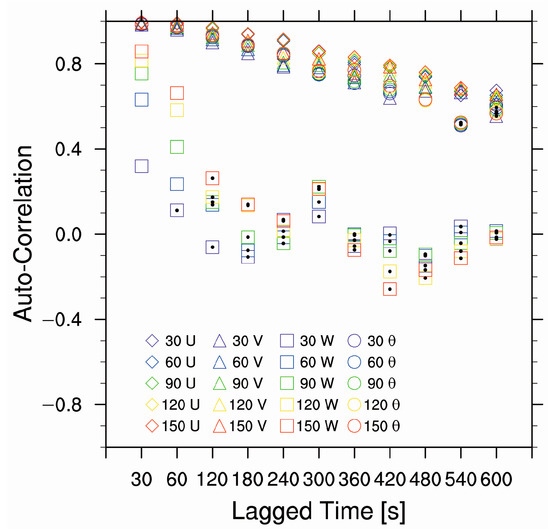
Figure 3.
Several time lagged autocorrelations after 30, 60, 90, 120, and 150 s moving average. Hollow diamonds, squares, triangles, and circles represent u wind, v wind, w wind, and potential temperature, respectively. Black dots mean reject by 99% confidence.
The arithmetic mean was used as a data thinning method to produce super observations [19]. In the following subsections, we also used arithmetic mean to reduce the representative error and serial correlation in aircraft observations instead of moving average because (1) assimilating thousands of aircraft observations in a small area has an extremely low computational efficiency in ensemble data assimilation; and (2) filter divergence could be a serious issue when high density observations are assimilated, because we only generated 60 ensemble members. It then becomes of interest to examine the properties of aircraft observations thinned by the arithmetic mean.
To examine the best time to assimilate aircraft observations, the root mean square errors (RMSEs) computed between the priors and averaged horizontal wind are shown in Figure 4. It is found that the minimum RMSEs occur at 0800 UTC regardless of the time interval of the arithmetic mean (Figure 4a,b). In contrast, minimum RMSEs for temperature and pressure could be at either 0800 or 0900 UTC, even at 0700 UTC for pressure, which depends on the time interval (Figure 4c,d). Therefore, we can conclude that u and v wind are more consistent with priors than temperature and pressure. Furthermore, to avoid deformation of the tropical cyclone’s circulation, we assimilated u and v wind at 0800 UTC.
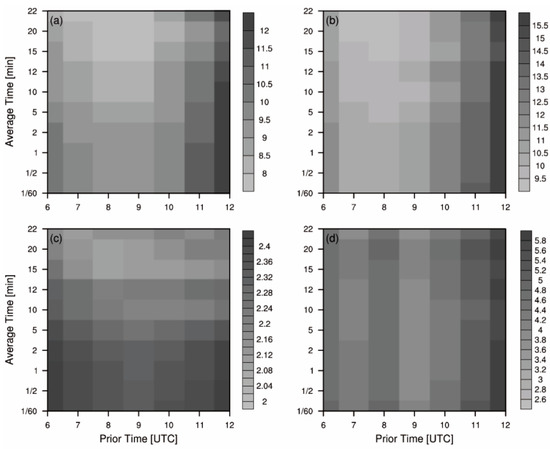
Figure 4.
Root mean square errors (RMSEs) of (a) u (unit: m s−1), (b) v (unit: m s−1), (c) temperature (unit: °C), and (d) pressure (unit: hPa) between priors and observations averaged over different time intervals at various times.
Figure 5 demonstrates that spatial intervals between aircraft observations can increase from several kilometers to over 100 km when different time intervals are used for the arithmetic mean. The maximum wind speed averaged over 1 s is nearly 50 m s−1, which indicates the Typhoon Nida’s intensity at the 100-m scale (Figure 5). A short (long) time interval for arithmetic mean leads to a high (low) spatial resolution (Figure 5) and a small (large) variance used as the observational error in this study (Table 1), which can reveal the strong (weak) intensity of tropical cyclone and significant (insignificant) serial correlation in aircraft observation errors. We can also find in Table 1 that variances for pressure rapidly increase with time intervals. The representation of pressure becomes poor in long time intervals. For data assimilation, a small observational error corresponds to a greater weight of observations in the analysis, and vice versa. The subsequent track and intensity forecasts could be closely related to the time interval of the arithmetic mean. Therefore, it is important to identify an optimal time interval length that provides a better representation of aircraft observations, as posterior errors of ensemble data assimilation closely depend on the tropical cyclone advection velocity and spatial interval between observations with high frequency that have serially correlated errors [16].
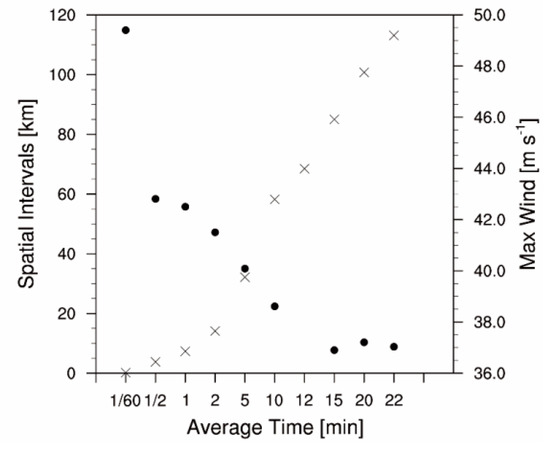
Figure 5.
Spatial intervals (crosses; unit: km) and maximum winds (dots; unit: m s−1) of aircraft observations averaged over different time intervals.

Table 1.
Observation errors (variances) when aircraft observations are averaged over different time intervals.
The distributions of horizontal wind speeds averaged over 1 s, 2 min, 12 min, and 22 min are shown in Figure 6. Despite the decrease in maximum horizontal wind speed, the patterns of aircraft observations averaged over 1 s and 2 min are consistent with the wind speed in Figure 2. In comparison with the wind speed in Figure 2, distributions of horizontal wind averaged over 12 and 22 min cannot describe the quasi stationary wind speed in the tropical cyclone center or maximum wind speed in the eye wall, because their spatial intervals are too large. Similar conclusions are found when comparing temperature and pressure data. High temperature and low pressure in the tropical cyclone center are over-smoothed in 12 and 22 min averages (figures omitted).
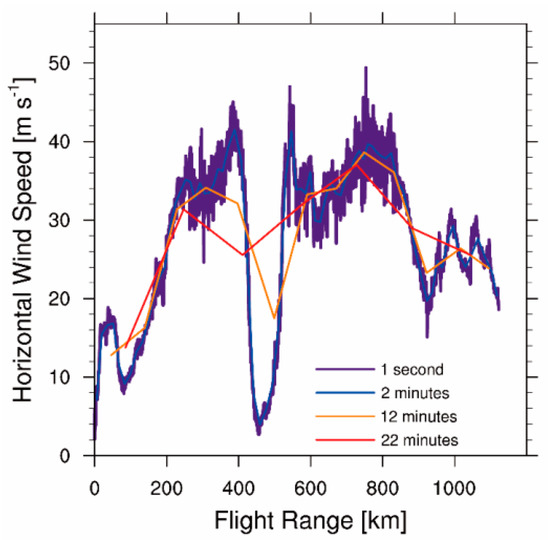
Figure 6.
Distributions of horizontal wind speeds (m s−1) along the flight path. The purple, blue, orange, and red lines represent the aircraft observations averaged over 1 s, 2 min, 12 min, and 22 min, respectively.
2.2. Independent Observations
To verify and evaluate track and intensity forecasts, the best-track data [20] produced by the Shanghai Typhoon Institute of the CMA was used in this study, which is a postseason analysis dataset included in the International Best Track Archive for Climate Stewardship (IBTrACS) project [21]. The composite radar reflectivity, i.e., the constant altitude plan position indicator (CAPPI), at 3 km altitude produced by the Guangdong Meteorology Service was also used to verify the precipitation forecasts and hydrometeors when Nida approached the south coast of China. This CAPPI dataset is a real-time product merged from 11 radars near to the Pearl River Delta, including that at the Hong Kong Observatory, which covers the offshore areas at 0.01° resolution. The highest tower observation in Asia near a reservoir (22.62 °N 113.9 °E), which is indicated with a diamond in Figure 1, recorded the pressure evolution during the landfall of Typhoon Nida. The tower observation was used to evaluate the intensity forecasts, because it was the only in situ measurement without terrain interference. The brightness temperature collected by VISSR on the FY2G was used to identify the cloud area of tropical cyclone.
The Global and Regional Assimilation and Prediction System (GRAPES) developed by the Research Center for Numerical Meteorological Prediction of Chinese Academy of Meteorological Sciences of CMA is a next-generation non-hydrostatic multi-scale community model based on fully compressible atmospheric equations [22]. A semi-implicit semi-Lagrangian algorithm, including vector discretization, and latitude–longitude grid points with horizontal Arakawa C staggering are used in GRAPES. A terrain following height coordinate discretized using Charney–Phillips staggering is used in the vertical direction. A three-dimensional reference profile for atmosphere that does not change with time and satisfies the hydrostatic balance is used to reduce the large perturbations in dimensionless pressure and potential temperature. This technology decreases the nonlinear terms and thus improves the time integration accuracy [23]. Various physical parameterizations, including the simplified Arakawa–Schubert convection scheme [24], single-moment six-class microphysics with graupel [25], Medium-Range Forecast for nonlocal planetary boundary layer process [26], and Rapid Radiative Transfer Model [27], are used in the GRAPES model.
In previous studies [28,29], the ensemble Kalman filter, utilizing the flow-dependent covariance estimated using short-range ensemble forecasts to present “errors of the day” [30,31], has been successfully used to assimilate aircraft observations. Provided that the model and observational errors are known and not serially correlated, although could be spatially correlated, the optimal posteriors of the Ensemble Square Root Filter (EnSRF) are as follows [32]:
where:
where the superscripts a and b in Equations (3) and (4) represent the posterior and prior vectors, respectively; and are the ensemble mean and perturbation of the model variables, respectively; and are the gain matrices for the ensemble mean and perturbation, respectively; Superscripts −1 and T in Equations (5) and (6) represent the inverse and transport of matrix, respectively; is the covariance of the priors, which can be computed directly using an ensemble forecast; , the covariance of observational error, is a diagonal matrix because the observational errors are assumed to be uncorrelated in space and time. The EnSRF will thus degrade to a sub-optimal scheme by producing a falsely large increment for correlated aircraft observations in this study. The forward operator , which interpolates the model variables to observational locations, is linear in this study. However, can be a nonlinear operator, such as radar reflectivity [33], because it is not applied to , but to the model variables individually.
The most efficient computation for Equations (3) and (4) has to assimilate the observations one at a time. Then, there is no need to compute the inverse or square root of matrices because the gain matrix reduces to a scalar. The covariance relaxation [34] is also used to inflate the ensemble priors of the analysis. To eliminate the false correlation estimated from the finite ensemble members, a compact fifth-order polynomial [35] is used to localize the aircraft observation information in horizontal direction. When assimilating the data, a quality control threshold for observations is usually used to prevent large increment posteriors, which might lead to an imbalance in initial conditions. Then, an observation should not be assimilated in this study if the absolute difference between the observation and priors is larger than a product of quality control threshold and observational errors.
3. Experiments
3.1. Control Experiment
A single 433 × 322 mesh with a 0.09° horizontal grid size from a left corner point at (97 °E, 5 °N) was set as the model domain of GRAPES for all experiments. This area was configured with a vertical structure of 65 unequally spaced sigma (terrain following height) levels from the surface to 32,000 m (about 13.48 hPa). Initial and boundary conditions in all simulations were taken from the European Centre for Medium Range Weather Forecasts (ECMWF) with a 0.125° horizontal resolution and 17 vertical layers from 1000 to 10 hPa. An ensemble with 60 members was generated using randomly balanced perturbations from a GRAPES three-dimensional variational assimilation based on a global analysis and forecasts. An 8-h GRAPES ensemble forecast with multiple convective parameterizations (simplified Arakawa–Schubert scheme for members 1–20, Betts–Miller–Janjić scheme for members 21–40, and Kain–Fritsch scheme for members 41–60) from 0000 UTC to 0800 UTC on 1 August provided the “errors of the day” in priors for EnSRF. Then, a 24-h deterministic forecast driven by the ensemble mean at 0800 UTC without data assimilation was taken as the control experiment, termed “NE” in Table 2, which was distinguished from experiments after assimilating aircraft observations.

Table 2.
Summary of experiments. The first and second columns are the experiment name and resolution of observation, respectively. The quality control threshold is in the third column. In the last column, the letters Y and N indicate if the observational error has changed.
3.2. Data Assimilation Experiments
Several data assimilation experiments were conducted, as listed in Table 2. We selected aircraft observations averaged over 1 s (E1S), 2 min (E2M), 12 min (E12M), and 22 min (E22M) to illustrate the tropical cyclone structures at the sub-grid scale (0.1 times the grid size), grid scale, resolvable scale (5 times the grid size), and super-grid scale (10 times the grid size) and discuss their impacts on EnSRF and subsequent forecasts. The corresponding spatial resolutions are provided in Table 2. For each experiment, the same 60 ensemble members in experiment NE were used as the priors for EnSRF.
We assumed that all aircraft observations were obtained at the same time in this study, as Typhoon Nida moved approximately 65 km (about 6 grid spaces) from 0700 UTC to 0900 UTC. Therefore, there is only one data assimilation cycle at 0800 UTC in this study. In addition, temperature and pressure observations are highly related to the flight altitude, because variations due to lapse rate with altitude may be larger than those caused by Typhoon Nida. The track and intensity forecasts then could worsen after assimilating temperature and pressure. Thus, only results using assimilation of u and v wind are discussed in the following sections.
3.3. Sensitivity Experiments
The combination of the quality control threshold (Table 2, column 3) and observational error can also affect the posterior error in EnSRF. To compare the effects of the arithmetic mean, the quality control threshold decreased to 2 in experiment E1S_qc2, wherein the weight of 1 s average aircraft observations in EnSRF decreases by lowering the number of observations. Augmenting the observational error can also reduce the observation weight, which also smooths the analysis, but more observations will be assimilated if the same quality control threshold is used. To evaluate the effect of augmenting observational error in assimilating aircraft observations, the observational error estimated for 1 s was replaced by that estimated for 22 min in experiment E1S_err. The differences and similarities in posteriors and subsequent forecasts between data assimilation experiments and sensitivity experiments are illustrated by comparing the results of these experiments; their comprehensive configurations are described in Table 2.
4. Results
4.1. Typhoon Nida Structures in the Posterior Ensemble Means
Figure 7 shows distributions of model-derived raw horizontal wind speeds with high frequency in the posterior ensemble means. By comparing the counterparts in the control experiment, it is clear that the horizontal wind speeds in all data assimilation experiments strengthen in the rain band and weaken in the eye of Typhoon Nida. The cyclonic circulation is enhanced by assimilating the aircraft observations. The distribution of model-derived horizontal wind speed in experiment E1S resembles the wind speed in Figure 2 because a small observational error was used. Despite the growth in intensity, the model-derived horizontal wind speeds after assimilating the wind structures in the resolvable scale (experiment E12M) and super-scale (experiment E22M) are similar to the pattern in experiment NE, rather than resembling the wind speed in Figure 2. The results from experiment E2M show enhanced horizontal wind speed in the eye wall and rain band, while also retaining the inner core structures. The distributions of model-derived horizontal wind speeds smooth with longer time intervals of the arithmetic mean, which outline different initial conditions for the tropical cyclone structures.
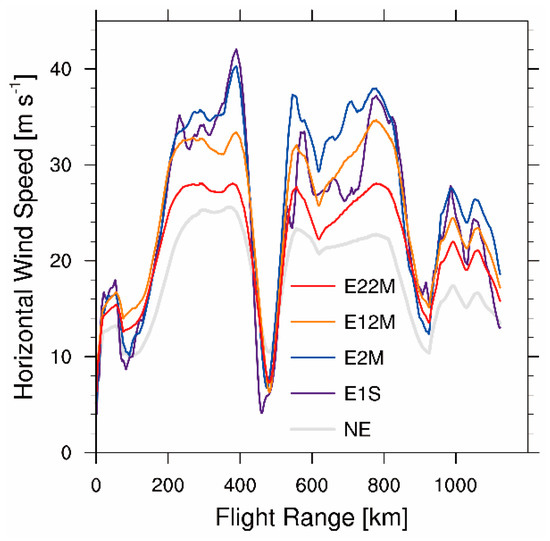
Figure 7.
Model-derived horizontal wind speeds (unit: m s−1) of raw observations computed using the posterior ensemble means. The gray line represents the experiment NE. The purple, blue, orange, and red lines represent experiments E1S, E2M, E12M, and E22M, respectively.
As shown in Table 3, the averaged RMSEs for u and v wind in these four data assimilation experiments clearly decline in comparison to experiment NE. Although the observational error in experiment E1S is the smallest among data assimilation experiments, experiment E2M achieves smaller RMSEs for u and v wind than experiment E1S. Thus, the tropical cyclone structures at the sub-grid scale are inappropriate for EnSRF with the 0.09° grid size covariance, because the linear combination of nonlinear components (sub-grid scale) in the priors results in a dynamic posterior imbalance in the nonlinear model [18]. The RMSEs for temperature and pressure in experiments E2M, E12M, and E22M also decrease, even when the temperature and pressure observations are not assimilated. This result demonstrates that the observations at greater than the grid scale appropriately propagate the information of cyclonic circulation to the temperature and pressure. However, the RMSEs for temperature and pressure increase in experiment E1S because observations do not propagate correctly at the sub-grid scale.

Table 3.
Averaged root mean square errors (RMSEs) of u and v wind, temperature, and pressure between posteriors and original aircraft observations in all experiments.
To further investigate the impact of thinning aircraft observations on the secondary circulation of tropical cyclone, Figure 8 shows the azimuthally averaged tangential and radial wind of the posterior ensemble mean. A weak secondary circulation in experiment NE consists of a shallow inflow and deep outflow to maintain the mass flux balance. Although the inflow and outflow clearly increase in experiment E1S, the secondary circulation inside the 100 km radial range is violated by providing a false account of the information at the sub-grid scale. This result can be also explained by the assumption in the EnSRF: A significant correlation between errors in the 1 s average aircraft observations reduces the information content from each observation and produces a falsely large increment, leading to a sub-optimal analysis for experiment E1S. The secondary circulations in experiment E12M and E22M also increase slightly when compared to that in experiment NE. The strong and smooth secondary circulation, corresponding to an improved intensity forecast, is produced by assimilating observations at the grid scale (in Figure 8c). The strongest tangential wind among data assimilation experiments, increasing to about 36 m s−1, is produced by experiment E2M. Thus, assimilation of aircraft observations at the grid scale both strengthens the horizontal rotation of tropical cyclone and adjusts the secondary circulation without extra noise related to observations at the sub-grid scale.
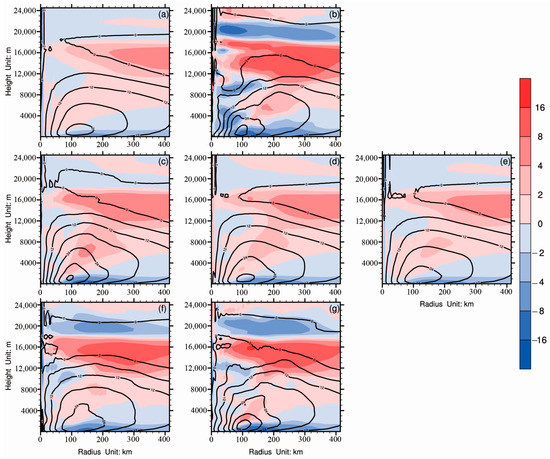
Figure 8.
Azimuthally averaged vertical cross-sections of tangential (black contours; unit: m s−1) and radial (shaded; unit: m s−1) wind at the analysis time computed by the posterior ensemble means in experiment (a) NE, (b) E1S, (c) E2M, (d) E12M, (e) E22M, (f) E1S_qc2, and (g) E1S_err.
To further demonstrate the imbalance problem generated from assimilating high resolution observations, the 6-h evolutions of the 5-min surface pressure trends averaged over the model domain are illustrated in Figure 9. The surface pressure trends in experiment E1S increase rapidly in the first 0.5 h, and GRAPES requires approximately 180 minmodel integration to adjust the noise to a dynamic balance. In this study, assimilating the observations averaged over 1 s is detrimental to the subsequent forecast, because the information at the sub-grid scale is misrepresented by the 0.09° grid size covariance. In contrast, the surface pressure trends in other data assimilation experiments decrease continually with some small fluctuations within 120 min. These relatively smooth evolutions in surface pressure trends describe the initial conditions after assimilating observations at either the grid or super-grid scale better fit the 0.09° grid size GRAPES. Divergence adjustment procedure or digital filter are often used to represent the model dynamical balance constraints for the analysis of EnKF [36]. By investigating Figure 9, we demonstrate that thinning observations, which have higher resolution than model grid size, can alleviate this issue as well.
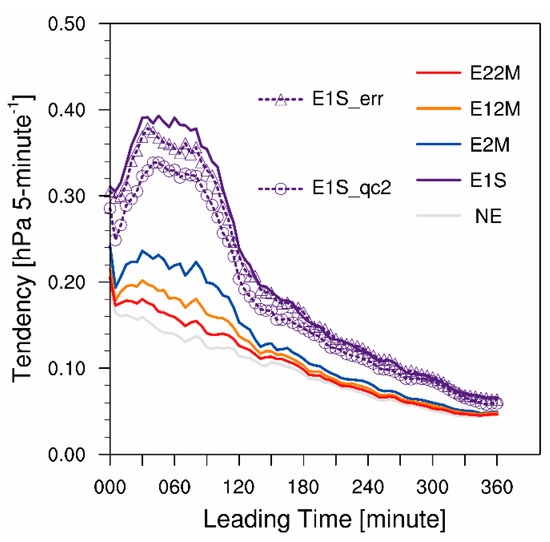
Figure 9.
Evolution of 5-min surface pressure trends (unit: hPa 5min−1) averaged over the whole model domain, initialized using the posterior ensemble mean.
4.2. Verifications Against Independent Observations
The most efficient way to evaluate the initial condition is to verify its subsequent forecasts against independent observations. Figure 10 compares the track and intensity forecasts with the best track data. In comparison with experiment NE, all track forecasts show improvements once aircraft observations are assimilated, except experiment E1S. The track forecast in experiment E1S exhibits an irregular swing in the first few hours, so that its northward movement is overpredicted due to the imbalance from information at the sub-grid scale. The northward bias in the track forecast decreased remarkably by assimilating aircraft observations at the grid size scale. In Figure 10b, the evolution in the track error from experiment E2M is smaller than other data assimilation experiments. Thus, assimilating aircraft observations at appropriate scales can decrease noise in the initial conditions and improve track forecasting. Notably, maximum wind speed and minimum sea level pressure also improved by assimilating aircraft observations. At the analysis time, the maximum wind speed in experiment E1S reaches 44 m s−1, much stronger than the best track data, but its minimum sea level pressure is 983 hPa, similar to experiment NE and weaker than the best track data. This inconsistency between maximum wind speed and minimum sea level pressure also results from noise at the sub-grid scale. The rapid decrease in maximum wind speed in the first 4 h demonstrates that GRAPES needs a few hours to dissipate the inappropriate tropical cyclone structures at the sub-grid scale. Experiment E12M clearly shows the best intensity forecast among the data assimilation experiments. The maximum wind speed in experiment E12M shows a similar evolution to the best track data, despite the disagreement in the forecast minimum sea level pressure, indicating a stronger intensity forecast.

Figure 10.
(a) Track forecasts, (b) errors in track forecasts (unit: km), (c) maximum surface winds (unit: m s−1), and (d) minimum sea level pressures (unit: hPa) for Typhoon Nida in the control experiment and data assimilation experiments. The black dashed lines represent the best track data.
To objectively examine the intensity forecasts, Figure 11 shows the verification against the pressure at 50 m detected by a tower in Shenzhen City, indicated with a diamond in Figure 1. The evolution of pressure observed by the tower declined to about 973 hPa when Nida passed Shenzhen City. The evolution in model-derived pressures from experiments E1S and NE share the same features. In contrast, the results from experiments E2M and E12M are more similar to the tower observations. Thus, the assimilation of aircraft observations at the grid or resolvable scale provide small RMSEs in posteriors and smooth and accurate initial conditions for the subsequent intensity forecast.
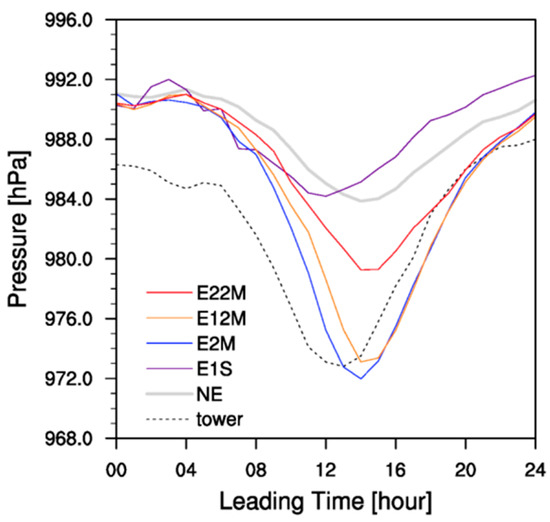
Figure 11.
The observed evolution in pressure (unit: hPa) at 50 m altitude at the tower and model-derived evolutions of pressure from experiments NE (gray line), E1S (purple line), E2M (blue line), E12M (orange line), and E22M (red line).
To show the impact of thinning aircraft observations on hydrometeors, the verification using CAPPI at 3 km from 1100 UTC on 1 August to 2000 UTC on 2 August is examined in Figure 12. The observations reveal that Typhoon Nida moved from the South China Sea and landed at Pearl River Delta with a clear eye and multiple rain bands (the first row in Figure 12). The model-derived CAPPI in experiment NE shows the weak rain bands and an incomplete eye wall in the first 12 h. Forecasts from experiment E1S show better cellular convection in the rain bands, but a poor eye wall near to the center of Typhoon Nida because of the false strong downdraft in Figure 8b. The corresponding results from experiment E2M exhibit an apparent eye and multiple rain bands after 6 h of simulation (Figure 12d2), instead of a sparse and fragmental distribution found in experiment E1S, though larger rain rates than observations in rain bands. In experiment E12M and E22M, where the spatial intervals of aircraft observations increased, the distributions of model-derived CAPPIs show less connection to observations compared with those from experiment E2M. Thus, assimilating aircraft observations at grid size scale can provide superior hydrometeors forecasts to other data assimilation experiments due to an appropriate secondary circulation of tropical cyclone.
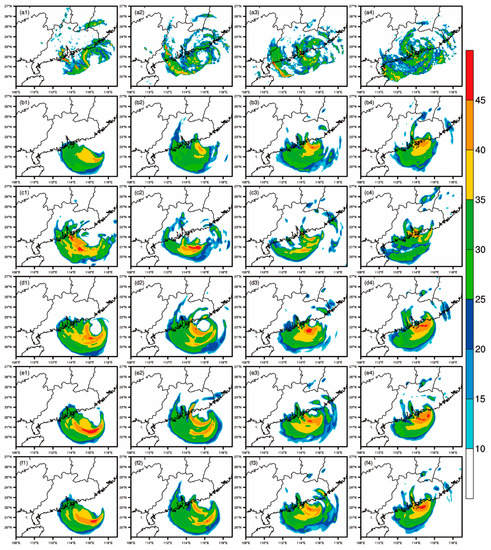
Figure 12.
CAPPI (unit: dBZ) at 3 km altitude at (a1) 1100, (a2) 1400, (a3) 1700, and (a4) 2000 UTC on 1 Aug 2016 and model-derived CAPPI in experiment NE (2nd row), E1S (3rd row), E2M (4th row), E12M (5th row), and E22M (6th row).
4.3. Sensitivity Experiments
Two sensitivity experiments were conducted to evaluate the effects of decreasing the quality control threshold and changing the observational error from assimilating the aircraft observations. Compared to experiment E1S, the averaged RMSEs for u and v wind are higher in experiment E1S_qc2 but lower in experiment E1S_err (Table 3). The risk of poor representativeness in the 1 s average aircraft observations is amplified by decreasing the number of observations in experiment E1S_qc2. However, decreasing the weight of observations by changing the observational errors results in lower RMSEs for u and v wind in experiment E1S_err because of the assumed uncorrelated observational errors in EnSRF. Although the secondary circulations in both experiments E1S_qc2 and E1S_err are contaminated by the sub-grid scale noise and serial correlation in aircraft observations (Figure 8f,g), the imbalance indicated by surface pressure trends was alleviated (Figure 9).
It is found in Figure 13 that the errors in track and intensity forecasts in experiments E1S_qc2 and E1S_err are lower than those in experiment E1S, but higher than those in experiment E2M. Reducing the weight given to aircraft observations by decreasing the number of observations and changing the observational error in the assimilated aircraft observations with high sampling frequency can improve the EnSRF analysis and its subsequent forecast, but still manifest inferior effects to the arithmetic mean.
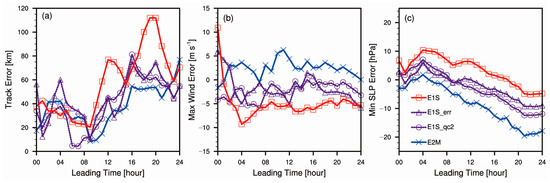
Figure 13.
Evolution in errors in (a) tracks (unit: km), (b) maximum surface winds (unit: m s−1), and (c) minimum sea level pressures (unit: hPa) computed using simulations after subtracting best track data.
5. Discussion
The objective verifications of the experiments in Section 4 show that thinning aircraft observations reduces errors in the posteriors of EnKF and improves the track and intensity forecasts for Typhoon Nida. In this section, we discuss what aspects are improved after assimilating aircraft observations by investigating dynamics and hydrometers of inner core structures of Typhoon Nida.
The mechanism for the movement of tropical cyclone over open water has been well studied: Environmental flow (steering flow), beta drift, and internal diabatic heating are the three main factors controlling the track of tropical cyclones [37,38]. The last factor is vital to intensity forecasting, but only the first two factors were investigated in this study. To better identify the components of tropical cyclone circulation that are improved by assimilating aircraft observations at 0800 UTC, the tangential and radial wind of the posterior ensemble mean averaged from 2 to 10 km in experiments NE and E2M were decomposed into the steering flow (wave number 0), axisymmetric (wave number 1), and asymmetric vortex structure (wave number 2) using Fourier decomposition as follows:
where:
where is the tangential or radial wind interpolated into the cylindrical coordinates centered at the tropical cyclone center with a 0.5° azimuthal interval and 6 km radial grid size; and and , respectively, represent the wave number and number of samples at each radial coordinate. Here, Equation (8) is the wave number 0.
After Fourier decomposition in cylindrical coordinates, the horizontal wind is transferred from tangential and radial wind and interpolated to Cartesian coordinates with a 6-km grid size. The steering flow in experiment NE is southeasterly, driving Typhoon Nida northwestward (Figure 14a1). After assimilating aircraft observations, the steering flow slows and shifts southward over the tropical cyclone center (Figure 14b1), leading to a decreasing track forecast error in experiment E2M. The asymmetric vortex structures in both experiments NE and E2M show a similar pattern, a pair of cyclonic and anticyclonic gyres, the cyclonic gyre to the northeast of Typhoon Nida and anticyclonic gyre to the southwest. Thus, ventilation flow passing the center of Typhoon Nida, between the pair of gyres, also leads the tropical cyclone to the northwest. However, the gyres in experiment E2M rotate anticlockwise around the tropical cyclone center (Figure 14b3), and the cyclonic (anticyclonic) one is located more toward the west (east) with the same intensity; therefore, there is a southward shift in ventilation flow. This evaluation of the steering and ventilation flows thus substantiates the improvement in track forecast shown in Figure 10a,b. In addition, in comparison with experiment NE, E2M shows an approximate 30 m s−1 rotation wind in Figure 14b2, because assimilating aircraft observations strengthens the axisymmetric structure of Typhoon Nida, which is consistent with the improved maximum wind forecast in Figure 10c.
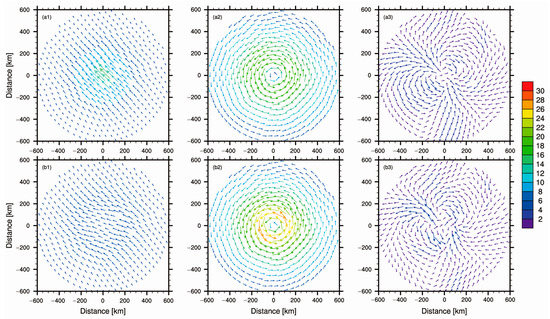
Figure 14.
Decompositions of horizontal wind (unit: m s−1) at analysis time averaged from 2 to 10 km in altitude for steering flow (1st column), axisymmetric vortex (2nd column), and asymmetric vortex (3rd column) generated by experiment NE (1st row) and E2M (2nd row).
Precipitation is influenced by hydrometeor physical processes, such as condensation, collision, and coalescence. Droplet growth by condensation can increase the chance of droplet colliding so that the rate of collision increases rapidly with size. Coalescence can become significant after the droplet spectrum evolves widely. Eventually, rain droplets are produced and grow by accretion [39]. Exploring the distributions of hydrometeors (Figure 15) can aid in understanding improvements in precipitation forecasts after assimilating aircraft observations. In comparison to results from experiment NE, the mixing ratios of hydrometeors in experiment E2M increase remarkably within a 400-km radial range, resulting in a clear eye wall, indicated by CAPPI in Figure 12. It is also found in Figure 15 that the increase in the mixing ratio of ice water at 12 km over the eye of tropical cyclone is consistent with the distribution of brightness temperature observed by FY2G (Figure 1), while the decrease in the mixing ratio of cloud water at approximate 1 km in the inner-eye area suggests a more intense secondary circulation, i.e., downdraft in eye and updraft in rain band (Figure 8c).
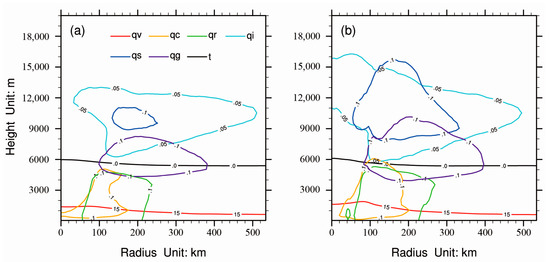
Figure 15.
Azimuthally averaged vertical cross sections of mixing ratio (unit: g/kg) of water vapor (red lines), cloud water (yellow lines), rain water (green lines), ice water (light blue lines), snow water (blue lines), and graupel water (purple lines) computed using the posterior ensemble means in experiments (a) NE and (b) E2M. The black lines represent the zero line of temperature (unit: °C).
6. Conclusions
J41 collected observations of the inner core structures of Typhoon Nida in the South China Sea, penetrating the center of tropical cyclone at low altitude for approximately 2.5 h. To reduce representative errors in aircraft observations, this study used the arithmetic mean over different time intervals to identify structures of tropical cyclone at different scales. The performances of the 0.09° grid size GRAPES model, driven by the posterior ensemble mean of all data assimilation experiments (Table 2), were evaluated using the dynamical structures of tropical cyclone and verified against independent observations. Furthermore, decreasing the quality control threshold and augmenting the observational error were also used to decrease the weight given to aircraft observations in the data assimilation.
In comparison with the control experiment, data assimilation experiments show that both horizontal cyclonic circulation and vertical secondary circulation are improved by assimilating aircraft observations. However, assimilating aircraft observations averaged over 1 s results in high frequency noise imposed on the secondary circulation, despite similarities in the model-derived raw observations, due to the small observational error in experiment E1S. The information at the sub-grid scale, which is misrepresented by the 0.09° grid size covariance, results in the largest errors in track and intensity forecasts among the data assimilation experiments. In contrast, experiment E2M, wherein thinned aircraft observations at the grid scale enhance the representation of inner core structures of Typhoon Nida, obtains superior track and intensity forecasts compared to other data assimilation experiments. Therefore, thinning aircraft observations using a 2-min arithmetic mean generates an appropriate posterior ensemble mean of EnSRF for the 0.09° grid size GRAPES model in terms of independent observations in this case study. More generally, data thinning has also been shown to provide improvements in satellite and radar assimilations for tropical cyclones [9,40].
To explain improvements indicated by independent observations, we investigated more refined dynamical structures and distribution of hydrometeors in posteriors of EnSRF than previous studies [10,11,41]. The decomposition of horizontal wind further illustrates that the decrease in track forecast error in experiment E2M results from the southward shift in both environmental and ventilation (anticlockwise rotation) flows. The distribution of hydrometeors in experiment E2M further confirms improvements in the model-derived CAPPI. This result is also consistent with the dynamical analysis, because the information contained by u and v wind at the grid scale propagates correctly to hydrometeors using the cross-variable covariance with a 0.09° grid size.
Two sensitivity experiments were performed to evaluate the impact of the aircraft observations, as the quality control threshold decreases and observational error increases. We found that these two methods can alleviate the imbalance in the posterior ensemble mean, similar to the impact of the arithmetic mean. Although the errors in track and intensity forecasts decreased in experiments E1S_qc2 and E1S_err when compared with experiment E1S, they are still inferior to those of experiment E2M. Therefore, the arithmetic mean over the grid size of model is recommended to reduce the serial correlation in observational errors and enhance the representation of observations with high sampling frequency.
Similar to previous achievements in the eastern Atlantic Ocean [3,8] this study confirms results that aircraft observations over the South China Sea play an important role in the progress of track and intensity forecasts of tropical cyclones. The conclusions based on data for Typhoon Nida suggest that thinning aircraft observations, which have higher resolution than model grid size, is necessary to achieve optimal posteriors and subsequent forecasts. Although intensity forecasts are improved by assimilating wind observations, radar reflectivity forecasts exhibit obvious errors in rain bands. Combination of in situ aircraft observations and other remoting observations should be assimilated to further evaluate their contributions to high impact weather. Further, research using additional case studies applied to different model grid sizes should be conducted to support these conclusions.
Author Contributions
Conceptualization, Y.G. and Q.W.; methodology, Y.G. and G.D.; validation, H.X. and D.J.; formal analysis, Y.G. and H.X.; investigation, Y.G. and D.J.; data curation, P.W.C. and K.K.H.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G. and P.W.C.; founding acquisition, Y.G., Q.W. and G.D.
Funding
This study was jointly funded by the National Key Research and Development Program of China (2017YFC1502001 and 2018YFC1506904), the National Natural Science Foundation of China (41705089 and 41475097), the Science and Technology Planning Project of Guangdong Province, China (2015B020217001 and 2017B020218003), the Natural Science Foundation of Guangdong Province, China (2016A030313140 and 2014A030313775), and the Special Fund for Meteorological Scientific Research in the Public Interest [GYHY201506005].
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Landsea, C.W.; Cangialosi, J.P. Have we reached the limits of predictability for tropical cyclone track forecasting? Bull. Am. Meteor. Soc. 2018, 99, 2237–2243. [Google Scholar] [CrossRef]
- Cavallo, S.M.; Torn, R.D.; Snyder, C.; Davis, C.; Wang, W.; Done, J. Evaluation of the Advanced Hurricane WRF Data Assimilation System for the 2009 Atlantic Hurricane Season. Mon. Weather Rev. 2013, 141, 523–541. [Google Scholar] [CrossRef]
- Aberson, S.D.; Black, M.L.; Black, R.A.; Cione, J.J.; Landsea, C.W.; Marks, F.D.; Burpee, R.W. Thirty years of tropical cyclone research with the NOAA P-3 aircraft. Bull. Am. Meteor. Soc. 2006, 87, 1039–1055. [Google Scholar] [CrossRef]
- Wu, C.C.; Chou, K.H.; Lin, P.H.; Aberson, S.D.; Peng, M.S.; Nakazawa, T. The impact of dropwindsonde data on typhoon track forecasts in DOTSTAR. Weather Forecast. 2007, 22, 1157–1176. [Google Scholar] [CrossRef]
- Jung, B.J.; Kim, H.M.; Zhang, F.; Wu, C.C. Effect of targeted dropsonde observations and best track data on the track forecasts of Typhoon Sinlaku (2008) using an Ensemble Kalman Filter. Tellus A 2012, 64, 14984. [Google Scholar] [CrossRef]
- Pu, Z.; Li, X.; Sun, J. Impact of Airborne Doppler Radar Data Assimilation on the Numerical Simulation of Intensity Changes of Hurricane Dennis near a Landfall. J. Atmos. Sci. 2009, 66, 3351–3365. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, X.; Davis, C.; Tuttle, J.; Holland, G.; Fitzpatrick, P.J. Experiments of Hurricane Initialization with Airborne Doppler Radar Data for the Advanced Research Hurricane WRF (AHW) Model. Mon. Weather Rev. 2009, 137, 2758–2777. [Google Scholar] [CrossRef]
- Aksoy, A.; Lorsolo, S.; Vukicevic, T.; Sellwood, K.J.; Aberson, S.D.; Zhang, F. The HWRF Hurricane Ensemble Data Assimilation System (HEDAS) for high-resolution data: The impact of airborne Doppler radar observations in an OSSE. Mon. Weather Rev. 2012, 140, 1843–1862. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, F. Assimilating airborne Doppler radar observations with an ensemble Kalman filter for convection-permitting hurricane initialization and prediction: Katrina (2005). Mon. Weather Rev. 2012, 140, 841–859. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y. Predicting Hurricane Intensity and Associated Hazards: A Five-Year Real-Time Forecast Experiment with Assimilation of Airborne Doppler Radar Observations. Bull. Am. Meteor. Soc. 2015, 96, 25–32. [Google Scholar] [CrossRef]
- Aberson, S.D.; Aksoy, A.; Kathryn, J.; Vukicevic, T.; Zhang, X. Assimilation of High-Resolution Tropical Cyclone Observations with an Ensemble Kalman Filter Using HEDAS: Evaluation of 2008–11 HWRF Forecasts. Mon. Weather Rev. 2015, 143, 511–523. [Google Scholar] [CrossRef]
- Chan, P.W.; Hon, K.K.; Foster, S. Wind data collected by a fixed-wing aircraft in the vicinity of a tropical cyclone over the south china coastal waters. Meteorol. Z. 2011, 20, 313–321. [Google Scholar] [CrossRef]
- Sparks, N.; Hon, K.K.; Chan, P.W.; Wang, S.; Chan, J.C.; Lee, T.C.; Toumi, R. Aircraft Observations of Tropical Cyclone Boundary Layer Turbulence over the South China Sea. J. Atmos. Sci. 2019. accepted. [Google Scholar] [CrossRef]
- Gamache, J. Evaluation of a fully-three dimensional variational Doppler analysis technique. In Proceedings of the 28th Conference on Radar Meteorology, Austin, TX, USA, 9–13 September 1997; American Meteorological Society: Boston, MA, USA, 1997; pp. 422–423. [Google Scholar]
- Daley, R. Estimating observation error statistics for atmospheric data assimilation. Ann. Geophys. 1993, 11, 634–647. [Google Scholar]
- Liu, Z.Q.; Rabier, F. The interaction between model resolution, observation resolution and observation density in data assimilation: A one-dimensional study. Q. J. R. Meteorol. Soc. 2002, 128, 1367–1386. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Rabier, F. The potential of high-density observations on Numerical Weather Prediction: A study with simulated observations. Q. J. R. Meteorol. Soc. 2003, 129, 3013–3035. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Sippel, J.; Meng, Z.; Bishop, C. Cloud-resolving hurricane initialization and prediction through assimilation of Doppler radar observations with an ensemble Kalman filter. Mon. Weather Rev. 2009, 137, 2105–2125. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone data. Bull. Am. Meteor. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Xue, J. Progresses of researches on numerical weather prediction in china: 1999–2002. Adv. Atmos. Sci. 2004, 21, 467–474. [Google Scholar]
- Su, Y.; Shen, X.; Chen, Z.; Zhang, H. A study on the three-dimensional reference atmosphere in GRAPES_GFS: Theoretical design and ideal test. Acta Meteorol. Sin. 2018, 76, 241–254. [Google Scholar]
- Pan, H.L.; Wu, W.S. Implementing a Mass Flux Convective Parameterization Package for the NMC Medium-Range Forecast Model; NMC Office Note 409: Washington, DC, USA, 1995. [Google Scholar]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice-microphysical processes for the bulk parameterization of cloud and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Vukicevic, T.; Aksoy, A.; Reasor, P.; Aberson, S.D.; Sellwood, K.J.; Marks, F. Joint Impact of Forecast Tendency and State Error Biases in Ensemble Kalman Filter Data Assimilation of Inner-Core Tropical Cyclone Observations. Mon. Weather Rev. 2013, 141, 2992–3006. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, F. Advances in Convection-permitting Tropical Cyclone Analysis and Prediction through EnKF Assimilation of Reconnaissance Aircraft Observations. J. Meteor. Soc. Jpn. 2016, 94, 345–358. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Zhang, F. Review of the Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather Rev. 2016, 144, 4490–4530. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble data assimilation without perturbed observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of Reflectivity Data in a Convective-Scale, Cycled 3DVAR Framework with Hydrometeor Classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of Initial Estimate and Observation Availability on Convective-Scale Data Assimilation with an Ensemble Kalman Filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Hamrud, M.; Bonavita, M.; Isaksen, L. EnKF and hybrid gain ensemble data assimilation. Part I: EnKF implementation. Mon. Weather Rev. 2015, 143, 4847–4864. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Williams, R.T. Analytical and numerical studies of the beta-effect in tropical cyclone motion. Part I: Zero mean flow. J. Atmos. Sci. 1987, 44, 1257–1265. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Ko, F.M.F.; Lei, Y.M. Relationship between potential vorticity tendency and tropical cyclone motion. J. Atmos. Sci. 2002, 59, 1317–1336. [Google Scholar] [CrossRef]
- Rogers, R.R.; Yau, M.K. A Short Course in Cloud Physics, 3rd ed.; Butterworth-Heinemann: Woburn, MA, USA, 2008; pp. 110–130. [Google Scholar]
- Lu, Y.; Zhang, F. Toward Ensemble Assimilation of Hyperspectral Satellite Observations with Data Compression and Dimension Reduction Using Principal Component Analysis. Mon. Weather Rev. 2019, 147, 3505–3518. [Google Scholar] [CrossRef]
- Aksoy, A. Storm-relative observations in tropical cyclone data assimilation with an ensemble kalman filter. Mon. Weather Rev. 2013, 141, 506–522. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).