How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses
Abstract
1. Introduction
2. Methods
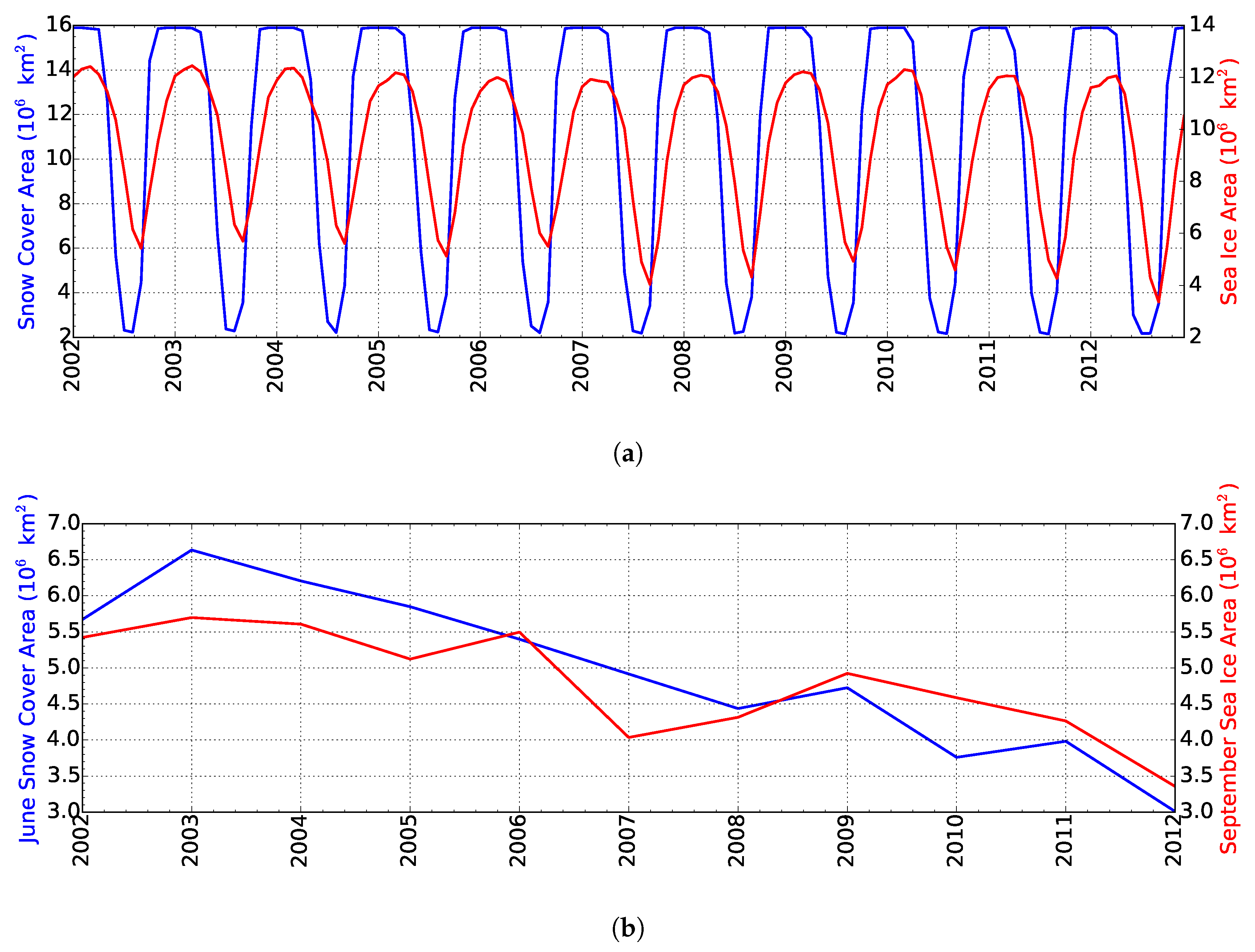
2.1. Datasets
2.2. Reanalyses
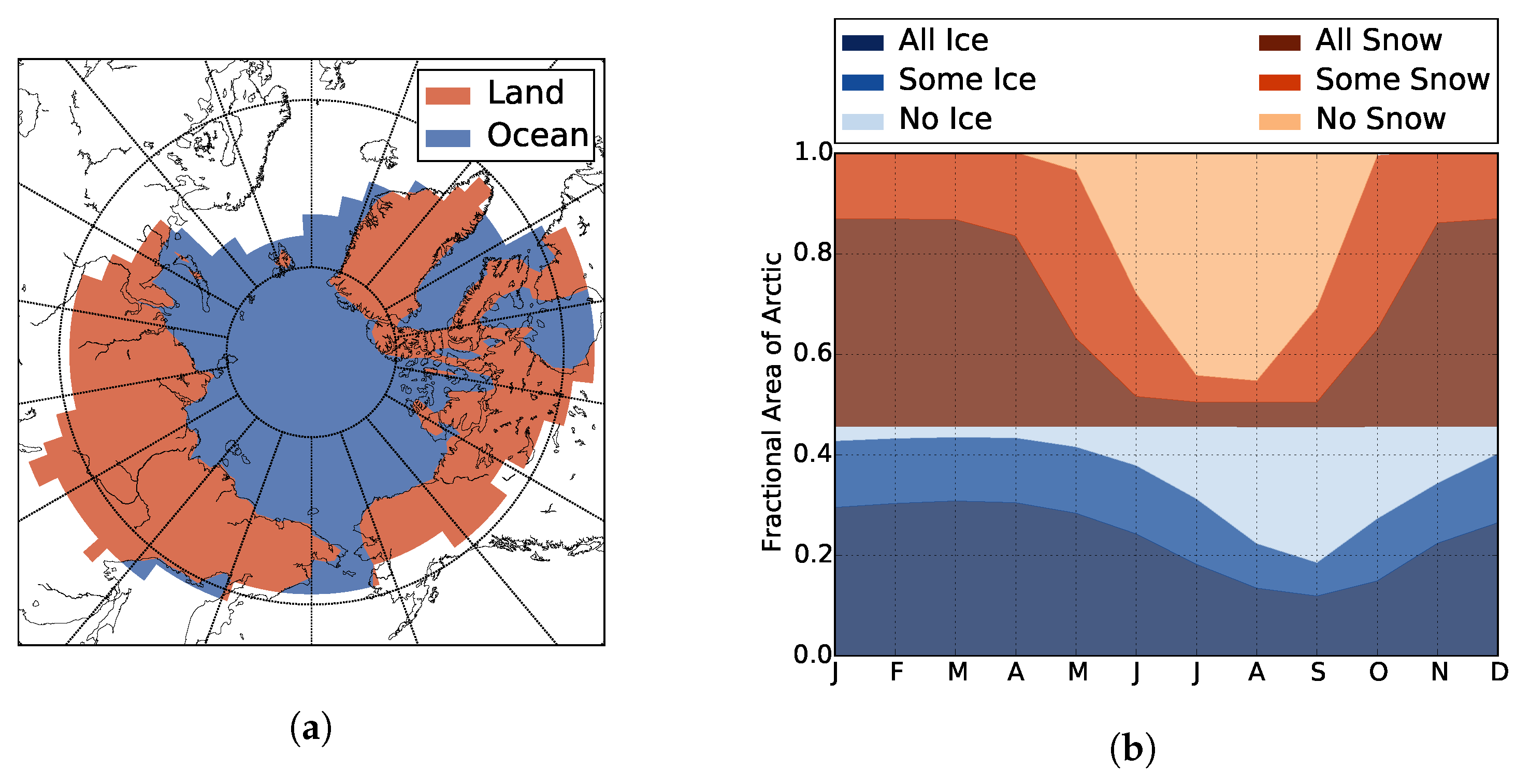
2.3. Surface Partitioning
2.4. Albedo Partitioning
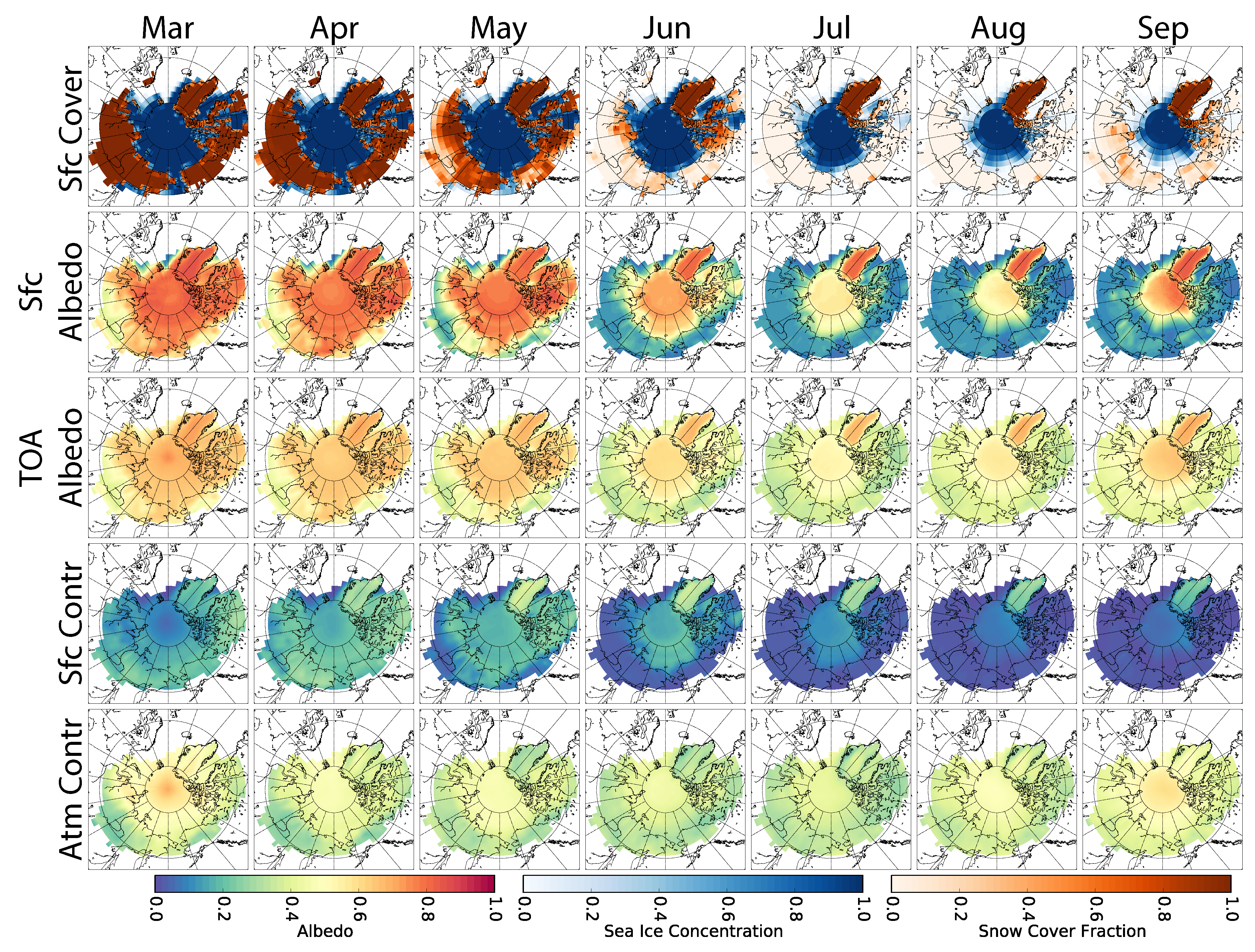
3. How Does Planetary Albedo Respond to Surface Cover?
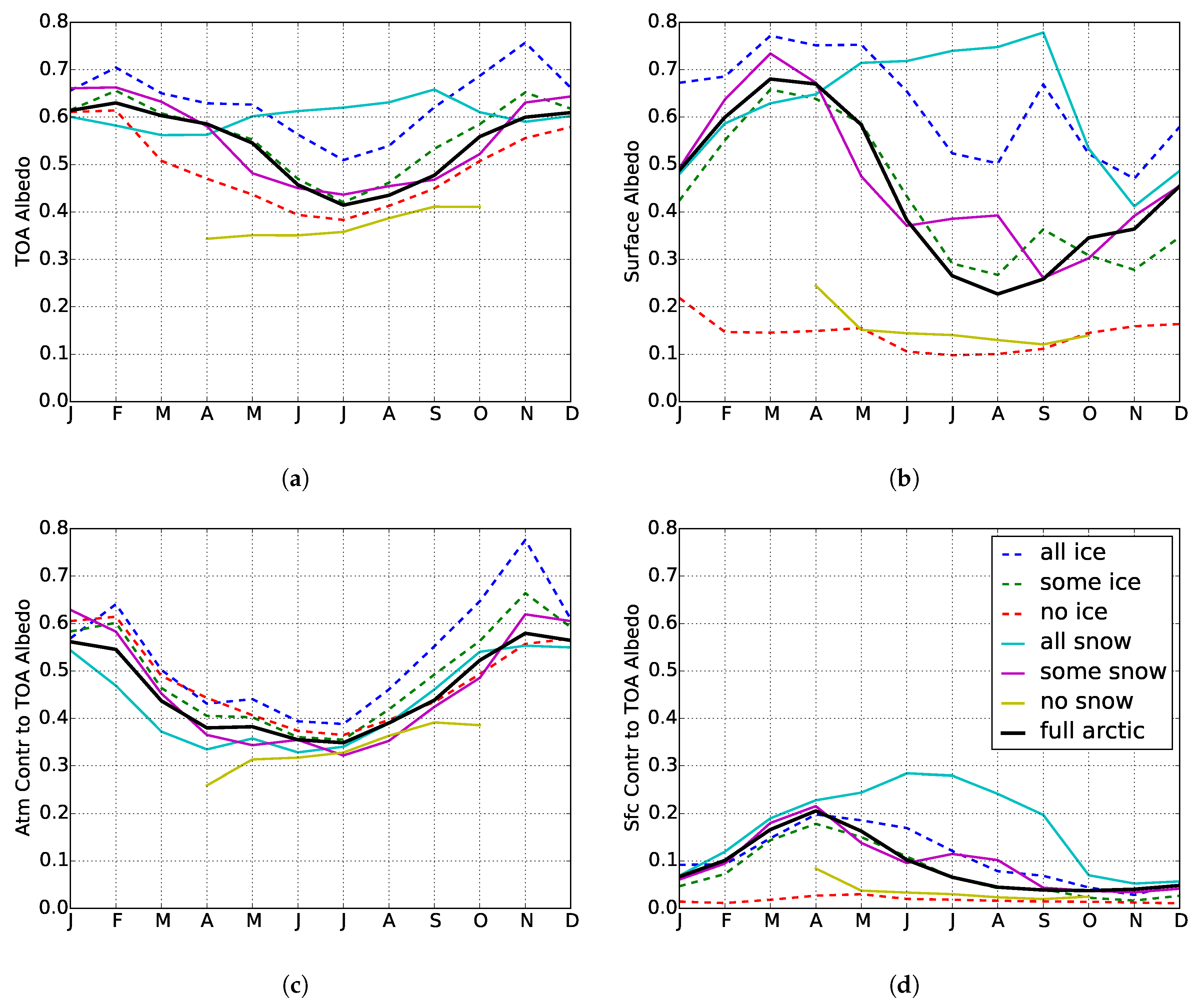
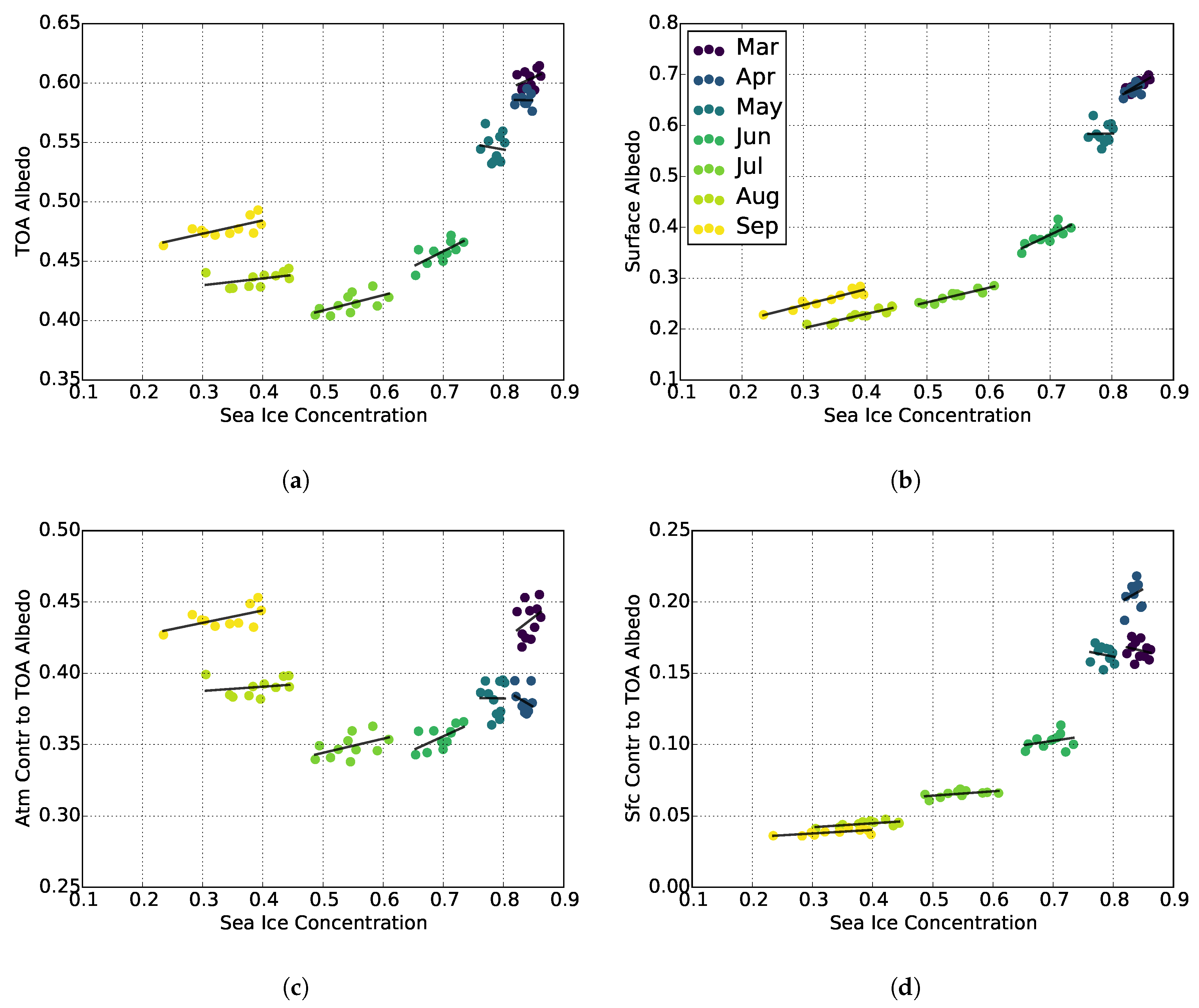
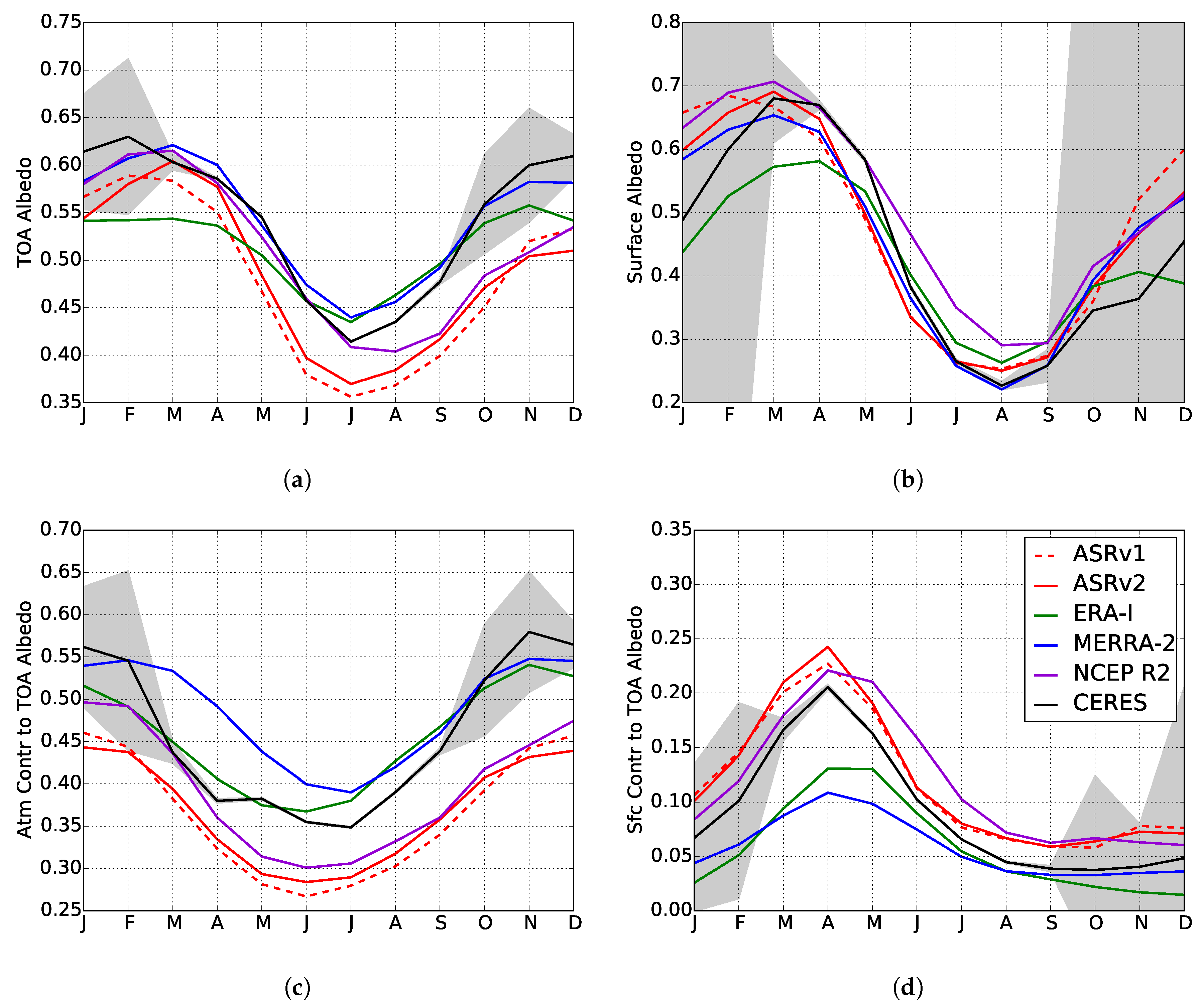
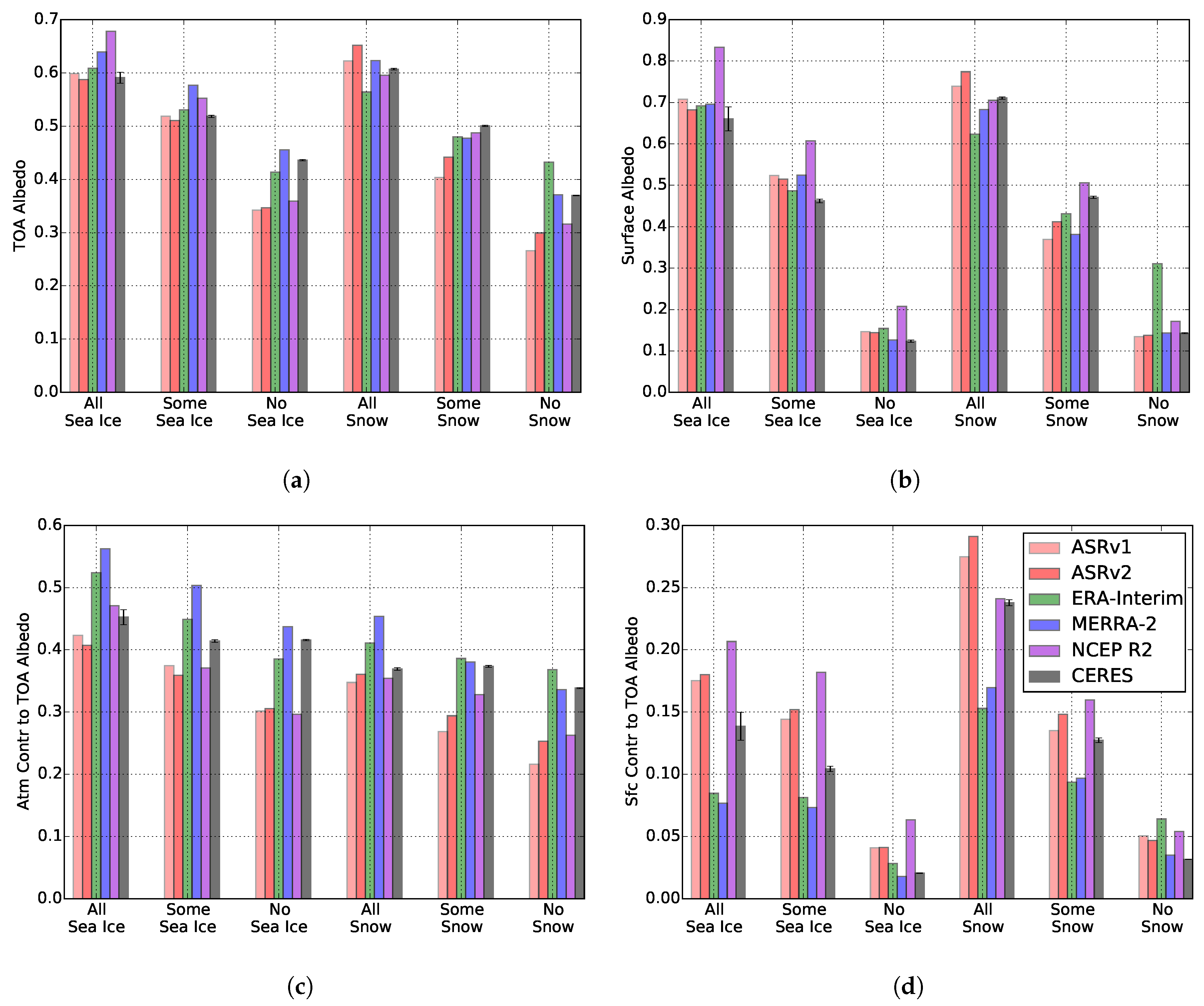
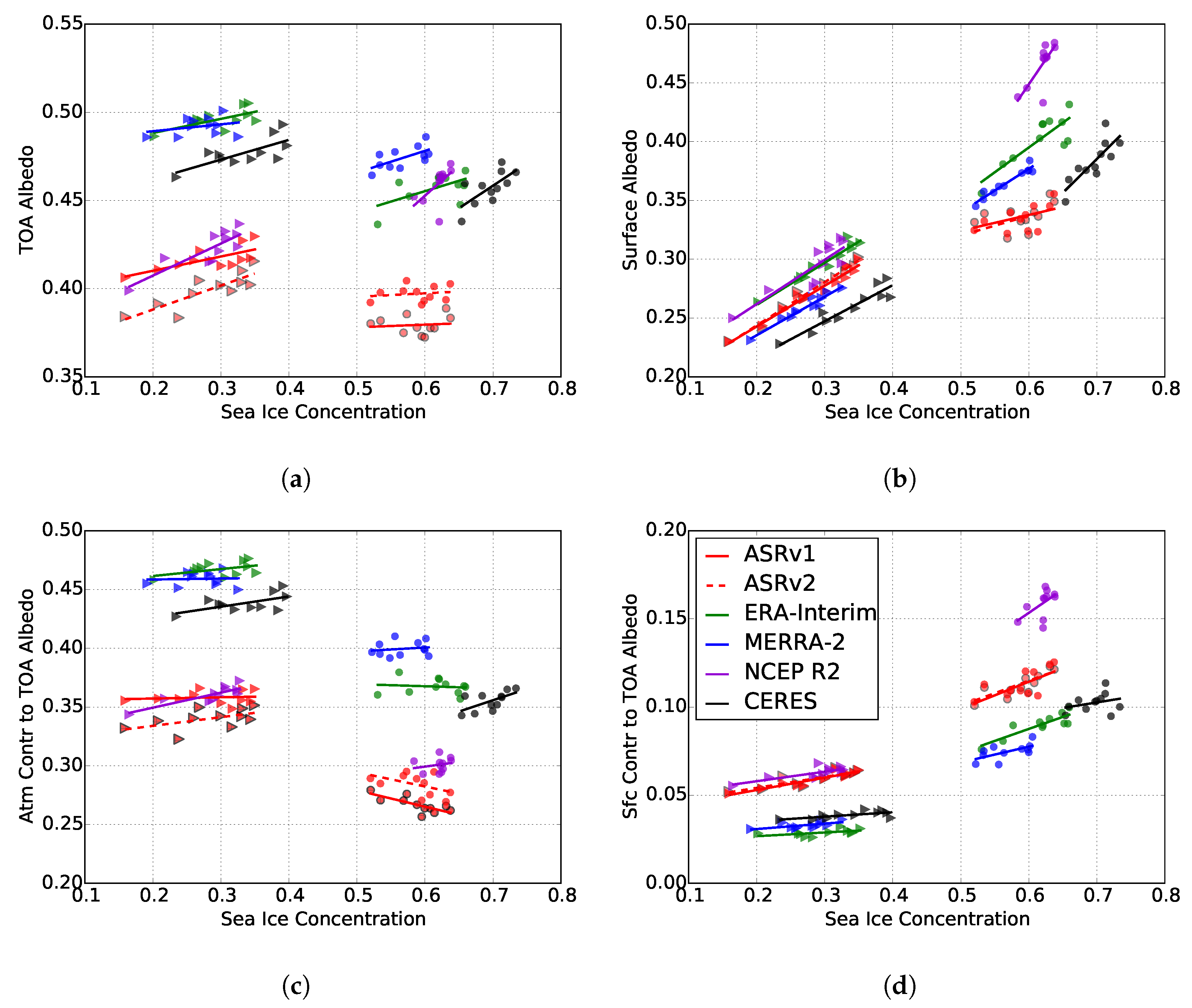
3.1. Effects of Surface Cover on TOA Albedo
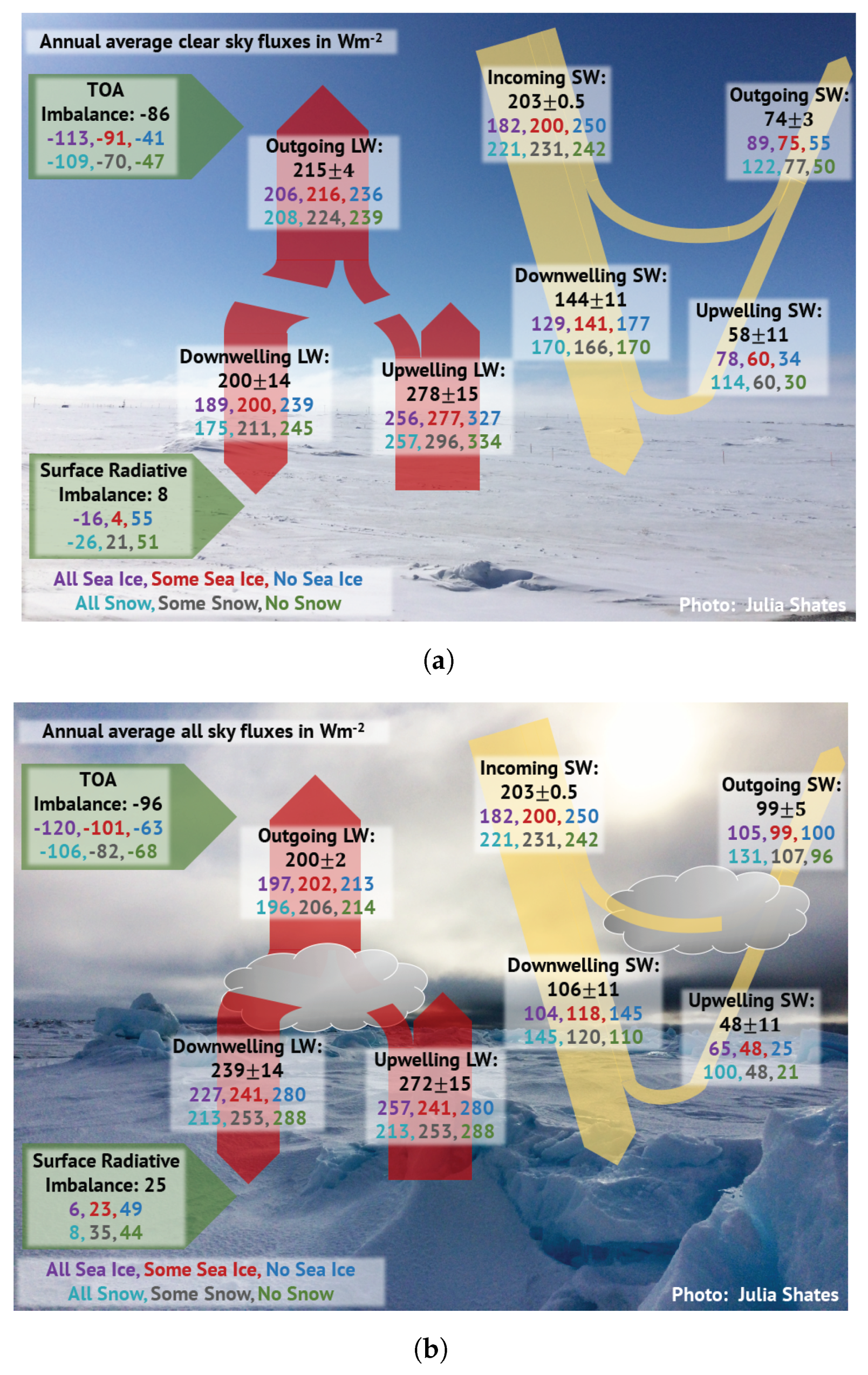
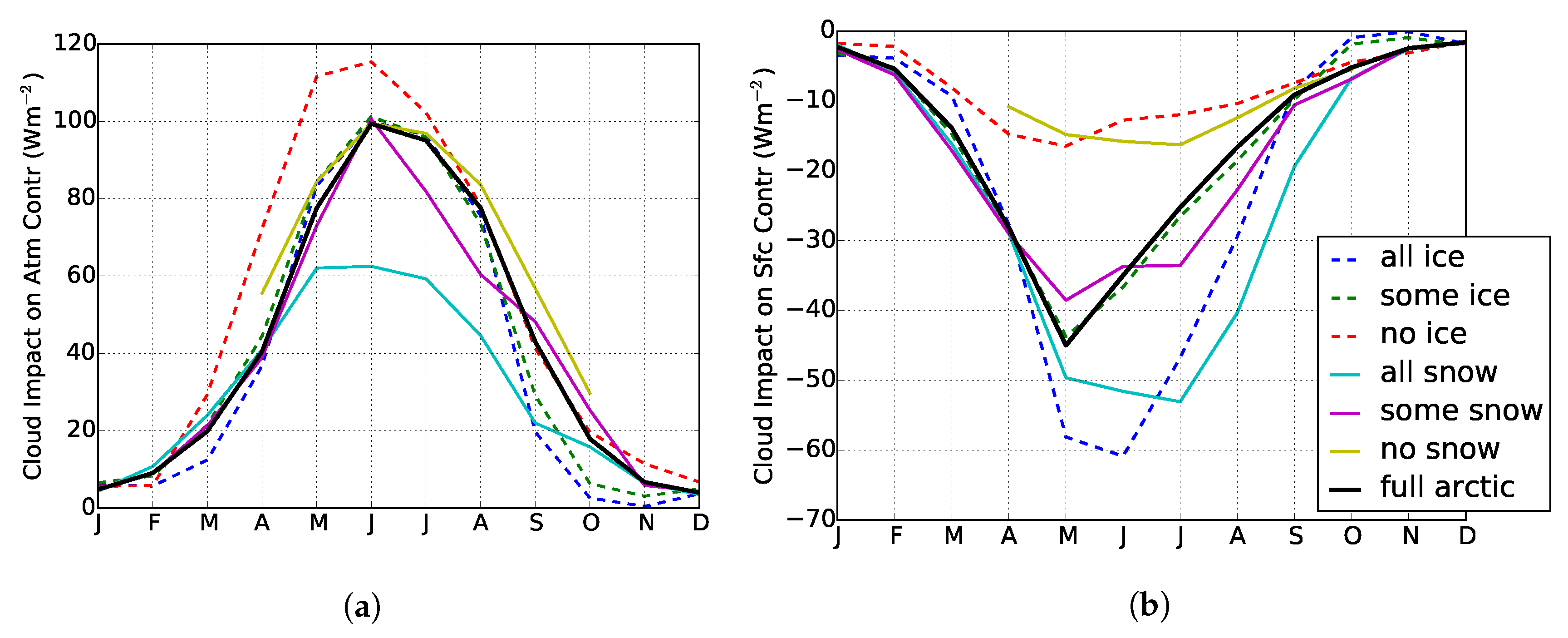
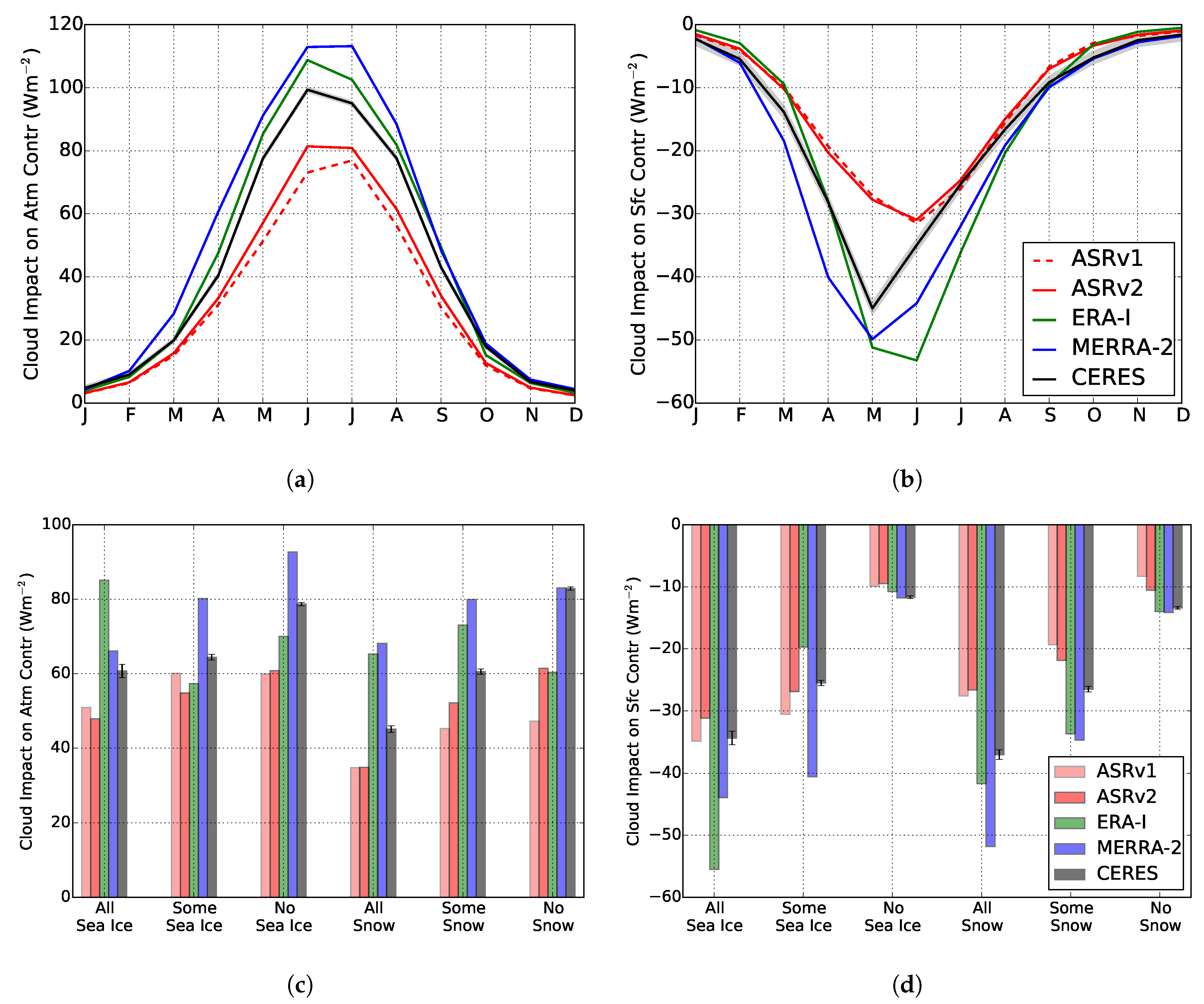
3.2. Cloud Modulation of Ice-Albedo Relationships
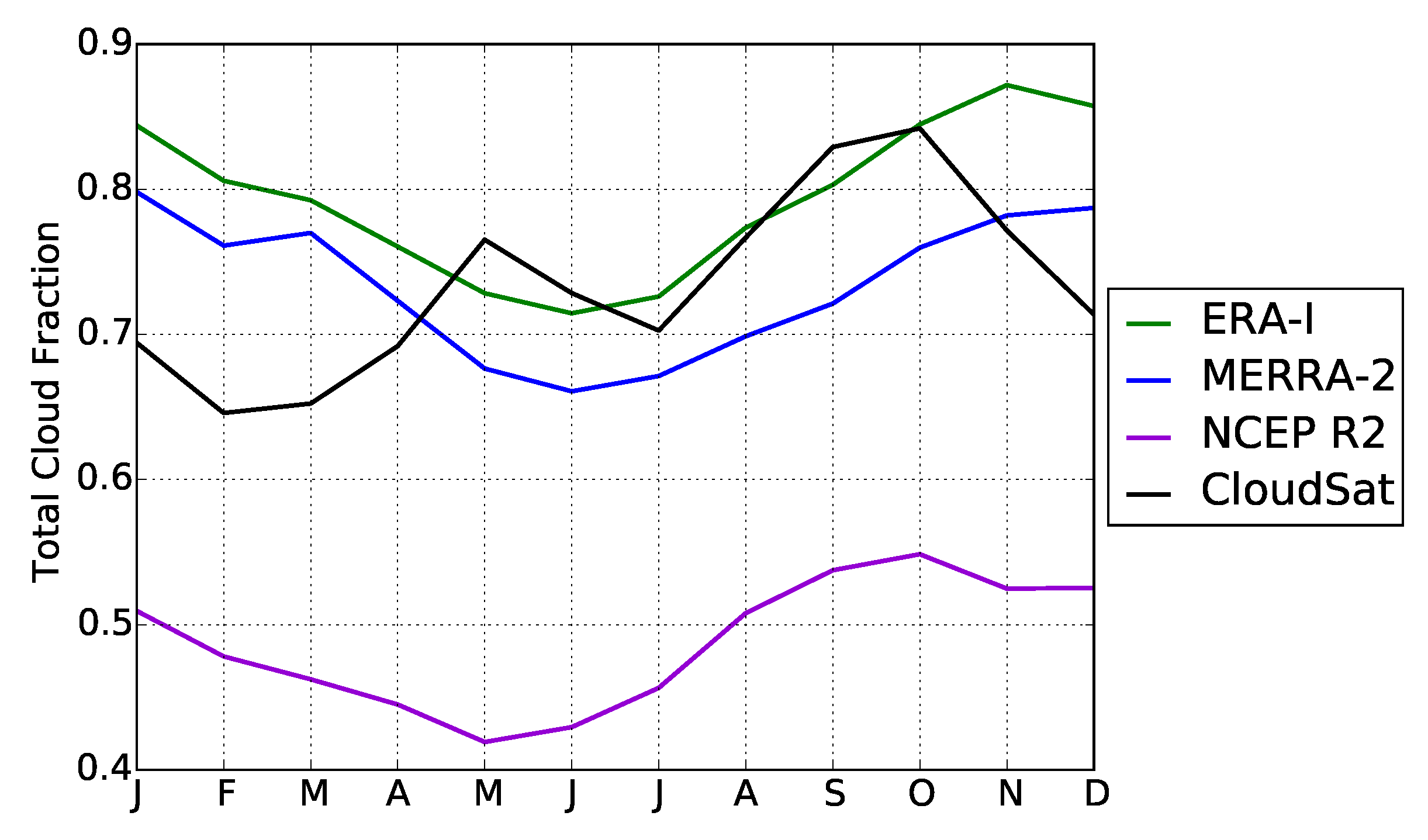
3.3. Representation in Reanalyses
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stroeve, J.C.; Serreze, M.C.; Holland, M.M.; Kay, J.E.; Malanik, J.; Barrett, A.P. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Chang. 2012, 110, 1005–1027. [Google Scholar] [CrossRef]
- Markus, T.; Stroeve, J.C.; Miller, J. Recent changes in Arctic sea ice melt onset, freezeup, and melt season length. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Liang, H.; Sun, Y.; Feng, Q.; Liang, T. Tracking Snow Variations in the Northern Hemisphere Using Multi-Source Remote Sensing Data (2000–2015). Remote Sens. 2018, 10, 136. [Google Scholar] [CrossRef]
- Noël, B.; Van De Berg, W.; Van Meijgaard, E.; Kuipers Munneke, P.; Van De Wal, R.; Van Den Broeke, M. Evaluation of the updated regional climate model RACMO2. 3: Summer snowfall impact on the Greenland Ice Sheet. Cryosphere 2015, 9, 1831–1844. [Google Scholar] [CrossRef]
- Serreze, M.; Barrett, A.; Stroeve, J.; Kindig, D.; Holland, M. The emergence of surface-based Arctic amplification. Cryosphere 2009, 3, 11. [Google Scholar] [CrossRef]
- Blunden, J.; Arndt, D.S. State of the Climate in 2016. Bull. Am. Meteorol. Soc. 2016, 98, Si-S280. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet. Chang. 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Gorodetskaya, I.V.; Cane, M.A.; Tremblay, L.B.; Kaplan, A. The effects of sea-ice and land-snow concentrations on planetary albedo from the earth radiation budget experiment. Atmos. Ocean 2006, 44, 195–205. [Google Scholar] [CrossRef]
- Riihelä, A.; Manninen, T.; Laine, V. Observed changes in the albedo of the Arctic sea-ice zone for the period 1982–2009. Nat. Clim. Chang. 2013, 3, 895. [Google Scholar] [CrossRef]
- Pistone, K.; Eisenman, I.; Ramanathan, V. Observational determination of albedo decrease caused by vanishing Arctic sea ice. Proc. Natl. Acad. Sci. USA 2014, 111, 3322–3326. [Google Scholar] [CrossRef]
- Curry, J.A.; Schramm, J.L.; Ebert, E.E. Sea ice-albedo climate feedback mechanism. J. Clim. 1995, 8, 240–247. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334. [Google Scholar] [CrossRef]
- Sedlar, J.; Tjernström, M.; Mauritsen, T.; Shupe, M.D.; Brooks, I.M.; Persson, P.O.G.; Birch, C.E.; Leck, C.; Sirevaag, A.; Nicolaus, M. A transitioning Arctic surface energy budget: The impacts of solar zenith angle, surface albedo and cloud radiative forcing. Clim. Dyn. 2011, 37, 1643–1660. [Google Scholar] [CrossRef]
- Intrieri, J.; Fairall, C.; Shupe, M.; Persson, P.; Andreas, E.; Guest, P.; Moritz, R. An annual cycle of Arctic surface cloud forcing at SHEBA. J. Geophys. Res. Oceans 2002, 107, SHE-13. [Google Scholar] [CrossRef]
- Perovich, D.K. Sunlight, clouds, sea ice, albedo, and the radiative budget: The umbrella versus the blanket. Cryosphere 2018, 12, 2159–2165. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Minnis, P.; Francis, J.A.; Charlock, T.P.; Rutan, D.A.; Clothiaux, E.E.; Sun-Mack, S. Seasonal and interannual variations of top-of-atmosphere irradiance and cloud cover over polar regions derived from the CERES data set. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Soden, B.J.; Held, I.M.; Colman, R.; Shell, K.M.; Kiehl, J.T.; Shields, C.A. Quantifying climate feedbacks using radiative kernels. J. Clim. 2008, 21, 3504–3520. [Google Scholar] [CrossRef]
- Hwang, J.; Choi, Y.S.; Kim, W.; Su, H.; Jiang, J.H. Observational estimation of radiative feedback to surface air temperature over Northern High Latitudes. Clim. Dyn. 2018, 50, 615–628. [Google Scholar] [CrossRef]
- Kay, J.E.; L’Ecuyer, T.; Chepfer, H.; Loeb, N.; Morrison, A.; Cesana, G. Recent advances in Arctic cloud and climate research. Curr. Clim. Chang. Rep. 2016, 2, 159–169. [Google Scholar] [CrossRef]
- Kay, J.E.; L’Ecuyer, T.; Gettelman, A.; Stephens, G.; O’Dell, C. The contribution of cloud and radiation anomalies to the 2007 Arctic sea ice extent minimum. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Perovich, D.K.; Richter-Menge, J.A.; Jones, K.F.; Light, B. Sunlight, water, and ice: Extreme Arctic sea ice melt during the summer of 2007. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Graversen, R.G.; Mauritsen, T.; Drijfhout, S.; Tjernström, M.; Mårtensson, S. Warm winds from the Pacific caused extensive Arctic sea-ice melt in summer 2007. Clim. Dyn. 2011, 36, 2103–2112. [Google Scholar] [CrossRef]
- Schweiger, A.; Zhang, J.; Lindsay, R.; Steele, M. Did unusually sunny skies help drive the record sea ice minimum of 2007? Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Ding, Q.; Schweiger, A.; L’Heureux, M.; Battisti, D.S.; Po-Chedley, S.; Johnson, N.C.; Blanchard-Wrigglesworth, E.; Harnos, K.; Zhang, Q.; Eastman, R.; et al. Influence of high-latitude atmospheric circulation changes on summertime Arctic sea ice. Nat. Clim. Chang. 2017, 7, 289. [Google Scholar] [CrossRef]
- Lenaerts, J.; Van Tricht, K.; Lhermitte, S.; L’Ecuyer, T.S. Polar clouds and radiation in satellite observations, reanalyses, and climate models. Geophys. Res. Lett. 2017, 44, 3355–3364. [Google Scholar] [CrossRef]
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J.L. The albedo of Earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef]
- Qu, X.; Hall, A. Surface contribution to planetary albedo variability in cryosphere regions. J. Clim. 2005, 18, 5239–5252. [Google Scholar] [CrossRef]
- Donohoe, A.; Battisti, D.S. Atmospheric and surface contributions to planetary albedo. J. Clim. 2011, 24, 4402–4418. [Google Scholar] [CrossRef]
- Serreze, M.C.; Lynch, A.H.; Clark, M.P. The Arctic frontal zone as seen in the NCEP–NCAR reanalysis. J. Clim. 2001, 14, 1550–1567. [Google Scholar] [CrossRef]
- Tilinina, N.; Gulev, S.K.; Bromwich, D.H. New view of Arctic cyclone activity from the Arctic system reanalysis. Geophys. Res. Lett. 2014, 41, 1766–1772. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, X.; Xi, B.; Deng, Y. A survey of the atmospheric physical processes key to the onset of Arctic sea ice melt in spring. Clim. Dyn. 2018, 1–16. [Google Scholar] [CrossRef]
- Walsh, J.E.; Chapman, W.L.; Portis, D.H. Arctic cloud fraction and radiative fluxes in atmospheric reanalyses. J. Clim. 2009, 22, 2316–2334. [Google Scholar] [CrossRef]
- Zib, B.J.; Dong, X.; Xi, B.; Kennedy, A. Evaluation and intercomparison of cloud fraction and radiative fluxes in recent reanalyses over the Arctic using BSRN surface observations. J. Clim. 2012, 25, 2291–2305. [Google Scholar] [CrossRef]
- Wesslén, C.; Tjernström, M.; Bromwich, D.; De Boer, G.; Ekman, A.M.; Bai, L.S.; Wang, S.H. The Arctic summer atmosphere: An evaluation of reanalyses using ASCOS data. Atmos. Chem. Phys. 2014, 14, 2605–2624. [Google Scholar] [CrossRef]
- Chernokulsky, A.; Mokhov, I.I. Climatology of total cloudiness in the Arctic: An intercomparison of observations and reanalyses. Adv. Meteorol. 2012, 2012. [Google Scholar] [CrossRef]
- Lindsay, R.; Wensnahan, M.; Schweiger, A.; Zhang, J. Evaluation of seven different atmospheric reanalysis products in the Arctic. J. Clim. 2014, 27, 2588–2606. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, X.; Xi, B.; Dolinar, E.K.; Stanfield, R.E.; Qiu, S. Quantifying the Uncertainties of Reanalyzed Arctic Cloud and Radiation Properties Using Satellite Surface Observations. J. Clim. 2017, 30, 8007–8029. [Google Scholar] [CrossRef]
- Tjernström, M.; Sedlar, J.; Shupe, M.D. How well do regional climate models reproduce radiation and clouds in the Arctic? An evaluation of ARCMIP simulations. J. Appl. Meteorol. Climatol. 2008, 47, 2405–2422. [Google Scholar] [CrossRef]
- Cao, Y.; Liang, S.; He, T.; Chen, X. Evaluation of Four Reanalysis Surface Albedo Data Sets in Arctic Using a Satellite Product. IEEE Geosci. Remote Sens. Lett. 2016, 13, 384–388. [Google Scholar] [CrossRef]
- Christensen, M.W.; Behrangi, A.; L’ecuyer, T.S.; Wood, N.B.; Lebsock, M.D.; Stephens, G.L. Arctic observation and reanalysis integrated system: A new data product for validation and climate study. Bull. Am. Meteorol. Soc. 2016, 97, 907–916. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Rose, F.G.; Doelling, D.R.; Rutan, D.A.; Caldwell, T.E.; Yu, L.; Weller, R.A. Surface irradiances consistent with CERES-derived top-of-atmosphere shortwave and longwave irradiances. J. Clim. 2013, 26, 2719–2740. [Google Scholar] [CrossRef]
- CERES. CERES_EBAF_Ed2.8 Data Quality Summary. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_EBAF_Ed2.8_DQS.pdf (accessed on 16 February 2017).
- L’Ecuyer, T.S.; Beaudoing, H.K.; Rodell, M.; Olson, W.; Lin, B.; Kato, S.; Clayson, C.A.; Wood, E.; Sheffield, J.; Adler, R.; et al. The observed state of the energy budget in the early twenty-first century. J. Clim. 2015, 28, 8319–8346. [Google Scholar] [CrossRef]
- CERES. CERES_EBAF_Surface_Ed2.8 Data Quality Summary. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_EBAF-Surface_Ed2.8_DQS.pdf (accessed on 16 February 2017).
- Tanelli, S.; Durden, S.L.; Im, E.; Pak, K.S.; Reinke, D.G.; Partain, P.; Haynes, J.M.; Marchand, R.T. CloudSat’s cloud profiling radar after two years in orbit: Performance, calibration, and processing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3560–3573. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO mission and CALIOP data processing algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kållberg, P.; Simmons, A.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.; Haseler, J.; Hernandez, A.; Kelly, G.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Dutra, E.; Balsamo, G.; Viterbo, P.; Miranda, P.M.; Beljaars, A.; Schär, C.; Elder, K. An improved snow scheme for the ECMWF land surface model: Description and offline validation. J. Hydrometeorol. 2010, 11, 899–916. [Google Scholar] [CrossRef]
- Ebert, E.E.; Curry, J.A. An intermediate one-dimensional thermodynamic sea ice model for investigating ice-atmosphere interactions. J. Geophys. Res. Oceans 1993, 98, 10085–10109. [Google Scholar] [CrossRef]
- Hogan, R. Radiation Quantities in the ECMWF Model and MARS, 2017. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2015/18490-radiation-quantities-ecmwf-model-and-mars.pdf (accessed on 6 January 2017).
- Tiedtke, M. Representation of clouds in large-scale models. Mon. Weather Rev. 1993, 121, 3040–3061. [Google Scholar] [CrossRef]
- Gregory, D.; Morcrette, J.J.; Jakob, C.; Beljaars, A.; Stockdale, T. Revision of convection, radiation and cloud schemes in the ECMWF Integrated Forecasting System. Q. J. R. Meteorol. Soc. 2000, 126, 1685–1710. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Duynkerke, P.G.; de Roode, S.R. Surface energy balance and turbulence characteristics observed at the SHEBA Ice Camp during FIRE III. J. Geophys. Res. Atmos. 2001, 106, 15313–15322. [Google Scholar] [CrossRef]
- Bosilovich, M.G. MERRA-2: Initial Evaluation of the Climate; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MA, USA, 2015. [Google Scholar]
- Bacmeister, J.T.; Suarez, M.J.; Robertson, F.R. Rain reevaporation, boundary layer–convection interactions, and Pacific rainfall patterns in an AGCM. J. Atmos. Sci. 2006, 63, 3383–3403. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.; Fiorino, M.; Potter, G. Ncep–doe amip-ii reanalysis (r-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Bromwich, D.; Kuo, Y.H.; Serreze, M.; Walsh, J.; Bai, L.S.; Barlage, M.; Hines, K.; Slater, A. Arctic system reanalysis: Call for community involvement. Eos Trans. Am. Geophys. Union 2010, 91, 13–14. [Google Scholar] [CrossRef]
- Bromwich, D.; Wilson, A.; Bai, L.; Liu, Z.; Barlage, M.; Shih, C.F.; Maldonado, S.; Hines, K.; Wang, S.H.; Woollen, J.; et al. The Arctic System Reanalysis, Version 2. Bull. Am. Meteorol. Soc. 2018, 99, 805–828. [Google Scholar] [CrossRef]
- Morrison, A.; Kay, J.; Chepfer, H.; Guzman, R.; Yettella, V. Isolating the liquid cloud response to recent Arctic sea ice variability using spaceborne lidar observations. J. Geophys. Res. Atmos. 2018, 123, 473–490. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barry, R.G. The Arctic Climate System; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Smithson, P.; Addison, K.; Atkinson, K. Fundamentals of the Physical Environment; Routledge: Abingdon-on-Thames, UK, 2013. [Google Scholar]
- Sedlar, J. Spring Arctic Atmospheric Preconditioning: Do Not Rule Out Shortwave Radiation Just Yet. J. Clim. 2018, 31, 4225–4240. [Google Scholar] [CrossRef]
- Curry, J.A.; Schramm, J.L.; Rossow, W.B.; Randall, D. Overview of Arctic cloud and radiation characteristics. J. Clim. 1996, 9, 1731–1764. [Google Scholar] [CrossRef]
- Zhang, J.; Rothrock, D. Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates. Mon. Weather Rev. 2003, 131, 845–861. [Google Scholar] [CrossRef]
- Box, J.E.; Bromwich, D.H.; Bai, L.S. Greenland ice sheet surface mass balance 1991–2000: Application of Polar MM5 mesoscale model and in situ data. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Liu, Y.; Key, J.R. Assessment of Arctic cloud cover anomalies in atmospheric reanalysis products using satellite data. J. Clim. 2016, 29, 6065–6083. [Google Scholar] [CrossRef]
- Hines, K.M.; Bromwich, D.H. Simulation of late summer Arctic clouds during ASCOS with Polar WRF. Mon. Weather Rev. 2017, 145, 521–541. [Google Scholar] [CrossRef]

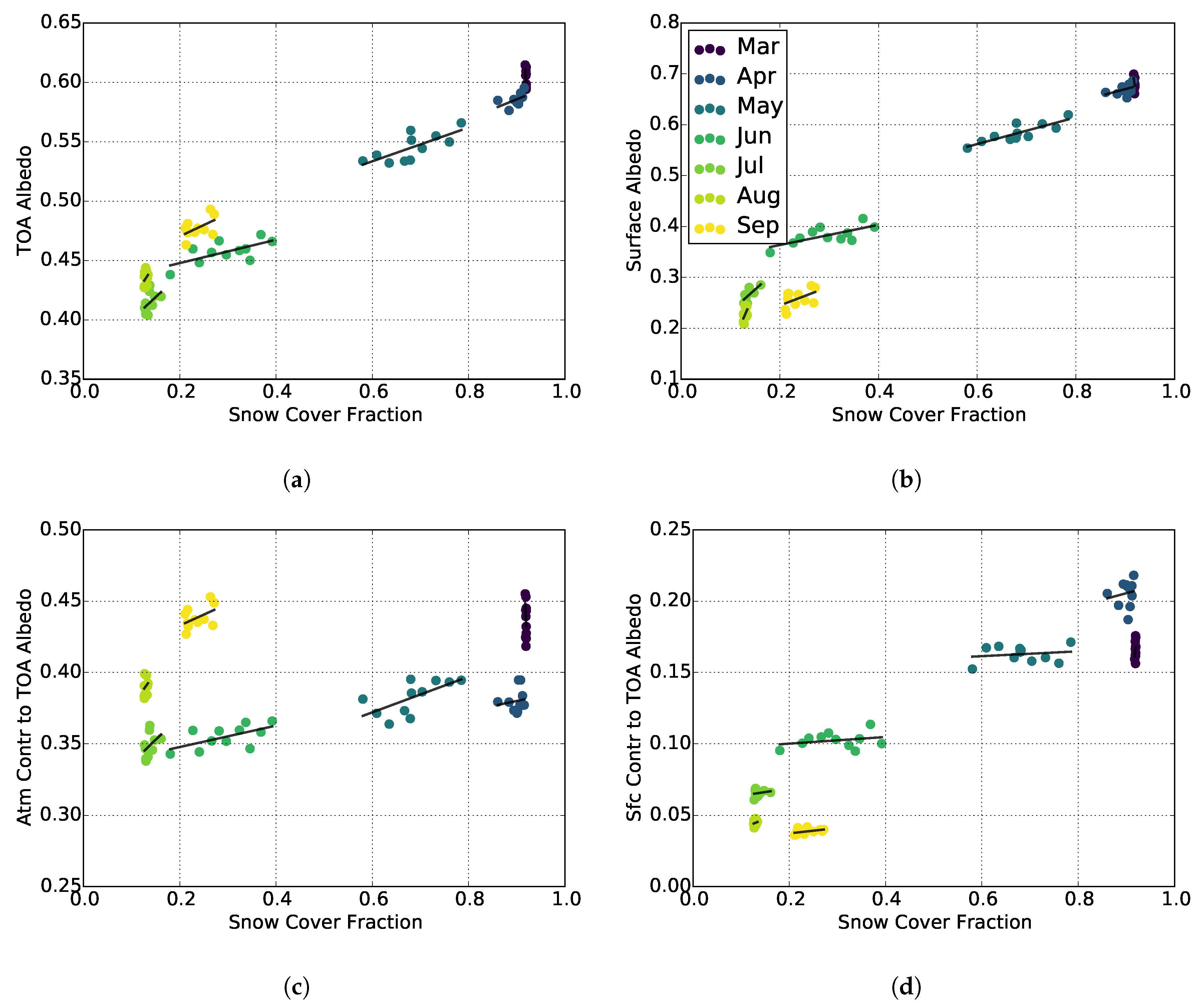
| Name | Original Resolution | Sea Ice Concentration | Sea Ice Albedo | Snow Cover Fraction | Snow Albedo | Clouds |
|---|---|---|---|---|---|---|
| ASR v1, v2 | 30 km (v1), 15 km (v2) | Prescribed from SSMI and AMSRE | Annually varying seasonal cycle | Vary seasonally with assimilations from NESDIS observations | PWRF single-moment 5-class microphysics scheme (v1), PWR 2-moment Morrison scheme (v2) | |
| ERA-Interim | 0.75° × 0.75° | Assimilated from various NCEP datasets | Monthly climatology | Calculated from snow water equivalent and snow density | Monthly climatology | Fully prognostic equations using 3-class two-moment scheme |
| MERRA-2 | 1.25° × 1.25° | Prescribed from various ocean datasets | Seasonal cycle from SHEBA observations | NASA Catchment land surface model | MODIS climatology | Prognostic scheme and single-phase condensate with two species |
| NCEP R2 | 1.25° × 1.25° | Prescribed from AMP-II | NSIDC snow cover fraction | Fixed with latitude dependent values | Diagnostic cloud scheme with parameterized relative humidity-cloud cover (empirical) relationship | |
| Month | Surface Albedo | TOA Albedo | Atm Contr to TOA Albedo | Sfc Contr to TOA Albedo |
|---|---|---|---|---|
| March | 0.72 (0.68) | 0.23 (0.15) | 0.32 (0.12) | −0.10 (0.04) |
| April | 0.49 (0.23) | −0.01 (0.00) | −0.25 (0.08) | 0.24 (0.06) |
| May | 0.01 (0.00) | −0.09 (0.01) | −0.01 (0.00) | −0.08 (0.03) |
| June | 0.57 (0.67) | 0.25 (0.48) | 0.19 (0.38) | 0.06 (0.09) |
| July | 0.29 (0.88) | 0.13 (0.39) | 0.10 (0.23) | 0.03 (0.28) |
| August | 0.27 (0.88) | 0.06 (0.18) | 0.03 (0.04) | 0.03 (0.41) |
| September | 0.31 (0.88) | 0.11 (0.52) | 0.09 (0.36) | 0.02 (0.52) |
| Month | Surface Albedo | TOA Albedo | Atm Contr to TOA Albedo | Sfc Contr to TOA Albedo |
|---|---|---|---|---|
| March | −7.33 (0.18) | −4.72 (0.17) | −7.82 (0.17) | 3.10 (0.10) |
| April | −0.26 (0.19) | 0.16 (0.27) | 0.07 (0.02) | 0.09 (0.03) |
| May | 0.26 (0.72) | 0.14 (0.55) | 0.12 (0.43) | 0.02 (0.03) |
| June | 0.20 (0.51) | 0.10 (0.45) | 0.07 (0.37) | 0.02 (0.08) |
| July | 0.87 (0.55) | 0.38 (0.23) | 0.33 (0.18) | 0.05 (0.05) |
| August | 2.24 (0.24) | 0.62 (0.08) | 0.48 (0.05) | 0.14 (0.04) |
| September | 0.37 (0.26) | 0.19 (0.30) | 0.15 (0.22) | 0.04 (0.19) |
| CERES | ASR | ASRv2 | ERA-Int | MERRA-2 | NCEP R2 | ||
|---|---|---|---|---|---|---|---|
| Surface Albedo | Jun | 0.57 (0.67) | 0.13 (0.20) | 0.17 (0.32) | 0.42 (0.71) | 0.37 (0.93) | 0.85 (0.57) |
| Sep | 0.31 (0.88) | 0.37 (0.98) | 0.35 (0.97) | 0.36 (0.94) | 0.33 (0.94) | 0.38 (0.77) | |
| TOA Albedo | Jun | 0.25 (0.47) | 0.01 (0.01) | 0.02 (0.03) | 0.12 (0.33) | 0.12 (0.40) | 0.34 (0.39) |
| Sep | 0.11 (0.52) | 0.14 (0.71) | 0.08 (0.51) | 0.08 (0.43) | 0.04 (0.08) | 0.18 (0.72) | |
| Atm Contr to TOA Albedo | Jun | 0.19 (0.38) | −0.14 (0.57) | −0.12 (0.23) | −0.02 (0.01) | 0.03 (0.03) | 0.08 (0.04) |
| Sep | 0.09 (0.36) | 0.07 (0.28) | 0.01 (0.01) | 0.06 (0.22) | 0.01 (0.00) | 0.13 (0.70) | |
| Sfc Contr to TOA Albedo | Jun | 0.06 (0.09) | 0.15 (0.70) | 0.12 (0.44) | 0.14 (0.76) | 0.09 (0.40) | 0.26 (0.30) |
| Sep | 0.02 (0.43) | 0.06 (0.72) | 0.07 (0.87) | 0.02 (0.28) | 0.03 (0.39) | 0.05 (0.57) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sledd, A.; L’Ecuyer, T. How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses. Atmosphere 2019, 10, 12. https://doi.org/10.3390/atmos10010012
Sledd A, L’Ecuyer T. How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses. Atmosphere. 2019; 10(1):12. https://doi.org/10.3390/atmos10010012
Chicago/Turabian StyleSledd, Anne, and Tristan L’Ecuyer. 2019. "How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses" Atmosphere 10, no. 1: 12. https://doi.org/10.3390/atmos10010012
APA StyleSledd, A., & L’Ecuyer, T. (2019). How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses. Atmosphere, 10(1), 12. https://doi.org/10.3390/atmos10010012





