Selection for Protein Stability Enriches for Epistatic Interactions
Abstract
:1. Introduction
2. Methods
Simulations
3. Results
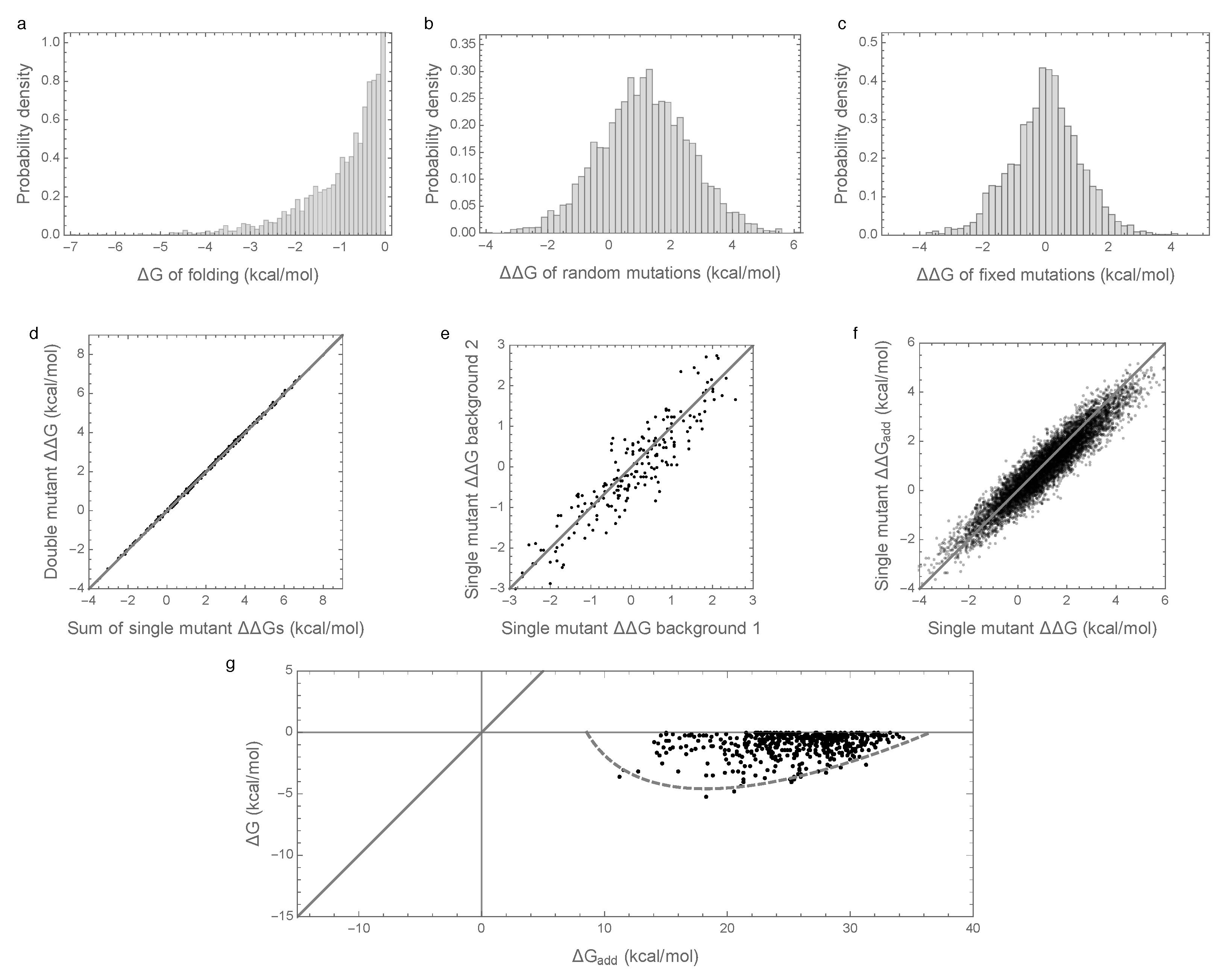
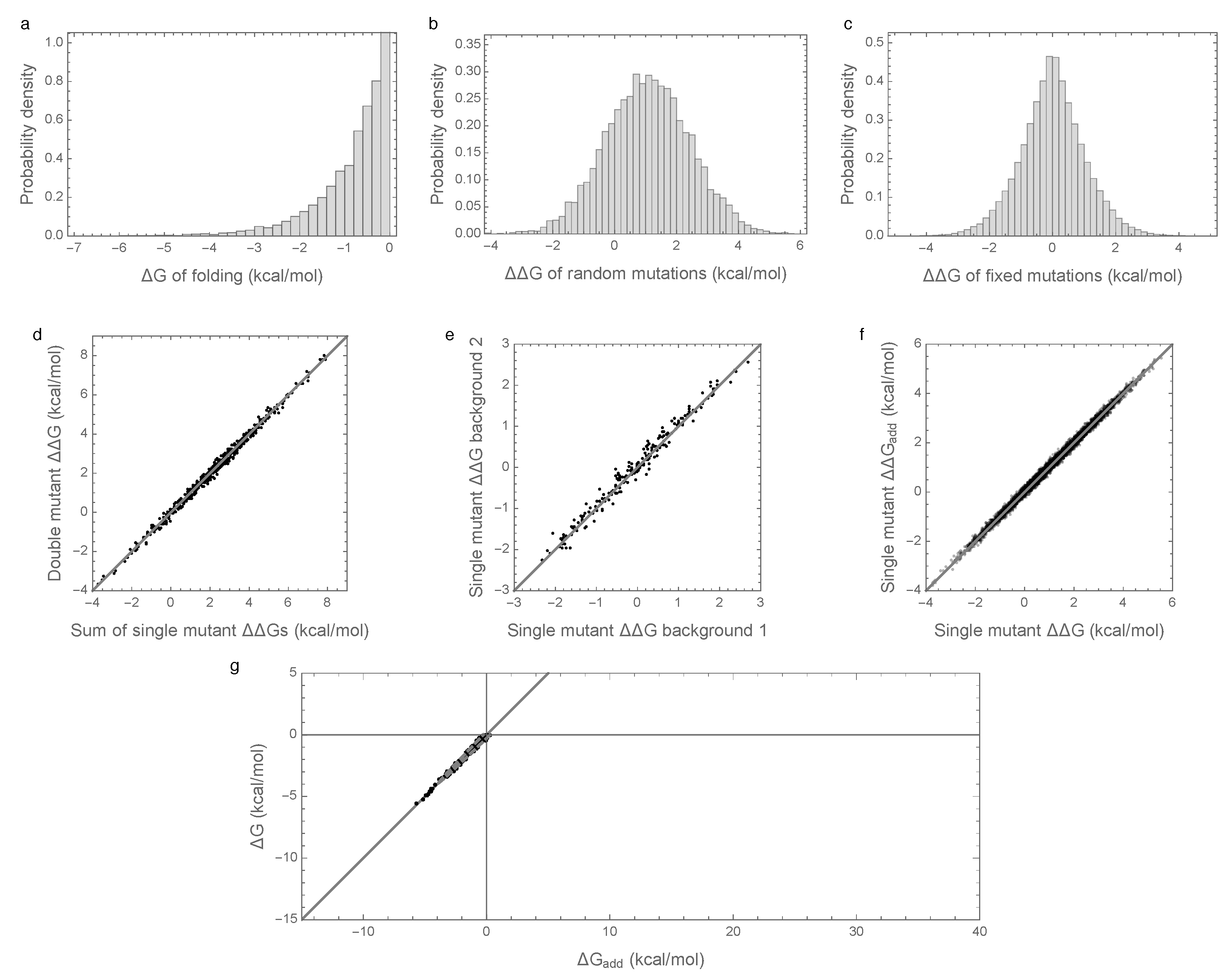
3.1. Epistasis Is Essential for Proper Folding of Evolved Sequences
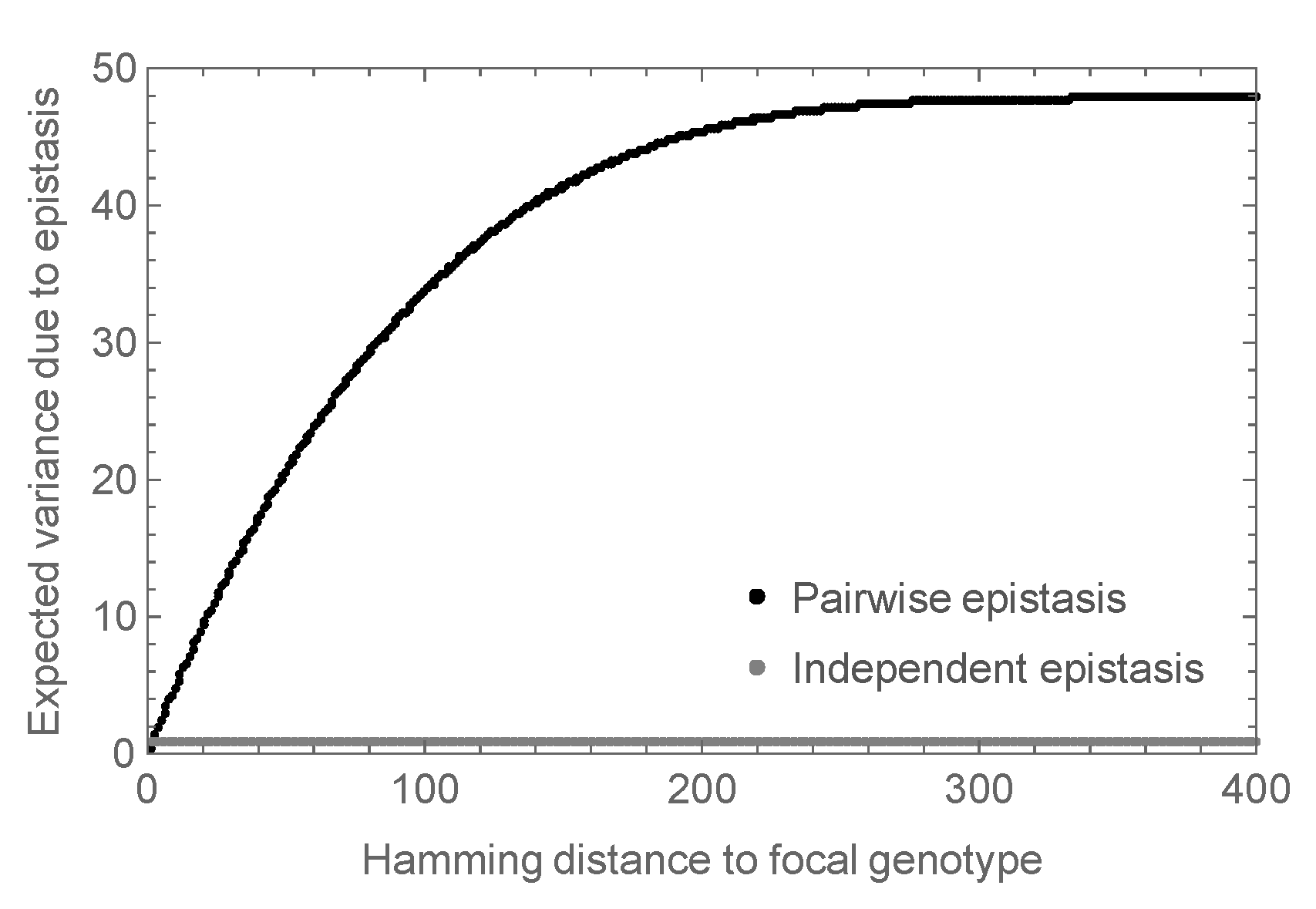
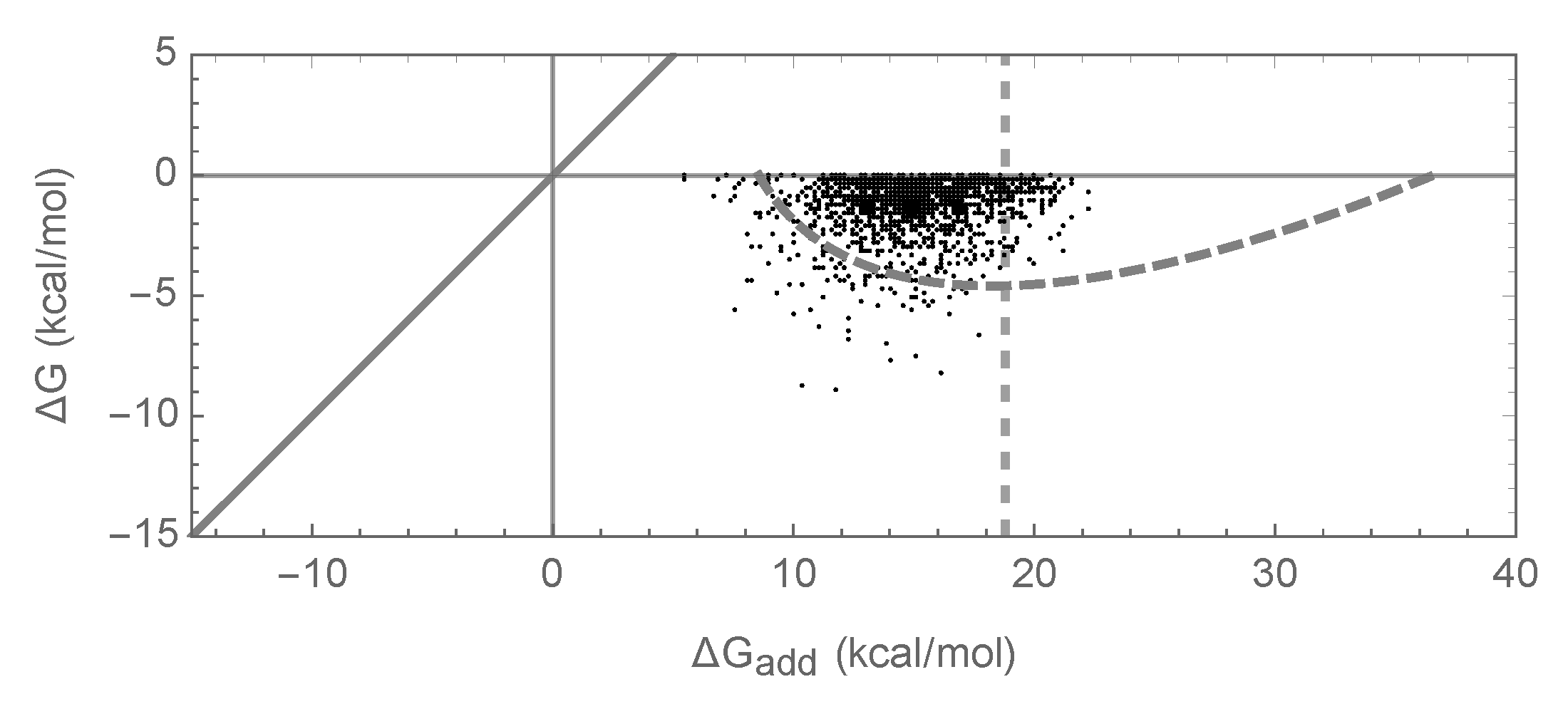
3.2. Enrichment for Epistasis Observed under the Pairwise Model, but Not the Independent Model
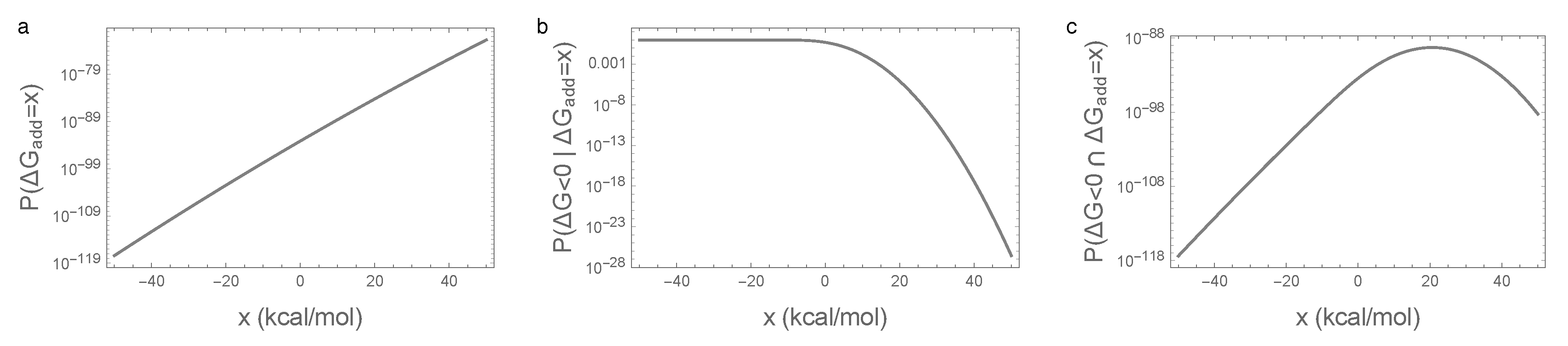
3.3. Bivariate Normal Approximation for the Joint Distribution of Additive and Epistatic Contributions to the Free Energy of Folding Captures Impact of Sequence Entropy
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Model for the Free Energy of Folding
Appendix A.2. Properties of the and
Appendix B
Appendix B.1. Expected Variance of Epistatic Energy of Distance Classes under the Random Field Model
Appendix C
Appendix C.1. Bivariate Normal Approximation
References
- Sikosek, T.; Chan, H.S. Biophysics of protein evolution and evolutionary protein biophysics. J. R. Soc. Interface 2014, 11, 20140419. [Google Scholar] [CrossRef] [PubMed]
- Bastolla, U.; Dehouck, Y.; Echave, J. What evolution tells us about protein physics, and protein physics tells us about evolution. Curr. Opin. Struct. Biol. 2017, 42, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Starr, T.N.; Thornton, J.W. Epistasis in protein evolution. Protein Sci. 2016, 25, 1204–1218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Echave, J.; Wilke, C.O. Biophysical models of protein evolution: Understanding the patterns of evolutionary sequence divergence. Ann. Rev. Biophys. 2017, 46, 85–103. [Google Scholar] [CrossRef] [PubMed]
- Storz, J.F. Compensatory mutations and epistasis for protein function. Curr. Opin. Struct. Biol. 2018, 50, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Tang, C.; Wingreen, N.S. Are protein folds atypical? Proc. Natl. Acad. Sci. USA 1998, 95, 4987–4990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tokuriki, N.; Tawfik, D.S. Stability effects of mutations and protein evolvability. Curr. Opin. Struct. Biol. 2009, 19, 596–604. [Google Scholar] [CrossRef] [PubMed]
- Taverna, D.M.; Goldstein, R.A. Why are proteins marginally stable? Proteins Struct. Funct. Bioinform. 2002, 46, 105–109. [Google Scholar] [CrossRef] [PubMed]
- Shakhnovich, E.I. Protein design: A perspective from simple tractable models. Fold. Des. 1998, 3, R45–R58. [Google Scholar] [CrossRef]
- Govindarajan, S.; Goldstein, R.A. On the thermodynamic hypothesis of protein folding. Proc. Natl. Acad. Sci. USA 1998, 95, 5545–5549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldstein, R.A. The evolution and evolutionary consequences of marginal thermostability in proteins. Proteins Struct. Funct. Bioinform. 2011, 79, 1396–1407. [Google Scholar] [CrossRef] [PubMed]
- Serohijos, A.W.; Shakhnovich, E.I. Merging molecular mechanism and evolution: Theory and computation at the interface of biophysics and evolutionary population genetics. Curr. Opin. Struct. Biol. 2014, 26, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.A.; Pollock, D.D. Sequence entropy of folding and the absolute rate of amino acid substitutions. Nat. Ecol. Evol. 2017, 1, 1923. [Google Scholar] [CrossRef] [PubMed]
- Ashenberg, O.; Gong, L.I.; Bloom, J.D. Mutational effects on stability are largely conserved during protein evolution. Proc. Natl. Acad. Sci. USA 2013, 110, 21071–21076. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollock, D.D.; Thiltgen, G.; Goldstein, R.A. Amino acid coevolution induces an evolutionary Stokes shift. Proc. Natl. Acad. Sci. USA 2012, 109, E1352–E1359. [Google Scholar] [CrossRef] [PubMed]
- Shah, P.; McCandlish, D.M.; Plotkin, J.B. Contingency and entrenchment in protein evolution under purifying selection. Proc. Natl. Acad. Sci. USA 2015, 112, E3226–E3235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breen, M.S.; Kemena, C.; Vlasov, P.K.; Notredame, C.; Kondrashov, F.A. Epistasis as the primary factor in molecular evolution. Nature 2012, 490, 535–538. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.A. Additivity of mutational effects in proteins. Biochemistry 1990, 29, 8509–8517. [Google Scholar] [CrossRef] [PubMed]
- Risso, V.A.; Manssour-Triedo, F.; Delgado-Delgado, A.; Arco, R.; Barroso-delJesus, A.; Ingles-Prieto, A.; Godoy-Ruiz, R.; Gavira, J.A.; Gaucher, E.A.; Ibarra-Molero, B.; et al. Mutational studies on resurrected ancestral proteins reveal conservation of site-specific amino acid preferences throughout evolutionary history. Mol. Biol. Evol. 2015, 32, 440–455. [Google Scholar] [CrossRef] [PubMed]
- Stadler, P.F.; Happel, R. Random field models for fitness landscapes. J. Math. Biol. 1999, 38, 435–478. [Google Scholar] [CrossRef] [Green Version]
- Neidhart, J.; Szendro, I.G.; Krug, J. Exact results for amplitude spectra of fitness landscapes. J. Theor. Biol. 2013, 332, 218–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aita, T.; Uchiyama, H.; Inaoka, T.; Nakajima, M.; Kokubo, T.; Husimi, Y. Analysis of a local fitness landscape with a model of the rough Mt. Fuji-type landscape: Application to prolyl endopeptidase and thermolysin. Biopolymers 2000, 54, 64–79. [Google Scholar] [CrossRef]
- Neidhart, J.; Szendro, I.G.; Krug, J. Adaptation in tunably rugged fitness landscapes: The rough Mount Fuji model. Genetics 2014, 198, 699–721. [Google Scholar] [CrossRef] [PubMed]
- Kingman, J. A simple model for the balance between selection and mutation. J. Appl. Probab. 1978, 15, 1–12. [Google Scholar] [CrossRef]
- Guerois, R.; Nielsen, J.E.; Serrano, L. Predicting changes in the stability of proteins and protein complexes: A study of more than 1000 mutations. J. Mol. Biol. 2002, 320, 369–387. [Google Scholar] [CrossRef]
- Miyazawa, S.; Jernigan, R.L. Residue—Residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996, 256, 623–644. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.; Bornberg-Bauer, E. Perspectives on protein evolution from simple exact models. Appl. Bioinform. 2002, 1, 121–144. [Google Scholar]
- Tokuriki, N.; Stricher, F.; Schymkowitz, J.; Serrano, L.; Tawfik, D.S. The stability effects of protein mutations appear to be universally distributed. J. Mol. Biol. 2007, 369, 1318–1332. [Google Scholar] [CrossRef] [PubMed]
- Zeldovich, K.B.; Chen, P.; Shakhnovich, E.I. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc. Natl. Acad. Sci. USA 2007, 104, 16152–16157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wylie, C.S.; Shakhnovich, E.I. A biophysical protein folding model accounts for most mutational fitness effects in viruses. Proc. Natl. Acad. Sci. USA 2011, 108, 9916–9921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazawa, S. Selection maintaining protein stability at equilibrium. J. Theor. Biol. 2016, 391, 21–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bloom, J.D.; Raval, A.; Wilke, C.O. Thermodynamics of neutral protein evolution. Genetics 2007, 175, 255–266. [Google Scholar] [CrossRef] [PubMed]
- Serrano, L.; Day, A.G.; Fersht, A.R. Step-wise mutation of barnase to binase: A procedure for engineering increased stability of proteins and an experimental analysis of the evolution of protein stability. J. Mol. Biol. 1993, 233, 305–312. [Google Scholar] [CrossRef] [PubMed]
- Serohijos, A.W.; Shakhnovich, E.I. Contribution of selection for protein folding stability in shaping the patterns of polymorphisms in coding regions. Mol. Biol. Evol. 2013, 31, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Van Nimwegen, E.; Crutchfield, J.P.; Huynen, M. Neutral evolution of mutational robustness. Proc. Natl. Acad. Sci. USA 1999, 96, 9716–9720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galton, F. Regression towards mediocrity in hereditary stature. J. Anthropol. Inst. G. B. Irel. 1886, 15, 246–263. [Google Scholar] [CrossRef]
- Lynch, M.; Walsh, B. Genetics and Analysis of Quantitative Traits; Sinauer: Sunderland, MA, USA, 1998; Volume 1. [Google Scholar]
- Kimura, M.; Crow, J.F. Effect of overall phenotypic selection on genetic change at individual loci. Proc. Natl. Acad. Sci. USA 1978, 75, 6168–6171. [Google Scholar] [CrossRef] [PubMed]
- Draghi, J.A.; Plotkin, J.B. Selection biases the prevalence and type of epistasis along adaptive trajectories. Evolution 2013, 67, 3120–3131. [Google Scholar] [CrossRef] [PubMed]
- Greene, D.; Crona, K. The changing geometry of a fitness landscape along an adaptive walk. PLoS Comput. Biol. 2014, 10, e1003520. [Google Scholar] [CrossRef] [PubMed]
- Blanquart, F.; Achaz, G.; Bataillon, T.; Tenaillon, O. Properties of selected mutations and genotypic landscapes under Fisher’s geometric model. Evolution 2014, 68, 3537–3554. [Google Scholar] [CrossRef] [PubMed]
- Drummond, D.A.; Wilke, C.O. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 2008, 134, 341–352. [Google Scholar] [CrossRef] [PubMed]
- Gavrilets, S.; Gravner, J. Percolation on the fitness hypercube and the evolution of reproductive isolation. J. Theor. Biol. 1997, 184, 51–64. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.A.; Pollock, D.D. The tangled bank of amino acids. Protein Sci 2016, 25, 1354–1362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teufel, A.I.; Wilke, C.O. Accelerated simulation of evolutionary trajectories in origin-fixation models. J. R. Soc. Interface 2017, 14, 20160906. [Google Scholar] [CrossRef] [PubMed]
- Naumenko, S.A.; Kondrashov, A.S.; Bazykin, G.A. Fitness conferred by replaced amino acids declines with time. Biol. Lett. 2012, 8, 825–828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McCandlish, D.M.; Shah, P.; Plotkin, J.B. Epistasis and the dynamics of reversion in molecular evolution. Genetics 2016, 203, 1335–1351. [Google Scholar] [CrossRef] [PubMed]
- Berg, O.G.; von Hippel, P.H. Selection of DNA binding sites by regulatory proteins: Statistical-mechanical theory and application to operators and promoters. J. Mol. Biol. 1987, 193, 723–743. [Google Scholar] [CrossRef]
- Wunderlich, Z.; Mirny, L.A. Different gene regulation strategies revealed by analysis of binding motifs. Trends Genet. 2009, 25, 434–440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Socolich, M.; Lockless, S.W.; Russ, W.P.; Lee, H.; Gardner, K.H.; Ranganathan, R. Evolutionary information for specifying a protein fold. Nature 2005, 437, 512. [Google Scholar] [CrossRef] [PubMed]
- Bradley, R.S. Estimation of bias and variance of measurements made from tomography scans. Meas. Sci. Technol. 2016, 27. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posfai, A.; Zhou, J.; Plotkin, J.B.; Kinney, J.B.; McCandlish, D.M. Selection for Protein Stability Enriches for Epistatic Interactions. Genes 2018, 9, 423. https://doi.org/10.3390/genes9090423
Posfai A, Zhou J, Plotkin JB, Kinney JB, McCandlish DM. Selection for Protein Stability Enriches for Epistatic Interactions. Genes. 2018; 9(9):423. https://doi.org/10.3390/genes9090423
Chicago/Turabian StylePosfai, Anna, Juannan Zhou, Joshua B. Plotkin, Justin B. Kinney, and David M. McCandlish. 2018. "Selection for Protein Stability Enriches for Epistatic Interactions" Genes 9, no. 9: 423. https://doi.org/10.3390/genes9090423




