Dual Graph Partitioning Highlights a Small Group of Pseudoknot-Containing RNA Submotifs
Abstract
1. Introduction
2. Materials and Methods
2.1. RNA Dual Graph Representation
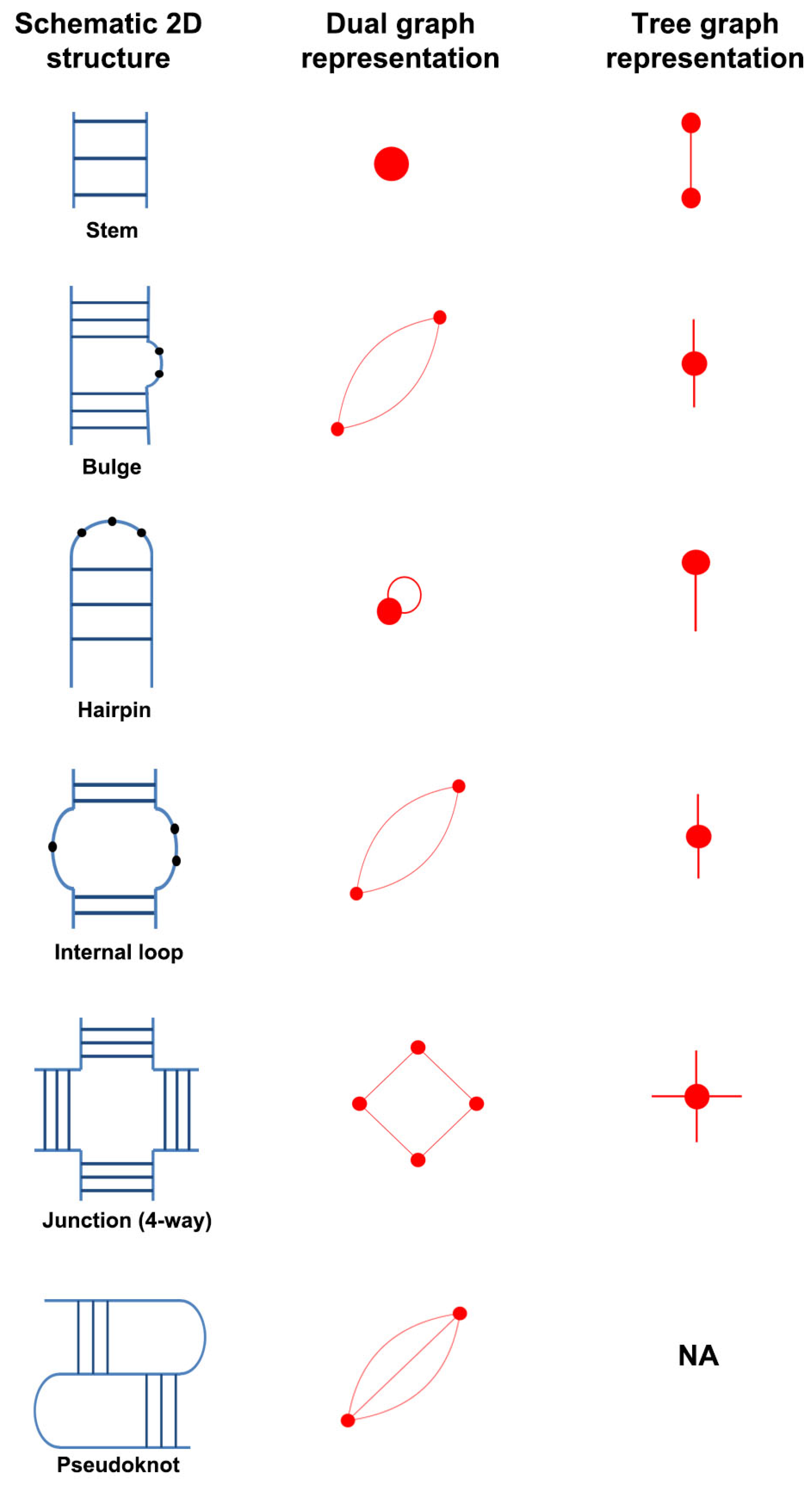
- An RNA stem (or helix) with at least two canonical base pairs is considered as a vertex.
- Each loop strand between two helices is denoted as an edge. Single-residue bulges and internal loops with only one nucleotide in each strand are ignored.
- Uninterrupted hairpin loops (including helical ends) are represented as self loops.
- Unpaired bases or helical ends at the 5 and 3 ends of RNA molecules are not represented.
2.2. Dual Graph Enumeration
2.3. Dual Graph Partitioning Algorithm
2.4. Representative Set of RNA Structures
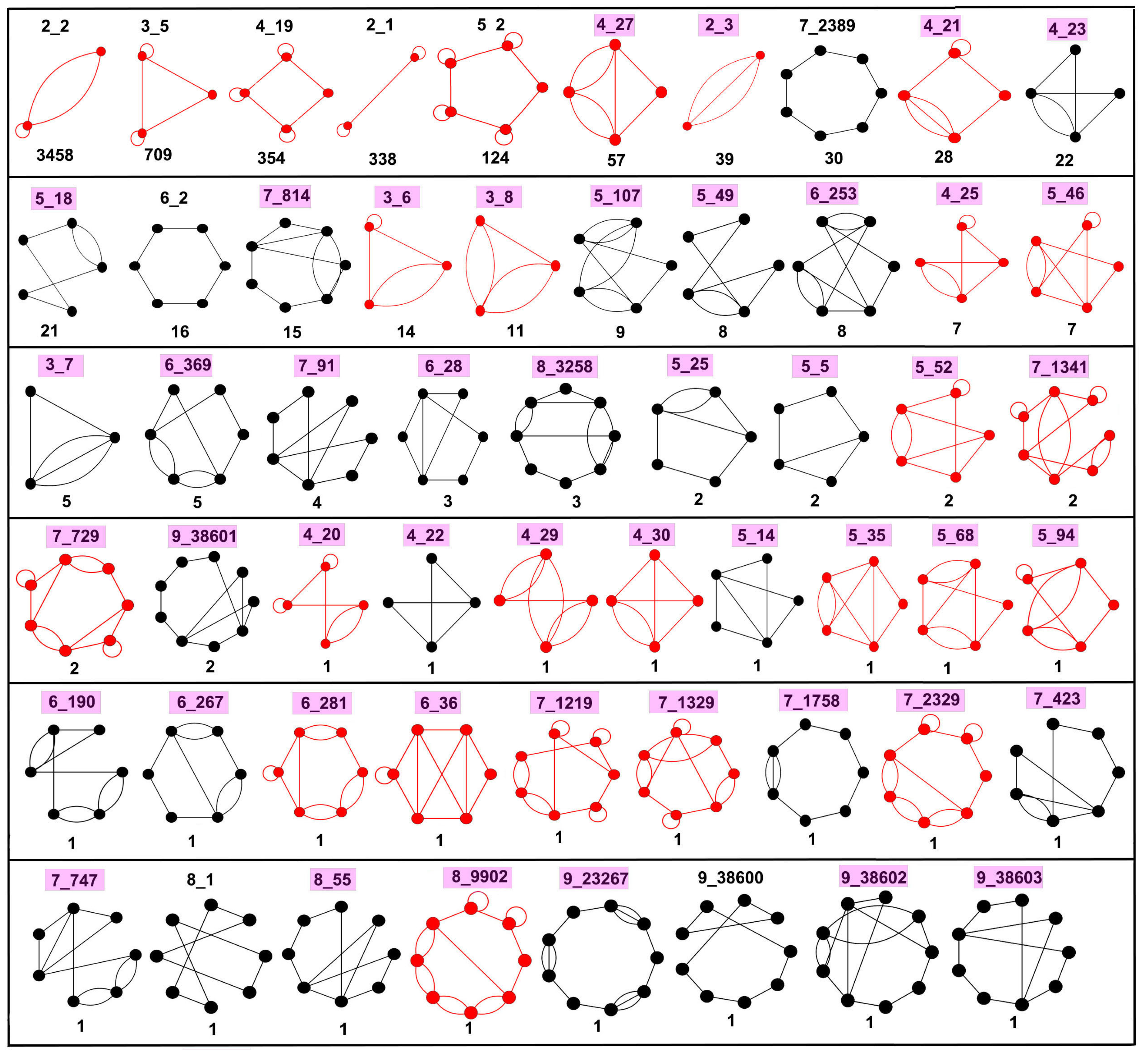
2.5. Defining Existing Dual Graph Topologies
3. Results
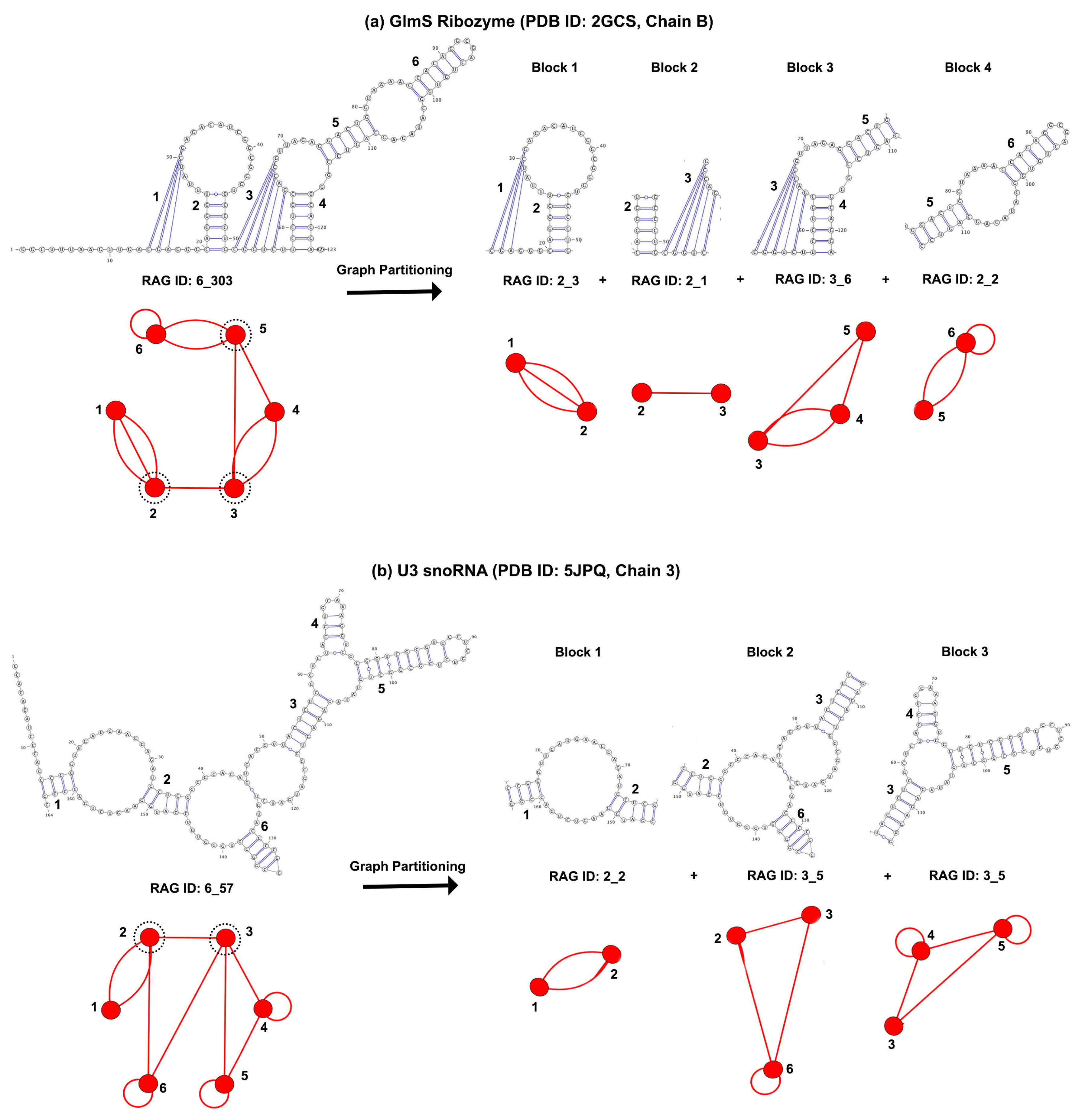
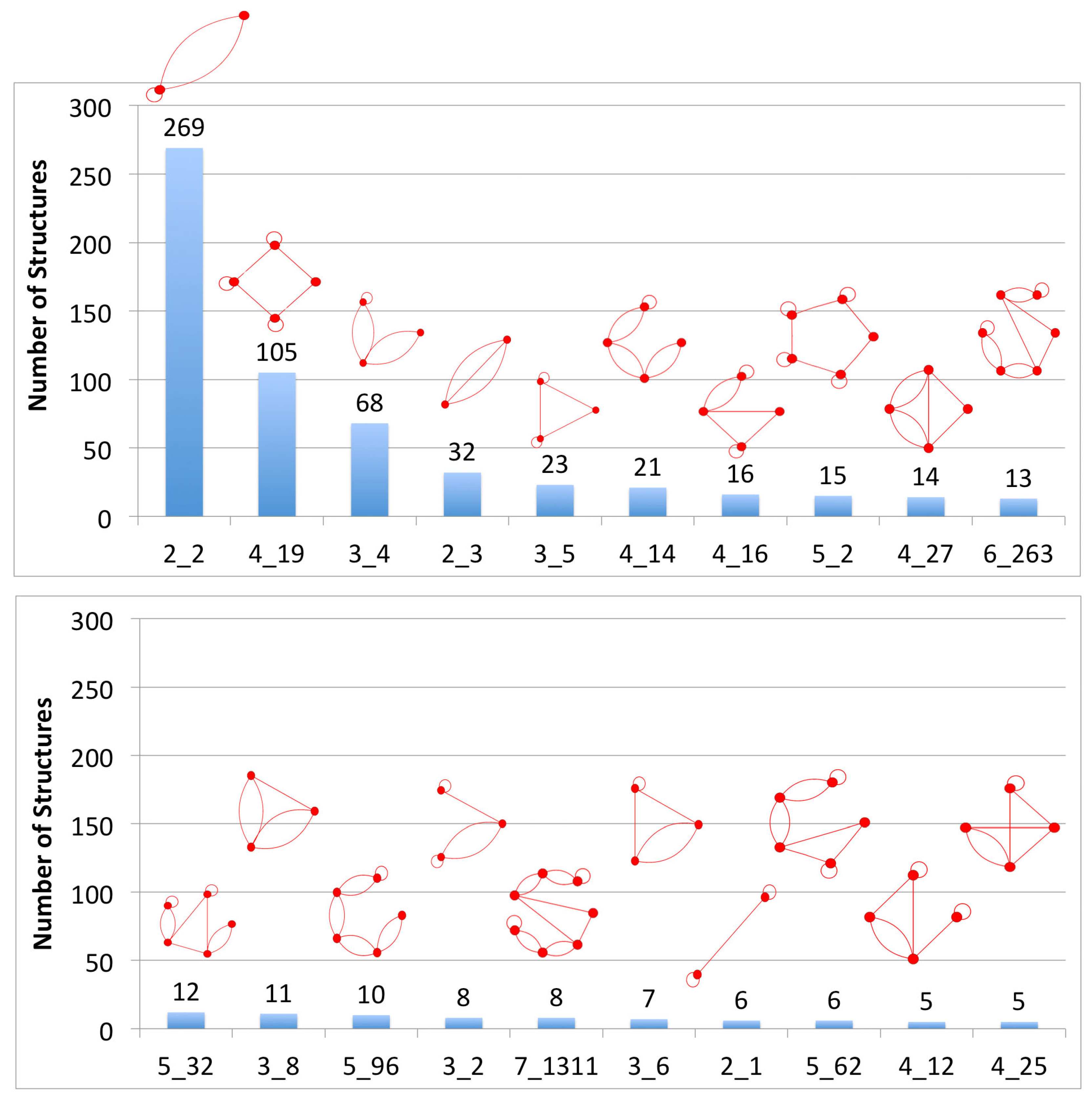
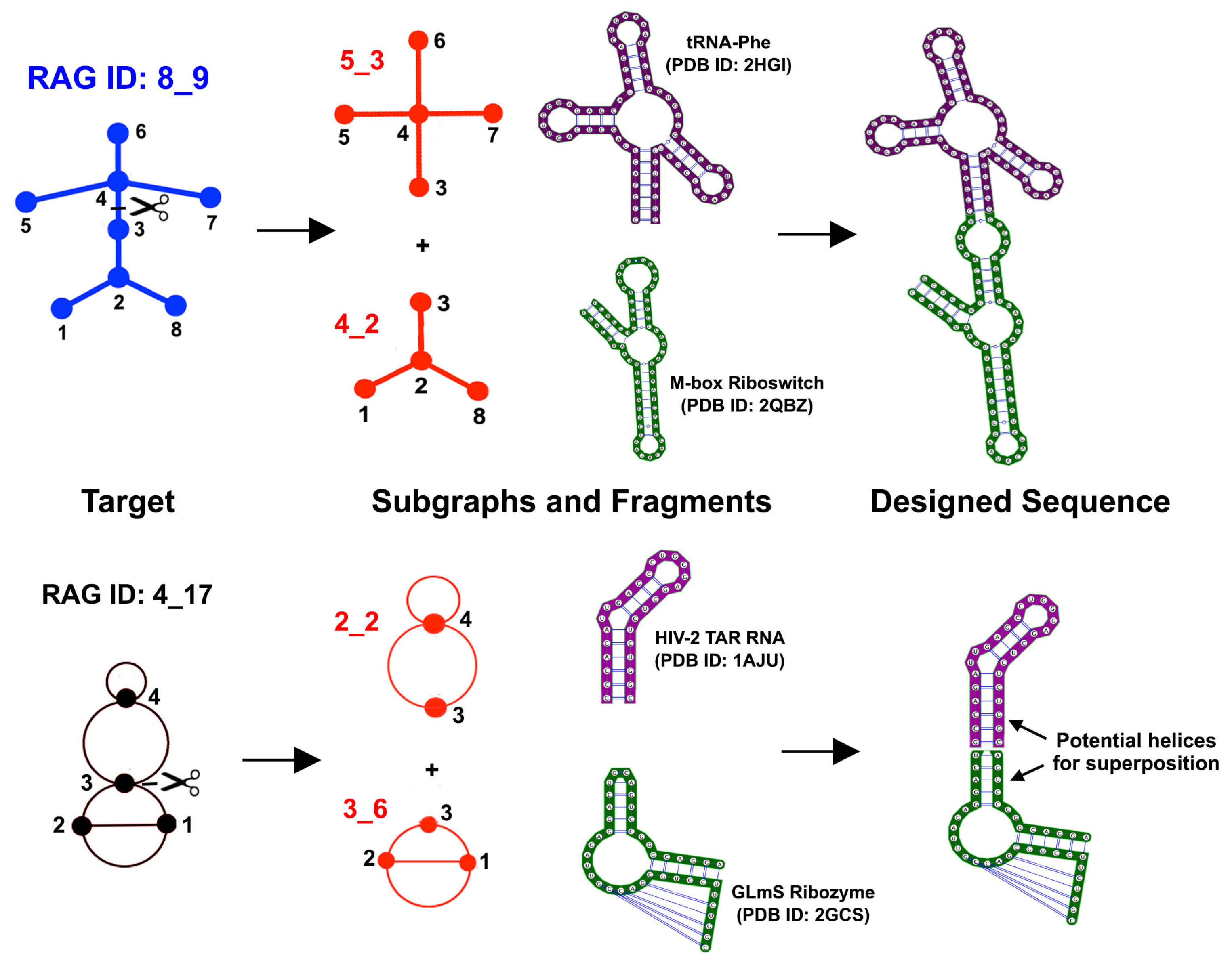
3.1. Partitioning Dual Graphs into Subgraphs
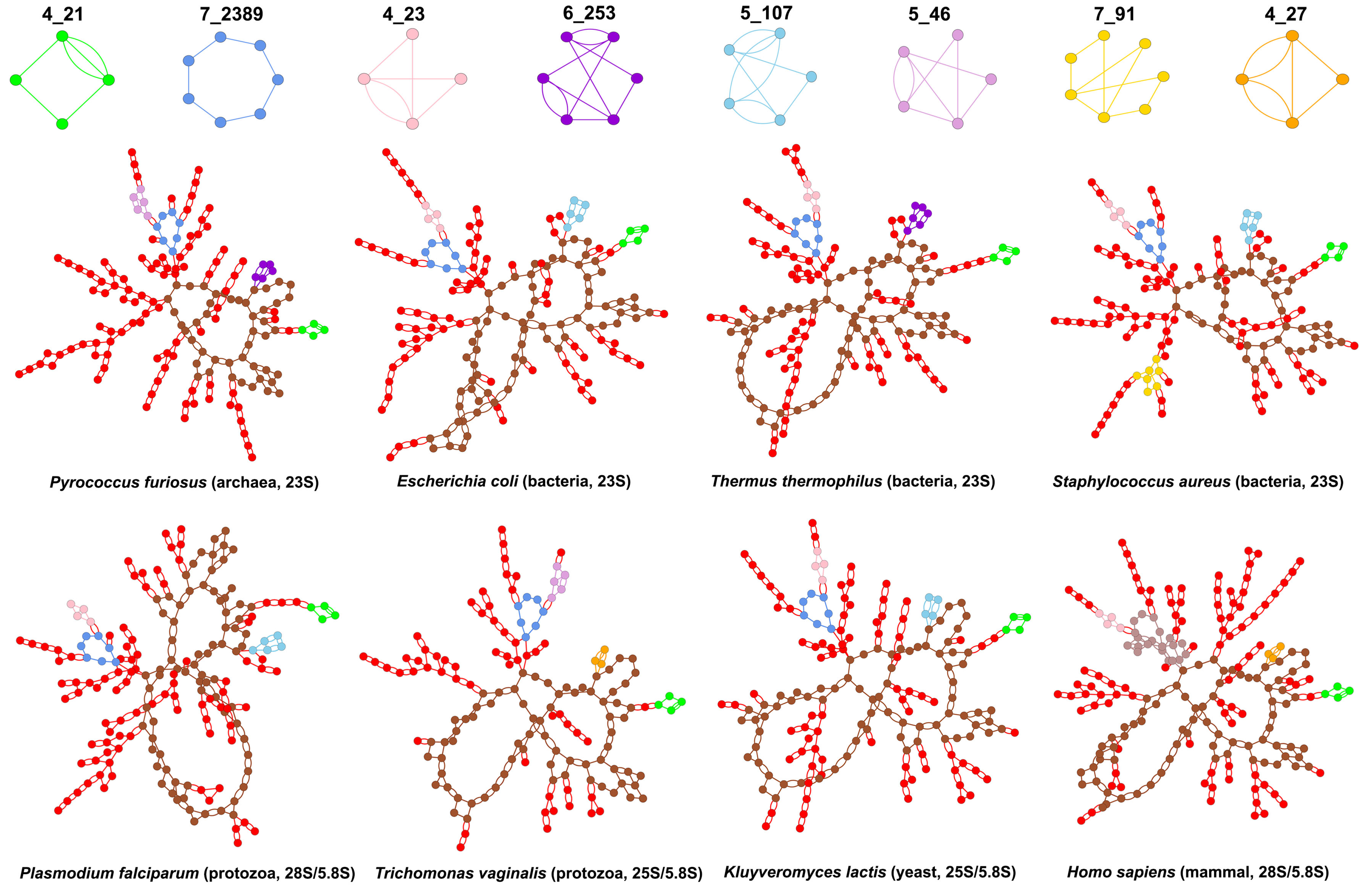
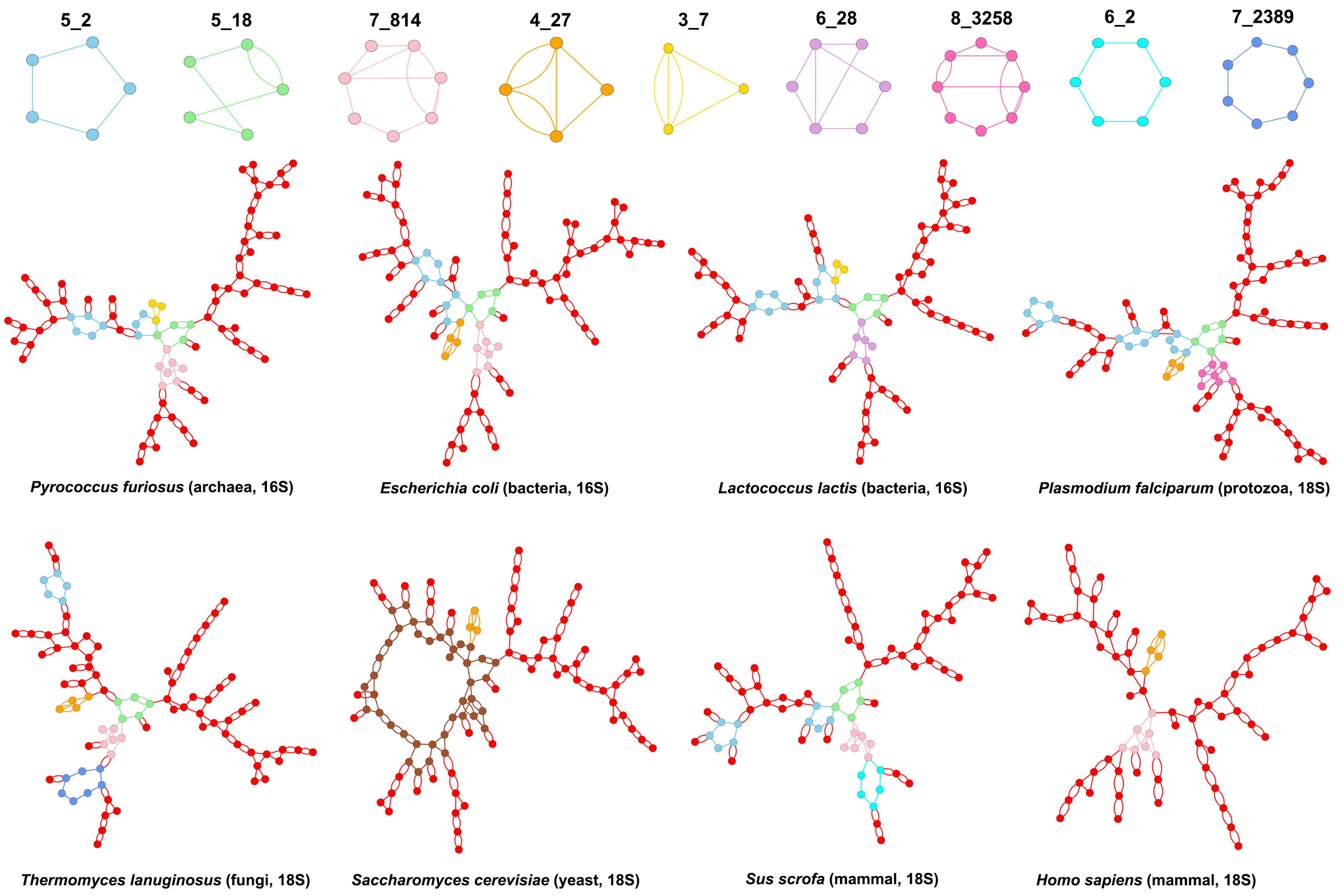
3.2. Submotifs in Ribosomal RNAs
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crick, F. Central dogma of molecular biology. Nature 1970, 227, 561–563. [Google Scholar] [CrossRef] [PubMed]
- Kaikkonen, M.U.; Lam, M.T.; Glass, C.K. Non-coding RNAs as regulators of gene expression and epigenetics. Cardiovasc. Res. 2011, 90, 430–440. [Google Scholar] [CrossRef] [PubMed]
- Patil, V.S.; Zhou, R.; Rana, T.M. Gene regulation by non-coding RNAs. Crit. Rev. Biochem. Mol. Biol. 2014, 49, 16–32. [Google Scholar] [CrossRef] [PubMed]
- Lilley, D.M.J. Mechanisms of RNA catalysis. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 2910–2917. [Google Scholar] [CrossRef] [PubMed]
- Wilson, T.J.; Liu, Y.; Lilley, D.M.J. Ribozymes and the mechanisms that underlie RNA catalysis. Front. Chem. Sci. Eng. 2016, 10, 178–185. [Google Scholar] [CrossRef]
- Tinoco, I.; Bustamante, C. How RNA folds. J. Mol. Biol. 1999, 293, 271–281. [Google Scholar] [CrossRef] [PubMed]
- Brion, P.; Westhof, E. Hierarchy and dynamics of RNA folding. Ann. Rev. Biophys. Biomol. Struct. 1997, 26, 113–137. [Google Scholar] [CrossRef] [PubMed]
- Schlick, T.; Pyle, A.M. Opportunities and challenges in RNA structural modeling and design. Biophys. J. 2017, 113, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Pyle, A.M.; Schlick, T. Challenges in RNA structural modeling and design. J. Mol. Biol. 2016, 428, 733–735. [Google Scholar] [CrossRef] [PubMed]
- Laing, C.; Schlick, T. Computational approaches to RNA structure prediction, analysis, and design. Curr. Opin. Struct. Biol. 2011, 21, 306–318. [Google Scholar] [CrossRef] [PubMed]
- Dawson, W.K.; Maciejczyk, M.; Jankowska, E.J.; Bujnicki, J.M. Coarse-grained modeling of RNA 3D structure. Methods 2016, 103, 138–156. [Google Scholar] [CrossRef] [PubMed]
- Tan, R.K.; Petrov, A.S.; Harvey, S.C. YUP: A Molecular simulation program for coarse-grained and multi-scaled models. J. Chem. Theory Comput. 2006, 2, 529–540. [Google Scholar] [CrossRef] [PubMed]
- Jonikas, M.A.; Radmer, R.J.; Laederach, A.; Das, R.; Pearlman, S.; Herschlag, D.; Altman, R.B. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA 2009, 15, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Krokhotin, A.; Houlihan, K.; Dokholyan, N.V. iFoldRNA v2: Folding RNA with constraints. Bioinformatics 2015, 31, 2891–2893. [Google Scholar] [CrossRef] [PubMed]
- Mustoe, A.M.; Al-Hashimi, H.M.; Brooks, C.L. Coarse grained models reveal essential contributions of topological constraints to the conformational free energy of RNA Bulges. J. Phys. Chem. B 2014, 118, 2615–2627. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, S.J. Physics-based RNA structure prediction. Biophys. Rep. 2015, 1, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Boniecki, M.J.; Lach, G.; Dawson, W.K.; Tomala, K.; Lukasz, P.; Soltysinski, T.; Rother, K.M.; Bujnicki, J.M. SimRNA: A coarse-grained method for RNA folding simulations and 3D structure prediction. Nucl. Acid. Res. 2015, 44, e63. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Bell, D.R.; Shi, Y.; Ren, P. RNA 3D Structure prediction by using a coarse-grained model and experimental data. J. Phys. Chem. B 2013, 117, 3135–3144. [Google Scholar] [CrossRef] [PubMed]
- Cragnolini, T.; Laurin, Y.; Derreumaux, P.; Pasquali, S. Coarse-grained HiRE-RNA model for ab Initio RNA folding beyond simple molecules, including noncanonical and multiple base pairings. J. Chem. Theory Comput. 2015, 11, 3510–3522. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Fuhr, K.N.; Schlick, T. Graph applications to RNA structure and function. In Biophysics of RNA Folding; Russell, R., Ed.; Springer: New York, NY, USA, 2013; pp. 23–51. [Google Scholar]
- Kim, N.; Petingi, L.; Schlick, T. Network theory tools for RNA modeling. WSEAS Trans. Math. 2013, 9, 941–955. [Google Scholar] [PubMed]
- Schlick, T. Adventures with RNA Graphs. Methods 2018. [Google Scholar] [CrossRef] [PubMed]
- Waterman, M. Secondary structure of single-stranded nucleic acids. Adv. Math. Suppl. Stud. 1978, 1, 167–212. [Google Scholar]
- Nussinov, R.; Jacobson, A.B. Fast algorithm for predicting the secondary structure of single-stranded RNA. Proc. Natl. Acad. Sci. USA 1980, 77, 6309–6313. [Google Scholar] [CrossRef] [PubMed]
- Le, S.; Nussinov, R.; Maizel, J. Tree graphs of RNA secondary structures and their comparisons. Comput. Biomed. Res. 1989, 22, 461–473. [Google Scholar] [CrossRef]
- Shapiro, B.A.; Zhang, K. Comparing multiple RNA secondary structures using tree comparisons. Bioinformatics 1990, 6, 309–318. [Google Scholar] [CrossRef]
- Reinharz, V.; Soulé, A.; Westhof, E.; Waldispühl, J.; Denise, A. Mining for recurrent long-range interactions in RNA structures reveals embedded hierarchies in network families. Nucl. Acids Res. 2018, 46, 3841–3851. [Google Scholar] [CrossRef] [PubMed]
- Gan, H.H.; Pasquali, S.; Schlick, T. Exploring the repertoire of RNA secondary motifs using graph theory; implications for RNA design. Nucl. Acids Res. 2003, 31, 2926–2943. [Google Scholar] [CrossRef] [PubMed]
- Gan, H.H.; Fera, D.; Zorn, J.; Shiffeldrim, N.; Tang, M.; Laserson, U.; Kim, N.; Schlick, T. RAG: RNA-As-Graphs database—Concepts, analysis, and features. Bioinformatics 2004, 20, 1285–1291. [Google Scholar] [CrossRef] [PubMed]
- Pasquali, S.; Gan, H.H.; Schlick, T. Modular RNA architecture revealed by computational analysis of existing pseudoknots and ribosomal RNAs. Nucl. Acids Res. 2005, 33, 1384–1398. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Zheng, Z.; Elmetwaly, S.; Schlick, T. RNA Graph Partitioning for the discovery of RNA modularity: A novel application of graph partition algorithm to biology. PLoS ONE 2014, 9, e106074. [Google Scholar] [CrossRef] [PubMed]
- Shu, W.; Bo, X.; Zheng, Z.; Wang, S. A novel representation of RNA secondary structure based on element-contact graphs. BMC Bioinform. 2008, 9, 188. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Li, K.; Gribskov, M. Accurate classification of RNA structures using topological fingerprints. PLoS ONE 2016, 11, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Shiffeldrim, N.; Gan, H.H.; Schlick, T. Candidates for novel RNA topologies. J. Mol. Biol. 2004, 341, 1129–1144. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Laederach, A.; Ramos, S.B.V.; Schlick, T. A pipeline for computational design of novel RNA-like topologies. Nucl. Acid. Res. 2018. [Google Scholar] [CrossRef]
- Baba, N.; Elmetwaly, S.; Kim, N.; Schlick, T. Predicting large RNA-Like topologies by a knowledge-based clustering approach. J. Mol. Biol. 2016, 428, 811–821. [Google Scholar] [CrossRef] [PubMed]
- Fera, D.; Kim, N.; Shiffeldrim, N.; Zorn, J.; Laserson, U.; Gan, H.H.; Schlick, T. RAG: RNA-As-Graphs web resource. BMC Bioinform. 2004, 5, 88. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Laing, C.; Elmetwaly, S.; Jung, S.; Curuksu, J.; Schlick, T. Graph-based sampling for approximating global helical topologies of RNA. Proc. Natl. Acad. Sci. USA 2014, 111, 4079–4084. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Zahran, M.; Schlick, T. Chapter five—Computational Prediction of Riboswitch Tertiary Structures Including Pseudoknots by RAGTOP: A Hierarchical Graph Sampling Approach. In Computational Methods for Understanding Riboswitches; Chen, S.J., Burke-Aguero, D.H., Eds.; Methods in Enzymology; Academic Press: Waltham, MA, USA, 2015; Volume 553, pp. 115–135. [Google Scholar] [CrossRef]
- Bayrak, C.S.; Kim, N.; Schlick, T. Using sequence signatures and kink-turn motifs in knowledge-based statistical potentials for RNA structure prediction. Nucl. Acids Res. 2017, 45, 5414–5422. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Schlick, T. F-RAG: Generating atomic models from RNA graphs using fragment assembly. J. Mol. Biol. 2017, 429, 3587–3605. [Google Scholar] [CrossRef] [PubMed]
- Izzo, J.A.; Kim, N.; Elmetwaly, S.; Schlick, T. RAG: An update to the RNA-As-Graphs resource. BMC Bioinform. 2011, 12, 219. [Google Scholar] [CrossRef] [PubMed]
- Staple, D.W.; Butcher, S.E. Pseudoknots: RNA structures with diverse functions. PLoS Biol. 2005, 3, e213. [Google Scholar] [CrossRef] [PubMed]
- Brierley, I.; Gilbert, R.J.; Pennell, S. RNA pseudoknots and the regulation of protein synthesis. Biochem. Soc. Trans. 2008, 36, 684–689. [Google Scholar] [CrossRef] [PubMed]
- Gultyaev, A.P.; Olsthoorn, R.C.; Pleij, C.W.; Westhof, E. RNA Structure: Pseudoknots. eLS 2012. [Google Scholar] [CrossRef]
- Zahran, M.; Bayrak, C.S.; Elmetwaly, S.; Schlick, T. RAG-3D: A search tool for RNA 3D substructures. Nucl. Acids Res. 2015, 43, 9474–9488. [Google Scholar] [CrossRef] [PubMed]
- Petingi, L.; Schlick, T. Partitioning RNAs into pseudonotted and pseudoknot-free regions modeled as Dual Graphs. arXiv, 2016; arXiv:1601.04259. [Google Scholar]
- Petingi, L.; Schlick, T. Partitioning and classification of RNA secondary structures into pseudonotted and pseudoknot-free regions using a graph-theoretical approach. IAENG Int. J. Comput. Sci. 2017, 44, 241–246. [Google Scholar]
- Database of RNA Dual Graphs. Available online: http://www.biomath.nyu.edu/?q=rag/dual_vertices.php (accesed on 19 July 2018).
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar]
- Hopcroft, J.; Tarjan, R. Algorithm 447: Efficient algorithms for graph manipulation. Commun. ACM 1973, 16, 372–378. [Google Scholar] [CrossRef]
- Petingi, L. Dual Graph Partitioning Code. Available online: https://github.com/Louis-Petingi/Partition-Algorithm-2/ (accesed on 19 July 2018).
- Representative Set of RNA 3D Structures. Available online: http://rna.bgsu.edu/rna3dhub/nrlist/ (accesed on 19 July 2018).
- Leontis, N.B.; Zirbel, C.L. Nonredundant 3D structure datasets for RNA knowledge extraction and benchmarking. In RNA 3D Structure Analysis and Prediction; Leontis, N., Westhof, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 281–298. [Google Scholar]
- Yang, H.; Jossinet, F.; Leontis, N.; Chen, L.; Westbrook, J.; Berman, H.; Westhof, E. Tools for the automatic identification and classification of RNA base pairs. Nucl. Acids Res. 2003, 31, 3450–3460. [Google Scholar] [CrossRef] [PubMed]
- Butcher, S.E.; Pyle, A.M. The molecular interactions that stabilize RNA tertiary structure: RNA motifs, patterns, and networks. Acc. Chem. Res. 2011, 44, 1302–1311. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, C.; Mohan, S.; Kalahar, B.K.; Williams, L.D. Peeling the onion: Ribosomes are ancient molecular fossils. Mol. Biol. Evol. 2009, 26, 2415–2425. [Google Scholar] [CrossRef] [PubMed]
- Petrov, A.S.; Bernier, C.R.; Hsiao, C.; Norris, A.M.; Kovacs, N.A.; Waterbury, C.C.; Stepanov, V.G.; Harvey, S.C.; Fox, G.E.; Wartell, R.M.; et al. Evolution of the ribosome at atomic resolution. Proc. Natl. Acad. Sci. USA 2014, 111, 10251–10256. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.K.; Lam, T.; Sung, W.K.; Cheung, B.W.; Yiu, S. Structural alignment of RNA with complex pseudoknot structure. J. Comput. Biol. 2011, 18, 97–108. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Byun, Y. PseudoViewer2: Visualization of RNA pseudoknots of any type. Nucl. Acids Res. 2003, 31, 3432–3440. [Google Scholar] [CrossRef] [PubMed]
- Kucharík, M.; Hofacker, I.L.; Stadler, P.F.; Qin, J. Pseudoknots in RNA folding landscapes. Bioinformatics 2016, 32, 187–194. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, S.; Bayrak, C.S.; Petingi, L.; Schlick, T. Dual Graph Partitioning Highlights a Small Group of Pseudoknot-Containing RNA Submotifs. Genes 2018, 9, 371. https://doi.org/10.3390/genes9080371
Jain S, Bayrak CS, Petingi L, Schlick T. Dual Graph Partitioning Highlights a Small Group of Pseudoknot-Containing RNA Submotifs. Genes. 2018; 9(8):371. https://doi.org/10.3390/genes9080371
Chicago/Turabian StyleJain, Swati, Cigdem S. Bayrak, Louis Petingi, and Tamar Schlick. 2018. "Dual Graph Partitioning Highlights a Small Group of Pseudoknot-Containing RNA Submotifs" Genes 9, no. 8: 371. https://doi.org/10.3390/genes9080371
APA StyleJain, S., Bayrak, C. S., Petingi, L., & Schlick, T. (2018). Dual Graph Partitioning Highlights a Small Group of Pseudoknot-Containing RNA Submotifs. Genes, 9(8), 371. https://doi.org/10.3390/genes9080371





