CoreProbe: A Novel Algorithm for Estimating Relative Abundance Based on Metagenomic Reads
Abstract
1. Introduction
2. Methods
2.1. A Finite Mixture and Latent Dirichlet Model
| Algorithm 1 (A finite mixture and latent Dirichlet model for metagenomics). |
| Require the hyperparameter, the total number of reads, the species set, the read-composition distributions Ensure the read dataset R sample the species mixture parametersfor a metagenome repeat 1. sample species 2. sample read untilthe total number of metagenomic readsis reached returnthe read dataset |
2.2. Mixture Parameter Inference and Gibbs Sampling
| Algorithm 2 (Gibbs Sampling Algorithm for the Metagenomic Model). |
| Require:references species, metagenomic reads, hyperparameter Global data:count statistics, read-composition distributions, memory for full conditionals Ensure:mixture parameters //initialization: obtain read-composition distributionsaccording to alignment results zero all count statistics fortodo sample the species indexincrement sampled species count end for//Gibbs sampling whilenot finished do fortododecrement target species count sample a new species index increment sampled species’ count end for ifconverged and a given number of samples generated then returnmixture parameteraccording to the equation end if end while |
3. Results
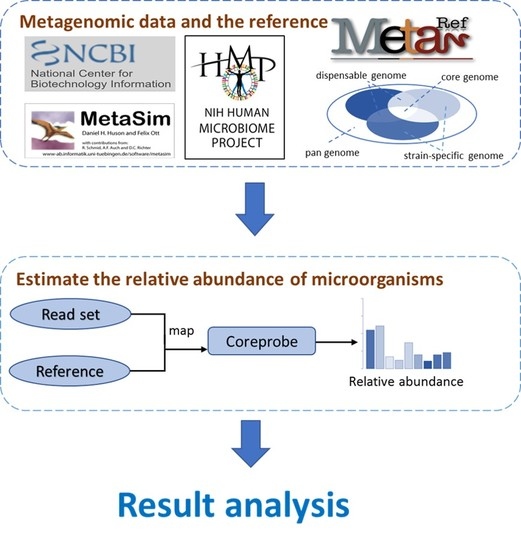
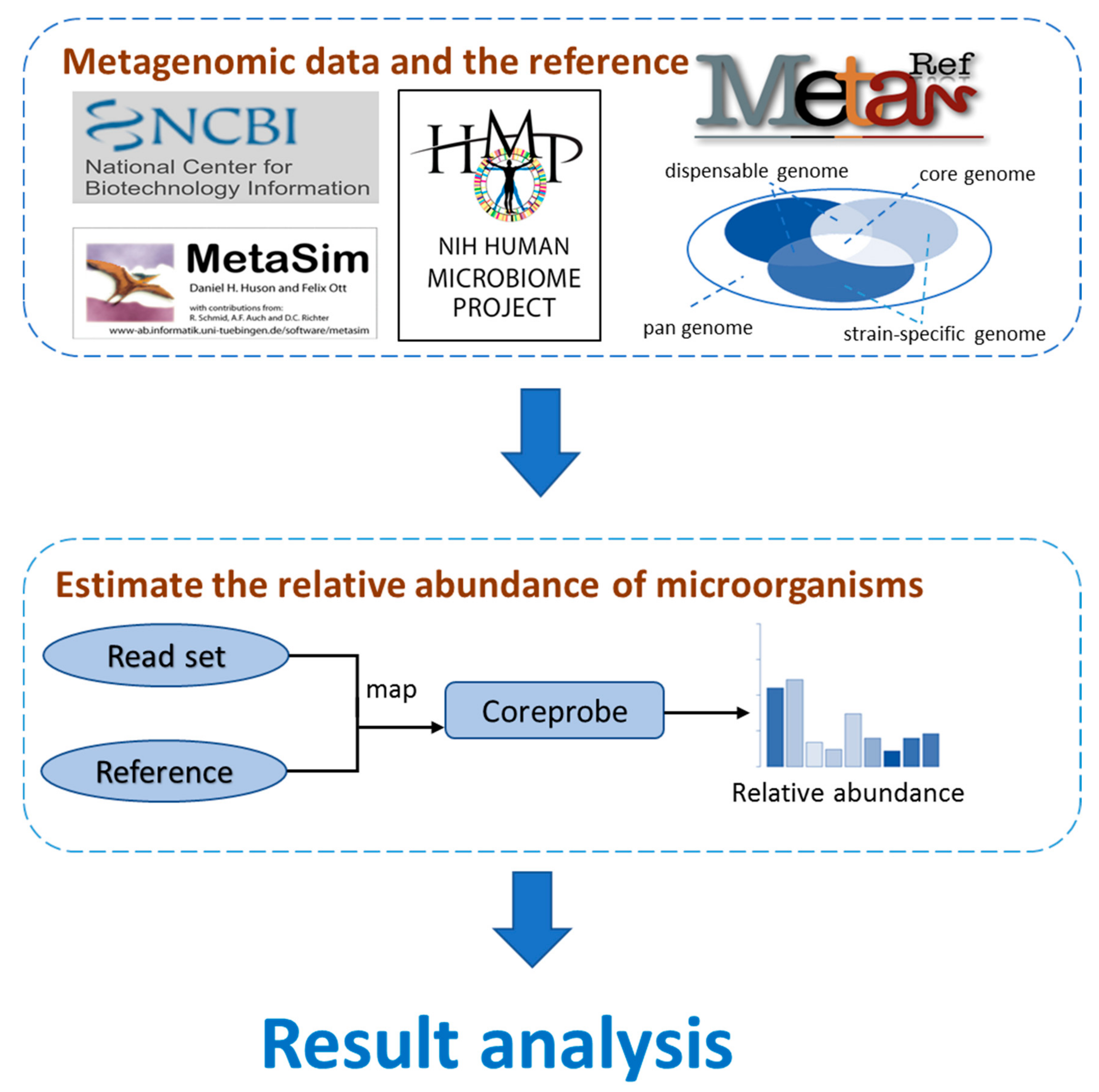
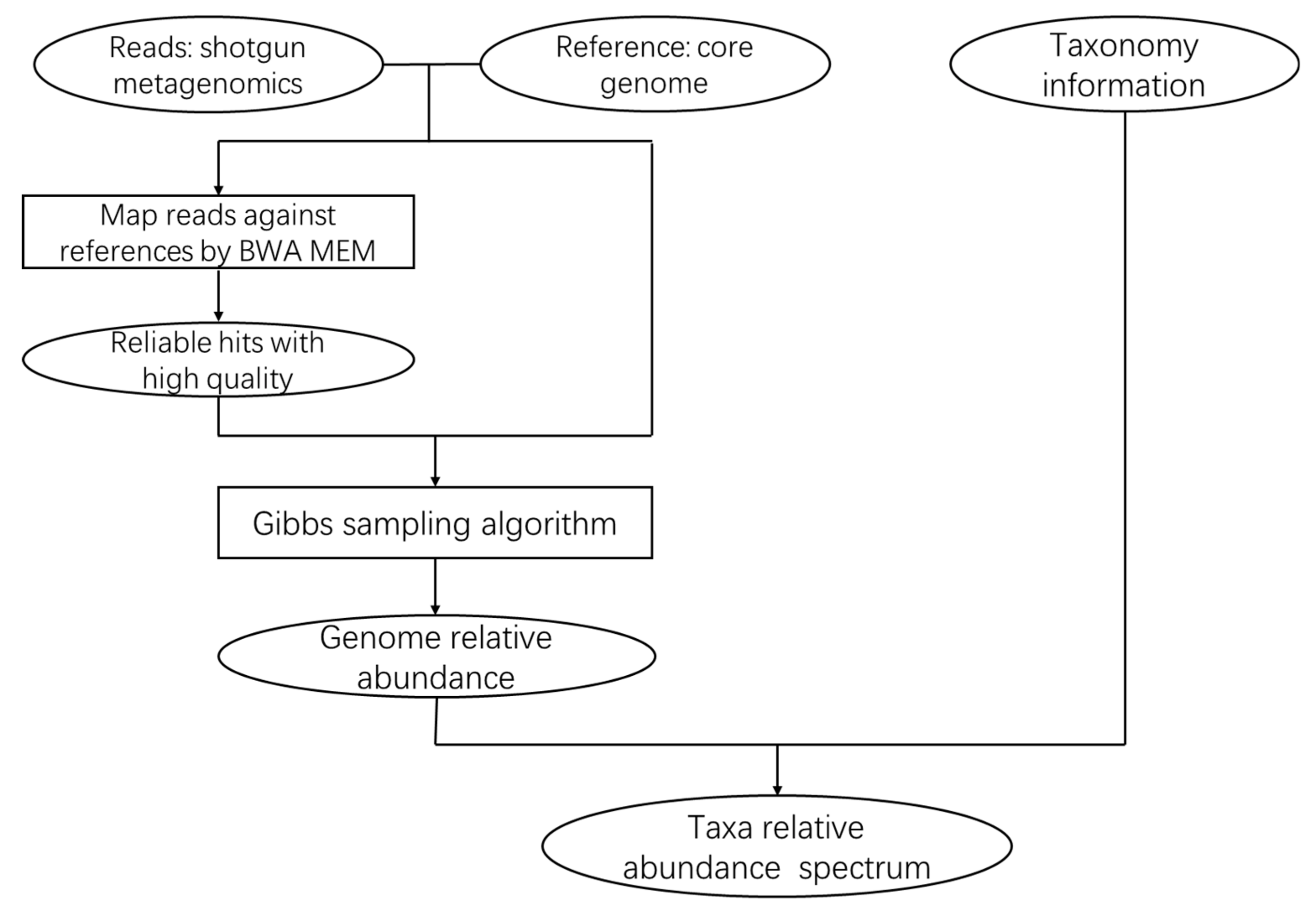
3.1. The CoreProbe Framework
3.2. Simulation Result
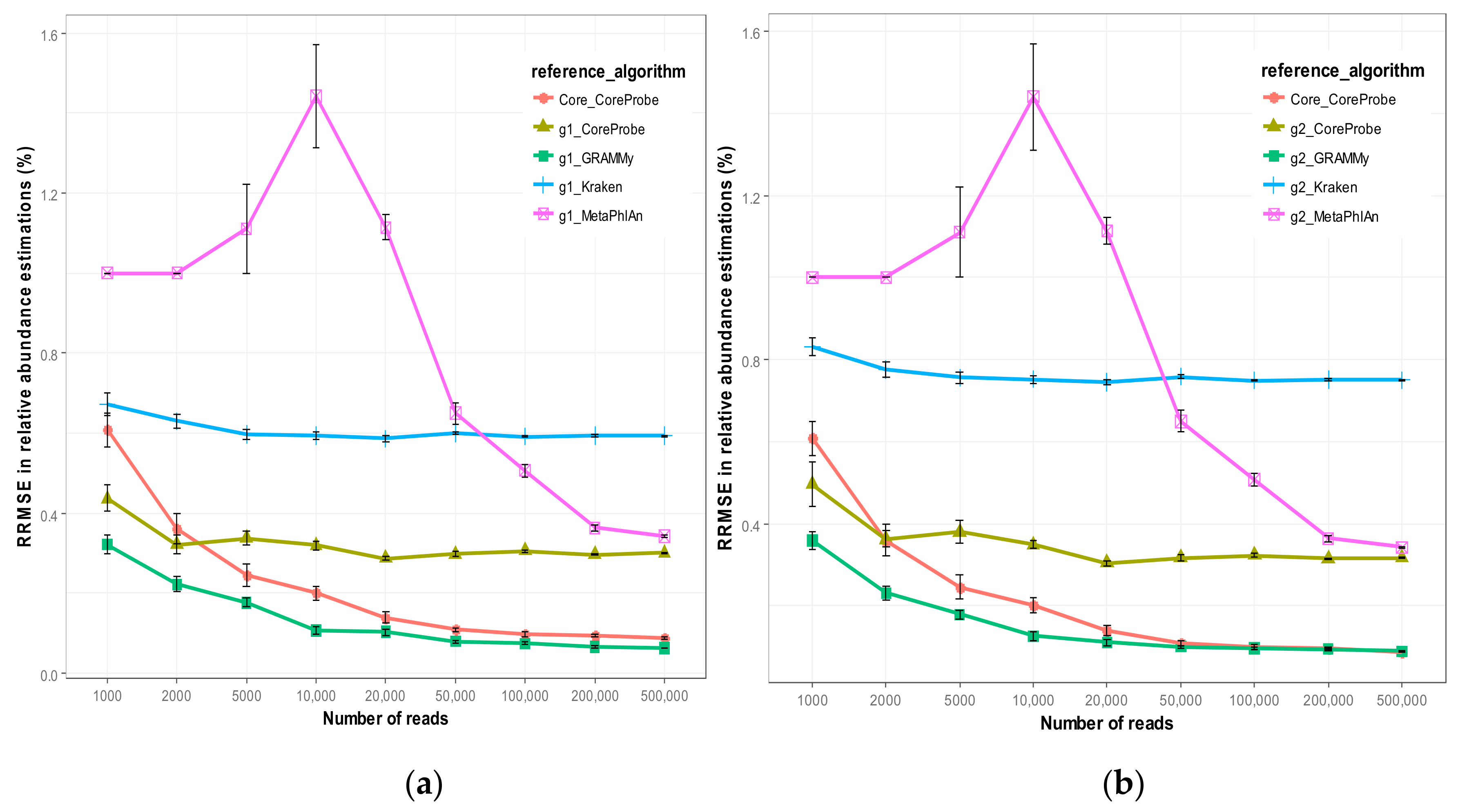
3.2.1. Comparison of Algorithm Accuracy
3.2.2. Comparison of Algorithm Speeds
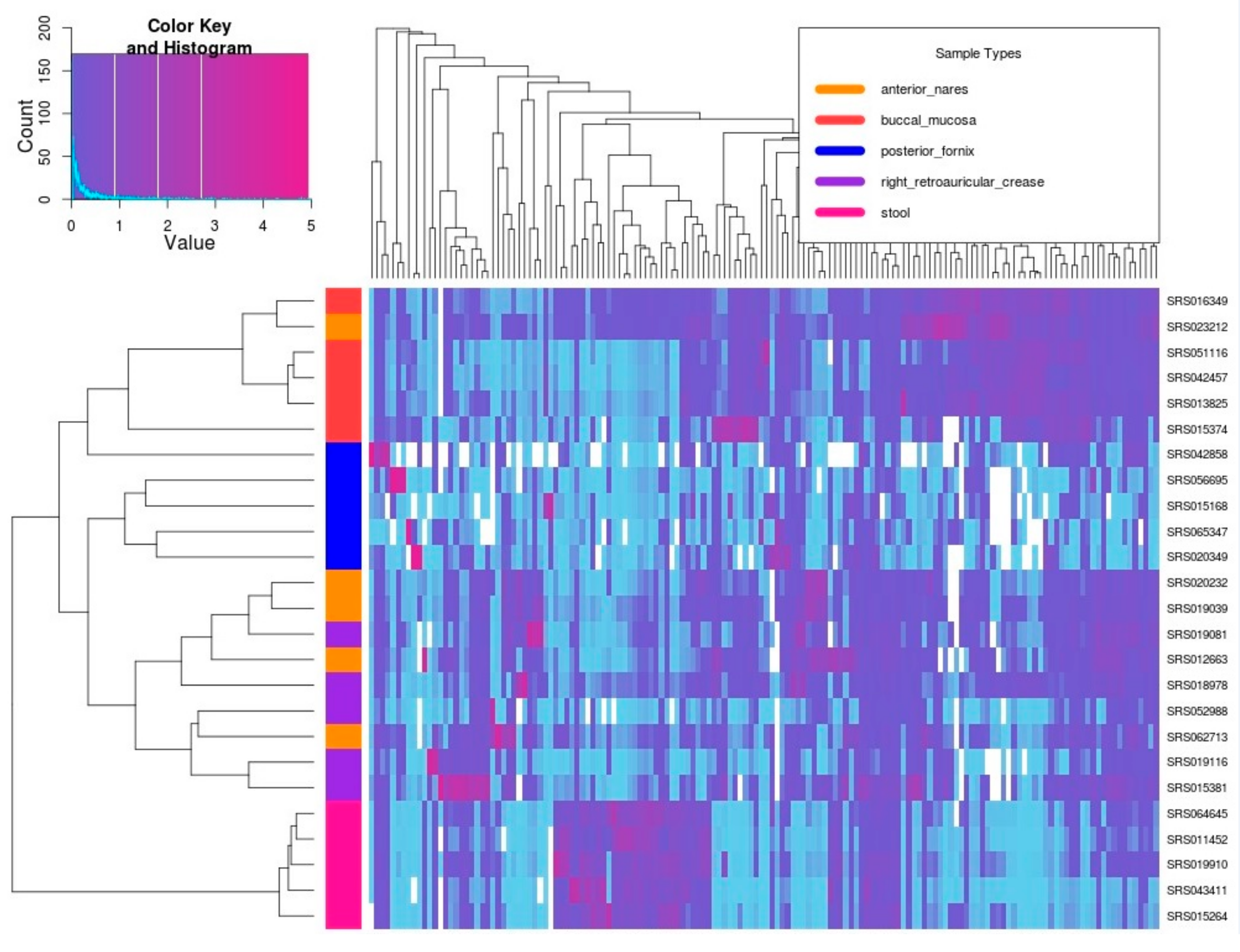
3.3. Real Metagenomic Datasets Analysis
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Barberán, A.; Bates, S.T.; Casamayor, E.O.; Fierer, N. Using network analysis to explore co-occurrence patterns in soil microbial communities. ISME J. 2012, 6, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Allison, S.D.; Lu, Y.; Weihe, C.; Goulden, M.L.; Martiny, A.C.; Treseder, K.K.; Martiny, J.B. Microbial abundance and composition influence litter decomposition response to environmental change. Ecology 2013, 94, 714–725. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yan, Q.; Xie, S.; Hu, W.; Yu, Y.; Hu, Z. Gut microbiota contributes to the growth of fast-growing transgenic common carp (Cyprinus carpio L.). PLoS ONE 2013, 8, e64577. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.I.; Yatsunenko, T.; Manary, M.J.; Trehan, I.; Mkakosya, R.; Cheng, J.; Kau, A.L.; Rich, S.S.; Concannon, P.; Mychaleckyj, J.C. Gut microbiomes of Malawian twin pairs discordant for kwashiorkor. Science 2013, 339, 548–554. [Google Scholar] [CrossRef] [PubMed]
- Vaarala, O. Human intestinal microbiota and type 1 diabetes. Curr. Diabetes Rep. 2013, 13, 601–607. [Google Scholar] [CrossRef] [PubMed]
- Ghoshal, U.C.; Shukla, R.; Ghoshal, U.; Gwee, K.-A.; Ng, S.C.; Quigley, E.M. The gut microbiota and irritable bowel syndrome: Friend or foe? Int. J. Inflamm. 2012, 2012. [Google Scholar] [CrossRef] [PubMed]
- Manichanh, C.; Borruel, N.; Casellas, F.; Guarner, F. The gut microbiota in IBD. Nat. Rev. Gastroenterol. Hepatol. 2012, 9, 599–608. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, C.; Tang, C.; Li, N.; Li, J. Molecular-phylogenetic characterization of the microbiota in ulcerated and non-ulcerated regions in the patients with Crohn’s disease. PLoS ONE 2012, 7, e34939. [Google Scholar] [CrossRef] [PubMed]
- Kostic, A.D.; Gevers, D.; Pedamallu, C.S.; Michaud, M.; Duke, F.; Earl, A.M.; Ojesina, A.I.; Jung, J.; Bass, A.J.; Tabernero, J. Genomic analysis identifies association of Fusobacterium with colorectal carcinoma. Genome Res. 2012, 22, 292–298. [Google Scholar] [CrossRef] [PubMed]
- Kostic, A.D.; Chun, E.; Robertson, L.; Glickman, J.N.; Gallini, C.A.; Michaud, M.; Clancy, T.E.; Chung, D.C.; Lochhead, P.; Hold, G.L. Fusobacterium nucleatum potentiates intestinal tumorigenesis and modulates the tumor-immune microenvironment. Cell Host Microbe 2013, 14, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Marshall, B.J.; Windsor, H.M. The relation of Helicobacter pylori to gastric adenocarcinoma and lymphoma: Pathophysiology, epidemiology, screening, clinical presentation, treatment, and prevention. Med. Clin. 2005, 89, 313–344. [Google Scholar] [CrossRef] [PubMed]
- Teeling, H.; Waldmann, J.; Lombardot, T.; Bauer, M.; Glöckner, F.O. TETRA: A web-service and a stand-alone program for the analysis and comparison of tetranucleotide usage patterns in DNA sequences. BMC Bioinform. 2004, 5, 163. [Google Scholar] [CrossRef] [PubMed]
- Chatterji, S.; Yamazaki, I.; Bai, Z.; Eisen, J. CompostBin: A DNA composition-based algorithm for binning environmental shotgun reads. In Research in Computational Molecular Biology; Springer: Berlin, Germany, 2008; pp. 17–28. [Google Scholar]
- Kelley, D.R.; Salzberg, S.L. Clustering metagenomic sequences with interpolated Markov models. BMC Bioinform. 2010, 11, 544. [Google Scholar] [CrossRef] [PubMed]
- Leung, H.C.; Yiu, S.-M.; Yang, B.; Peng, Y.; Wang, Y.; Liu, Z.; Chen, J.; Qin, J.; Li, R.; Chin, F.Y. A robust and accurate binning algorithm for metagenomic sequences with arbitrary species abundance ratio. Bioinformatics 2011, 27, 1489–1495. [Google Scholar] [CrossRef] [PubMed]
- McHardy, A.C.; Martin, H.G.; Tsirigos, A.; Hugenholtz, P.; Rigoutsos, I. Accurate phylogenetic classification of variable-length DNA fragments. Nat. Methods 2007, 4, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Rosen, G.; Garbarine, E.; Caseiro, D.; Polikar, R.; Sokhansanj, B. Metagenome Fragment Classification Using N-Mer Frequency Profiles. Adv. Bioinf. 2008. [Google Scholar] [CrossRef] [PubMed]
- Diaz, N.N.; Krause, L.; Goesmann, A.; Niehaus, K.; Nattkemper, T.W. TACOA—Taxonomic classification of environmental genomic fragments using a kernelized nearest neighbor approach. BMC Bioinform. 2009, 10, 56. [Google Scholar] [CrossRef] [PubMed]
- Nalbantoglu, O.U.; Way, S.F.; Hinrichs, S.H.; Sayood, K. RAIphy: Phylogenetic classification of metagenomics samples using iterative refinement of relative abundance index profiles. BMC Bioinform. 2011, 12, 41. [Google Scholar] [CrossRef] [PubMed]
- Ames, S.K.; Hysom, D.A.; Gardner, S.N.; Lloyd, G.S.; Gokhale, M.B.; Allen, J.E. Scalable metagenomic taxonomy classification using a reference genome database. Bioinformatics 2013, 29, 2253–2260. [Google Scholar] [CrossRef] [PubMed]
- Wood, D.E.; Salzberg, S.L. Kraken: Ultrafast metagenomic sequence classification using exact alignments. Genome Biol. 2014, 15, R46. [Google Scholar] [CrossRef] [PubMed]
- Ounit, R.; Wanamaker, S.; Close, T.J.; Lonardi, S. CLARK: Fast and accurate classification of metagenomic and genomic sequences using discriminative k-mers. BMC Genom. 2015, 16, 236. [Google Scholar] [CrossRef] [PubMed]
- Brady, A.; Salzberg, S.L. Phymm and PhymmBL: Metagenomic phylogenetic classification with interpolated Markov models. Nat. Methods 2009, 6, 673–676. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, N.J.; Parks, D.H.; Beiko, R.G. Rapid identification of high-confidence taxonomic assignments for metagenomic data. Nucleic Acids Res. 2012, 40, e111. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Chuai, G.; Qi, T.; Shao, F.; Zhou, C.; Zhu, C.; Yang, J.; Yu, Y.; Shi, C.; Kang, N. MetaTopics: An integration tool to analyze microbial community profile by topic model. BMC Genom. 2017, 18, 962. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Fast and accurate short read alignment with Burrows—Wheeler transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef] [PubMed]
- Langmead, B.; Salzberg, S.L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 2012, 9, 357–359. [Google Scholar] [CrossRef] [PubMed]
- Huson, D.H.; Auch, A.F.; Qi, J.; Schuster, S.C. MEGAN analysis of metagenomic data. Genome Res. 2007, 17, 377–386. [Google Scholar] [CrossRef] [PubMed]
- Krause, L.; Diaz, N.N.; Goesmann, A.; Kelley, S.; Nattkemper, T.W.; Rohwer, F.; Edwards, R.A.; Stoye, J. Phylogenetic classification of short environmental DNA fragments. Nucleic Acids Res. 2008, 36, 2230–2239. [Google Scholar] [CrossRef] [PubMed]
- Berger, S.A.; Stamatakis, A. Aligning short reads to reference alignments and trees. Bioinformatics 2011, 27, 2068–2075. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Folino, G.; Jetten, M.S.; Marchiori, E. MTR: Taxonomic annotation of short metagenomic reads using clustering at multiple taxonomic ranks. Bioinformatics 2010, 27, 196–203. [Google Scholar] [CrossRef] [PubMed]
- Angly, F.E.; Willner, D.; Prieto-Davó, A.; Edwards, R.A.; Schmieder, R.; Vega-Thurber, R.; Antonopoulos, D.A.; Barott, K.; Cottrell, M.T.; Desnues, C. The GAAS metagenomic tool and its estimations of viral and microbial average genome size in four major biomes. PLoS Comput. Biol. 2009, 5, e1000593. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.C.; Cram, J.A.; Chen, T.; Fuhrman, J.A.; Sun, F. Accurate genome relative abundance estimation based on shotgun metagenomic reads. PLoS ONE 2011, 6, e27992. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.; Manimaran, S.; Shen, Y.; Perez-Rogers, J.F.; Byrd, A.L.; Castro-Nallar, E.; Crandall, K.A.; Johnson, W.E. PathoScope 2.0: A complete computational framework for strain identification in environmental or clinical sequencing samples. Microbiome 2014, 2, 33. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.S.; Renard, B.Y. Metagenomic abundance estimation and diagnostic testing on species level. Nucleic Acids Res. 2012, 41, e10. [Google Scholar] [CrossRef] [PubMed]
- Morfopoulou, S.; Plagnol, V. Bayesian mixture analysis for metagenomic community profiling. Bioinformatics 2015, 31, 2930–2938. [Google Scholar] [CrossRef] [PubMed]
- Segata, N.; Waldron, L.; Ballarini, A.; Narasimhan, V.; Jousson, O.; Huttenhower, C. Metagenomic microbial community profiling using unique clade-specific marker genes. Nat. Methods 2012, 9, 811–814. [Google Scholar] [CrossRef] [PubMed]
- Sunagawa, S.; Mende, D.R.; Zeller, G.; Izquierdo-Carrasco, F.; Berger, S.A.; Kultima, J.R.; Coelho, L.P.; Arumugam, M.; Tap, J.; Nielsen, H.B. Metagenomic species profiling using universal phylogenetic marker genes. Nat. Methods 2013, 10, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Tettelin, H.; Riley, D.; Cattuto, C.; Medini, D. Comparative genomics: The bacterial pan-genome. Curr. Opin. Microbiol. 2008, 11, 472–477. [Google Scholar] [CrossRef] [PubMed]
- Kashtan, N.; Roggensack, S.E.; Rodrigue, S.; Thompson, J.W.; Biller, S.J.; Coe, A.; Ding, H.; Marttinen, P.; Malmstrom, R.R.; Stocker, R. Single-cell genomics reveals hundreds of coexisting subpopulations in wild Prochlorococcus. Science 2014, 344, 416–420. [Google Scholar] [CrossRef] [PubMed]
- Ley, R.E.; Peterson, D.A.; Gordon, J.I. Ecological and evolutionary forces shaping microbial diversity in the human intestine. Cell 2006, 124, 837–848. [Google Scholar] [CrossRef] [PubMed]
- Vernikos, G.; Medini, D.; Riley, D.R.; Tettelin, H. Ten years of pan-genome analyses. Curr. Opin. Microbiol. 2015, 23, 148–154. [Google Scholar] [CrossRef] [PubMed]
- Stecher, B.; Denzler, R.; Maier, L.; Bernet, F.; Sanders, M.J.; Pickard, D.J.; Barthel, M.; Westendorf, A.M.; Krogfelt, K.A.; Walker, A.W. Gut inflammation can boost horizontal gene transfer between pathogenic and commensal Enterobacteriaceae. Proc. Natl. Acad. Sci. USA 2012, 109, 1269–1274. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar] [PubMed]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Heinrich, G. Parameter Estimation for Text Analysis; Technical Report; University of Leipzig and Vsonix GmbH: Darmstadt, Germany, 2008. [Google Scholar]
- Richter DC, Ott F, Auch AF, Schmid R, Huson DH: MetaSim—A sequencing simulator for genomics and metagenomics. PLoS ONE 2008, 3, e3373.
- Shakya, M.; Quince, C.; Campbell, J.H.; Yang, Z.K.; Schadt, C.W.; Podar, M. Comparative metagenomic and rRNA microbial diversity characterization using archaeal and bacterial synthetic communities. Environ. Microbiol. 2013, 15, 1882–1899. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Schirmer, M.; Ijaz, U.Z.; D’Amore, R.; Hall, N.; Sloan, W.T.; Quince, C. Insight into biases and sequencing errors for amplicon sequencing with the Illumina MiSeq platform. Nucleic Acids Res. 2015, 43, e37. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Oshima, T.; Morimoto, T.; Ikeda, S.; Yoshikawa, H.; Shiwa, Y.; Ishikawa, S.; Linak, M.C.; Hirai, A.; Takahashi, H. Sequence-specific error profile of Illumina sequencers. Nucleic Acids Res. 2011, 39, e90. [Google Scholar] [CrossRef] [PubMed]
- Minoche, A.E.; Dohm, J.C.; Himmelbauer, H. Evaluation of genomic high-throughput sequencing data generated on Illumina HiSeq and genome analyzer systems. Genome Biol. 2011, 12, R112. [Google Scholar] [CrossRef] [PubMed]
- Consortium, H.M.P. Structure, function and diversity of the healthy human microbiome. Nature 2012, 486, 207–214. [Google Scholar]
- Arumugam, M.; Raes, J.; Pelletier, E.; Le Paslier, D.; Yamada, T.; Mende, D.R.; Fernandes, G.R.; Tap, J.; Bruls, T.; Batto, J.-M. Addendum: Enterotypes of the human gut microbiome. Nature 2014, 506, 516. [Google Scholar] [CrossRef]
- Hu, B.; Xie, G.; Lo, C.-C.; Starkenburg, S.R.; Chain, P.S. Pathogen comparative genomics in the next-generation sequencing era: Genome alignments, pangenomics and metagenomics. Brief. Funct. Genom. 2011, 10, 322–333. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, D.; Pan, H.; Huang, R.; Xia, L.C. CoreProbe: A Novel Algorithm for Estimating Relative Abundance Based on Metagenomic Reads. Genes 2018, 9, 313. https://doi.org/10.3390/genes9060313
Ai D, Pan H, Huang R, Xia LC. CoreProbe: A Novel Algorithm for Estimating Relative Abundance Based on Metagenomic Reads. Genes. 2018; 9(6):313. https://doi.org/10.3390/genes9060313
Chicago/Turabian StyleAi, Dongmei, Hongfei Pan, Ruocheng Huang, and Li C. Xia. 2018. "CoreProbe: A Novel Algorithm for Estimating Relative Abundance Based on Metagenomic Reads" Genes 9, no. 6: 313. https://doi.org/10.3390/genes9060313
APA StyleAi, D., Pan, H., Huang, R., & Xia, L. C. (2018). CoreProbe: A Novel Algorithm for Estimating Relative Abundance Based on Metagenomic Reads. Genes, 9(6), 313. https://doi.org/10.3390/genes9060313