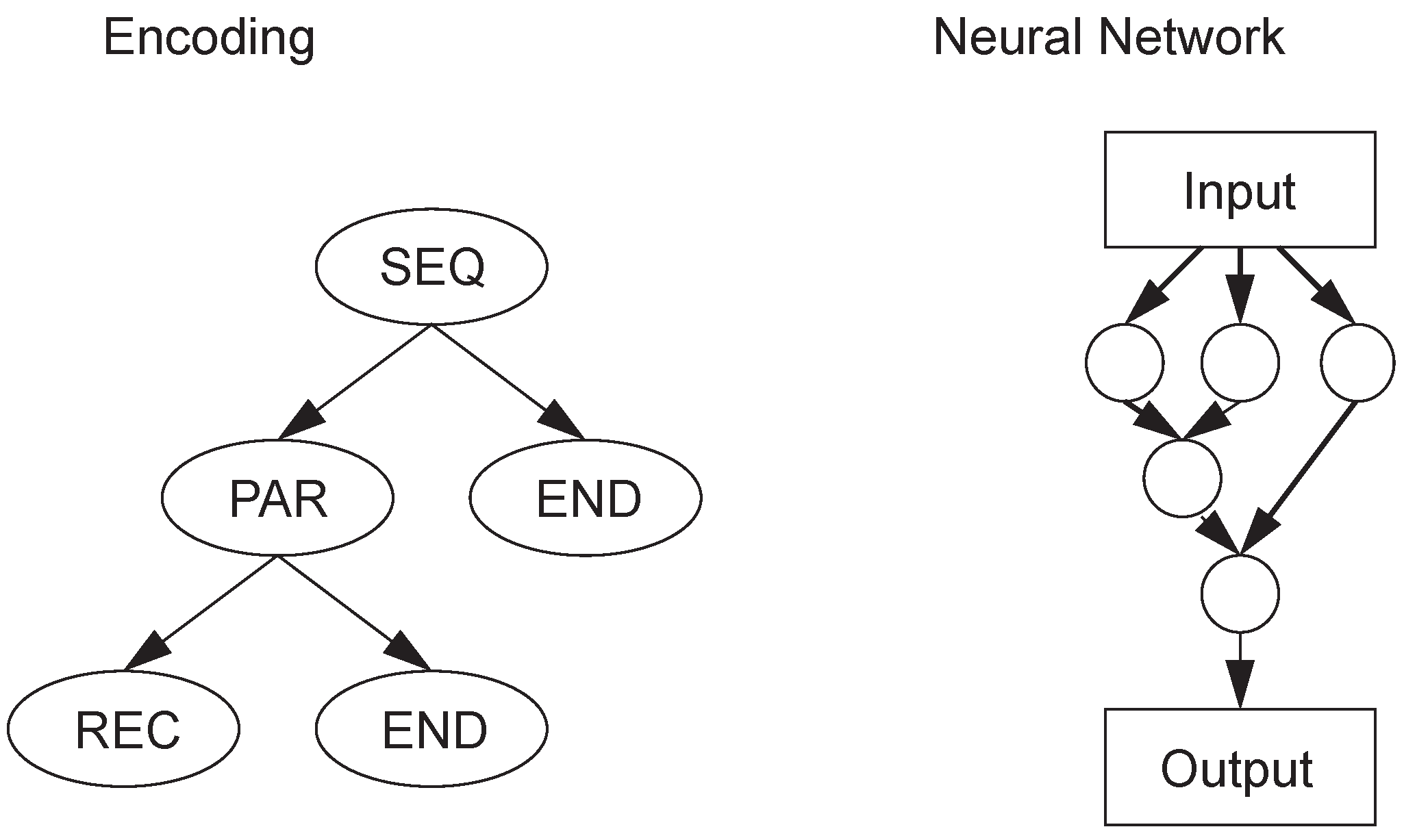
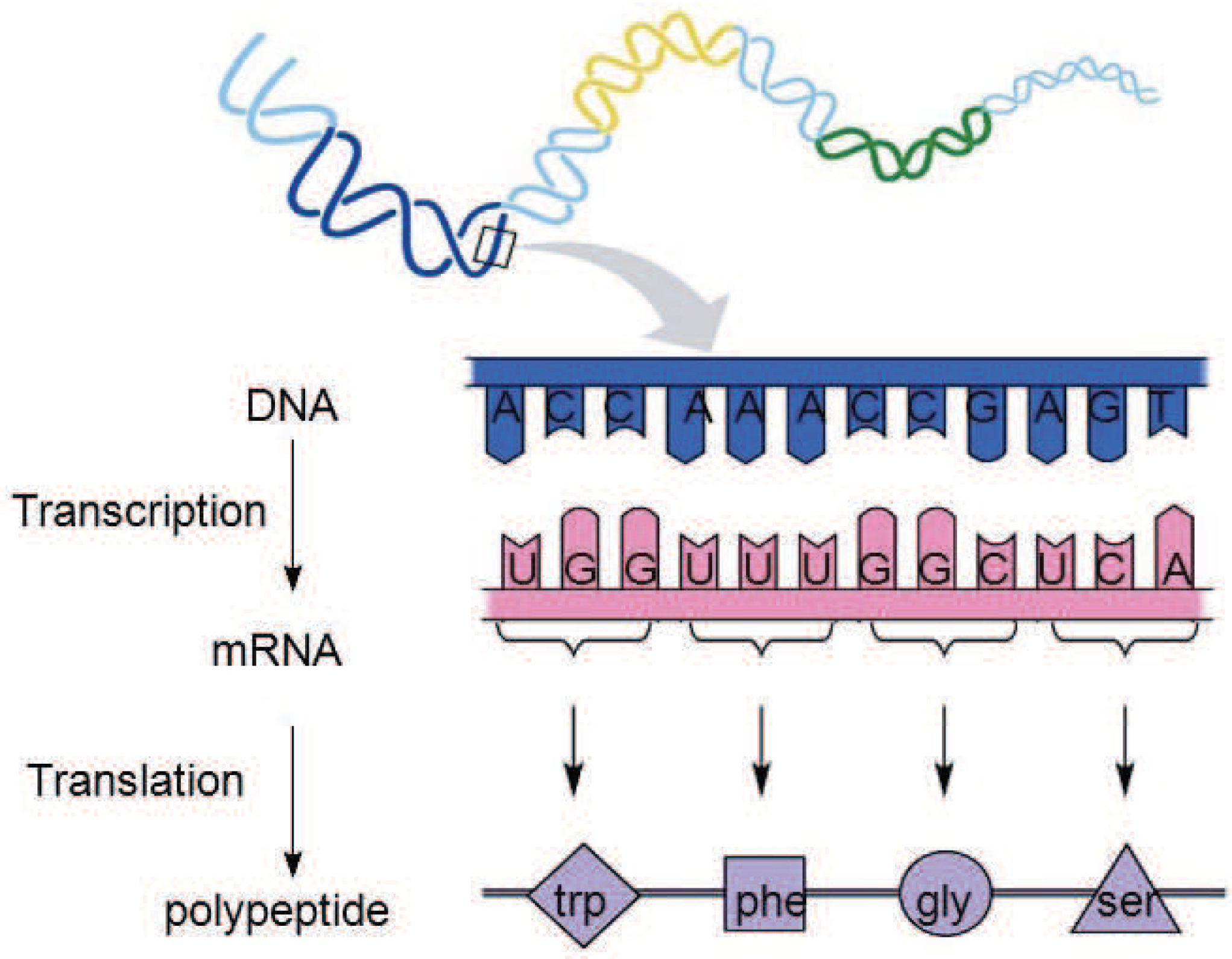
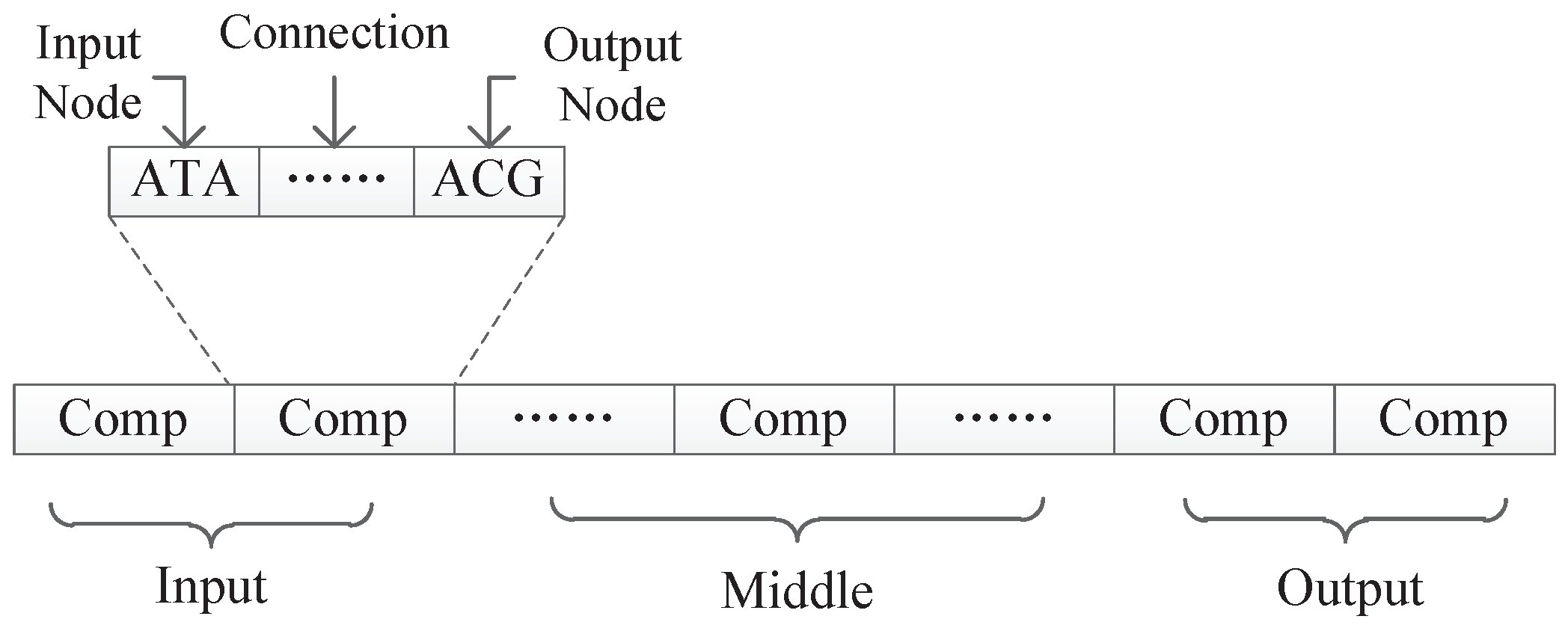
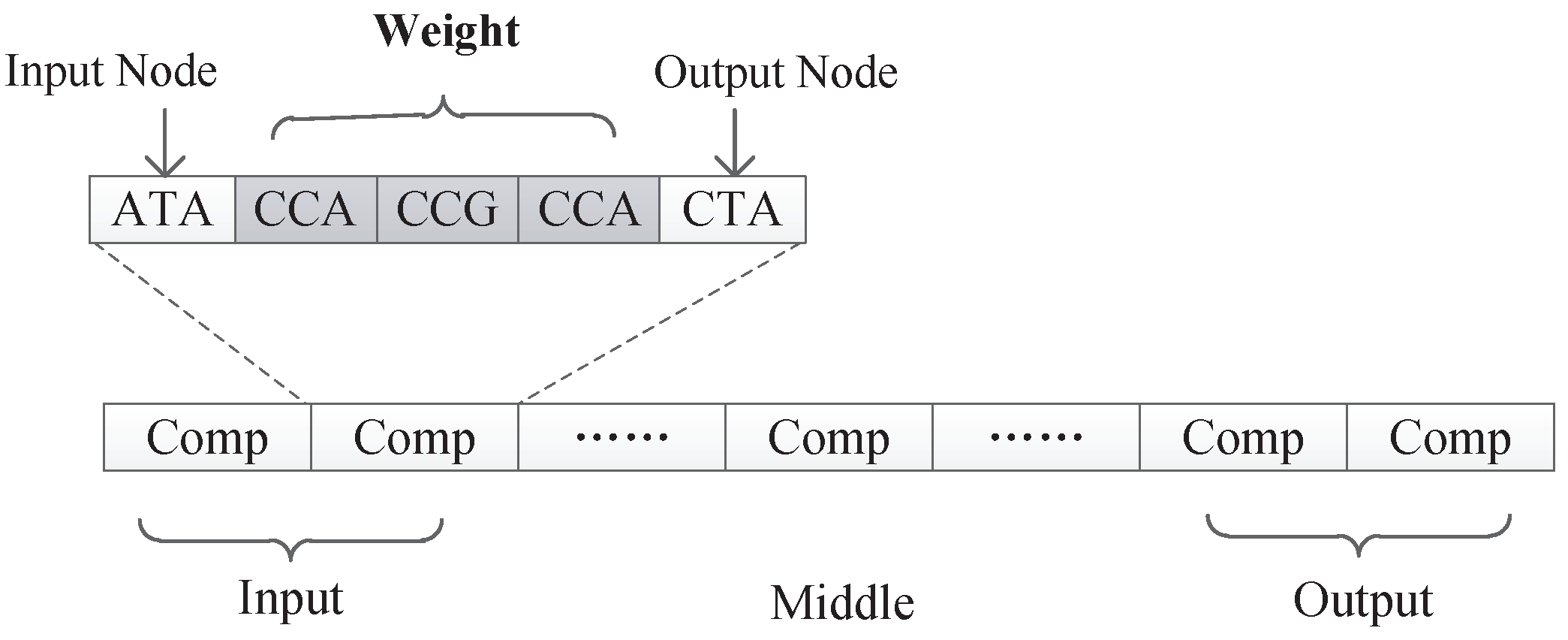
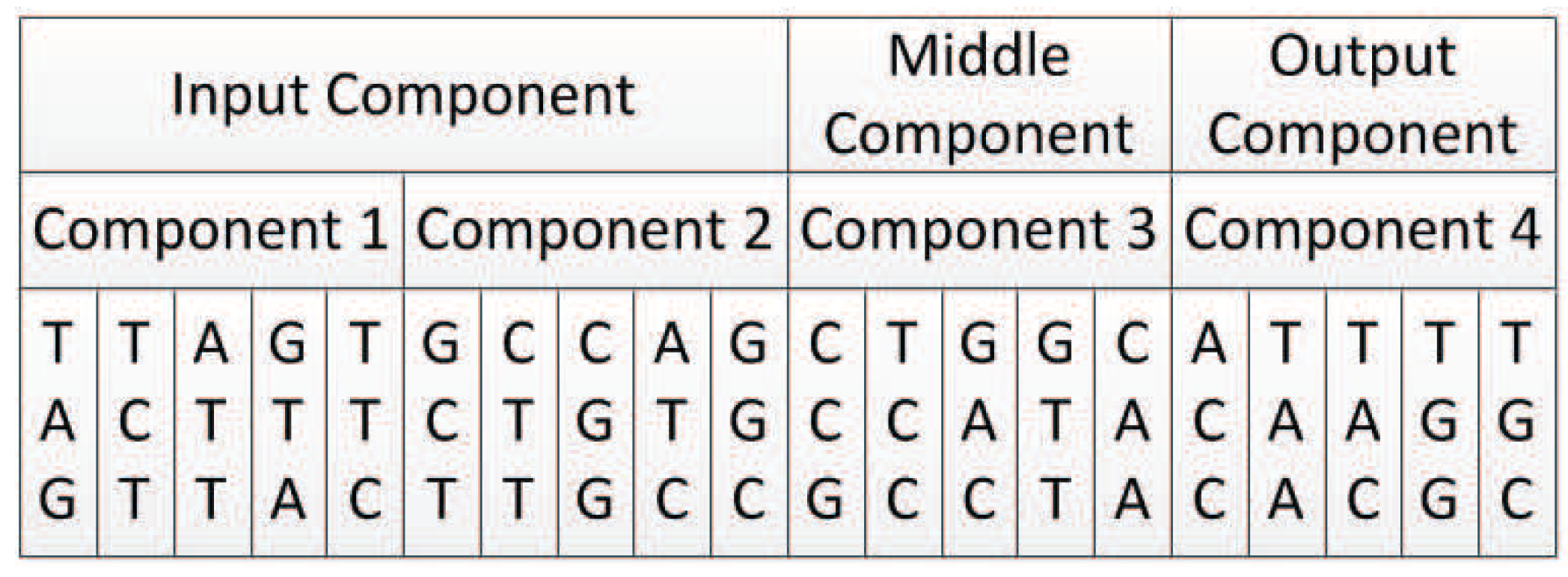
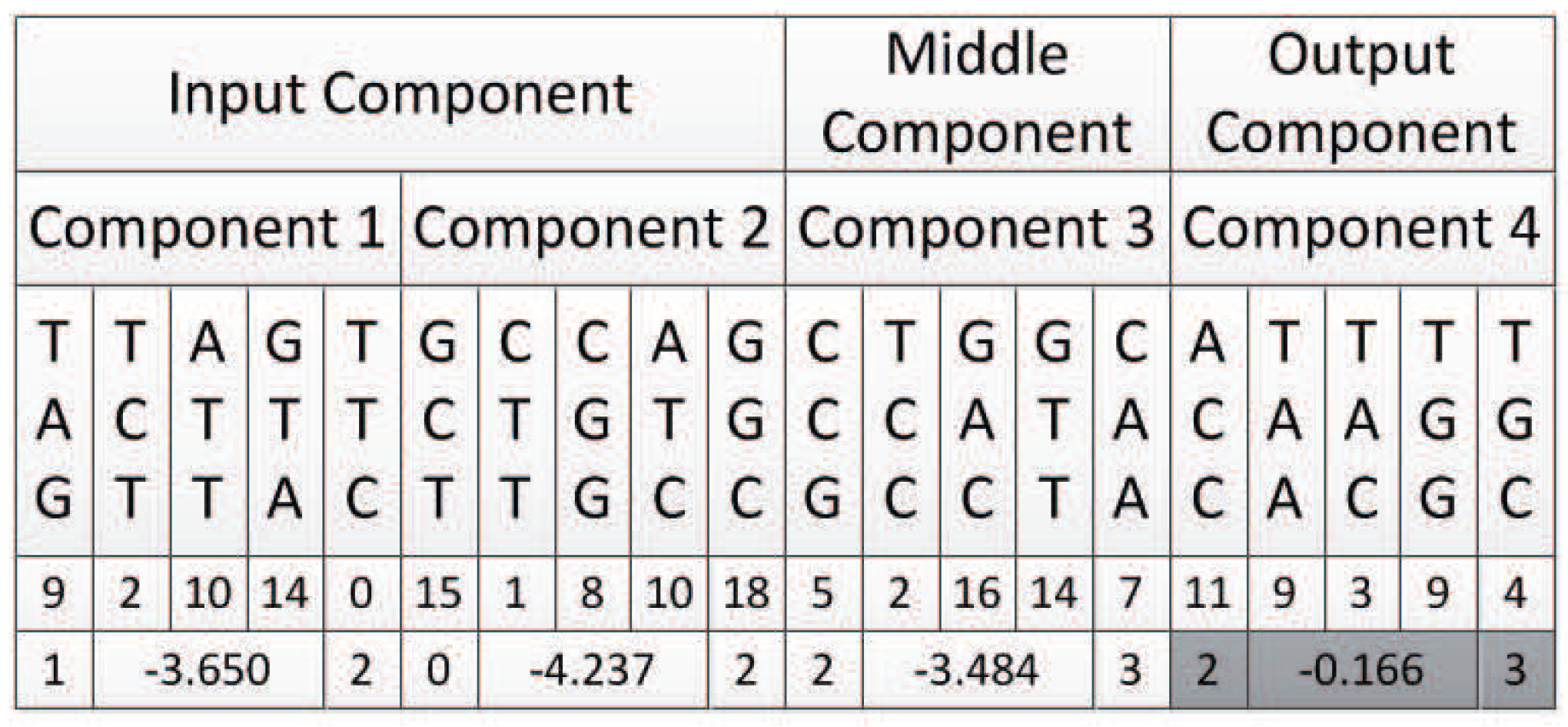
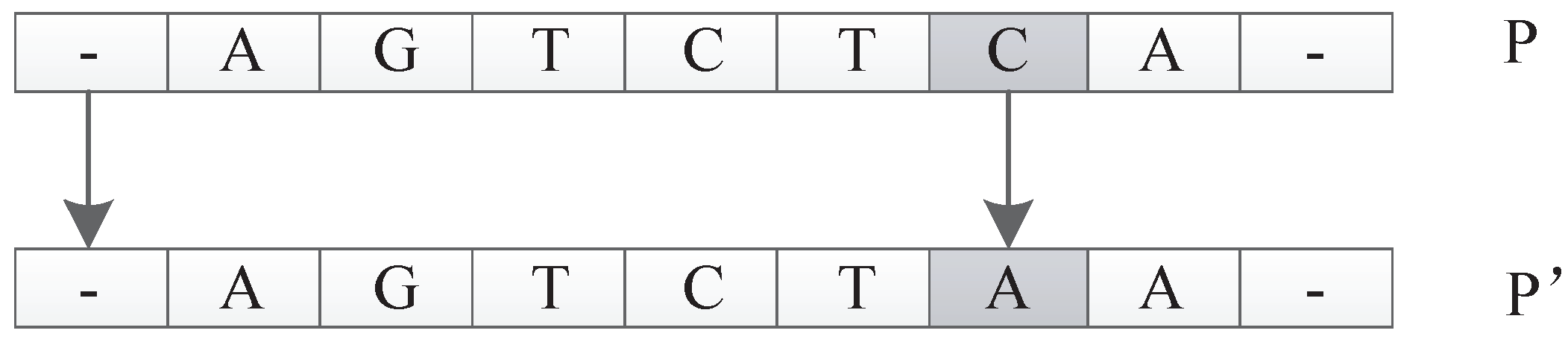
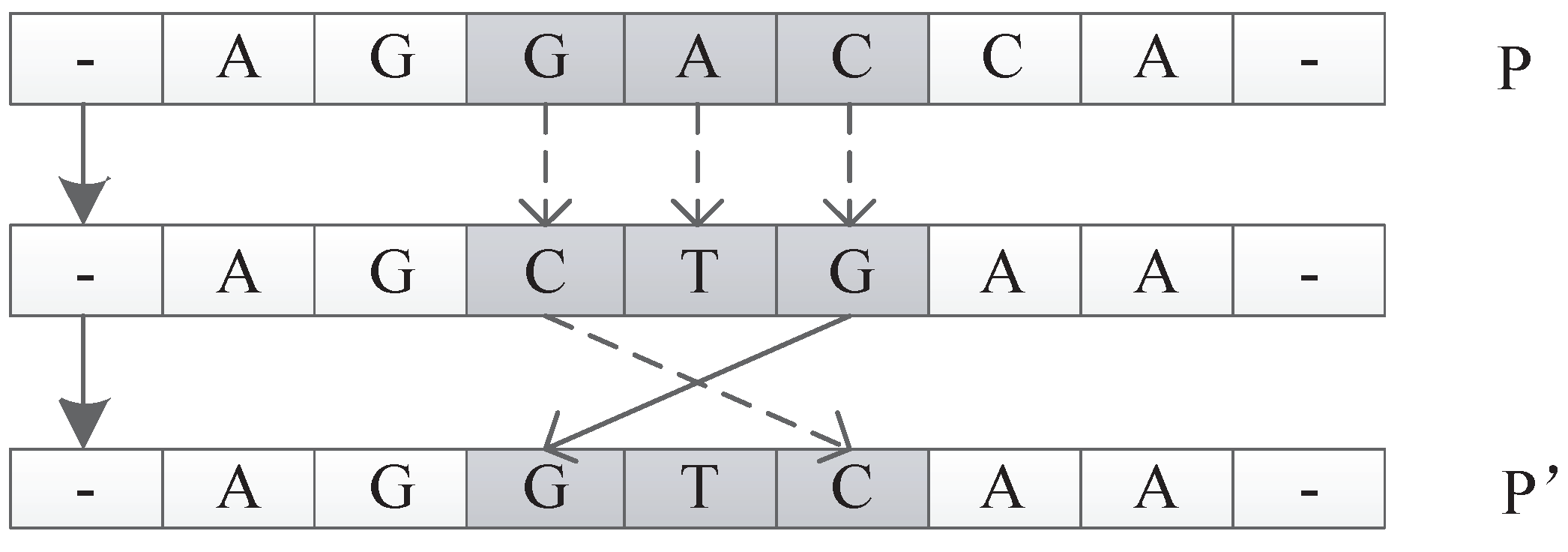
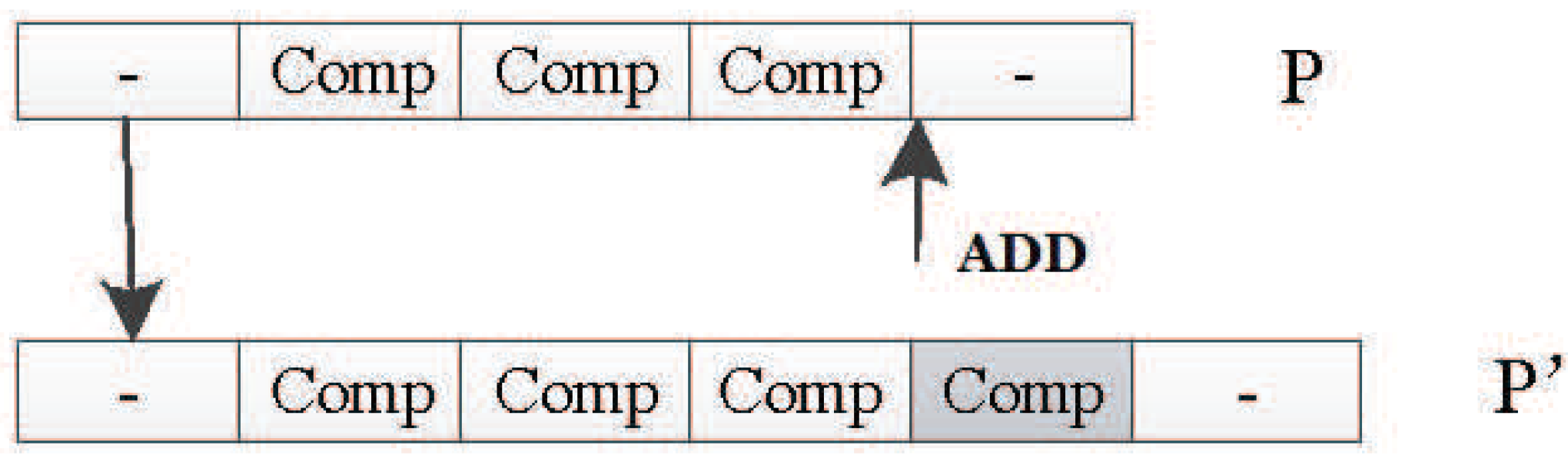
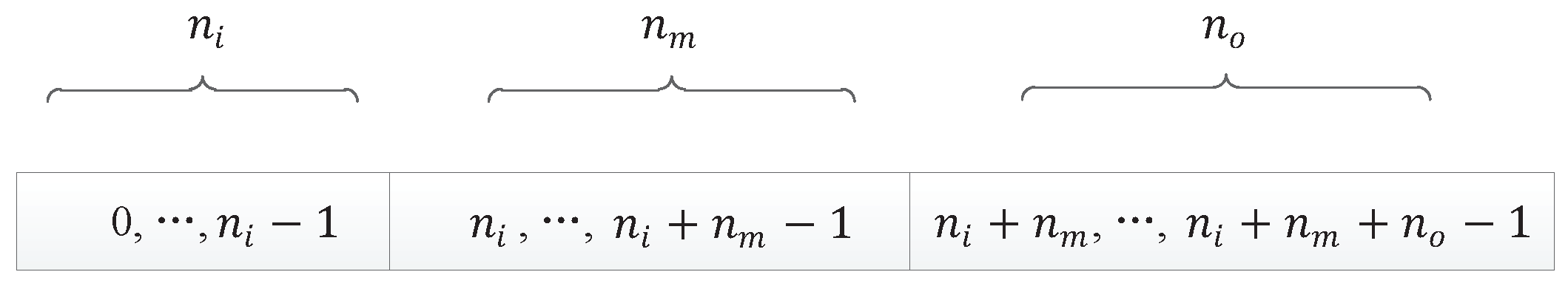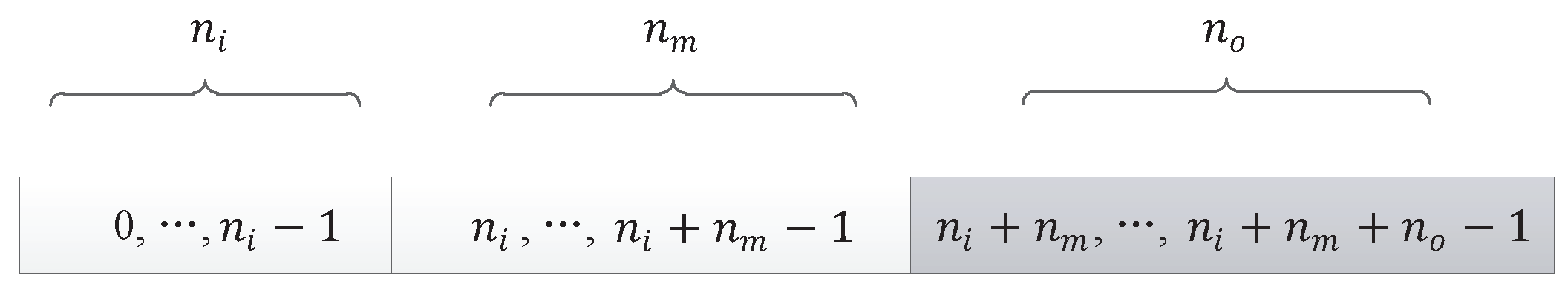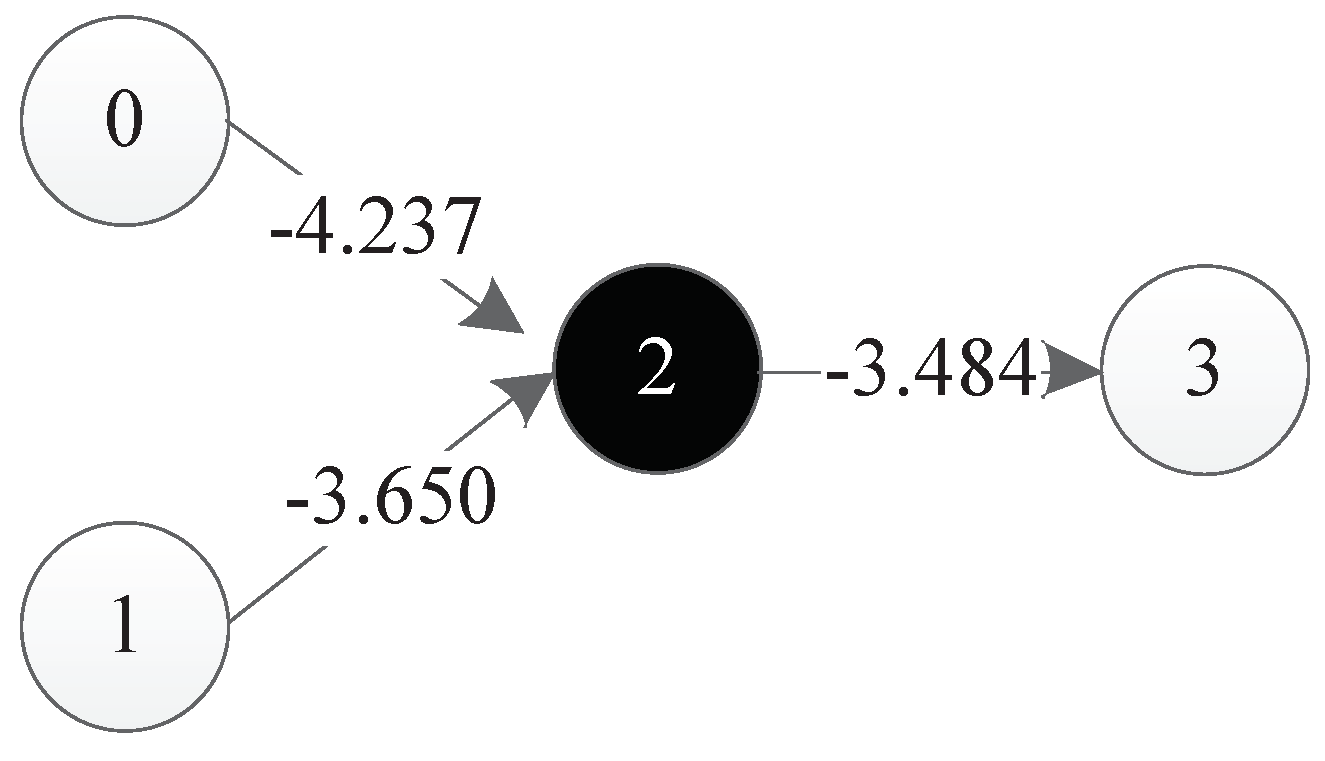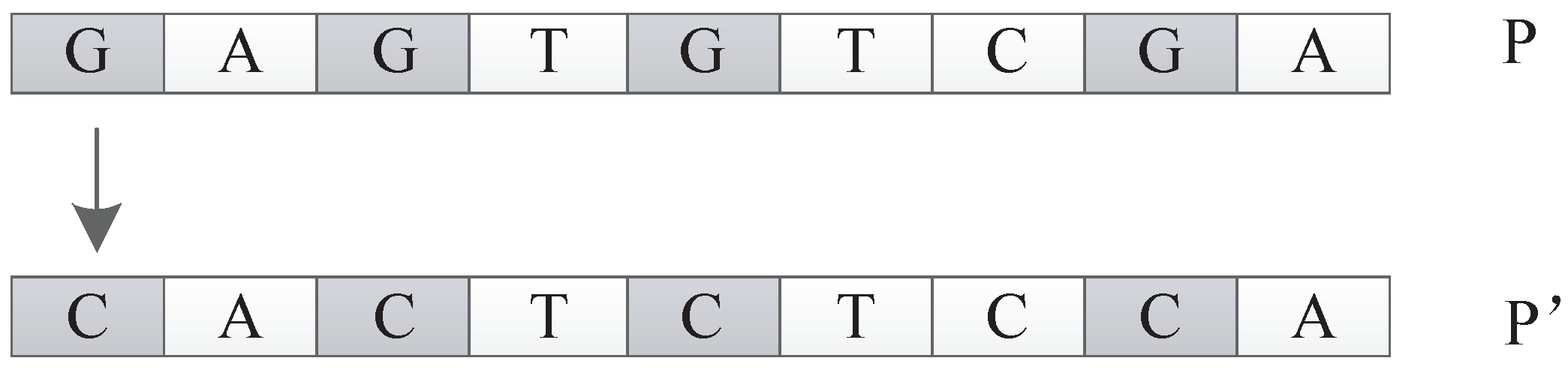8.1. Experiment Setup
In this paper, we want to verify two hypotheses: (1) This encoding scheme can make the network evolve into a necessary structure; (2) compared with other neural evolutionary systems, this encoding can find a solution more effectively.
The XOR network construction experiment was chosen to verify hypothesis 1. This task is relatively simple, but it needs to add hidden neurons to the neural network. Therefore, this experiment can be used to test whether the proposed triplet codon encoding can evolve hidden neurons and to further verify whether the evolutionary algorithm based on this encoding method can properly evolve new structures to solve the target problem.
Double Pole Balancing with Velocity (DPV) and the more difficult Double Pole Balancing without Velocity without speed (DPNV) were chosen to verify hypothesis 2. The goal was to balance the two rods connected to the car by moving it in the right direction. Two-bar balance is a good benchmark experiment, and other neural evolution systems were tested in the experiment, so it is easy to compare the results of the algorithm. Among them, the task of balancing a two-pole car without speed is more difficult. This problem is a non-Markov chain task, so it is difficult to estimate the state of the next moment; thus, there is a higher requirement to keep the balance of the system. Therefore, this experiment can provide very powerful evidence for the effectiveness of the algorithm, that is, it can not only prove that the encoding strategy can improve the ability to find the optimal structure, but also is effective in very difficult control tasks.
The experiments conducted in this paper used the same parameters setting as in [
34,
35,
36]. These three experiments can be solved by the reinforcement learning algorithm, but because the neural evolutionary algorithm can also solve this kind of problem very effectively, the neural evolution field usually regards it as the benchmark experiment.
All experiments in this paper adopted the encoding strategy with connection weights, because this encoding strategy can realize the co-evolution of weights and structures and there are suitable experimental data for comparison. The first encoding strategy with subnet structure can only evolve the network structure, and if the encoding method with connection weight proves to be effective, it must be able to prove that the first encoding can also maximize the evolution of the structure.
8.2. Results for the XOR Network Construction Experiment
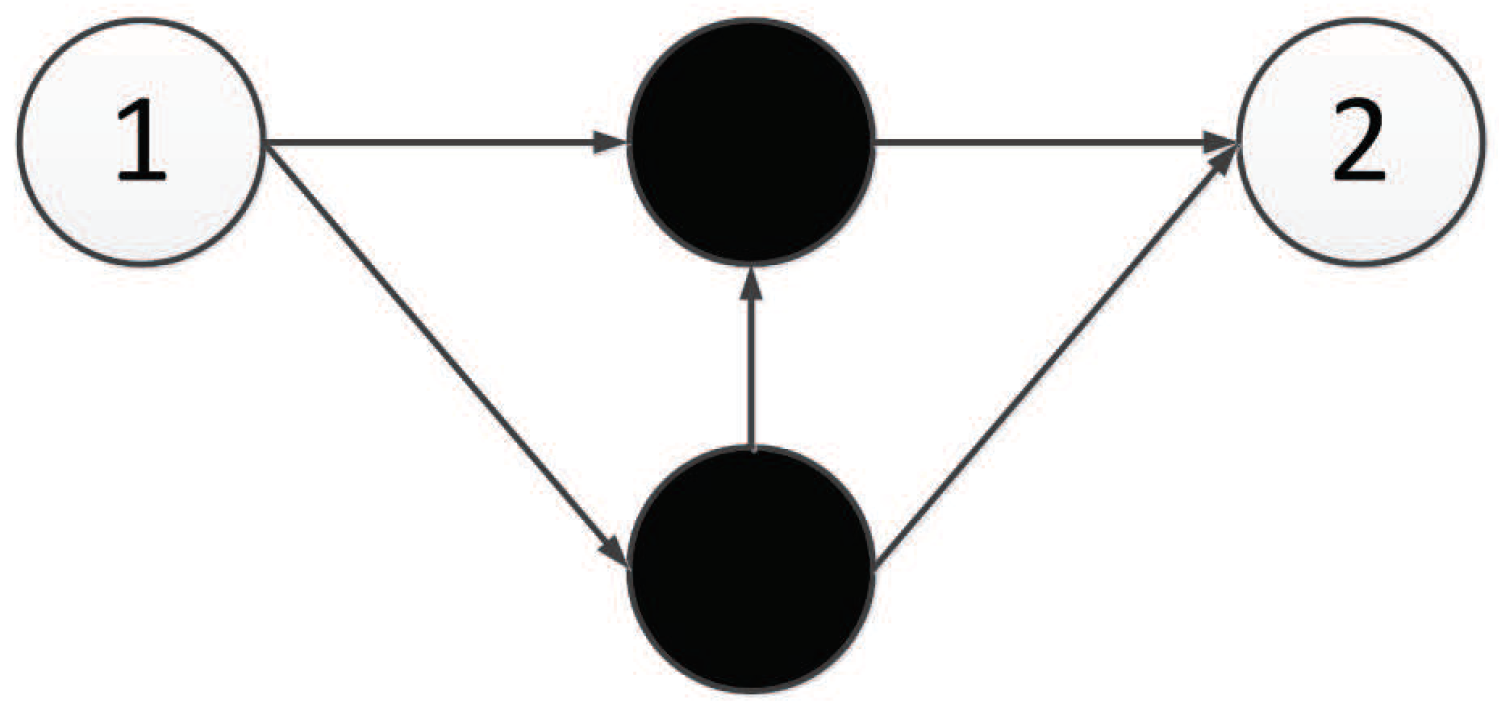
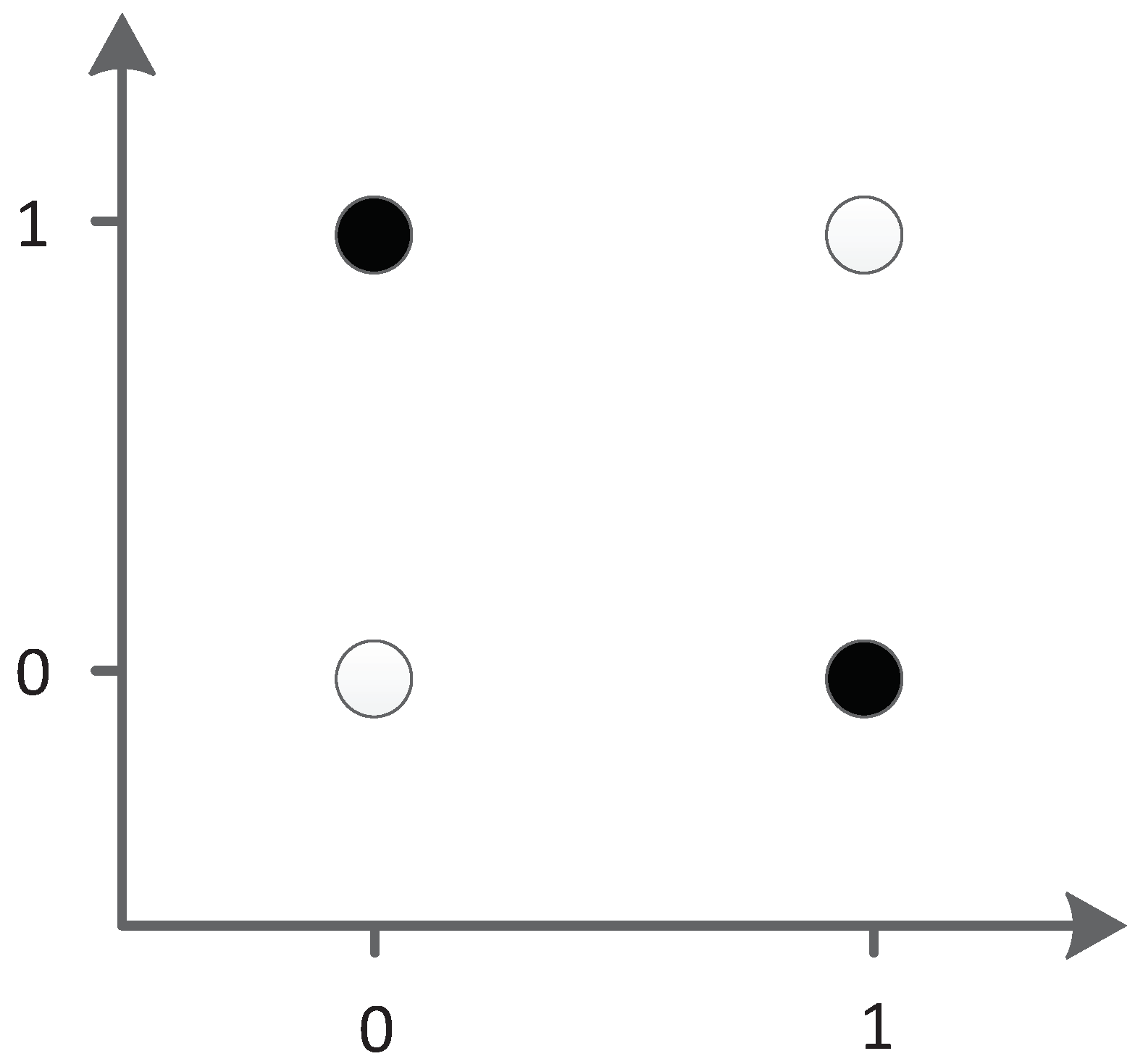
The XOR problem is a typical linear inseparability problem, as shown in
Figure 35, so it is necessary to add hidden neurons to solve the problem in neural networks. This requirement makes XOR suitable for testing the ability of algorithm structure evolution.
In the XOR experiment, the efficiency of the algorithm was compared by the average number of evaluation times.
Table 7 compares different methods for a solution with the XOR network. Because this task was significantly easier to solve, we used a smaller population of 150. The results are averages over 100 runs.
The experimental results show that the structure of XOR was obtained by an average of 24 iterations in 100 XOR experiments, and the average number of evaluations was 3571 for our TCENNE algorithm. It can be seen from the data that the average number of times of evaluation and the number of iterations of the TCENNE algorithm were less than those of the NEAT algorithm with the same population size. Therefore, the TCENNE algorithm performs well in the simple neural network evolution problem.
In the 100 experiments completed, the network had 2.5 hidden nodes, on average. Additionally, there was no failure. The worst performance was 16,050 evaluation times, the population iteration was 107 times (average 23 generations), and all of the others were less than 10,000 evaluation times.
The experimental results show that TCENNE can effectively use 1 to 3 hidden nodes to construct XOR networks.
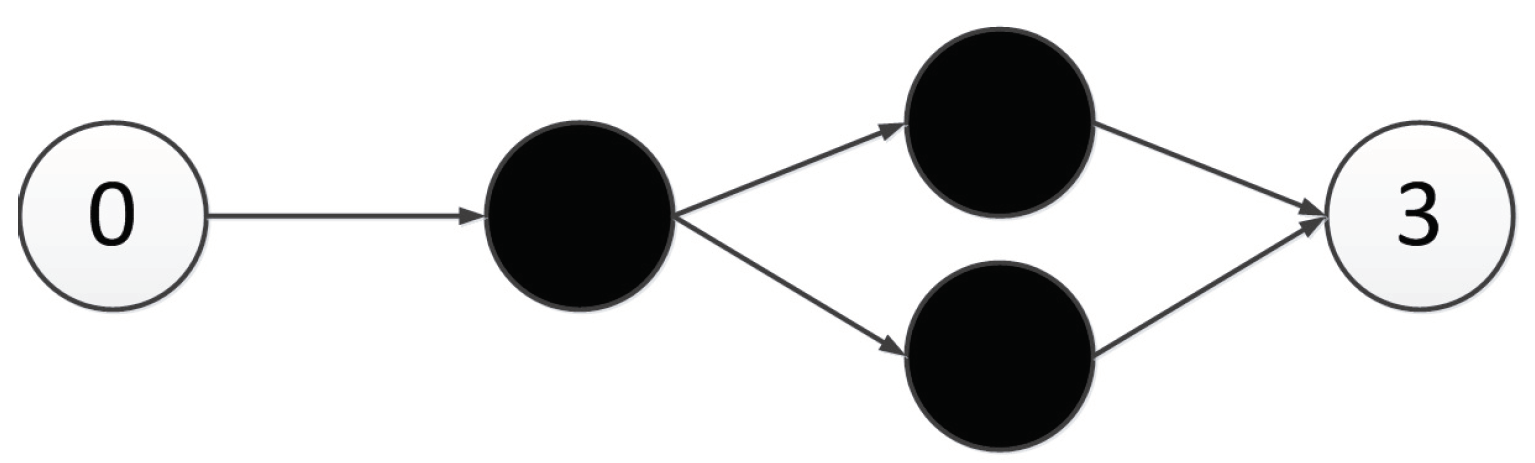
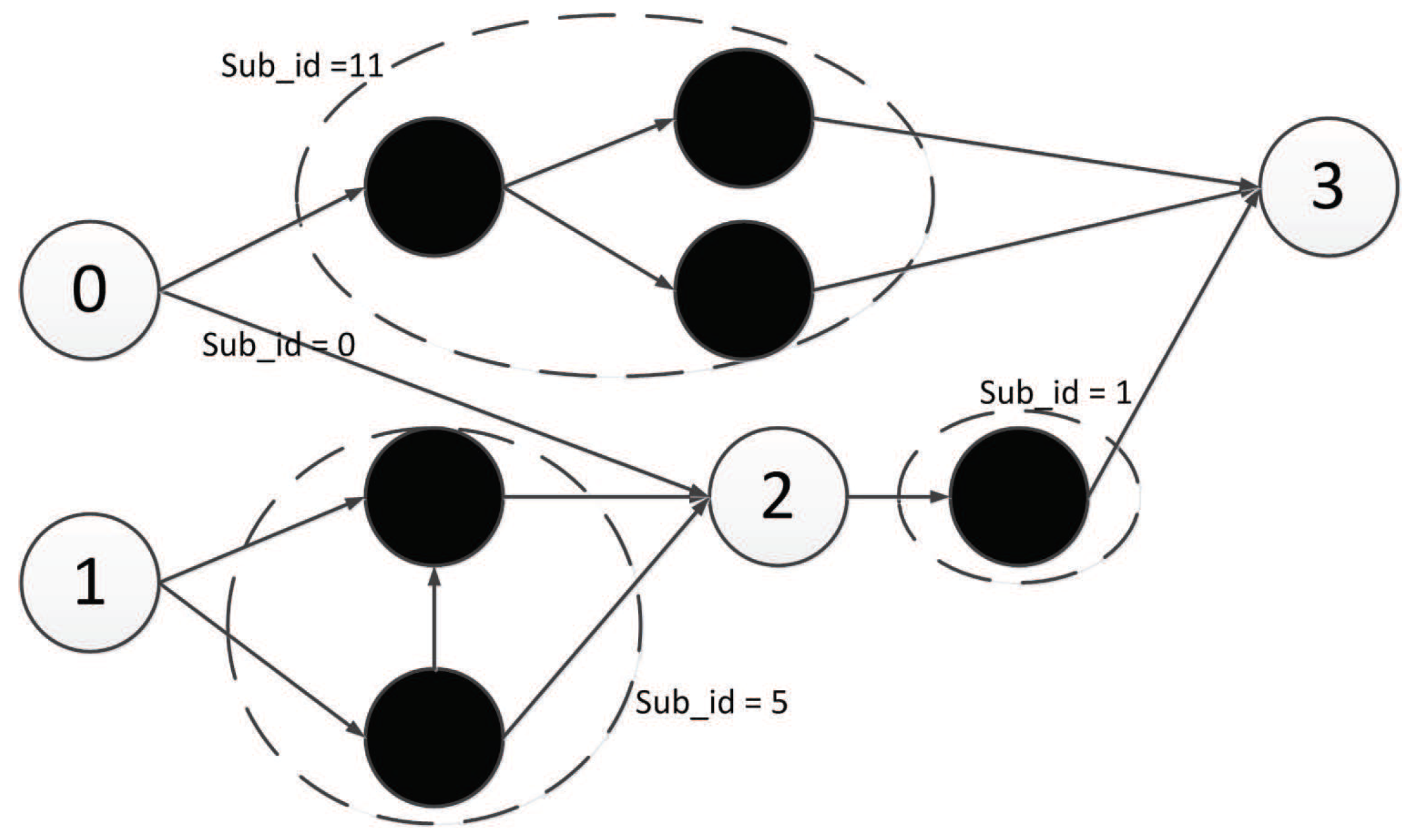
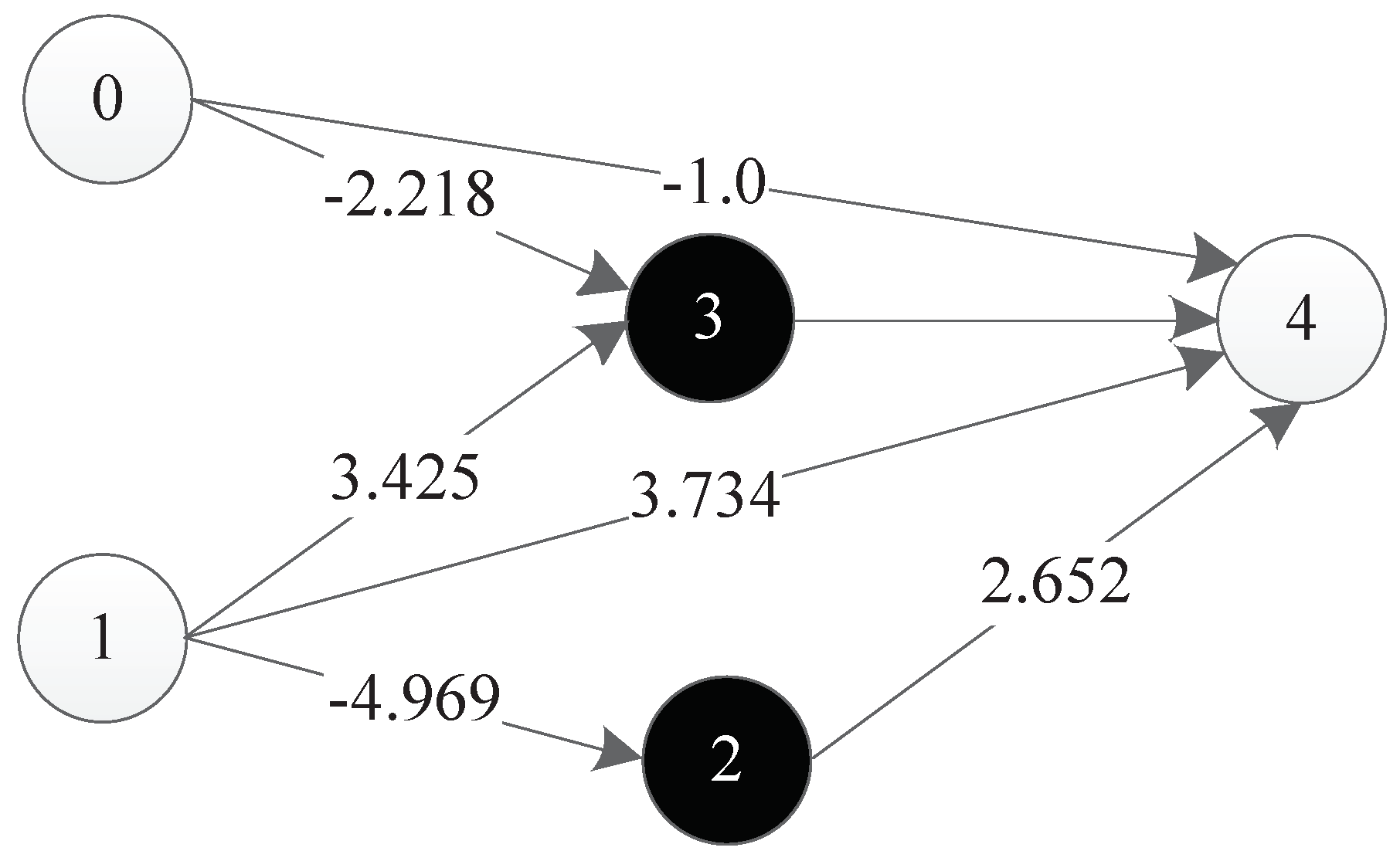
Figure 36 is a representation network of an optimal individual obtained from an experiment, where 0 and 1 represent input points, 4 represents output points, 2 and 3 represent hidden nodes obtained in the course of evolution, and each line has a corresponding weight.
The XOR problem has been used to prove the validity of neural network encoding and the performance of evolutionary neural network algorithm with topological weights. Although TCENNE can effectively solve the XOR problem, the design of the problem is too simple. In order to prove that TCENNE has the ability of continuous co-evolution of topology and weights, and that this triplet codon encoding method is actually beneficial to the evolution of network topology and weights, it needs to be verified for more difficult tasks.
8.3. Results for Double Pole Balancing with Velocity
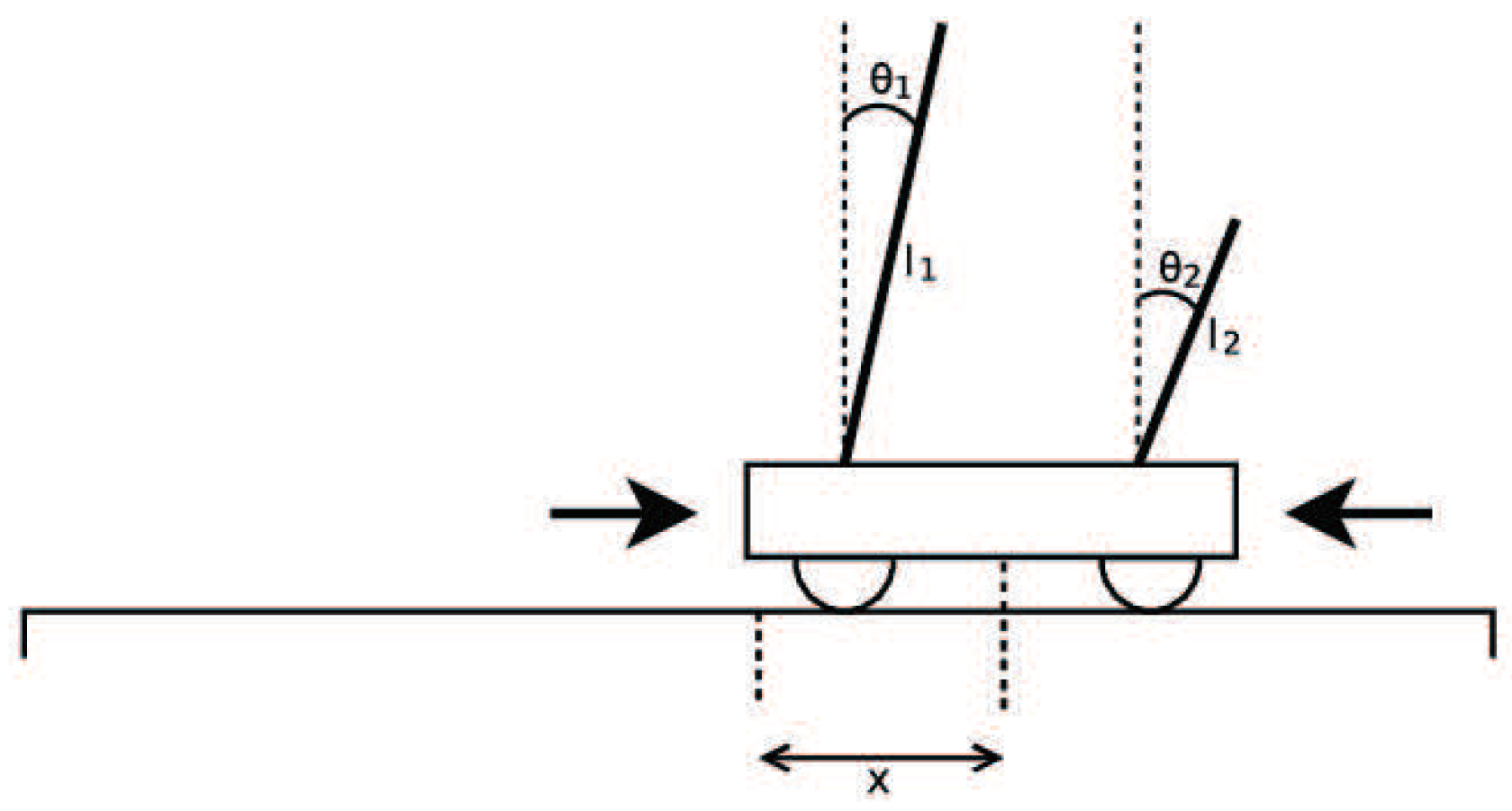
Double Pole Balancing with Velocity (DPV) is a Markov problem. The experimental diagram is as shown in
Figure 37. The standard of success of the task is to keep the system balanced by 100,000 time steps (30 minutes of simulation time). The vertical direction of the rod is considered to be balanced between
and
. The more time steps that the two bars keep in balance, the higher the fitness value is.
In the experiments, the number of individuals evaluated from the initial state to the optimal solution is represented by the number of evaluations. Iterations represent the algebra of population evolution in the algorithm. The population size represents the number of individuals in each generation. The relationship between the number of evaluations and the two can be expressed as
Here, the relationship is smaller or equal, because in the last generation of populations, it is likely that the solution to the target problem can be found without having to evaluate all the individuals. In the experiment of DPV, if the evaluation time of the algorithm is smaller, the algorithm is more efficient.
In the DPV experiment, TCENNE was compared with five other published results of NE systems, as shown in
Table 8.
For the statistical methods of the experimental data, the results of the first four systems are the average values of more than 50 experimental data. The results of the NEAT algorithm are the average values of more than 120 experimental data, while the results of the TCENNE algorithm are the average values of 242 experimental data. From the comparison of the experimental results, we can see that the experimental effect of the first three NE systems was much lower than that of the latter three.
Although there was no significant difference in the number of evaluations between the latter three neural evolutionary systems, and the number of TCENNE iterations was relatively high, TCENNE’s population size was set at 100 in the DPV experiment—less than the other two systems. Moreover, TCENNE was still superior to ESP and NEAT in terms of the evaluating time. Therefore, TCENNE is still competitive with the other two NE systems. Moreover, TCENNE selects the average value of more experiments, but the result was still better than the other two, which shows that this DNA encoding strategy based on triplet codon can ensure the stability and effectiveness of the algorithm.
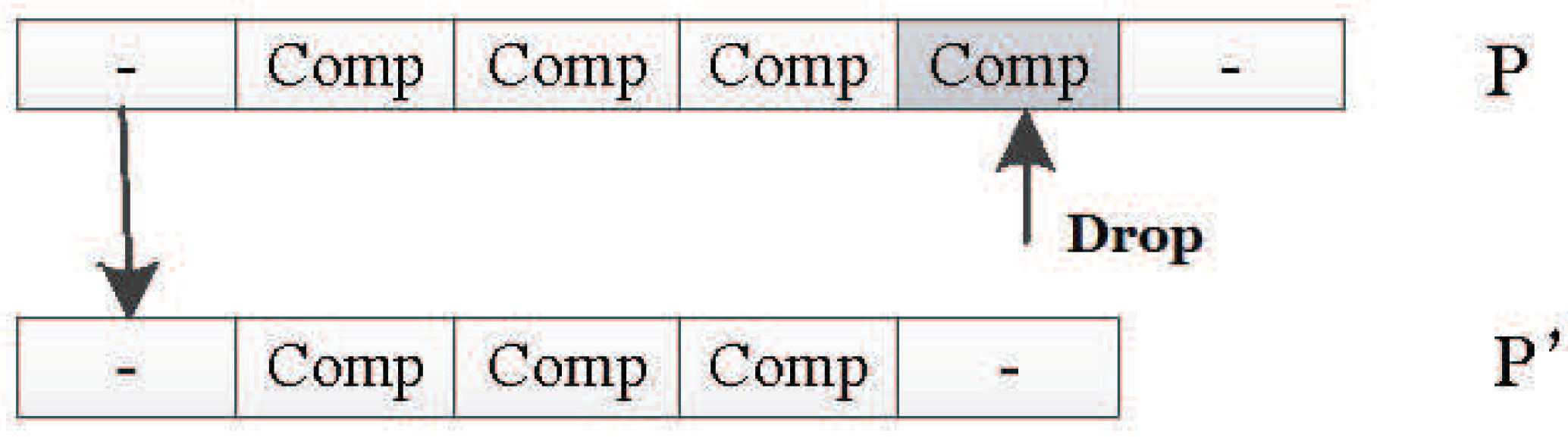
In this encoding method, multiple codons can be decoded into the same amino acid, so the mutation of codons can keep the decoding invariance in a small range, and, at the same time, it keeps the diversity of the whole encoding. Because the mutation operation of DNA includes the adding mutation and the drop mutation, the network size will be different with the adding and drop mutation operation in the iterative process. As a result, smaller solutions can be found with the same performance.
Therefore, TCENNE can quickly find a small scale network to prove the effectiveness of the proposed encoding strategy.
8.4. Results for Double Pole Balancing without Velocity
Double Pole Balancing without Velocity (DPNV) is a non-Markov problem, that is, it is impossible to predict the state of the next moment through the historical state of the system. The input of the system is only the position of the car, the angle of the short rod and the angle of the long rod, so the system needs to keep its internal stability without speed. In the experiment, the TCENNE system needs to output a force acting on the car each time to control the direction and speed of the car and the double rods.
In 1996, Gruau et al. [
41] introduced a special fitness function for this problem to prevent the system from simply moving the vehicle back and forth to keep the balance of the bar. This fitness evaluation method, which does not need to calculate the missing velocity value, has been used in many experiments of neural evolutionary systems. The fitness function
F is composed of two subfitness functions,
and
, and we can set
. Within 1000 time steps, the two subfitness functions are defined as
where
t is the number of time steps in which the two rods are balanced in 1000 total time steps.
K is a constant which is set to 0.75. The denominator in Equation (
7) is the sum of the absolute values of the state variables of the running car and the long rod. Summation involves the sum of the absolute values of state variables in the last 100 time steps of the run. Therefore, by minimizing damping oscillation, the system can maximize its fitness value.
According to Gruau’s solution standards, the best individuals of each generation need to perform generalization tests to ensure the robustness of their systems. Generalization testing takes more time than fitness testing, so it usually applies only to the best individuals of each generation. In the generalization test, in addition to requiring the two poles on the car to balance 100,000 time steps, the best individual network must balance the two poles in 625 different initial states. In each different initial state, success is achieved if the car has 1000 steps to keep both poles balanced. The total number of successes is the generalization performance of the solution. The system under test is generally required to succeed at least 200 times in 625 different states.
Therefore, there are two main criteria for evaluating DPNV: the number of evaluations and the number of generalizations. The number of evaluations is the number of individuals evaluated from the beginning to the end of the algorithm, and the number of generalizations is the number of times the optimal individual passes the generalization test. If the number of generalization is qualified, the smaller the number of evaluations is, the more efficient the algorithm is. If the number of generalizations is larger, the stability of the optimal individual is more stable, which indicates that the stability of the algorithm is stronger.
Since the non-Markov problem is more difficult than the Markov problem, the initial DNA chain should be set longer, which can make the variation of individual populations a little larger, so the initial component length of the DNA chain for our encoding method was set to 30.
Our proposed TCENNE algorithm was compared with five standard neuroevolutionary systems that can successfully solve DPNV problems. The experimental results are shown in
Table 9.
The success of Cellular Encoding (CE) [
41] is due first and foremost to the ability of its evolutionary structure. The fixed topology neural evolutionary system ESP can accomplish the task five times faster than CE by random startup of hidden layer nodes [
40]. NEAT uses direct coding of the network topology and weight information and uses historical feature markers to make its structure evolve effectively [
34]. AGE (Analog Genetic Encoding) [
35] is a new implicit neural network evolutionary method based on the observation of biological genetic regulatory networks. The effect of this method on DPNV experiments is better than that of NEAT. The Echo State Network (ESN) is a kind of cyclic neural network based on a large number of sparse random connections. Unsupervised learning of ESN (UESN) applies the evolutionary continuous parameter optimization method to the evolutionary learning of ESN and verifies it effectively on the two-bar equilibrium system [
36].
All of the algorithms in
Table 9 use the same experimental settings, including the car, the parameters of the two rods, and the calculation method of the fitness function. The experimental results of TCENNE were taken as the average of 26 times, and the results of other algorithms were taken as the average of 20 times.
The average number of evaluations of the TCENNE algorithm was only 19074 times, which is only of CE, which indicates that the improvement of structure evolution has great influence on the performance. This DNA encoding design based on the triplet codon can greatly improve the evolution efficiency of the structure. The average evaluation number of TCENNE was nearly of that of ESP, which shows that the method of structure and weight evolution at the same time is better than that of fixed topology and evolution weight alone. The TCENNE algorithm was shown to be 1.7 times faster than NEAT and 1.2 times faster than UESN. Thus, the effectiveness of this encoding strategy is proved.
In the NEAT system, the connection and weight are coded directly, and the individual cross is realized by the unique mark of connection. The network structure of the population can evolve effectively in the iterative process. Although NEAT is a highly efficient neural evolutionary algorithm, it needs to encode a large amount of specific information to ensure the transmission of information between generations. The triplet codon based the encoding method designed in this paper adopts a more abstract encoding and decoding strategy. It can effectively evolve the individual structure and weight of the population by simply encoding a small amount of information.
In the TCNNE algorithm, different individuals can evolve into different structures, and each structure represents a different dimension space. Additionally, the simple genetic operator makes TCENNE try to solve the problem in many different ways. The change space is very large, and it is beneficial to the search of the optimal solution, which further reflects its advantages.
There were no significant differences in the performance of the previous four methods in the generalization test, but the average generalization time of the TCENNE experiment was 610, very close to the maximum 625, and far higher than the other four. Actually, in the 26 generalization experiments of TCENNE, only in one test was the number of generalizations 241, and the result for the others was 625. Thus, the optimal solution selected by the TCENNE algorithm can not only meet the requirements of the basic equilibrium time of the experiment, but can also maintain a balance of 1000 steps under most initial state conditions of the car systems. The stability of individuals also reflects the stability of the whole algorithm to a great extent.
TCENNE was determined to be the most efficient and more stable algorithm in these systems by comparing the number of evaluation times and the number of generalizations. This shows that the design of this triplet codon based coding is helpful for the co-evolution of weights and topologies. Additionally, it can make the remaining individual more stable.