Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients
Abstract
1. Introduction
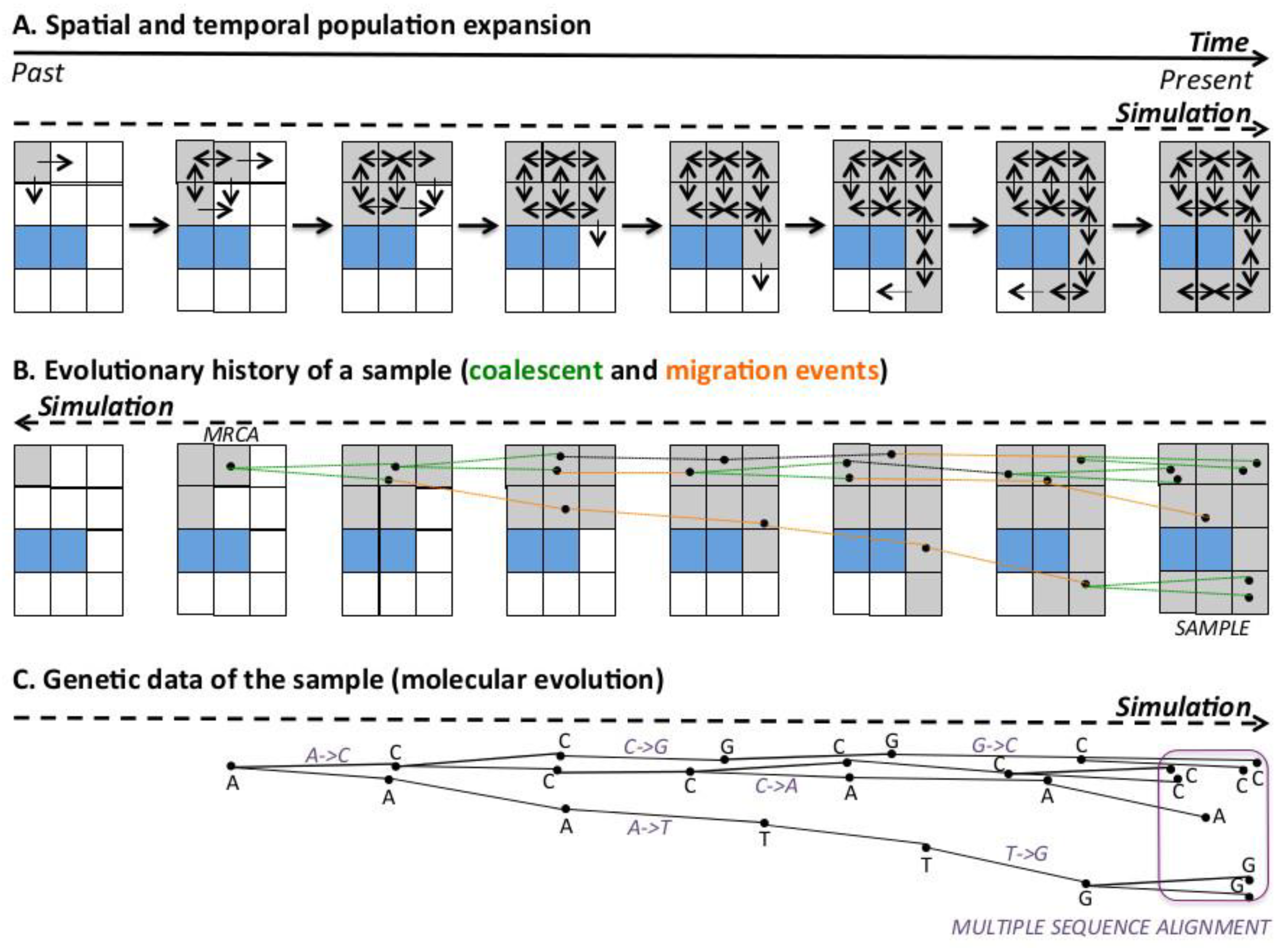
2. Simulation of Genetic Gradients
2.1. Simulation of Genetic Data under Diverse Evolutionary Scenarios of Human Evolution
Spatially-Explicit Computer Simulations
2.2. Estimation of Genetic Gradients in Studies of Human Evolution
3. Selecting among Alternative Scenarios of Population Admixture through Simulated Genetic Gradients
4. Selecting among Alternative Scenarios of Presence and Absence of the Last Glacial Period through Simulated Genetic Gradients
5. Selecting among Alternative Scenarios of Other Evolutionary Processes through Simulated Genetic Gradients
5.1. Influence of a Paleolithic Expansion from the Iberian Peninsula on the European Genetic Gradient
5.2. Influence of Varying Evolutionary Parameters on Genetic Gradients
5.3. Influence of Long-Distance Dispersal on Genetic Gradients
5.4. Evolutionary Information from the Second and Third Principal Components
6. Conclusions and Future Prospects
Funding
Acknowledgments
Conflicts of Interest
References
- Novembre, J.; Stephens, M. Response to Cavalli-Sforza interview [Human Biology 82(3):245-266 (June 2010)]. Hum. Biol. 2010, 82, 469–470. [Google Scholar] [CrossRef] [PubMed]
- Relethford, J.H. Genetic evidence and the modern human origins debate. Heredity (Edinb.) 2008, 100, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Lopez, S.; van Dorp, L.; Hellenthal, G. Human Dispersal Out of Africa: A Lasting Debate. Evol. Bioinform. Online 2015, 11, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Perez-Losada, M.; Posada, D.; Arenas, M.; Jobes, D.V.; Sinangil, F.; Berman, P.W.; Crandall, K.A. Ethnic differences in the adaptation rate of HIV gp120 from a vaccine trial. Retrovirology 2009, 6, 67. [Google Scholar] [CrossRef] [PubMed]
- Wiencke, J.K. Impact of race/ethnicity on molecular pathways in human cancer. Nat. Rev. Cancer 2004, 4, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Cavalli-Sforza, L.L.; Menozzi, P.; Piazza, A. Demic expansions and human evolution. Science 1993, 259, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Cavalli-Sforza, L.L.; Menozzi, P.; Piazza, A. The History and Geography of Human Genes; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Piazza, A.; Rendine, S.; Minch, E.; Menozzi, P.; Mountain, J.; Cavalli-Sforza, L.L. Genetics and the origin of European languages. Proc. Natl. Acad. Sci. USA 1995, 92, 5836–5840. [Google Scholar] [CrossRef] [PubMed]
- Chikhi, L.; Nichols, R.A.; Barbujani, G.; Beaumont, M.A. Y genetic data support the Neolithic demic diffusion model. Proc. Natl. Acad. Sci. USA 2002, 99, 11008–11013. [Google Scholar] [CrossRef] [PubMed]
- Sokal, R.R.; Menozzi, P. Spatial Autocorrelations of HLA Frequencies in Europe Support Demic Diffusion of Early Farmers. Am. Nat. 1982, 119, 1–17. [Google Scholar] [CrossRef]
- Novembre, J.; Stephens, M. Interpreting principal component analyses of spatial population genetic variation. Nat. Genet. 2008, 40, 646–649. [Google Scholar] [CrossRef] [PubMed]
- François, O.; Currat, M.; Ray, N.; Han, E.; Excoffier, L.; Novembre, J. Principal component analysis under population genetic models of range expansion and admixture. Mol. Biol. Evol. 2010, 27, 1257–1268. [Google Scholar] [CrossRef] [PubMed]
- McVean, G. A genealogical interpretation of principal components analysis. PLoS Genet. 2009, 5, e1000686. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M.; Francois, O.; Currat, M.; Ray, N.; Excoffier, L. Influence of admixture and paleolithic range contractions on current European diversity gradients. Mol. Biol. Evol. 2013, 30, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Reich, D.; Price, A.L.; Patterson, N. Principal component analysis of genetic data. Nat. Genet. 2008, 40, 491–492. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, C.A.; Lillie, A.S.; Cavalli-Sforza, L.L. Mutations arising in the wave front of an expanding population. Proc. Natl. Acad. Sci. USA 2004, 101, 975–979. [Google Scholar] [CrossRef] [PubMed]
- Excoffier, L.; Ray, N. Surfing during population expansions promotes genetic revolutions and structuration. Trends Ecol. Evol. 2008, 23, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Branco, C.; Velasco, M.; Benguigui, M.; Currat, M.; Ray, N.; Arenas, M. Consequences of diverse evolutionary processes on american genetic gradients of modern humans. Heredity 2018, in press. [Google Scholar] [CrossRef] [PubMed]
- Beaumont, M.A.; Zhang, W.; Balding, D.J. Approximate Bayesian computation in population genetics. Genetics 2002, 162, 2025–2035. [Google Scholar] [PubMed]
- Beaumont, M.A. Approximate Bayesian computation in evolution and ecology. Annu. Rev. Ecol. Evol. Syst. 2010, 41, 379–405. [Google Scholar] [CrossRef]
- Alves, I.; Arenas, M.; Currat, M.; Sramkova Hanulova, A.; Sousa, V.C.; Ray, N.; Excoffier, L. Long-distance dispersal shaped patterns of human genetic diversity in Eurasia. Mol. Biol. Evol. 2016, 33, 946–958. [Google Scholar] [CrossRef] [PubMed]
- Pimenta, J.; Lopes, A.M.; Comas, D.; Amorim, A.; Arenas, M. Evaluating the Neolithic Expansion at Both Shores of the Mediterranean Sea. Mol. Biol. Evol. 2017, 34, 3232–3242. [Google Scholar] [CrossRef] [PubMed]
- Fagundes, N.J.; Ray, N.; Beaumont, M.; Neuenschwander, S.; Salzano, F.M.; Bonatto, S.L.; Excoffier, L. Statistical evaluation of alternative models of human evolution. Proc. Natl. Acad. Sci. USA 2007, 104, 17614–17619. [Google Scholar] [CrossRef] [PubMed]
- Ray, N.; Wegmann, D.; Fagundes, N.J.; Wang, S.; Ruiz-Linares, A.; Excoffier, L. A statistical evaluation of models for the initial settlement of the american continent emphasizes the importance of gene flow with Asia. Mol. Biol. Evol. 2010, 27, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Gamba, C.; Fernandez, E.; Tirado, M.; Deguilloux, M.F.; Pemonge, M.H.; Utrilla, P.; Edo, M.; Molist, M.; Rasteiro, R.; Chikhi, L.; et al. Ancient DNA from an Early Neolithic Iberian population supports a pioneer colonization by first farmers. Mol. Ecol. 2012, 21, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Kingman, J.F.C. The coalescent. Stoch. Process. Appl. 1982, 13, 235–248. [Google Scholar] [CrossRef]
- Kendall, D.G. On the Generalized “Birth-and-Death” Process. Ann. Math. Stat. 1948, 19, 1–15. [Google Scholar] [CrossRef]
- Epperson, B.K.; McRae, B.H.; Scribner, K.; Cushman, S.A.; Rosenberg, M.S.; Fortin, M.J.; James, P.M.; Murphy, M.; Manel, S.; Legendre, P.; et al. Utility of computer simulations in landscape genetics. Mol. Ecol. 2010, 19, 3549–3564. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Amos, C.I.; Kimmel, M. Forward-time simulations of human populations with complex diseases. PLoS Genet. 2007, 3, e47. [Google Scholar] [CrossRef] [PubMed]
- Rasteiro, R.; Bouttier, P.A.; Sousa, V.C.; Chikhi, L. Investigating sex-biased migration during the Neolithic transition in Europe, using an explicit spatial simulation framework. Proc. Biol. Sci. 2012, 279, 2409–2416. [Google Scholar] [CrossRef] [PubMed]
- Calafell, F.; Grigorenko, E.L.; Chikanian, A.A.; Kidd, K.K. Haplotype evolution and linkage disequilibrium: A simulation study. Hum. Hered. 2001, 51, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Ray, N.; Excoffier, L. A first step towards inferring levels of long-distance dispersal during past expansions. Mol. Ecol. Resour. 2010, 10, 902–914. [Google Scholar] [CrossRef] [PubMed]
- Mona, S.; Ray, N.; Arenas, M.; Excoffier, L. Genetic consequences of habitat fragmentation during a range expansion. Heredity 2014, 112, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Padhukasahasram, B.; Marjoram, P.; Wall, J.D.; Bustamante, C.D.; Nordborg, M. Exploring population genetic models with recombination using efficient forward-time simulations. Genetics 2008, 178, 2417–2427. [Google Scholar] [CrossRef] [PubMed]
- Laval, G.; Patin, E.; Barreiro, L.B.; Quintana-Murci, L. Formulating a historical and demographic model of recent human evolution based on resequencing data from noncoding regions. PLoS ONE 2010, 5, e10284. [Google Scholar] [CrossRef] [PubMed]
- Slatkin, M. Simulating genealogies of selected alleles in a population of variable size. Genet. Res. 2001, 78, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 1983, 23, 183–201. [Google Scholar] [CrossRef]
- Arenas, M. The importance and application of the ancestral recombination graph. Front. Genet. 2013, 4, 206. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R. Island models and the coalescent process. Mol. Ecol. 1998, 7, 413–418. [Google Scholar] [CrossRef]
- Arenas, M.; Posada, D. Recodon: Coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinform. 2007, 8, 458. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M.; Posada, D. Simulation of genome-wide evolution under heterogeneous substitution models and complex multispecies coalescent histories. Mol. Biol. Evol. 2014, 31, 1295–1301. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.R.; Kaplan, N.L. The coalescent process in models with selection and recombination. Genetics 1988, 120, 831–840. [Google Scholar] [PubMed]
- Arenas, M.; Posada, D. Coalescent simulation of intracodon recombination. Genetics 2010, 184, 429–437. [Google Scholar] [CrossRef] [PubMed]
- Ewing, G.; Hermisson, J. MSMS: A coalescent simulation program including recombination, demographic structure and selection at a single locus. Bioinformatics 2010, 26, 2064–2065. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M. Applications of the Coalescent for the Evolutionary Analysis of Genetic Data. In Reference Module in Life Sciences; Elsevier: Amsterdam, The Netherlands, 2019; Volume 2, pp. 746–758. [Google Scholar]
- Arenas, M. Simulation of Molecular Data under Diverse Evolutionary Scenarios. PLoS Comput. Biol. 2012, 8, e1002495. [Google Scholar] [CrossRef] [PubMed]
- Hoban, S.; Bertorelle, G.; Gaggiotti, O.E. Computer simulations: Tools for population and evolutionary genetics. Nat. Rev. Genet. 2012, 13, 110–122. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M. Computer programs and methodologies for the simulation of DNA sequence data with recombination. Front. Genet. 2013, 4, 9. [Google Scholar] [CrossRef] [PubMed]
- Ray, N.; Currat, M.; Foll, M.; Excoffier, L. SPLATCHE2: A spatially explicit simulation framework for complex demography, genetic admixture and recombination. Bioinformatics 2010, 26, 2993–2994. [Google Scholar] [CrossRef] [PubMed]
- Currat, M.; Ray, N.; Excoffier, L. SPLATCHE: A program to simulate genetic diversity taking into account environmental heterogeneity. Mol. Ecol. Notes 2004, 4, 139–142. [Google Scholar] [CrossRef]
- Benguigui, M.; Arenas, M. Spatial and temporal simulation of human evolution. Methods, frameworks and applications. Curr. Genom. 2014, 15, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z. Computational Molecular Evolution; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Arenas, M.; Posada, D. Simulation of coding sequence evolution. In Codon Evolution; Cannarozzi, G.M., Schneider, A., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 126–132. [Google Scholar]
- Arenas, M. Trends in substitution models of molecular evolution. Front. Genet. 2015, 6, 319. [Google Scholar] [CrossRef] [PubMed]
- Dunning, J.B.; Stewart, D.J.; Danielson, B.J.; Noon, B.R.; Root, T.L.; Lamberson, R.H.; Stevens, E.E. Spatially explicit population models: Current forms and future uses. Ecol. Appl. 1995, 5, 3–11. [Google Scholar] [CrossRef]
- Excoffier, L.; Foll, M.; Petit, R.J. Genetic consequences of range expansions. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 481–501. [Google Scholar] [CrossRef]
- Ray, N.; Excoffier, L. Inferring past demography using spatially explicit population genetic models. Hum. Biol. 2009, 81, 141–157. [Google Scholar] [CrossRef] [PubMed]
- Landguth, E.L.; Cushman, S.A. CDPOP: A spatially explicit cost distance population genetics program. Mol. Ecol. Resour. 2010, 10, 156–161. [Google Scholar] [CrossRef] [PubMed]
- Strand, A.E.; Niehaus, J.M. KERNELPOP, a spatially explicit population genetic simulation engine. Mol. Ecol. Notes 2007, 7, 969–973. [Google Scholar] [CrossRef]
- Leblois, R.; Estoup, A.; Rousset, F. IBDSim: A computer program to simulate genotypic data under isolation by distance. Mol. Ecol. Resour. 2009, 9, 107–109. [Google Scholar] [CrossRef] [PubMed]
- Rendine, S.; Piazza, A.; Cavalli-Sforza, L.L. Simulation and separation by principal components of multiple demic expansions in europe. Am. Nat. 1986, 128, 681–706. [Google Scholar] [CrossRef]
- Landguth, E.L.; Bearlin, A.; Day, C.C.; Dunham, J. CDMetaPOP: An individual-based, eco-evolutionary model for spatially explicit simulation of landscape demogenetics. Methods Ecol. Evol. 2016, 8, 4–11. [Google Scholar] [CrossRef]
- Leempoel, K.; Duruz, S.; Rochat, E.; Widmer, I.; Orozco-terWengel, P.; Joost, S. Simple rules for an efficient use of geographic information systems in molecular ecology. Front. Ecol. Evol. 2017, 5, 33. [Google Scholar] [CrossRef]
- Kimura, M.; Weiss, G.H. The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 1964, 49, 561–576. [Google Scholar] [PubMed]
- Cavalli-Sforza, L.L. Population structure and human evolution. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1966, 164, 362–379. [Google Scholar] [CrossRef]
- Jakobsson, M.; Scholz, S.W.; Scheet, P.; Gibbs, J.R.; VanLiere, J.M.; Fung, H.C.; Szpiech, Z.A.; Degnan, J.H.; Wang, K.; Guerreiro, R.; et al. Genotype, haplotype and copy-number variation in worldwide human populations. Nature 2008, 451, 998–1003. [Google Scholar] [CrossRef] [PubMed]
- Novembre, J.; Ramachandran, S. Perspectives on human population structure at the cusp of the sequencing era. Annu. Rev. Genom. Hum. Genet. 2011, 12, 245–274. [Google Scholar] [CrossRef] [PubMed]
- Patterson, N.; Price, A.L.; Reich, D. Population structure and eigenanalysis. PLoS Genet. 2006, 2, e190. [Google Scholar] [CrossRef] [PubMed]
- Petkova, D.; Novembre, J.; Stephens, M. Visualizing spatial population structure with estimated effective migration surfaces. Nat. Genet. 2016, 48, 94–100. [Google Scholar] [CrossRef] [PubMed]
- Bradburd, G.S.; Ralph, P.L.; Coop, G.M. A spatial framework for understanding population structure and admixture. PLoS Genet. 2016, 12, e1005703. [Google Scholar] [CrossRef] [PubMed]
- Duforet-Frebourg, N.; Blum, M.G. Nonstationary patterns of isolation-by-distance: Inferring measures of local genetic differentiation with Bayesian kriging. Evolution 2014, 68, 1110–1123. [Google Scholar] [CrossRef] [PubMed]
- Messina, F.; Finocchio, A.; Akar, N.; Loutradis, A.; Michalodimitrakis, E.I.; Brdicka, R.; Jodice, C.; Novelletto, A. Spatially Explicit Models to Investigate Geographic Patterns in the Distribution of Forensic STRs: Application to the North-Eastern Mediterranean. PLoS ONE 2016, 11, e0167065. [Google Scholar] [CrossRef] [PubMed]
- Jeong, C.; Peter, B.M.; Basnyat, B.; Neupane, M.; Beall, C.M.; Childs, G.; Craig, S.R.; Novembre, J.; Di Rienzo, A. A longitudinal cline characterizes the genetic structure of human populations in the Tibetan plateau. PLoS ONE 2017, 12, e0175885. [Google Scholar]
- Uren, C.; Kim, M.; Martin, A.R.; Bobo, D.; Gignoux, C.R.; van Helden, P.D.; Moller, M.; Hoal, E.G.; Henn, B.M. Fine-Scale Human Population Structure in Southern Africa Reflects Ecogeographic Boundaries. Genetics 2016, 204, 303–314. [Google Scholar] [CrossRef] [PubMed]
- Richards, M. The Neolithic Invasion of Europe. Annu. Rev. Anthropol. 2003, 32, 135–162. [Google Scholar] [CrossRef]
- Lazaridis, I.; Patterson, N.; Mittnik, A.; Renaud, G.; Mallick, S.; Kirsanow, K.; Sudmant, P.H.; Schraiber, J.G.; Castellano, S.; Lipson, M.; et al. Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature 2014, 513, 409–413. [Google Scholar] [CrossRef] [PubMed]
- Dupanloup, I.; Bertorelle, G.; Chikhi, L.; Barbujani, G. Estimating the impact of prehistoric admixture on the genome of Europeans. Mol. Biol. Evol. 2004, 21, 1361–1372. [Google Scholar] [CrossRef] [PubMed]
- Currat, M.; Excoffier, L. The effect of the Neolithic expansion on European molecular diversity. Proc. Biol. Sci. 2005, 272, 679–688. [Google Scholar] [CrossRef] [PubMed]
- Sokal, R.R.; Oden, N.L.; Wilson, C. Genetic evidence for the spread of agriculture in Europe by demic diffusion. Nature 1991, 351, 143–145. [Google Scholar] [CrossRef] [PubMed]
- Salas, A.; Lovo-Gomez, J.; Alvarez-Iglesias, V.; Cerezo, M.; Lareu, M.V.; Macaulay, V.; Richards, M.B.; Carracedo, A. Mitochondrial echoes of first settlement and genetic continuity in El Salvador. PLoS ONE 2009, 4, e6882. [Google Scholar] [CrossRef] [PubMed]
- Dillehay, T.D. Probing deeper into first American studies. Proc. Natl. Acad. Sci. USA 2009, 106, 971–978. [Google Scholar] [CrossRef] [PubMed]
- Forster, P.; Harding, R.; Torroni, A.; Bandelt, H.J. Origin and evolution of Native American mtDNA variation: A reappraisal. Am. J. Hum. Genet. 1996, 59, 935–945. [Google Scholar] [PubMed]
- Straus, L.G. Southwestern Europe at the Last Glacial Maximum. Curr. Anthropol. 1991, 32, 189–199. [Google Scholar] [CrossRef]
- Barbujani, G.; Bertorelle, G. Genetics and the population history of Europe. Proc. Natl. Acad. Sci. USA 2001, 98, 22–25. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M.; Ray, N.; Currat, M.; Excoffier, L. Consequences of range contractions and range shifts on molecular diversity. Mol. Biol. Evol. 2012, 29, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Arenas, M.; Mona, S.; Trochet, A.; Sramkova Hanulova, A.; Currat, M.; Ray, N.; Chikhi, L.; Rasteiro, R.; Schmeller, D.S.; Excoffier, L. The scaling of genetic diversity in a changing and fragmented world. In Scaling in Ecology and Biodiversity Conservation; Henle, K., Potts, S.G., Kunin, W.E., Matsinos, Y.G., Similä, J., Pantis, J.D., Grobelnik, V., Penev, L., Settele, J., Eds.; Pensoft Publishers: Sofia, Bulgaria, 2014; pp. 55–60. [Google Scholar]
- Ray, N.; Adams, J.M. A GIS-Based Vegetation Map of the World at the Last Glacial Maximum (25,000–15,000 BP). Internet Archaeol. 2001, 11. [Google Scholar] [CrossRef]
- Marshall, S.J.; James, T.S.; Clarke, G.K.C. North American Ice Sheet reconstructions at the Last Glacial Maximum. Quat. Sci. Rev. 2002, 21, 175–192. [Google Scholar] [CrossRef]
- Bodner, M.; Perego, U.A.; Huber, G.; Fendt, L.; Rock, A.W.; Zimmermann, B.; Olivieri, A.; Gomez-Carballa, A.; Lancioni, H.; Angerhofer, N.; et al. Rapid coastal spread of First Americans: Novel insights from South America’s Southern Cone mitochondrial genomes. Genome Res. 2012, 22, 811–820. [Google Scholar] [CrossRef] [PubMed]
- Fagundes, N.J.; Kanitz, R.; Eckert, R.; Valls, A.C.; Bogo, M.R.; Salzano, F.M.; Smith, D.G.; Silva, W.A., Jr.; Zago, M.A.; Ribeiro-dos-Santos, A.K.; et al. Mitochondrial population genomics supports a single pre-Clovis origin with a coastal route for the peopling of the Americas. Am. J. Hum. Genet. 2008, 82, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, M.W.; Ruter, A.; Schweger, C.; Friebe, H.; Staff, R.A.; Kjeldsen, K.K.; Mendoza, M.L.; Beaudoin, A.B.; Zutter, C.; Larsen, N.K.; et al. Postglacial viability and colonization in North America’s ice-free corridor. Nature 2016, 537, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Rogers, R.A.; Rogers, L.A.; Hoffmann, R.S.; Martin, L.D. Native american biological diversity and the biogeographic influence of ice age refugia. J. Biogeogr. 1991, 18, 623–630. [Google Scholar] [CrossRef]
- Balme, J. Of boats and string: The maritime colonisation of Australia. Quat. Int. 2013, 285, 68–75. [Google Scholar] [CrossRef]
- Novembre, J.; Galvani, A.P.; Slatkin, M. The geographic spread of the CCR5 Delta32 HIV-resistance allele. PLoS Biol. 2005, 3, e339. [Google Scholar] [CrossRef] [PubMed]
- Binney, H.; Edwards, M.; Macias-Fauria, M.; Lozhkin, A.; Anderson, P.; Kaplan, J.O.; Andreev, A.; Bezrukova, E.; Blyakharchuk, T.; Jankovska, V.; et al. Vegetation of Eurasia from the last glacial maximum to present: Key biogeographic patterns. Quat. Sci. Rev. 2017, 157, 80–97. [Google Scholar] [CrossRef]
- Wegmann, D.; Currat, M.; Excoffier, L. Molecular diversity after a range expansion in heterogeneous environments. Genetics 2006, 174, 2009–2020. [Google Scholar] [CrossRef] [PubMed]
- Zalloua, P.A.; Platt, D.E.; El Sibai, M.; Khalife, J.; Makhoul, N.; Haber, M.; Xue, Y.; Izaabel, H.; Bosch, E.; Adams, S.M.; et al. Identifying genetic traces of historical expansions: Phoenician footprints in the Mediterranean. Am. J. Hum. Genet. 2008, 83, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Nebel, A.; Landau-Tasseron, E.; Filon, D.; Oppenheim, A.; Faerman, M. Genetic evidence for the expansion of Arabian tribes into the Southern Levant and North Africa. Am. J. Hum. Genet. 2002, 70, 1594–1596. [Google Scholar] [CrossRef] [PubMed]
- Hunley, K.; Healy, M. The impact of founder effects, gene flow, and European admixture on native American genetic diversity. Am. J. Phys. Anthropol. 2011, 146, 530–538. [Google Scholar] [CrossRef] [PubMed]
- Lindo, J.; Huerta-Sanchez, E.; Nakagome, S.; Rasmussen, M.; Petzelt, B.; Mitchell, J.; Cybulski, J.S.; Willerslev, E.; DeGiorgio, M.; Malhi, R.S. A time transect of exomes from a Native American population before and after European contact. Nat. Commun. 2016, 7, 13175. [Google Scholar] [CrossRef] [PubMed]
- O’Fallon, B.D.; Fehren-Schmitz, L. Native Americans experienced a strong population bottleneck coincident with European contact. Proc. Natl. Acad. Sci. USA 2011, 108, 20444–20448. [Google Scholar] [CrossRef] [PubMed]
- Ammerman, A.J.; Cavalli-Sforza, L.L. The Neolithic Transition and the Genetics of Populations in Europe; Princeton University Press: Princeton, NJ, USA, 1984. [Google Scholar]
- Regueiro, M.; Alvarez, J.; Rowold, D.; Herrera, R.J. On the origins, rapid expansion and genetic diversity of Native Americans from hunting-gatherers to agriculturalists. Am. J. Phys. Anthropol. 2013, 150, 333–348. [Google Scholar] [CrossRef] [PubMed]
- Weaver, T.D.; Roseman, C.C. New developments in the genetic evidence for modern human origins. Evol. Anthropol. Issues News Rev. 2008, 17, 69–80. [Google Scholar] [CrossRef]
- Schlebusch, C.M.; Malmstrom, H.; Gunther, T.; Sjodin, P.; Coutinho, A.; Edlund, H.; Munters, A.R.; Vicente, M.; Steyn, M.; Soodyall, H.; et al. Southern African ancient genomes estimate modern human divergence to 350,000 to 260,000 years ago. Science 2017, 358, 652–655. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branco, C.; Arenas, M. Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients. Genes 2018, 9, 506. https://doi.org/10.3390/genes9100506
Branco C, Arenas M. Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients. Genes. 2018; 9(10):506. https://doi.org/10.3390/genes9100506
Chicago/Turabian StyleBranco, Catarina, and Miguel Arenas. 2018. "Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients" Genes 9, no. 10: 506. https://doi.org/10.3390/genes9100506
APA StyleBranco, C., & Arenas, M. (2018). Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients. Genes, 9(10), 506. https://doi.org/10.3390/genes9100506





