Genomic Anomaly Detection with Functional Data Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Preprocessing and Computation of Summary Statistics
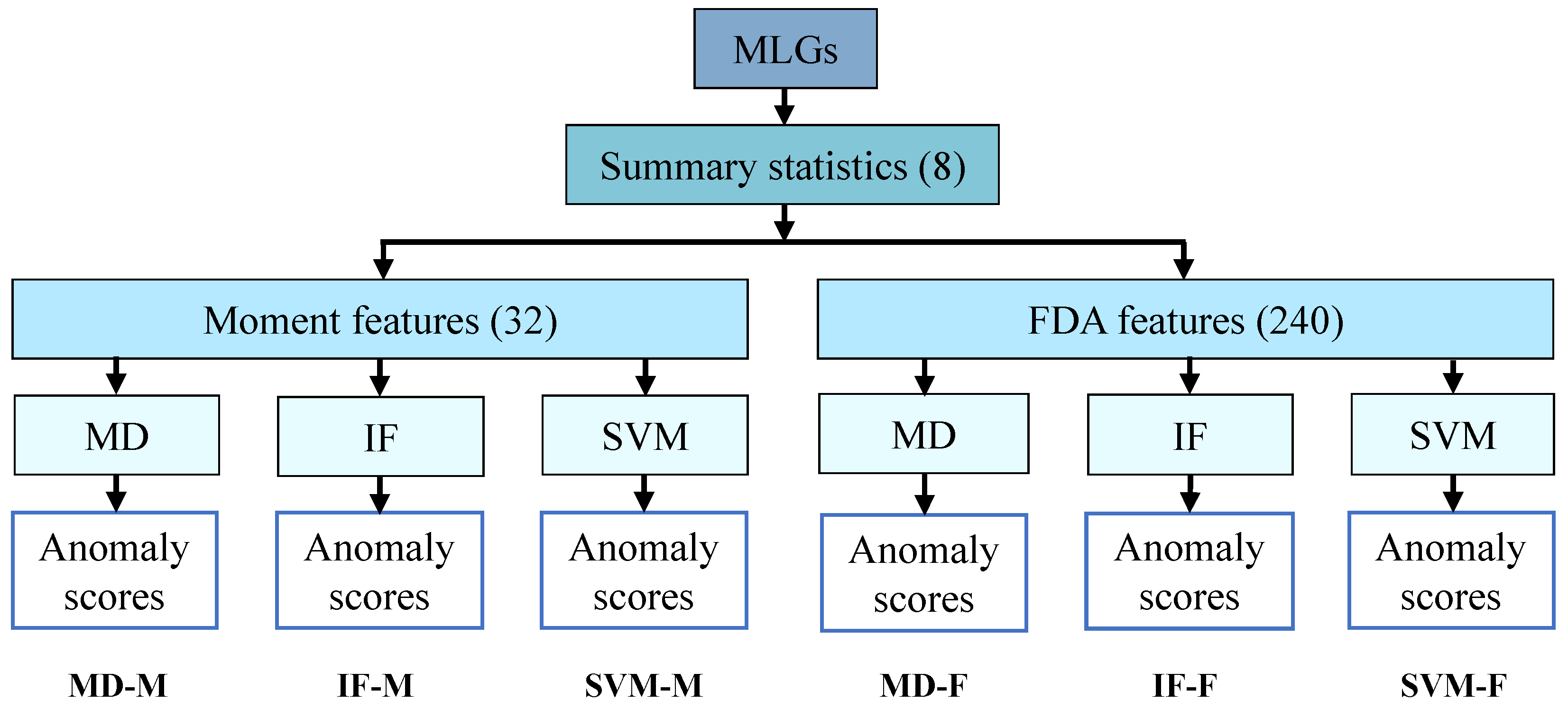
2.2. Feature Generation from Summary Statistics
2.3. Construction of Anomaly Detection Algorithms
2.4. Identification of Anomalous Regions
2.5. Application of Methods to Empirical Data
2.6. Statistical Analyses
2.7. Gene Ontology Enrichment Analyses
3. Results
3.1. Design of Anomaly Detection Algorithms
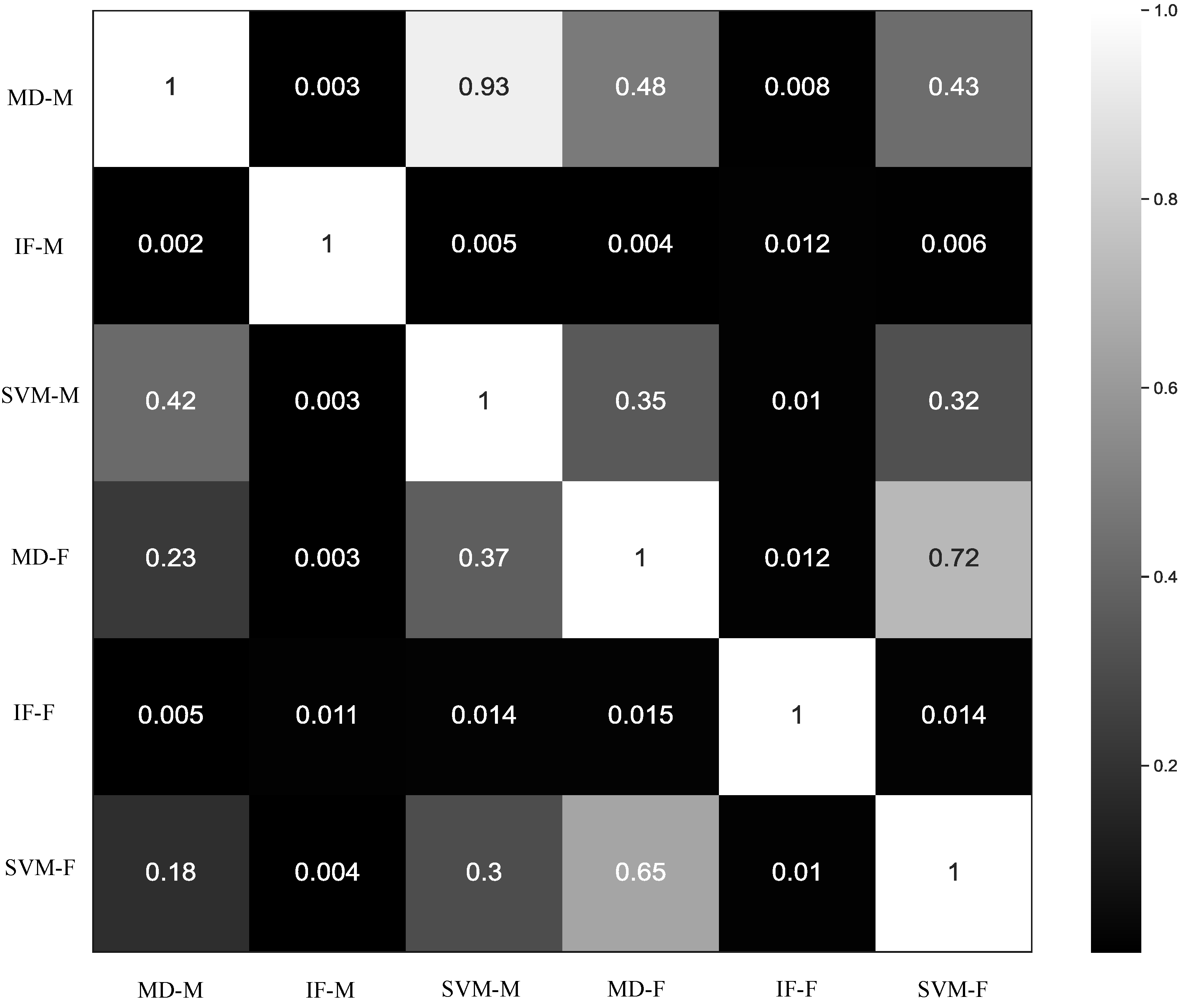
3.2. Comparison of Anomaly Detection Methods
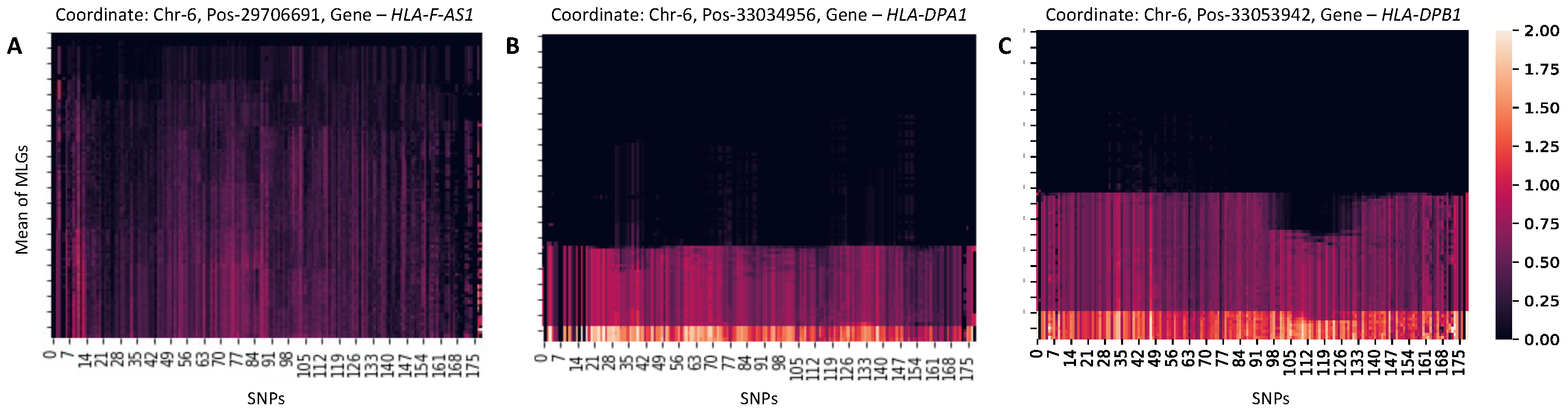
3.3. Characterization of Anomalous Regions
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hartl, D.L.; Clark, A.G. Principles of Population Genetics; Sinauer Associates: Sunderland, MA, USA, 1997; Volume 116. [Google Scholar]
- Endler, J.A. Natural Selection in the Wild; Number 21; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Gillespie, J.H. Population Genetics: A Concise Guide; JHU Press: Baltimore, MD, USA, 2004. [Google Scholar]
- Stearns, S.C.; Ebert, D. Evolution in health and disease: Work in progress. Q. Rev. Biol. 2001, 76, 417–432. [Google Scholar] [CrossRef]
- Meacham, F.; Boffelli, D.; Dhahbi, J.; Martin, D.I.; Singer, M.; Pachter, L. Identification and correction of systematic error in high-throughput sequence data. BMC Bioinform. 2011, 12, 451. [Google Scholar] [CrossRef]
- Nakamura, K.; Oshima, T.; Morimoto, T.; Ikeda, S.; Yoshikawa, H.; Shiwa, Y.; Ishikawa, S.; Linak, M.C.; Hirai, A.; Takahashi, H.; et al. Sequence-specific error profile of Illumina sequencers. Nucleic Acids Res. 2011, 39, e90. [Google Scholar] [CrossRef]
- Lee, H.; Schatz, M.C. Genomic dark matter: The reliability of short read mapping illustrated by the genome mappability score. Bioinformatics 2012, 28, 2097–2105. [Google Scholar] [CrossRef]
- Flickinger, M.; Jun, G.; Abecasis, G.R.; Boehnke, M.; Kang, H.M. Correcting for sample contamination in genotype calling of DNA sequence data. Am. J. Hum. Genet. 2015, 97, 284–290. [Google Scholar] [CrossRef][Green Version]
- Tajima, F. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 1989, 123, 585–595. [Google Scholar] [CrossRef]
- Fay, J.C.; Wu, C.I. Hitchhiking under positive Darwinian selection. Genetics 2000, 155, 1405–1413. [Google Scholar] [CrossRef]
- Bitarello, B.D.; De Filippo, C.; Teixeira, J.C.; Schmidt, J.M.; Kleinert, P.; Meyer, D.; Andrés, A.M. Signatures of long-term balancing selection in human genomes. Genome Biol. Evol. 2018, 10, 939–955. [Google Scholar] [CrossRef]
- Cheng, X.; DeGiorgio, M. Detection of shared balancing selection in the absence of trans-species polymorphism. Mol. Biol. Evol. 2019, 36, 177–199. [Google Scholar] [CrossRef]
- Hejase, H.A.; Dukler, N.; Siepel, A. From summary statistics to gene trees: Methods for inferring positive selection. Trends Genet. 2020, 36, 243–258. [Google Scholar] [CrossRef]
- Schneider, K.; White, T.J.; Mitchell, S.; Adams, C.E.; Reeve, R.; Elmer, K.R. The pitfalls and virtues of population genetic summary statistics: Detecting selective sweeps in recent divergences. J. Evol. Biol. 2021, 34, 893–909. [Google Scholar] [CrossRef]
- Xue, A.T.; Schrider, D.R.; Kern, A.D. Discovery of ongoing selective sweeps within anopheles mosquito populations using deep learning. Mol. Biol. Evol. 2021, 38, 1168–1183. [Google Scholar] [CrossRef]
- Fu, Y.X. Variances and covariances of linear summary statistics of segregating sites. Theor. Popul. Biol. 2022, 145, 95–108. [Google Scholar] [CrossRef]
- Hancock, A.M.; Di Rienzo, A. Detecting the genetic signature of natural selection in human populations: Models, methods, and data. Annu. Rev. Anthropol. 2008, 37, 197–217. [Google Scholar] [CrossRef][Green Version]
- Hill, W.; Robertson, A. Linkage disequilibrium in finite populations. Theor. Appl. Genet. 1968, 38, 226–231. [Google Scholar] [CrossRef]
- Slatkin, M. Linkage disequilibrium—Understanding the evolutionary past and mapping the medical future. Nat. Rev. Genet. 2008, 9, 477–485. [Google Scholar] [CrossRef]
- Messer, P.W.; Petrov, D.A. Population genomics of rapid adaptation by soft selective sweeps. Trends Ecol. Evol. 2013, 28, 659–669. [Google Scholar] [CrossRef]
- Garud, N.R.; Messer, P.W.; Buzbas, E.O.; Petrov, D.A. Recent selective sweeps in North American Drosophila melanogaster show signatures of soft sweeps. PLoS Genet. 2015, 11, e1005004. [Google Scholar] [CrossRef]
- Kim, Y.; Stephan, W. Detecting a local signature of genetic hitchhiking along a recombining chromosome. Genetics 2002, 160, 765–777. [Google Scholar] [CrossRef]
- Kim, Y.; Nielsen, R. Linkage disequilibrium as a signature of selective sweeps. Genetics 2004, 167, 1513–1524. [Google Scholar] [CrossRef]
- Alachiotis, N.; Stamatakis, A.; Pavlidis, P. OmegaPlus: A scalable tool for rapid detection of selective sweeps in whole-genome datasets. Bioinformatics 2012, 28, 2274–2275. [Google Scholar] [CrossRef]
- Pavlidis, P.; Živković, D.; Stamatakis, A.; Alachiotis, N. SweeD: Likelihood-based detection of selective sweeps in thousands of genomes. Mol. Biol. Evol. 2013, 30, 2224–2234. [Google Scholar] [CrossRef]
- DeGiorgio, M.; Huber, C.D.; Hubisz, M.J.; Hellmann, I.; Nielsen, R. SweepFinder2: Increased sensitivity, robustness and flexibility. Bioinformatics 2016, 32, 1895–1897. [Google Scholar] [CrossRef]
- Schrider, D.R.; Kern, A.D. Supervised machine learning for population genetics: A new paradigm. Trends Genet. 2018, 34, 301–312. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Sheehan, S.; Song, Y.S. Deep learning for population genetic inference. PLoS Comput. Biol. 2016, 12, e1004845. [Google Scholar] [CrossRef]
- Korfmann, K.; Gaggiotti, O.E.; Fumagalli, M. Deep learning in population genetics. Genome Biol. Evol. 2023, 15, evad008. [Google Scholar] [CrossRef]
- Lin, K.; Li, H.; Schlotterer, C.; Futschik, A. Distinguishing positive selection from neutral evolution: Boosting the performance of summary statistics. Genetics 2011, 187, 229–244. [Google Scholar] [CrossRef]
- Pybus, M.; Luisi, P.; Dall’Olio, G.M.; Uzkudun, M.; Laayouni, H.; Bertranpetit, J.; Engelken, J. Hierarchical boosting: A machine-learning framework to detect and classify hard selective sweeps in human populations. Bioinformatics 2015, 31, 3946–3952. [Google Scholar] [CrossRef]
- Schrider, D.R.; Kern, A.D. S/HIC: Robust identification of soft and hard sweeps using machine learning. PLoS Genet. 2016, 12, e1005928. [Google Scholar] [CrossRef]
- Chan, J.; Perrone, V.; Spence, J.; Jenkins, P.; Mathieson, S.; Song, Y. A likelihood-free inference framework for population genetic data using exchangeable neural networks. Adv. Neural Inf. Process. Syst. 2018, 31, 8594–8605. [Google Scholar]
- Sugden, L.A.; Atkinson, E.G.; Fischer, A.P.; Rong, S.; Henn, B.M.; Ramachandran, S. Localization of adaptive variants in human genomes using averaged one-dependence estimation. Nature Commun. 2018, 9, 703. [Google Scholar] [CrossRef]
- Flagel, L.; Brandvain, Y.; Schrider, D.R. The unreasonable effectiveness of convolutional neural networks in population genetic inference. Mol. Biol. Evol. 2019, 36, 220–238. [Google Scholar] [CrossRef]
- Mughal, M.R.; DeGiorgio, M. Localizing and classifying adaptive targets with trend filtered regression. Mol. Biol. Evol. 2019, 36, 252–270. [Google Scholar] [CrossRef]
- Torada, L.; Lorenzon, L.; Beddis, A.; Isildak, U.; Pattini, L.; Mathieson, S.; Fumagalli, M. ImaGene: A convolutional neural network to quantify natural selection from genomic data. BMC Bioinform. 2019, 20, 337. [Google Scholar] [CrossRef]
- Mughal, M.R.; Koch, H.; Huang, J.; Chiaromonte, F.; DeGiorgio, M. Learning the properties of adaptive regions with functional data analysis. PLoS Genet. 2020, 16, e1008896. [Google Scholar] [CrossRef]
- Gower, G.; Picazo, P.I.; Fumagalli, M.; Racimo, F. Detecting adaptive introgression in human evolution using convolutional neural networks. eLife 2021, 10, e64669. [Google Scholar] [CrossRef]
- Isildak, U.; Stella, A.; Fumagalli, M. Distinguishing between recent balancing selection and incomplete sweep using deep neural networks. Mol. Ecol. Resour. 2021, 21, 2706–2718. [Google Scholar] [CrossRef]
- Amin, M.R.; Hasan, M.; Arnab, S.P.; DeGiorgio, M. Tensor Decomposition-based Feature Extraction and Classification to Detect Natural Selection from Genomic Data. Mol. Biol. Evol. 2023, 40, msad216. [Google Scholar] [CrossRef]
- Arnab, S.P.; Amin, M.R.; DeGiorgio, M. Uncovering footprints of natural selection through spectral analysis of genomic summary statistics. Mol. Biol. Evol. 2023, 40, msad157. [Google Scholar] [CrossRef]
- Cecil, R.M.; Sugden, L.A. On convolutional neural networks for selection inference: Revealing the effect of preprocessing on model learning and the capacity to discover novel patterns. PLoS Comput. Biol. 2023, 19, e1010979. [Google Scholar] [CrossRef]
- Lauterbur, M.E.; Munch, K.; Enard, D. Versatile detection of diverse selective sweeps with flex-sweep. Mol. Biol. Evol. 2023, 40, msad139. [Google Scholar] [CrossRef] [PubMed]
- Riley, R.; Mathieson, I.; Mathieson, S. Interpreting generative adversarial networks to infer natural selection from genetic data. Genetics 2024, 226, iyae024. [Google Scholar] [CrossRef]
- Whitehouse, L.S.; Schrider, D.R. Timesweeper: Accurately identifying selective sweeps using population genomic time series. Genetics 2023, 224, iyad084. [Google Scholar] [CrossRef]
- Amin, M.R.; Hasan, M.; DeGiorgio, M. Digital image processing to detect adaptive evolution. Mol. Biol. Evol. 2024, 41, msae242. [Google Scholar] [CrossRef]
- Arnab, S.P.; Campelos dos Santos, A.L.; Fumgalli, M.; DeGiorgio, M. Efficient detection and characterization of targets of natural selection using transfer learning. Mol. Biol. Evol. 2025, 42, msaf094. [Google Scholar] [CrossRef]
- Goldstein, M.; Uchida, S. A comparative evaluation of unsupervised anomaly detection algorithms for multivariate data. PLoS ONE 2016, 11, e0152173. [Google Scholar] [CrossRef] [PubMed]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Hunter-Zinck, H.; Clark, A.G. Aberrant Time to Most Recent Common Ancestor as a Signature of Natural Selection. Mol. Biol. Evol. 2015, 32, 2784–2797. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Ralph, P. Local PCA Shows How the Effect of Population Structure Differs Along the Genome. Genetics 2018, 211, 289–304. [Google Scholar] [CrossRef]
- Shetta, O.; Niranjan, M. Robust subspace methods for outlier detection in genomic data circumvents the curse of dimensionality. R. Soc. Open Sci. 2020, 7, 190714. [Google Scholar] [CrossRef]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 372–378. [Google Scholar]
- Cremona, M.A.; Xu, H.; Makova, K.D.; Reimherr, M.; Chiaromonte, F.; Madrigal, P. Functional data analysis for computational biology. Bioinformatics 2019, 35, 3211. [Google Scholar] [CrossRef] [PubMed]
- Ramsay, J.O.; Silverman, B.W. Fitting Differential Equations to Functional Data: Principal Differential Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Wang, J.L.; Chiou, J.M.; Müller, H.G. Functional data analysis. Annu. Rev. Stat. Its Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef]
- Castrillon-Candas, J.E.; Kon, M. Anomaly detection: A functional analysis perspective. J. Multivar. Anal. 2022, 189, 104885. [Google Scholar] [CrossRef]
- Austin, E.; Eckley, I.A.; Bardwell, L. Detection of emergent anomalous strcuture in functional data. Technometrics 2024, 66, 614–624. [Google Scholar] [CrossRef]
- Siddique, M.F.; Saleem, F.; Umar, M.; Kim, C.H.; Kim, J.M. A hybrid deep learning approach for bearing fault diagnosis using continuous wavelet transform and attention-enhanced spatiotemporal feature extraction. Sensors 2025, 25, 2712. [Google Scholar] [CrossRef]
- Harris, A.M.; Garud, N.R.; DeGiorgio, M. Detection and classification of hard and soft sweeps from unphased genotypes by multilocus genotype identity. Genetics 2018, 210, 1429–1452. [Google Scholar] [CrossRef] [PubMed]
- Kern, A.D.; Schrider, D.R. diploS/HIC: An updated approach to classifying selective sweeps. G3 Genes Genomes Genet. 2018, 8, 1959–1970. [Google Scholar] [CrossRef]
- Sassenhagen, I.; Erdner, D.L.; Lougheed, B.C.; Richlen, M.L.; SjÖqvist, C. Estimating genotypic richness and proportion of identical multi-locus genotypes in aquatic microalgal populations. J. Plankton Res. 2022, 44, 559–572. [Google Scholar] [CrossRef]
- Mountain, J.L.; Cavalli-Sforza, L.L. Multilocus genotypes, a tree of individuals, and human evolutionary history. Am. J. Hum. Genet. 1997, 61, 705–718. [Google Scholar] [CrossRef]
- Gao, X.; Martin, E.R. Using allele sharing distance for detecting human population stratification. Hum. Hered. 2009, 68, 182–191. [Google Scholar] [CrossRef]
- Schaid, D.J. Genomic similarity and kernel methods I: Advancements by building on mathematical and statistical foundations. Hum. Hered. 2010, 70, 109–131. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Yang, K.; Kpotufe, S.; Feamster, N. An efficient one-class SVM for anomaly detection in the Internet of Things. arXiv 2021, arXiv:2104.11146. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, B.; Gong, J. An anomaly detection model based on one-class svm to detect network intrusions. In Proceedings of the 2015 11th International Conference on Mobile Ad-hoc and Sensor Networks (MSN), Shenzhen, China, 16–18 December 2015; pp. 102–107. [Google Scholar]
- Chandra, M.P. On the generalised distance in statistics. Proc. Natl. Inst. Sci. India 1936, 2, 49–55. [Google Scholar]
- Hotelling, H. The Generalization of Student’s Ratio; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Joseph, E.; Galeano San Miguel, P.; Lillo Rodríguez, R.E. Two-sample Hotelling’s T2 statistics based on the functional Mahalanobis semi-distance. In Working Paper; Universidad Carlos III de Madrid: Madrid, Spain, 2015; Available online: https://researchportal.uc3m.es/display/act428899 (accessed on 10 June 2025).
- Brereton, R.G. Hotelling’s T squared distribution, its relationship to the F distribution and its use in multivariate space. J. Chemom. 2016, 30, 18–21. [Google Scholar] [CrossRef]
- Klammer, A.A.; Park, C.Y.; Noble, W.S. Statistical calibration of the SEQUEST XCorr function. J. Proteome Res. 2009, 8, 2106–2113. [Google Scholar] [CrossRef]
- Yang, J.; Weedon, M.N.; Purcell, S.; Lettre, G.; Estrada, K.; Willer, C.J.; Smith, A.V.; Ingelsson, E.; O’connell, J.R.; Mangino, M.; et al. Genomic inflation factors under polygenic inheritance. Eur. J. Hum. Genet. 2011, 19, 807–812. [Google Scholar] [CrossRef]
- Neyman, J.; Pearson, E.S. On the use and interpretation of certain test criteria for purposes of statistical inference: Part I. Biometrika 1928, 20, 175–240. [Google Scholar]
- Altshuler, D.; Daly, M.J.; Lander, E.S. Genetic mapping in human disease. Science 2008, 322, 881–888. [Google Scholar] [CrossRef]
- Auton, A.; Brooks, L.; Durbin, R.; Garrison, E.; Kang, H.; Korbel, J.; Marchini, J.; McCarthy, S.; McVean, G.; Abecasis, G. A global reference for human genetic variation. 1000 Genomes Project Consortium. Nature 2015, 526, 68. [Google Scholar] [PubMed]
- Miles, A.; pyup.io bot.; R., M.; Ralph, P.; Kelleher, J.; Schelker, M.; Pisupati, R.; Rae, S.; Millar, T. cggh/scikit-allel, v1.3.7, 2023. [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Ramsay, J.; Hooker, G.; Graves, S. Introduction to functional data analysis. In Functional Data Analysis with R and MATLAB; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–19. [Google Scholar]
- Ramsay, J.; Hooker, G.; Graves, S. Functional Data Analysis with R and Matlab. J. Stat. Softw. 2009, 34, 1–2. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kent, W.J.; Sugnet, C.W.; Furey, T.S.; Roskin, K.M.; Pringle, T.H.; Zahler, A.M.; Haussler, D. The human genome browser at UCSC. Genome Res. 2002, 12, 996–1006. [Google Scholar] [CrossRef]
- Talkowski, M.E.; Ernst, C.; Heilbut, A.; Chiang, C.; Hanscom, C.; Lindgren, A.; Kirby, A.; Liu, S.; Muddukrishna, B.; Ohsumi, T.K.; et al. Next-generation sequencing strategies enable routine detection of balanced chromosome rearrangements for clinical diagnostics and genetic research. Am. J. Hum. Genet. 2011, 88, 469–481. [Google Scholar] [CrossRef]
- Schwartz, U.; Németh, A.; Diermeier, S.; Exler, J.H.; Hansch, S.; Maldonado, R.; Heizinger, L.; Merkl, R.; Längst, G. Characterizing the nuclease accessibility of DNA in human cells to map higher order structures of chromatin. Nucleic Acids Res. 2019, 47, 1239–1254. [Google Scholar] [CrossRef] [PubMed]
- Eden, E.; Lipson, D.; Yogev, S.; Yakhini, Z. Discovering motifs in ranked lists of DNA sequences. PLoS Comput. Biol. 2007, 3, e39. [Google Scholar] [CrossRef]
- Eden, E.; Navon, R.; Steinfeld, I.; Lipson, D.; Yakhini, Z. GOrilla: A tool for discovery and visualization of enriched GO terms in ranked gene lists. BMC Bioinform. 2009, 10, 48. [Google Scholar] [CrossRef]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D.L. The mahalanobis distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Li, K.L.; Huang, H.K.; Tian, S.F.; Xu, W. Improving one-class SVM for anomaly detection. In Proceedings of the 2003 International Conference on Machine Learning and Cybernetics (IEEE Cat. No. 03EX693), Xi’an, China, 5 November 2003; Volume 5, pp. 3077–3081. [Google Scholar]
- Ghorbani, H. Mahalanobis distance and its application for detecting multivariate outliers. Facta Univ. Ser. Math. Inform. 2019, 583–595. [Google Scholar] [CrossRef]
- Pierini, F.; Lenz, T.L. Divergent allele advantage at human MHC genes: Signatures of past and ongoing selection. Mol. Biol. Evol. 2018, 35, 2145–2158. [Google Scholar] [CrossRef]
- Taliun, D.; Harris, D.N.; Kessler, M.D.; Carlson, J.; Szpiech, Z.A.; Torres, R.; Taliun, S.A.G.; Corvelo, A.; Gogarten, S.M.; Kang, H.M.; et al. Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. Nature 2021, 590, 290–299. [Google Scholar] [CrossRef]
- Hughes, A.L.; Nei, M. Pattern of nucleotide substitution at major histocompatibility complex class I loci reveals overdominant selection. Nature 1988, 335, 167–170. [Google Scholar] [CrossRef]
- Klein, J.; Satta, Y.; O’hUigin, C.; Takahata, N. The molecular descent of the major histocompatibility complex. Annu. Rev. Immunol. 1993, 11, 269–295. [Google Scholar] [CrossRef] [PubMed]
- DeGiorgio, M.; Lohmueller, K.E.; Nielsen, R. A model-based approach for identifying signatures of ancient balancing selection in genetic data. PLoS Genet. 2014, 10, e1004561. [Google Scholar] [CrossRef]
- Li, Y.; Wu, D.D.; Boyko, A.R.; Wang, G.D.; Wu, S.F.; Irwin, D.M.; Zhang, Y.P. Population variation revealed high-altitude adaptation of Tibetan mastiffs. Mol. Biol. Evol. 2014, 31, 1200–1205. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Liu, Y.H.; Wang, G.D.; Yang, C.T.; Otecko, N.O.; Liu, F.; Wu, S.F.; Wang, L.; Yu, L.; Zhang, Y.P. Identifying molecular signatures of hypoxia adaptation from sex chromosomes: A case for Tibetan Mastiff based on analyses of X chromosome. Sci. Rep. 2016, 6, 35004. [Google Scholar] [CrossRef]
- Edea, Z.; Dadi, H.; Dessie, T.; Kim, K.S. Genomic signatures of high-altitude adaptation in Ethiopian sheep populations. Genes Genom. 2019, 41, 973–981. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, H.; Ye, J.; Liu, C.; Wei, R.; Chen, C.; Huang, L. Genetic diversity and signatures of selection in 15 Chinese indigenous dog breeds revealed by genome-wide SNPs. Front. Genet. 2019, 10, 1174. [Google Scholar] [CrossRef]
- Gaughran, S.J. Patterns of Adaptive and Purifying Selection in the Genomes of Phocid Seals. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2021. [Google Scholar]
- Hsu, W.T.; Williamson, P.; Khatkar, M.S. Analysis of dog breed diversity using a composite selection index. Sci. Rep. 2023, 13, 1674. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.Y.; Stern, A.J.; Racimo, F.; Nielsen, R. Detecting selection in multiple populations by modeling ancestral admixture components. Mol. Biol. Evol. 2022, 39, msab294. [Google Scholar] [CrossRef] [PubMed]
- Dokas, P.; Ertoz, L.; Kumar, V.; Lazarevic, A.; Srivastava, J.; Tan, P.N. Data mining for network intrusion detection. In Proceedings of the NSF Workshop on Next Generation Data Mining; Citeseer: Baltimore, MD, USA, 2002; pp. 21–30. [Google Scholar]
- Kamoi, R.; Kobayashi, K. Why is the mahalanobis distance effective for anomaly detection? arXiv 2020, arXiv:2003.00402. [Google Scholar]
- Fisher, R.A. On the Dominance Ratio. Proc. R. Soc. Edinb. 1922, 42, 321–341. [Google Scholar] [CrossRef]
- Dilthey, A.; Cox, C.; Iqbal, Z.; Nelson, M.R.; McVean, G. Improved genome inference in the MHC using a population reference graph. Nat. Genet. 2015, 47, 682–688. [Google Scholar] [CrossRef]
- Soto, D.C.; Uribe-Salzar, J.M.; Shew, C.J.; Sekar, A.; McGinty, S.P.; Dennis, M.Y. Genomic structural variation: A copmlex but important driver of human evolution. Am. J. Biol. Anthropol. 2023, 181, 118–144. [Google Scholar] [CrossRef]
- Enard, D.; Messer, P.W.; Petrov, D.A. Genome-wide signals of positive selection in human evolution. Genome Res 2014, 24, 885–895. [Google Scholar] [CrossRef]
- Nord, A.S.; Pattabriaman, K.; Visel, A.; Rubenstein, J.L.R. Genomic perspectives of transcriptional regulation in forebrain devleopment. Neuron 2015, 85, 27–47. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanjilal, R.; Campelo dos Santos, A.L.; Arnab, S.P.; DeGiorgio, M.; Assis, R. Genomic Anomaly Detection with Functional Data Analysis. Genes 2025, 16, 710. https://doi.org/10.3390/genes16060710
Kanjilal R, Campelo dos Santos AL, Arnab SP, DeGiorgio M, Assis R. Genomic Anomaly Detection with Functional Data Analysis. Genes. 2025; 16(6):710. https://doi.org/10.3390/genes16060710
Chicago/Turabian StyleKanjilal, Ria, Andre Luiz Campelo dos Santos, Sandipan Paul Arnab, Michael DeGiorgio, and Raquel Assis. 2025. "Genomic Anomaly Detection with Functional Data Analysis" Genes 16, no. 6: 710. https://doi.org/10.3390/genes16060710
APA StyleKanjilal, R., Campelo dos Santos, A. L., Arnab, S. P., DeGiorgio, M., & Assis, R. (2025). Genomic Anomaly Detection with Functional Data Analysis. Genes, 16(6), 710. https://doi.org/10.3390/genes16060710





