Internal Validation of MaSTR™ Probabilistic Genotyping Software for the Interpretation of 2–5 Person Mixed DNA Profiles
Abstract
:1. Introduction
2. Materials and Methods
2.1. DNA Procurement and Preparation
2.2. DNA Amplification
2.3. Capillary Electrophoresis and STR Genotyping
2.4. DNA Mixture Preparation
2.5. Graphical User Interface
2.6. Protocol Dataset
2.7. Likelihood Ratio Calculations
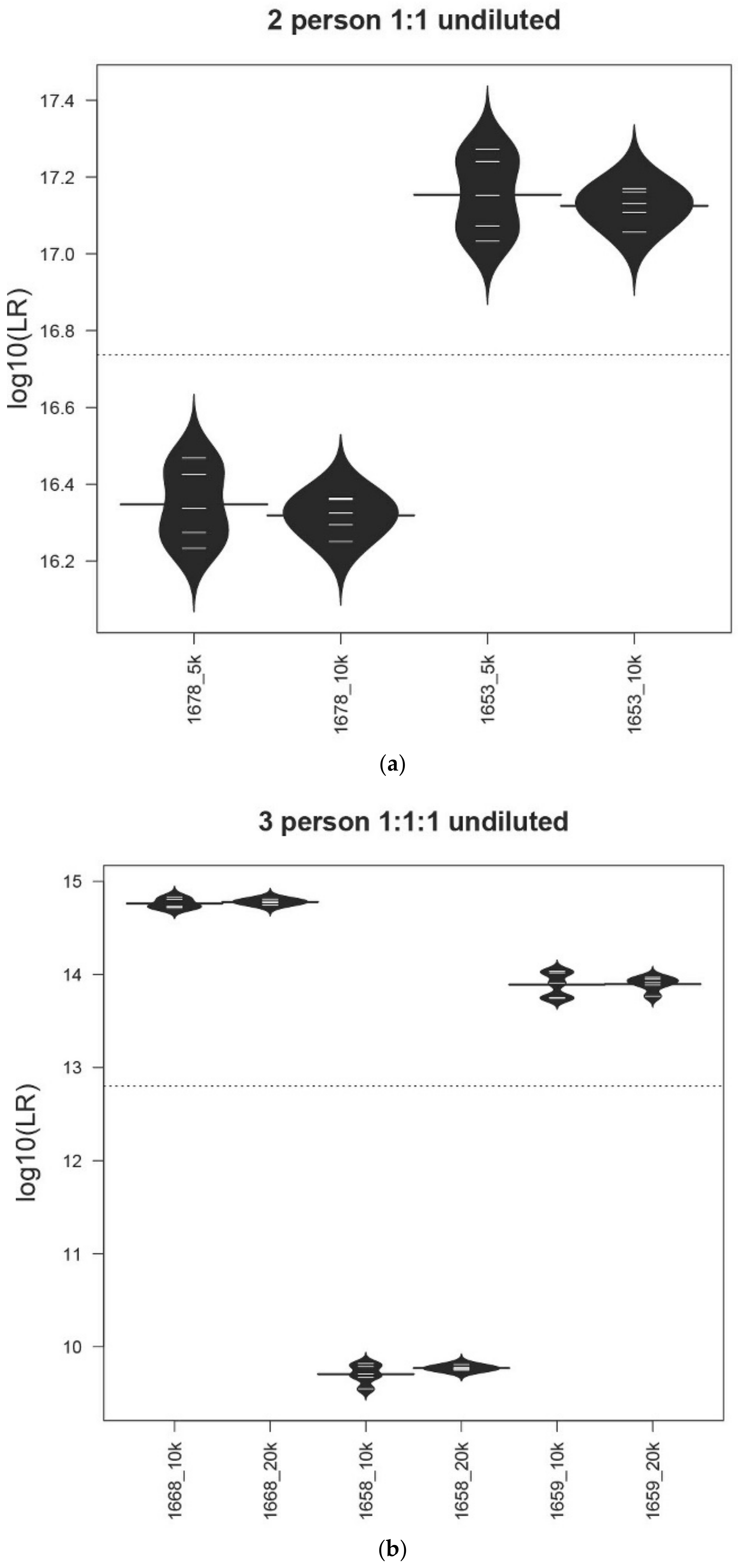
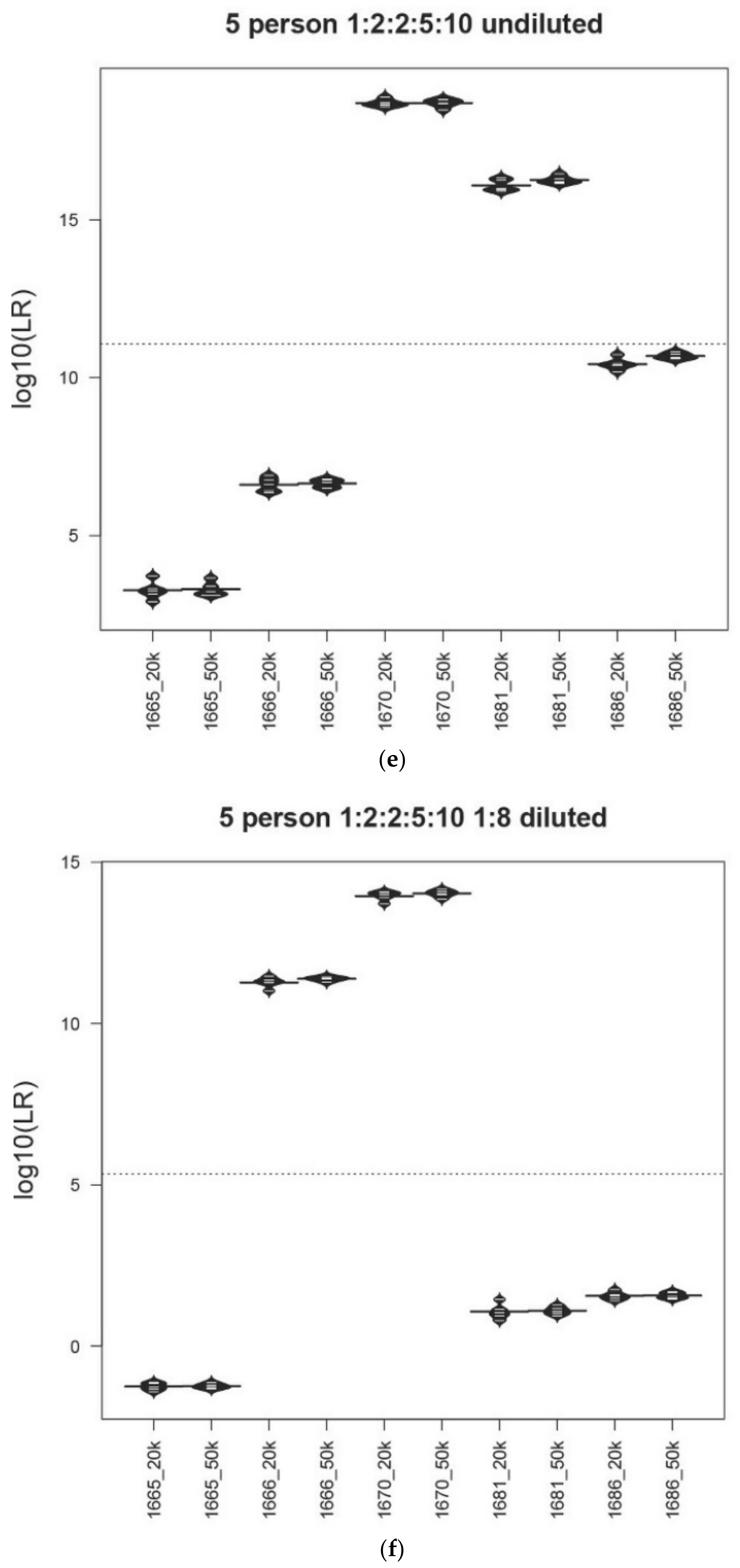
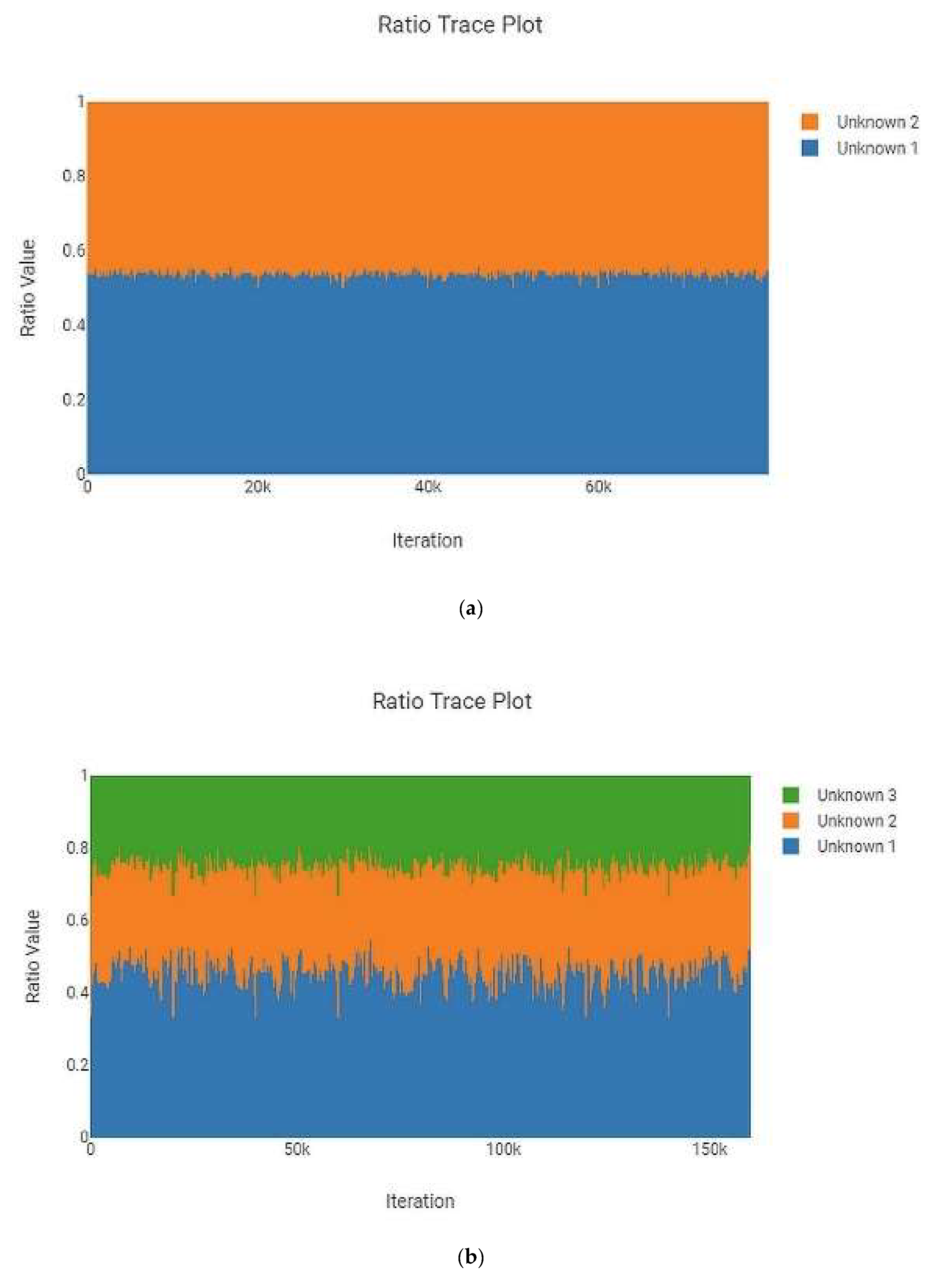
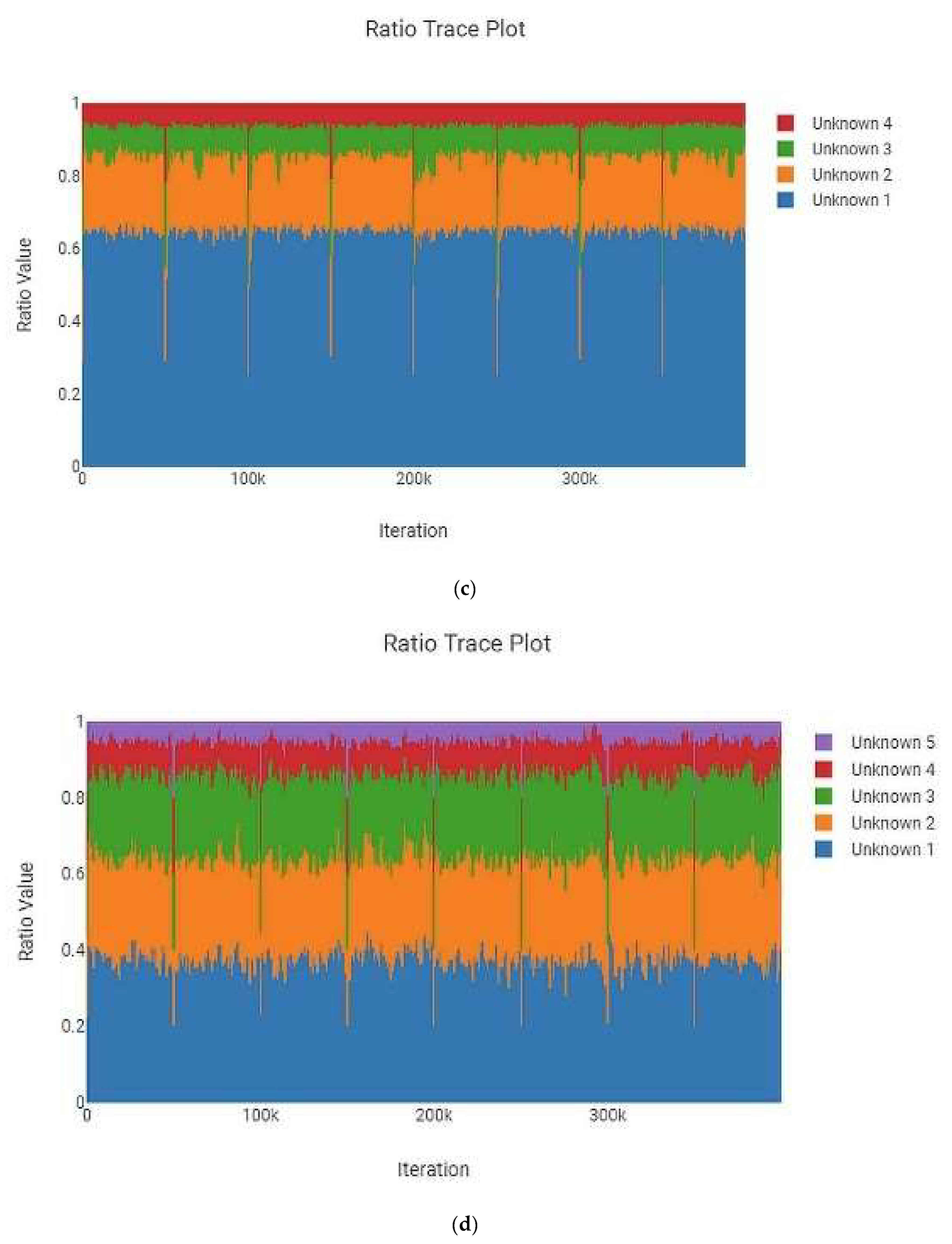
2.8. Statistical Visualizations
3. Results
3.1. Variance Factor Results
3.2. Number of MCMC Iterations and Precision
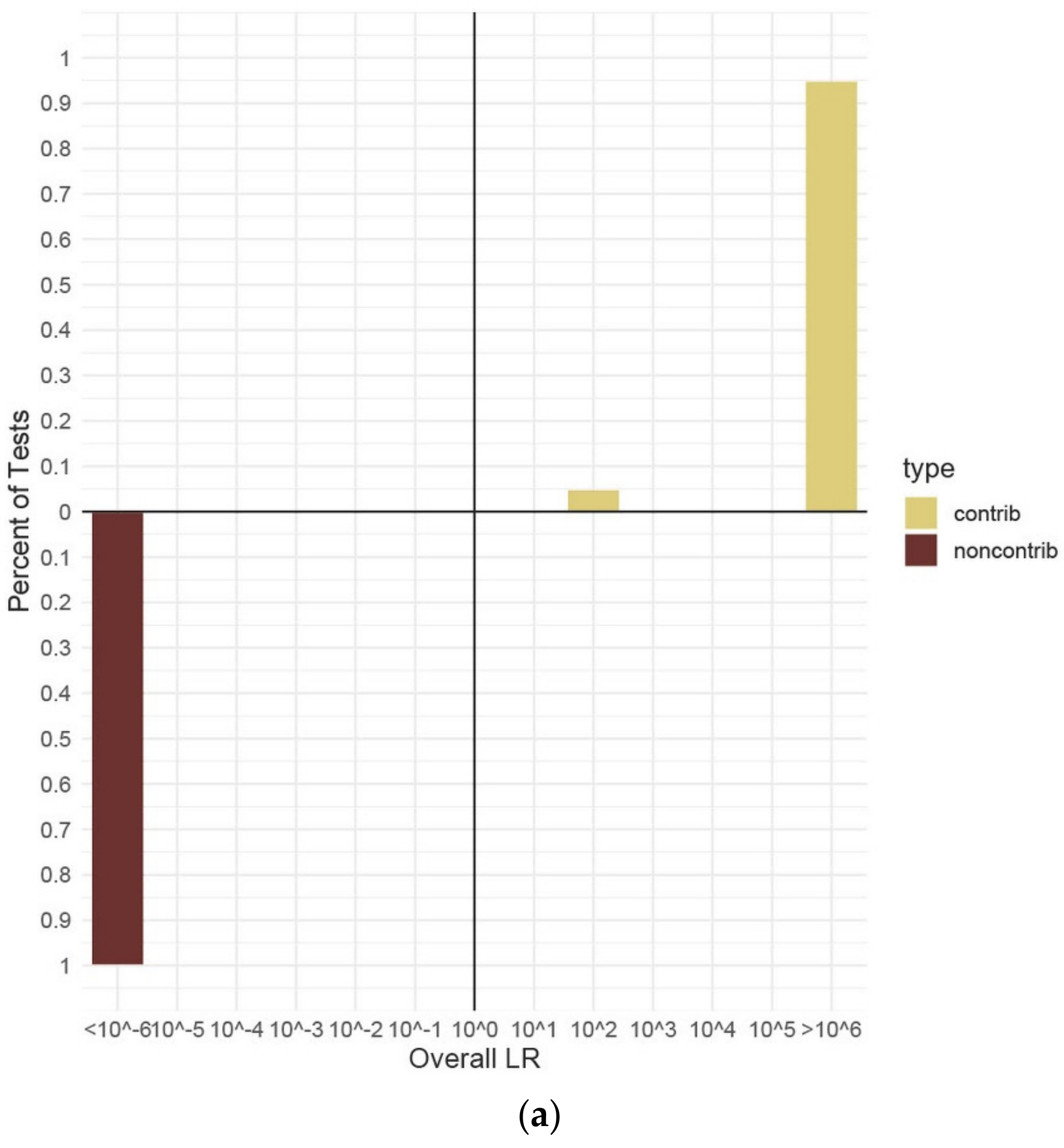
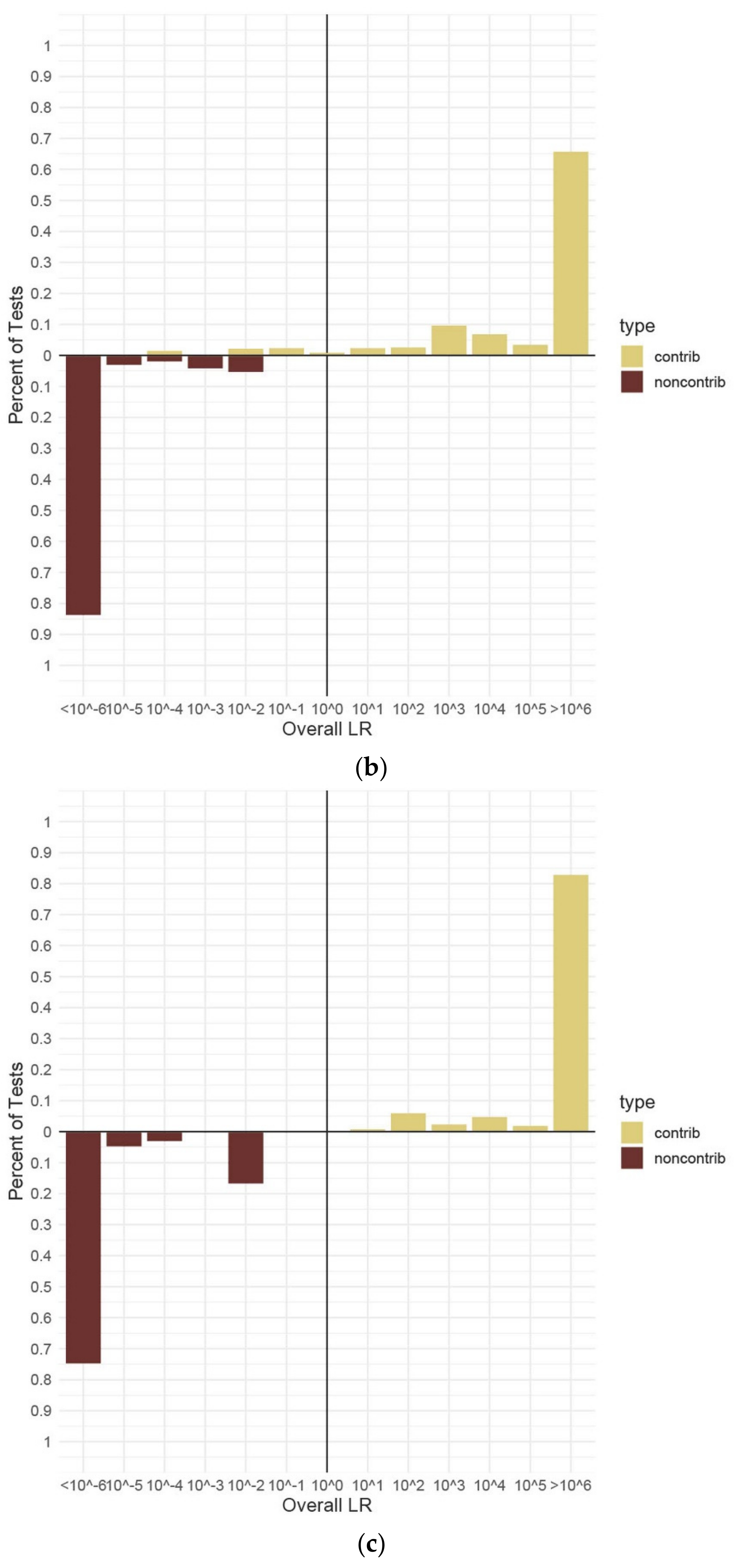
3.3. Accuracy Assessment
3.4. Testing Sensitivity and Specificity
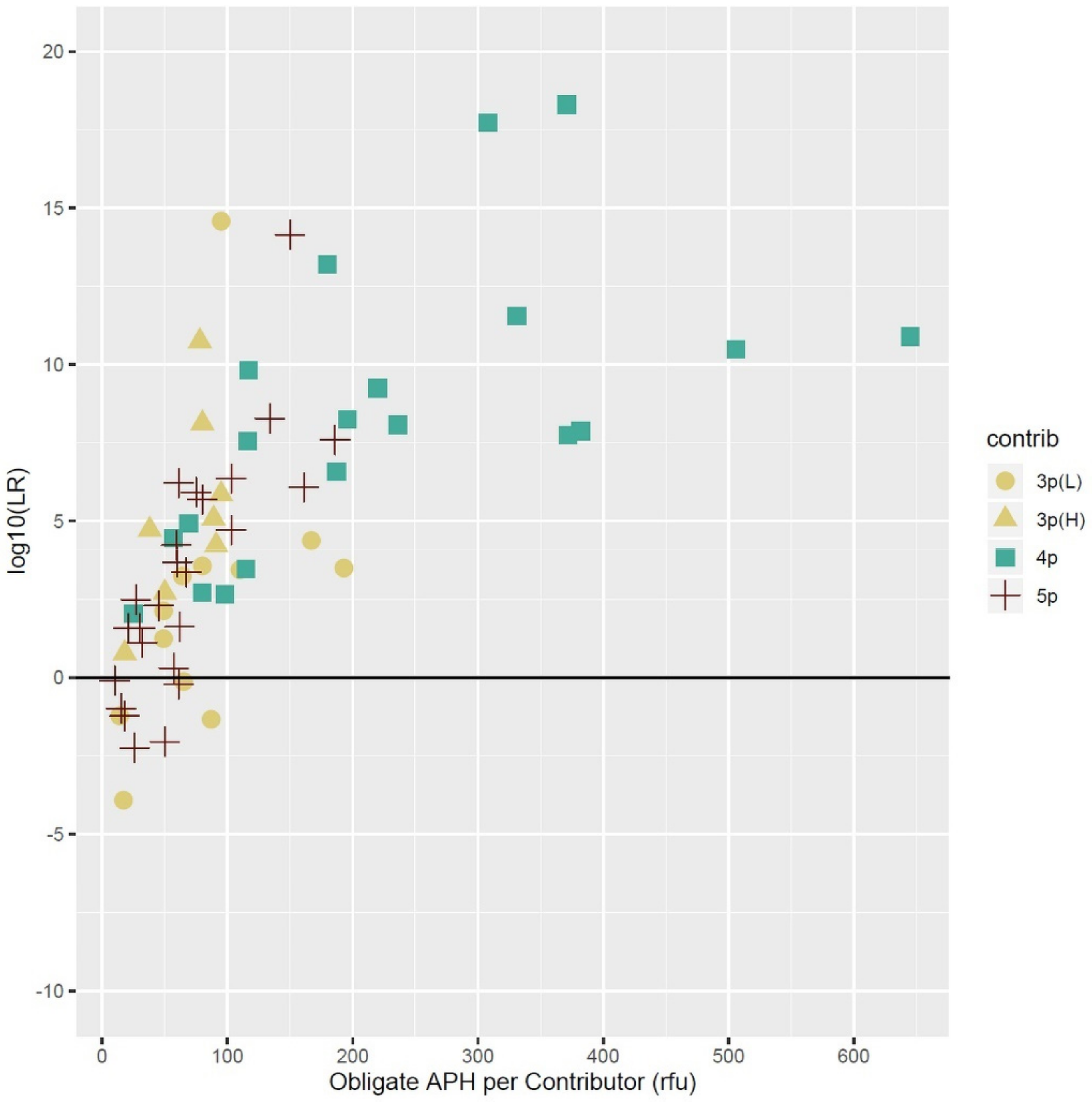
3.5. Allele Peak Height, Allele Sharing, and Template Amount
3.6. Number of Contributors
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coble, M.D.; Bright, J. Probabilistic genotyping software: An Overview. Forensic Sci. Int. Genet. 2019, 38, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Evett, I.W.; Buffery, C.; Willott, G.; Stoney, D. A guide to Interpreting Single Locus Profiles of DNA Mixtures in Forensic Cases. J. Forensic Sci. 1991, 31, 41–47. [Google Scholar] [CrossRef]
- Weir, B.S.; Triggs, C.M.; Starling, L.; Stowell, L.I.; Walsh, K.A.J.; Buckleton, J.S. Interpreting DNA Mixtures. J. Forensic Sci. 1997, 42, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Ladd, C.; Lee, H.C.; Yang, N.; Bieber, F.R. Interpretation of Complex Forensic DNA Mixtures. Croat. Med. J. 2001, 42, 244–246. Available online: www.scopus.com (accessed on 18 May 2022).
- Bieber, F.R.; Buckleton, J.S.; Budowle, B.; Butler, J.M.; Coble, M.D. Evaluation of Forensic DNA Mixture Evidence: Protocol for Evaluation, Interpretation, and Statistical Calculations Using the Combined Probability of Inclusion. BMC Genet. 2016, 17, 125. [Google Scholar] [CrossRef]
- Gill, P.; Whitaker, J.P.; Flaxman, C.; Brown, N.; Buckleton, J.S. An Investigation of the Rigor of Interpretation Rules for STR’s Derived from Less Than 100pg of DNA. Forensic Sci. Int. 2000, 112, 17–40. [Google Scholar] [CrossRef]
- Gill, P.; Brenner, C.H.; Buckleton, J.S.; Carracedo, A.; Krawczak, M.; Mayr, W.R.; Morling, N.; Prinz, M.; Schneider, P.M.; Weir, B.S. DNA Commission of the International Society of Forensic Genetics: Recommendations on the Interpretation of Mixtures. Forensic Sci. Int. 2006, 160, 90–101. [Google Scholar] [CrossRef]
- Buckleton, J.; Curran, J. A Discussion of the Merits of Random Man Not Excluded and Likelihood Ratios. Forensic Sci. Int. Genet. 2008, 2, 343–348. [Google Scholar] [CrossRef]
- Scientific Working Group on DNA Analysis Methods (SWGDAM). Guidelines for the Validation of Probabilistic Genotyping Systems. 2015. Available online: http://media.wix.com/ugd/4344b0_22776006b67c4a32a5ffc04fe3b56515.pdf (accessed on 21 April 2021).
- Coble, M.D.; Buckleton, J.; Butler, J.M.; Egeland, T.; Fimmers, R.; Gill, P.; Gusmão, L.; Guttman, B.; Krawczak, M.; Morling, N.; et al. DNA Commission of the International Society for Forensic Genetics: Recommendations on the Validation of Software Programs Performing Biostatistical Calculations for Forensic Genetics Applications. Forensic Sci. Int. Genet. 2016, 25, 191–197. [Google Scholar] [CrossRef]
- ANSI/ASB Standard 018 Standard for Validation of Probabilistic Genotyping Systems. 2020. Available online: www.asbstandardsboard.org (accessed on 22 April 2021).
- Inman, K.; Rudin, N.; Cheng, K.; Robinson, C.; Kirschner, A.; Inman-Semerau, L.; Lohmueller, K.E. Lab Retriever: A Software Tool for Calculating Likelihood Ratios Incorporating a Probability of Drop-out for Forensic DNA Profiles. BMC Bioinform. 2015, 16, 298. [Google Scholar] [CrossRef]
- Gill, P.; Haned, H. A New Methodological Framework to Interpret Complex DNA Profiles Using Likelihood Ratios. Forensic Sci. Int. Genet. 2013, 7, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Prieto, L.; Haned, H.; Mosquera, A.; Crespillo, M.; Aleman, M.; Aler, M.; Alvarez, F.; Baeza-Richer, C.; Dominguez, A.; Doutremepuich, C.; et al. Euroforgen-NoE Collaborative Exercise on LRmix to Demonstrate Standardization of the Interpretation of Complex DNA Profiles. Forensic Sci. Int. Genet. 2014, 9, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Barrio, P.A.; Crespillo, M.; Luque, J.A.; Aler, M.; Baeza-Richer, C.; Baldassarri, L.; Carnevali, E.; Coufalova, P.; Flores, I.; García, O.; et al. GHEP-ISFG Collaborative Exercise on Mixture Profiles (GHEP-MIX06). Reporting Conclusions: Results and Evaluation. Forensic Sci. Int. Genet. 2018, 35, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Perlin, M.W.; Sinelnikov, A. An Information Gap in DNA Evidence Interpretation. PLoS ONE 2009, 4, e8327. [Google Scholar] [CrossRef]
- Perlin, M.W.; Legler, M.M.; Spencer, C.E.; Smith, J.L.; Allan, W.P.; Belrose, J.L.; Duceman, B.W. Validating TrueAllele® DNA Mixture Interpretation. J. Forensic Sci. 2011, 56, 1430–1447. [Google Scholar] [CrossRef]
- Perlin, M.W.; Belrose, J.L.; Duceman, B.W. New York State TrueAllele® Casework Validation Study. J. Forensic Sci. 2013, 58, 1458–1466. [Google Scholar] [CrossRef]
- Perlin, M.W.; Hornyak, J.M.; Sugimoto, G.; Miller, K.W.P. TrueAllele_ Genotype Identification on DNA Mixtures Containing Up to Five Unknown Contributors. J. Forensic Sci. 2015, 60, 857–868. [Google Scholar] [CrossRef]
- Bleka, Ø.; Storvik, G.; Gill, P. EuroForMix: An Open Source Software Based on a Continuous Model to Evaluate STR DNA Profiles from a Mixture of Contributors with Artefacts. Forensic Sci. Int. Genet. 2016, 21, 35–44. [Google Scholar] [CrossRef]
- Benschop, C.C.G.; Nijveld, A.; Duijs, F.E.; Sijen, T. An Assessment of the Performance of the Probabilistic Genotyping Software EuroForMix: Trends in Likelihood Ratios and Analysis of Type I & II Errors. Forensic Sci. Int. Genet. 2019, 42, 31–38. [Google Scholar] [CrossRef]
- Taylor, D.; Bright, J.A.; Buckleton, J. The Interpretation of Single Source and Mixed DNA Profiles. Forensic Sci. Int. Genet. 2013, 7, 516–528. [Google Scholar] [CrossRef]
- Bright, J.A.; Taylor, D.; McGovern, C.; Cooper, S.; Russell, L.; Abarno, D.; Buckleton, J. Developmental Validation of STRmixTM, Expert Software for the Interpretation of Forensic DNA Profiles. Forensic Sci. Int. Genet. 2016, 23, 226–239. [Google Scholar] [CrossRef] [PubMed]
- Buckleton, J.S.; Bright, J.A.; Gittelson, S.; Moretti, T.R.; Onorato, A.J.; Bieber, F.R.; Budowle, B.; Taylor, D.A. The Probabilistic Genotyping Software STRmix: Utility and Evidence for its Validity. J. Forensic Sci. 2019, 64, 393–405. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Richey, M. The Evolution of Markov Chain Monte Carlo Methods. Am. Math Mon. 2010, 117, 383–413. [Google Scholar] [CrossRef]
- Taylor, D.; Bright, J.A.; Buckleton, J. The ‘Factor of Two’ Issue in Mixed DNA Profiles. J. Theor. Biol. 2014, 363, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.; Bright, J.A.; Buckleton, J. Considering Relatives When Assessing the Evidential Strength of Mixed DNA Profiles. Forensic Sci. Int. Genet. 2014, 13, 259–263. [Google Scholar] [CrossRef]
- Clayton, T.; Whitaker, J.P.; Sparkes, R.L.; Gill, P. Analysis and Interpretation of Mixed Forensic Stains Using DNA STR Profiling. Forensic Sci. Int. 1998, 91, 55–70. [Google Scholar] [CrossRef]
- Quantifiler® Human DNA Quantification Kit and Quantifiler® Y Human Male DNA Quantification Kit User’s Manual. 2014. Available online: https://tools.thermofisher.com/content/sfs/manuals/cms_041395.pdf (accessed on 4 April 2022).
- PowerPlex® Fusion System for Use on the Applied Biosystems® Genetic Analyzers Instructions for Use of Products. 2020. Available online: https://www.promega.com/~/media/Files/Resources/Protocols/Technical%20Manuals/101/PowerPlex%20Fusion%20System%20Protocol.pdf (accessed on 4 April 2022).
- Applied Biosystems 3130/3130xl Genetic Analyzers Getting Started Guide. 2012. Available online: https://tools.thermofisher.com/content/sfs/manuals/4477796.pdf (accessed on 4 April 2022).
- Budowle, B.; Shea, B.; Niezgoda, S.J.; Chakraborty, R. CODIS STR Loci Data from 41 Sample Populations. J. Forensic Sci. 2001, 46, 453–489. [Google Scholar] [CrossRef]
- Hill, C.R.; Duewer, D.L.; Kline, M.C.; Coble, M.D.; Butler, J.M. U.S. Population Data for 29 Autosomal STR Loci. Forensic Sci. Int. Genet. 2013, 7, e82–e83. [Google Scholar] [CrossRef]
- Moretti, T.R.; Moreno, L.I.; Smerick, J.B.; Pignone, M.L.; Hizon, R.; Buckleton, J.S.; Bright, J.A.; Onorato, A.J. Population Data on the Expanded CODIS Core STR Loci for Eleven Populations of Significance for Forensic DNA Analyses in the United States. Forensic Sci. Int. Genet. 2016, 25, 175–181. [Google Scholar] [CrossRef] [PubMed]
- National Research Council II, National Research Council Committee on DNA Forensic Science. The Evaluation of Forensic DNA Evidence; National Academy Press: Washington, DC, USA, 1996. [Google Scholar]
- Balding, D.J.; Nichols, R.A. DNA profile match probability calculation: How to allow for population stratification, relatedness, database selection and single bands. Forensic Sci. Int. 1994, 64, 125–140. [Google Scholar] [CrossRef]
- Taylor, D.; Buckleton, J.; Bright, J.A. Factors Affecting Peak Height Variability for Short Tandem Repeat Data. Forensic Sci. Int. Genet. 2016, 21, 126–133. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.; Kokshoorn, B.; Biedermann, A. Evaluation of forensic genetics findings given activity level propositions: A review. Forensic Sci. Int. Genet. 2018, 36, 34–49. [Google Scholar] [CrossRef]
- Roy, V. Convergence Diagnostics for Markov Chain Monte Carlo. Annu. Rev. Stat. Appl. 2020, 7, 387–412. [Google Scholar] [CrossRef]
- MaSTR™ User’s Manual. 2019. Available online: https://softgenetics.com/downloads.php (accessed on 12 April 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org (accessed on 2 May 2022).
- Moretti, T.R.; Just, R.S.; Kehl, S.C.; Willis, L.E.; Buckleton, J.S.; Bright, J.A.; Taylor, D.A.; Onorato, A.J. Internal Validation of STRmix for the Interpretation of Single Source and Mixed DNA Profiles. Forensic Sci. Int. Genet. 2017, 29, 126–144. [Google Scholar] [CrossRef]
- Taylor, D.; Bright, J.A.; Buckleton, J.; Curran, J. An Illustration of the Effect of Various Sources of Uncertainty on DNA Likelihood Ratio Calculations. Forensic Sci. Int. Genet. 2014, 11, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Bright, J.A.; Stevenson, K.E.; Curran, J.M.; Buckleton, J.S. The Variability in Likelihood Ratios Due to Different Mechanisms. Forensic Sci. Int. Genet. 2015, 14, 187–190. [Google Scholar] [CrossRef]
- Recommendations of the SWGDAM ad hoc Working Group on Genotyping Results Reported as Likelihood Ratios. 2018. Available online: https://www.swgdam.org/_files/ugd/4344b0_dd5221694d1448588dcd0937738c9e46.pdf (accessed on 10 January 2022).
- Bright, J.A.; Richards, R.; Kruijver, M.; Kelly, H.; McGovern, C.; Magee, A.; McWhorter, A.; Ciecko, A.; Peck, B.; Baumgartner, C.; et al. Internal Validation of STRmix™—A Multi Laboratory Response to PCAST. Forensic Sci. Int. Genet. 2018, 34, 11–24. [Google Scholar] [CrossRef]
- Bright, J.A.; Curran, J.M.; Buckleton, J.S. The Effect of the Uncertainty in the Number of Contributors to Mixed DNA Profiles on Profile Interpretation. Forensic Sci. Int. Genet. 2014, 12, 208–214. [Google Scholar] [CrossRef]
- Greenspoon, S.A.; Schiermeier-Wood, L.; Jenkins, B.C. Establishing the Limits of TrueAllele® Casework: A Validation Study. J. Forensic Sci. 2015, 60, 1263–1276. [Google Scholar] [CrossRef] [PubMed]
- Quintin, D.M.; Scheinman, J.E.; Adamowicz, M.S.; San Pietro, D. Assessment of PowerPlex® Fusion 5C’s Ability to Type Degraded DNA. Sci. Justice 2020, 60, 423–431. [Google Scholar] [CrossRef] [PubMed]
- Buckleton, J.S.; Curran, J.M.; Gill, P. Towards Understanding the Effect of Uncertainty in the Number of Contributors to DNA Stains. Forensic Sci. Int. Genet. 2007, 1, 20–28. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.; Bright, J.A.; Buckleton, J. Interpreting Forensic DNA Profiling Evidence Without Specifying the Number of Contributors. Forensic Sci. Int. Genet. 2014, 13, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Dembinski, G.M.; Sobieralski, C.; Picard, C.J. Estimation of the Number of Contributors of Theoretical Mixture Profiles Based on Allele Counting: Does Increasing the Number of Loci Increase Success Rate of Estimates? Forensic Sci. Int. Genet. 2018, 33, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Lynch, P.C.; Cotton, R.W. Determination of the Possible Number of Genotypes Which can Contribute to DNA Mixtures: Non-computer Assisted Deconvolution Should Not be Attempted for Greater Than Two Person Mixtures. Forensic Sci. Int. Genet. 2018, 37, 235–240. [Google Scholar] [CrossRef]
- Buckleton, J.S.; Bright, J.A.; Cheng, K.; Kelly, H.; Taylor, D.A. The Effect of Varying the Number of Contributors in the Prosecution and Alternate Propositions. Forensic Sci. Int. Genet. 2019, 38, 225–231. [Google Scholar] [CrossRef]
- Haned, H.; Pene, L.; Sauvage, F.; Pontier, D. The Predictive Value of the Maximum Likelihood Estimator of the Number of Contributors to a DNA Mixture. Forensic Sci. Int. Genet. 2011, 5, 281–284. [Google Scholar] [CrossRef]
- Haned, H.; Pene, L.P.; Lobry, J.R.; Dufour, A.B.; Pontier, D. Estimating the Number of Contributors to Forensic DNA Mixtures: Does Maximum Likelihood Perform Better Than Maximum Allele Count? J. Forensic Sci. 2011, 56, 23–28. [Google Scholar] [CrossRef]
- Biedermann, A.; Bozza, S.; Konis, K.; Taroni, F. Inference About the Number of Contributors to a DNA Mixture: Comparative Analyses of a Bayesian Network Approach and the Maximum Allele Count Method. Forensic Sci. Int. Genet. 2012, 6, 689–696. [Google Scholar] [CrossRef]
- Swaminathan, H.; Grgicak, C.M.; Medard, M.; Lun, D.S. NOCIt: A Computational Method to Infer the Number of Contributors to DNA Samples Analyzed by STR Genotyping. Forensic Sci. Int. Genet. 2015, 16, 172–180. [Google Scholar] [CrossRef] [PubMed]
- Marciano, M.A.; Adelman, J.D. PACE: Probabilistic Assessment for Contributor Estimation— A Machine Learning-based Assessment of the Number of Contributors in DNA Mixtures. Forensic Sci. Int. Genet. 2017, 27, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Alfonse, L.E.; Tejada, G.; Swaminathan, H.; Lun, D.S.; Grgicak, C.M. Inferring the Number of Contributors to Complex DNA Mixtures Using Three Methods: Exploring the Limits of Low-template DNA Interpretation. J. Forensic Sci. 2017, 62, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Marciano, M.A.; Adelman, J.D. Developmental Validation of PACE™: Automated Artifact Identification and Contributor Estimation for Use with GlobalFiler™ and PowerPlex® Fusion 6c Generated Data. Forensic Sci. Int. Genet. 2019, 43, 102140. [Google Scholar] [CrossRef] [PubMed]
- Benschop, C.C.G.; van der Linden, J.; Hoogenboom, J.; Ypma, R.; Haned, H. Automated Estimation of the Number of Contributors in Autosomal Short Tandem Repeat Profiles Using a Machine Learning Approach. Forensic Sci. Int. Genet. 2019, 43, 102150. [Google Scholar] [CrossRef] [PubMed]
- Gittelson, S.; Kalafut, T.; Myers, S.; Taylor, D.; Hicks, T.; Taroni, F.; Evett, I.W.; Bright, J.A.; Buckleton, J. A Practical Guide for the Formulation of Propositions in the Bayesian Approach to DNA Evidence Interpretation in an Adversarial Environment. J. Forensic Sci. 2016, 61, 186–195. [Google Scholar] [CrossRef]
- Alladio, E.; Omedei, M.; Cisana, S.; D’Amico, G.; Caneparo, D.; Vincenti, M.; Garofano, P. DNA Mixtures Interpretation—A Proof-of-concept Multi-software Comparison Highlighting Different Probabilistic Methods’ Performances on Challenging Samples. Forensic Sci. Int. Genet. 2018, 37, 143–150. [Google Scholar] [CrossRef]
- Holland, M.; Tiedge, T.; Bender, A.; Gaston-Sanchez, S.; McElhoe, J. MaSTR™: An Effective Probabilistic Genotyping Tool for Interpretation of STR Mixtures Associated with Differentially Degraded DNA. Int. J. Legal Med. 2022, 136, 433–446. [Google Scholar] [CrossRef]

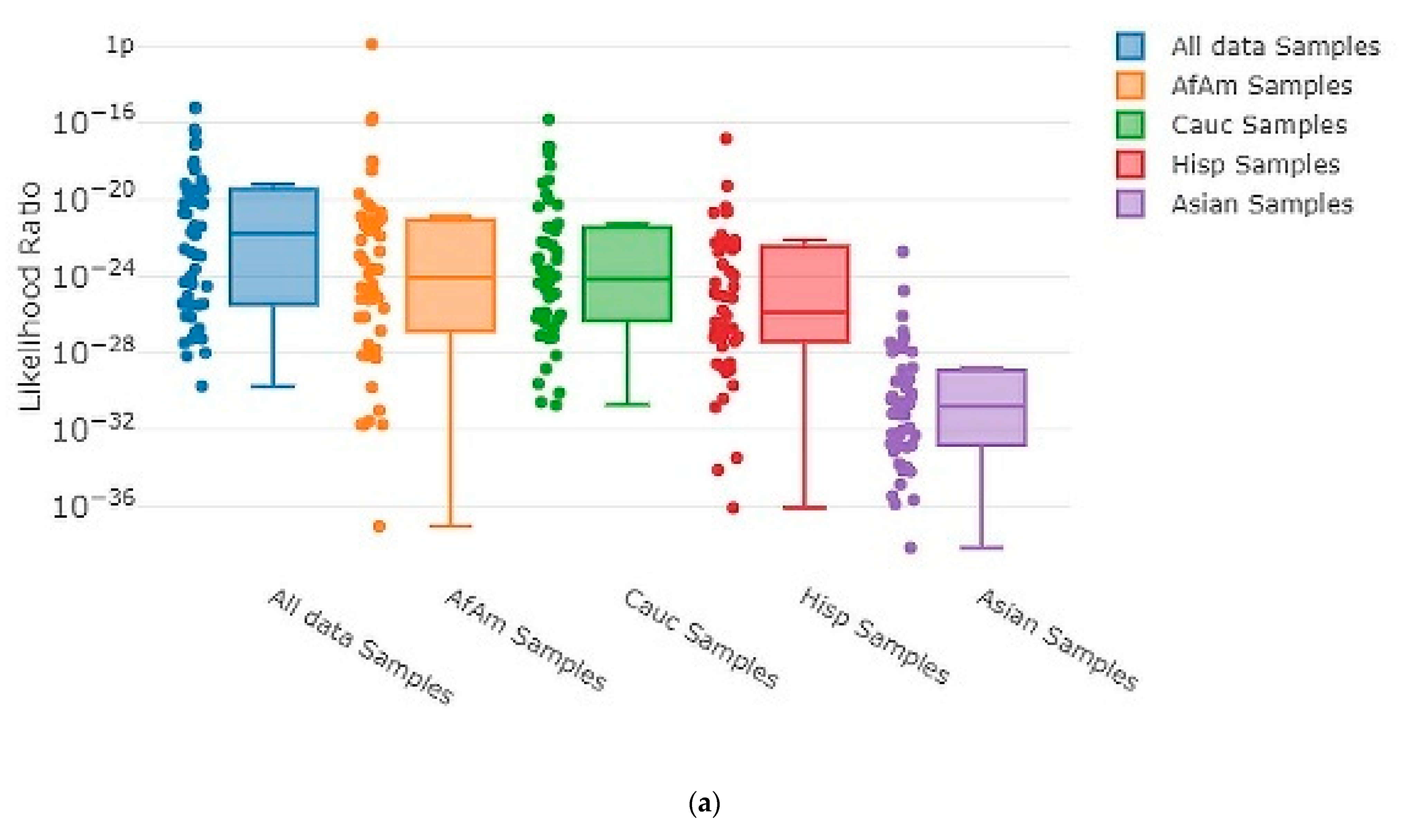
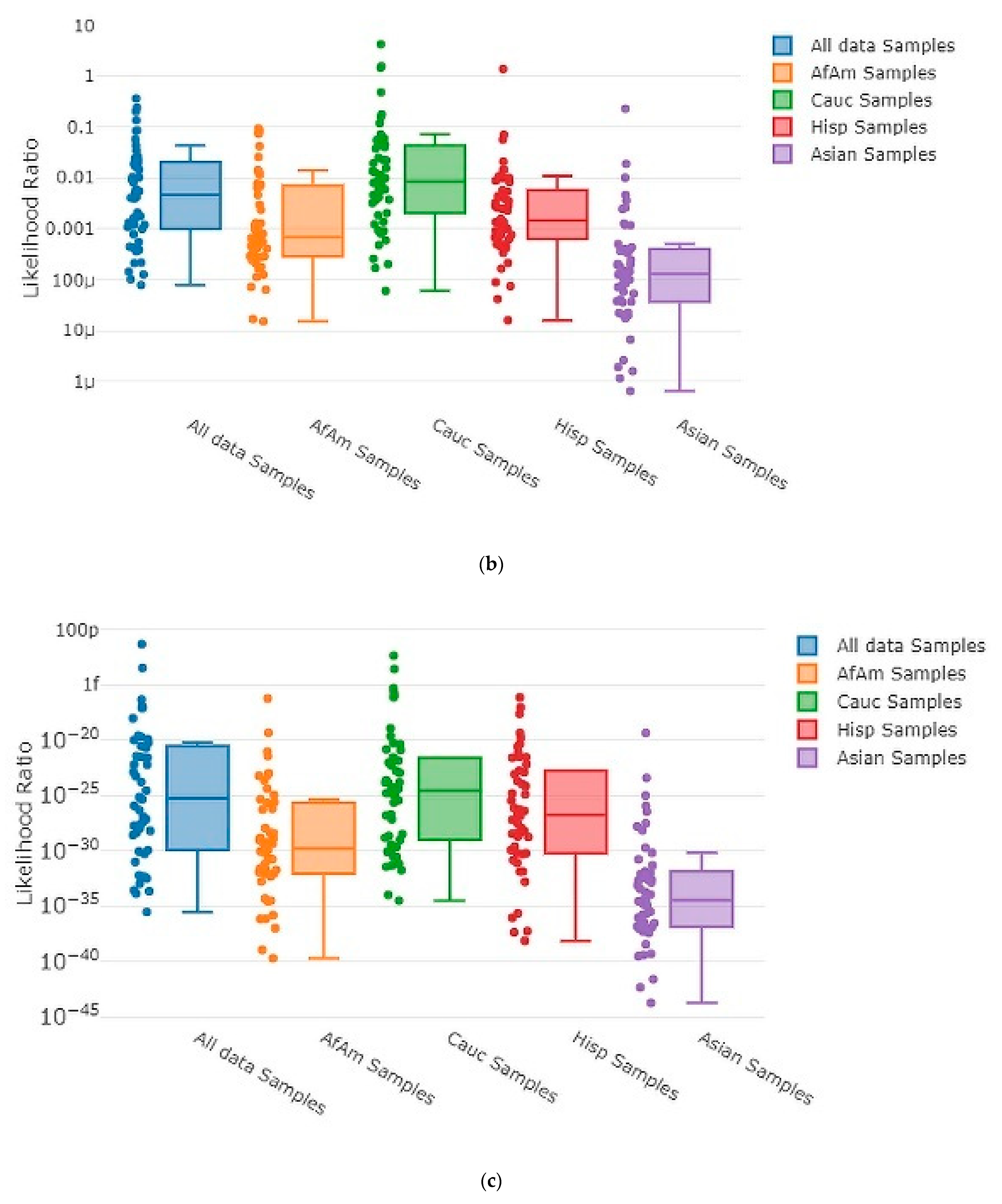
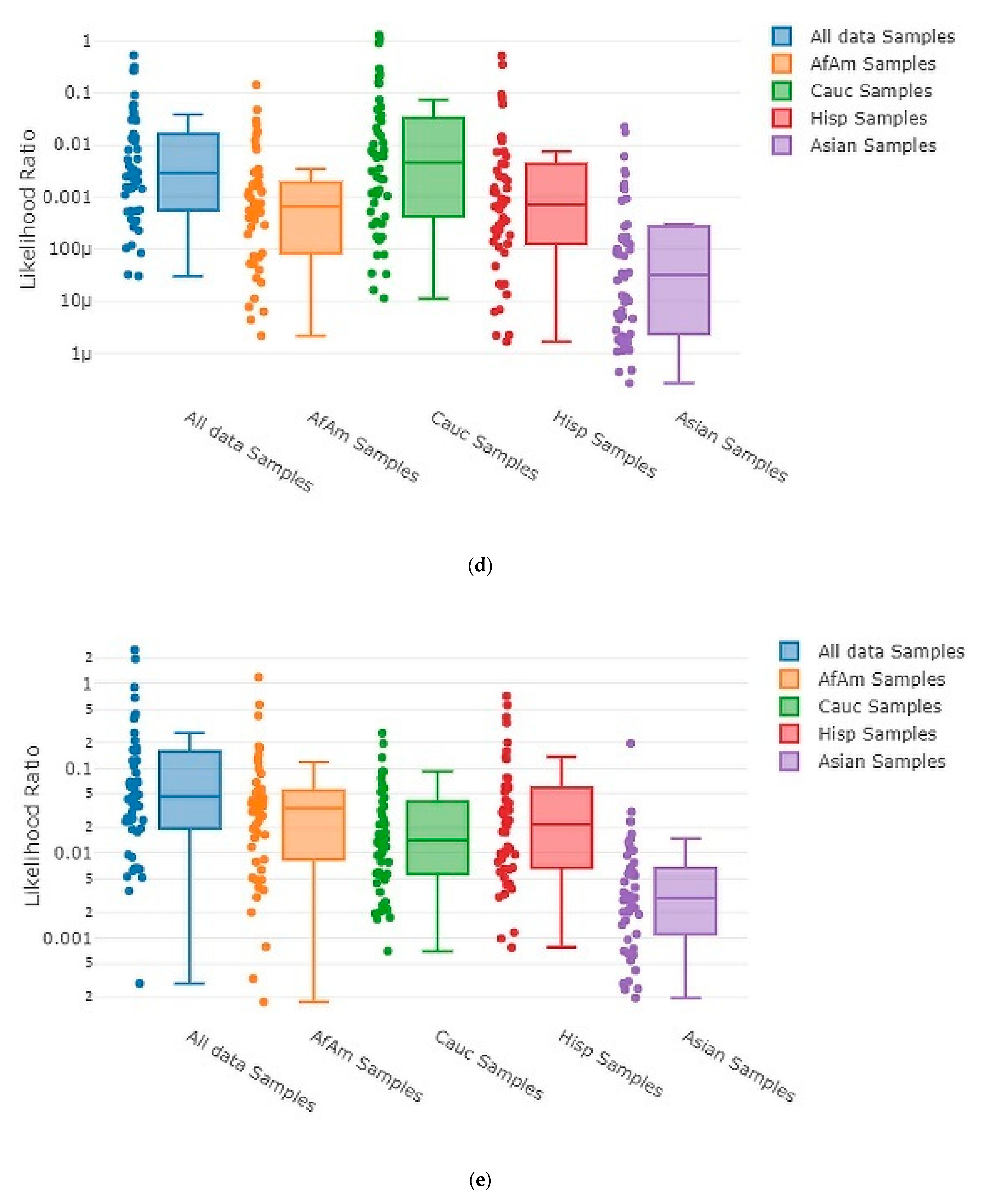
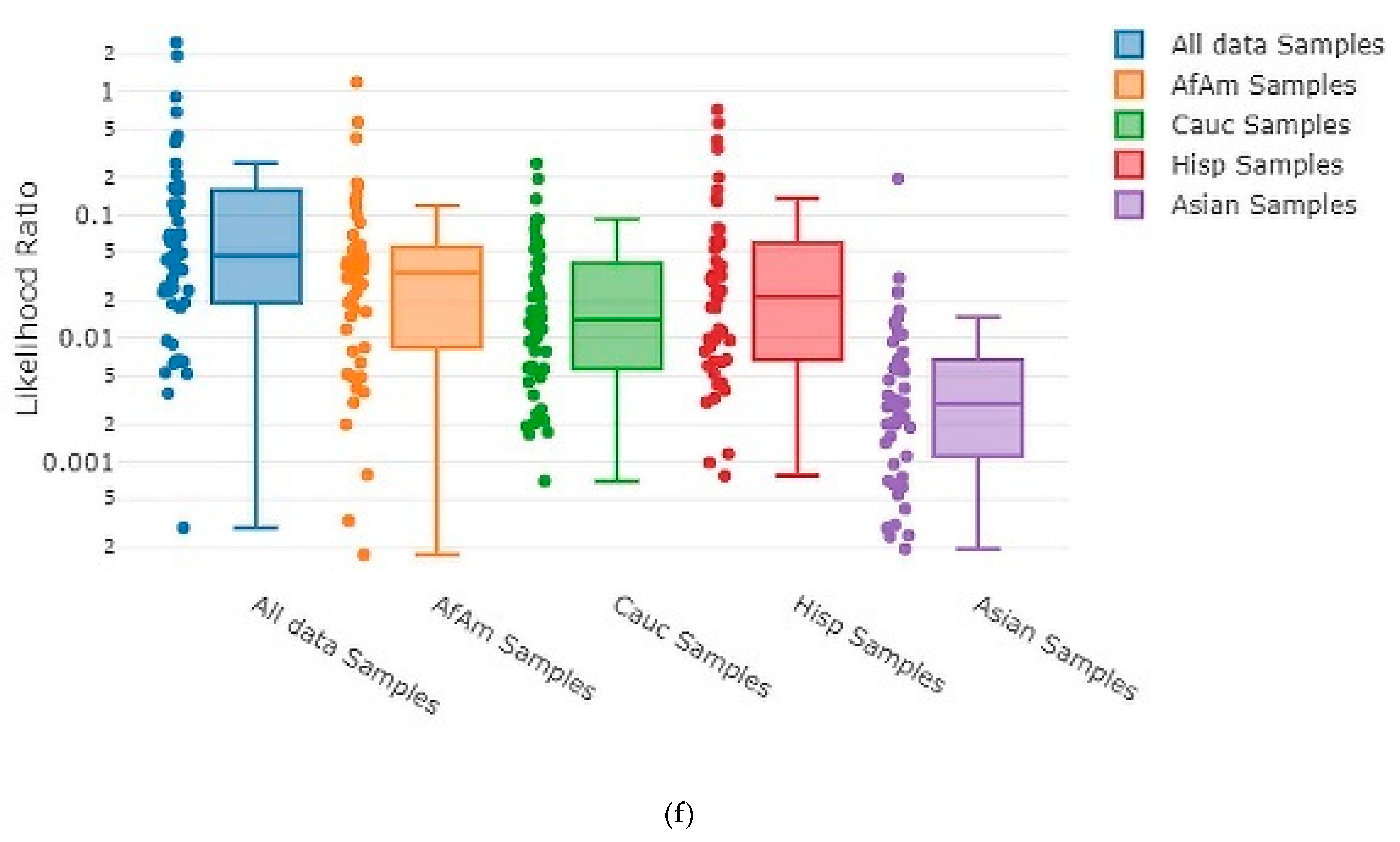

| Type of Mixture | Contributor Code | ||||
|---|---|---|---|---|---|
| Contributor 1 | Contributor 2 | Contributor 3 | Contributor 4 | Contributor 5 | |
| Low share, 2 person | 1678 | 1653 | N/A | N/A | N/A |
| High share, 2 person | 1660 | 1693 | N/A | N/A | N/A |
| Low share, 3 person | 1679 | 1683 | 1657 | N/A | N/A |
| High share, 3 person | 1668 | 1658 | 1659 | N/A | N/A |
| Random, 4 person | 1669 | 1682 | 1683 | 1690 | N/A |
| Random, 5 person | 1665 | 1666 | 1670 | 1681 | 1686 |
| Number of Contributors | Contributor Ratios | Approximate Undiluted Contributor DNA Template in Picograms | Approximate undiluted Total Picograms DNA Template | Sample Serial Dilutions | Total Number of Mixture Conditions Tested | Number of Mixtures for Interpretation |
|---|---|---|---|---|---|---|
| 2 allele low share | 1:1, 1:2, 1:3, 1:5, 1:10 | 500:500, 250:500, 160:500, 100:500, 50:500 | 1000, 750, 660, 600, 550 | 1:2, 1:4, 1:8 | 20 | 60 |
| 2 allele high share | 1:1, 1:2, 1:3, 1:5, 1:10 | 500:500, 250:500, 160:500, 100:500, 50:500 | 1000, 750, 660, 600, 550 | 1:2, 1:4, 1:8 | 20 | 60 |
| 3 allele low share | 1:1:1, 1:1:2, 1:2:10, 1:3:5 | 500:500:500, 250:250:500, 50:100:500, 100:300:500 | 1500, 1000, 650, 900 | 1:2, 1:4, 1:8 | 16 | 48 |
| 3 allele high share | 1:1:1, 1:1:2, 1:2:10, 1:3:5 | 500:500:500, 250:250:500, 50:100:500, 100:300:500 | 1500, 1000, 650, 900 | 1:2, 1:4, 1:8 | 16 | 48 |
| 4 | 1:1:1:1:1, 1:1:3:10, 1:2:2:5 | 500:500:500:500, 50:50:150:500, 100:200:200:500 | 2000, 750, 1000 | 1:2, 1:4, 1:8 | 12 | 36 |
| 5 | 1:1:1:1:1, 1:1:5:5:10, 1:2:2:5:10 | 500:500:500:500:500, 50:50:250:250:500, 50:100:100:250:500 | 2500, 1100, 1000 | 1:2, 1:4, 1:8 | 12 | 36 |
| Number of Contributors | H1/H2 Propositions | H1/H2 Propositions |
|---|---|---|
| 2 Person | 1 POI and 1 Unknown * | 1 Known and 1 POI |
| 2 Unknowns | 1 Known and 1 POI | |
| 3 Person | 1 POI and 2 Unknowns * | 1 Known and 1 POI and 1 Unknown |
| 3 Unknowns | 1 Known and 2 Unknowns | |
| 4 Person | 1 POI and 3 Unknowns * | 1 Known and 1 POI and 2 Unknowns * |
| 4 Unknowns | 1 Known and 3 Unknowns | |
| 5 Person | 1 POI and 4 Unknowns * | 1 Known and 1 POI and 3 Unknowns |
| 5 unknowns | 1 Known and 4 Unknowns |
| Number of Contributors | Total Number of MaSTR™ Analyses | Number of H1 True Tests with No Conditioning | Number of H1 True Tests Conditioned with a Known Contributor | Number of H2 True Tests with No Conditioning | Number of H2 True Tests Conditioned with a Known Contributor |
|---|---|---|---|---|---|
| 2 | 195 | 300 | 50 | 40 | 0 |
| 3 | 276 | 538 | 200 | 90 | 0 |
| 4 | 135 | 420 | 40 | 60 | 20 |
| 5 | 181 | 730 | 80 | 95 | 0 |
| Number of True Contributors | Mixture Ratio (Mixture Quantities) | Contributor | N-1 True Contributor Overall Ave. LR | N True Contributor Overall Ave. LR | N-1 True Contributor Simple Ave. LR |
|---|---|---|---|---|---|
| 3 | 1:1:1 (~500:500:500 pg) | 1668 | 4.94 × 10−1 | 1.76 × 1012 | 4.97 × 105 |
| 1658 | 1.18 × 10−23 | 5.09 × 1015 | 1.64 × 10−14 | ||
| 1659 | 1.67 × 10−19 | 2.62 × 1010 | 1.58 × 10−3 | ||
| 3 | 1:1:2 (~250:250:500 pg) | 1668 | 8.87 × 10−13 | 3.18 × 1013 | 1.11 × 10−3 |
| 1658 | 3.93 × 10−20 | 4.14 × 1011 | 1.50 × 10−16 | ||
| 1659 | 3.85 × 106 | 1.67 × 1021 | 1.76 × 1012 | ||
| 3 | 1:2:10 (~50:100:500 pg) | 1668 | 2.46 × 10−16 | 9.7 × 104 | 8.87 × 10−14 |
| 1658 | 1.02 × 103 | 1.67 × 1012 | 3.94 × 105 | ||
| 1659 | 3.55 × 1030 | 2.27 × 1030 | 4.18 × 1031 | ||
| 3 | 1:3:5 (~100:300:500 pg) | 1668 | 3.59 × 10−23 | 1.56 × 104 | 3.67 × 10−13 |
| 1658 | 4.21 × 1011 | 7.85 × 1010 | 3.94 × 1018 | ||
| 1659 | 2.65 × 1026 | 2.89 × 1021 | 4.18 × 1027 | ||
| 4 | 1:1:1:1 (~500:500:500:500 pg) | 1669 | 2.08 × 10−9 | 8.00 × 109 | 8.89 × 1015 |
| 1682 | 9.77 × 10−9 | 1.32 × 1012 | 3.16 × 1017 | ||
| 1683 | 4.38 × 10−2 | 5.16 × 1010 | 1.27 × 1015 | ||
| 1690 | 1.76 × 10−12 | 1.19 × 107 | 1.56 × 103 | ||
| 4 | 1:1:3:10 (~50:50:150:500 pg) | 1682 | 1.70 × 10−5 | 4.4 × 1010 | 2.03 × 106 |
| 1683 | 8.64 × 10−12 | 1.15 × 106 | 1.09 × 102 | ||
| 1690 | 3.45 × 1018 | 7.61 × 1021 | 1.85 × 1022 | ||
| 1669 | 1.26 × 0128 | 7.77 × 1027 | 1.44 × 1030 | ||
| 4 | 1:2:2:5 (~100:200:200:500 pg) | 1669 | 8.15 × 10−18 | 8.98 × 1011 | 1.23 × 105 |
| 1682 | 1.10 × 1013 | 7.27 × 1017 | 3.29 × 1019 | ||
| 1683 | 9.05 × 10−6 | 5.32 × 1010 | 2.36 × 106 | ||
| 1690 | 1.63 × 1025 | 4.89 × 1025 | 1.55 × 1028 |
| Number of True Contributors | Mixture Ratio | Sample | N + 1 True Contributor Overall Ave. LR | N True Contributor Overall Ave. LR |
|---|---|---|---|---|
| 3 | 1:1:1 (~500:500:500 pg) | 1668 | 1.78 × 1013 | 1.76 × 1012 |
| 1658 | 1.89 × 1010 | 5.09 × 1015 | ||
| 1659 | 4.81 × 1014 | 2.62 × 1010 | ||
| 3 | 1:1:2 (~250:250:500 pg) | 1668 | 7.13 × 1013 | 3.18 × 1013 |
| 1658 | 7.10 × 1010 | 4.14 × 1011 | ||
| 1659 | 2.31 × 1021 | 1.67 × 1021 | ||
| 3 | 1:2:10 (~50:100:500 pg) | 1668 | 1.01 × 105 | 9.76 × 104 |
| 1658 | 8.28 × 1011 | 1.67 × 1012 | ||
| 1659 | 1.67 × 1030 | 2.27 × 1030 | ||
| 3 | 1:3:5 (~100:300:500 pg) | 1668 | 3.35 × 104 | 7.85 × 1010 |
| 1658 | 9.55 × 1011 | 1.56 × 104 | ||
| 1659 | 6.11 × 1023 | 2.89 × 1021 | ||
| 4 | 1:1:1:1 (~500:500:500:500pg) | 1669 | 4.51 × 1011 | 8.00 × 109 |
| 1682 | 3.70 × 1012 | 1.32 × 1012 | ||
| 1683 | 3.95 × 1010 | 5.16 × 1010 | ||
| 1690 | 5.60 × 108 | 1.19 × 107 | ||
| 4 | 1:1:3:10 (~50:50:150:500 pg) | 1682 | 1.66 × 1010 | 4.40 × 1010 |
| 1683 | 3.73 × 105 | 1.15 × 106 | ||
| 1690 | 3.63 × 1021 | 7.61 × 1021 | ||
| 1669 | 5.54 × 1027 | 7.77 × 1027 | ||
| 4 | 1:2:2:5 (~100:200:200:500 pg) | 1669 | 5.15 × 109 | 8.98 × 1011 |
| 1682 | 5.98 × 1014 | 7.27 × 1017 | ||
| 1683 | 9.47 × 108 | 5.32 × 1010 | ||
| 1690 | 4.93 x1024 | 4.89 × 1025 |
| Number of True Contributors | Mixture Ratio | Sample | N-1 True Contributor Overall Ave. LR Conditioned w/Known | N-1 True Contributor Simple Ave. LR Conditioned w/Known |
|---|---|---|---|---|
| 3 | 1:1:1 (~500:500:500 pg) | 1668 | Known | Known |
| 1658 | 4.01 × 10−12 | 4.01 × 10−12 | ||
| 1659 | 2.45 × 10−26 | 2.45 × 10−26 | ||
| 3 | 1:1:2 (~250:250:500 pg) | 1668 | Known | Known |
| 1658 | 5.36 × 10−24 | 5.36 × 10−24 | ||
| 1659 | 4.18 × 10−4 | 4.18 × 10−4 | ||
| 3 | 1:2:10 (~50:100:500 pg) | 1668 | Known | Known |
| 1658 | 4.87 × 10−27 | 4.87 × 10−27 | ||
| 1659 | 1.57 × 101 | 1.57 × 101 | ||
| 3 | 1:3:5 (~100:300:500 pg) | 1668 | Known | Known |
| 1658 | 8.67 × 10−18 | 8.67 × 10−18 | ||
| 1659 | 1.95 × 10−4 | 1.95 × 10−4 | ||
| 4 | 1:1:1:1 (~500:500:500:500pg) | 1669 | Known | Known |
| 1682 | 6.95 × 10−18 | 1.86 × 103 | ||
| 1683 | 4.26 × 10−25 | 4.05 × 10−7 | ||
| 1690 | 6.44 × 10−24 | 2.49 × 10−7 | ||
| 4 | 1:1:3:10 (~50:50:150:500 pg) | 1682 | Known | Known |
| 1683 | 3.33 × 10−25 | 1.17 × 10−17 | ||
| 1690 | 4.88 × 101 | 5.61 × 105 | ||
| 1669 | 8.52 × 1026 | 2.01 × 1028 | ||
| 4 | 1:2:2:5 (~100:200:200:500 pg) | 1669 | Known | Known |
| 1682 | 6.78 × 10−10 | 1.80 × 10−2 | ||
| 1683 | 1.45 × 10−29 | 1.13 × 10−21 | ||
| 1690 | 2.51 × 1023 | 5.20 × 10+23 |
| Number of True Contributors | Mixture Ratio | Sample | N + 1 Contributor Overall Ave. LR | N + 1 Contributor Simple Ave. LR | True NOC Overall Ave. LR |
|---|---|---|---|---|---|
| 3 | 1:1:1 (~500:500:500 pg) | 1668 | 1.88 × 1013 | 2.00 × 1027 | 9.49 × 1011 |
| 1658 | 1.95 × 1010 | 6.30 × 1022 | 1.53 × 1010 | ||
| 1637 * | 3.50 × 10−3 | 1.19 × 104 | 1.79 × 10−26 | ||
| 3 | 1:1:2 (~250:250:500 pg) | 1668 | 7.30 × 1013 | 3.88 × 1025 | 3.49 × 1013 |
| 1658 | 5.19 × 1010 | 1.03 × 1021 | 5.80 × 1011 | ||
| 1651 * | 3.11 × 10−1 | 6.23 × 107 | 5.49 × 10−19 | ||
| 3 | 1:2:10 (~50:100:500 pg) | 1668 | 1.26 × 105 | 9.26 × 1015 | 1.11 × 105 |
| 1658 | 8.35 × 1011 | 1.24 × 1021 | 1.79 × 1012 | ||
| 1618 * | 1.28 × 1000 | 3.46 × 1010 | 1.13 × 10−4 | ||
| 3 | 1:3:5 (~100:300:500 pg) | 1668 | 4.55 × 104 | 2.05 × 1016 | 5.05 × 105 |
| 1658 | 7.01 × 1011 | 8.45 × 1021 | 6.14 × 1012 | ||
| 1687 * | 8.43 × 10−2 | 2.74 × 105 | 2.29 × 10−16 | ||
| 4 | 1:1:1:1 (~500:500:500:500pg) | 1669 | 3.97 × 1011 | 7.47 × 1025 | 3.09 × 1010 |
| 1682 | 3.74 × 1012 | 1.60 × 1026 | 1.50 × 1012 | ||
| 1683 | 3.77 × 1010 | 2.98 × 1024 | 4.34 × 1010 | ||
| 1689 * | 1.88 × 10−1 | 2.87 × 108 | 3.43 × 10−22 | ||
| 4 | 1:1:3:10 (~50:50:150:500 pg) | 1682 | 1.67 × 1010 | 9.06 × 1022 | 4.75 × 1010 |
| 1683 | 1.03 × 106 | 1.67 × 1020 | 1.16 × 105 | ||
| 1690 | 2.95 × 1021 | 1.56 × 1029 | 6.74 × 1021 | ||
| 1625 * | 2.89 × 10−2 | 9.82 × 108 | 1.22 × 10−17 | ||
| 4 | 1:2:2:5 (~100:200:200:500 pg) | 1669 | 6.33 × 109 | 1.27 × 1023 | 1.08 × 1012 |
| 1682 | 1.25 × 1015 | 3.11 × 1026 | 7.16 × 1017 | ||
| 1683 | 1.87 × 109 | 3.31 × 1022 | 4.58 × 1010 | ||
| 1677 * | 1.89 × 10−6 | 1.96 × 104 | 5.49 × 10−17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamowicz, M.S.; Rambo, T.N.; Clarke, J.L. Internal Validation of MaSTR™ Probabilistic Genotyping Software for the Interpretation of 2–5 Person Mixed DNA Profiles. Genes 2022, 13, 1429. https://doi.org/10.3390/genes13081429
Adamowicz MS, Rambo TN, Clarke JL. Internal Validation of MaSTR™ Probabilistic Genotyping Software for the Interpretation of 2–5 Person Mixed DNA Profiles. Genes. 2022; 13(8):1429. https://doi.org/10.3390/genes13081429
Chicago/Turabian StyleAdamowicz, Michael S., Taylor N. Rambo, and Jennifer L. Clarke. 2022. "Internal Validation of MaSTR™ Probabilistic Genotyping Software for the Interpretation of 2–5 Person Mixed DNA Profiles" Genes 13, no. 8: 1429. https://doi.org/10.3390/genes13081429
APA StyleAdamowicz, M. S., Rambo, T. N., & Clarke, J. L. (2022). Internal Validation of MaSTR™ Probabilistic Genotyping Software for the Interpretation of 2–5 Person Mixed DNA Profiles. Genes, 13(8), 1429. https://doi.org/10.3390/genes13081429






