MarZIC: A Marginal Mediation Model for Zero-Inflated Compositional Mediators with Applications to Microbiome Data
Abstract
:1. Introduction
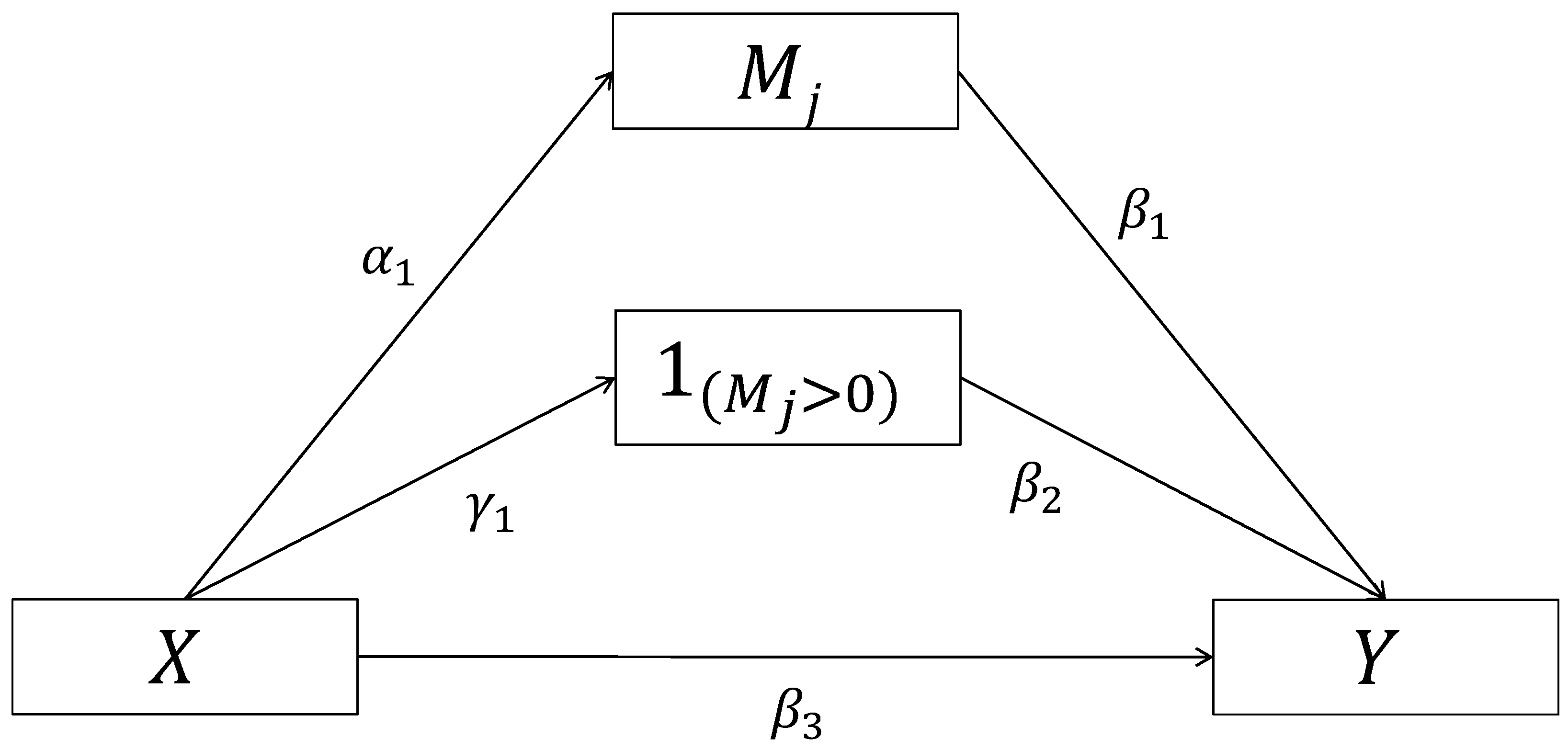
2. Model and Notation
2.1. Model for Data without Zeros
2.2. Model for Data with Zeros
2.3. Mechanism for Observing Zeros of the Mediator
2.4. Marginal Mediation Effect and Direct Effect
2.5. Sequential Ignorability Assumption
3. Parameter Estimation
4. Simulation
4.1. Simulation Setting 1: Univariate ZIB Distribution
4.2. Simulation Setting 2: Multivariate Zero-Inflated Dirichlet-Multinomial Distribution
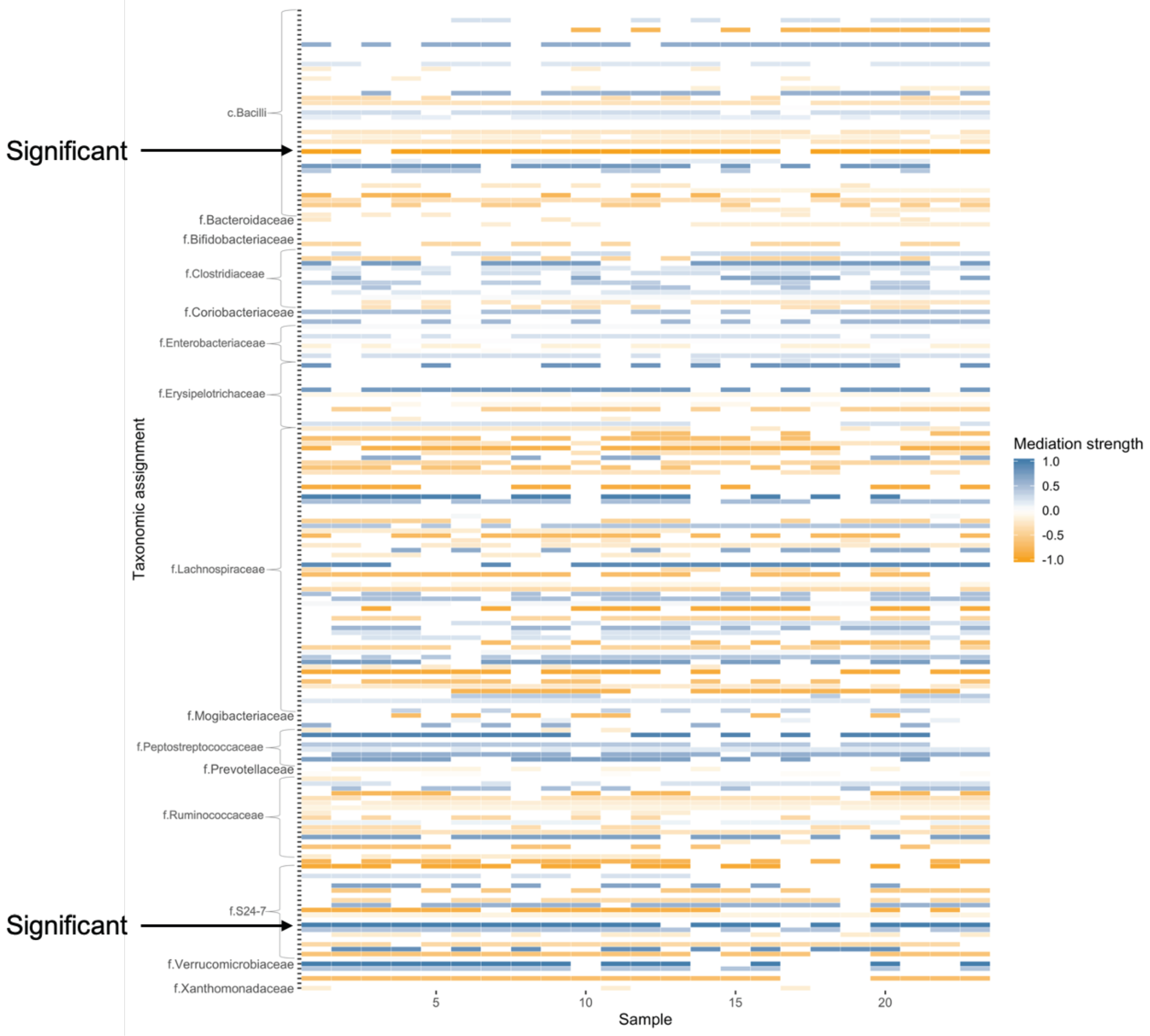
5. Real Study Application
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Marginal Association beween Y and Mj
Appendix B. Multivariate Delta Method for Obtaining 95% CI of NIE1, NIE2, NDE and CDE
Appendix C. Microbiome Data Generation Process for Simulation Setting 2
References
- Belkaid, Y.; Hand, T.W. Role of the microbiota in immunity and inflammation. Cell 2014, 157, 121–141. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, G.; Feng, T.; Zhang, J.; Huang, X.; Wang, T.; Xie, Z.; Chu, X.; Yang, J.; Wang, H.; et al. Sodium oligomannate therapeutically remodels gut microbiota and suppresses gut bacterial amino acids-shaped neuroinflammation to inhibit Alzheimer’s disease progression. Cell Res. 2019, 29, 787–803. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Lagoudas, G.K.; Zhao, C.; Bullman, S.; Bhutkar, A.; Hu, B.; Ameh, S.; Sandel, D.; Liang, X.S.; Mazzilli, S.; et al. Commensal Microbiota Promote Lung Cancer Development via GammaDelta T Cells. Cell 2019, 176, 998–1013.e16. [Google Scholar] [CrossRef] [PubMed]
- Tanoue, T.; Morita, S.; Plichta, D.R.; Skelly, A.N.; Suda, W.; Sugiura, Y.; Narushima, S.; Vlamakis, H.; Motoo, I.; Sugita, K.; et al. A defined commensal consortium elicits CD8 T cells and anti-cancer immunity. Nature 2019, 565, 600–605. [Google Scholar] [CrossRef]
- Li, H. Statistical and Computational Methods in Microbiome and Metagenomics. Handb. Stat. Genom. 2018. [Google Scholar] [CrossRef]
- Sohn, M.B.; Li, H. Compositional mediation analysis for microbiome studies. Ann. Appl. Stat. 2019, 13, 661–681. [Google Scholar] [CrossRef]
- Wang, C.; Hu, J.; Blaser, M.J.; Li, H. Estimating and testing the microbial causal mediation effect with high-dimensional and compositional microbiome data. Bioinformatics 2019, 36, 347–355. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Li, Z.; Liu, L. Testing for mediation effect with application to human microbiome data. Stat. Biosci. 2019; in press. [Google Scholar]
- VanderWeele, T.J. Marginal structural models for the estimation of direct and indirect effects. Epidemiology 2009, 20, 18–26. [Google Scholar] [CrossRef]
- Imai, K.; Keele, L.; Tingley, D. A General Approach to Causal Mediation Analysis. Psychol. Methods 2010, 15, 309–334. [Google Scholar] [CrossRef]
- VanderWeele, T.J. Explanation in Causal Inference: Methods for Mediation and Interaction; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Baron, R.M.; Kenny, D.A. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. J. Personal. Soc. Psychol. 1986, 51, 1173–1182. [Google Scholar] [CrossRef]
- MacKinnon, D.P. Introduction to Statistical Mediation Analysis; Erlbaum: New York, NY, USA, 2008. [Google Scholar]
- MacKinnon, D.P.; Fairchild, A.J.; Fritz, M.S. Mediation analysis. Annu. Rev. Psychol. 2007, 58, 593–614. [Google Scholar] [CrossRef] [PubMed]
- VanderWeele, T.J. Mediation Analysis: A Practitioner’s Guide. Annu. Rev. Public Health 2016, 37, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Lange, T.; Hansen, K.W.; Sørensen, R.; Galatius, S. Applied mediation analyses: A review and tutorial. Epidemiol. Health 2017, 39, e2017035. [Google Scholar] [CrossRef] [PubMed]
- Dalrymple, M.L.; Hudson, I.L.; Ford, R.P.K. Finite mixture, zero-inflated Poisson and hurdle models with application to SIDS. Comput. Stat. Data Anal. 2003, 41, 491–504. [Google Scholar] [CrossRef]
- Chai, H.; Jiang, H.; Lin, L.; Liu, L. A marginalized two-part Beta regression model for microbiome compositional data. PLoS Comput. Biol. 2018, 14, e1006329. [Google Scholar] [CrossRef]
- Chen, E.Z.; Li, H. A two-part mixed-effects model for analyzing longitudinal microbiome compositional data. Bioinformatics 2016, 32, 2611–2617. [Google Scholar] [CrossRef]
- Tang, Z.Z.; Chen, G. Zero-inflated generalized Dirichlet multinomial regression model for microbiome compositional data analysis. Biostatistics 2018, 20, 698–713. [Google Scholar] [CrossRef]
- Peng, X.; Li, G.; Liu, Z. Zero-Inflated Beta Regression for Differential Abundance Analysis with Metagenomics Data. J. Comput. Biol. 2016, 23, 102–110. [Google Scholar] [CrossRef]
- Chen, J.; Li, H. Variable Selection for Sparse Dirichlet-Multinomial Regression with an Application to Microbiome Data Analysis. Ann. Appl. Stat. 2013, 7, 418–442. [Google Scholar] [CrossRef]
- Martin, B.D.; Witten, D.; Willis, A.D. Modeling Microbial Abundances and Dysbiosis with Beta-Binomial Regression. Ann. Appl. Stat. 2020, 14, 94–115. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta Regression for Modelling Rates and Proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Zeileis, A. Beta Regression in R. J. Stat. Softw. 2010, 34, 24848. [Google Scholar] [CrossRef]
- Terhorst, H.J. On Stieltjes Integration in Euclidean-Space. J. Math. Anal. Appl. 1986, 114, 57–74. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Imai, K.; Keele, L.; Yamamoto, T. Identification, Inference and Sensitivity Analysis for Causal Mediation Effects. Stat. Sci. 2010, 25, 51–71. [Google Scholar] [CrossRef]
- Pearl, J. Direct and indirect effects. In Proceedings of the Seventh Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 26–29 August 2001; Breese, J., Koller, D., Eds.; Morgan Kaufman: San Francisco, CA, USA, 2001; pp. 411–420. [Google Scholar]
- Robins, J. Semantics of causal DAG models and the identification of direct and indirect effects. In Proceedings of the Highly Structured Stochastic Systems; Green, P., Hjort, N., Richardson, S., Eds.; Oxford University Press: Oxford, UK, 2003; pp. 70–81. [Google Scholar]
- Peterson, M.; Sinisi, S.; van der Laan, M. Estimation of Direct Causal Effects. Epidemiology 2006, 17, 276–284. [Google Scholar] [CrossRef]
- Hafeman, D.M.; VanderWeele, T.J. Alternative Assumptions for the Identification of Direct and Indirect Effects. Epidemiology 2011, 22, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Tingley, D.; Yamamoto, T.; Hirose, K.; Keele, L.; Imai, K. mediation: R Package for Causal Mediation Analysis. 2017. Available online: https://cran.r-project.org/web/packages/mediation/vignettes/mediation.pdf (accessed on 6 June 2022).
- Martinez, M.N.; Bartholomew, M.J. What does it “mean”? A review of interpreting and calculating different types of means and standard deviations. Pharmaceutics 2017, 9, 14. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A Practical and powerful approach to multiple testing. J. Roy. Statist. Soc. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Gionchetti, P.; Rizzello, F.; Venturi, A.; Brigidi, P.; Matteuzzi, D.; Bazzocchi, G.; Poggioli, G.; Miglioli, M.; Campieri, M. Oral bacteriotherapy as maintenance treatment in patients with chronic pouchitis: A double-blind, placebo-controlled trial. Gastroenterology 2000, 119, 305–309. [Google Scholar] [CrossRef]
- Sood, A.; Midha, V.; Makharia, G.K.; Ahuja, V.; Singal, D.; Goswami, P.; Tandon, R.K. The probiotic preparation, VSL# 3 induces remission in patients with mild-to-moderately active ulcerative colitis. Clin. Gastroenterol. Hepatol. 2009, 7, 1202–1209. [Google Scholar] [PubMed]
- Madsen, K.; Cornish, A.; Soper, P.; McKaigney, C.; Jijon, H.; Yachimec, C.; Doyle, J.; Jewell, L.; De Simone, C. Probiotic bacteria enhance murine and human intestinal epithelial barrier function. Gastroenterology 2001, 121, 580–591. [Google Scholar] [CrossRef] [PubMed]
- Pagnini, C.; Saeed, R.; Bamias, G.; Arseneau, K.O.; Pizarro, T.T.; Cominelli, F. Probiotics promote gut health through stimulation of epithelial innate immunity. Proc. Natl. Acad. Sci. USA 2010, 107, 454–459. [Google Scholar] [CrossRef] [PubMed]
- Arthur, J.C.; Gharaibeh, R.Z.; Uronis, J.M.; Perez-Chanona, E.; Sha, W.; Tomkovich, S.; Mühlbauer, M.; Fodor, A.A.; Jobin, C. VSL# 3 probiotic modifies mucosal microbial composition but does not reduce colitis-associated colorectal cancer. Sci. Rep. 2013, 3, 2868. [Google Scholar] [PubMed]
- Caporaso, J.G.; Kuczynski, J.; Stombaugh, J.; Bittinger, K.; Bushman, F.D.; Costello, E.K.; Fierer, N.; Pena, A.G.; Goodrich, J.K.; Gordon, J.I.; et al. QIIME allows analysis of high-throughput community sequencing data. Nat. Methods 2010, 7, 335. [Google Scholar] [CrossRef] [PubMed]
- Bokulich, N.A.; Subramanian, S.; Faith, J.J.; Gevers, D.; Gordon, J.I.; Knight, R.; Mills, D.A.; Caporaso, J.G. Quality-filtering vastly improves diversity estimates from Illumina amplicon sequencing. Nat. Methods 2013, 10, 57. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Garrity, G.M.; Tiedje, J.M.; Cole, J.R. Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl. Environ. Microbiol. 2007, 73, 5261–5267. [Google Scholar] [CrossRef]
- Peters, B.A.; Dominianni, C.; Shapiro, J.A.; Church, T.R.; Wu, J.; Miller, G.; Yuen, E.; Freiman, H.; Lustbader, I.; Salik, J.; et al. The gut microbiota in conventional and serrated precursors of colorectal cancer. Microbiome 2016, 4, 69. [Google Scholar] [CrossRef]
- Bråten, L.S.; Sødring, M.; Paulsen, J.E.; Snipen, L.G.; Rudi, K. Cecal microbiota association with tumor load in a colorectal cancer mouse model. Microb. Ecol. Health Dis. 2017, 28, 1352433. [Google Scholar] [CrossRef]
- Gianola, D. Least-Squares Means Vs Population Marginal Means. Am. Stat. 1982, 36, 65–66. [Google Scholar]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2014; Volume 333. [Google Scholar]
- Aitchison, J. The Statistical Analysis of Compositional Data. J. R. Stat. Soc. Ser. B-Stat. Methodol. 1982, 44, 139–177. [Google Scholar] [CrossRef]
| Low Relative Abundance (Mean = 0.0025) | High Relative Abundance (Mean = 0.5) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | True | Mean | Bias | Bias | SE | Mean | CP (%) | True | Mean | Bias | Bias | SE | Mean | CP (%) |
| /Effect | Estimate | % | SE | Estimate | % | SE | ||||||||
| MarZIC | ||||||||||||||
| NIE1 | 0.10 | 0.11 | 0.01 | 10.0 | 0.08 | 0.07 | 91 | 9.30 | 9.11 | −0.18 | −1.98 | 2.68 | 2.70 | 96 |
| NIE2 | 0.55 | 0.52 | −0.03 | −5.67 | 0.55 | 0.56 | 97 | 0.55 | 0.50 | −0.06 | −10.15 | 0.62 | 0.56 | 94 |
| NIE | 0.65 | 0.63 | −0.02 | −3.31 | 0.58 | 0.58 | 96 | 9.85 | 9.61 | −0.24 | −2.44 | 3.25 | 3.20 | 95 |
| −2.00 | −2.05 | −0.05 | −2.45 | 0.32 | 0.33 | 96 | −2.00 | −1.92 | 0.07 | 3.82 | 0.32 | 0.29 | 94 | |
| 100.00 | 101.89 | 1.89 | 1.89 | 18.04 | 19.04 | 97 | 100.00 | 99.96 | −0.04 | −0.04 | 1.89 | 1.74 | 91 | |
| 4.00 | 4.05 | 0.05 | 1.37 | 0.38 | 0.36 | 94 | 4.00 | 3.93 | −0.07 | −1.73 | 0.58 | 0.57 | 91 | |
| 5.00 | 5.08 | 0.08 | 1.53 | 0.53 | 0.51 | 94 | 5.00 | 4.97 | −0.03 | −0.62 | 0.46 | 0.46 | 99 | |
| 3.00 | 2.93 | −0.07 | −2.40 | 0.58 | 0.55 | 92 | 3.00 | 3.02 | 0.02 | 0.55 | 0.53 | 0.54 | 99 | |
| 1.00 | 0.99 | −0.01 | −1.00 | 0.07 | 0.07 | 90 | 1.00 | 0.97 | −0.03 | −2.99 | 0.07 | 0.07 | 89 | |
| −6.20 | −6.24 | −0.04 | −0.69 | 0.36 | 0.36 | 94 | −1.00 | −1.01 | −0.01 | −0.93 | 0.05 | 0.05 | 90 | |
| 0.40 | 0.42 | 0.02 | 5.52 | 0.33 | 0.29 | 92 | 0.40 | 0.41 | 0.01 | 1.69 | 0.06 | 0.07 | 95 | |
| 50.00 | 56.42 | 6.42 | 12.83 | 24.21 | 19.35 | 97 | 50.00 | 53.37 | 3.37 | 6.74 | 8.22 | 8.40 | 96 | |
| −1.16 | −1.23 | −0.07 | −5.75 | 0.35 | 0.36 | 99 | −1.16 | −1.20 | −0.04 | −3.18 | 0.37 | 0.34 | 95 | |
| −0.50 | −0.53 | −0.03 | −5.10 | 0.55 | 0.55 | 97 | −0.50 | −0.47 | 0.03 | 6.91 | 0.58 | 0.53 | 91 | |
| IKT | ||||||||||||||
| NIE | 0.65 | 0.10 | −0.55 | −84.81 | - | - | 9 | 9.85 | 9.20 | −0.65 | −6.62 | - | - | 94 |
| Recall (%) | Precision (%) | F1 (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | MarZIC | MarZIC | CCMM | IKT | MarZIC | MarZIC | CCMM | IKT | MarZIC | MarZIC | CCMM | IKT | |
| (NIE1) | (NIE2) | (NIE1) | (NIE2) | (NIE1) | (NIE2) | ||||||||
| 10 | 200 | 99.00 | 100.00 | 100.00 | 58.00 | 97.70 | 98.00 | 38.80 | 99.70 | 97.90 | 98.60 | 55.30 | 68.10 |
| 25 | 200 | 99.50 | 100.00 | 96.00 | 39.50 | 98.20 | 99.50 | 52.40 | 100.00 | 98.50 | 99.60 | 66.10 | 48.30 |
| 50 | 200 | 97.50 | 100.00 | 97.00 | 44.00 | 100.00 | 100.00 | 46.40 | 100.00 | 98.30 | 100.00 | 60.60 | 54.70 |
| 100 | 200 | 96.00 | 98.90 | 100.00 | 32.50 | 95.50 | 100.00 | 42.80 | 100.00 | 94.50 | 98.90 | 58.00 | 41.30 |
| 300 | 200 | 86.00 | 97.80 | - | 25.00 | 90.80 | 99.50 | - | 100.00 | 85.80 | 97.50 | - | 31.30 |
| 500 | 200 | 77.50 | 94.70 | - | 23.50 | 97.80 | 87.20 | - | 99.00 | 83.00 | 87.30 | - | 30.00 |
| Recall (%) | Precision (%) | F1 (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Taxa | MarZIC | MarZIC | CCMM | IKT | MarZIC | MarZIC | CCMM | IKT | MarZIC | MarZIC | CCMM | IKT | |
| with Non-Zero NIE1 | (NIE1) | (NIE2) | (NIE1B) | (NIE2) | (NIE1) | (NIE2) | |||||||
| 50 | 5 | 95.00 | 100.00 | 89.00 | 66.20 | 99.00 | 98.50 | 27.90 | 99.60 | 96.60 | 99.00 | 42.20 | 78.20 |
| 50 | 10 | 95.70 | 92.00 | 66.00 | 62.40 | 98.80 | 91.80 | 33.20 | 99.60 | 97.10 | 86.20 | 43.90 | 75.70 |
| 100 | 5 | 96.60 | 99.00 | 89.40 | 60.60 | 92.70 | 98.30 | 19.00 | 99.10 | 94.10 | 97.80 | 31.20 | 73.30 |
| 100 | 10 | 92.10 | 91.00 | 80.10 | 46.00 | 93.70 | 97.80 | 27.20 | 100.00 | 92.50 | 89.50 | 40.40 | 61.20 |
| 300 | 5 | 94.20 | 96.00 | - | 56.10 | 80.50 | 97.00 | - | 99.70 | 85.20 | 94.00 | - | 69.90 |
| 300 | 10 | 85.30 | 93.00 | - | 29.30 | 77.10 | 91.00 | - | 99.60 | 79.60 | 86.60 | - | 43.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; O’Malley, J.; Datta, S.; Gharaibeh, R.Z.; Jobin, C.; Karagas, M.R.; Coker, M.O.; Hoen, A.G.; Christensen, B.C.; Madan, J.C.; et al. MarZIC: A Marginal Mediation Model for Zero-Inflated Compositional Mediators with Applications to Microbiome Data. Genes 2022, 13, 1049. https://doi.org/10.3390/genes13061049
Wu Q, O’Malley J, Datta S, Gharaibeh RZ, Jobin C, Karagas MR, Coker MO, Hoen AG, Christensen BC, Madan JC, et al. MarZIC: A Marginal Mediation Model for Zero-Inflated Compositional Mediators with Applications to Microbiome Data. Genes. 2022; 13(6):1049. https://doi.org/10.3390/genes13061049
Chicago/Turabian StyleWu, Quran, James O’Malley, Susmita Datta, Raad Z. Gharaibeh, Christian Jobin, Margaret R. Karagas, Modupe O. Coker, Anne G. Hoen, Brock C. Christensen, Juliette C. Madan, and et al. 2022. "MarZIC: A Marginal Mediation Model for Zero-Inflated Compositional Mediators with Applications to Microbiome Data" Genes 13, no. 6: 1049. https://doi.org/10.3390/genes13061049
APA StyleWu, Q., O’Malley, J., Datta, S., Gharaibeh, R. Z., Jobin, C., Karagas, M. R., Coker, M. O., Hoen, A. G., Christensen, B. C., Madan, J. C., & Li, Z. (2022). MarZIC: A Marginal Mediation Model for Zero-Inflated Compositional Mediators with Applications to Microbiome Data. Genes, 13(6), 1049. https://doi.org/10.3390/genes13061049






