A Multi-Trait Gaussian Kernel Genomic Prediction Model under Three Tunning Strategies
Abstract
1. Introduction
2. Material and Methods
2.1. Dataset 1. Japonica
2.2. Dataset 2. Indica
2.3. Dataset 3. Groundnut
2.4. Dataset 4. Cotton
2.5. Dataset 5. Disease
2.6. Multi-Trait Kernel Model
2.7. Evaluation of Prediction Performance
3. Results
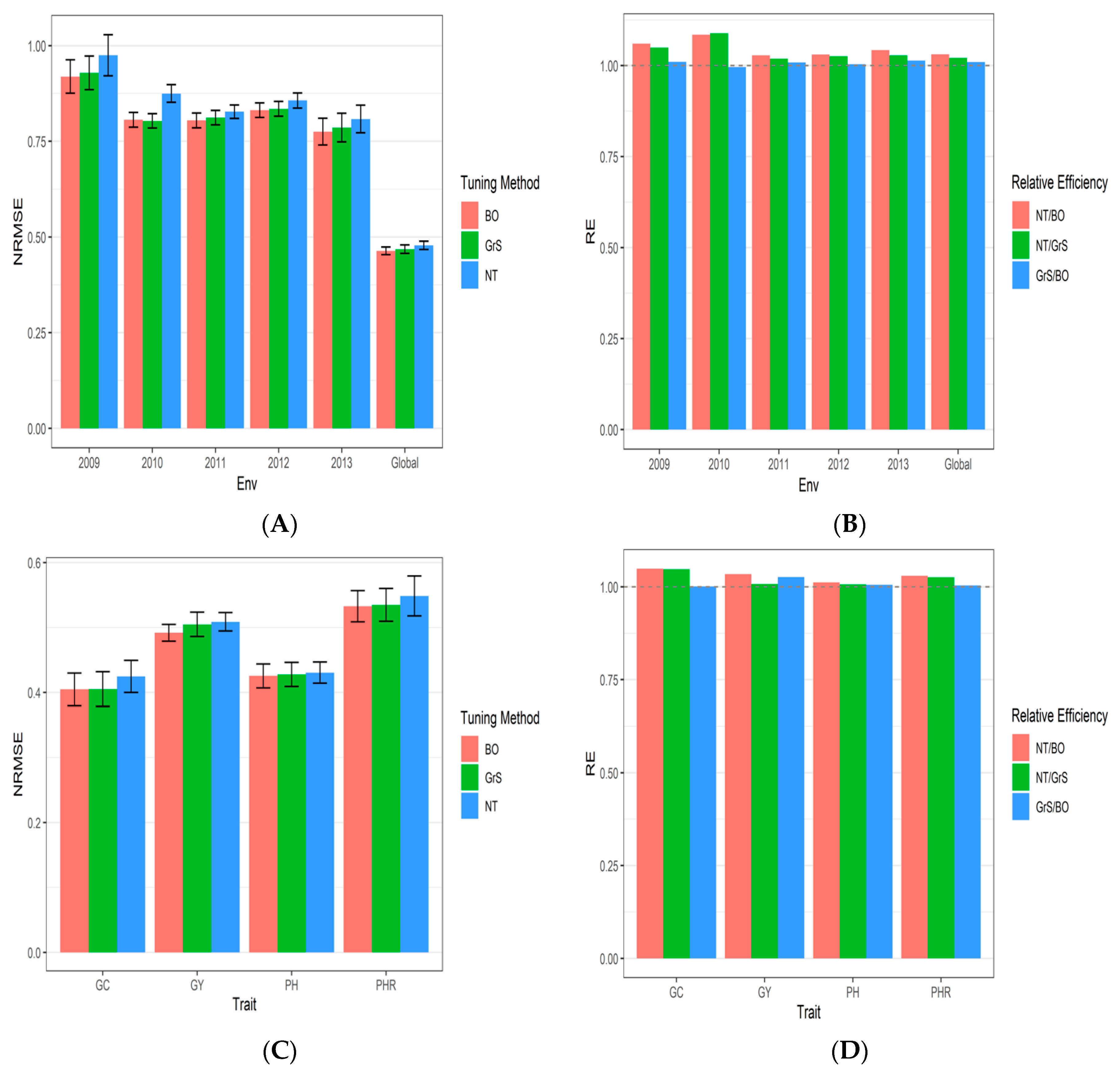
3.1. Dataset 1 Japonica
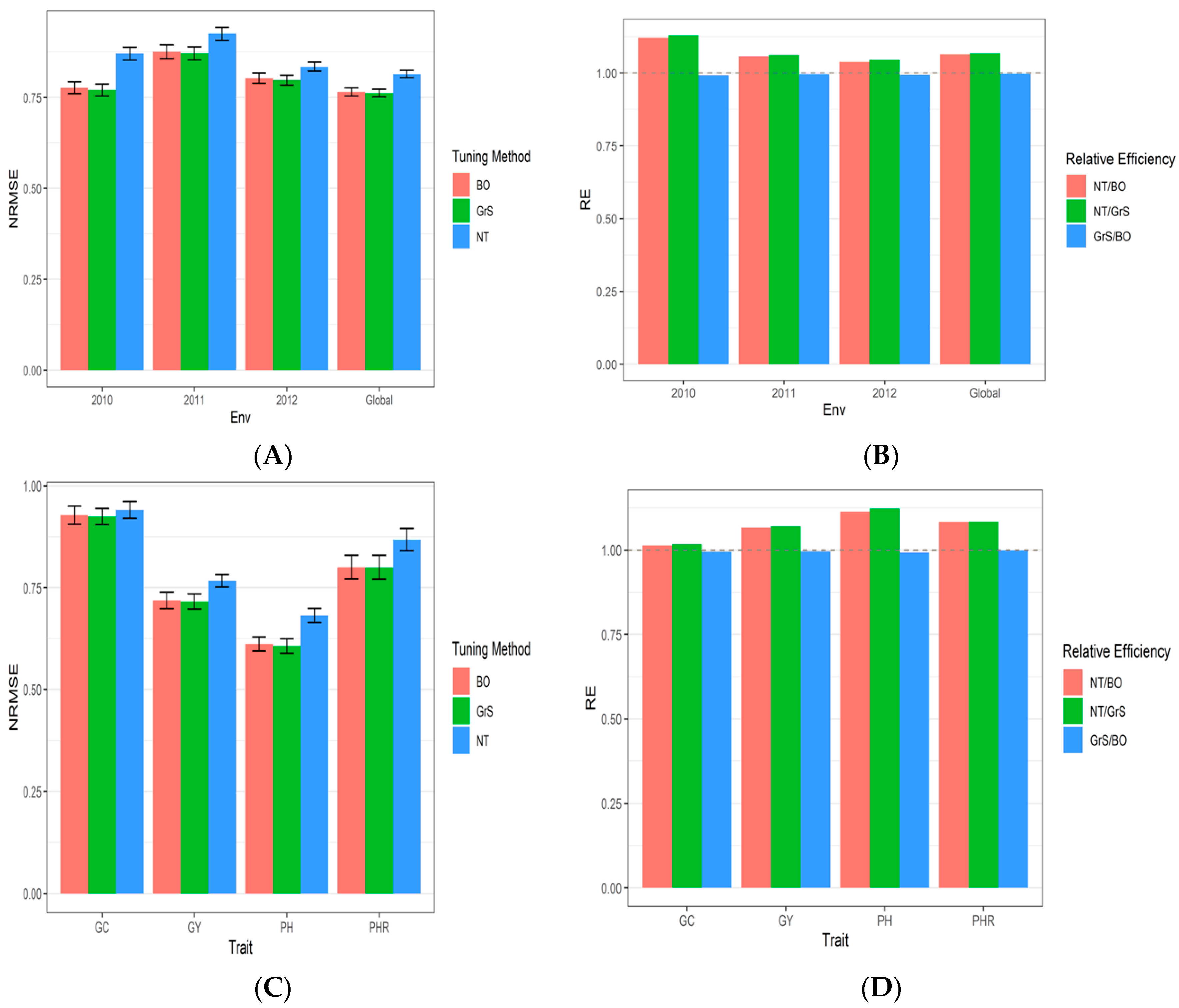
3.2. Dataset 2 Indica
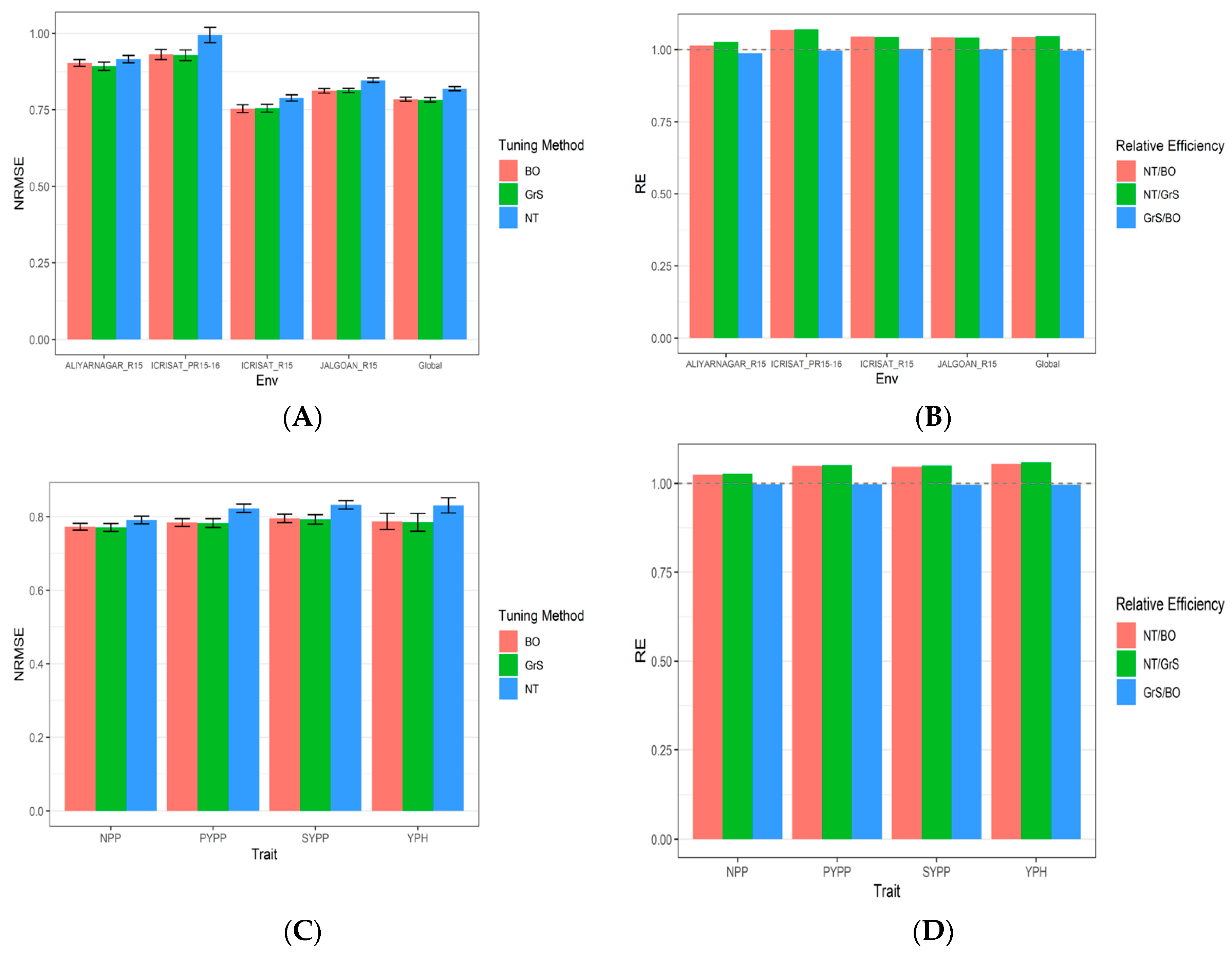
3.3. Dataset 3 Groundnut
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Tuning Type | Year | NRMSE_GC | NRMSE_GY | NRMSE_PH | NRMSE_PHR | NRMSE | RE |
|---|---|---|---|---|---|---|---|
| Bayesian Optimization | 2009 | 1.1256 | 0.9846 | 0.7289 | 0.8383 | 0.919350 | 1.0603959 |
| Bayesian Optimization | 2010 | 0.9377 | 0.8181 | 0.6398 | 0.8298 | 0.806350 | 1.0849197 |
| Bayesian Optimization | 2011 | 0.7741 | 0.8752 | 0.7574 | 0.8119 | 0.804650 | 1.0283353 |
| Bayesian Optimization | 2012 | 0.8877 | 0.8585 | 0.6541 | 0.9253 | 0.831400 | 1.0304306 |
| Bayesian Optimization | 2013 | 0.7327 | 0.8658 | 0.6643 | 0.8374 | 0.775050 | 1.0427714 |
| Bayesian Optimization | Global | 0.4048 | 0.4919 | 0.4255 | 0.5328 | 0.463750 | 1.0310512 |
| Grid Search | 2009 | 1.1246 | 1.0185 | 0.7283 | 0.8445 | 0.928975 | 1.0494093 |
| Grid Search | 2010 | 0.9130 | 0.8299 | 0.6436 | 0.8270 | 0.803375 | 1.0889373 |
| Grid Search | 2011 | 0.7787 | 0.8943 | 0.7585 | 0.8156 | 0.811775 | 1.0193095 |
| Grid Search | 2012 | 0.8877 | 0.8689 | 0.6530 | 0.9298 | 0.834850 | 1.0261724 |
| Grid Search | 2013 | 0.7305 | 0.9151 | 0.6578 | 0.8401 | 0.785875 | 1.0284078 |
| Grid Search | Global | 0.4053 | 0.5049 | 0.4278 | 0.5348 | 0.468200 | 1.0212516 |
| No Tuning | 2009 | 1.3539 | 0.9841 | 0.6954 | 0.8661 | 0.974875 | 1.0104694 |
| No Tuning | 2010 | 1.1494 | 0.8527 | 0.6445 | 0.8527 | 0.874825 | 0.9963105 |
| No Tuning | 2011 | 0.8013 | 0.9069 | 0.7661 | 0.8355 | 0.827450 | 1.0088548 |
| No Tuning | 2012 | 0.9123 | 0.8961 | 0.6673 | 0.9511 | 0.856700 | 1.0041496 |
| No Tuning | 2013 | 0.7988 | 0.9049 | 0.6741 | 0.8550 | 0.808200 | 1.0139668 |
| No Tuning | Global | 0.4246 | 0.5088 | 0.4306 | 0.5486 | 0.478150 | 1.0095957 |
| Tuning Type | Year | NRMSE_GC | NRMSE_GY | NRMSE_PH | NRMSE_PHR | NRMSE | RE |
|---|---|---|---|---|---|---|---|
| Bayesian Optimization | 2010 | 0.9201 | 0.9234 | 0.4439 | 0.8195 | 0.776725 | 1.1207956 |
| Bayesian Optimization | 2011 | 0.9305 | 0.8324 | 0.8707 | 0.8687 | 0.875575 | 1.0563344 |
| Bayesian Optimization | 2012 | 0.9492 | 0.7529 | 0.6981 | 0.8116 | 0.802950 | 1.0391058 |
| Bayesian Optimization | Global | 0.9287 | 0.7190 | 0.6117 | 0.8006 | 0.765000 | 1.0645425 |
| Grid Search | 2010 | 0.9181 | 0.9154 | 0.4229 | 0.8253 | 0.770425 | 1.1299607 |
| Grid Search | 2011 | 0.9206 | 0.8250 | 0.8728 | 0.8668 | 0.871300 | 1.0615173 |
| Grid Search | 2012 | 0.9433 | 0.7542 | 0.6926 | 0.8004 | 0.797625 | 1.0460429 |
| Grid Search | Global | 0.9248 | 0.7165 | 0.6070 | 0.8002 | 0.762125 | 1.0685583 |
| No Tuning | 2010 | 0.9470 | 1.0435 | 0.5777 | 0.9140 | 0.870550 | 0.9918890 |
| No Tuning | 2011 | 0.9390 | 0.8394 | 0.9642 | 0.9570 | 0.924900 | 0.9951175 |
| No Tuning | 2012 | 0.9461 | 0.8031 | 0.7495 | 0.8387 | 0.834350 | 0.9933682 |
| No Tuning | Global | 0.9409 | 0.7669 | 0.6816 | 0.8681 | 0.814375 | 0.9962418 |
| Tuning Type | Environment | NRMSE_NPP | NRMSE_PYPP | NRMSE_SYPP | NRMSE_YPH | NRMSE | RE |
|---|---|---|---|---|---|---|---|
| Bayesian Optimization | ALIYARNAGAR_R15 | 0.8992 | 0.9442 | 0.9452 | 0.8242 | 0.9032 | 1.0139781 |
| Bayesian Optimization | ICRISAT_R15 | 0.7872 | 0.7729 | 0.786 | 0.6701 | 0.75405 | 1.0458524 |
| No Tuning | ALIYARNAGAR_R15 | 0.9152 | 0.9554 | 0.9597 | 0.833 | 0.915825 | 0.9879318 |
| Bayesian Optimization | ICRISAT_PR15-16 | 0.9025 | 0.9547 | 0.9469 | 0.9191 | 0.9308 | 1.068194 |
| Bayesian Optimization | JALGOAN_R15 | 0.8081 | 0.8361 | 0.8383 | 0.7674 | 0.812475 | 1.0423705 |
| No Tuning | ICRISAT_PR15-16 | 0.9331 | 1.0378 | 1.0184 | 0.9878 | 0.994275 | 0.9975827 |
| Grid Search | ALIYARNAGAR_R15 | 0.8902 | 0.9342 | 0.9337 | 0.8111 | 0.89230 | 1.0263645 |
| Grid Search | ICRISAT_R15 | 0.7862 | 0.7755 | 0.7873 | 0.6737 | 0.755675 | 1.0436034 |
| No Tuning | ICRISAT_R15 | 0.7866 | 0.823 | 0.8324 | 0.7125 | 0.788625 | 1.002155 |
| Grid Search | ICRISAT_PR15-16 | 0.9026 | 0.9517 | 0.9441 | 0.9158 | 0.92855 | 1.0707824 |
| Grid Search | JALGOAN_R15 | 0.8091 | 0.8377 | 0.8404 | 0.7671 | 0.813575 | 1.0409612 |
| No Tuning | JALGOAN_R15 | 0.827 | 0.8753 | 0.8758 | 0.8095 | 0.8469 | 1.0013539 |
| Bayesian Optimization | Global | 0.7726 | 0.7841 | 0.7952 | 0.7871 | 0.78475 | 1.0440268 |
| Grid Search | Global | 0.7707 | 0.7825 | 0.7925 | 0.7845 | 0.78255 | 1.0469619 |
| No Tuning | Global | 0.7912 | 0.8229 | 0.8324 | 0.8307 | 0.8193 | 0.9971966 |
Appendix B
| Tuning Type | Year | NRMSE_SE_GC | NRMSE_SE_GY | NRMSE_SE_PH | NRMSE_SE_PHR | NRMSE_SE |
|---|---|---|---|---|---|---|
| Bayesian Optimization | 2009 | 0.1457 | 0.0531 | 0.1201 | 0.0303 | 0.0436500 |
| Bayesian Optimization | 2010 | 0.0475 | 0.0239 | 0.0580 | 0.0244 | 0.0192250 |
| Bayesian Optimization | 2011 | 0.0344 | 0.0405 | 0.0606 | 0.0173 | 0.0191000 |
| Bayesian Optimization | 2012 | 0.0176 | 0.0408 | 0.0630 | 0.0317 | 0.0191375 |
| Bayesian Optimization | 2013 | 0.0594 | 0.0850 | 0.1139 | 0.0211 | 0.0349250 |
| Bayesian Optimization | Global | 0.0251 | 0.0129 | 0.0184 | 0.0240 | 0.0100500 |
| Grid Search | 2009 | 0.1326 | 0.0701 | 0.1150 | 0.0328 | 0.0438125 |
| Grid Search | 2010 | 0.0378 | 0.0296 | 0.0580 | 0.0227 | 0.0185125 |
| Grid Search | 2011 | 0.0353 | 0.0399 | 0.0619 | 0.0152 | 0.0190375 |
| Grid Search | 2012 | 0.0182 | 0.0410 | 0.0623 | 0.0310 | 0.0190625 |
| Grid Search | 2013 | 0.0599 | 0.1058 | 0.1102 | 0.0246 | 0.0375625 |
| Grid Search | Global | 0.0266 | 0.0187 | 0.0186 | 0.0253 | 0.0111500 |
| No Tuning | 2009 | 0.2366 | 0.0583 | 0.0931 | 0.0406 | 0.0535750 |
| No Tuning | 2010 | 0.0825 | 0.0189 | 0.0522 | 0.0315 | 0.0231375 |
| No Tuning | 2011 | 0.0325 | 0.0328 | 0.0587 | 0.0164 | 0.0175500 |
| No Tuning | 2012 | 0.0122 | 0.0419 | 0.0702 | 0.0332 | 0.0196875 |
| No Tuning | 2013 | 0.0614 | 0.0880 | 0.1179 | 0.0201 | 0.0359250 |
| No Tuning | Global | 0.0246 | 0.0141 | 0.0162 | 0.0307 | 0.0107000 |
| Tuning Type | Year | NRMSE_SE_GC | NRMSE_SE_GY | NRMSE_SE_PH | NRMSE_SE_PHR | NRMSE_SE |
|---|---|---|---|---|---|---|
| Bayesian Optimization | 2010 | 0.0272 | 0.0275 | 0.0314 | 0.0428 | 0.0161125 |
| Bayesian Optimization | 2011 | 0.0300 | 0.0300 | 0.0333 | 0.0574 | 0.0188375 |
| Bayesian Optimization | 2012 | 0.0261 | 0.0125 | 0.0297 | 0.0457 | 0.0142500 |
| Bayesian Optimization | Global | 0.0225 | 0.0201 | 0.0172 | 0.0292 | 0.0111250 |
| Grid Search | 2010 | 0.0280 | 0.0264 | 0.0299 | 0.0481 | 0.0165500 |
| Grid Search | 2011 | 0.0245 | 0.0270 | 0.0356 | 0.0557 | 0.0178500 |
| Grid Search | 2012 | 0.0253 | 0.0133 | 0.0317 | 0.0398 | 0.0137625 |
| Grid Search | Global | 0.0197 | 0.0184 | 0.0177 | 0.0295 | 0.0106625 |
| No Tuning | 2010 | 0.0328 | 0.0168 | 0.0382 | 0.0528 | 0.0175750 |
| No Tuning | 2011 | 0.0235 | 0.0271 | 0.0366 | 0.0521 | 0.0174125 |
| No Tuning | 2012 | 0.0295 | 0.0077 | 0.0228 | 0.0387 | 0.0123375 |
| No Tuning | Global | 0.0207 | 0.0157 | 0.0176 | 0.0273 | 0.0101625 |
| Tuning Type | Environment | NRMSE_SE_NPP | NRMSE_SE_PYPP | NRMSE_SE_SYPP | NRMSE_SE_YPH | NRMSE_SE |
|---|---|---|---|---|---|---|
| Bayesian Optimization | ALIYARNAGAR_R15 | 0.0269 | 0.0164 | 0.0185 | 0.0287 | 0.0113125 |
| Bayesian Optimization | ICRISAT_PR15-16 | 0.0299 | 0.0342 | 0.0386 | 0.0283 | 0.0163750 |
| Bayesian Optimization | ICRISAT_R15 | 0.0228 | 0.0282 | 0.0255 | 0.0255 | 0.0127500 |
| Bayesian Optimization | JALGOAN_R15 | 0.0249 | 0.0089 | 0.0110 | 0.0169 | 0.0077125 |
| Bayesian Optimization | Global | 0.0094 | 0.0105 | 0.0114 | 0.0222 | 0.0066875 |
| Grid Search | ALIYARNAGAR_R15 | 0.0312 | 0.0228 | 0.0253 | 0.0310 | 0.0137875 |
| Grid Search | ICRISAT_PR15-16 | 0.0322 | 0.0366 | 0.0403 | 0.0288 | 0.0172375 |
| Grid Search | ICRISAT_R15 | 0.0223 | 0.0288 | 0.0268 | 0.0241 | 0.0127500 |
| Grid Search | JALGOAN_R15 | 0.0246 | 0.0077 | 0.0086 | 0.0166 | 0.0071875 |
| Grid Search | Global | 0.0106 | 0.0119 | 0.0126 | 0.0241 | 0.0074000 |
| No Tuning | ALIYARNAGAR_R15 | 0.0294 | 0.0205 | 0.0202 | 0.0262 | 0.0120375 |
| No Tuning | ICRISAT_PR15-16 | 0.0429 | 0.0555 | 0.0581 | 0.0452 | 0.0252125 |
| No Tuning | ICRISAT_R15 | 0.0239 | 0.0198 | 0.0216 | 0.0176 | 0.0103625 |
| No Tuning | JALGOAN_R15 | 0.0224 | 0.0086 | 0.0078 | 0.0195 | 0.0072875 |
| No Tuning | Global | 0.0104 | 0.0113 | 0.0113 | 0.0205 | 0.0066875 |
References
- Caamal-Pat, D.; Pérez-Rodríguez, P.; Crossa, J.; Velasco-Cruz, C.; Pérez-Elizalde, S.; Vázquez-Peña, M. lme4GS: An R-Package for Genomic Selection. Front. Genet. 2021, 12, 680569. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Cano-Paez, B.; Hernández-Suárez, C.M.; Santana-Mancilla, P.C.; Crossa, J. A Comparison of Three Machine Learning Methods for Multivariate Genomic Prediction Using the Sparse Kernels Method (SKM) Library. Genes 2022, 13, 1494. [Google Scholar] [CrossRef] [PubMed]
- Cordell, H.J. Epistasis: What it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002, 11, 2463–2468. [Google Scholar] [CrossRef] [PubMed]
- Golan, D.; Rosset, S. Effective genetic-risk prediction using mixed models. Am. J. Hum. Genet. 2014, 95, 383–393. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D.; Fernando, R.L.; Stella, A. Genomic-assisted prediction of genetic value with semi parametric procedures. Genetics 2006, 173, 1761–1776. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D.; van Kaam, J.B.C.H.M. Reproducing kernel Hilbert spaces regression methods for genomic assisted prediction of quantitative traits. Genetics 2008, 178, 2289–2303. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Long, N.; Gianola, D.; Rosa, G.J.; Weigel, K.A.; Kranis, A.; González-Recio, O. Radial basis function regression methods for predicting quantitative traits using SNP markers. Genet. Res. 2010, 92, 209–225. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; de los Campos, G.; Pérez, P.; Gianola, D.; Burgueño, J.; Araus, J.L. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 2010, 186, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.; Montesinos-López, O.A.; Juliana, P.; Guzmán, C.; Pérez-Rodríguez, P.; González-Bucio, J.; Burgueño, J.; Montesinos-López, A.; Crossa, J. Deep Kernel for Genomic and Near Infrared Predictions in Multi-environment Breeding Trials. G3-Genes Genomes Genet. 2019, 9, 2913–2924. [Google Scholar] [CrossRef] [PubMed]
- Tusell, L.; Pérez-Rodríguez, P.; Wu, S.F.X.-L.; Gianola, D. Genome-enabled methods for predicting litter size in pigs: A comparison. Animal 2013, 7, 1739–1749. [Google Scholar] [CrossRef] [PubMed]
- Morota, G.; Koyama, M.; Rosa, G.J.M.; Weigel, K.A.; Gianola, D. Predicting complex traits using a diffusion kernel on genetic markers with an application to dairy cattle and wheat data. Genet. Sel. Evol. 2013, 45, 17. [Google Scholar] [CrossRef] [PubMed]
- Arojju, S.K.; Cao, M.; Trolove, M.; Barrett, B.A.; Inch, C.; Eady, C.; Stewart, A.; Faville, M.J. Multi-Trait Genomic Prediction Improves Predictive Ability for Dry Matter Yield and Water-Soluble Carbohydrates in Perennial Ryegrass. Front. Plant Sci. 2020, 11, 1197. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J.; Cuevas, J.; Montesinos-López, J.C.; Salas-Gutiérrez, Z.; Lillemo, M.; Philomin, J.; Singh, R. A Bayesian Genomic Multi-output Regressor Stacking Model for Predicting Multi-trait Multi-environment Plant Breeding Data. G3-Genes Genomes Genet. 2019, 9, 3381–3393. [Google Scholar] [CrossRef] [PubMed]
- Monteverde, E.; Gutierrez, L.; Blanco, P.; Pérez de Vida, F.; Rosas, J.E.; Bonnecarrère, V.; Quero, G.; McCouch, S. Integrating Molecular Markers and Environmental Covariates To Interpret Genotype by Environment Interaction in Rice (Oryza sativa L.) Grown in Subtropical Areas. G3 Genes Genomes Genet. 2019, 9, 1519–1531. [Google Scholar] [CrossRef]
- Pandey, M.K.; Chaudhari, S.; Jarquin, D.; Janila, P.; Crossa, J.; Patil, S.C.; Sundravadana, S.; Khare, D.; Bhat, R.S.; Radhakrishnan, T.; et al. Genome-based trait prediction in multi- environment breeding trials in groundnut. Theor. Appl. Genet. 2020, 133, 3101–3117. [Google Scholar] [CrossRef] [PubMed]
- Gapare, W.; Liu, S.; Conaty, W.; Zhu, Q.H.; Gillespie, V.; Llewellyn, D.; Stiller, W.; Wilson, I. Historical Datasets Support Genomic Selection Models for the Prediction of Cotton Fiber Quality Phenotypes Across Multiple Environments. G3 Genes Genomes Genet. 2018, 8, 1721–1732. [Google Scholar] [CrossRef] [PubMed]
- VanRaden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J. (Eds.) Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-89010-0. [Google Scholar]
- Montesinos-López, O.A.; Carter, A.H.; Bernal-Sandoval, D.A.; Cano-Paez, B.; Montesinos-López, A.; Crossa, J. A Comparison Between Three Tuning Strategies for Gaussian kernels in the Context of Univariate Genomic Prediction. Genes, 2022; submitted for publication. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Pérez, P.; de los Campos, G. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kismiantini; Montesinos-López, A.; Cano-Páez, B.; Montesinos-López, J.C.; Chavira-Flores, M.; Montesinos-López, O.A.; Crossa, J. A Multi-Trait Gaussian Kernel Genomic Prediction Model under Three Tunning Strategies. Genes 2022, 13, 2279. https://doi.org/10.3390/genes13122279
Kismiantini, Montesinos-López A, Cano-Páez B, Montesinos-López JC, Chavira-Flores M, Montesinos-López OA, Crossa J. A Multi-Trait Gaussian Kernel Genomic Prediction Model under Three Tunning Strategies. Genes. 2022; 13(12):2279. https://doi.org/10.3390/genes13122279
Chicago/Turabian StyleKismiantini, Abelardo Montesinos-López, Bernabe Cano-Páez, J. Cricelio Montesinos-López, Moisés Chavira-Flores, Osval A. Montesinos-López, and José Crossa. 2022. "A Multi-Trait Gaussian Kernel Genomic Prediction Model under Three Tunning Strategies" Genes 13, no. 12: 2279. https://doi.org/10.3390/genes13122279
APA StyleKismiantini, Montesinos-López, A., Cano-Páez, B., Montesinos-López, J. C., Chavira-Flores, M., Montesinos-López, O. A., & Crossa, J. (2022). A Multi-Trait Gaussian Kernel Genomic Prediction Model under Three Tunning Strategies. Genes, 13(12), 2279. https://doi.org/10.3390/genes13122279




