Classification of Protein Sequences by a Novel Alignment-Free Method on Bacterial and Virus Families
Abstract
1. Introduction
2. Materials and Methods
2.1. Accumulated Natural Vector for Protein Sequences
2.1.1. Related Definitions
2.1.2. Accumulated Natural Vector
2.2. Convex Hull Method
2.3. Convex Hull Distance
2.4. Linear Discriminant Analysis
2.5. Maximum Margin Criterion
2.6. Knn Classification
3. Results and Discussion
3.1. Convex Hull Analysis of Bacterial Families
3.2. Classification of Protein Enzyme Classes
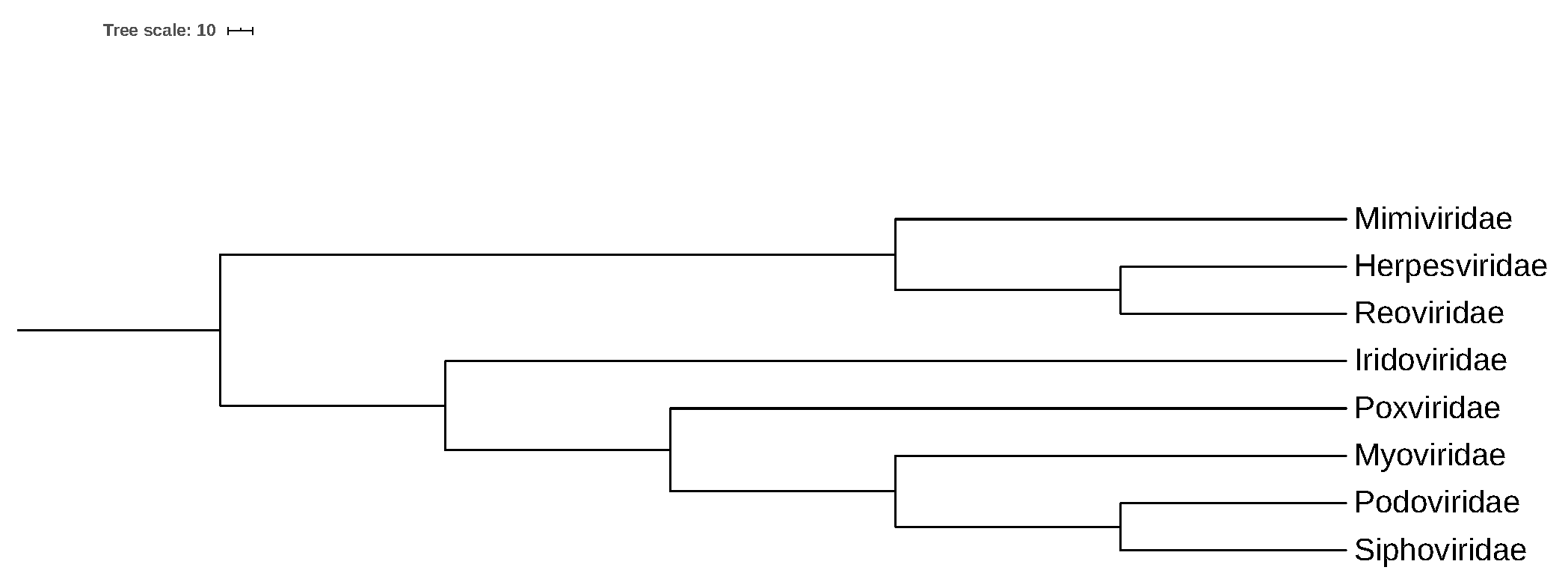
3.3. Convex Hull Analysis of Virus Families
3.3.1. Intersection of Virus Families in a 250-Dimensional Space
3.3.2. Intersection of Virus Families in a 2-Dimensional Space
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mount, D.W. Bioinformatics: Sequence and Genome Analysis, 2nd ed.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2004. [Google Scholar]
- Lodish, H.; Berk, A.; Kaiser, C.A.; Krieger, M. Molecular Cell Biology; W.H. Freeman and Company: New York, NY, USA, 2004. [Google Scholar]
- Bairoch, A. The ENZYME database in 2000. Nucleic Acids Res. 2000, 28, 304–305. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry; W.H. Freeman and Company: New York, NY, USA, 2008. [Google Scholar]
- Ng, P.C.; Henikoff, S. SIFT: Predicting amino acid changes that affect protein function. Nucleic Acids Res. 2003, 31, 3812–3814. [Google Scholar] [CrossRef] [PubMed]
- Black, D.L. Protein Diversity from Alternative Splicing: A Challenge for Bioinformatics and Post-Genome biology. Cell 2000, 103, 367–370. [Google Scholar] [CrossRef]
- Wu, C.; Gao, R.; De Marinis, Y.; Zhang, Y. A novel model for protein sequence similarity analysis based on spectral radius. J. Theor. Biol. 2018, 446, 61–70. [Google Scholar] [CrossRef]
- Yao, Y.H.; Dai, Q.; Li, L.; Nan, X.Y.; He, P.A.; Zhang, Y.Z. Similarity/dissimilarity studies of protein sequences based on a new 2D graphical representation. J. Comput. Chem. 2010, 31, 1045–1052. [Google Scholar] [CrossRef]
- Pham, T.D.; Zuegg, J. A probabilistic measure for alignment-free sequence comparison. Bioinformatics 2004, 20, 3455–3461. [Google Scholar] [CrossRef]
- Schwende, I.; Pham, T.D. Pattern recognition and probabilistic measures in alignment-free sequence analysis. Brief. Bioinform. 2014, 15, 354–368. [Google Scholar] [CrossRef][Green Version]
- Sims, G.E.; Jun, S.R.; Wu, G.A.; Kim, S.H. Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl. Acad. Sci. USA 2009, 106, 2677–2682. [Google Scholar] [CrossRef]
- Steinegger, M.; Söding, J. Clustering huge protein sequence sets in linear time. Nat. Commun. 2018, 9, 2542. [Google Scholar] [CrossRef]
- Yau, S.S.T.; Yu, C.; He, R. A protein map and its application. DNA Cell Biol. 2008, 27, 241–250. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Yau, S.S.T. Phylogenetic analysis of protein sequences based on a novel k-mer natural vector method. Genomics 2019, 111, 1298–1305. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Tian, K.; He, R.L.; Yau, S.S.T. Convex hull principle for classification and phylogeny of eukaryotic proteins. Genomics 2019, 111, 1777–1784. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; He, L.; He, R.L.; Yau, S.S.T. A Novel Approach to Clustering Genome Sequences Using Inter-nucleotide Covariance. Front. Genet. 2019, 10, 234. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition. J. Theor. Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Tian, K.; Zhao, X.; Yau, S.S.T. Convex hull analysis of evolutionary and phylogenetic relationships between biological groups. J. Theor. Biol. 2018, 456, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Chen, L.F.; Liao, H.Y.M.; Ko, M.T.; Lin, J.C.; Yu, G.J. New LDA-based face recognition system which can solve the small sample size problem. Pattern Recognit. 2000, 33, 1713–1726. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient knn classification with different numbers of nearest neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef]
- Alexander, C.; Rietschel, E.T. Invited review: Bacterial lipopolysaccharides and innate immunity. J. Endotoxin Res. 2001, 7, 167–202. [Google Scholar] [CrossRef]
- Palmer, B.R.; Marinus, M.G. The dam and dcm strains of Escherichia coli—A review. Gene 1994, 143, 1–12. [Google Scholar] [CrossRef]
- Li, M.; Yuan, B. 2D-LDA: A statistical linear discriminant analysis for image matrix. Pattern Recognit. Lett. 2005, 26, 527–532. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, K.; Yau, S.S.T. Protein Sequence Classification Using Natural Vector and Convex Hull Method. J. Comput. Biol. 2019, 26, 315–321. [Google Scholar] [CrossRef] [PubMed]


| Sequence S | A | R | R | N | A | D | C | D | C | C |
|---|---|---|---|---|---|---|---|---|---|---|
| Position(i) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Sequence S | A | R | R | N | A | D | C | D | C | C |
|---|---|---|---|---|---|---|---|---|---|---|
| Position(i) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 0 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 |
| Enzyme Class | Total Number | Correct Number | Accuracy |
|---|---|---|---|
| Oxidoreductases | 1829 | 1720 | 0.940404 |
| Transferases | 4054 | 3905 | 0.963246 |
| Hydrolases | 2783 | 2632 | 0.945742 |
| Lyases | 1387 | 1354 | 0.976208 |
| Isomerases | 823 | 788 | 0.957473 |
| Ligases | 906 | 893 | 0.985651 |
| Translocases | 502 | 490 | 0.976096 |
| Total | 12,284 | 11,782 | 0.959134 |
| Virus Classification | Samples | Number of Virus Families |
|---|---|---|
| dsDNA virus | Herelleviridae | 23 |
| ssDNA virus | Microviridae | 7 |
| dsRNA virus | Totiviridae | 8 |
| ssRNA(+) virus | Alphatetraviridae | 30 |
| ssRNA(-) virus | Bornaviridae | 1 |
| ssRNA-RT virus | Metaviridae | 1 |
| dsDNA-RT virus | Caulimoviridae | 2 |
| Virus Family | Percentage | Virus Family | Percentage |
|---|---|---|---|
| Adenoviridae | 0.6667 | Hepeviridae | 0.9861 |
| Alloherpesviridae | 0.8472 | Herelleviridae | 0.8472 |
| Alphaflexiviridae | 0.8056 | Herpesviridae | 0.1389 |
| Alphatetraviridae | 1.0000 | Hypoviridae | 1.0000 |
| Ampullaviridae | 0.8472 | Inoviridae | 0.8056 |
| Anelloviridae | 0.9861 | Iridoviridae | 0.5333 |
| Arteriviridae | 0.9583 | Kitaviridae | 0.9861 |
| Ascoviridae | 0.9444 | Lavidaviridae | 0.9583 |
| Astroviridae | 1.0000 | Leviviridae | 0.9444 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, M.; Zhao, L.; Yau, S.S.-T. Classification of Protein Sequences by a Novel Alignment-Free Method on Bacterial and Virus Families. Genes 2022, 13, 1744. https://doi.org/10.3390/genes13101744
Guan M, Zhao L, Yau SS-T. Classification of Protein Sequences by a Novel Alignment-Free Method on Bacterial and Virus Families. Genes. 2022; 13(10):1744. https://doi.org/10.3390/genes13101744
Chicago/Turabian StyleGuan, Mengcen, Leqi Zhao, and Stephen S.-T. Yau. 2022. "Classification of Protein Sequences by a Novel Alignment-Free Method on Bacterial and Virus Families" Genes 13, no. 10: 1744. https://doi.org/10.3390/genes13101744
APA StyleGuan, M., Zhao, L., & Yau, S. S.-T. (2022). Classification of Protein Sequences by a Novel Alignment-Free Method on Bacterial and Virus Families. Genes, 13(10), 1744. https://doi.org/10.3390/genes13101744






