Feature Selection for Topological Proximity Prediction of Single-Cell Transcriptomic Profiles in Drosophila Embryo Using Genetic Algorithm
Abstract
1. Introduction
2. Method
2.1. DREAM Dataset Description
2.2. Selection of Gene Sets
2.3. Data Preprocessing
2.4. Training Model
2.4.1. Genetic Algorithm
2.4.2. Fitness Function
2.4.3. Metric-1 Based on Root Mean Squared Deviation
2.4.4. Metric-2 Based on Spearman Correlation
2.4.5. Metric-3 Based on Jaccard Index
2.4.6. Metric-4 Based on Euclidean Distance
2.4.7. Final Fitness Function
2.4.8. Parameters
- Initial population:Initial population was a set of sequences of length n, carrying indexes of different columns we need to incorporate. Hence, we could set the exact length of the number of features to be selected by this. The initial population is defined by randomly generating 500 chromosomes of feature indexes of size n.
- Crossover:A crossover is done between two chromosomes in the population, generating two offspring. A single point crossover is done between two randomly selected chromosomes, at a randomly selected point one minus the length of the chromosome. The chromosomes are further crossed over if the offspring chromosomes do not have a repetition of gene sets and added to the next generation. 200 offspring are generated by crossing over chromosomes 100 times.
- Mutation:A mutation is introduced in the population set every third generation. For every chromosome in the generation, a location is randomly selected and replaced with a new feature index not already present in the chromosome.
- Elitism:At the end of each generation, we selected only the top 20% of the offspring as parents for the next generation.
- Gene Ontology Analysis:The GA-based approach is a simple data-driven approach which may not produce the most biologically meaningful results. For this purpose, GA optimized top sets (from last few generations of GA) were re-prioritized to ensure that the pathway enrichment in the final set of genes also has the best overlap with the enrichments produced by 84 driver genes. Hence, the last three unique gene sets obtained for each subset size were analyzed for gene set/GO-based enrichment analysis, using the FlyMine enrichment tool [40]. The set with the maximum overlap of GO terms was selected as the final set of genes.
2.5. Post Competition Assessment of GA Hyperparameters
2.6. Creating Baseline Gene Sets to Evaluate Performance Gains in a Complex Method
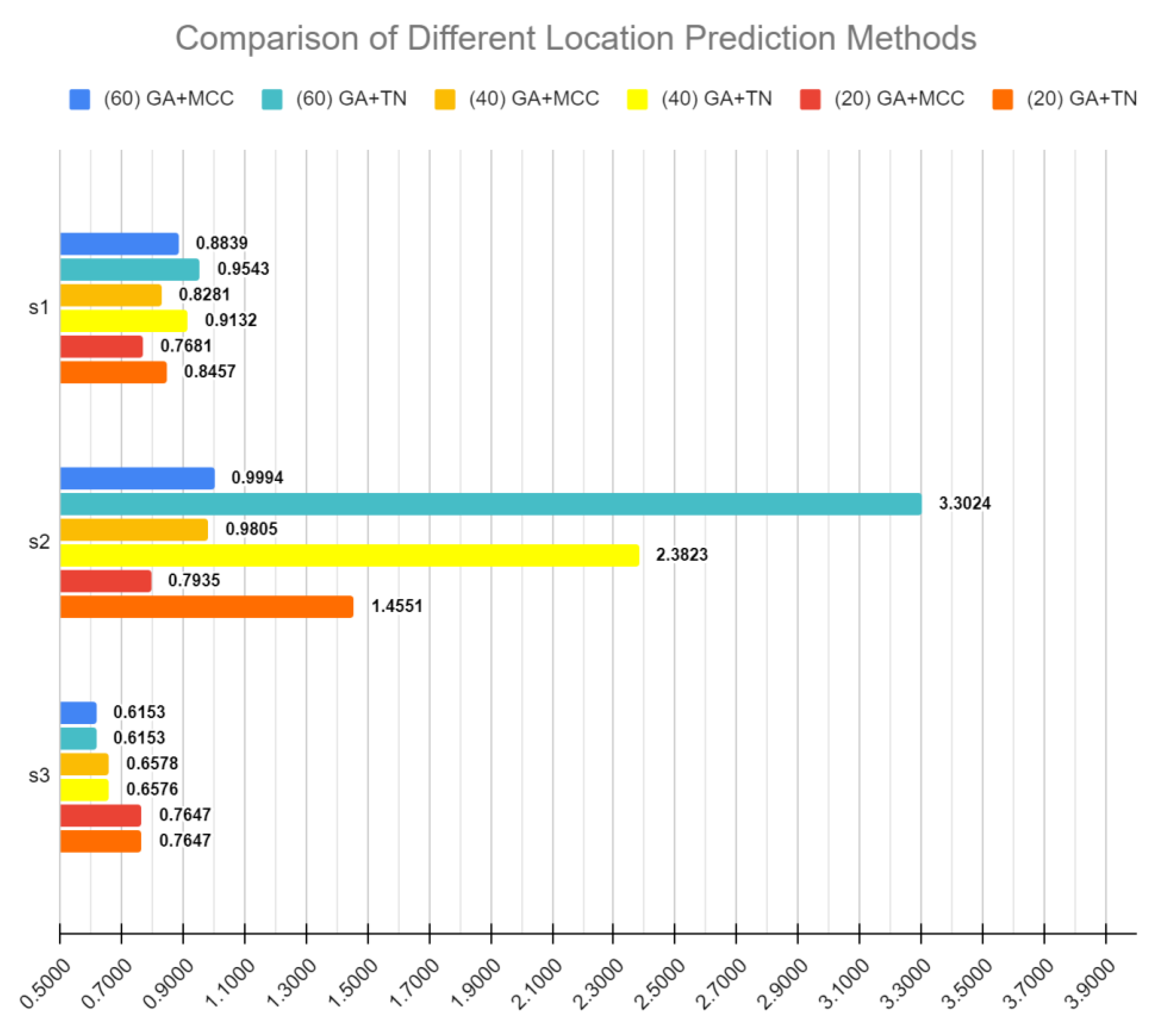
2.7. Evaluating Performance of Selected Gene Sets by Comparing with Different Location Prediction Methods
3. Result
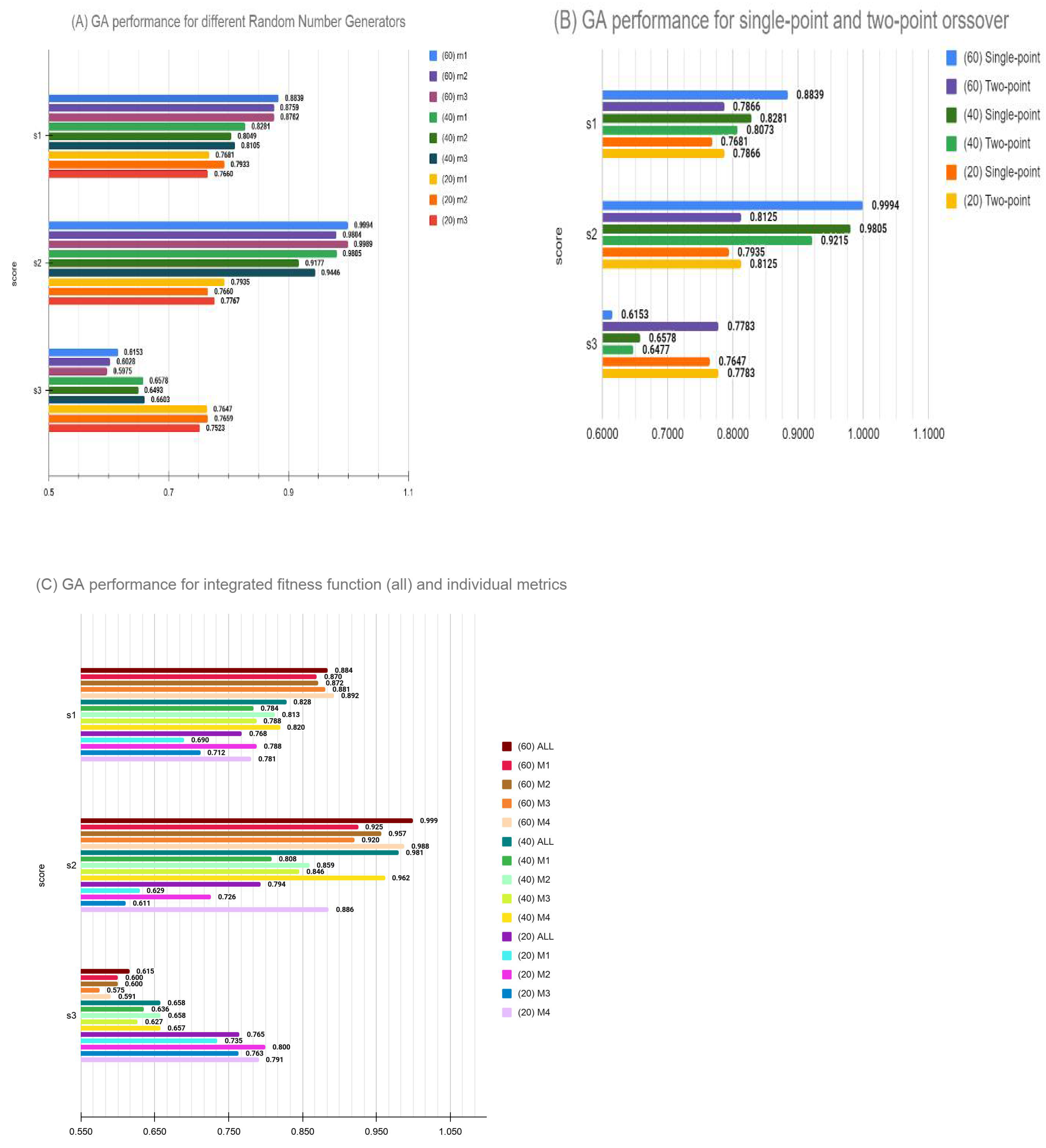
3.1. GA Optimization of Fixed Sized Gene Sets
3.2. Ranking of Proposed GA Method in DREAM Challenge and Post-Competition Experimentation
3.3. Feature Selection versus Location Assignment
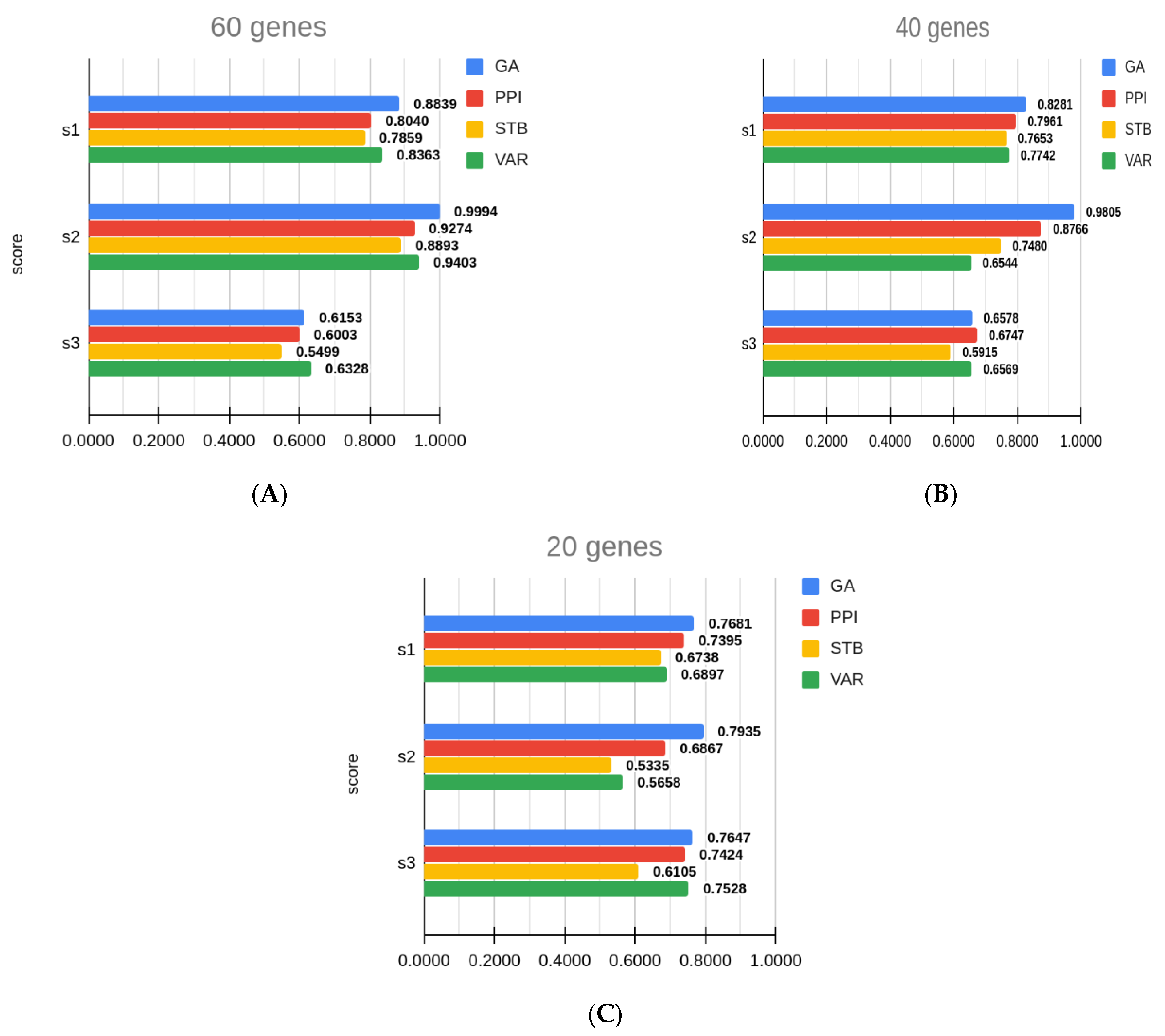
3.4. Comparison with Other Gene Sets
3.5. Parameter Evaluation Post DREAM Challenge
- (a)
- The initialization conditions and GA robustness: In these experiments, we performed 10 runs of GA optimization with random initialization every time. Overall, 30 experiments (10 for each of the 20, 40 and 60 feature sets) were carried out, and three scores, namely s1, s2 and s3, were compared. Overall, 90 comparisons shown in Supplementary Table S4 and represented in Supplementary Figure S1 clearly indicate the GA has successfully avoided local minima as the variance in 10 runs in each case is less than 5% of the mean performance score with the average variance across all runs being less than 2%. This demonstrates that GA algorithm can be safely employed for a few runs to get an optimal solution when the computing cost for feature selection is too high.
- (b)
- Variation of performance was also examined by a combination of crossover and mutation rates, as well as elitism in the model. Our original model used 100% crossover with no parents allowed to cross over for a faster convergence within the time limit of DREAM challenge. Post-challenge, we examined these variations and found that, for the small feature set target of 20 genes, results are not too sensitive to hyperparameters. However, larger feature set selections are somewhat unstable and a combination better than our challenge submission did exist. Thus, we conclude that GA optimization may benefit from larger scan of hyperparameter space when permissible. Nonetheless, an intuitively selected set of hyperparameters did perform well enough to remain competitive in the blind competition.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, F.; Barbacioru, C.; Wang, Y.; Nordman, E.; Lee, C.; Xu, N.; Wang, X.; Bodeau, J.; Touch, B.B.; Siddiqui, A.; et al. mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods 2009, 6, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Jaitin, D.A.; Kenigsberg, E.; Keren-Shaul, H.; Elefant, N.; Paul, F.; Zaretsky, I.; Mildner, A.; Cohen, N.; Jung, S.; Tanay, A.; et al. Massively Parallel Single-Cell RNA-Seq for Marker-Free Decomposition of Tissues into Cell Types. Science 2014, 343, 776–779. [Google Scholar] [CrossRef] [PubMed]
- Pollen, A.A.; Nowakowski, T.J.; Shuga, J.; Wang, X.; Leyrat, A.A.; Lui, J.H.; Li, N.; Szpankowski, L.; Fowler, B.; Chen, P.; et al. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nat. Biotechnol. 2014, 32, 1053–1058. [Google Scholar] [CrossRef] [PubMed]
- Lovatt, D.; Ruble, B.K.; Lee, J.; Dueck, H.; Kim, T.K.; Fisher, S.; Francis, C.; Spaethling, J.M.; Wolf, J.A.; Grady, M.S.; et al. Transcriptome in vivo analysis (TIVA) of spatially defined single cells in live tissue. Nat. Methods 2014, 11, 190–196. [Google Scholar] [CrossRef]
- Ståhl, P.L.; Salmén, F.; Vickovic, S.; Lundmark, A.; Fernández Navarro, J.; Magnusson, J.; Giacomello, S.; Asp, M.; Westholm, J.O.; Huss, M.; et al. Visualization and Analysis of Gene Expression in Tissue Sections by Spatial Tran-Scriptomics; American Association for the Advancement of Science: Washington, DC, USA, 2016; pp. 78–82. [Google Scholar]
- Rodriques, S.G.; Stickels, R.R.; Goeva, A.; Martin, C.A.; Murray, E.; Vanderburg, C.; Welch, J.; Chen, L.M.; Chen, F.; Macosko, E.Z. Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science 2019, 363, 1463–1467. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, M.; Deng, Y.; Su, G.; Guo, C.C.; Zhang, D.; Kim, D.; Bai, Z.; Xiao, Y.; Fan, R. High-Spatial-Resolution Multi-Omics Atlas Sequencing of Mouse Embryos via De-terministic Barcoding in Tissue. SSRN Electron. J. 2019. [Google Scholar] [CrossRef]
- Nitzan, M.; Karaiskos, N.; Friedman, N.; Rajewsky, N. Charting a tissue from single-cell transcriptomes. bioRxiv 2018, 456350. [Google Scholar] [CrossRef]
- Bageritz, J.; Willnow, P.; Valentini, E.; Leible, S.; Boutros, M.; Teleman, A.A. Gene expression atlas of a developing tissue by single cell expression correlation analysis. Nat. Methods 2019, 16, 750–756. [Google Scholar] [CrossRef]
- Moor, A.E.; Harnik, Y.; Ben-Moshe, S.; Massasa, E.E.; Rozenberg, M.; Eilam, R.; Halpern, K.B.; Itzkovitz, S. Spatial Reconstruction of Single Enterocytes Uncovers Broad Zonation along the Intestinal Villus Axis. Cell 2018, 175, 1156–1167.e15. [Google Scholar] [CrossRef] [PubMed]
- Achim, K.; Pettit, J.B.; Saraiva, L.; Gavriouchkina, D.; Larsson, T.; Arendt, D.; Marioni, J.C. High-throughput spatial mapping of single-cell RNA-seq data to tissue of origin. Nat. Biotechnol. 2015, 33, 503–509. [Google Scholar] [CrossRef] [PubMed]
- Halpern, K.B.; Shenhav, R.; Matcovitch-Natan, O.; Tóth, B.; Lemze, D.; Golan, M.; Massasa, E.E.; Baydatch, S.; Landen, S.; Moor, A.E.; et al. Single-cell spatial reconstruction reveals global division of labour in the mammalian liver. Nat. Cell Biol. 2017, 542, 352–356. [Google Scholar] [CrossRef] [PubMed]
- Karaiskos, N.; Wahle, P.; Alles, J.; Boltengagen, A.; Ayoub, S.; Kipar, C.; Kocks, C.; Rajewsky, N.; Zinzen, P.R. The Drosophila embryo at single-cell transcriptome resolution. Science 2017, 358, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Papalexi, E.; Mauck, W.M.; Hao, Y.; Stoeckius, M.; Smibert, P.; Satija, R. Comprehensive Integration of Single-Cell Data. Cell 2019, 177, 1888–1902.e21. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.X.Y.; Zheng, J.M.; Belgrader, T.P.; Ryvkin, P.; Bent, Z.W.; Wilson, R.; Ziraldo, S.B.; Wheeler, T.D.; McDermott, G.P.; Zhu, J.; et al. Massively parallel digital transcriptional profiling of single cells. Nat. Commun. 2017, 8, 14049. [Google Scholar] [CrossRef]
- Iacono, G.; Mereu, E.; Guillaumet-Adkins, A.; Corominas, R.; Cusco, I.; Rodríguez-Esteban, G.; Gut, M.; Pérez-Jurado, L.A.; Gut, I.; Heyn, H. bigSCale: An analytical framework for big-scale single-cell data. Genome Res. 2018, 28, 878–890. [Google Scholar] [CrossRef]
- Svensson, V.; Vento-Tormo, R.; Teichmann, S.A. Exponential scaling of single-cell RNA-seq in the past decade. Nat. Protoc. 2018, 13, 599–604. [Google Scholar] [CrossRef]
- Cao, J.; Packer, J.S.; Ramani, V.; Cusanovich, D.A.; Huynh, C.; Daza, R.; Qiu, X.; Lee, C.; Furlan, S.N.; Steemers, F.J.; et al. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 2017, 357, 661–667. [Google Scholar] [CrossRef]
- Davie, K.; Janssens, J.; Koldere, D.; De Waegeneer, M.; Pech, U.; Kreft, Ł.; Aibar, S.; Makhzami, S.; Christiaens, V.; González-Blas, C.B.; et al. A Single-Cell Transcriptome Atlas of the Aging Drosophila Brain. Cell 2018, 174, 982–998.e20. [Google Scholar] [CrossRef]
- Tabula Muris Consortium; Overall Coordination; Logistical Coordination; Organ Collection and Processing; Library Preparation and Sequencing; Computational Data Analysis; Cell Type Annotation; Writing Group; Supplemental Text Writing Group; Principal Investigators. Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature 2018, 562, 367–372. [Google Scholar] [CrossRef]
- Han, X.; Wang, R.; Zhou, Y.; Fei, L.; Sun, H.; Lai, S.; Saadatpour, A.; Zhou, Z.; Chen, H.; Ye, F.; et al. Mapping the Mouse Cell Atlas by Microwell-Seq. Cell 2018, 172, 1091–1107.e17. [Google Scholar] [CrossRef]
- Regev, A.; Teichmann, S.A.; Lander, E.S.; Amit, I.; Benoist, C.; Birney, E.; Bodenmiller, B.; Campbell, P.J.; Carninci, P.; Clatworthy, M.; et al. The Human Cell Atlas. eLife 2017, 6, e27041. [Google Scholar] [CrossRef] [PubMed]
- Stuart, T.; Satija, R. Integrative single-cell analysis. Nat. Rev. Genet. 2019, 20, 257–272. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, V.Y.; Andrews, T.S.; Hemberg, M. Challenges in unsupervised clustering of single-cell RNA-seq data. Nat. Rev. Genet. 2019, 20, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.; Zeisel, A.; Joost, S.; La Manno, G.; Zajac, P.; Kasper, M.; Lönnerberg, P.; Linnarsson, S. Quantitative single-cell RNA-seq with unique molecular identifiers. Nat. Methods 2014, 11, 163–166. [Google Scholar] [CrossRef]
- Subramanian, A.; Narayan, R.; Corsello, S.M.; Peck, D.D.; Natoli, T.E.; Lu, X.; Gould, J.; Davis, J.F.; Tubelli, A.A.; Asiedu, J.K.; et al. A Next Generation Connectivity Map: L1000 Platform and the First 1,000,000 Profiles. Cell 2017, 171, 1437–1452.e17. [Google Scholar] [CrossRef]
- Satija, R.; Farrell, J.A.; Gennert, D.; Schier, A.F.; Regev, A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 2015, 33, 495–502. [Google Scholar] [CrossRef]
- Yang, J.; Honavar, V.G. Feature Subset Selection Using a Genetic Algorithm; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1998; pp. 117–136. [Google Scholar]
- Tangherloni, A.; Spolaor, S.; Rundo, L.; Nobile, M.S.; Cazzaniga, P.; Mauri, P.; Liò, P.; Merelli, I.; Besozzi, D. GenHap: A novel computational method based on genetic algorithms for haplotype assembly. BMC Bioinform. 2019, 20, 1–14. [Google Scholar] [CrossRef]
- Rundo, L.; Tangherloni, A.; Cazzaniga, P.; Nobile, M.S.; Russo, G.; Gilardi, M.C.; Vitabile, S.; Mauri, G.; Besozzi, D.; Militello, C. A novel framework for MR image segmentation and quantification by using MedGA. Comput. Methods Programs Biomed. 2019, 176, 159–172. [Google Scholar] [CrossRef]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M.S. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. 2019, 81, 105494. [Google Scholar] [CrossRef]
- Li, L.; Weinberg, C.R.; Darden, T.A.; Pedersen, L.G. Gene selection for sample classification based on gene expression data: Study of sen-sitivity to choice of parameters of the GA/KNN method. Bioinformatics 2001, 17, 1131–1142. [Google Scholar] [CrossRef]
- Ooi, C.H.; Tan, P. Genetic algorithms applied to multi-class prediction for the analysis of gene expression data. Bioinformatics 2003, 19, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Dolled-Filhart, M.; Rydén, L.; Cregger, M.; Jirström, K.; Harigopal, M.; Camp, R.L.; Rimm, D.L. Classification of breast cancer using genetic algorithms and tissue mi-croarrays. Clin. Cancer Res. 2006, 12, 6459–6468. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.C.; Liu, R.S.; Chao, Y.T.; Chen, S.Y. Classifying subtypes of acute lymphoblastic leukemia using silhouette statistics and genetic algorithms. Gene 2013, 518, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Latkowski, T.; Osowski, S. Computerized system for recognition of autism on the basis of gene expression microarray data. Comput. Biol. Med. 2015, 56, 82–88. [Google Scholar] [CrossRef]
- Tanevski, J.; Nguyen, T.; Truong, B.; Karaiskos, N.; Ahsen, M.E.; Zhang, X.; Shu, C.; Xu, K.; Liang, X.; Hu, Y.; et al. Predicting cellular position in the Drosophila embryo from Single-Cell Tran-scriptomics data. bioRxiv 2019, 796029. [Google Scholar] [CrossRef]
- Stolovitzky, G.; Monroe, D.; Califano, A. Dialogue on Reverse-Engineering Assessment and Methods: The DREAM of High-Throughput Pathway Inference. Ann. N. Y. Acad. Sci. 2007, 1115, 1–22. [Google Scholar] [CrossRef]
- Fowlkes, C.C.; Hendriks, C.L.L.; Keränen, S.V.; Weber, G.H.; Rübel, O.; Huang, M.Y.; Chatoor, S.; DePace, A.H.; Simirenko, L.; Henriquez, C.; et al. A Quantitative Spatiotemporal Atlas of Gene Expression in the Drosophila Blastoderm. Cell 2008, 133, 364–374. [Google Scholar] [CrossRef]
- Lyne, R.; Smith, R.; Rutherford, K.M.; Wakeling, M.; Varley, A.; Guillier, F.; Janssens, H.; Ji, W.; McLaren, P.; North, P.; et al. FlyMine: An integrated database for Drosophila and Anopheles genomics. Genome Biol. 2007, 8, R129. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Gable, A.L.; Lyon, D.; Junge, A.; Wyder, S.; Huerta-Cepas, J.; Simonovic, M.; Doncheva, N.T.; Morris, J.H.; Bork, P.; et al. STRING v11: Protein–protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. 2019, 47, D607–D613. [Google Scholar] [CrossRef]
- Shannon, P.; Markiel, A.; Ozier, O.; Baliga, N.S.; Wang, J.T.; Ramage, D.; Amin, N.; Schwikowski, B.; Ideker, T. Cytoscape: A software Environment for integrated models of biomolecular in-teraction networks. Genome Res. 2003, 13, 2498–2504. [Google Scholar] [CrossRef]
- Hafemeister, C.; Satija, R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol. 2019, 20, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Liao, M.; Liu, Y.; Yuan, J.; Wen, Y.; Xu, G.; Zhao, J.; Cheng, L.; Li, J.; Wang, X.; Wang, F.; et al. Single-cell landscape of bronchoalveolar immune cells in patients with COVID-19. Nat. Med. 2020, 26, 842–844. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.V.H.; Li, X.; Truong, B.; Nguyen, T.; Liu, L.; Li, J.; Le, T. The winning methods for predicting cellular position in the DREAM single-cell transcriptomics challenge. Brief. Bioinform. 2020. [Google Scholar] [CrossRef] [PubMed]

| n = 60 | aay, Ama, Ance, Blimp-1, bmm, brk, Btk29A, bun, cad, CG10479, CG11208, CG14427, CG43394, CG8147, croc, Cyp310a1, D, dan, danr, Dfd, Doc2, edl, erm, eve, fj, fkh, ftz, gk, gt, h, hb, Ilp4, ImpE2, ImpL2, kni, Kr, lok, Mes2, MESR3, mfas, NetA, noc, nub, numb, oc, odd, prd, pxb, rau, rho, run, sna, tkv, tll, toc, Traf4, trn, tsh, twi, zen |
| n = 40 | Ama, Antp, Blimp-1, brk, Btk29A, CG10479, CG43394, CG8147, danr, disco, Doc3, edl, eve, fkh, ftz, gt, h, Ilp4, ImpE2, ImpL2, ken, kni, lok, Mdr49, MESR3, Nek2, noc, nub, numb, oc, pxb, rau, rho, run, sna, toc, Traf4, trn, tsh, twi |
| n = 20 | brk, CG43394, CG8147, dan, Doc2, h, Ilp4, ImpL2, kni, Kr, Mdr49, MESR3, Nek2, noc, oc, odd, rho, sna, trn, tsh |
| Sub_Challenge | Subset_Size | Score 1 | Score 2 | Score 3 | Rank |
|---|---|---|---|---|---|
| 1 | 60 | 0.6991 ± 0.0057 | 0.9997 ± 0.0057 | 0.6142 ± 0.0057 | 8 |
| 2 | 40 | 0.6532 ± 0.0064 | 0.9815 ± 0.0064 | 0.6572 ± 0.0064 | 7 |
| 3 | 20 | 0.6137 ± 0.0083 | 0.7943 ± 0.0083 | 0.7646 ± 0.0083 | 12 |
| Subset | Name of the Team | S1 | S2 | S3 | Rank |
|---|---|---|---|---|---|
| 60 | GA + TN | (0.7929) | (3.3008) | 0.6141382 | - |
| Thin Nguyen | ((0.776)) | ((3.0637)) | 0.6178 | 1 | |
| WhatATeam | 0.7002 | 1.5327 | (((0.6268))) | 2 | |
| NAD | 0.7504 | 1.6614 | 0.5916 | 3 | |
| Christoph Hafemeister | 0.667 | 1.0624 | (0.6506) | 4 | |
| zho_team | (((0.7663))) | (((2.5973))) | 0.5635 | 5 | |
| MLB | 0.6826 | 1.0245 | 0.6469 | 5 | |
| OmicsEngineering | 0.6738 | 1.0188 | 0.6258 | 6 | |
| Challengers18 | 0.661 | 1.4522 | 0.6122 | 10 | |
| DeepCMC | 0.6668 | 1.0194 | 0.6271 | 10 | |
| BCBU | 0.6506 | 1.2276 | 0.6037 | 13 | |
| 40 | GA + TN | (0.7442) | (2.3817) | 0.6570 | - |
| WhatATeam | (((0.6869))) | 1.164 | 0.6672 | 1 | |
| OmicsEngineering | 0.6511 | 0.9991 | ((0.6899)) | 2 | |
| NAD | ((0.7367)) | (((1.4341))) | 0.5968 | 3 | |
| Christoph Hafemeister | 0.6587 | 0.976 | 0.6837 | 4 | |
| Challengers18 | 0.6552 | 1.3176 | 0.6538 | 4 | |
| MLB | 0.647 | 0.909 | (0.7076) | 5 | |
| DeepCMC | 0.6524 | 0.9846 | (((0.6846))) | 6 | |
| zho_team | 0.6657 | ((1.6043)) | 0.5353 | 9 | |
| BCBU | 0.625 | 1.1918 | 0.6241 | 11 | |
| Thin Nguyen | 0.6265 | 1.258 | 0.5836 | 12 | |
| 20 | GA + TN | ((0.6923)) | (1.4546) | 0.7646 | - |
| OmicsEngineering | 0.6554 | 0.9534 | (((0.7934))) | 1 | |
| NAD | (0.7217) | ((1.2445)) | 0.6534 | 2 | |
| Challengers18 | 0.662 | 1.0166 | 0.7928 | 2 | |
| WhatATeam | 0.6504 | 0.9327 | 0.7783 | 3 | |
| DeepCMC | (((0.6621))) | 0.8411 | (0.818) | 4 | |
| BCBU | 0.6406 | (((1.1456))) | 0.6393 | 5 | |
| MLB | 0.642 | 0.7579 | ((0.8156)) | 7 | |
| Thin Nguyen | 0.6462 | 0.8791 | 0.6302 | 9 | |
| Christoph Hafemeister | 0.6017 | 0.9056 | 0.6341 | 14 | |
| Zho team | 0.5234 | 0.8545 | 0.4546 | 18 |
| Sub_Challenge | Subset_Size | Method | Score 1 | Score 2 | Score 3 |
|---|---|---|---|---|---|
| 1 | 60 | GA | 0.8839 ± 0.0056 | 0.9994 ± 0.0191 | 0.6153 ± 0.0042 |
| 60 | PPI | 0.8040 ± 0.0075 | 0.9274 ± 0.0275 | 0.6003 ± 0.0050 | |
| 60 | STB | 0.7859 ± 0.0076 | 0.8893 ± 0.0188 | 0.5499 ± 0.0043 | |
| 60 | VAR | 0.8363 ± 0.0074 | 0.9403 ± 0.0319 | 0.6328 ± 0.0047 | |
| 2 | 40 | GA | 0.8281 ± 0.0065 | 0.9805 ± 0.0247 | 0.6578 ± 0.0037 |
| 40 | PPI | 0.7961 ± 0.0068 | 0.8766 ± 0.0259 | 0.6747 ± 0.0058 | |
| 40 | STB | 0.7653 ± 0.0088 | 0.7480 ± 0.0215 | 0.5915 ± 0.0042 | |
| 40 | VAR | 0.7742 ± 0.0082 | 0.6544 ± 0.0206 | 0.6569 ± 0.0066 | |
| 3 | 20 | GA | 0.7681 ± 0.0088 | 0.7935 ± 0.0245 | 0.7647 ± 0.0040 |
| 20 | PPI | 0.7395 ± 0.0122 | 0.6867 ± 0.0299 | 0.7424 ± 0.0065 | |
| 20 | STB | 0.6738 ± 0.0133 | 0.5335 ± 0.0211 | 0.6105 ± 0.0060 | |
| 20 | VAR | 0.6897 ± 0.0114 | 0.5658 ± 0.0305 | 0.7528 ± 0.0079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Verma, A.K.; Ahmad, S. Feature Selection for Topological Proximity Prediction of Single-Cell Transcriptomic Profiles in Drosophila Embryo Using Genetic Algorithm. Genes 2021, 12, 28. https://doi.org/10.3390/genes12010028
Gupta S, Verma AK, Ahmad S. Feature Selection for Topological Proximity Prediction of Single-Cell Transcriptomic Profiles in Drosophila Embryo Using Genetic Algorithm. Genes. 2021; 12(1):28. https://doi.org/10.3390/genes12010028
Chicago/Turabian StyleGupta, Shruti, Ajay Kumar Verma, and Shandar Ahmad. 2021. "Feature Selection for Topological Proximity Prediction of Single-Cell Transcriptomic Profiles in Drosophila Embryo Using Genetic Algorithm" Genes 12, no. 1: 28. https://doi.org/10.3390/genes12010028
APA StyleGupta, S., Verma, A. K., & Ahmad, S. (2021). Feature Selection for Topological Proximity Prediction of Single-Cell Transcriptomic Profiles in Drosophila Embryo Using Genetic Algorithm. Genes, 12(1), 28. https://doi.org/10.3390/genes12010028





