Feature Selection for High-Dimensional and Imbalanced Biomedical Data Based on Robust Correlation Based Redundancy and Binary Grasshopper Optimization Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Filtering Methods
2.1.1. ReliefF
2.1.2. Chi-Square
2.1.3. Fisher Score
2.2. Grasshopper Optimisation Algorithm (GOA)
2.2.1. Coefficient Parameter
| Algorithm 1 The main steps of the GOA algorithm |
| Initializes the swarm |
| Initialize , and maximum number of iterations |
| Calculate the fitness of each search agent |
| T = the best search agent |
| while () |
| Update using Equation (11) |
| For each search agent |
| Normalize the distance between grasshopper in [1,4] |
| Update the position of current search agent by the Equation (10) |
| Bring the current search agent back if it goes outside the boundaries |
| End for |
| update if a better solution is achieved |
| solution |
| End while |
| Return |
2.2.2. Binary GOA
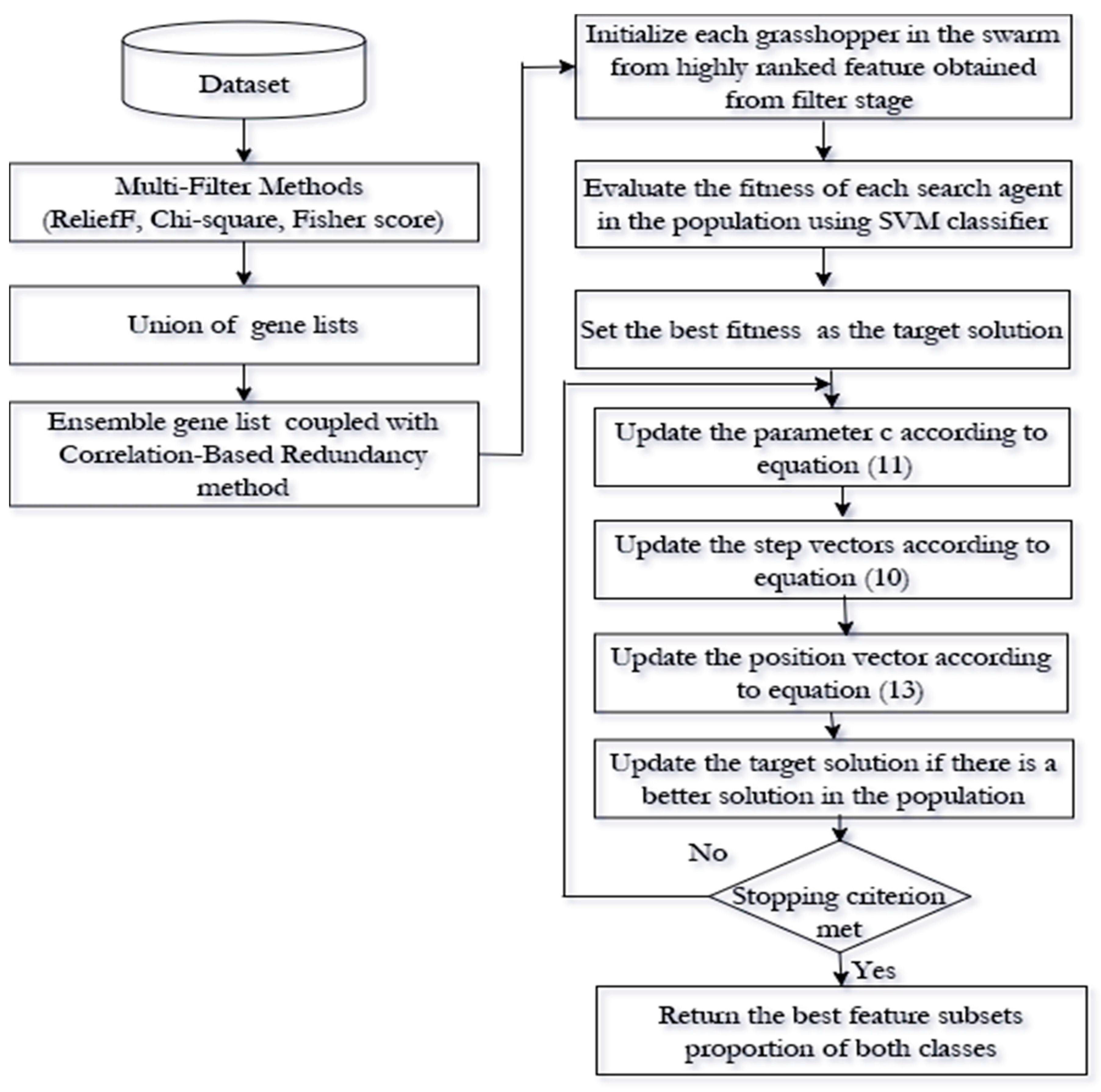
3. The Proposed Method for High Dimensional and Imbalanced Data Using Feature Selection Approach
3.1. Stage I: Filter Approach
3.1.1. Symmetric Uncertainty
3.1.2. Combination of Multi-Filter Approaches Phase
| Algorithm 2 |
| 1: For each feature in the training set D{ , ,..., } and class |
| 2: Initialize parameters, = , = , |
| 3: number of selected filters |
| 4: selected filters |
| Ensemble of filters |
| 5: for |
| 6: for |
| Employ to calculate the statistical scores of each gene |
| End of for |
| 7: Rank genes based on its scores in descending order and get a new gene list , |
| End of for |
| 8: produce a new ranking list by combining filter methods , using union operator, in order to consolidate the overlapping genes. |
3.1.3. Correlation-Based Redundancy Method
| Algorithm 3 |
| 1: Initialize parameter = , |
| 2: For each candidate feature in , calculate between feature-feature and feature-class to eliminate redundant features using AMb. |
| 3: For tofirst featuresecond feature |
| 4: calculateand |
| 5: &then |
| 6: remove i.e.,. |
| 7: else |
| 8: Insert into output selected features list |
| 9: end |
| 10: End of for |
| 11: Return: The optimal subset of non-redundant genes S. |
3.1.4. Hybrid of Multi-Filter Approaches and Correlation-Based Redundancy Analysis
- (1)
- Redundancy: A feature is redundant if it has approximate Markov Blanket ().
- (2)
- Irrelevance: A feature is irrelevant if it is ranking score is below the top ranking score in all the filter methods.
- (3)
- Relevance: A feature is relevant if it is ranking score is amongst the top ranking-score in at least one filter method.
- (4)
- Strong relevance: A feature is strongly relevant if it is the Markov Blanket of the target (class).
| Algorithm 4 Hybrid Multi-filter approaches and Correlation-Based Redundancy |
| Input: DA dataset with m features, number of filter h, number of union filtered gene n, number of genes subset (, classifier C |
| Output: optimal feature subset |
| for |
| for |
| employ filter to compute the statistical scores of each gene |
| end for |
| select the top-ranking score in each list and get a new gene list , |
| end for |
| produce a new ranking list by aggregating the output filter methods , using union the operator. |
| R/* the union of the list genes */ |
| for each candidate feature in , compute the interaction between feature-feature and feature-class, to discard redundant features based on Correlation-Based Redundancy using . |
| Initialize = , |
| For |
| first feature, second feature |
| ifthen |
| remove . |
| else |
| insert into output selected features list |
| end if |
| End of For |
| Return optimal feature subsets |
3.2. Stage II: Wrapper Approach
3.2.1. Solution Representation
3.2.2. Fitness Function
4. Experimental Results and Discussion
4.1. Dataset
4.2. Effect of the Proposed Filtering rCBR Method and Contribution of the Individual Filter Method
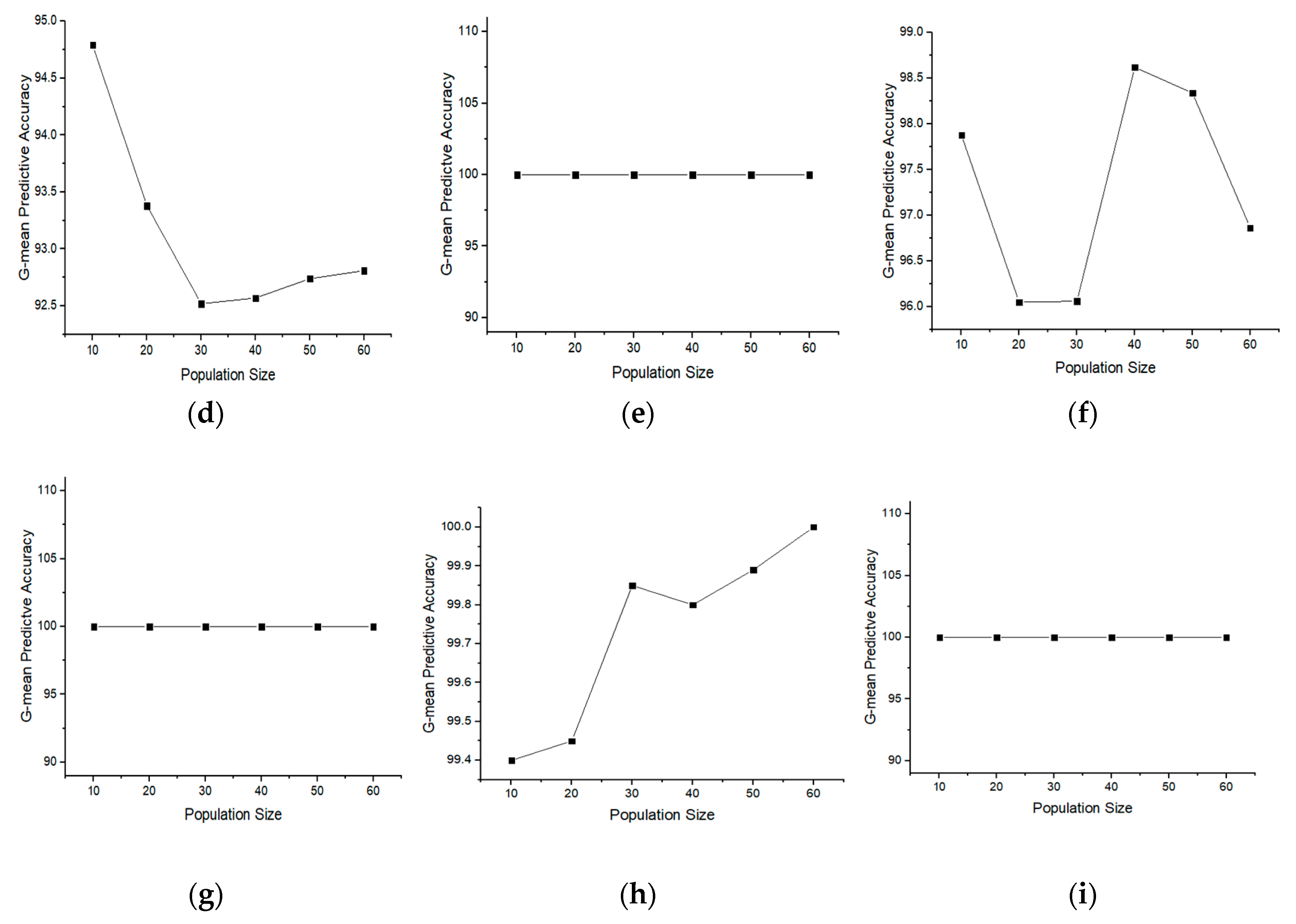
4.3. Effect on the Performance of BGOA
4.4. Statistical Analysis
4.5. Execution Time
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, H.; Ni, J. An improved ensemble learning method for classifying high-dimensional and imbalanced biomedicine data. IEEE/ACM Trans. Comput. Biol. Bioinform. (TCBB) 2014, 11, 657–666. [Google Scholar] [CrossRef] [PubMed]
- Van Hulse, J.; Khoshgoftaar, T.M.; Napolitano, A.; Wald, R. Feature selection with high-dimensional imbalanced data. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops, Miami, FL, USA, 6 December 2009; IEEE Computer Society: Washington, DC, USA; pp. 507–514. [Google Scholar]
- Silva, D.A.; Souza, L.C.; Motta, G.H. An instance selection method for large datasets based on markov geometric diffusion. Data Knowl. Eng. 2016, 101, 24–41. [Google Scholar] [CrossRef]
- Moayedikia, A.; Ong, K.-L.; Boo, Y.L.; Yeoh, W.G.; Jensen, R. Feature selection for high dimensional imbalanced class data using harmony search. Eng. Appl. Artif. Intell. 2017, 57, 38–49. [Google Scholar] [CrossRef]
- Chawla, N.; Japkowicz, N.; Kolcz, A. Workshop learning from imbalanced data sets II. In Proceedings of the International Conference on Machine Learning, ICML’2003 Workshop, Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Wang, S.; Minku, L.L.; Chawla, N.; Yao, X. Proceedings of the IJCAI 2017 Workshop on Learning in the Presence of Class Imbalance and Concept Drift (LPCICD’17), Melbourne, Australia, 20 August 2017. arXiv 2017, arXiv:1707.09425. [Google Scholar]
- Brefeld, U.; Curry, E.; Daly, E.; MacNamee, B.; Marascu, A.; Pinelli, F.; Berlingerio, M.; Hurley, N. Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2018, Dublin, Ireland, September 10–14, 2018, Proceedings; Springer: Berlin/Heidelberg, Germany, 2018; Volume 11053. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.-Y.; Mao, B.-H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Yen, S.-J.; Lee, Y.-S. Cluster-based under-sampling approaches for imbalanced data distributions. Expert Syst. Appl. 2009, 36, 5718–5727. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.; Li, S.A. Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks, 2008 (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008. [Google Scholar]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving prediction of the minority class in boosting. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Cavtat-Dubrovnik, Croatia, 22–26 September 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 107–119. [Google Scholar]
- Tao, D.; Tang, X.; Li, X.; Wu, X. Asymmetric bagging and random subspace for support vector machines-based relevance feedback in image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1088–1099. [Google Scholar]
- Hanifah, F.S.; Wijayanto, H.; Kurnia, A. Smotebagging algorithm for imbalanced dataset in logistic regression analysis (case: Credit of bank x). Appl. Math. Sci. 2015, 9, 6857–6865. [Google Scholar]
- Li, G.-Z.; Meng, H.-H.; Lu, W.-C.; Yang, J.Y.; Yang, M.Q. Asymmetric bagging and feature selection for activities prediction of drug molecules. BMC Bioinform. 2008, 9, S7. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Liu, X.-Y. Training cost-sensitive neural networks with methods addressing the class imbalance problem. IEEE Trans. Knowl. Data Eng. 2006, 18, 63–77. [Google Scholar] [CrossRef]
- Elkan, C. The foundations of cost-sensitive learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; Lawrence Erlbaum Associates Ltd.: Mahwah, NJ, USA, 2001; Volume 17. No. 1. [Google Scholar]
- Ling, C.; Sheng, V. Cost-sensitive learning and the class imbalance problem. In Encyclopedia of Machine Learning; Springer: Berlin/Heidelberg, Germany, 2011; Volume 24. [Google Scholar]
- Hempstalk, K.; Frank, E.; Witten, I.H. One-class classification by combining density and class probability estimation. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Antwerp, Belgium, 14–18 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 505–519. [Google Scholar]
- Shin, H.J.; Eom, D.-H.; Kim, S.-S. One-class support vector machines—an application in machine fault detection and classification. Comput. Ind. Eng. 2005, 48, 395–408. [Google Scholar] [CrossRef]
- Seo, K.-K. An application of one-class support vector machines in content-based image retrieval. Expert Syst. Appl. 2007, 33, 491–498. [Google Scholar] [CrossRef]
- Ertekin, S.; Huang, J.; Bottou, L.; Giles, L. Learning on the border: Active learning in imbalanced data classification. In Proceedings of the Sixteenth ACM Conference on Information and Knowledge Management, Lisbon, Portugal, 6–10 November 2007; ACM: New York, NY, USA, 2007; pp. 127–136. [Google Scholar]
- Ertekin, S.; Huang, J.; Giles, C.L. Active learning for class imbalance problem. Proc. SIGIR 2007, 7, 823–824. [Google Scholar]
- Attenberg, J.; Ertekin, S. Class imbalance and active learning. In Imbalanced Learning: Foundations, Algorithms, and Applications; He, H., Ma, Y., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 101–149. [Google Scholar]
- Van Hulse, J.; Khoshgoftaar, T. Knowledge discovery from imbalanced and noisy data. Data Knowl. Eng. 2009, 68, 1513–1542. [Google Scholar] [CrossRef]
- Maldonado, S.; Weber, R.; Famili, F. Feature selection for high-dimensional class-imbalanced data sets using Support Vector Machines. Inf. Sci. 2014, 286, 228–246. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Kanellopoulos, D.; Pintelas, P. Handling imbalanced datasets: A review. GESTS Int. Trans. Comput. Sci. Eng. 2006, 30, 25–36. [Google Scholar]
- Basgall, M.J.; Hasperué, W.; Naiouf, M.; Fernández, A.; Herrera, F. SMOTE-BD: An Exact and Scalable Oversampling Method for Imbalanced Classification in Big Data. In Proceedings of the VI Jornadas de Cloud Computing & Big Data (JCC&BD), La Plata, Argentina, 25–29 June 2018. [Google Scholar]
- Thong, N.T. Intuitionistic fuzzy recommender systems: An effective tool for medical diagnosis. Knowl. Based Syst. 2015, 74, 133–150. [Google Scholar]
- Lusa, L. Class prediction for high-dimensional class-imbalanced data. BMC Bioinform. 2010, 11, 523. [Google Scholar]
- Lin, W.-J.; Chen, J.J. Class-imbalanced classifiers for high-dimensional data. Brief. Bioinform. 2012, 14, 13–26. [Google Scholar] [CrossRef]
- Wasikowski, M.; Chen, X.-w. Combating the small sample class imbalance problem using feature selection. IEEE Trans. Knowl. Data Eng. 2009, 22, 1388–1400. [Google Scholar] [CrossRef]
- Tomczak, A.; Mortensen, J.M.; Winnenburg, R.; Liu, C.; Alessi, D.T.; Swamy, V.; Vallania, F.; Lofgren, S.; Haynes, W.; Shah, N.H. Interpretation of biological experiments changes with evolution of the Gene Ontology and its annotations. Sci. Rep. 2018, 8, 5115. [Google Scholar] [CrossRef] [PubMed]
- Koprinska, I.; Rana, M.; Agelidis, V.G. Correlation and instance based feature selection for electricity load forecasting. Knowl. Based Syst. 2015, 82, 29–40. [Google Scholar] [CrossRef]
- Dittman, D.J.; Khoshgoftaar, T.M.; Napolitano, A. Selecting the appropriate data sampling approach for imbalanced and high-dimensional bioinformatics datasets. In Proceedings of the 2014 IEEE International Conference on Bioinformatics and Bioengineering, Boca Raton, FL, USA, 10–12 November 2014; pp. 304–310. [Google Scholar]
- Shanab, A.A.; Khoshgoftaar, T. Is Gene Selection Enough for Imbalanced Bioinformatics Data? In Proceedings of the 2018 IEEE International Conference on Information Reuse and Integration (IRI), Salt Lake City, UT, USA, 7–9 July 2018; pp. 346–355. [Google Scholar]
- Maldonado, S.; López, J. Dealing with high-dimensional class-imbalanced datasets: Embedded feature selection for SVM classification. Appl. Soft Comput. 2018, 67, 94–105. [Google Scholar] [CrossRef]
- Braytee, A.; Liu, W.; Kennedy, P.J. Supervised context-aware non-negative matrix factorization to handle high-dimensional high-correlated imbalanced biomedical data. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 4512–4519. [Google Scholar]
- Yang, P.; Liu, W.; Zhou, B.B.; Chawla, S.; Zomaya, A.Y. Ensemble-based wrapper methods for feature selection and class imbalance learning. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 544–555. [Google Scholar]
- Yang, J.; Zhou, J.; Zhu, Z.; Ma, X.; Ji, Z. Iterative ensemble feature selection for multiclass classification of imbalanced microarray data. J. Biol. Res. Thessalon. 2016, 23, 13. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Maldonado, S.; López, J. Imbalanced data classification using second-order cone programming support vector machines. Pattern Recognit. 2014, 47, 2070–2079. [Google Scholar] [CrossRef]
- Yin, L.; Ge, Y.; Xiao, K.; Wang, X.; Quan, X. Feature selection for high-dimensional imbalanced data. Neurocomputing 2013, 105, 3–11. [Google Scholar] [CrossRef]
- Alibeigi, M.; Hashemi, S.; Hamzeh, A. DBFS: An effective Density Based Feature Selection scheme for small sample size and high dimensional imbalanced data sets. Data Knowl. Eng. 2012, 81, 67–103. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, G.; Zhou, Y.; Yao, L.; Jiang, Z.L.; Liao, Q.; Wang, X. Feature selection for high dimensional imbalanced class data based on F-measure optimization. In Proceedings of the 2017 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Shenzhen, China, 15–17 December 2017; pp. 278–283. [Google Scholar]
- Viegas, F.; Rocha, L.; Gonçalves, M.; Mourão, F.; Sá, G.; Salles, T.; Andrade, G.; Sandin, I. A genetic programming approach for feature selection in highly dimensional skewed data. Neurocomputing 2018, 273, 554–569. [Google Scholar] [CrossRef]
- Yu, H.; Hong, S.; Yang, X.; Ni, J.; Dan, Y.; Qin, B. Recognition of multiple imbalanced cancer types based on DNA microarray data using ensemble classifiers. BioMed Res. Int. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, D.; Cai, Y.; Wang, R.; Chen, F. A hybrid method based on ensemble WELM for handling multi class imbalance in cancer microarray data. Neurocomputing 2017, 266, 641–650. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The feature selection problem: Traditional methods and a new algorithm. Proc. AAAI 1992, 2, 129–134. [Google Scholar]
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef] [PubMed]
- Su, C.-T.; Hsu, J.-H. An extended chi2 algorithm for discretization of real value attributes. IEEE Trans. Knowl. Data Eng. 2005, 17, 437–441. [Google Scholar]
- Jin, X.; Xu, A.; Bie, R.; Guo, P. Machine learning techniques and chi-square feature selection for cancer classification using SAGE gene expression profiles. In Proceedings of the International Workshop on Data Mining for Biomedical Applications, Singapore, 9 April 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 106–115. [Google Scholar]
- Gu, Q.; Li, Z.; Han, J. Generalized Fisher Score for Feature Selection; Cornell University: Ithaca, NY, USA, 2012; arXiv preprint arXiv:1202.3725. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Trigg, L.E.; Hall, M.A.; Holmes, G.; Cunningham, S.J. Weka: Practical Machine Learning Tools and Techniques with Java Implementations; University of Waikato: Hamilton, New Zealand, 1999. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Piao, Y.; Piao, M.; Park, K.; Ryu, K.H. An ensemble correlation-based gene selection algorithm for cancer classification with gene expression data. Bioinformatics 2012, 28, 3306–3315. [Google Scholar] [CrossRef]
- Kannan, S.S.; Ramaraj, N. A novel hybrid feature selection via Symmetrical Uncertainty ranking based local memetic search algorithm. Knowl. Based Syst. 2010, 23, 580–585. [Google Scholar] [CrossRef]
- Koller, D.; Sahami, M. Toward Optimal Feature Selection; Stanford InfoLab: Stanford, CA, USA, 1996. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Duval, B.; Hao, J.-K.; Hernandez Hernandez, J.C. A memetic algorithm for gene selection and molecular classification of cancer. In Proceedings of the 11th Annual conference on Genetic and evolutionary computation, Montreal, QC, Canada, 8–12 July 2009; ACM: New York, NY, USA, 2009; pp. 201–208. [Google Scholar]
- Amaldi, E.; Kann, V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theor. Comput. Sci. 1998, 209, 237–260. [Google Scholar] [CrossRef]
- Alomari, O.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A. A novel gene selection method using modified MRMR and hybrid bat-inspired algorithm with β-hill climbing. Appl. Intell. 2018, 48, 4429–4447. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2018. [Google Scholar] [CrossRef]
- Gu, Q.; Zhu, L.; Cai, Z. Evaluation measures of the classification performance of imbalanced data sets. In Proceedings of the International symposium on intelligence computation and applications, Huangshi, China, 23–25 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 461–471. [Google Scholar]
- Chan, P.K.; Stolfo, S.J. Toward Scalable Learning with Non-Uniform Class and Cost Distributions: A Case Study in Credit Card Fraud Detection. Proc. KDD 1998, 1998, 164–168. [Google Scholar]
- Lu, J.Z. The elements of statistical learning: Data mining, inference, and prediction. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2010, 173, 693–694. [Google Scholar] [CrossRef]
- Butler-Yeoman, T.; Xue, B.; Zhang, M. Particle swarm optimisation for feature selection: A hybrid filter-wrapper approach. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 2428–2435. [Google Scholar]
- Mathworks. Global Optimization Toolbox: User’s Guide (r2019b); Mathworks: Natick, MA, USA, 2019. [Google Scholar]
- Li, J.; Liu, H. Kent Ridge Bio-Medical Data Set Repository. Institute for Infocomm Research. 2002. Available online: http://sdmc.lit.org.sg/GEDatasets/Datasets.html (accessed on 11 July 2019).
- Li, T.; Zhang, C.; Ogihara, M. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics 2004, 20, 2429–2437. [Google Scholar] [CrossRef]
- Statnikov, A.; Tsamardinos, I.; Dosbayev, Y.; Aliferis, C.F. GEMS: A system for automated cancer diagnosis and biomarker discovery from microarray gene expression data. Int. J. Med. Inform. 2005, 74, 491–503. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Chawla, N.V.; Japkowicz, N.; Kotcz, A. Special issue on learning from imbalanced data sets. ACM Sigkdd Explor. Newsl. 2004, 6, 1–6. [Google Scholar] [CrossRef]
- Deepa, T.; Punithavalli, M. An E-SMOTE technique for feature selection in high-dimensional imbalanced dataset. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; pp. 322–324. [Google Scholar]
- Hou, W.; Wei, Y.; Jin, Y.; Zhu, C. Deep features based on a DCNN model for classifying imbalanced weld flaw types. Measurement 2019, 131, 482–489. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Imbalanced Classification with Multiple Classes. In Learning from Imbalanced Data Sets; Springer: Berlin/Heidelberg, Germany, 2018; pp. 197–226. [Google Scholar]
- Feng, W.; Huang, W.; Ren, J. Class imbalance ensemble learning based on the margin theory. Appl. Sci. 2018, 8, 815. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Multiclass imbalance problems: Analysis and potential solutions. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Rifkin, R.; Klautau, A. In defense of one-vs-all classification. J. Mach. Learn. Res. 2004, 5, 101–141. [Google Scholar]
- Sáez, J.A.; Galar, M.; Luengo, J.; Herrera, F. Analyzing the presence of noise in multi-class problems: Alleviating its influence with the one-vs-one decomposition. Knowl. Inf. Syst. 2014, 38, 179–206. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Classification by pairwise coupling. In Proceedings of the Advances in Neural Information Processing Systems; Cornell University: Ithaca, NY, USA, 1998; pp. 507–513. [Google Scholar]
- Galar, M.; Fernández, A.; Barrenechea, E.; Bustince, H.; Herrera, F. An overview of ensemble methods for binary classifiers in multi-class problems: Experimental study on one-vs-one and one-vs-all schemes. Pattern Recognit. 2011, 44, 1761–1776. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Bakiri, G. Solving multiclass learning problems via error-correcting output codes. J. Artif. Intell. Res. 1994, 2, 263–286. [Google Scholar] [CrossRef]
- Kijsirikul, B.; Ussivakul, N. Multiclass support vector machines using adaptive directed acyclic graph. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN’02 (Cat. No. 02CH37290), Honolulu, HI, USA, 12–17 May 2002; pp. 980–985. [Google Scholar]
- Statnikov, A.; Aliferis, C.F.; Tsamardinos, I.; Hardin, D.; Levy, S. A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics 2004, 21, 631–643. [Google Scholar] [CrossRef]

| Predicted Positive Class 1 | Predictive Negative Class 2 | |
|---|---|---|
| Actual positive class | TP (True Positive) | FN (False Negative) |
| Actual negative class | FP (False Positive) | TN (True Negative) |
| Data Sets | #Features | #Samples | #Classes | IR |
|---|---|---|---|---|
| Colon | 2000 | 62 | 2 | 1.82 |
| DLBCL | 7129 | 59 | 2 | 1.04 |
| CNS | 7129 | 60 | 2 | 1.86 |
| Leukaemia | 7129 | 72 | 2 | 1.88 |
| Breast | 24482 | 97 | 2 | 1.11 |
| CAR | 9182 | 174 | 2 | 14.82 |
| LUNG | 12534 | 181 | 2 | 4.84 |
| GLIOMA | 4433 | 50 | 2 | 2.43 |
| SRBCT | 2308 | 83 | 2 | 6.55 |
| Brain_Tumor1 | 5920 | 90 | 5 | 15.00 |
| Brain_Tumor2 | 10367 | 50 | 4 | 2.14 |
| SRBCT_4 | 2308 | 83 | 4 | 2.64 |
| LUNG Cancer | 12601 | 203 | 5 | 23.17 |
| Dataset | Measures | ReliefF | Fisher Score | Chi Square | rCBR |
|---|---|---|---|---|---|
| Breast | G-mean | 66.9 | 67.2 | 61.3 | 66.7 |
| AUC | 66.7 | 67.3 | 61.5 | 67.4 | |
| Sens | 61.6 | 68.1 | 59.7 | 65.2 | |
| Spec | 71.8 | 66.4 | 63.4 | 69.3 | |
| Colon | G-mean | 80.5 | 82.1 | 68.1 | 83.9 |
| AUC | 81.1 | 82.9 | 69.4 | 84.9 | |
| Sens | 80.4 | 85.1 | 70.9 | 97.1 | |
| Spec | 81.6 | 80.7 | 68.0 | 72.6 | |
| AUC | 30.8 | 73.2 | 71.5 | 83.9 | |
| CAR | G-mean | 30.7 | 67.7 | 50.9 | 73.5 |
| Sens | 30.7 | 47.1 | 46.6 | 70.0 | |
| Spec | 95.9 | 99.4 | 96.4 | 97.6 | |
| CNS | AUC | 77.1 | 74.2 | 66.4 | 85.6 |
| G-mean | 76.4 | 71.1 | 65.6 | 85.1 | |
| Sens | 78.3 | 55.1 | 54.0 | 83.8 | |
| Spec | 75.9 | 93.3 | 79.7 | 88.1 | |
| DLBCL | AUC | 98.0 | 96.7 | 86.0 | 98.0 |
| G-mean | 97.9 | 96.5 | 85.1 | 97.9 | |
| Sens | 96.0 | 93.3 | 83.4 | 96.0 | |
| Spec | 100 | 100 | 66.7 | 100 | |
| AUC | 89.7 | 97.2 | 87.6 | 99.8 | |
| Leukemia | G-mean | 89.1 | 97.0 | 86.9 | 99.0 |
| Sens | 100 | 100 | 77.6 | 100 | |
| Spec | 79.6 | 94.4 | 97.5 | 98.8 | |
| Lung | AUC | 97.8 | 99.0 | 94.9 | 97.3 |
| G-mean | 97.8 | 99.0 | 94.7 | 97.2 | |
| Sens | 95.6 | 98.0 | 89.8 | 94.5 | |
| Spec | 100 | 100 | 100 | 100 | |
| Glioma | AUC | 30.8 | 81.7 | 30.4 | 95.0 |
| G-mean | 30.9 | 81.7 | 30.9 | 95.0 | |
| Sens | 30.7 | 63.3 | 30.7 | 90.0 | |
| Spec | 89.3 | 100 | 86.1 | 100 | |
| SRBCT | AUC | 98.7 | 96.7 | 90.8 | 100 |
| G-mean | 98.6 | 96.3 | 89.9 | 100 | |
| Sens | 100 | 93.3 | 81.7 | 100 | |
| Spec | 97.4 | 100 | 100 | 100 | |
| Brain Tumour1 | AUC | 89.6 | 85.9 | 74.00 | 86.2 |
| G-mean | 88.9 | 85.1 | 72.9 | 86.2 | |
| Sens | 100 | 83.3 | 70.0 | 90.0 | |
| Spec | 79.1 | 88.5 | 78.0 | 82.4 |
| Data Sets | d | rCBR-BGOA | SYMON | SSVM-FS | FRHS | SVM-RFE | SVM-BFE | D-HELL | SMOTE-RLF | SMOTE-PCA |
|---|---|---|---|---|---|---|---|---|---|---|
| BREAST | F/5 | 92.8 | 62.6 | - | - | 56.0 | 66.4 | 62.6 | 52.4 | 52.4 |
| 2F/5 | 91.8 | 62.6 | - | - | 62.6 | 58.0 | 62.6 | 58.5 | 52.4 | |
| 3F/5 | 90.5 | 62.6 | - | - | 62.6 | 52.0 | 66.4 | 52.4 | 52.4 | |
| CAR | F/5 | 97.1 | 93.5 | 96.4 | 100 | 90.5 | 95.3 | 88.7 | 98.5 | 90.5 |
| 2F/5 | 97.4 | 93.5 | 98.2 | 100 | 92.4 | 93.6 | 90.5 | 95.3 | 90.5 | |
| 3F/5 | 97.4 | 93.5 | 98.2 | 96.5 | 92.4 | 92.4 | 88.7 | 95.3 | 90.5 | |
| CNS | F/5 | 95.2 | 79.0 | - | - | 74.5 | 74.5 | 70.7 | 57.7 | 62.4 |
| 2F/5 | 94.1 | 79.0 | - | - | 74.5 | 69.7 | 74.5 | 66.7 | 74.5 | |
| 3F/5 | 94.2 | 79.0 | - | - | 74.5 | 74.5 | 74.5 | 74.5 | 74.5 | |
| Colon | F/5 | 94.6 | 67.4 | 78.2 | 74.6 | 60.0 | 56.0 | 67.0 | 60.3 | 58.5 |
| 2F/5 | 93.1 | 71.5 | 71.4 | 74.6 | 60.0 | 60.0 | 60.0 | 60.3 | 63.0 | |
| 3F/5 | 93.1 | 67.4 | 71.4 | 74.6 | 56.0 | 56.0 | 64.0 | 60.3 | 63.0 | |
| DLBCL | F/5 | 100 | 29.6 | 54.3 | 76.2 | 25.0 | 25.0 | 22.3 | 27.4 | 38.7 |
| 2F/5 | 100 | 29.6 | 58.8 | 76.2 | 27.3 | 25.0 | 25.0 | 27.4 | 54.7 | |
| 3F/5 | 100 | 29.6 | 62.6 | 78.4 | 27.3 | 25.0 | 25.0 | 2.4 | 29.6 | |
| Leukemia | F/5 | 99.4 | 100 | - | - | 31.6 | 31.6 | 50.0 | 0.7 | 0.7 |
| 2F/5 | 99.7 | 100 | - | - | 31.6 | 31.6 | 83.6 | 0.7 | 0.7 | |
| 3F/5 | 99.7 | 100 | - | - | 31.6 | 31.6 | 44.7 | 0.7 | 0.7 | |
| LUNG | F/5 | 100 | 100 | - | - | 97.3 | 100 | 100 | 96.8 | 96.8 |
| 2F/5 | 100 | 100 | - | - | 97.3 | 100 | 100 | 96.8 | 96.8 | |
| 3F/5 | 100 | 100 | - | - | 97.3 | 100 | 100 | 96.8 | 96.8 | |
| GLIOMA | F/5 | 96.6 | 88.7 | 85.6 | 91.5 | 75.4 | 92.6 | 72.6 | 82.5 | 84.2 |
| 2F/5 | 96.5 | 85.4 | 83.4 | 92.8 | 73.8 | 90.2 | 80.6 | 82.5 | 84.2 | |
| 3F/5 | 97.3 | 81.3 | 79.3 | 89.6 | 73.2 | 86.7 | 82.6 | 79.4 | 84.2 |
| Data Sets | d | rCBR-BGOA | SYMON | SVM-RFE | SVM-BFE | D-HELL | SMOTE-RLF | SMOTE-PCA |
|---|---|---|---|---|---|---|---|---|
| BRE | F/5 | 78.1(0.2) | 79.2(0.8) | 75.0(0.2) | 29.1(0.4) | 75.0(0.4) | 65.2(0.8) | 59.3(0.2) |
| CAR | F/5 | 96.9(0.2) | 100(0.2) | 75.0(0.2) | 29.1(0.4) | 75.0(0.4) | 93.7(0.2) | 93.7(0.20 |
| CNS | F/5 | 94.1(0.2) | 65.2(0.2) | 46.0(0.6) | 65.2(0.4) | 65.2(0.6) | 75.2(0.2) | 75.0(0.4) |
| Col | F/5 | 96.4(0.2) | 72.0(0.8) | 61.3(0.2) | 67.0(0.4) | 73.8(0.4) | 61.6(0.2) | 67.6(0.8) |
| DLBCL | F/5 | 100(0.2) | 78.7(0.2) | 68.7(0.6) | 68.7(0.4) | 68.7(0.6) | 63.4(0.2) | 63.7(0.8) |
| LEU | F/5 | 99.0(0.2) | 93.5(0.2) | 87.5(0.2) | 87.5(0.2) | 87.5(0.2) | 87.5(0.2) | 87.5(0.2) |
| LUG | F/5 | 100(0.2) | 96.8(0.2) | 96.8(0.2) | 96.8(0.2) | 96.8(0.2) | 96.8(0.2) | 96.8(0.2) |
| SRBCT | F/5 | 100(0.2) | 100(0.2) | 100(0.2) | 100(0.2) | 100(0.2) | 100(0.2) | 100(0.2) |
| Evaluation Metric | Comparison | Hypothesis | p-Value | Significant Difference |
|---|---|---|---|---|
| G-mean | rCBR-BGOA vs. SYMON | Reject at 5% | 2.2689 × 10−4 (1) | Yes |
| rCBR-BGOA vs. SSVM-FS | Reject at 5% | 0.0049 (1) | Yes | |
| rCBR-BGOA vs. FRHS | Retain at 5% | 0.0078 (1) | No | |
| rCBR-BGOA vs. SVM-RFE | Reject at 5% | 1.8162 × 10−5 (1) | Yes | |
| rCBR-BGOA vs. SVM-BFE | Reject at 5% | 3.8662 × 10−5 (1) | Yes | |
| rCBR-BGOA vs. D-HELL | Retain at 5% | 3.8767 × 10−5 (1) | Yes | |
| rCBR-BGOA vs. SMOTE-ReliefF | Retain at 5% | 2.0645 × 10−5 (1) | Yes | |
| rCBR-BGOA vs. SMOTE-PCA | Retain at 5% | 1.816 × 10−5(1) | Yes |
| Evaluation Metric | Comparison | Hypothesis Decision | p-Value | Significant Difference |
|---|---|---|---|---|
| AUC | rCBR-BGOA vs. SYMON | Retain at 5% | 0.0781 | No |
| rCBR-BGOA vs. SVM-RFE | Reject at 5% | 0.0156 | Yes | |
| rCBR-BGOA vs. SVM-BFE | Reject at 5% | 0.0156 | Yes | |
| rCBR-BGOA vs. D-HELL | Reject at 5% | 0.0156 | Yes | |
| rCBR-BGOA vs. SMOTE-ReliefF | Reject at 5% | 0.0156 | Yes | |
| rCBR-BGOA vs. SMOTE-PCA | Reject at 5% | 0.0156 | Yes |
| Execution Time | Algorithms | Data Sets | |||
|---|---|---|---|---|---|
| 2K (COL) | 7K (DLBCL) | 12 K (LUG) | 24 K (BC) | ||
| Execution time | SVM-REF | 2.6 | 7.58 | 16.67 | 28.68 |
| SVM-BFE | 80.64 | 358.52 | 25,066.6 | 48,569.73 | |
| D-HELL | 2.51 | 7.57 | 12.57 | 21.58 | |
| SYMON | 289 | 2622 | 17,023 | 31,805 | |
| SMOTE-RLF | 5.045 | 11.778 | 196.05 | 92.32 | |
| SMOTE-PCA | 2.755 | 11.305 | 59.466 | 1134.15 | |
| rCBR-BGOA | 12.92 | 17.39 | 143.19 | 76.67 | |
| Data Sets | rCBR-BGOA | EnSVM-OAA(RUS) | C-E-MWELM |
|---|---|---|---|
| Brain-Tumor1 | 97.9 | 40.3 | 83.0 |
| Brain-Tumor2 | 98.8 | 64.6 | 92.4 |
| Lung-Cancer | 96.9 | 96.2 | 97.2 |
| SRBCT | 100 | 100 | 99.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulrauf Sharifai, G.; Zainol, Z. Feature Selection for High-Dimensional and Imbalanced Biomedical Data Based on Robust Correlation Based Redundancy and Binary Grasshopper Optimization Algorithm. Genes 2020, 11, 717. https://doi.org/10.3390/genes11070717
Abdulrauf Sharifai G, Zainol Z. Feature Selection for High-Dimensional and Imbalanced Biomedical Data Based on Robust Correlation Based Redundancy and Binary Grasshopper Optimization Algorithm. Genes. 2020; 11(7):717. https://doi.org/10.3390/genes11070717
Chicago/Turabian StyleAbdulrauf Sharifai, Garba, and Zurinahni Zainol. 2020. "Feature Selection for High-Dimensional and Imbalanced Biomedical Data Based on Robust Correlation Based Redundancy and Binary Grasshopper Optimization Algorithm" Genes 11, no. 7: 717. https://doi.org/10.3390/genes11070717
APA StyleAbdulrauf Sharifai, G., & Zainol, Z. (2020). Feature Selection for High-Dimensional and Imbalanced Biomedical Data Based on Robust Correlation Based Redundancy and Binary Grasshopper Optimization Algorithm. Genes, 11(7), 717. https://doi.org/10.3390/genes11070717





