Genomic Selection for Optimum Index with Dry Biomass Yield, Dry Mass Fraction of Fresh Material, and Plant Height in Biomass Sorghum
Abstract
1. Introduction
2. Materials and Methods
2.1. Phenotypic and Genotypic Data
2.2. Phenotypic Data Analysis
2.3. Molecular Data
2.4. Construction of Genomic Selection Indices
2.5. Genomic Selection Models
3. Results
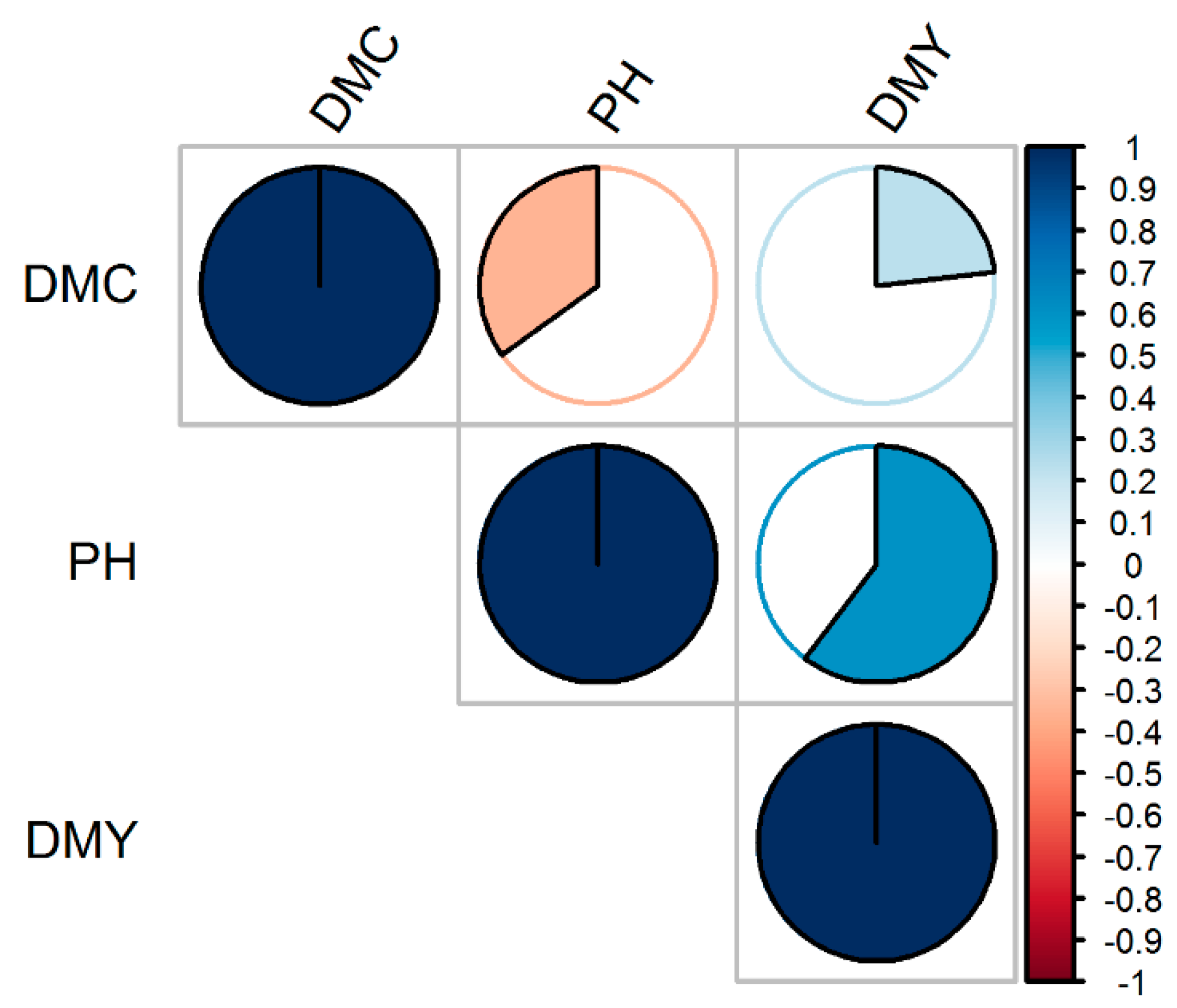
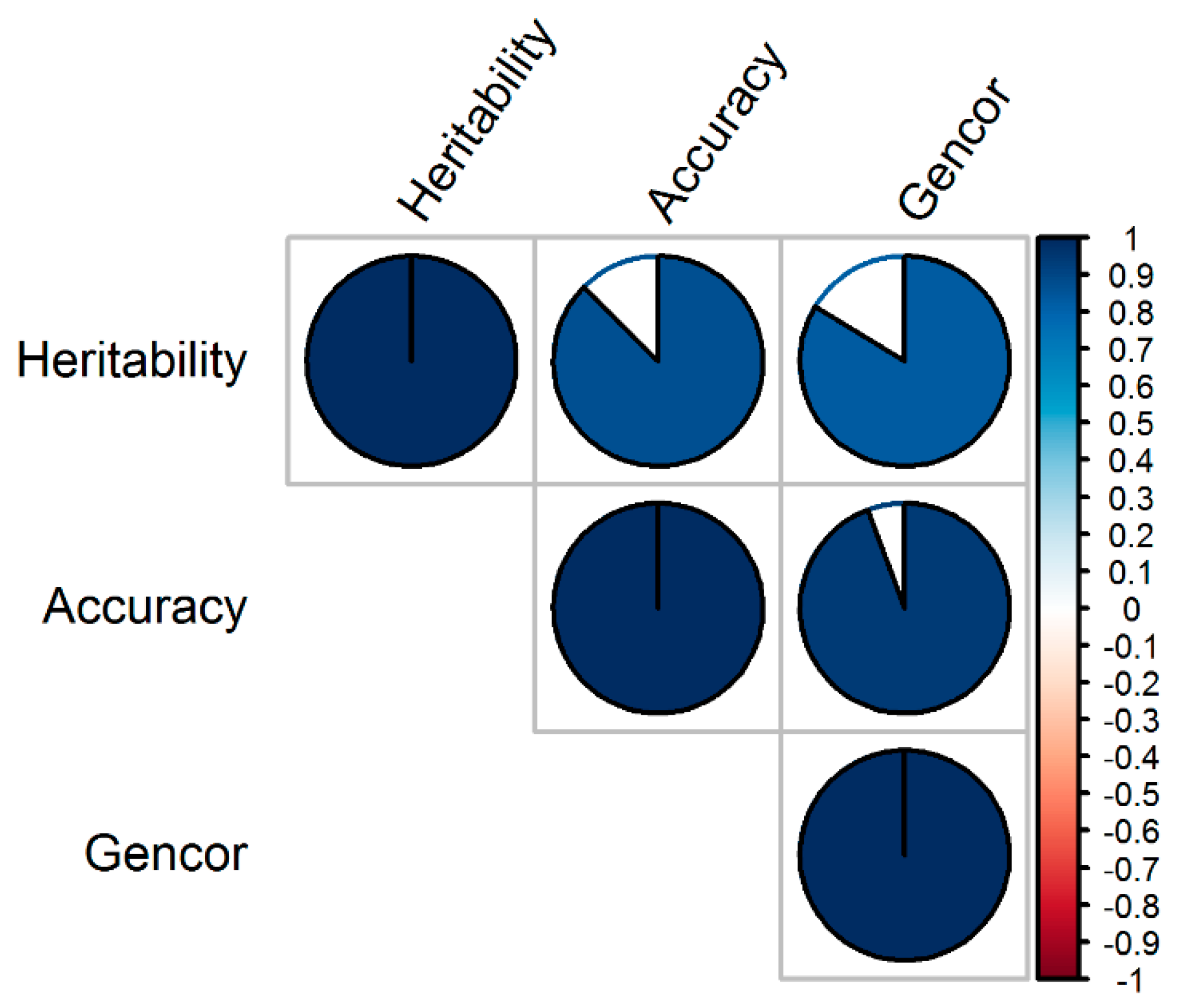
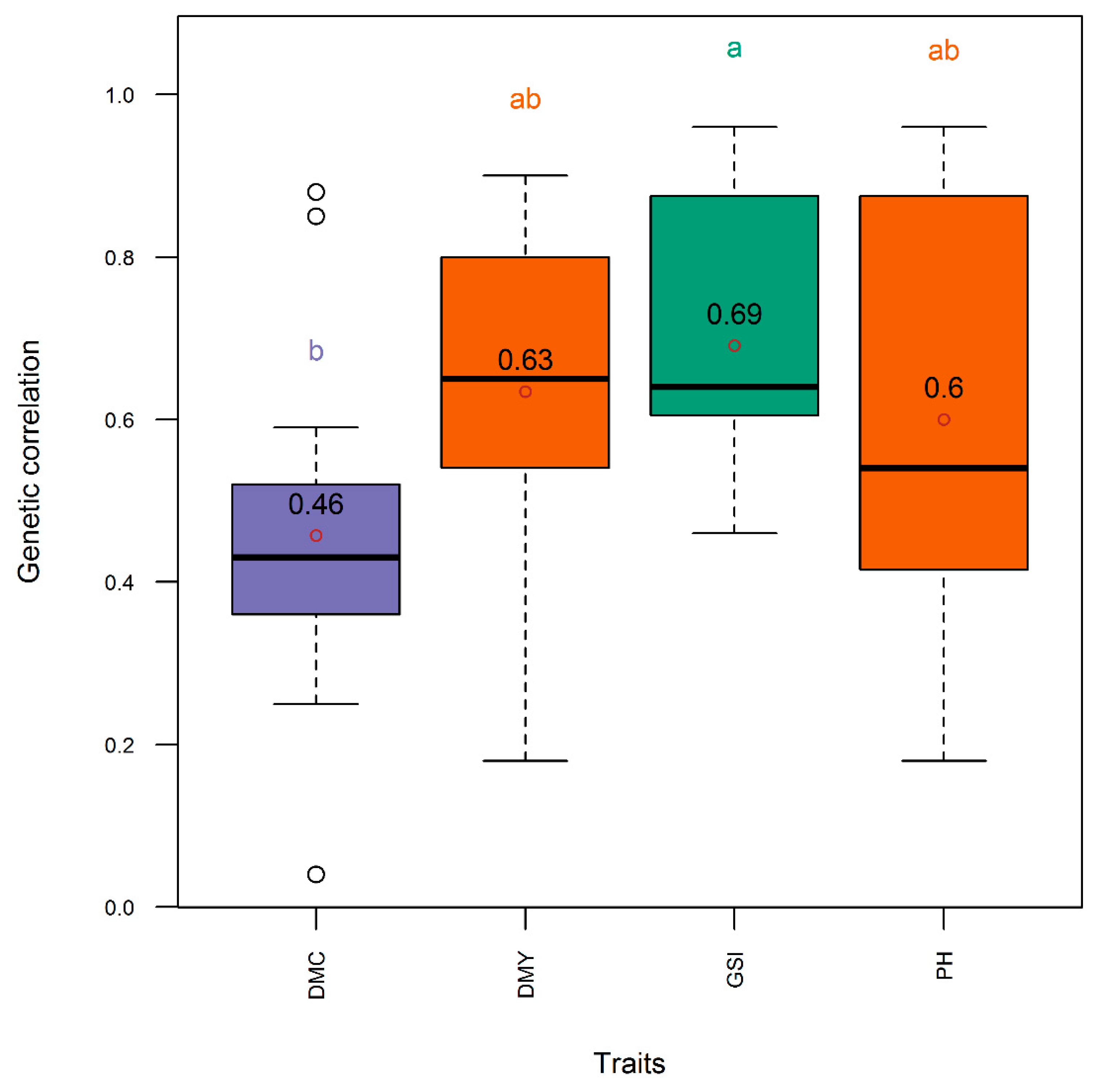
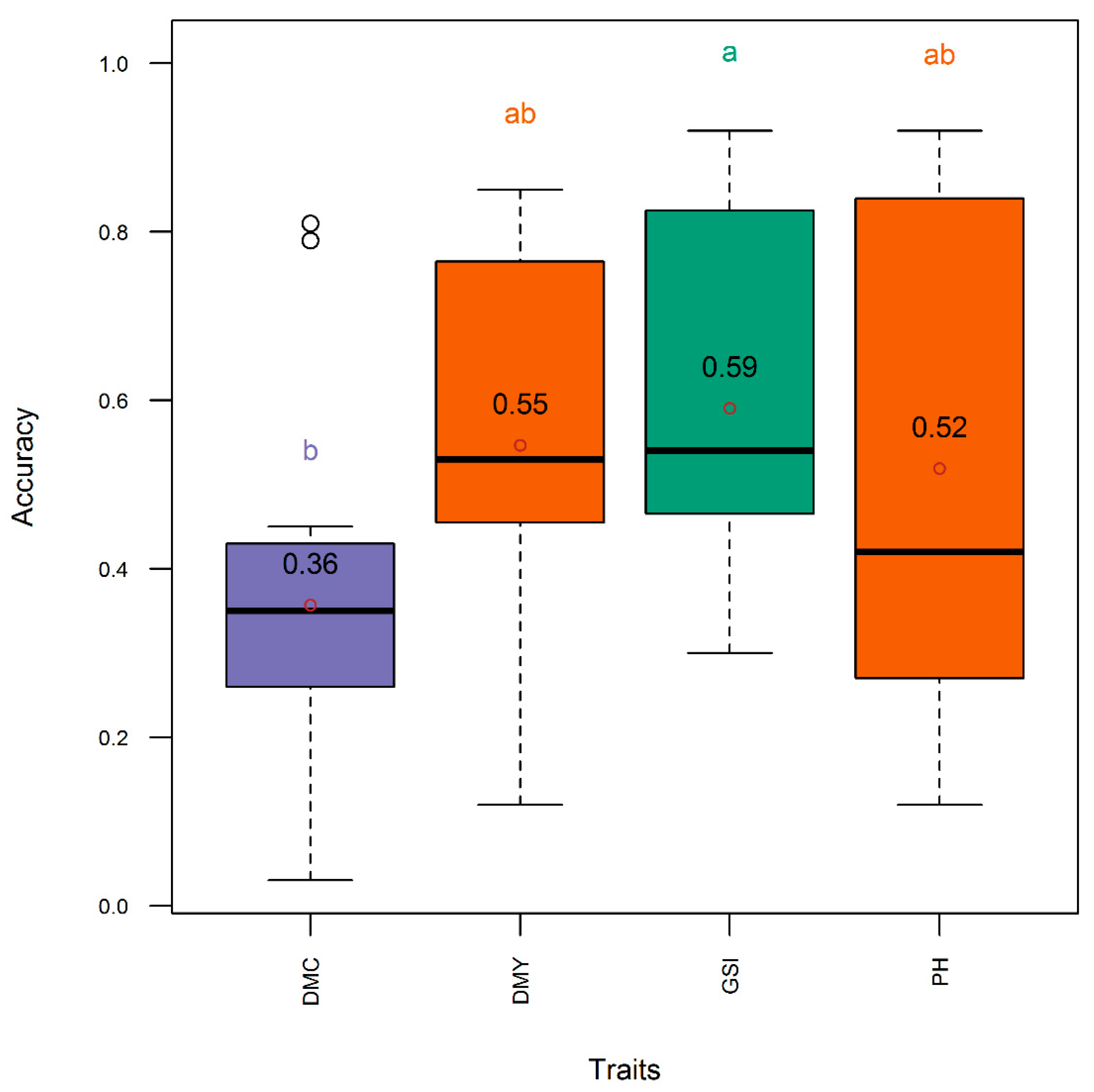
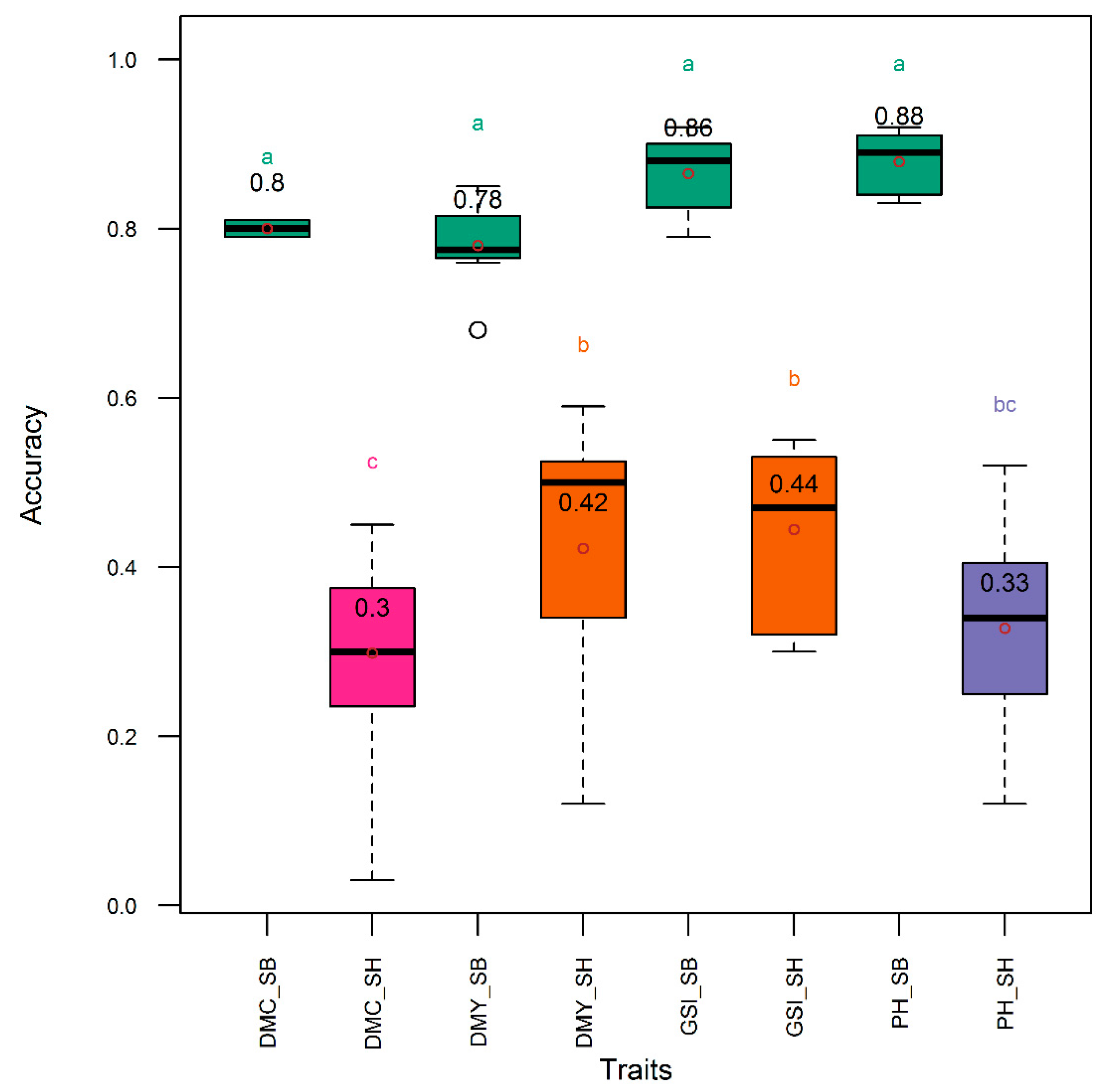
3.1. Comparison of Traits, Genetic Metrics, and Genomic Selection Approaches
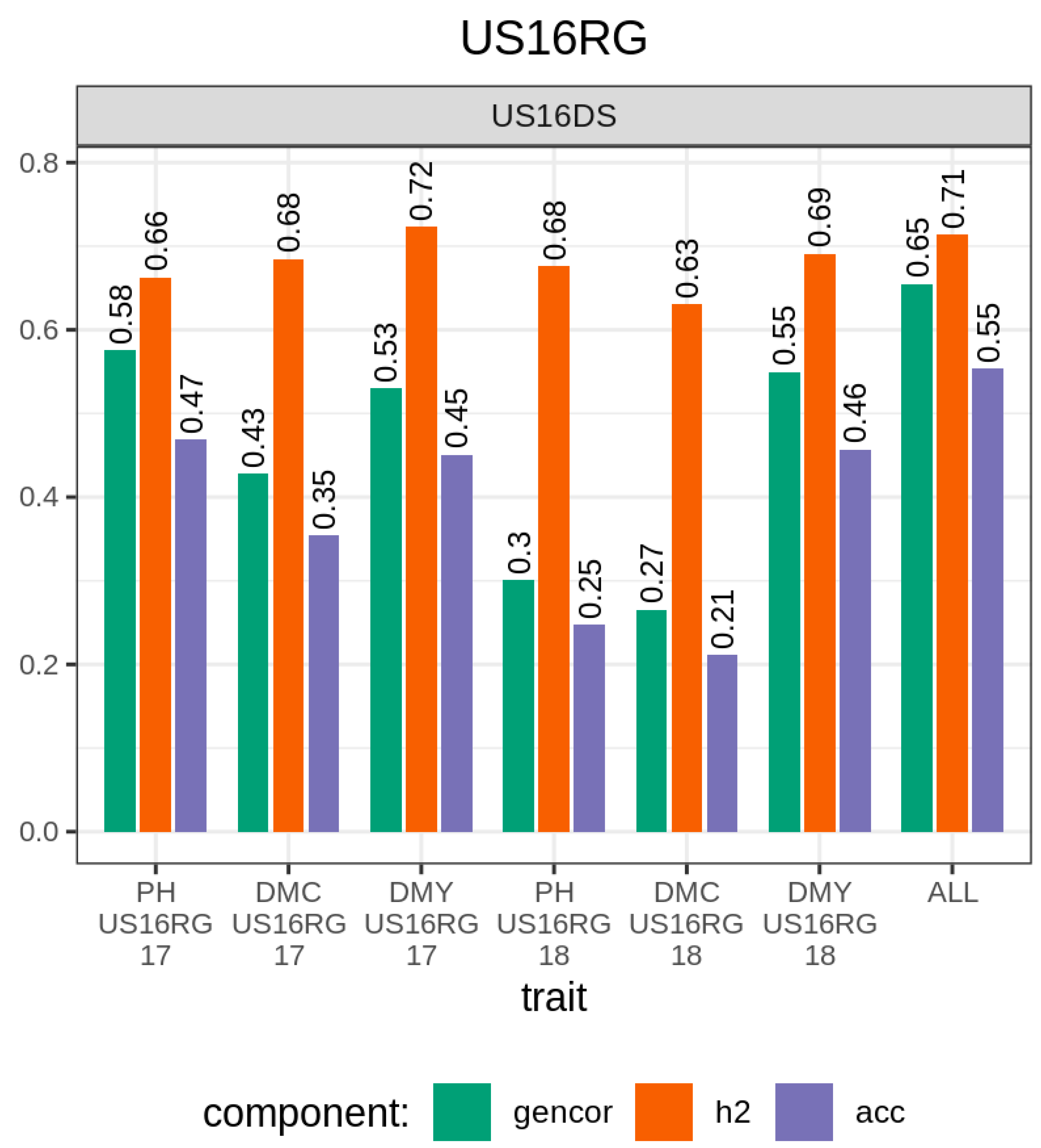
3.2. Predicting Regrowth Performance in Perennial Sorghum Bicolor × Sorghum Halepense
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Habyarimana, E.; Lorenzoni, C.; Marudelli, M.; Redaelli, R.; Amaducci, S. A meta-analysis of bioenergy conversion relevant traits in sorghum landraces, lines and hybrids in the Mediterranean region. Ind. Crops Prod. 2016, 81, 100–109. [Google Scholar] [CrossRef]
- Habyarimana, E.; Lorenzoni, C.; Redaelli, R.; Alfieri, M.; Amaducci, S.; Cox, S. Towards a perennial biomass sorghum crop: A comparative investigation of biomass yields and overwintering of Sorghum bicolor × S. halepense lines relative to long term S. bicolor trials in northern Italy. Biomass Bioenergy 2018, 111, 187–195. [Google Scholar] [CrossRef]
- Fernandes, S.B.; Dias, K.O.G.; Ferreira, D.F.; Brown, P.J. Efficiency of multi-trait, indirect, and trait-assisted genomic selection for improvement of biomass sorghum. Theor. Appl. Genet. 2018, 131, 747–755. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, R. Breeding for Quantitative Traits in Plants; Stemma Pr: Woodbury, MN, USA, 2002; ISBN 978-0-9720724-0-3. [Google Scholar]
- Lynch, M.; Walsh, B. Genetics and Analysis of Quantitative Traits, 1st ed.; Sinauer Associates is an Imprint of Oxford University Press: Sunderland, MA, USA, 1998; ISBN 978-0-87893-481-2. [Google Scholar]
- Habyarimana, E. Genomic prediction for yield improvement and safeguarding genetic diversity in CIMMYT spring wheat (Triticum aestivum L.). Aust. J. Crop Sci. 2016, 10, 127–136. [Google Scholar]
- Habyarimana, E.; Parisi, B.; Mandolino, G. Genomic prediction for yields, processing and nutritional quality traits in cultivated potato (Solanum tuberosum L.). Plant Breed. 2017, 136, 245–252. [Google Scholar] [CrossRef]
- Meuwissen, T.; Hayes, B.; Goddard, M. Genomic selection: A paradigm shift in animal breeding. Anim. Front. 2016, 6, 6–14. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de Los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic Selection in Plant Breeding: Methods, Models, and Perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- Habyarimana, E.; Lopez-Cruz, M. Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines. Genes 2019, 10, 841. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar]
- Velazco, J.G.; Jordan, D.R.; Mace, E.S.; Hunt, C.H.; Malosetti, M.; van Eeuwijk, F.A. Genomic Prediction of Grain Yield and Drought-Adaptation Capacity in Sorghum Is Enhanced by Multi-Trait Analysis. Front. Plant Sci. 2019, 10, 997. [Google Scholar] [CrossRef]
- De los Campos, G.; Gianola, D.; Rosa, G.J.M.; Weigel, K.A.; Crossa, J. Semi-parametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genet. Res. 2010, 92, 295–308. [Google Scholar] [CrossRef]
- Pérez, P.; de los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Gianola, D. Priors in Whole-Genome Regression: The Bayesian Alphabet Returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef] [PubMed]
- Kulwal, P.L. Association Mapping and Genomic Selection—Where Does Sorghum Stand. In The Sorghum Genome; Rakshit, S., Wang, Y.-H., Eds.; Compendium of Plant Genomes; Springer International Publishing: Cham, Switzerland, 2016; pp. 137–148. ISBN 978-3-319-47789-3. [Google Scholar]
- Hunt, C.H.; van Eeuwijk, F.A.; Mace, E.S.; Hayes, B.J.; Jordan, D.R. Development of Genomic Prediction in Sorghum. Crop Sci. 2018, 58, 690–700. [Google Scholar] [CrossRef]
- Ceron-Rojas, J.J.; Crossa, J.; Arief, V.N.; Basford, K.; Rutkoski, J.; Jarquín, D.; Alvarado, G.; Beyene, Y.; Semagn, K.; DeLacy, I. A Genomic Selection Index Applied to Simulated and Real Data. G3 2015, 5, 2155–2164. [Google Scholar] [CrossRef] [PubMed]
- Céron-Rojas, J.J.; Hiriart, J.C. Linear Selection Indices in Modern Plant Breeding; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-91222-6. [Google Scholar]
- Safari, P.; Honarnejad, R.; Esfahani, M. Indirect selection for increased oil yield in peanut: Comparison selection indices and biplot analysis for simultaneous improvement multiple traits. Int. J. Biosci. 2013, 3, 87–96. [Google Scholar]
- Hazel, L.N.; Lush, J.L. The efficiency of three methods of selection. J. Hered. 1942, 33, 393–399. [Google Scholar] [CrossRef]
- Henderson, C.R.; Quaas, R.L. Multiple Trait Evaluation Using Relatives’ Records. J. Anim. Sci. 1976, 43, 1188–1197. [Google Scholar] [CrossRef]
- Thompson, R.; Meyer, K. A review of theoretical aspects in the estimation of breeding values for multi-trait selection. Livest. Prod. Sci. 1986, 15, 299–313. [Google Scholar] [CrossRef]
- Mrode, R.A. Linear Models for the Prediction of Animal Breeding Values, 3rd ed.; CABI: Boston, MA, USA, 2014. [Google Scholar]
- Calus, M.P.; Veerkamp, R.F. Accuracy of multi-trait genomic selection using different methods. Genet. Sel. Evol. 2011, 43, 26. [Google Scholar] [CrossRef]
- Jia, Y.; Jannink, J.-L. Multiple-trait genomic selection methods increase genetic value prediction accuracy. Genetics 2012, 192, 1513–1522. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Yang, Z.; Zheng, X.; Yu, S.; Xu, C.; Hu, Z. Predicting rice hybrid performance using univariate and multivariate GBLUP models based on North Carolina mating design II. Heredity 2017, 118, 302–310. [Google Scholar] [CrossRef] [PubMed]
- Schulthess, A.W.; Zhao, Y.; Longin, C.F.H.; Reif, J.C. Advantages and limitations of multiple-trait genomic prediction for Fusarium head blight severity in hybrid wheat (Triticum aestivum L.). Theor. Appl. Genet. 2018, 131, 685–701. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, J.P.R.; de Castro Vasconcellos, R.C.; Pires, L.P.M.; Balestre, M.; Von Pinho, R.G. Inclusion of Dominance Effects in the Multivariate GBLUP Model. PLoS ONE 2016, 11, e0152045. [Google Scholar] [CrossRef] [PubMed]
- Federer, W.T.; Cornell University, Biometrics Unit; Cornell University, Dept. of Biometrics; Cornell University, Dept. of Biological Statistics and Computational Biology. Augmented (or Hoonuiaku) Designs. Biom. Unit Tech. Rep. 1956, 33, 1. [Google Scholar]
- Descriptors for Sorghum [Sorghum bicolor (L.) Moench]. Available online: https://www.bioversityinternational.org/e-library/publications/detail/descriptors-for-sorghum-sorghum-bicolor-l-moench/ (accessed on 24 November 2019).
- Smith, H.F. A Discriminant Function for Plant Selection. Ann. Eugen. 1936, 7, 240–250. [Google Scholar] [CrossRef]
- Tomar, S.S. Restricted selection index in animal system—A review. Agric. Rev. 1983, 4, 109–118. [Google Scholar]
- Cartuche Macas, L. Economic weights in rabbit meat production. World Rabbit Sci. 2014, 22, 165–177. [Google Scholar] [CrossRef]
- Bradshaw, J.E. Plant breeding: Past, present and future. Euphytica 2017, 213, 60. [Google Scholar] [CrossRef]
- Kang, M.S. Applied Quantitative Genetics; Kang, M.S., Ed.; MS Kang: Baton Rouge, LA, USA, 1994; ISBN 978-0-9642970-4-3. [Google Scholar]
- Baker, R.J. Selection Indices in Plant Breeding; CRC Press: Boca Raton, FL, USA, 1986; ISBN 978-0-8493-6377-1. [Google Scholar]
- de Los Campos, G.; Grüneberg, A. QuantGen/MTM: MTM Version 1.0.0 from GitHub. Available online: https://rdrr.io/github/QuantGen/MTM/ (accessed on 24 November 2019).
- Montesinos-López, O.A.; Montesinos-López, A.; Luna-Vázquez, F.J.; Toledo, F.H.; Pérez-Rodríguez, P.; Lillemo, M.; Crossa, J. An R Package for Bayesian Analysis of Multi-environment and Multi-trait Multi-environment Data for Genome-Based Prediction. G3 2019, 9, 1355–1369. [Google Scholar] [CrossRef]
- Scutari, M.; Mackay, I.; Balding, D. Using Genetic Distance to Infer the Accuracy of Genomic Prediction. PLoS Genet. 2016, 12, e1006288. [Google Scholar] [CrossRef] [PubMed]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 27 September 2019).
- Gomez, K.A.; Gomez, A.A. Statistical Procedures for Agricultural Research, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1984; ISBN 978-0-471-87092-0. [Google Scholar]
- Habyarimana, E.; Dall’Agata, M.; De Franceschi, P.; Baloch, F.S. Genome-wide association mapping of total antioxidant capacity, phenols, tannins, and flavonoids in a panel of Sorghum bicolor and S. bicolor × S. halepense populations using multi-locus models. PLoS ONE 2019, 14, e0225979. [Google Scholar] [CrossRef] [PubMed]
- Wricke, G.; Weber, E. Quantitative Genetics and Selection in Plant Breeding, Reprint 2010 ed.; De Gruyter: Berlin, Germany, 1986; ISBN 978-3-11-007561-8. [Google Scholar]
- Saeidnia, M.; Emami, H.; Honarnejad, R.; Esfahani, M. Comparing Economical Coefficients to Select the Best Optimum Selection Index in Peanut. Am. Eurasian J. Agric. Environ. Sci. 2012, 12, 393–398. [Google Scholar]
- Piper, J.; Kulakow, P. Seed yield and biomass allocation in Sorghum bicolor and F1 and backcross generations of S. bicolor × S. halepense hybrids. Can. J. Bot. 2011, 72, 468–474. [Google Scholar] [CrossRef]


| Trials | PH | DMC | DMY 1 |
|---|---|---|---|
| IT14 | 174 | 123 | 123 |
| IT15 | 179 | 179 | 179 |
| IT16 | 180 | NA | 180 |
| IT17 | 168 | 168 | 168 |
| US15_DS | 90 | 90 | 90 |
| US15_RG16 | 89 | 89 | 89 |
| US15_RG17 | 85 | 85 | 85 |
| US15_RG18 | 85 | 85 | 85 |
| US16_DS | 189 | 189 | 189 |
| US16_RG17 | 189 | 189 | 189 |
| US16_RG18 | 189 | 189 | 189 |
| US17_DS | 189 | 189 | 189 |
| US17_RG18 | 189 | 189 | 189 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habyarimana, E.; Lopez-Cruz, M.; Baloch, F.S. Genomic Selection for Optimum Index with Dry Biomass Yield, Dry Mass Fraction of Fresh Material, and Plant Height in Biomass Sorghum. Genes 2020, 11, 61. https://doi.org/10.3390/genes11010061
Habyarimana E, Lopez-Cruz M, Baloch FS. Genomic Selection for Optimum Index with Dry Biomass Yield, Dry Mass Fraction of Fresh Material, and Plant Height in Biomass Sorghum. Genes. 2020; 11(1):61. https://doi.org/10.3390/genes11010061
Chicago/Turabian StyleHabyarimana, Ephrem, Marco Lopez-Cruz, and Faheem S. Baloch. 2020. "Genomic Selection for Optimum Index with Dry Biomass Yield, Dry Mass Fraction of Fresh Material, and Plant Height in Biomass Sorghum" Genes 11, no. 1: 61. https://doi.org/10.3390/genes11010061
APA StyleHabyarimana, E., Lopez-Cruz, M., & Baloch, F. S. (2020). Genomic Selection for Optimum Index with Dry Biomass Yield, Dry Mass Fraction of Fresh Material, and Plant Height in Biomass Sorghum. Genes, 11(1), 61. https://doi.org/10.3390/genes11010061







