Multi-Objective Optimized Fuzzy Clustering for Detecting Cell Clusters from Single-Cell Expression Profiles
Abstract
1. Introduction
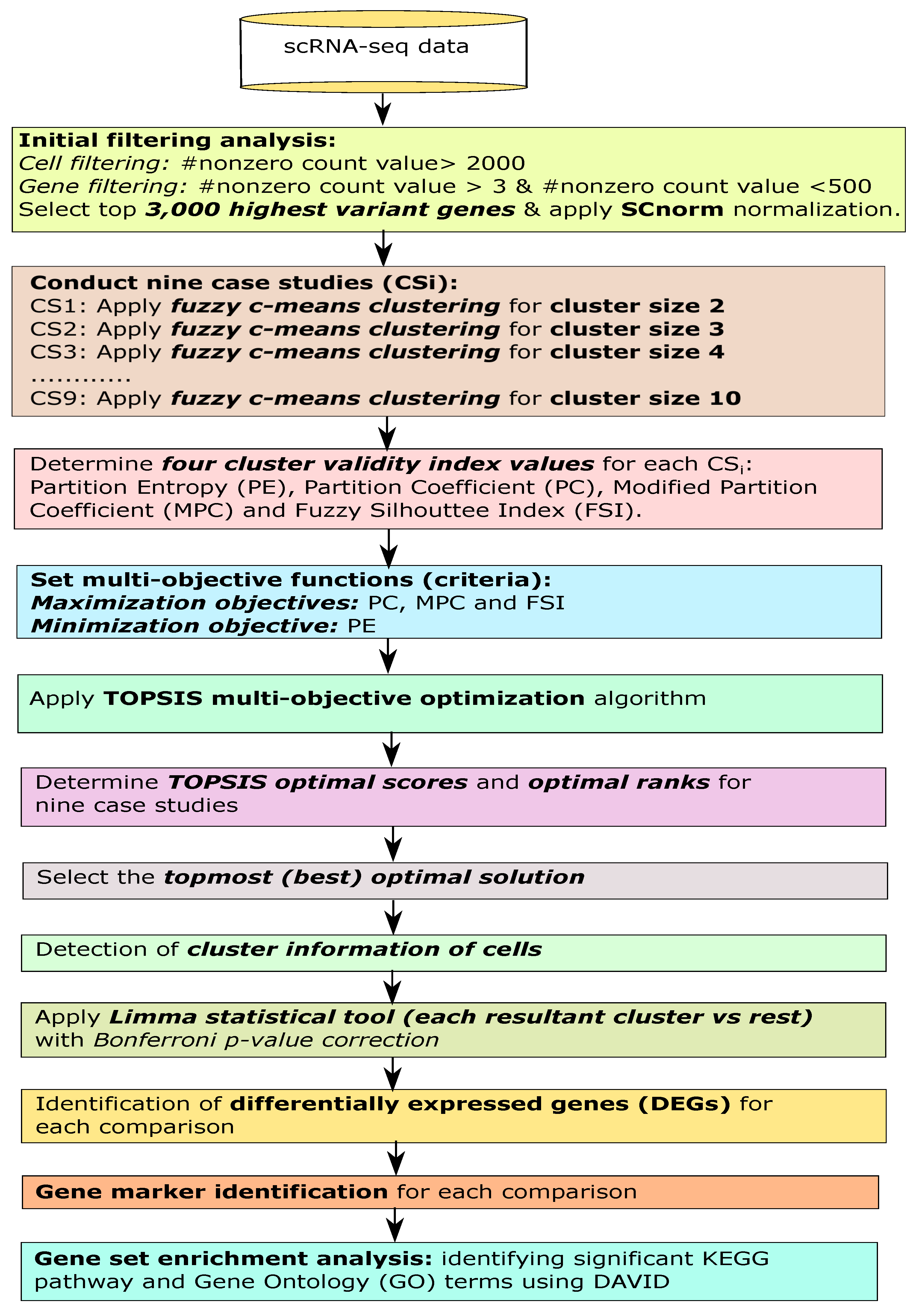
2. Materials and Methods
2.1. Initial Filtering
2.2. Fuzzy Clustering for Finding Optimized Cell Clusters
2.3. Measuring Cluster Validity Index Measures
2.4. Identifying Optimal Fuzzy Clustering Solution Using Multi-Objective Decision-Making Model
2.5. Identification of Differentially Expressed Genes through Statistical Test
2.6. Gene Set Enrichment Analysis
2.7. Identification of Novel Gene Markers
3. Results
3.1. Source Dataset
3.2. Filtering Analysis
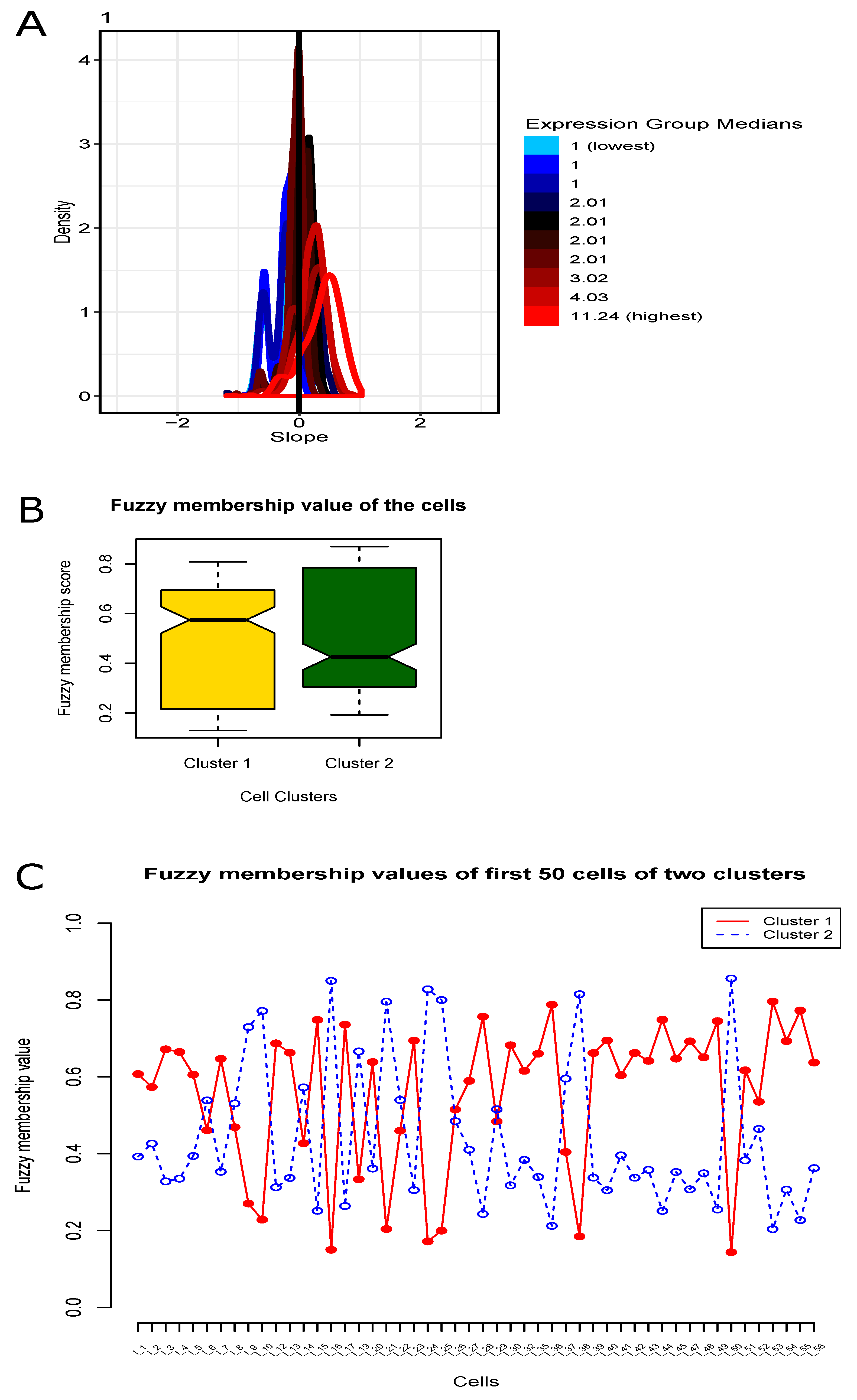
3.3. Fuzzy Clustering of Cells
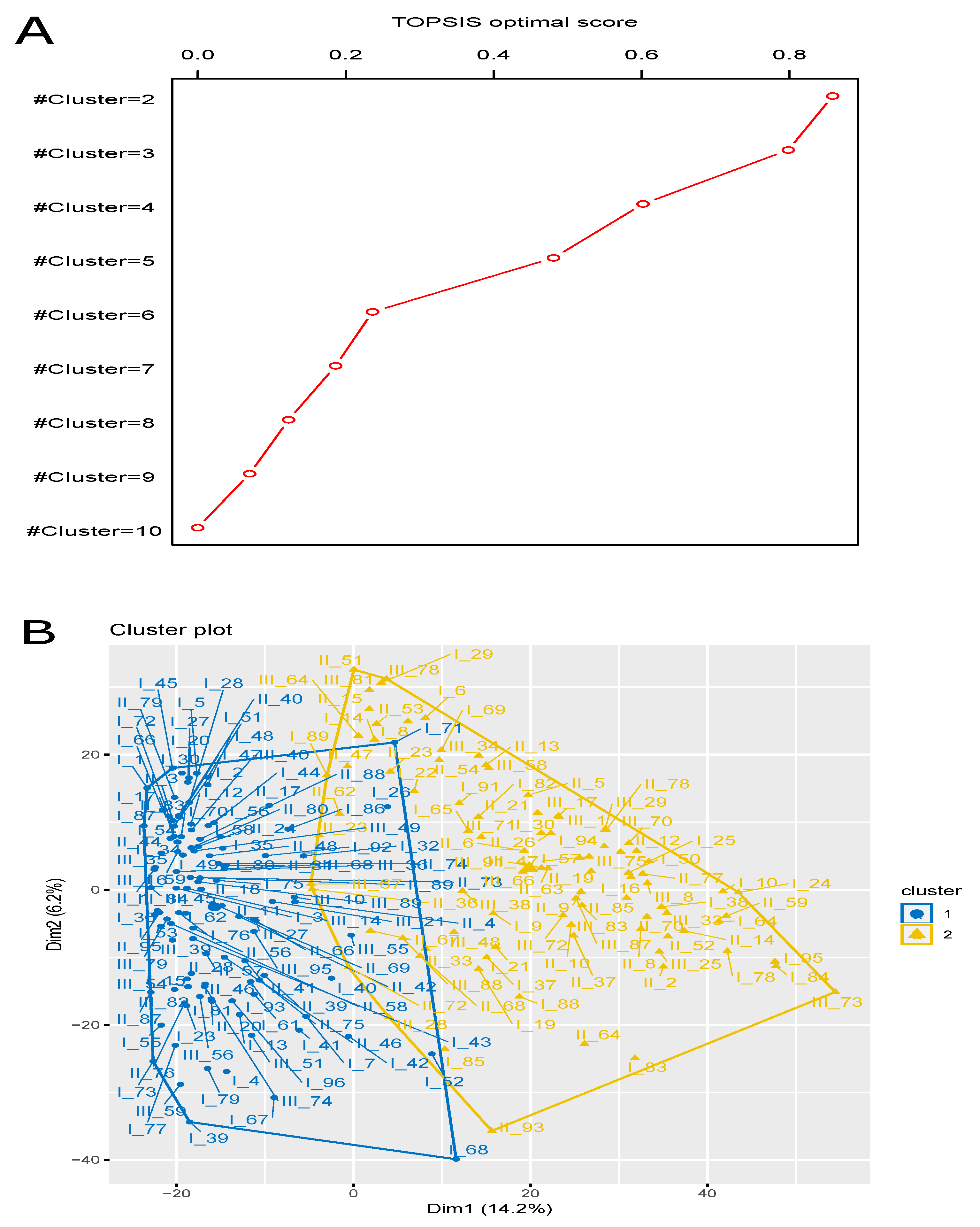
3.4. Finding Optimal Clustering (Solution) Using Multi-Objective Optimization
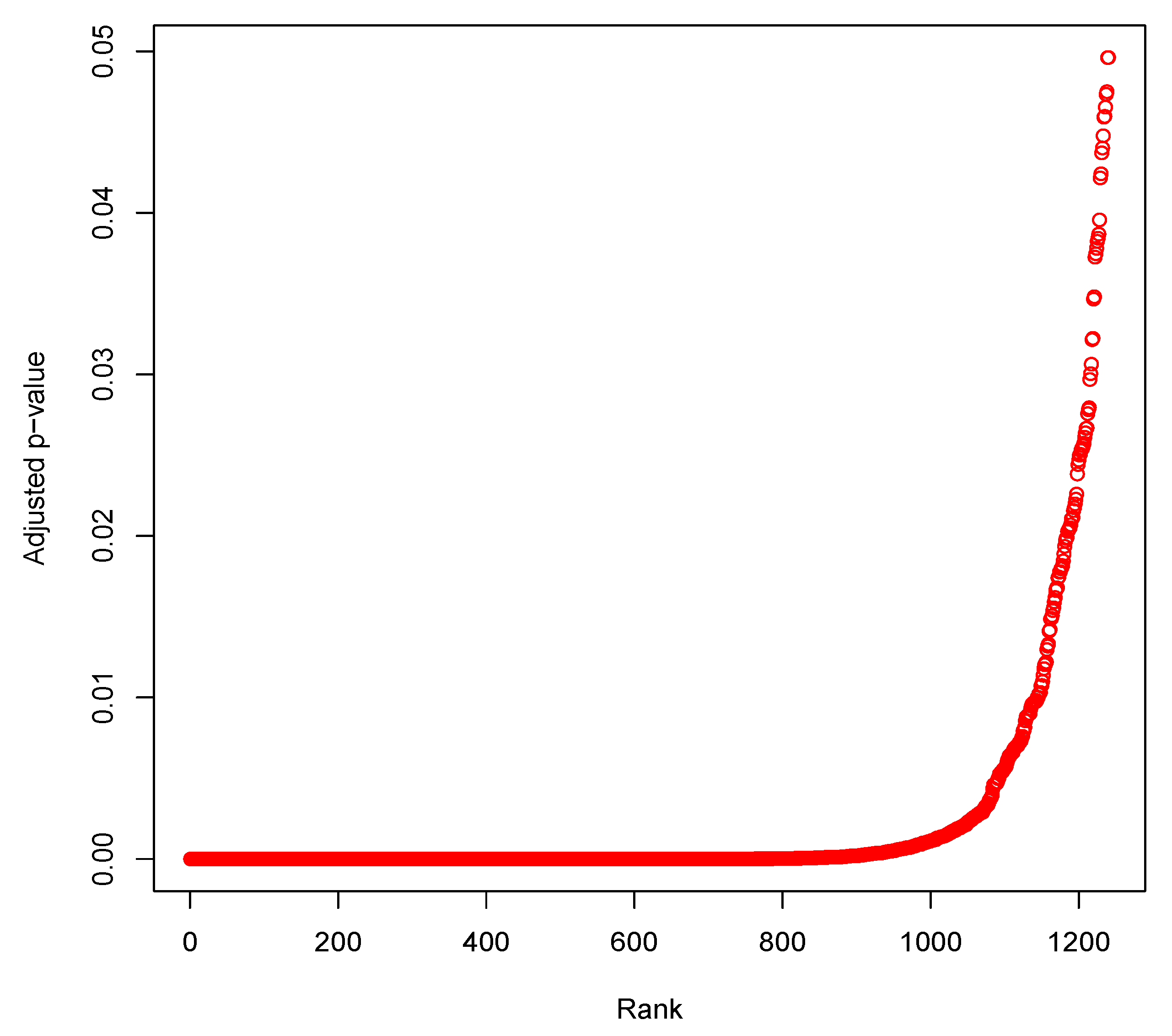
3.5. Identification of Differentially Expressed Genes through Statistical Test
3.6. Gene Set Enrichment Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wagner, A.; Regev, A.; Yosef, N. Revealing the vectors of cellular identity with single-cell genomics. Nat. Biotechnol. 2016, 34, 1145–1160. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, A.A.; Kim, J.K.; Svensson, V.; Marioni, J.C.; Teichmann, S.A. The technology and biology of single-cell RNA sequencing. Mol. Cell 2015, 58, 610–620. [Google Scholar] [CrossRef] [PubMed]
- Picelli, S.; Bjorklund, A.K.; Faridani, O.R.; Sagasser, S.; Winberg, G.; Sandberg, R. Smart-seq2 for sensitive full-length transcriptome profiling in single cells. Nat. Methods 2013, 10, 1096–1098. [Google Scholar] [CrossRef] [PubMed]
- Picelli, S.; Faridani, O.R.; Bjorklund, A.K.; Winberg, G.; Sagasser, S.; Sandberg, R. Full-length RNA-seq from single cells using Smartseq2. Nat. Protoc. 2014, 9, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Gokce, O.; Stanley, G.M.; Treutlein, B.; Neff, N.F.; Camp, J.G.; Malenka, R.C.; Rothwell, P.E.; Fuccillo, M.V.; Sdhof, T.C.; Quake, S.R. Cellular Taxonomy of the Mouse Striatum as Revealed by Single-Cell RNA-Seq. Cell Rep. 2016, 16, 1126–1137. [Google Scholar] [CrossRef] [PubMed]
- Reinius, B.; Mold, J.E.; Ramskold, D.; Deng, Q.; Johnsson, P.; Michalsson, J.; Frisen, J.; Sandberg, R. Analysis of allelic expression patterns in clonal somatic cells by single-cell RNA-seq. Nat. Genet. 2016, 48, 1430–1435. [Google Scholar] [CrossRef] [PubMed]
- Tirosh, I.; Izar, B.; Prakadan, S.M.; Wadsworth, M.H., 2nd; Treacy, D.; Trombetta, J.J.; Rotem, A.; Rodman, C.; Lian, C.; Murphy, G.; et al. Dissecting the multicellular ecosystem of metastatic melanoma by single cell RNA-seq. Science 2016, 352, 189–196. [Google Scholar] [CrossRef]
- Shapiro, E.; Biezuner, T.; Linnarsson, S. Single-cell sequencing-based technologies will revolutionize whole-organism science. Nat. Rev. Genet. 2013, 14, 618–630. [Google Scholar] [CrossRef]
- Zheng, G.X.; Terry, J.M.; Belgrader, P.; Ryvkin, P.; Bent, Z.W.; Wilson, R.; Ziraldo, S.B.; Wheeler, T.D.; McDermott, G.P.; Zhu, J.; et al. Massively parallel digital transcriptional profiling of single cells. Nat. Commun. 2017, 8, 140–149. [Google Scholar] [CrossRef]
- Macosko, E.Z.; Basu, A.; Satija, R.; Nemesh, J.; Shekhar, K.; Goldman, M.; Tirosh, I.; Bialas, A.R.; Kamitaki, N.; Martersteck, E.M.; et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 2015, 161, 1202–1214. [Google Scholar] [CrossRef]
- Campbell, J.N.; Macosko, E.Z.; Fenselau, H.; Pers, T.H.; Lyubetskaya, A.; Tenen, D.; Goldman, M.; Verstegen, A.M.; Resch, J.M.; McCarroll, S.A.; et al. A molecular census of arcuate hypothalamus and median eminence cell types. Nat. Neurosci. 2017, 20, 484–496. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, V.Y.; Andrews, T.S.; Hemberg, M. Challenges in unsupervised clustering of single-cell RNA-seq data. Nat. Rev. Genet. 2019, 20, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Andrews, T.S.; Hemberg, M. Identifying cell populations with scRNASeq. Mol. Asp. Med. 2018, 59, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Lei, J.; Klei, L.; Devlin, B.; Roeder, K. Semisoft clustering of single-cell data. Proc. Natl. Acad. Sci. USA 2019, 116, 466–471. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Mejia, J.J.; Meng, E.C.; Pico, A.R.; MacParland, S.A.; Ketela, T.; Pugh, T.J.; Bader, G.D.; Morris, J.H. Evaluation of methods to assign cell type labels to cell clusters from single-cell RNA-sequencing data. Mol. Cell 2019, 8, 1–17. [Google Scholar] [CrossRef]
- Slansky, J. Antigen-specific t cells: Analyses of the needles in the haystack. PLoS Biol. 2003, 1, e78. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Altman, J.; Moss, P.A.; Goulder, P.J.; Barouch, D.H.; McHeyzer-Williams, M.G.; Bell, J.; McMichael, A.J.; Davis, M.M. Phenotypic analysis of antigen-specific t lymphocytes. Science 1996, 274, 94–96. [Google Scholar] [CrossRef]
- Manzo, T.; Heslop, H.E.; Rooney, C.M. Antigen-specific t cell therapies for cancer. Hum. Mol. Genet. 2015, 24, R67–R73. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Lin, C.H.; Shau, W.Y.; Chen, T.J.; Yang, S.H.; Huang, S.M.; Cheng, A.L. Dynamics of circulating endothelial cells and endothelial progenitor cells in breast cancer patients receiving cytotoxic chemotherapy. BMC Cancer 2012, 12, 620. [Google Scholar] [CrossRef]
- Cima, I.; Kong, S.L.; Sengupta, D.; Tan, I.B.; Phyo, W.M.; Lee, D.; Hu, M.; Iliescu, C.; Alexander, I.; Goh, W.L.; et al. Tumor-derived circulating endothelial cell clusters in colorectal cancer. Sci. Transl. Med. 2016, 8, 345ra89. [Google Scholar] [CrossRef]
- Krebs, M.; Hou, J.M.; Ward, T.H.; Blackhall, F.H.; Dive, C. Circulating tumour cells: Their utility in cancer management and predicting outcomes. Ther. Adv. Med. Oncol. 2010, 2, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.Y.; Sharkis, S. Stem cell plasticity: A rare cell, not a rare event. Stem. Cell Rev. 2005, 1, 45–51. [Google Scholar] [CrossRef]
- Grun, D.; Lyubimova, A.; Kester, L.; Wiebrands, K.; Basak, O.; Sasaki, N.; Clevers, H.; van Oudenaarden, A. Single-cell messenger rna sequencing reveals rare intestinal cell types. Nature 2015, 525, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Chen, H.; Pinello, L.; Yuan, G.C. Giniclust: Detecting rare cell types from single-cell gene expression data with gini index. Genome Biol. 2016, 17, 144. [Google Scholar] [CrossRef] [PubMed]
- Mallik, S.; Zhao, Z. Identification of gene signatures from RNA-seq data using Pareto-optimal cluster algorithm. BMC Syst. Biol. 2018, 12, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Mallik, S.; Zhao, Z. Graph- and rule-based learning algorithms: A comprehensive review of their applications for cancer type classification and prognosis using genomic data. Brief. Bioinform. 2018, bby120. [Google Scholar] [CrossRef] [PubMed]
- Mallik, S.; Bhadra, T.; Seth, S.; Bandyopadhyay, S.; Chen, J. Multi-Objective Optimization Approaches in Biological Learning System on Microarray Data. In Multi-Objective Optimization; Springer: Singapore, 2018; pp. 159–180. [Google Scholar]
- Mallik, S.; Maulik, U. Module-Based Knowledge Discovery for Multiple-Cytosine-Variant Methylation Profile. In Soft Computing for Biological Systems; Springer: Singapore, 2018. [Google Scholar]
- Mallik, S.; Zhao, Z. Towards integrated oncogenic marker recognition through mutual information-based statistically significant feature extraction: An ARM-based study on leukemia expression and methylation profiles. Quant. Biol. 2017, 5, 302–327. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, S.; Mallik, S. Integrating Multiple Data Sources for Combinatorial Marker Discovery: A Study in Tumorigenesis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 673–687. [Google Scholar]
- Mallik, S.; Bhadra, T.; Maulik, U. Identifying Epigenetic Biomarkers using Maximal Relevance and Minimal Redundancy Based Feature Selection for Multi-Omics Data. IEEE Trans. Nanobiosci. 2017, 16, 3–10. [Google Scholar] [CrossRef]
- Mallik, S.; Zhao, Z. ConGEMs: Condensed Gene Co-Expression Module Discovery Through Rule-Based Learning and Its Application to Lung Squamous Cell Carcinoma. Genes 2017, 9, 7. [Google Scholar] [CrossRef]
- Maulik, U.; Sen, S.; Mallik, S.; Bandyopadhyay, S. Detecting TF-MiRNA-Gene Network Based Modules for 5hmC and 5mC Brain Samples: A Intra- and Inter-Species Case-Study Between Human and Rhesus. BMC Genet. 2018, 19, 9. [Google Scholar] [CrossRef] [PubMed]
- Aqil, M.; Naqvi, A.R.; Mallik, S.; Bandyopadhyay, S.; Maulik, U.; Jameel, S. The HIV Nef protein modulates cellular and exosomal miRNA profiles in human monocytic cells. J. Extracell. Vesicles 2014, 3, 23129. [Google Scholar] [CrossRef] [PubMed]
- Aqil, M.; Mallik, S.; Bandyopadhyay, S.; Maulik, U.; Jameel, S. Transcriptomic Analysis of mRNAs in Human Monocytic Cells Expressing the HIV-1 Nef Protein and Their Exosomes. BioMed Res. Int. 2015, 2015, 492395. [Google Scholar] [CrossRef] [PubMed]
- Maulik, U.; Mallik, S.; Mukhopadhyay, A.; Bandyopadhyay, S. Analyzing Gene Expression and Methylation Data Profiles using StatBicRM: Statistical Biclustering-based Rule Mining. PLoS ONE 2015, 10, e0119448. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mallik, S.; Sen, S.; Maulik, U. IDPT: Insights into Potential Intrinsically Disordered Proteins Through Transcriptomic Analysis of Genes for Prostate Carcinoma Epigenetic Data. Gene 2016, 586, 87–96. [Google Scholar] [CrossRef]
- Mallik, S.; Zhao, Z. TrapRM: Transcriptomic and Proteomic Rule Mining using Weighted Shortest Distance Based Multiple Minimum Supports for Multi-Omics Dataset. In Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017. [Google Scholar]
- Mallik, S.; Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S. Integrated Analysis of Gene Expression and Genome-wide DNA Methylation for Tumor Prediction: An Association Rule Mining-based Approach. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Singapore, 16–19 April 2013; pp. 120–127. [Google Scholar]
- Mallik, S.; Mukhopadhyay, A.; Maulik, U. Integrated Statistical and Rule-Mining Techniques for DNA Methylation and Gene Expression Data Analysis. JAISCR 2013, 3, 101–115. [Google Scholar] [CrossRef]
- Khan, A.; Katanic, D.; Thakar, J. Meta-analysis of cell- specific transcriptomic data using fuzzy c-means clustering discovers versatile viral responsive genes. BMC Bioinform. 2017, 18, 295. [Google Scholar] [CrossRef]
- Fu, L.; Medico, E. FLAME, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinform. 2007, 8, 1–15. [Google Scholar] [CrossRef]
- Talwar, D.; Mongia, A.; Sengupta, D.; Majumdar, A. AutoImpute: Autoencoder based imputation of single-cell RNA-seq data. Sci. Rep. 2008, 8, 16329. [Google Scholar] [CrossRef]
- Bacher, R.; Chu, L.F.; Leng, N.; Gasch, A.P.; Thomson, J.A.; Stewart, R.M.; Newton, M.; Kendziorski, C. SCnorm: Robust normalization of single-cell RNA-seq data. Nat. Methods 2017, 14, 584–586. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Bezdek, J.C. Cluster validity with fuzzy sets. J. Cybern. 1974, 3, 58–78. [Google Scholar] [CrossRef]
- Joopudi, S.; Rathi, S.S.; Narasimhan, S.; Rengaswamy, R. A New Cluster Validity Index for Fuzzy Clustering. In Proceedings of the 10th IFAC Int Symp on Dynamics and Control of Process Systems, Mumbai, India, 18–20 December 2013. [Google Scholar]
- Bezdek, J.C. Numerical taxonomy with fuzzy sets. Math. Biol. 1974, 1, 57–71. [Google Scholar] [CrossRef]
- Dave, R.N. Validating fuzzy partitions obtained through c-shells clustering. Pattern Recognit. Lett. 1996, 17, 613–623. [Google Scholar] [CrossRef]
- Eustaquio, F. On Fuzzy Cluster Validity Indexes for High Dimensional Feature Space. Adv. Fuzzy Log. Technol. Adv. Intell. Syst. Comput. 2017, 642, 1–13. [Google Scholar]
- Campello, R.; Hruschka, E. A fuzzy extension of the silhouette width criterion for cluster analysis. Fuzzy Sets Syst. 2006, 157, 2858–2875. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Yoon, K.P.; Hwang, C. Multiple Attribute Decision Making: An Introduction; SAGE Publications: Thousand Oaks, CA, USA, 1995. [Google Scholar]
- Smyth, G. Linear Models and Empirical Bayes Methods for Assessing Differential Expression in Microarray Experiments. Stat. Appl. Genet. Mol. Biol. 2004, 3, 3. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Mallik, S.; Mukhopadhyay, A. A Survey and Comparative Study of Statistical Tests for Identifying Differential Expression from Microarray Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2013, 11, 95–115. [Google Scholar] [CrossRef]
- Thess, A. Artificial Nucleic Acid Molecules. U.S. Patents US 2017/0029847 A1, 2 February 2017. [Google Scholar]
- Sloan, K. The Exosome and Human Ribosome Biogenesis. Ph.D. Thesis, University of Newcastle upon Tyne, Newcastle upon Tyne, UK, 2012. [Google Scholar]
- Alonso, M.M. Role of the Protease MT4-MMP in the Arterial Vasculature. Ph.D. Thesis, Autonomous University of Madrid, Madrid, Spain, 2016. [Google Scholar]
- Cesar-Razquin, A.; Snijder, B.; Frappier-Brinton, T.; Isserlin, R.; Gyimesi, G.; Bai, X.; Reithmeier, R.A.; Hepworth, D.; Hediger, M.A.; Edwards, A.M.; et al. A Call for Systematic Research on Solute Carriers. Cell 2015, 162, 478–487. [Google Scholar] [CrossRef]
- Hempel, A.; Kuhl, A.J. Comparative expression analysis of cysteine-rich intestinal protein family members crip1, 2 and 3 during Xenopus laevis embryogenesis. Int. J. Dev. Biol. 2014, 58, 841–849. [Google Scholar] [CrossRef]
- Venticinque, L.; Meruelo, D. Comprehensive Proteomic Analysis of Nonintegrin Laminin Receptor Interacting Proteins. J. Proteome Res. 2012, 11, 4863–4872. [Google Scholar] [CrossRef]
- Peng, S.Y.; Hsu, H.C. ALDOB (aldolase B, fructose-bisphosphate). Atlas Genet. Cytogenet. Oncol. Haematol. 2009, 13, 704–708. [Google Scholar] [CrossRef]
- Jaakkola, M.K.; Seyednasrollah, F.; Mehmood, A.; Elo, L.L. Comparison of methods to detect differentially expressed genes between single-cell populations. Brief. Bioinform. 2017, 18, 735–743. [Google Scholar] [CrossRef]
| Case Study (CS) ID | (↑ ) | (↓ ) | (↑ ) | (↑ ) | |
|---|---|---|---|---|---|
| CS1 | 2 | 0.482 | 0.578 | 0.607 | 0.215 |
| CS2 | 3 | 0.543 | 0.886 | 0.482 | 0.224 |
| CS3 | 4 | 0.588 | 0.117 | 0.373 | 0.164 |
| CS4 | 5 | 0.632 | 0.139 | 0.304 | 0.130 |
| CS5 | 6 | 0.333 | 0.157 | 0.246 | 0.095 |
| CS6 | 7 | 0.364 | 0.172 | 0.215 | 0.085 |
| CS7 | 8 | 0.340 | 0.185 | 0.190 | 0.075 |
| CS8 | 9 | 0.328 | 0.197 | 0.165 | 0.061 |
| CS9 | 10 | 0.267 | 0.209 | 0.153 | 0.059 |
| Case Study (CS) ID | TOPSIS Optimal Score | Optimal Rank | |
|---|---|---|---|
| CS1 | 2 | 0.858 | 1 |
| CS2 | 3 | 0.798 | 2 |
| CS3 | 4 | 0.602 | 3 |
| CS4 | 5 | 0.481 | 4 |
| CS5 | 6 | 0.236 | 5 |
| CS6 | 7 | 0.186 | 6 |
| CS7 | 8 | 0.123 | 7 |
| CS8 | 9 | 0.070 | 8 |
| CS9 | 10 | 0 | 9 |
| Cluster ID | # Cells | Cell IDs |
|---|---|---|
| Cluster 1 | 115 | I_1, I_2, I_3, I_4, I_5, I_7, I_12, I_13, I_15, I_17, I_20, I_23, I_26, I_27, I_28, I_30, I_32, I_35, I_36, I_39, I_40, I_41, I_42, I_43, I_44, I_45, I_47, I_48, I_49, I_51, I_52, I_53, I_54, I_55, I_56, I_58, I_59, I_61, I_62, I_66, I_67, I_68, I_70, I_71, I_72, I_73, I_75, I_76, I_77, I_79, I_80, I_81, I_86, I_87, I_92, I_93, I_96, II_1, II_3, II_4, II_11, II_17, II_18, II_20, II_24, II_27, II_28, II_31, II_34, II_39, II_40, II_41, II_42, II_44, II_46, II_48, II_56, II_57, II_58, II_66, II_69, II_73, II_74, II_75, II_76, II_79, II_80, II_83, II_87, II_88, II_89, II_95, III_10, III_14, III_16, III_21, III_35, III_36, III_39, III_40, III_45, III_46, III_49, III_51, III_54, III_55, III_56, III_59, III_68, III_74, III_79, III_82, III_84, III_89, III_95 |
| Cluster 2 | 91 | I_6, I_8, I_9, I_10, I_14, I_16, I_19, I_21, I_22, I_24, I_25, I_29, I_37, I_38, I_50, I_57, I_64, I_65, I_69, I_78, I_82, I_83, I_84, I_85, I_88, I_89, I_91, I_94, I_95, II_2, II_5, II_6, II_8, II_9, II_10, II_12, II_13, II_14, II_15, II_19, II_21, II_23, II_26, II_30, II_33, II_36, II_37, II_47, II_51, II_52, II_53, II_54, II_59, II_62, II_63, II_64, II_67, II_68, II_70, II_72, II_77, II_78, II_85, II_93, III_1, III_8, III_17, III_23, III_25, III_28, III_29, III_33, III_34, III_38, III_47, III_48, III_58, III_64, III_66, III_67, III_70, III_71, III_72, III_73, III_75, III_78, III_81, III_83, III_87, III_88, III_91 |
| KEGG Pathway | Count | p-Value | Bonferroni p-Value | Gene Symbols |
|---|---|---|---|---|
| mmu03010:Ribosome | 94 | 3.91 | 1.08 | RPL18, RPL17, RPL36A, RPL19, RPL14, RPL13, RPL15, RPLP2, RPS27L, RPL22L1, etc. |
| mmu03040:Spliceosome | 54 | 3.72 | 1.02 | SRSF1, LSM6, U2AF2, SNRPD3, LSM7, SNRPD1, SNRPD2, RBM8A, PCBP1, U2AF1, etc. |
| mmu01130:Biosynthesis of antibiotics | 52 | 5.87 | 1.61 | SC5D, LDHA, EHHADH, PGAM1, OGDH, CMBL, PKM, IDH3G, PDHA1, CAT, etc. |
| mmu03050:Proteasome | 21 | 3.95 | 1.09 | SHFM1, PSMB5, PSMA2, PSMB4, PSMA1, PSMD14, PSMB7, PSMB6, PSMC5, PSMB1, etc. |
| mmu01200:Carbon metabolism | 33 | 5.49 | 1.51 | ALDOA, ALDOC, EHHADH, ALDOB, PGAM1, OGDH, GPI1, ACAT1, PKM, TPI1, etc. |
| mmu00010:Glycolysis /Gluconeogenesis | 23 | 3.32 | 9.13 | ALDOA, LDHA, ALDOC, HKDC1, ALDOB, FBP1, PGAM1, PFKP, FBP2, GPI1, etc. |
| mmu01100:Metabolic pathways | 168 | 7.42 | 2.04 | CYP2C66, CYP2C65, GDA, LDHA, SC5D, CNDP2, EHHADH, CYP2C68, DTYMK, PGAM1, etc. |
| mmu00480:Glutathione metabolism | 20 | 1.51 | 4.16 | GSTA1, GSTA2, ODC1, GSTA4, SRM, GGT1, ANPEP, GSTM6, GSTM1, GPX2, etc. |
| mmu05204:Chemical carcinogenesis | 26 | 3.58 | 9.85 | CYP2C66, CYP2C65, CYP3A25, CYP2C68, GSTM6, GSTM1, GSTM3, CBR1, GSTM4, ADH1, etc. |
| mmu01230:Biosynthesis of amino acids | 22 | 2.30 | 6.33 | ALDOA, SHMT2, MAT2A, ALDOC, ALDOB, PFKP, PGAM1, CPS1, IDH3A, PKM, etc. |
| Gene Ontology | Count | p-Value | Bonferroni Correction | Gene Symbols |
|---|---|---|---|---|
| GO:BP : GO:0006412 translation | 145 | 3.83 | 1.34 | RPL18, RPL17, RPL36A, RPL19, RPL14, RPL13, RBM3, EIF5, RPL15, EIF5A, etc. |
| GO:BP : GO:0008380 RNA splicing | 67 | 2.68 | 9.38 | RALY, SRSF1, LSM6, SNRPD3, U2AF2, SNRPD1, SYNCRIP, SNRPD2, YBX1, NONO, etc. |
| GO:BP : GO:0006397 mRNA processing | 75 | 3.36 | 1.18 | RALY, SRSF1, LSM6, U2AF2, SNRPD3, SNRPD1, SYNCRIP, SNRPD2, YBX1, NONO, etc. |
| GO:BP : GO:0055114 oxidation-reduction process | 101 | 2.51 | 8.79 | SC5D, LDHA, EHHADH, OGDH, UQCR10, IDH3G, CPOX, PDHA1, HADH, NQO1, etc. |
| GO:BP : GO:0006413 translational initiation | 25 | 1.07 | 3.88 | ABCE1, EIF5, DENR, EIF1A, LARP1, EIF4B, EIF4G2, EIF3D, EIF3A, EIF3B, etc. |
| GO:CC : GO:0030529 intracellular ribonucleoprotein complex | 151 | 1.35 | 9.24 | RPL18, MRPL40, RALY, SRP14, RPL17, MRPL42, RPL19, RPL14, RPL13, SNRPD3, etc. |
| GO:CC : GO:0070062 extracellular exosome | 401 | 3.28 | 2.26 | PRDX5, PRDX2, RPS2, SYNGR2, PTMA, RPS3, SLC1A5, RHOC, TREH, CAT, etc. |
| GO:CC : GO:0005840 ribosome | 101 | 3.93 | 2.70 | RPL18, MRPL40, RPL17, RPL36A, MRPL42, RPL19, RPL14, RPL13, RPL15, RPLP2, etc. |
| GO:CC : GO:0022625 cytosolic large ribosomal subunit | 50 | 1.34 | 9.19 | RPL18, RPL17, RPL36A, RPL19, RPL14, RPL13, RPL15, RPLP2, RPL22L1, RPLP0, etc. |
| GO:CC : GO:0005730 nucleolus | 148 | 1.01 | 6.91 | RPL18, MRPL40, RPL19, LSM6, RBM3, MORF4L2, CBX5, NONO, EBNA1BP2, IMP3, etc. |
| GO:MF : GO:0044822 poly(A) RNA binding | 295 | 5.08 | 6.64 | RPS25, RPS26, RPS28, PABPC1, RPS20, RPS21, RPS23, HNRNPAB, RPS24, DHX9, etc. |
| GO:MF : GO:0003735 structural constituent of ribosome | 104 | 2.15 | 2.81 | RPL18, RPL17, RPL36A, RPL19, RPL14, RPL13, RPL15, RPLP2, RPS27L, RPL22L1, etc. |
| GO:MF : GO:0003723 RNA binding | 165 | 5.82 | 7.61 | RPL18, RALY, SRP14, RPL13, SNRPD3, U2AF2, LSM6, RBM3, LSM7, SNRPD1, etc. |
| GO:MF : GO:0003729 mRNA binding | 46 | 6.85 | 8.95 | SRSF1, TRA2B, RPL35, RPS2, YBX1, RPS3, HNRNPA3, RPS26, MRPL13, EIF3A, etc. |
| GO:MF : GO:0098641 cadherin binding involved in cell-cell adhesion | 64 | 4.66 | 6.09 | HSP90AB1, LDHA, RPL14, RPL15, EIF5, PDLIM1, RANGAP1, RPS2, LARP1, BZW2, etc. |
| Gene | Literature Evidence | KEGG Pathway & Gene Ontology Terms | Status |
|---|---|---|---|
| (Connected with) | |||
| Rps21 | Biological functions: artificial nucleic acid molecules [56], exosome and human ribosome biogenesis [57], arterial vasculature [58] | KEGG pathway: Ribosome (p-value = 3.91 ), GO:BP: GO:0006412 translation (p-value = 3.83 ), GO:CC: GO:0005622 intracellular (p-value = 6.8 ), GO:0022627 cytosolic small ribosomal subunit (p-value = 8.99 ), GO:MF: GO:0003735 structural constituent of ribosome (p-value = 2.15 ), GO:0044822 poly(A) RNA binding (p-value = 5.08 ). | Known |
| Slc5a1 | Solute carriers [59] | KEGG pathway: Mineral absorption (p-value = 1.11 ), mmu04973: Carbohydrate digestion and absorption (p-value = 9.90 ), GO:BP: GO:0006810 transport (p-value = 2.01 ), GO:0001951 intestinal D-glucose absorption (p-value = 2.01 ), GO:CC: GO:0070062 extracellular exosome (p-value = 3.28 ), GO:MF: GO:0015293 symporter activity (p-value = 1.93 ). | Known |
| Crip1 | Xenopus laevis embryogenesis [60] | GO:CC: GO:0005737 cytoplasm (p-value = 6.06 ), GO:MF: GO:0008301 DNA binding, bending (p-value = 2.11 ), GO:0042277 peptide binding (p-value = 4.27 ). | Known |
| Rpl15 | Artificial nucleic acid molecules [56] | KEGG pathway: Ribosome (pval=3.91 ), GO:BP: GO:0098609 cell-cell adhesion (p-value = 5.06 ), GO:0002181 cytoplasmic translation (p-value = 2.91 ), GO:CC: GO:0005739 mitochondrion (p-value = 2.25 ), GO:0030529 intracellular ribonucleoprotein complex (p-value = 1.35 ), GO:0070062 extracellular exosome (p-value = 3.28 ), GO:MF: GO:0003735 structural constituent of ribosome (p-value = 2.15 ). | Known |
| Rpl3 | Artificial nucleic acid molecules [56] | KEGG pathway: Ribosome (p-value = 3.91 ), GO:BP: GO:0002181 cytoplasmic translation (p-value = 2.91 ), GO:0042254 ribosome biogenesis (p-value = 1.81 ), GO:CC: GO:0070062 extracellular exosome (p-value = 3.28 ), GO:0031012 extracellular matrix (p-value = 2.06 ), GO:0005761 mitochondrial ribosome (p-value = 2.56 ), GO:MF: GO:0003735 structural constituent of ribosome (p-value = 2.15 ). | Known |
| Rpl27a | Arterial vasculature [58] | KEGG pathway: Ribosome (p-value = 3.91 ), GO:BP: GO:0006412 translation (p-value = 3.83 ), GO:CC: GO:0022626 cytosolic ribosome (p-value = 5.88 ), GO:0022625 cytosolic large ribosomal subunit (p-value = 1.34 ), GO:MF: GO:0003735 structural constituent of ribosome (p-value = 2.15 ). | Known |
| Rps3a1 | - | KEGG pathway: Ribosome (p-value = 3.91 ), GO:BP: GO:0006412 translation (p-value = 3.83 ), GO:0043066 negative regulation of apoptotic process (p-value = 5.39 ), GO:CC: GO:0070062 extracellular exosome (p-value = 3.28 ), GO:0022627 cytosolic small ribosomal subunit (p-value = 8.99 ), GO:0030529 intracellular ribonucleoprotein complex (p-value = 1.35 ), GO:MF: GO:0044822 poly(A) RNA binding (p-value = 5.08 ). | Known |
| Rps17 | Different biological functions: proteomic analysis [56,57,58,61] | KEGG pathway: Ribosome (p-value = 3.91 ), GO:BP: GO:0000028 ribosomal small subunit assembly (p-value = 1.17 ), GO:CC: GO:0070062 extracellular exosome (p-value = 3.28 ), GO:0005739 mitochondrion (p-value = 2.25 ), GO:0031012 extracellular matrix (p-value = 2.06 ), GO:MF: GO:0003735 structural constituent of ribosome (p-value = 2.15 ). | Known |
| Aldob | Hepatocellular cellular carcinoma [62]. | - | Known |
| Khk | - | - | Novel |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallik, S.; Zhao, Z. Multi-Objective Optimized Fuzzy Clustering for Detecting Cell Clusters from Single-Cell Expression Profiles. Genes 2019, 10, 611. https://doi.org/10.3390/genes10080611
Mallik S, Zhao Z. Multi-Objective Optimized Fuzzy Clustering for Detecting Cell Clusters from Single-Cell Expression Profiles. Genes. 2019; 10(8):611. https://doi.org/10.3390/genes10080611
Chicago/Turabian StyleMallik, Saurav, and Zhongming Zhao. 2019. "Multi-Objective Optimized Fuzzy Clustering for Detecting Cell Clusters from Single-Cell Expression Profiles" Genes 10, no. 8: 611. https://doi.org/10.3390/genes10080611
APA StyleMallik, S., & Zhao, Z. (2019). Multi-Objective Optimized Fuzzy Clustering for Detecting Cell Clusters from Single-Cell Expression Profiles. Genes, 10(8), 611. https://doi.org/10.3390/genes10080611





