Computational Methods for Detection of Differentially Methylated Regions Using Kernel Distance and Scan Statistics
Abstract
1. Introduction
2. Materials and Methods
2.1. Kernel Distance Method
2.2. Binomial Scan Statistic Method
2.3. Simulation
Simulation Parameters
3. Results
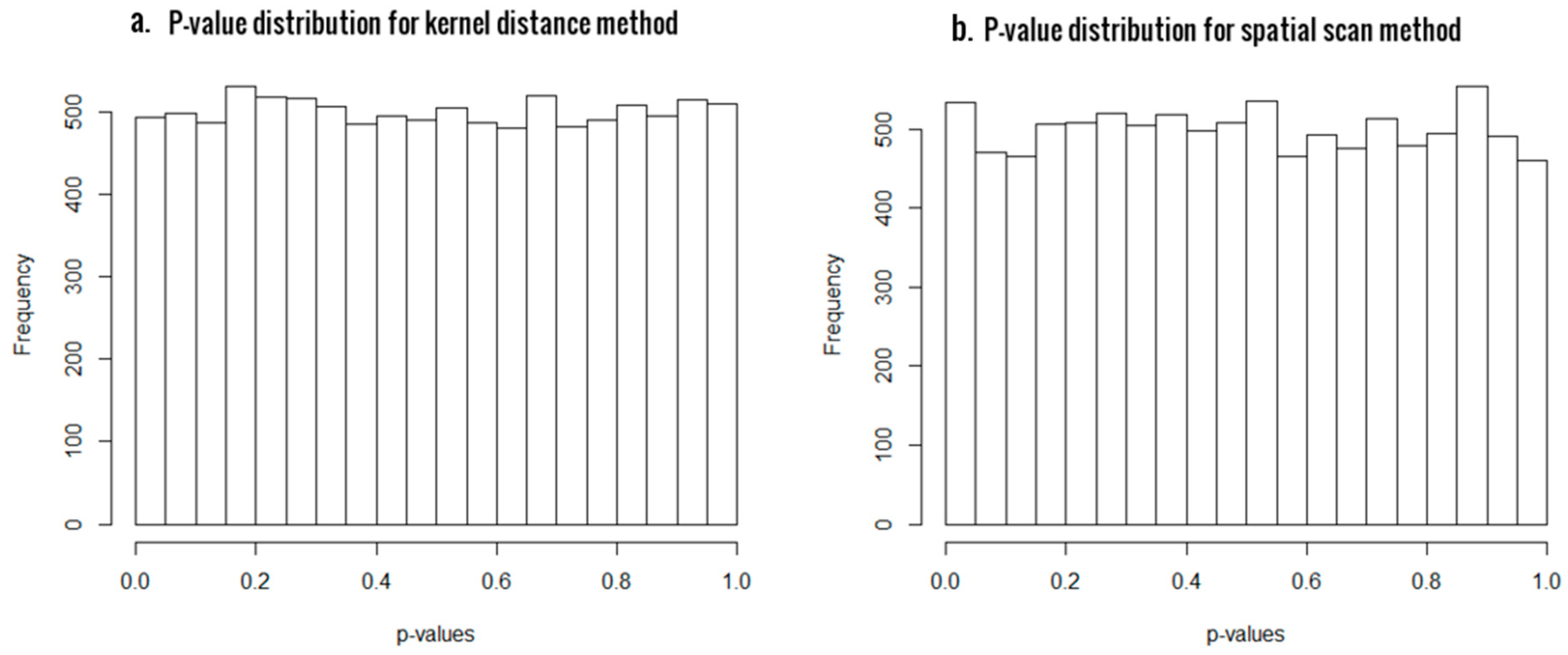
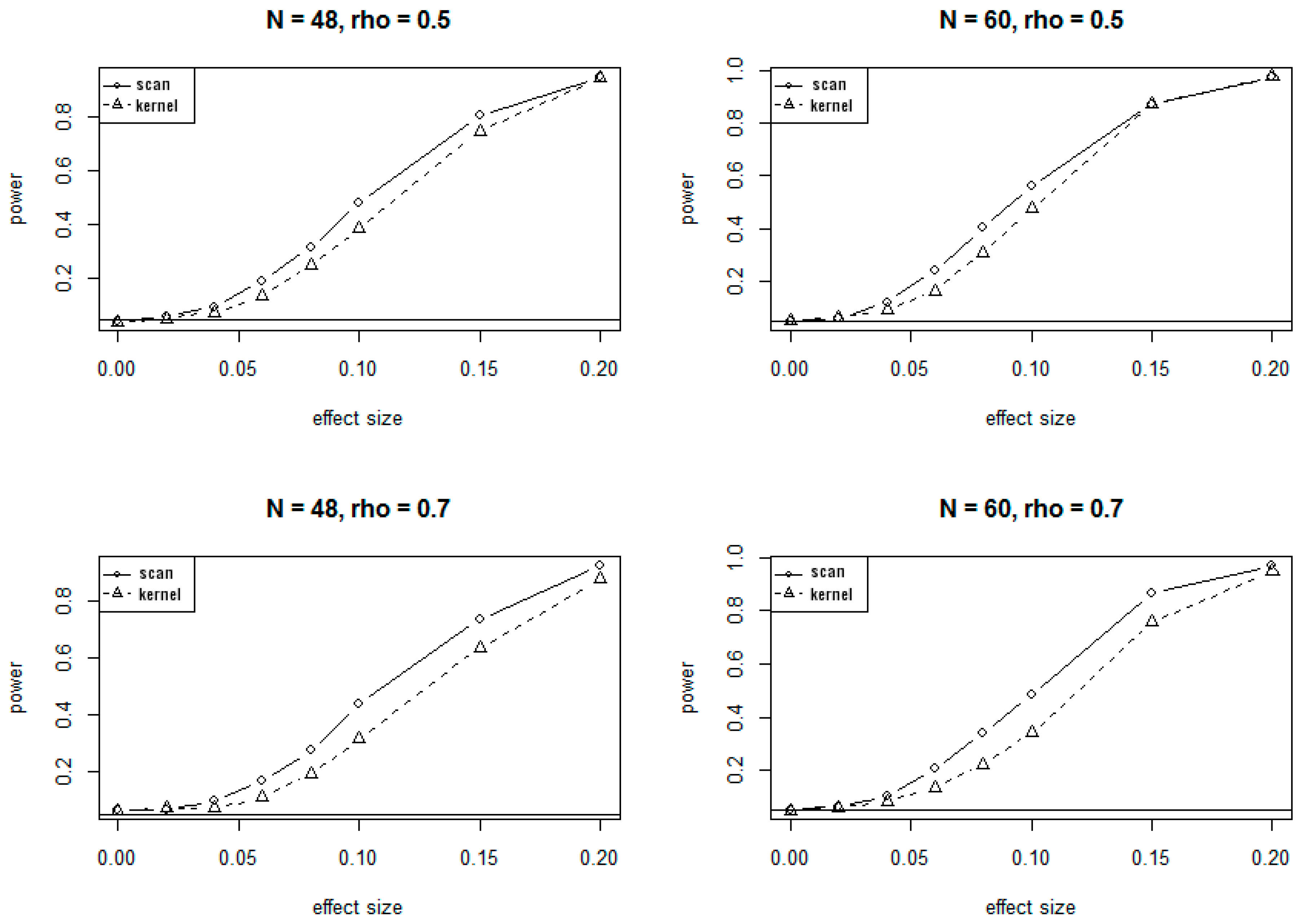
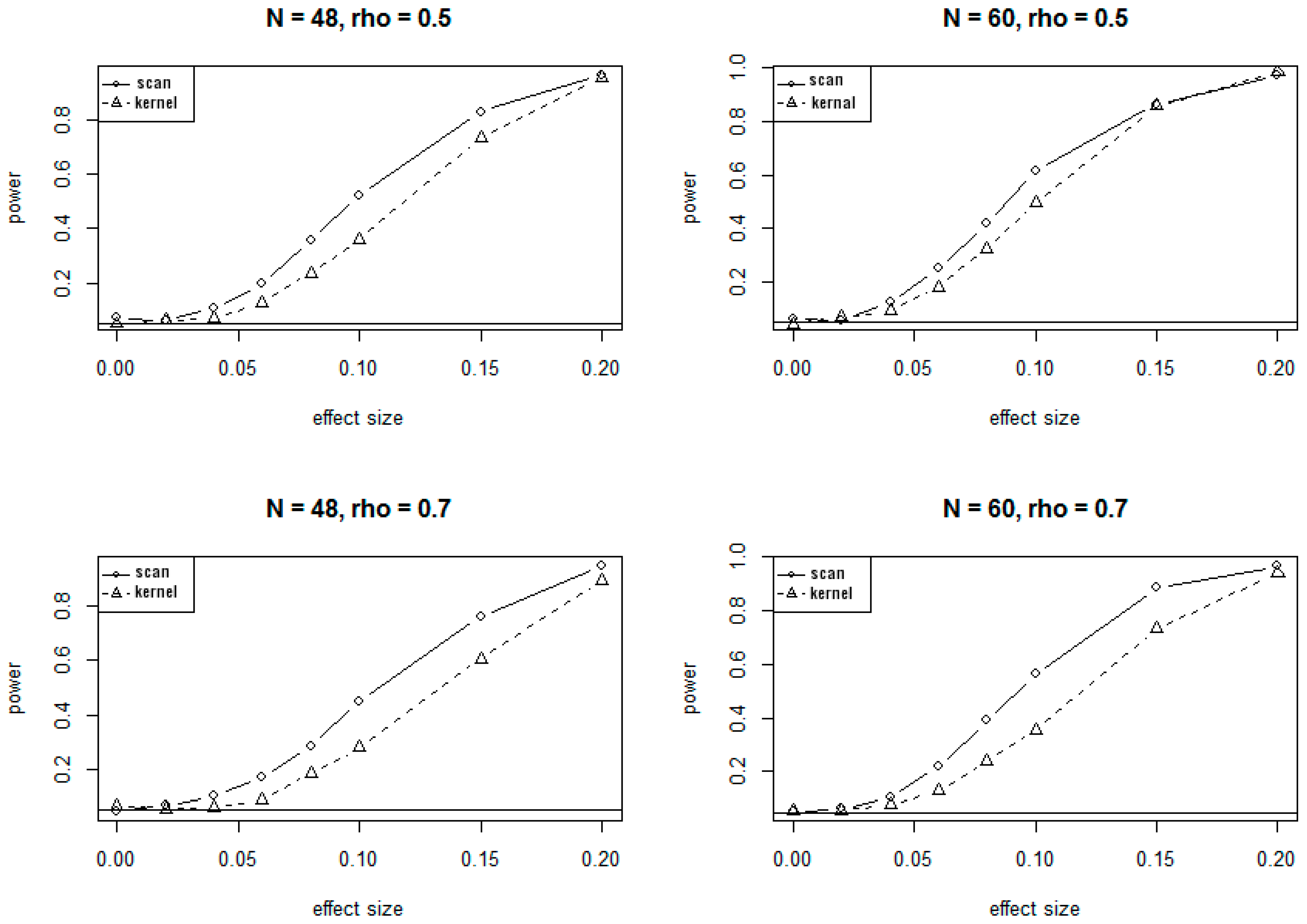
3.1. Simulation Results
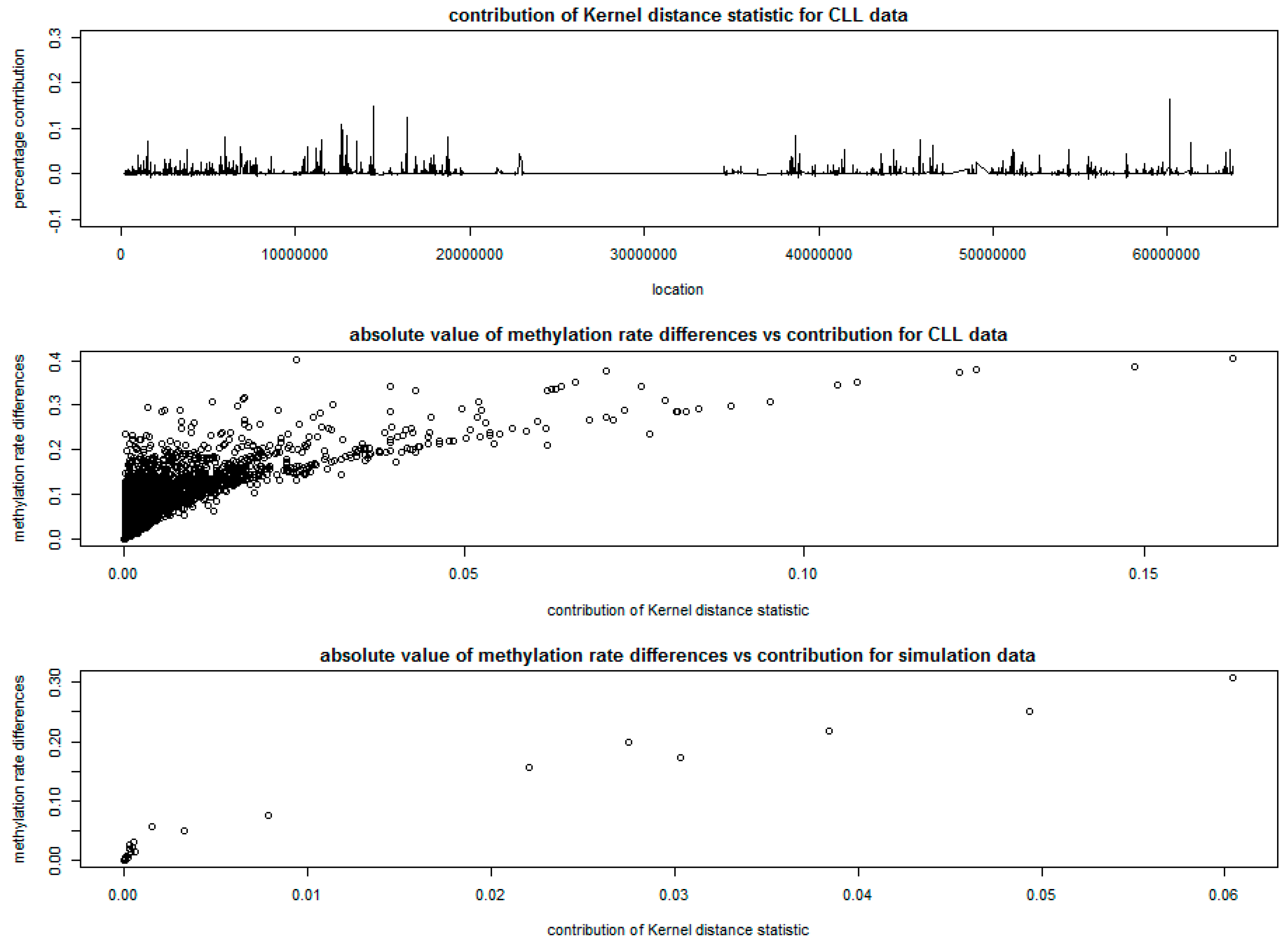
3.2. Analysis of Chronic Lymphocytic Leukemia Data
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
A.1. Adjusting for Correlation Between CpG sites with Mixed-Effects Model
A.2. Adjusting for Clustering Structure Within Each CpG Site
A.3. Binomial Scan Statistic for Case-Control Studies
A.4. SSM for Multinomial Responses
References
- Hindorff, L.A.; Sethupathy, P.; Junkins, H.A.; Ramos, E.M.; Mehta, J.P.; Collins, F.S.; Manolio, T.A. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. USA 2009, 106, 9362–9367. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.A.; Baylin, S.B. The epigenomics of cancer. Cell 2007, 128, 683–692. [Google Scholar] [CrossRef]
- Stricker, S.H.; Feber, A.; Engstrom, P.G.; Caren, H.; Kurian, K.M.; Takashima, Y.; Watts, C.; Way, M.; Dirks, P.; Bertone, P.; et al. Widespread resetting of DNA methylation in glioblastoma-initiating cells suppresses malignant cellular behavior in a lineage-dependent manner. Genes Dev. 2013, 27, 654–669. [Google Scholar] [CrossRef]
- Eckhardt, F.; Lewin, J.; Cortese, R.; Rakyan, V.K.; Attwood, J.; Burger, M.; Burton, J.; Cox, T.V.; Davies, R.; Down, T.A.; et al. DNA methylation profiling of human chromosomes 6, 20 and 22. Nat. Genet. 2006, 38, 1378–1385. [Google Scholar] [CrossRef]
- Leek, J.T.; Scharpf, R.B.; Bravo, H.C.; Simcha, D.; Langmead, B.; Johnson, W.E.; Geman, D.; Baggerly, K.; Irizarry, R.A. Tackling the widespread and critical impact of batch effects in high-throughput data. Nat. Rev. Genet. 2010, 11, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, A.E.; Murakami, P.; Lee, H.; Leek, J.T.; Fallin, M.D.; Feinberg, A.P.; Irizarry, R.A. Bump hunting to identify differentially methylated regions in epigenetic epidemiology studies. Int. J. Epidemiol. 2012, 41, 200–209. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.D.; Langmead, B.; Irizarry, R.A. BSmooth: From whole genome bisulfite sequencing reads to differentially methylated regions. Genome Biol. 2012, 13, R83. [Google Scholar] [CrossRef]
- Hebestreit, K.; Dugas, M.; Klein, H.U. Detection of significantly differentially methylated regions in targeted bisulfite sequencing data. Bioinformatics 2013, 29, 1647–1653. [Google Scholar] [CrossRef]
- Ryu, D.; Xu, H.; George, V.; Su, S.; Wang, X.; Shi, H.; Podolsky, R.H. Differential methylation tests of regulatory regions. Stat. Appl. Genet. Mol. Biol. 2016, 15, 237–251. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.T.; Tsai, P.C.; Yang, T.P.; Pidsley, R.; Nisbet, J.; Glass, D.; Mangino, M.; Zhai, G.; Zhang, F.; Valdes, A.; et al. Epigenome-wide scans identify differentially methylated regions for age and age-related phenotypes in a healthy ageing population. PLoS Genet. 2012, 8, e1002629. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Menon, U.; Gentry-Maharaj, A.; Ramus, S.J.; Weisenberger, D.J.; Shen, H.; Campan, M.; Noushmehr, H.; Bell, C.G.; Maxwell, A.P.; et al. Age-dependent DNA methylation of genes that are suppressed in stem cells is a hallmark of cancer. Genome Res. 2010, 20, 440–446. [Google Scholar] [CrossRef]
- Kibriya, M.G.; Raza, M.; Jasmine, F.; Roy, S.; Paul-Brutus, R.; Rahaman, R.; Dodsworth, C.; Rakibuz-Zaman, M.; Kamal, M.; Ahsan, H. A genome-wide DNA methylation study in colorectal carcinoma. BMC Med. Genom. 2011, 4, 50. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Morgan, M.; Hutchison, K.; Calhoun, V.D. A study of the influence of sex on genome wide methylation. PLoS ONE 2010, 5, e10028. [Google Scholar] [CrossRef] [PubMed]
- Tango, T. The detection of disease clustering in time. Biometrics 1984, 40, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Schaid, D.J.; Sinnwell, J.P.; McDonnell, S.K.; Thibodeau, S.N. Detecting genomic clustering of risk variants from sequence data: Cases versus controls. Hum. Genet. 2013, 132, 1301–1309. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Naus, J.I. The distribution of the size of the maximum cluster of points on a line. J. Am. Stat. Assoc. 1965, 60, 532–538. [Google Scholar] [CrossRef]
- Kulldorff, M. A spatial scan statistic. Commun. Stat. Theory Methods 1997, 26, 1481–1496. [Google Scholar] [CrossRef]
- Ionita-Laza, I.; Makarov, V.; Consortium, A.A.S.; Buxbaum, J.D. Scan-statistic approach identifies clusters of rare disease variants in LRP2, a gene linked and associated with autism spectrum disorders, in three datasets. Am. J. Hum. Genet. 2012, 90, 1002–1013. [Google Scholar] [CrossRef] [PubMed]
- Pei, L.; Choi, J.H.; Liu, J.; Lee, E.J.; McCarthy, B.; Wilson, J.M.; Speir, E.; Awan, F.; Tae, H.; Arthur, G.; et al. Genome-wide DNA methylation analysis reveals novel epigenetic changes in chronic lymphocytic leukemia. Epigenetics 2012, 7, 567–578. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tango, T. A test for spatial disease clustering adjusted for multiple testing. Stat. Med. 2000, 19, 191–204. [Google Scholar] [CrossRef]
- Xu, H.; Podolsky, R.H.; Ryu, D.; Wang, X.; Su, S.; Shi, H.; George, V. A method to detect differentially methylated loci with next-generation sequencing. Genet. Epidemiol. 2013, 37, 377–382. [Google Scholar] [CrossRef]
- Rao, J.N.; Scott, A.J. A simple method for the analysis of clustered binary data. Biometrics 1992, 48, 577–585. [Google Scholar] [CrossRef] [PubMed]
- Lacey, M.R.; Baribault, C.; Ehrlich, M. Modeling, simulation and analysis of methylation profiles from reduced representation bisulfite sequencing experiments. Stat. Appl. Genet. Mol. Biol. 2013, 12, 723–742. [Google Scholar] [CrossRef] [PubMed]
- Dohner, H.; Stilgenbauer, S.; Benner, A.; Leupolt, E.; Krober, A.; Bullinger, L.; Dohner, K.; Bentz, M.; Lichter, P. Genomic aberrations and survival in chronic lymphocytic leukemia. N. Engl. J. Med. 2000, 343, 1910–1916. [Google Scholar] [CrossRef] [PubMed]
- Hamblin, T.J.; Davis, Z.; Gardiner, A.; Oscier, D.G.; Stevenson, F.K. Unmutated Ig V(H) genes are associated with a more aggressive form of chronic lymphocytic leukemia. Blood 1999, 94, 1848–1854. [Google Scholar] [PubMed]
- Hamblin, T.J.; Orchard, J.A.; Gardiner, A.; Oscier, D.G.; Davis, Z.; Stevenson, F.K. Immunoglobulin V genes and CD38 expression in CLL. Blood 2000, 95, 2455–2457. [Google Scholar]
- Damle, R.N.; Wasil, T.; Fais, F.; Ghiotto, F.; Valetto, A.; Allen, S.L.; Buchbinder, A.; Budman, D.; Dittmar, K.; Kolitz, J.; et al. Ig V gene mutation status and CD38 expression as novel prognostic indicators in chronic lymphocytic leukemia. Blood 1999, 94, 1840–1847. [Google Scholar]
- Meissner, A.; Gnirke, A.; Bell, G.W.; Ramsahoye, B.; Lander, E.S.; Jaenisch, R. Reduced representation bisulfite sequencing for comparative high-resolution DNA methylation analysis. Nucleic Acids Res. 2005, 33, 5868–5877. [Google Scholar] [CrossRef]
- Shaw, D.J.; Harley, H.G.; Brook, J.D.; McKeithan, T.W. Long-range restriction map of a region of human chromosome 19 containing the apolipoprotein genes, a CLL-associated translocation breakpoint, and two polymorphic MluI sites. Hum. Genet. 1989, 83, 71–74. [Google Scholar] [CrossRef]
- Wallingford, M.C.; Filkins, R.; Adams, D.; Walentuk, M.; Salicioni, A.M.; Visconti, P.E.; Mager, J. Identification of a novel isoform of the leukemia-associated MLLT1 (ENL/LTG19) protein. Gene Expr. Patterns 2015, 17, 11–15. [Google Scholar] [CrossRef]
- Chin, L.K.; Cheah, C.Y.; Michael, P.M.; MacKinnon, R.N.; Campbell, L.J. 11q23 rearrangement and duplication of MLLT1-MLL gene fusion in therapy-related acute myeloid leukemia. Leuk. Lymphoma 2012, 53, 2066–2068. [Google Scholar] [CrossRef] [PubMed]
- Doty, R.T.; Vanasse, G.J.; Disteche, C.M.; Willerford, D.M. The leukemia-associated gene MLLT1/ENL: characterization of a murine homolog and demonstration of an essential role in embryonic development. Blood Cells Mol. Dis. 2002, 28, 407–417. [Google Scholar] [CrossRef] [PubMed]
- Crans-Vargas, H.N.; Landaw, E.M.; Bhatia, S.; Sandusky, G.; Moore, T.B.; Sakamoto, K.M. Expression of cyclic adenosine monophosphate response-element binding protein in acute leukemia. Blood 2002, 99, 2617–2619. [Google Scholar] [CrossRef] [PubMed]
- Mayr, B.; Montminy, M. Transcriptional regulation by the phosphorylation-dependent factor CREB. Nat. Rev. Mol. Cell Biol. 2001, 2, 599–609. [Google Scholar] [CrossRef] [PubMed]
- Chae, H.D.; Mitton, B.; Lacayo, N.J.; Sakamoto, K.M. Replication factor C3 is a CREB target gene that regulates cell cycle progression through the modulation of chromatin loading of PCNA. Leukemia 2015, 29, 1379–1389. [Google Scholar] [CrossRef] [PubMed]
- Kang, X.; Lu, Z.; Cui, C.; Deng, M.; Fan, Y.; Dong, B.; Han, X.; Xie, F.; Tyner, J.W.; Coligan, J.E.; et al. The ITIM-containing receptor LAIR1 is essential for acute myeloid leukaemia development. Nat. Cell Biol 2015, 17, 665–677. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, D.; Phillips, J.M.; Venkatasubramanian, S. The hunting of the bump: on maximizing statistical discrepancy. In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm; Society for Industrial and Applied Mathematics: Miami, FL, USA, 2006; pp. 1137–1146. [Google Scholar]
| Significance Level | 0.05 | 0.01 | |||||
|---|---|---|---|---|---|---|---|
| Total Sample Sizes | Total Number of Sites | KDM | SSM | KDM | SSM | ||
| 48 | 24 | 0.1 | 0.5 | 0.053 | 0.056 | 0.013 | 0.014 |
| 48 | 24 | 0.1 | 0.7 | 0.0514 | 0.0518 | 0.0116 | 0.0125 |
| Start | End | Window Size | p-Value | Start | End | Window Size | p-Value |
|---|---|---|---|---|---|---|---|
| 951,756 | 960,480 | 15 | 0.001 | 40,495,154 | 40,706,271 | 40 | 0.033 |
| 5,748,848 | 5,855,704 | 35 | 0.024 | 40,958,295 | 40,995,281 | 15 | 0.028 |
| 5,949,493 | 6,059,920 | 15 | 0.037 | 41,323,151 | 41,345,137 | 5 | 0.027 |
| 6,222,967 | 6,325,326 | 40 | 0.042 | 42,400,872 | 42,516,823 | 25 | 0.023 |
| 6,695,897 | 6,704,448 | 5 | 0.039 | 42,631,539 | 42,651,999 | 10 | 0.022 |
| 7,049,880 | 7,149,391 | 20 | 0.042 | 43,411,447 | 43,472,750 | 70 | 0.023 |
| 8,306,311 | 8,416,558 | 105 | 0.02 | 44,099,619 | 44,158,078 | 10 | 0.003 |
| 10,078,223 | 10,091,192 | 15 | 0.049 | 45,388,832 | 45,464,209 | 30 | 0.007 |
| 10,261,108 | 10,336,402 | 75 | 0.048 | 45,812,107 | 45,821,840 | 5 | 0.005 |
| 10,366,854 | 10,374,990 | 5 | 0.011 | 46,555,659 | 46,595,121 | 5 | 0.007 |
| 10,529,295 | 10,537,824 | 5 | 0.033 | 47,040,515 | 47,078,316 | 5 | 0.008 |
| 11,311,211 | 11,369,166 | 35 | 0.046 | 50,778,928 | 50,793,474 | 5 | 0.021 |
| 11,852,835 | 11,937,174 | 15 | 0.012 | 51,010,992 | 51,058,089 | 10 | 0.029 |
| 12,036,638 | 12,128,243 | 10 | 0.019 | 51,059,619 | 51,079,866 | 15 | 0.026 |
| 13,780,707 | 13,818,691 | 30 | 0.035 | 51,409,109 | 51,427,742 | 5 | 0.027 |
| 15,871,811 | 15,874,720 | 5 | 0.033 | 53,821,358 | 53,829,676 | 15 | 0.001 |
| 16,211,533 | 16,298,141 | 10 | 0.008 | 53,914,126 | 53,934,314 | 20 | 0.011 |
| 16,779,596 | 16,818,698 | 5 | 0.049 | 53,946,213 | 53,983,289 | 5 | 0.033 |
| 17,181,376 | 17,207,209 | 20 | 0.032 | 54,819,984 | 54,835,037 | 5 | 0.035 |
| 17,483,944 | 17,492,848 | 5 | 0.027 | 54,872,826 | 54,884,388 | 10 | 0.033 |
| 18,358,107 | 18,358,200 | 5 | 0.018 | 55,714,472 | 55,760,862 | 15 | 0.047 |
| 18,839,769 | 18,849,925 | 40 | 0.037 | 55,853,400 | 55,911,789 | 30 | 0.046 |
| 19,196,863 | 19,220,558 | 10 | 0.001 | 56,884,684 | 56,887,726 | 5 | 0.002 |
| 20,751,241 | 20,751,405 | 10 | 0.016 | 58,388,434 | 58,388,478 | 5 | 0.006 |
| 21,443,528 | 21,449,542 | 5 | 0.042 | 58,980,127 | 59,064,230 | 15 | 0.007 |
| 35,558,112 | 35,558,143 | 5 | 0.014 | 59,643,525 | 59,652,071 | 5 | 0.002 |
| 37,528,315 | 37,528,707 | 10 | 0.035 | 59,652,664 | 59,666,539 | 15 | 0.011 |
| 37,808,618 | 37,858,100 | 10 | 0.019 | 60,109,922 | 60,545,979 | 205 | 0.04 |
| 38,315,030 | 38,359,639 | 10 | 0.012 | 60,790,219 | 60,808,074 | 15 | 0.015 |
| 38,576,223 | 38,632,218 | 20 | 0.001 | 61,304,533 | 61,424,810 | 55 | 0.013 |
| 38,980,210 | 39,003,767 | 20 | 0.043 | 61,741,700 | 61,798,595 | 20 | 0.048 |
| 39,760,398 | 39,760,441 | 5 | 0.022 | 62,277,420 | 62,310,019 | 5 | 0.019 |
| 40,193,224 | 40,214,045 | 25 | 0.046 | 63,565,854 | 63,570,870 | 10 | 0.035 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunbar, F.; Xu, H.; Ryu, D.; Ghosh, S.; Shi, H.; George, V. Computational Methods for Detection of Differentially Methylated Regions Using Kernel Distance and Scan Statistics. Genes 2019, 10, 298. https://doi.org/10.3390/genes10040298
Dunbar F, Xu H, Ryu D, Ghosh S, Shi H, George V. Computational Methods for Detection of Differentially Methylated Regions Using Kernel Distance and Scan Statistics. Genes. 2019; 10(4):298. https://doi.org/10.3390/genes10040298
Chicago/Turabian StyleDunbar, Faith, Hongyan Xu, Duchwan Ryu, Santu Ghosh, Huidong Shi, and Varghese George. 2019. "Computational Methods for Detection of Differentially Methylated Regions Using Kernel Distance and Scan Statistics" Genes 10, no. 4: 298. https://doi.org/10.3390/genes10040298
APA StyleDunbar, F., Xu, H., Ryu, D., Ghosh, S., Shi, H., & George, V. (2019). Computational Methods for Detection of Differentially Methylated Regions Using Kernel Distance and Scan Statistics. Genes, 10(4), 298. https://doi.org/10.3390/genes10040298






