Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Materials
2.2. Determination of Antioxidants Concentration and Statistical Inferences
2.3. DNA Extraction
2.4. Whole-Genome GBS SNP Genotyping and Population Structure
2.5. GS Models and Prediction Accuracy
3. Results
3.1. Phenotypic Performance and Diversity
3.2. GBS SNP Whole-Genome Genotyping
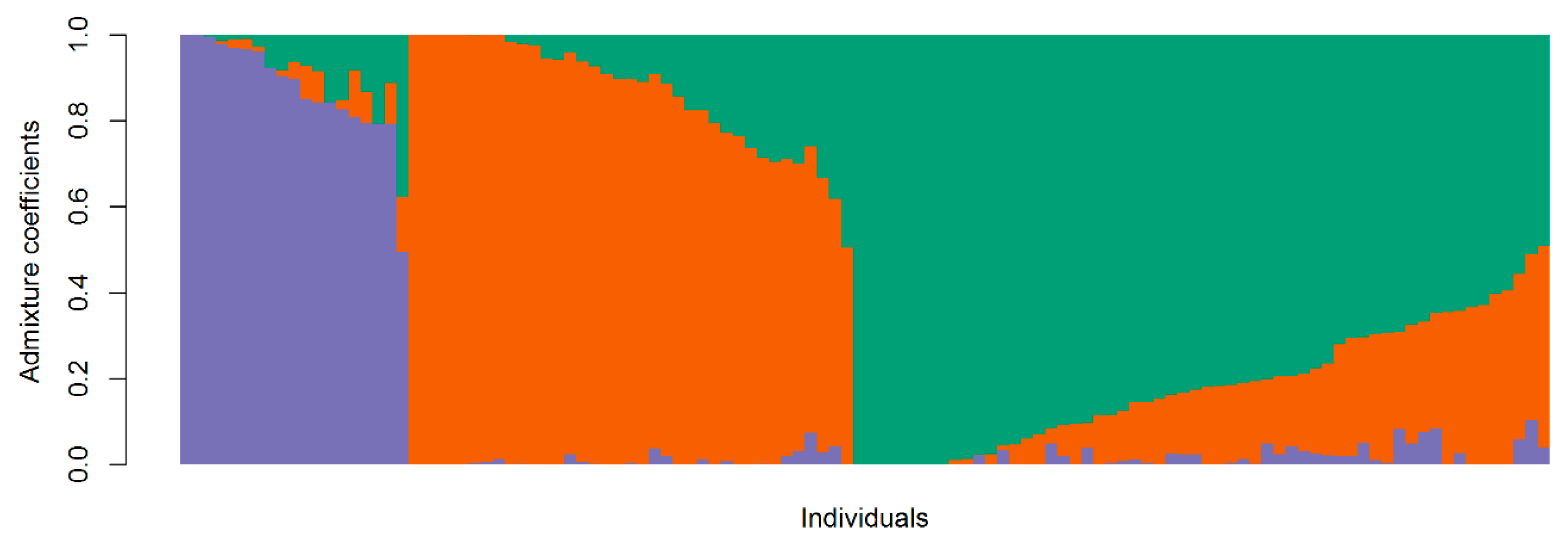
3.3. Population Structure
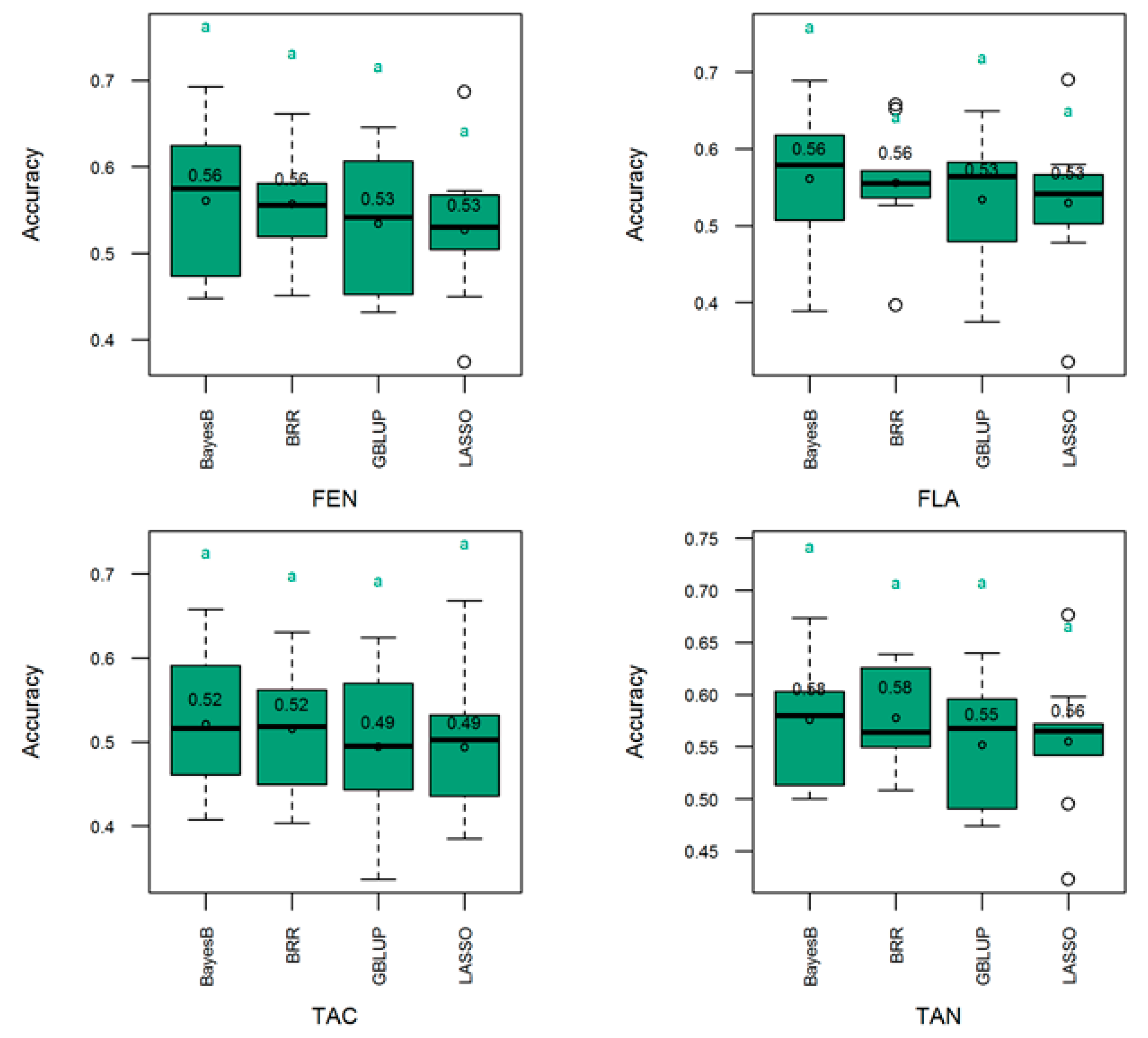
3.4. Genomic Prediction of Genetic Merit
4. Discussion
4.1. Contribution of S. halepense to Antioxidant Improvement in Sorghum
4.2. Genomic Selection Model Performance
Author Contributions
Funding
Conflicts of Interest
References
- Habyarimana, E.; Lorenzoni, C.; Marudelli, M.; Redaelli, R.; Amaducci, S. A meta-analysis of bioenergy conversion relevant traits in sorghum landraces, lines and hybrids in the Mediterranean region. Ind. Crops Prod. 2016, 81, 100–109. [Google Scholar] [CrossRef]
- Alfieri, M.; Balconi, C.; Cabassi, G.; Habyarimana, E.; Redaelli, R. Antioxidant activity in a set of sorghum landraces and breeding lines. Maydica 2017, 62, 1–7. [Google Scholar]
- Habyarimana, E.; Bonardi, P.; Laureti, D.; Di Bari, V.; Cosentino, S.; Lorenzoni, C. Multilocational evaluation of biomass sorghum hybrids under two stand densities and variable water supply in Italy. Ind. Crops Prod. 2004, 20, 3–9. [Google Scholar] [CrossRef]
- Paterson, A.H.; Bowers, J.E.; Bruggmann, R.; Dubchak, I.; Grimwood, J.; Gundlach, H.; Haberer, G.; Hellsten, U.; Mitros, T.; Poliakov, A.; et al. The Sorghum bicolor genome and the diversification of grasses. Nature 2009, 457, 551–556. [Google Scholar] [CrossRef]
- Mccormick, R.; Truong, S.; Sreedasyam, A.; Jenkins, J.; Shu, S.; Sims, D.; Kennedy, M.; Amirebrahimi, M.; Weers, B.; McKinley, B.; et al. The Sorghum bicolor reference genome: Improved assembly, gene annotations, a transcriptome atlas, and signatures of genome organization. Plant J. 2018, 93, 338–354. [Google Scholar] [CrossRef]
- Rhodes, D.H.; Hoffmann, L.; Rooney, W.L.; Ramu, P.; Morris, G.P.; Kresovich, S. Genome-wide association study of grain polyphenol concentrations in global sorghum [Sorghum bicolor (L.) Moench] germplasm. J. Agric. Food Chem. 2014, 62, 10916–10927. [Google Scholar] [CrossRef]
- Rhodes, D.; Gadgil, P.; Perumal, R.; Tesso, T.; Herald, T.J. Natural Variation and Genome-Wide Association Study of Antioxidants in a Diverse Sorghum Collection. Cereal Chem. J. 2017, 94, 190–198. [Google Scholar] [CrossRef]
- Velazco, J.G.; Malosetti, M.; Hunt, C.H.; Mace, E.S.; Jordan, D.R.; van Eeuwijk, F.A. Combining pedigree and genomic information to improve prediction quality: an example in sorghum. Theor. Appl. Genet. 2019, 132, 2055–2067. [Google Scholar] [CrossRef]
- Velazco, J.G.; Jordan, D.R.; Mace, E.S.; Hunt, C.H.; Malosetti, M.; van Eeuwijk, F.A. Genomic Prediction of Grain Yield and Drought-Adaptation Capacity in Sorghum Is Enhanced by Multi-Trait Analysis. Front. Plant Sci. 2019, 10, 997. [Google Scholar] [CrossRef]
- De Oliveira, A.A.; Pastina, M.M.; de Souza, V.F.; da Costa Parrella, R.A.; Noda, R.W.; Simeone, M.L.F.; Schaffert, R.E.; de Magalhães, J.V.; Damasceno, C.M.B.; Margarido, G.R.A. Genomic prediction applied to high-biomass sorghum for bioenergy production. Mol. Breed. 2018, 38, 49. [Google Scholar] [CrossRef]
- Muleta, K.T.; Pressoir, G.; Morris, G.P. Optimizing Genomic Selection for a Sorghum Breeding Program in Haiti: A Simulation Study. G3 Genes Genomes Genet. 2019, 9, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. Genomic Selection Using Low-Density Marker Panels. Genetics 2009, 182, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Heffner, E.L.; Sorrells, M.E.; Jannink, J.-L. Genomic Selection for Crop Improvement. Crop Sci. 2009, 49, 1. [Google Scholar] [CrossRef]
- Heffner, E.L.; Lorenz, A.J.; Jannink, J.-L.; Sorrells, M.E. Plant Breeding with Genomic Selection: Gain per Unit Time and Cost. Crop Sci. 2010, 50, 1681. [Google Scholar] [CrossRef]
- Crossa, J.; Campos, G.D.L.; Pérez, P.; Gianola, D.; Burgueño, J.; Araus, J.L.; Makumbi, D.; Singh, R.P.; Dreisigacker, S.; Yan, J.; et al. Prediction of Genetic Values of Quantitative Traits in Plant Breeding Using Pedigree and Molecular Markers. Genetics 2010, 186, 713–724. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Chao, S.; Asoro, F.G.; Heffner, E.L.; Hayashi, T.; Iwata, H.; Smith, K.P.; Sorrells, M.E.; Jannink, J.-L. Genomic Selection in Plant Breeding. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2011; Volume 110, pp. 77–123. ISBN 978-0-12-385531-2. [Google Scholar]
- Hayes, B.J.; Cogan, N.O.I.; Pembleton, L.W.; Goddard, M.E.; Wang, J.; Spangenberg, G.C.; Forster, J.W. Prospects for genomic selection in forage plant species. Plant Breed. 2013, 132, 133–143. [Google Scholar] [CrossRef]
- Lorenz, A.J. Resource Allocation for Maximizing Prediction Accuracy and Genetic Gain of Genomic Selection in Plant Breeding: A Simulation Experiment. G3 Genes Genomes Genet. 2013, 3, 481–491. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar]
- Barton, N.; Etheridge, A.; Véber, A. The infinitesimal model: Definition, derivation, and implications. Theor. Popul. Biol. 2017, 118, 50–73. [Google Scholar] [CrossRef]
- Collard, B.C.Y.; Mackill, D.J. Marker-assisted selection: an approach for precision plant breeding in the twenty-first century. Phil. Trans. R. Soc. B 2008, 363, 557–572. [Google Scholar] [CrossRef]
- Bernardo, R.; Yu, J. Prospects for Genomewide Selection for Quantitative Traits in Maize. Crop Sci. 2007, 47, 1082. [Google Scholar] [CrossRef]
- Grenier, C.; Cao, T.-V.; Ospina, Y.; Quintero, C.; Châtel, M.H.; Tohme, J.; Courtois, B.; Ahmadi, N. Accuracy of Genomic Selection in a Rice Synthetic Population Developed for Recurrent Selection Breeding. PLoS ONE 2015, 10, e0136594. [Google Scholar] [CrossRef] [PubMed]
- Hickey, J.M.; Chiurugwi, T.; Mackay, I.; Powell, W.; Implementing Genomic Selection in CGIAR Breeding Programs Workshop Participants. Genomic prediction unifies animal and plant breeding programs to form platforms for biological discovery. Nat. Genet. 2017, 49, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Morais, O.P., Jr.; Duarte, J.B.; Breseghello, F.; Coelho, A.S.G.; Morais, O.P.; Magalhães, A.M., Jr. Single-Step Reaction Norm Models for Genomic Prediction in Multienvironment Recurrent Selection Trials. Crop Sci. 2018, 58, 592. [Google Scholar] [CrossRef]
- Müller, D.; Schopp, P.; Melchinger, A.E. Persistency of Prediction Accuracy and Genetic Gain in Synthetic Populations under Recurrent Genomic Selection. G3 (Bethesda) 2017, 7, 801–811. [Google Scholar] [CrossRef] [PubMed]
- Windhausen, V.S.; Atlin, G.N.; Hickey, J.M.; Crossa, J.; Jannink, J.-L.; Sorrells, M.E.; Raman, B.; Cairns, J.E.; Tarekegne, A.; Semagn, K.; et al. Effectiveness of genomic prediction of maize hybrid performance in different breeding populations and environments. G3 (Bethesda) 2012, 2, 1427–1436. [Google Scholar] [CrossRef] [PubMed]
- Weyhrich, R.A.; Lamkey, K.R.; Hallauer, A.R. Responses to Seven Methods of Recurrent Selection in the BS11 Maize Population. Crop Sci. 1998, 38, 308. [Google Scholar] [CrossRef]
- Habyarimana, E.; Lorenzoni, C.; Redaelli, R.; Alfieri, M.; Amaducci, S.; Cox, S. Towards a perennial biomass sorghum crop: A comparative investigation of biomass yields and overwintering of Sorghum bicolor x S. halepense lines relative to long term S. bicolor trials in northern Italy. Biomass Bioenergy 2018, 111, 187–195. [Google Scholar] [CrossRef]
- Federer, W.T. Augmented (or hoonuiaku) designs. Hawaii. Plant. Rec. 1956, 55, 191–208. [Google Scholar]
- Alfieri, M.; Cabassi, G.; Habyarimana, E.; Quaranta, F.; Balconi, C.; Redaelli, R. Discrimination and prediction of polyphenolic compounds and total antioxidant capacity in sorghum grains. J. Near Infrared Spectrosc. 2019, 27, 46–53. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 27 September 2019).
- Duane, S.; Kennedy, A.D.; Pendleton, B.J.; Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Neal, R.M. MCMC using Hamiltonian dynamics. arXiv 2012, arXiv:1206.1901. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. arXiv 2011, arXiv:1111.4246. [Google Scholar]
- Bürkner, P.-C. Brms: An R Package for Bayesian Multilevel Models Using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef]
- Piepho, H.-P.; Möhring, J. Computing Heritability and Selection Response from Unbalanced Plant Breeding Trials. Genetics 2007, 177, 1881–1888. [Google Scholar] [CrossRef]
- Habyarimana, E. Genomic prediction for yield improvement and safeguarding genetic diversity in CIMMYT spring wheat (Triticum aestivum L.). Aust. J. Crop Sci. 2016, 10, 127–136. [Google Scholar]
- Habyarimana, E.; Parisi, B.; Mandolino, G. Genomic prediction for yields, processing and nutritional quality traits in cultivated potato (Solanum tuberosum L.). Plant Breed. 2017, 136, 245–252. [Google Scholar] [CrossRef]
- De los Campos, G.; Gianola, D.; Rosa, G.J.M.; Weigel, K.A.; Crossa, J. Semi-parametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genet. Res. 2010, 92, 295–308. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, D.; Zhang, Q. Predicting hybrid performance in rice using genomic best linear unbiased prediction. Proc. Natl. Acad. Sci. USA 2014, 111, 12456–12461. [Google Scholar] [CrossRef]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The variant call format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar]
- Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software STRUCTURE: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef]
- Excoffier, L.; Smouse, P.E.; Quattro, J.M. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 1992, 131, 479–491. [Google Scholar]
- Pérez, P.; de los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- VanRaden, P. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Gianola, D. Priors in Whole-Genome Regression: The Bayesian Alphabet Returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2008, 161, 209–228. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F.C. Introduction to Quantitative Genetics, 4th ed.; Pearson: Harlow, UK, 1996; ISBN 978-0-582-24302-6. [Google Scholar]
- De los Campos, G.; Naya, H.; Gianola, D.; Crossa, J.; Legarra, A.; Manfredi, E.; Weigel, K.; Cotes, J.M. Predicting quantitative traits with regression models for dense molecular markers and pedigree. Genetics 2009, 182, 375–385. [Google Scholar] [CrossRef]
- Clark, S.A.; Hickey, J.M.; Daetwyler, H.D.; van der Werf, J.H. The importance of information on relatives for the prediction of genomic breeding values and the implications for the makeup of reference data sets in livestock breeding schemes. Genet. Sel. Evol. 2012, 44, 4. [Google Scholar] [CrossRef]
- Scutari, M.; Mackay, I.; Balding, D. Using Genetic Distance to Infer the Accuracy of Genomic Prediction. PLoS Genet. 2016, 12, e1006288. [Google Scholar] [CrossRef]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Statist. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Xiang, W.; Zhu, C.; Lin, Z.; Wu, Y.; Li, J.; Pandravada, S.; Ridder, D.D.; Bai, G.; et al. Presence of tannins in sorghum grains is conditioned by different natural alleles of Tannin1. Proc. Natl. Acad. Sci. USA 2012, 109, 10281–10286. [Google Scholar] [CrossRef]
- Dia, V.P.; Pangloli, P.; Jones, L.; McClure, A.; Patel, A. Phytochemical concentrations and biological activities of Sorghum bicolor alcoholic extracts. Food Funct. 2016, 7, 3410–3420. [Google Scholar] [CrossRef]
- López-Contreras, J.J.; Zavala-García, F.; Urías-Orona, V.; Martínez-Ávila, G.C.G.; Rojas, R.; Niño-Medina, G. Chromatic, Phenolic and Antioxidant Properties of Sorghum bicolor Genotypes. Not. Bot. Horti Agrobo. 2015, 43, 366–370. [Google Scholar] [CrossRef]
- Dykes, L. Phenolic Compounds in Cereal Grains and Their Health Benefits. Cereal Food World 2007, 52, 105–111. [Google Scholar] [CrossRef]
- Piper, J.; Kulakow, P. Seed yield and biomass allocation in Sorghum bicolor and F1 and backcross generations of S.bicolor X S.halepense hybrids. Can. J. Bot. 2011, 72, 468–474. [Google Scholar] [CrossRef]
- Paterson, A.H. Genomics of Sorghum. Int. J. Plant Genom. 2008, 2008, 1–6. [Google Scholar] [CrossRef]
- Kaur, R.; Soodan, A.S. Reproductive biology of Sorghum halepense (L.) Pers. (Poaceae; Panicoideae; Andropogoneae) in relation to invasibility. Flora 2017, 229, 32–49. [Google Scholar] [CrossRef]
- Cox, S.; Nabukalu, P.; Paterson, A.; Kong, W.; Nakasagga, S. Development of Perennial Grain Sorghum. Sustainability 2018, 10, 172. [Google Scholar] [CrossRef]
- De Donato, M.; Peters, S.O.; Mitchell, S.E.; Hussain, T.; Imumorin, I.G. Genotyping-by-Sequencing (GBS): A Novel, Efficient and Cost-Effective Genotyping Method for Cattle Using Next-Generation Sequencing. PLoS ONE 2013, 8, e62137. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, T.; Zhou, Y.; Yin, S.; Li, P.; Liu, J.; Xu, S.; Yang, Z.; Xu, C. Genome-Wide Association Mapping of Starch Pasting Properties in Maize Using Single-Locus and Multi-Locus Models. Front. Plant Sci. 2018, 9, 1311. [Google Scholar] [CrossRef]
- Norman, A.; Taylor, J.; Edwards, J.; Kuchel, H. Optimising Genomic Selection in Wheat: Effect of Marker Density, Population Size and Population Structure on Prediction Accuracy. G3 2018, 8, 2889–2899. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.-L.; Sorrells, M.E. Genomic Selection Accuracy using Multifamily Prediction Models in a Wheat Breeding Program. Plant Genome 2011, 4, 65. [Google Scholar] [CrossRef]
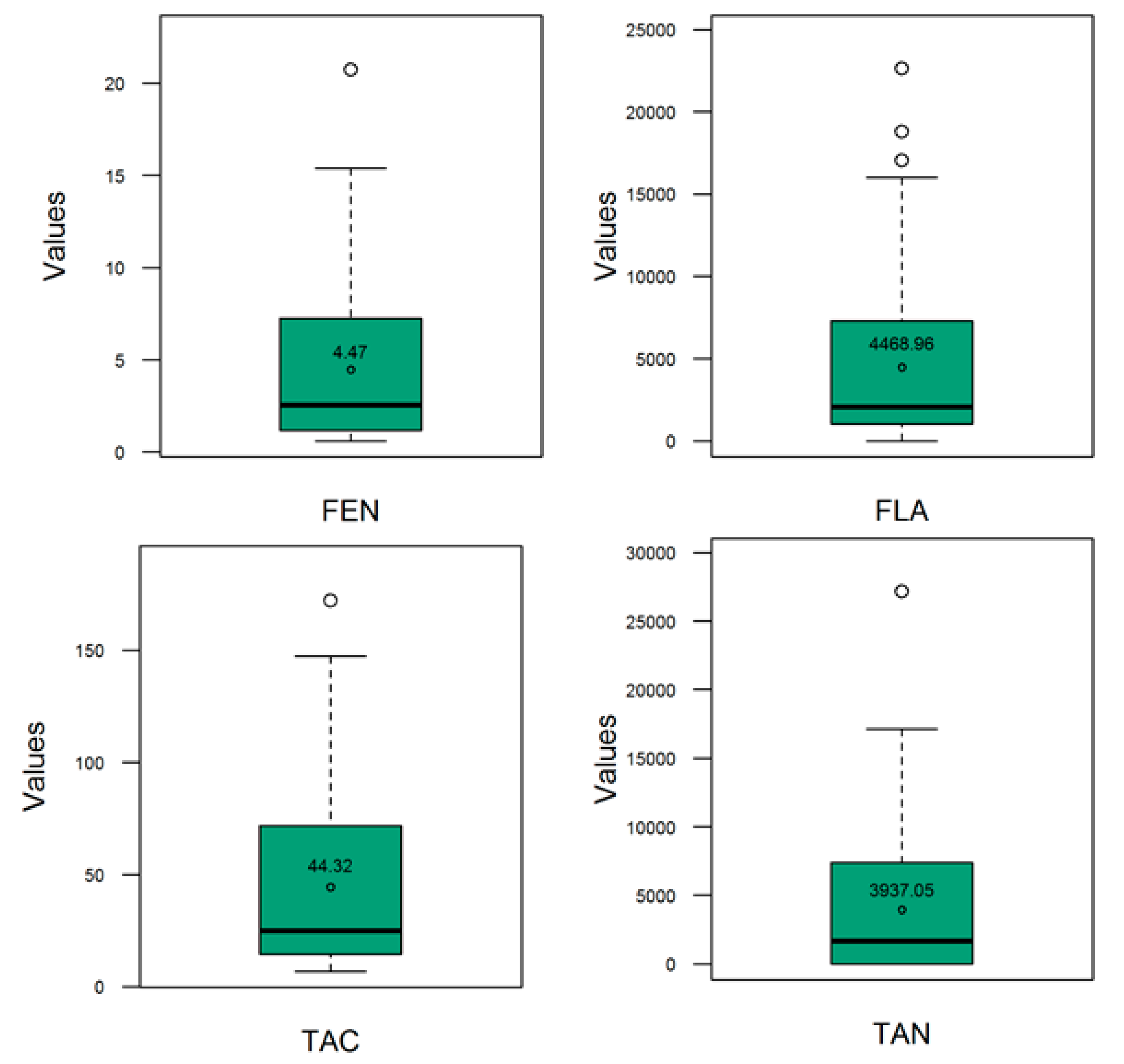
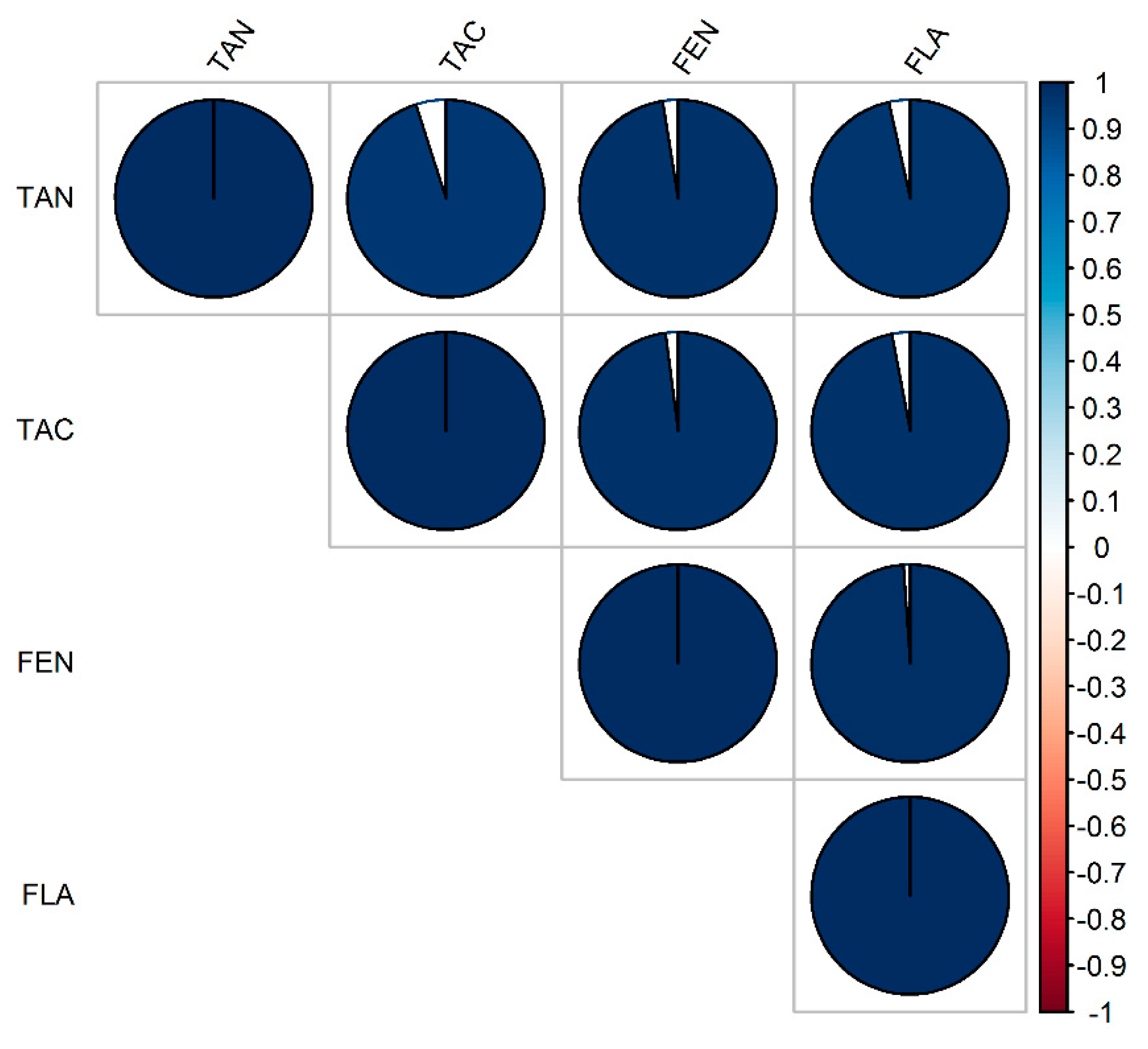
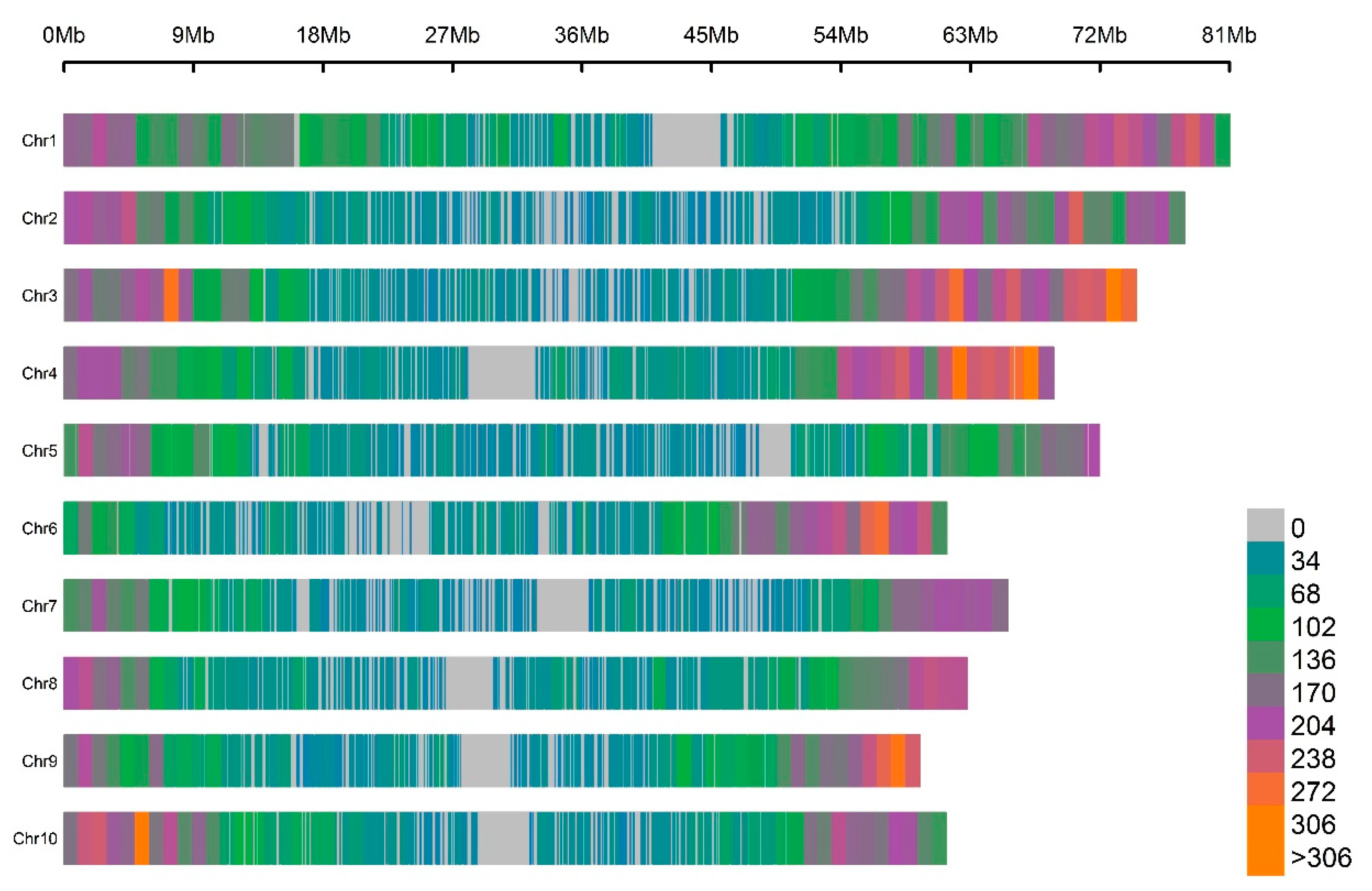
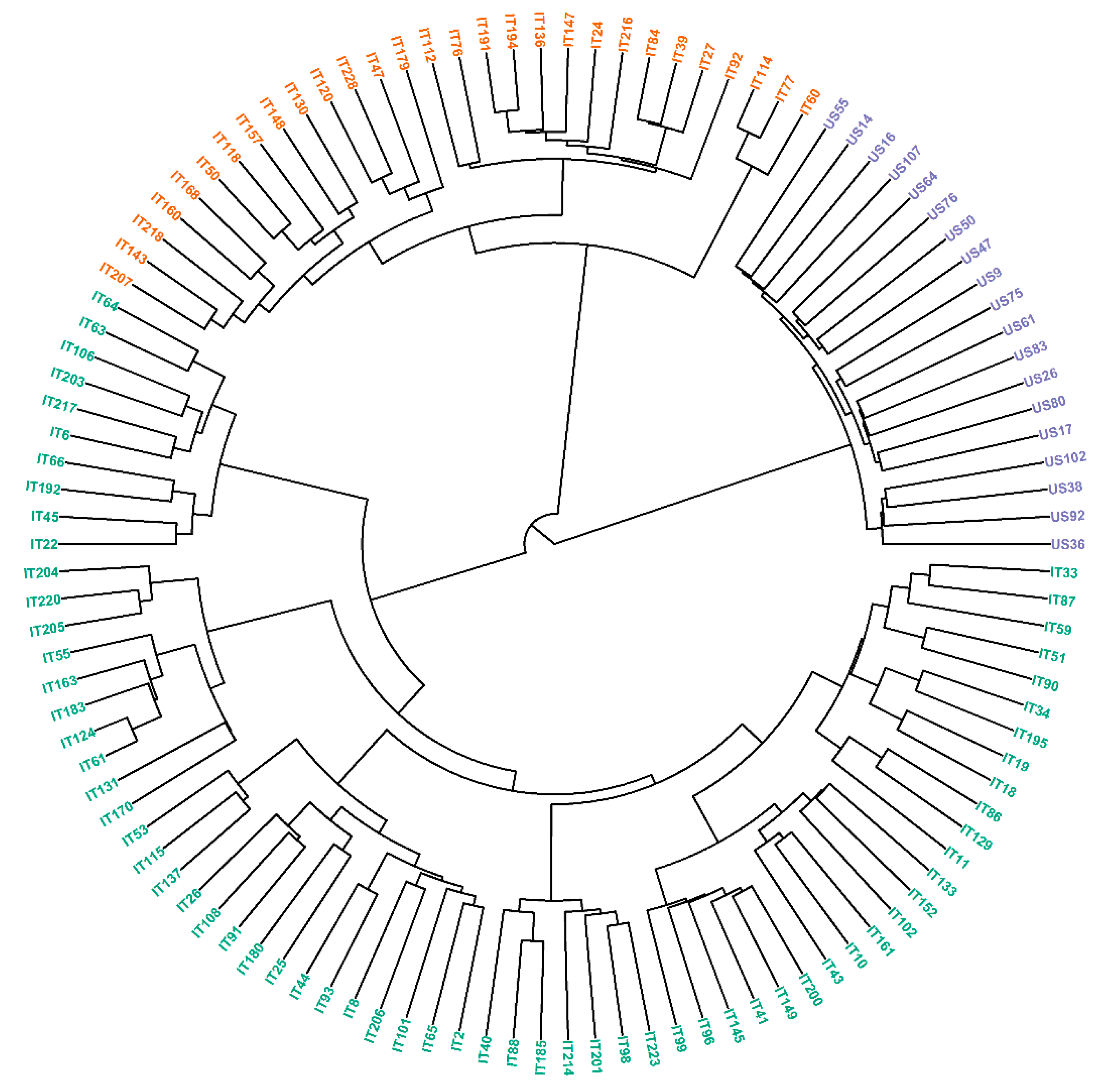
| Traits | Parameters | Estimate | Est. Error | l–95% CI | u–95% CI | Rhat | Bulk_ESS | Tail_ESS 1 |
|---|---|---|---|---|---|---|---|---|
| FLA | SD.G (intercept) | 4461.34 | 291.64 | 3932.56 | 5070.77 | 1 | 8469 | 18871 |
| Intercept | 5276.13 | 415.54 | 4448.66 | 6083.73 | 1 | 2793 | 5094 | |
| Sigma | 405.25 | 26.3 | 357.83 | 460.87 | 1 | 113,402 | 190,944 | |
| FEN | SD.G (intercept) | 4.26 | 0.28 | 3.75 | 4.86 | 1 | 2137 | 4694 |
| Intercept | 4.33 | 0.39 | 3.55 | 5.1 | 1.01 | 466 | 1355 | |
| Sigma | 0.22 | 0.01 | 0.19 | 0.25 | 1 | 45,376 | 84,449 | |
| TAC | SD.G (intercept) | 37.93 | 2.48 | 33.45 | 43.24 | 1 | 1787 | 3107 |
| Intercept | 43.21 | 3.56 | 36.33 | 50.26 | 1.01 | 599 | 1491 | |
| Sigma | 2.71 | 0.18 | 2.4 | 3.08 | 1 | 32,486 | 56,955 | |
| TAN | SD.G (intercept) | 3935.62 | 256.08 | 3469.61 | 4468.41 | 1 | 1555 | 3174 |
| Intercept | 5320.1 | 358.8 | 4630.73 | 6044.63 | 1 | 501 | 887 | |
| Sigma | 253.67 | 16.37 | 224.16 | 288.35 | 1 | 23,079 | 44,792 |
| Source of Variation | Degrees of Freedom | Sums of Squares | Mean Squares | F Value | R2 | p Value |
|---|---|---|---|---|---|---|
| Clusters | 2 | 37,773.14 | 37,773.14 | 11.47 | 0.09 | 0.001 |
| Residuals | 111 | 368,746.64 | 3292.38 | NA | 0.91 | NA |
| Total | 113 | 406,519.77 | NA | NA | 1 | NA |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habyarimana, E.; Lopez-Cruz, M. Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines. Genes 2019, 10, 841. https://doi.org/10.3390/genes10110841
Habyarimana E, Lopez-Cruz M. Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines. Genes. 2019; 10(11):841. https://doi.org/10.3390/genes10110841
Chicago/Turabian StyleHabyarimana, Ephrem, and Marco Lopez-Cruz. 2019. "Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines" Genes 10, no. 11: 841. https://doi.org/10.3390/genes10110841
APA StyleHabyarimana, E., & Lopez-Cruz, M. (2019). Genomic Selection for Antioxidant Production in a Panel of Sorghum bicolor and S. bicolor × S. halepense Lines. Genes, 10(11), 841. https://doi.org/10.3390/genes10110841






