A Random Walk Based Cluster Ensemble Approach for Data Integration and Cancer Subtyping
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Competitive Methods
2.3. Evaluation Metrics
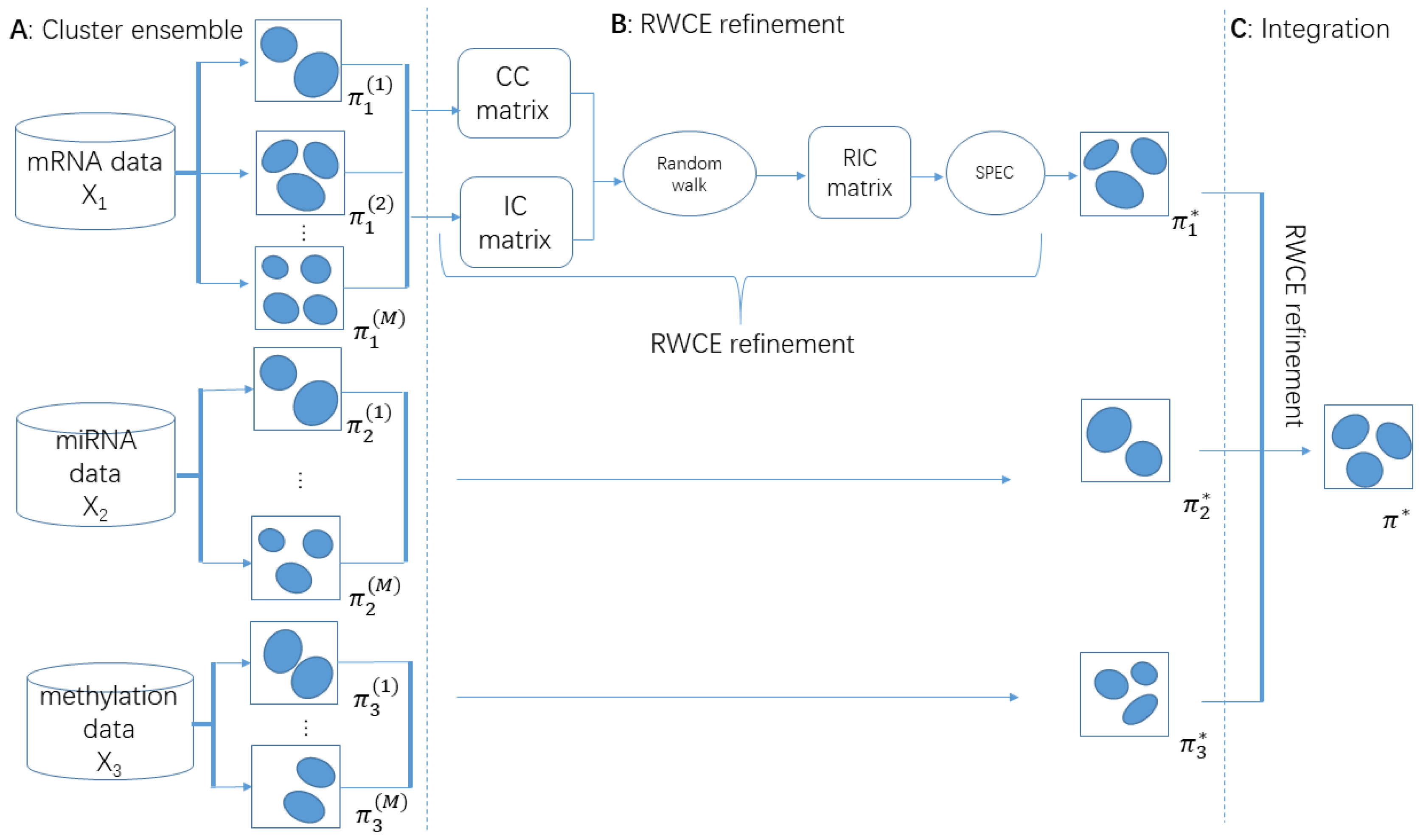
2.4. Methodology Overview of RWCE
2.5. Cluster Ensemble
2.6. RWCE Refinement
2.6.1. Generating a Refined Instance-Cluster Association (RIC) Matrix
2.6.2. Random-Walk Based Similarity Algorithm
2.6.3. Applying Spectral Clustering to RIC
2.7. Integrating Multiple Types of Omics Data for Subtyping
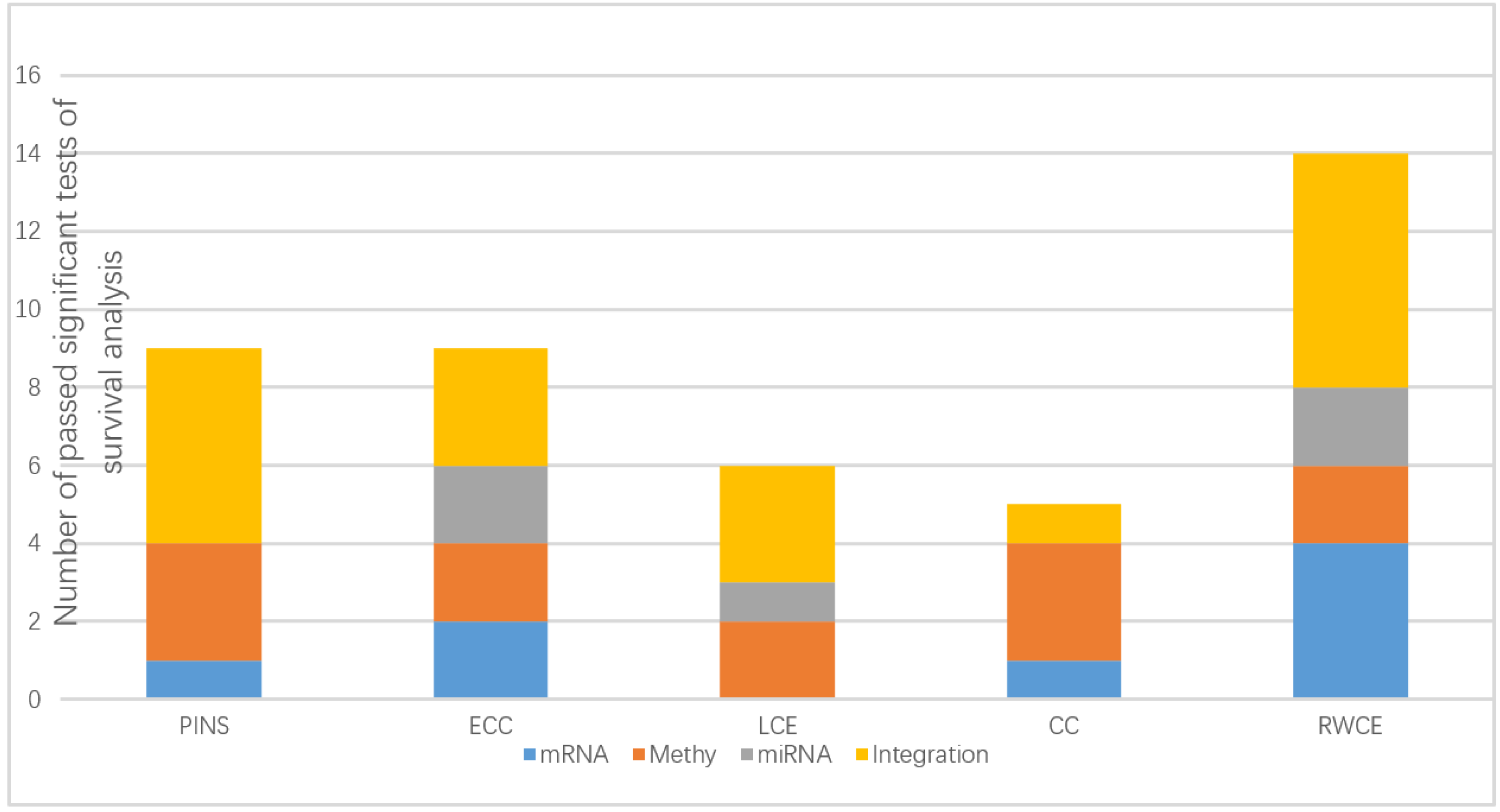
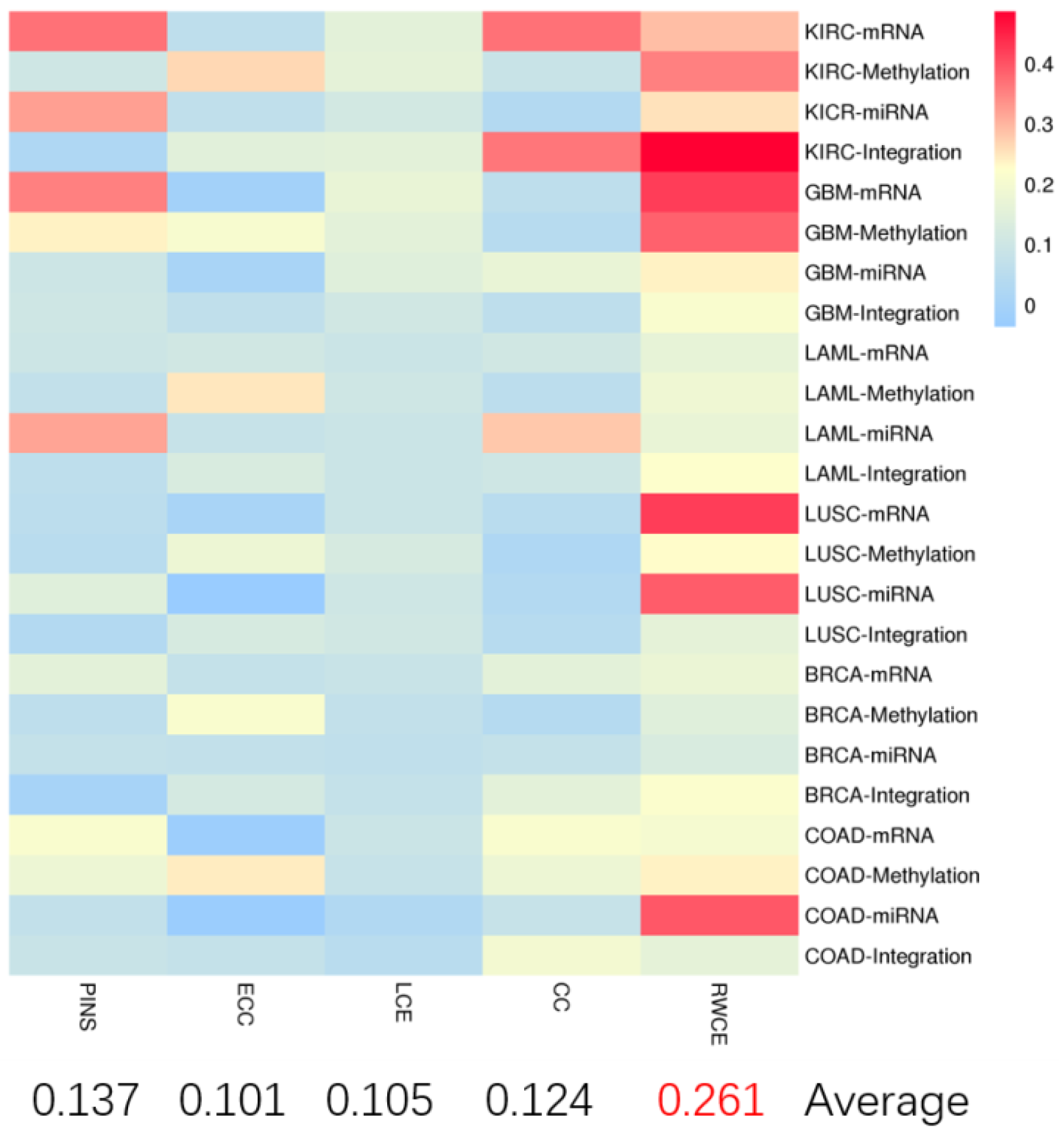
3. Results
3.1. Evaluation on TCGA Cancer Data Sets
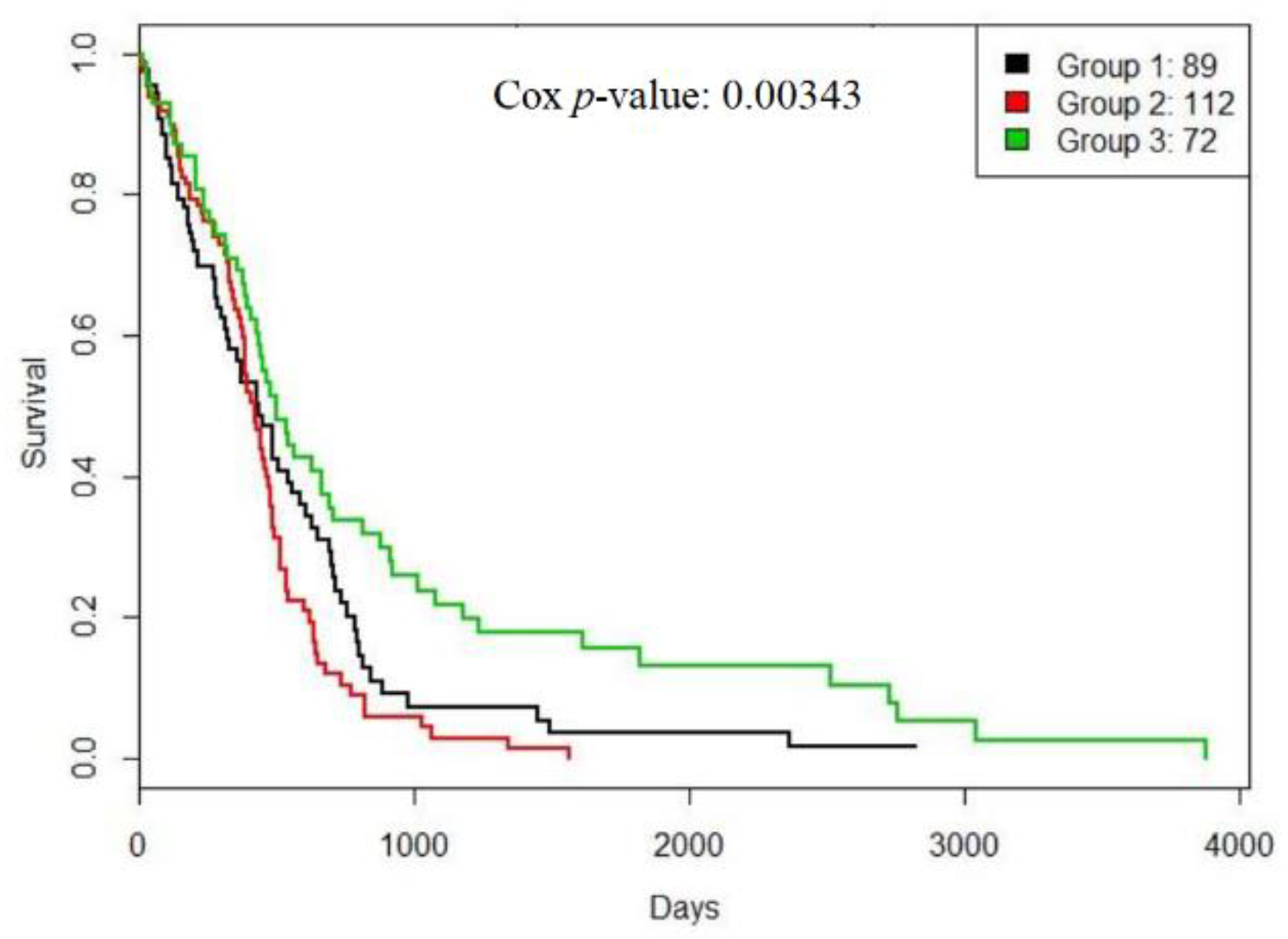
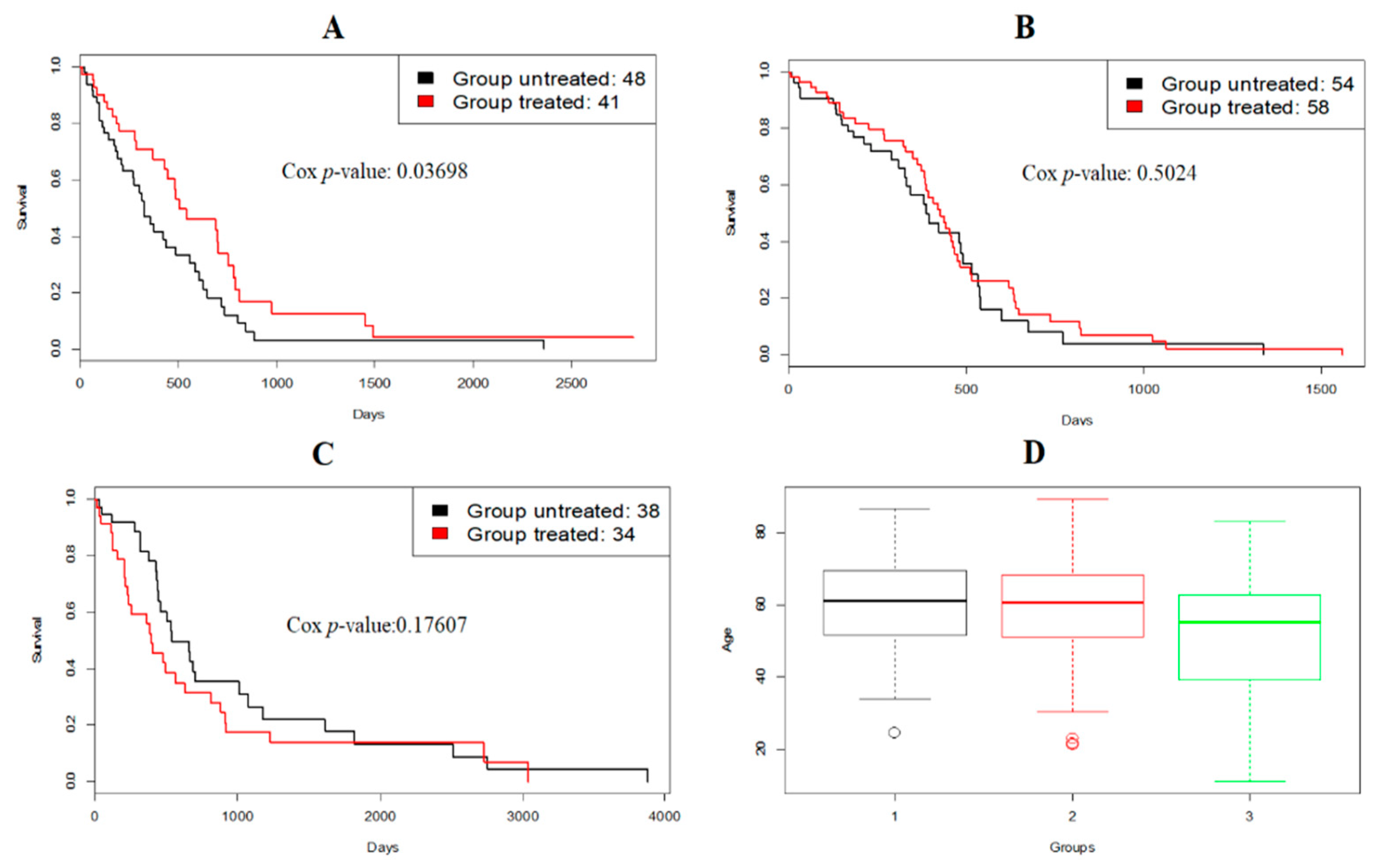
3.2. A Case Study: Glioblastoma Multiforme
3.3. Evaluation on METABRIC Data Set
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- The International Cancer Genome Consortium. International network of cancer genome projects. Nature 2010, 464, 993. [Google Scholar] [CrossRef] [PubMed]
- Levine, D.A. The Cancer Genom Atlas Research Network. Integrated genomic characterization of endometrial carcinoma. Nature 2013, 497, 67. [Google Scholar]
- The Cancer Genom Atlas Research. Integrated genomic analyses of ovarian carcinoma. Nature 2011, 474, 609. [Google Scholar] [CrossRef] [PubMed]
- Emig, D.; Ivliev, A.; Pustavalova, O.; Lanchasire, L.; Bureeva, S.; Nikolsky, Y.; Bessarabova, M. Drug target prediction and repositioning using an integrated network-based approach. PLoS ONE 2013, 8, e60618. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of drug–target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 2008, 24, i232–i240. [Google Scholar] [CrossRef] [PubMed]
- Bashashati, A.; Haffari, G.; Ding, J.; Ha, G.; Lui, K.; Rosner, J.; Huntsman, D.G.; Caldas, C.; Aparico, S.A.; Shah, S.P. DriverNet: Uncovering the impact of somatic driver mutations on transcriptional networks in cancer. Genome Biol. 2012, 13, R124. [Google Scholar] [CrossRef] [PubMed]
- Cho, A.; Shim, J.E.; Kim, E.; Supek, F.; Lehner, B.; Lee, I. MUFFINN: Cancer gene discovery via network analysis of somatic mutation data. Genome Biol. 2016, 17, 129. [Google Scholar] [CrossRef]
- Hou, J.P.; Ma, J. DawnRank: Discovering personalized driver genes in cancer. Genome Med. 2014, 6, 56. [Google Scholar] [CrossRef]
- Hofree, M.; Shen, J.P.; Carter, H.; Gross, A.; Ideker, T. Network-based stratification of tumor mutations. Nat. Methods 2013, 10, 1108. [Google Scholar] [CrossRef]
- Shen, R.; Olshen, A.B.; Ladanyi, M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 2009, 25, 2906–2912. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, R.; Fang, H.; Cheng, F.; Fu, Y.; Liu, Y.Y. Entropy-based consensus clustering for patient stratification. Bioinformatics 2017, 33, 2691–2698. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kins, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Gao, Y.L.; Zheng, C.H.; Xu, Y.; Yu, J. Block-constraint robust principal component analysis and its application to integrated analysis of TCGA Data. IEEE Trans. Nanobiosci. 2016, 15, 510–516. [Google Scholar] [CrossRef]
- Liu, J.X.; Xu, Y.; Zheng, C.H.; Kong, H.; Lai, Z.H. RPCA-based tumor classification using gene expression data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 964–970. [Google Scholar] [CrossRef]
- Iam-On, N.; Boongoen, T.; Garrett, S. LCE: A link-based cluster ensemble method for improved gene expression data analysis. Bioinformatics 2010, 26, 1513–1519. [Google Scholar] [CrossRef] [PubMed]
- Lock, E.F.; Dunson, D.B. Bayesian consensus clustering. Bioinformatics 2013, 29, 2610–2616. [Google Scholar] [CrossRef] [PubMed]
- Monti, S.; Tamayo, P.; Mesirov, J.; Golub, T. Consensus clustering: A resampling-based method for class discovery and visualization of gene expression microarray data. Mach. Learn. 2003, 52, 91–118. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 849–856. [Google Scholar]
- Curtis, C.; Shah, S.B.; Chin, S.F.; Gulisa, T.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346. [Google Scholar] [CrossRef]
- Nguyen, T.; Tagett, R.; Diaz, D.; Draghici, S. A novel approach for data integration and disease subtyping. Genome Res. 2017, 27, 2025. [Google Scholar] [CrossRef]
- Lappalainen, I.; Almeida-King, J.; Kumanduri, V.; Senf, A.; Spalding, J.D.; Ur-Rehman, S.; Saunders, G.; Kandasamy, J.; Caccamo, M.; Leinonen, R. The European genome-phenome archive of human data consented for biomedical research. Nat. Genet. 2015, 47, 692. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; May, S. Applied survival analysis: Regression modeling of time-to-event data, second edition. J. Stat. Plan. Inference 2000, 91, 173–175. [Google Scholar]
- Pencina, M.J.; D’Agostino, R.B. Overall C as a measure of discrimination in survival analysis: Model specific population value and confidence interval estimation. Stat. Med. 2004, 23, 2109–2123. [Google Scholar] [CrossRef] [PubMed]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. JMLR 2003, 3, 583–617. [Google Scholar]
- Topchy, A.; Jain, A.K.; Punch, W. Clustering ensembles: Models of consensus and weak partitions. IEEE Trans. Pattern. Anal. Mach. Intell. 2005, 27, 1866–1881. [Google Scholar] [CrossRef] [PubMed]
| mRNA | Methylation | miRNA | Integration | |
|---|---|---|---|---|
| KIRC | 0.008(2) | 0.79397(3) | 0.52883(2) | 0.00671(2) |
| GBM | 0.19041(2) | 0.00629(2) | 0.96568(2) | 0.00343 (3) |
| LAML | 0.00272(8) | 0.58721(2) | 0.00119(8) | 0.00158(2) |
| LUSC | 0.40747(3) | 0.04761(7) | 0.01666(2) | 0.00827(4) |
| BRCA | 0.04193(2) | 0.58412(2) | 0.15534(2) | 0.03006(2) |
| COAD | 0.01058(2) | 0.68703(2) | 0.81886(6) | 0.02818(3) |
| PAM50 (5, 5) | PINS (14, 7) | CC (10, 8) | ECC (10, 10) | LCE (10, 8) | RWCE (6, 6) | |||
|---|---|---|---|---|---|---|---|---|
| Discovery | p-value | DFS | 3.00 × 10−11 | 6.50 × 10−10 | 2.50 × 10−5 | 1.39 × 10−1 | 9.50 × 10−1 | 1.69 × 10−9 |
| Overall | 8.50 × 10−5 | 1.90 × 10−6 | 8.10 × 10−6 | 5.59 × 10−2 | 4.42 × 10−1 | 4.16 × 10−12 | ||
| CI | DFS | 0.620 | 0.634 | 0.598 | 0.521 | 0.506 | 0.594 | |
| Overall | 0.578 | 0.598 | 0.572 | 0.529 | 0.508 | 0.641 | ||
| Validation | p-value | DFS | 3.10 × 10−9 | 4.30 × 10−5 | 1.20 × 10−2 | 2.61 × 10−1 | 8.44 × 10−2 | 9.12 × 10−5 |
| Overall | 2.90 × 10−5 | 033.80 × 10−3 | 7.90 × 10−3 | 1.66 × 10−1 | 3.53 × 10−2 | 9.13 × 10−7 | ||
| CI | DFS | 0.636 | 0.589 | 0.572 | 0.521 | 0.520 | 0.560 | |
| Overall | 0.561 | 0.545 | 0.538 | 0.519 | 0.514 | 0.607 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wang, Y.-T.; Zheng, C.-H. A Random Walk Based Cluster Ensemble Approach for Data Integration and Cancer Subtyping. Genes 2019, 10, 66. https://doi.org/10.3390/genes10010066
Yang C, Wang Y-T, Zheng C-H. A Random Walk Based Cluster Ensemble Approach for Data Integration and Cancer Subtyping. Genes. 2019; 10(1):66. https://doi.org/10.3390/genes10010066
Chicago/Turabian StyleYang, Chao, Yu-Tian Wang, and Chun-Hou Zheng. 2019. "A Random Walk Based Cluster Ensemble Approach for Data Integration and Cancer Subtyping" Genes 10, no. 1: 66. https://doi.org/10.3390/genes10010066
APA StyleYang, C., Wang, Y.-T., & Zheng, C.-H. (2019). A Random Walk Based Cluster Ensemble Approach for Data Integration and Cancer Subtyping. Genes, 10(1), 66. https://doi.org/10.3390/genes10010066




