Viscosity of Plasma as a Key Factor in Assessment of Extracellular Vesicles by Light Scattering
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Exosome Standards
2.1.2. Blood Plasma Samples
2.1.3. Blood Plasma for the Ultracentrifugation Experiments and Viscosity Determination
2.1.4. Human Serum Albumin
2.2. Methods
2.2.1. Static and Dynamic Light Scattering Measurements
2.2.2. Viscosity and Density Measurements
2.2.3. Asymmetric Flow Field Flow Fractionation (AF4/UV-MALS)
2.2.4. Flow Cytometry (FCM)
2.2.5. Atomic Force Microscopy (AFM)
3. Results
3.1. LS Size Characterization of the Exosome Standard
3.2. LS Size Characterization of Particles in Blood Plasma
3.3. Determination of the Medium Viscosity for Correct Characterization of the EV size by DLS in Full Blood Plasma Samples
3.4. Shape Characterization of Particles by DLS/SLS
4. Discussion
4.1. Size Characterization
4.2. Identification of Subpopulations of Extracellular Vesicles in Blood Plasma
4.3. Structural Characterization
4.4. Further Considerations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Simpson, R.J.; Mathivanan, S. Extracellular Microvesicles: The Need for Internationally Recognised Nomenclature and Stringent Purification Criteria. J. Proteomics Bioinform. 2012. [Google Scholar] [CrossRef]
- Linares, R.; Tan, S.; Gounou, C.; Arraud, N.; Brisson, A.R. High-speed centrifugation induces aggregation of extracellular vesicles. J. Extracell. Vesicles 2015. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, K.B.; Gudbergsson, J.M.; Andresen, T.L.; Simonsen, J.B. What is the blood concentration of extracellular vesicles? Implications for the use of extracellular vesicles as blood-borne biomarkers of cancer. Biochim. Biophys. Acta 2019, 1871, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Černe, K.; Kobal, B. Chapter Eight-Implications of Microvesicle and Cell Surface Protein Shedding for Biomarker Studies, Cancerogenesis, and Therapeutic Target Discovery in Ovarian Cancer. In Advances in Planar Lipid Bilayers and Liposomes; Aleš, I., Ed.; Academic Press: Cambridge, MA, USA, 2012; Volume 16, pp. 239–274. [Google Scholar]
- Yáñez-Mó, M.; Siljander, P.R.M.; Andreu, Z.; Zavec, A.B.; Borràs, F.E.; Buzas, E.I.; Buzas, K.; Casal, E.; Cappello, F.; Carvalho, J.; et al. Biological properties of extracellular vesicles and their physiological functions. J. Extracell. Vesicles 2015. [Google Scholar] [CrossRef]
- Muller, L.; Hong, C.S.; Stolz, D.B.; Watkins, S.C.; Whiteside, T.L. Isolation of biologically-active exosomes from human plasma. J. Immunol. Methods 2014, 411, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Witwer, K.W.; Buzas, E.I.; Bemis, L.T.; Bora, A.; Lasser, C.; Lotvall, J.; Nolte-’t Hoen, E.N.; Piper, M.G.; Sivaraman, S.; Skog, J.; et al. Standardization of sample collection, isolation and analysis methods in extracellular vesicle research. J. Extracell. Vesicles 2013. [Google Scholar] [CrossRef] [PubMed]
- van der Pol, E.; Boing, A.N.; Harrison, P.; Sturk, A.; Nieuwland, R. Classification, functions, and clinical relevance of extracellular vesicles. Pharmacological reviews 2012, 64, 676–705. [Google Scholar] [CrossRef] [PubMed]
- Zeringer, E.; Barta, T.; Li, M.; Vlassov, A.V. Strategies for Isolation of Exosomes. Cold Spring Harb. Protoc. 2015. [Google Scholar] [CrossRef]
- Lacroix, R.; Judicone, C.; Mooberry, M.; Boucekine, M.; Key, N.S.; Dignat-George, F. Standardization of pre-analytical variables in plasma microparticle determination: Results of the International Society on Thrombosis and Haemostasis SSC Collaborative workshop. J. Thromb. Haemost. 2016, 11, 1190–1193. [Google Scholar] [CrossRef]
- Štukelj, R.; Schara, K.; Bedina-Zavec, A.; Šuštar, V.; Pajnič, M.; Pađen, L.; Krek, J.L.; Kralj-Iglič, V.; Mrvar-Brečko, A.; Janša, R. Effect of shear stress in the flow through the sampling needle on concentration of nanovesicles isolated from blood. Eur. J. Pharm. Sci. 2017, 98, 17–29. [Google Scholar] [CrossRef]
- Šuštar, V.; Bedina-Zavec, A.; Štukelj, R.; Frank, M.; Bobojević, G.; Janša, R.; Ogorevc, E.; Kruljc, P.; Mam, K.; Šimunič, B.; et al. Nanoparticles isolated from blood: A reflection of vesiculability of blood cells during the isolation process. Int. J. Nanomed. 2011, 6, 2737–2748. [Google Scholar] [CrossRef]
- Corrado, C.; Raimondo, S.; Chiesi, A.; Ciccia, F.; De Leo, G.; Alessandro, R. Exosomes as intercellular signaling organelles involved in health and disease: Basic science and clinical applications. Int. J. Mol. Sci. 2013, 14, 5338–5366. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Carpenter, E.; Issadore, D. Detection and isolation of circulating exosomes and microvesicles for cancer monitoring and diagnostics using micro-/nano-based devices. Analyst 2016, 141, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Kätzel, U.; Vorbau, M.; Stintz, M.; Gottschalk-Gaudig, T.; Barthel, H. Dynamic Light Scattering for the Characterization of Polydisperse Fractal Systems: II. Relation between Structure and DLS Results. Part. Part. Syst. Char. 2008, 25, 19–30. [Google Scholar] [CrossRef]
- Shibayama, M.; Karino, T.; Okabe, S. Distribution analyses of multi-modal dynamic light scattering data. Polymer 2006, 47, 6446–6456. [Google Scholar] [CrossRef]
- Schärtl, W. Light Scattering from Polymer Solutions and Nanoparticle Dispersions; Springer: Basel, Switzerland, 2007. [Google Scholar] [CrossRef]
- Kratochvil, P. Particle scattering functions. In Light scattering from polymer solutions; Huglin, M.B., Ed.; Academic Press: New York, NY, USA, 1972; pp. 333–384. [Google Scholar]
- Lawrie, A.S.; Albanyan, A.; Cardigan, R.A.; Mackie, I.J.; Harrison, P. Microparticle sizing by dynamic light scattering in fresh-frozen plasma. Vox Sang. 2009, 96, 206–212. [Google Scholar] [CrossRef]
- Erdbrugger, U.; Lannigan, J. Analytical challenges of extracellular vesicle detection: A comparison of different techniques. Cytometry A 2016, 89, 123–134. [Google Scholar] [CrossRef]
- Pencer, J.; Hallett, F.R. Effects of Vesicle Size and Shape on Static and Dynamic Light Scattering Measurements. Langmuir 2003, 19, 7488–7497. [Google Scholar] [CrossRef]
- Petersen, K.E.; Manangon, E.; Hood, J.L.; Wickline, S.A.; Fernandez, D.P.; Johnson, W.P.; Gale, B.K. A review of exosome separation techniques and characterization of B16-F10 mouse melanoma exosomes with AF4-UV-MALS-DLS-TEM. Anal. Bioanal. Chem. 2014, 406, 7855–7866. [Google Scholar] [CrossRef]
- Palmieri, V.; Lucchetti, D.; Gatto, I.; Maiorana, A.; Marcantoni, M.; Maulucci, G.; Papi, M.; Pola, R.; De Spirito, M.; Sgambato, A. Dynamic light scattering for the characterization and counting of extracellular vesicles: A powerful noninvasive tool. J. Nanopart. Res. 2014. [Google Scholar] [CrossRef]
- Kesimer, M.; Gupta, R. Physical characterization and profiling of airway epithelial derived exosomes using light scattering. Methods 2015, 87, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Fischer, K.; Schmidt, M. Pitfalls and novel applications of particle sizing by dynamic light scattering. Biomaterials 2016, 98, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Sun, X.; Liu, L.; Jiang, H.; Shen, Y.; Xu, X.; Li, J.; Zhang, G.; Huang, J.; Lin, Z.; et al. Exosomes and Their Therapeutic Potentials of Stem Cells. Stem Cells Int. 2016. [Google Scholar] [CrossRef]
- Bruning, B.; Stehle, R.; Falus, P.; Farago, B. Influence of charge density on bilayer bending rigidity in lipid vesicles: A combined dynamic light scattering and neutron spin-echo study. Eur Phys. J. E. Soft Matter. 2013. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Peng, P.; Kuang, Y.; Yang, J.; Cao, D.; You, Y.; Shen, K. Characterization of exosomes derived from ovarian cancer cells and normal ovarian epithelial cells by nanoparticle tracking analysis. Tumour Biol. 2016, 37, 4213–4221. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S. DLS and zeta potential-What they are and what they are not? J. Controlled Release 2016, 235, 337–351. [Google Scholar] [CrossRef] [PubMed]
- Filipe, V.; Hawe, A.; Jiskoot, W. Critical evaluation of Nanoparticle Tracking Analysis (NTA) by NanoSight for the measurement of nanoparticles and protein aggregates. Pharm Res. 2010, 27, 796–810. [Google Scholar] [CrossRef] [PubMed]
- Sitar, S.; Aseyev, V.; Kogej, K. Differences in association behavior of isotactic and atactic poly(methacrylic acid). Polymer 2014, 55, 848–854. [Google Scholar] [CrossRef]
- Sitar, S.; Aseyev, V.; Kogej, K. Microgel-like aggregates of isotactic and atactic poly(methacrylic acid) chains in aqueous alkali chloride solutions as evidenced by light scattering. Soft Matter 2014, 10, 7712–7722. [Google Scholar] [CrossRef]
- Brown, W. Dynamic light scattering: The method and some applications; Brown, W., Ed.; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Bosch, S.; de Beaurepaire, L.; Allard, M.; Mosser, M.; Heichette, C.; Chretien, D.; Jegou, D.; Bach, J.M. Trehalose prevents aggregation of exosomes and cryodamage. Sci Rep. 2016. [Google Scholar] [CrossRef]
- Klucker, R.; Munch, J.P.; Schosseler, F. Combined Static and Dynamic Light Scattering Study of Associating Random Block Copolymers in Solution. Macromolecules 1997, 30, 3839–3848. [Google Scholar] [CrossRef]
- Raspaud, E.; Lairez, D.; Adam, M.; Carton, J.P. Triblock Copolymers in a Selective Solvent. 1. Aggregation Process in Dilute Solution. Macromolecules 1994, 27, 2956–2964. [Google Scholar] [CrossRef]
- Tarassova, E.; Aseyev, V.; Filippov, A.; Tenhu, H. Structure of poly(vinyl pyrrolidone)–C70 complexes in aqueous solutions. Polymer 2007, 48, 4503–4510. [Google Scholar] [CrossRef]
- Kogej, K.; Šorl, S. Temperature dependence of solution properties of anionic polyelectrolyte-cationic surfactant complexes in ethanol. J. Mol. Liq. 2017, 228, 103–111. [Google Scholar] [CrossRef]
- Sitar, S.; Kejzar, A.; Pahovnik, D.; Kogej, K.; Tusek-Znidaric, M.; Lenassi, M.; Zagar, E. Size characterization and quantification of exosomes by asymmetrical-flow field-flow fractionation. Anal. Chem. 2015, 87, 9225–9233. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lyden, D. Asymmetric-flow field-flow fractionation technology for exomere and small extracellular vesicle separation and characterization. Nat. Protoc. 2019, 14, 1027–1053. [Google Scholar] [CrossRef] [PubMed]
- Gumz, H.; Boye, S.; Iyisan, B.; Krönert, V.; Formanek, P.; Voit, B.; Lederer, A.; Appelhans, D. Toward Functional Synthetic Cells: In-Depth Study of Nanoparticle and Enzyme Diffusion through a Cross-Linked Polymersome Membrane. Adv. Sci. 2019. [Google Scholar] [CrossRef]
- Elvang, P.A.; Stein, P.C.; Bauer-Brandl, A.; Brandl, M. Characterization of co-existing colloidal structures in fasted state simulated fluids FaSSIF: A comparative study using AF4/MALLS, DLS and DOSY. J. Pharm. Biomed. Anal. 2017, 145, 531–536. [Google Scholar] [CrossRef]
- Debye, P.; Bueche, A.M. Scattering by an Inhomogeneous Solid. J. Appl. Phys. 1949, 20, 518–525. [Google Scholar] [CrossRef]
- Debye, P.; Bueche, F. Distribution of Segments in a Coiling Polymer Molecule. J. Chem. Phys. 1952, 20, 1337–1338. [Google Scholar] [CrossRef]
- Savin, G.; Burchard, W. Uncommon Solution Behavior of Poly(N-vinylimidazole). Angular Dependence of Scattered Light from Aggregates in Ethanol. Macromolecules 2004, 37, 3005–3017. [Google Scholar] [CrossRef]
- Stauch, O.; Schubert, R.; Savin, G.; Burchard, W. Structure of Artificial Cytoskeleton Containing Liposomes in Aqueous Solution Studied by Static and Dynamic Light Scattering. Biomacromolecules 2002, 3, 565–578. [Google Scholar] [CrossRef] [PubMed]
- Ruckdeschel, P.; Dulle, M.; Honold, T.; Förster, S.; Karg, M.; Retsch, M. Monodisperse hollow silica spheres: An in-depth scattering analysis. Nano Res. 2016, 9, 1366–1376. [Google Scholar] [CrossRef]
- Holyst, R.; Bielejewska, A.; Szymanski, J.; Wilk, A.; Patkowski, A.; Gapinski, J.; Zywocinski, A.; Kalwarczyk, T.; Kalwarczyk, E.; Tabaka, M.; et al. Scaling form of viscosity at all length-scales in poly(ethylene glycol) solutions studied by fluorescence correlation spectroscopy and capillary electrophoresis. Phys. Chem. Chem. Phys. 2009, 11, 9025–9032. [Google Scholar] [CrossRef] [PubMed]
- Plantz, E. Brownian Motion, Dynamic Light Scattering and the Use of Viscosity Or…Would You Argue with Albert Einstein about how to use Viscosity in the DLS Formula? Available online: https://www.microtrac.com/MTWP/wp-content/uploads/2012/10/Microtrac-Application-Notes-Arguing-with-Einstein-How-to-Use-Viscosity-in-the-DLS-Formula.pdf (accessed on 1 September 2017).
- Fairhurst, D.; Weiner, B. A Guide to Determination of Particle Size–Making an Effective and Reliable Measurement. Available online: http://www.brookhaveninstruments.com/pdf/theory/Determination%20of%20Particle%20Size.pdf (accessed on 1 September 2017).
- Thery, C.; Amigorena, S.; Raposo, G.; Clayton, A. Isolation and characterization of exosomes from cell culture supernatants and biological fluids. Curr. Protoc. Cell Biol. 2006. [Google Scholar] [CrossRef] [PubMed]
- Varenne, F.; Makky, A.; Gaucher-Delmas, M.; Violleau, F.; Vauthier, C. Multimodal Dispersion of Nanoparticles: A Comprehensive Evaluation of Size Distribution with 9 Size Measurement Methods. Pharm. Res. 2016, 33, 1220–1234. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Shen, J.; Thomas, J.C.; Yin, Z.; Wang, X.; Wang, Y.; Liu, W.; Sun, X. Effect of scattering angle error on particle size determination by multiangle dynamic light scattering. Appl. Optics 2015, 54, 2824–2831. [Google Scholar] [CrossRef]



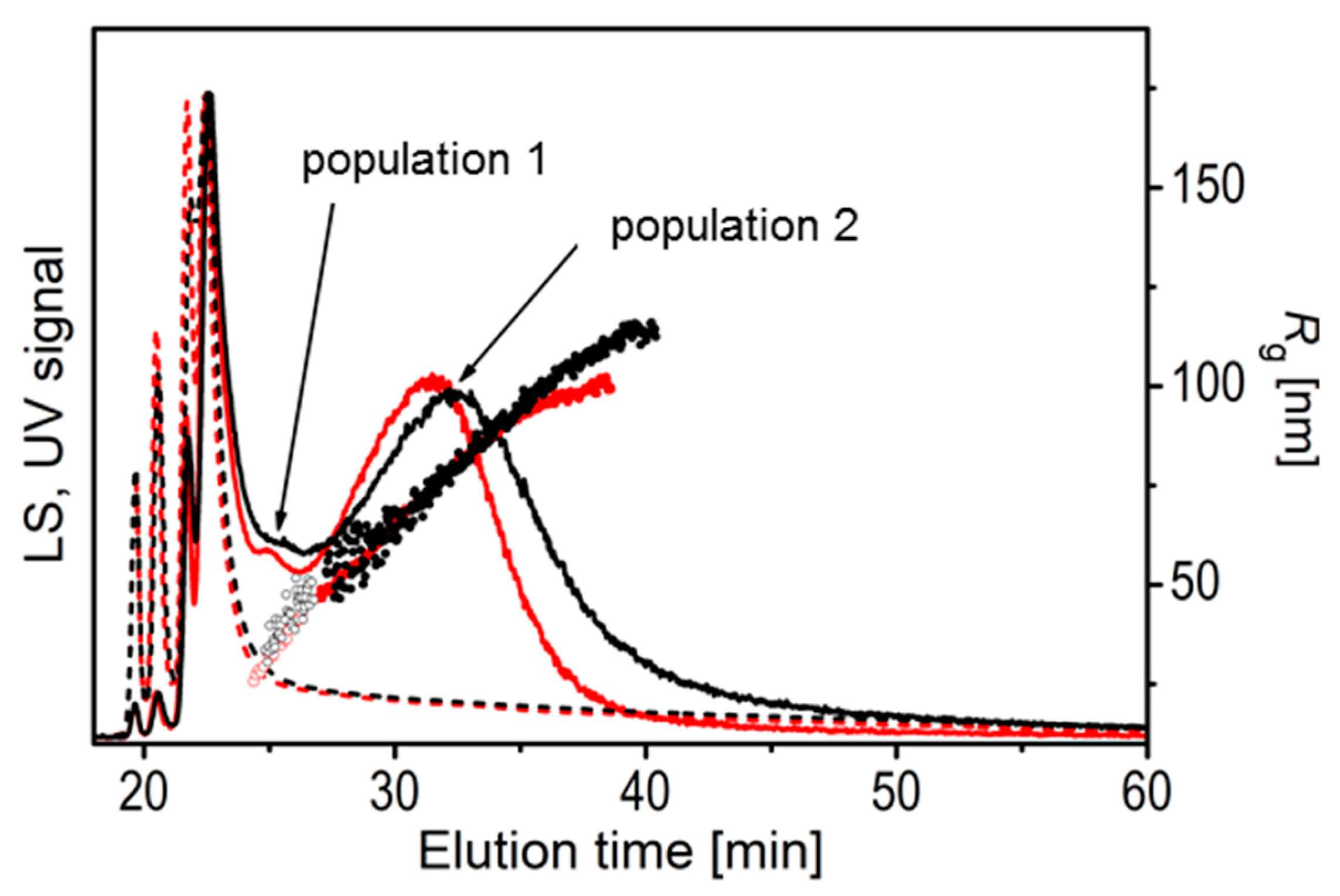

| AF4-MALS | Batch DLS/SLS | |||
|---|---|---|---|---|
| Sample | Rg (nm) | Rh,90 # (nm) | Rg (nm) | |
| unfiltered ES | larger EVs (population 2) | 93 | 119 | 152 |
| smaller EVs (population 1) | ~40 | 20 | ND * | |
| Average of short-time eluted particles; i.e., components with high UV signal and smaller EVs (population 1) | ~25 | |||
| filtered ES | larger EVs (population 2) | 84 | 101 | 138 |
| smaller EVs (population 1) | ~40 | 19 | ND * | |
| Average of short-time eluted particles; i.e., components with high UV signal and smaller EVs (population 1) | ~25 | |||
| Peak | I [%] | Rh,90 [nm] | Rh,90corr [nm] | Measured Viscosity, η [mPa/s] | |
|---|---|---|---|---|---|
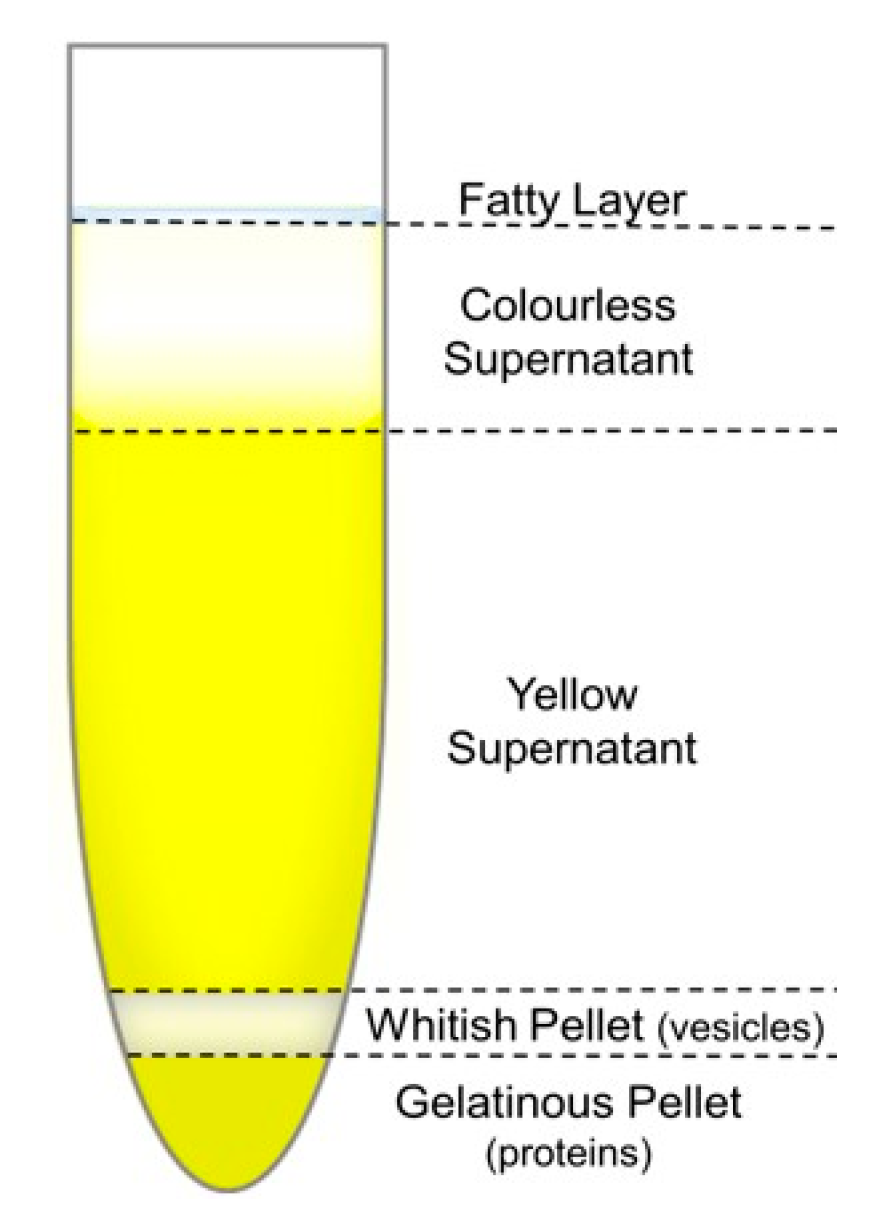
| Initial plasma sample I (total) = 792 kHz/mW | 0 | 5 (a) | 3 (a) | 3 (a) | 1.47 |
| 1 | 31 | 19 | 12 | ||
| 2 | 64 | 75 | 46 | ||
| Colourless supernatant I (total) = 904 kHz/mW | 1 | 46 | 21 | 20 | 0.94 |
| 2 | 54 (b) | 55 (b) | 52 (b) | ||
| Yellow supernatant I (total) = 746 kHz/mW | 0 | 3 (a) | 2 (a) | 2 (a) | 1.32 |
| 1 | 31 | 14 | 9 | ||
| 2 | 64 | 62 | 42 | ||
| Whitish pellet re-suspended in PBS I (total) = 490 kHz/mW | 1 | 17 (a) | 7 (a) | 7 (a) | NC c) |
| 2 | 77 | 44 | 44 | ||
| Gelatinous pellet re-suspended in PBS I (total) = 113 kHz/mW | 0 | 50 (a) | 7 (a) | 7 (a) | NC (c) |
| 1 | 49 | 40 | 40 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Božič, D.; Sitar, S.; Junkar, I.; Štukelj, R.; Pajnič, M.; Žagar, E.; Kralj-Iglič, V.; Kogej, K. Viscosity of Plasma as a Key Factor in Assessment of Extracellular Vesicles by Light Scattering. Cells 2019, 8, 1046. https://doi.org/10.3390/cells8091046
Božič D, Sitar S, Junkar I, Štukelj R, Pajnič M, Žagar E, Kralj-Iglič V, Kogej K. Viscosity of Plasma as a Key Factor in Assessment of Extracellular Vesicles by Light Scattering. Cells. 2019; 8(9):1046. https://doi.org/10.3390/cells8091046
Chicago/Turabian StyleBožič, Darja, Simona Sitar, Ita Junkar, Roman Štukelj, Manca Pajnič, Ema Žagar, Veronika Kralj-Iglič, and Ksenija Kogej. 2019. "Viscosity of Plasma as a Key Factor in Assessment of Extracellular Vesicles by Light Scattering" Cells 8, no. 9: 1046. https://doi.org/10.3390/cells8091046
APA StyleBožič, D., Sitar, S., Junkar, I., Štukelj, R., Pajnič, M., Žagar, E., Kralj-Iglič, V., & Kogej, K. (2019). Viscosity of Plasma as a Key Factor in Assessment of Extracellular Vesicles by Light Scattering. Cells, 8(9), 1046. https://doi.org/10.3390/cells8091046








