Reverse Engineering Cellular Networks with Information Theoretic Methods
Abstract
:1. Introduction
2. Background
2.1. Correlations, Probabilities and Entropies
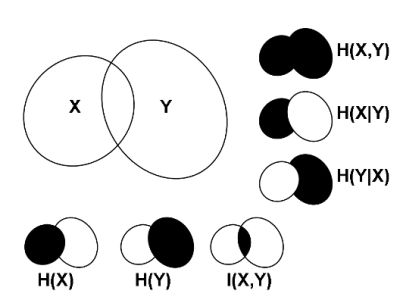
2.2. Mutual Information
2.3. Generalizations of Information Theory
3. Review of Network Inference Methods
3.1. Detecting Interactions: Correlations and Mutual Information
3.2. Distinguishing between Direct and Indirect Interactions
- Given a species Y, start with X* = ⊘
- Find X* : H(Y∣X*, X*) = minXH(Y∣X*,X*)
- Set X* = {X*, X*}
- Stop if H(Y∣X*, X*) = H(Y∣X*), or when all species except Y are already in X*; otherwise go to step 2
3.3. Detecting Causality
3.4. Previous Comparisons
4. Conclusions, Successes and Challenges
Acknowledgments
References
- Kitano, H. Foundations of Systems Biology; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Arkin, A.; Schaffer, D. Network news: Innovations in 21st century systems biology. Cell 2011, 144, 844–849. [Google Scholar]
- Gray, R. Entropy and Information Theory; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Quastler, H. Information Theory in Biology; University of Illinois Press: Urbana, IL, USA, 1953. [Google Scholar]
- Bekey, G.; Beneken, J. Identification of biological systems: A survey. Automatica 1978, 14, 41–47. [Google Scholar]
- D'haeseleer, P.; Liang, S.; Somogyi, R. Genetic network inference: From co-expression clustering to reverse engineering. Bioinformatics 2000, 16, 707–726. [Google Scholar]
- Crampin, E.; Schnell, S.; McSharry, P. Mathematical and computational techniques to deduce complex biochemical reaction mechanisms. Prog. Biophys. Mol. Biol. 2004, 86, 77–112. [Google Scholar]
- Ross, J. Determination of complex reaction mechanisms. Analysis of chemical, biological and genetic networks. J. Phys. Chem. A 2008, 112, 2134–2143. [Google Scholar]
- De Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar]
- Cho, K.; Choo, S.; Jung, S.; Kim, J.; Choi, H.; Kim, J. Reverse engineering of gene regulatory networks. IET Syst. Biol. 2007, 1, 149–163. [Google Scholar]
- Markowetz, F.; Spang, R. Inferring cellular networks–A review. BMC Bioinform. 2007, 8, S5:1–S5:17. [Google Scholar]
- Hecker, M.; Lambeck, S.; Toepfer, S.; van Someren, E.; Guthke, R. Gene regulatory network inference: Data integration in dynamic models–A review. Biosystems 2009, 96, 86–103. [Google Scholar]
- López-Kleine, L.; Leal, L.; López, C. Biostatistical approaches for the reconstruction of gene co-expression networks based on transcriptomic data. Brief. Funct. Genomics 2013. [Google Scholar] [CrossRef]
- Koyutürk, M. Algorithmic and analytical methods in network biology. WIREs Syst. Biol. Med. 2009, 2, 277–292. [Google Scholar]
- De Smet, R.; Marchal, K. Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 2010, 8, 717–729. [Google Scholar]
- Soranzo, N.; Bianconi, G.; Altafini, C. Comparing association network algorithms for reverse engineering of large-scale gene regulatory networks: Synthetic versus real data. Bioinformatics 2007, 23, 1640–1647. [Google Scholar]
- Altay, G.; Emmert-Streib, F. Revealing differences in gene network inference algorithms on the network level by ensemble methods. Bioinformatics 2010, 26, 1738–1744. [Google Scholar]
- Bansal, M.; Belcastro, V.; Ambesi-Impiombato, A.; di Bernardo, D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007, 3, 78:1–78:10. [Google Scholar]
- Hurley, D.; Araki, H.; Tamada, Y.; Dunmore, B.; Sanders, D.; Humphreys, S.; Affara, M.; Imoto, S.; Yasuda, K.; Tomiyasu, Y.; et al. Gene network inference and visualization tools for biologists: Application to new human transcriptome datasets. Nucleic Acids Res. 2012, 40, 2377–2398. [Google Scholar]
- Walter, E.; Pronzato, L. Identification of parametric models from experimental data. In Communications and Control Engineering Series; Springer: London, UK, 1997. [Google Scholar]
- Ljung, L. System Identification: Theory for the User; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Galton, F. Regression towards mediocrity in hereditary stature. J. Anthropol. Inst. Great Brit. Ire. 1886, 15, 246–263. [Google Scholar]
- Stigler, S. Francis Galton's account of the invention of correlation. Stat. Sci. 1989, 4, 73–79. [Google Scholar]
- Samoilov, M. Reconstruction and functional analysis of general chemical reactions and reaction networks. PhD thesis, Stanford University, Stanford, CA, USA, 1997. [Google Scholar]
- Samoilov, M.; Arkin, A.; Ross, J. On the deduction of chemical reaction pathways from measurements of time series of concentrations. Chaos 2001, 11, 108–114. [Google Scholar]
- Linfoot, E. An informational measure of correlation. Inf. Control 1957, 1, 85–89. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Numata, J.; Ebenhöh, O.; Knapp, E. Measuring correlations in metabolomic networks with mutual information. Genome Inform. 2008, 20, 112–122. [Google Scholar]
- Steuer, R.; Kurths, J.; Daub, C.; Weise, J.; Selbig, J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics 2002, 18, S231–S240. [Google Scholar]
- Fraser, A.; Swinney, H. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar]
- Cellucci, C.; Albano, A.; Rapp, P. Statistical validation of mutual information calculations: Comparison of alternative numerical algorithms. Phys. Rev. E 2005, 71, 066208:1–066208:14. [Google Scholar]
- Moon, Y.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318–2321. [Google Scholar]
- Hausser, J.; Strimmer, K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Olsen, C.; Meyer, P.; Bontempi, G. On the impact of entropy estimation on transcriptional regulatory network inference based on mutual information. EURASIP J. Bioinform. Syst. Biol. 2009, 2009, 308959:1–308959:9. [Google Scholar]
- De Matos Simoes, R.; Emmert-Streib, F. Influence of statistical estimators of mutual information and data heterogeneity on the inference of gene regulatory networks. PLoS One 2011, 6, e29279:1–e29279:14. [Google Scholar]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar]
- Margolin, A.; Wang, K.; Califano, A.; Nemenman, I. Multivariate dependence and genetic networks inference. IET Syst. Biol. 2010, 4, 428–440. [Google Scholar]
- Marko, H. Information theory and cybernetics. IEEE Spectrum 1967, 4, 75–83. [Google Scholar]
- Marko, H. The bidirectional communication theory–a generalization of information theory. IEEE Trans. Commun. 1973, 21, 1345–1351. [Google Scholar]
- Massey, J. Causality, feedback and directed information. Proceedings of the International Symposium on Information Theory and Its Applications (ISITA-90), Hawaii, HA, USA, 27–30 November 1990; pp. 303–305.
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Sci. USA 2005, 102, 15377–15382. [Google Scholar]
- Tsallis, C. Entropic nonextensivity: A possible measure of complexity. Chaos Soliton Fract. 2002, 13, 371–391. [Google Scholar]
- Barabási, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Barabási, A. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar]
- Farber, R.; Lapedes, A.; Sirotkin, K. Determination of eukaryotic protein coding regions using neural networks and information theory. J. Mol. Biol. 1992, 226, 471–479. [Google Scholar]
- Korber, B.; Farber, R.; Wolpert, D.; Lapedes, A. Covariation of mutations in the V3 loop of human immunodeficiency virus type 1 envelope protein: an information theoretic analysis. Proc. Natl. Acad. Sci. USA 1993, 90, 7176–7180. [Google Scholar]
- Liang, S.; Fuhrman, S.; Somogyi, R. REVEAL, a general reverse engineering algorithm for inference of genetic network architectures. Proceedings of the Pacific Symposium on Biocomputing, Hawaii, HA, USA, 4–9 January 1998; Volume 3, pp. 18–29.
- Michaels, G.; Carr, D.; Askenazi, M.; Fuhrman, S.; Wen, X.; Somogyi, R. Cluster analysis and data visualization of large scale gene expression data. Proceedings of the Pacific Symposium on Biocomputing, Hawaii, HA, USA, 4–9 January 1998; Volume 3, pp. 42–53.
- Butte, A.; Kohane, I. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. Proceedings of the Pacific Symposium on Biocomputing, Hawaii, HA, USA, 4–9 January 2000; Volume 5, pp. 418–429.
- Butte, A.; Tamayo, P.; Slonim, D.; Golub, T.; Kohane, I. Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proc. Natl. Acad. Sci. USA 2000, 97, 12182–12186. [Google Scholar]
- Stuart, J.; Segal, E.; Koller, D.; Kim, S. A gene-coexpression network for global discovery of conserved genetic modules. Science 2003, 302, 249–255. [Google Scholar]
- Belcastro, V.; Siciliano, V.; Gregoretti, F.; Mithbaokar, P.; Dharmalingam, G.; Berlingieri, S.; Iorio, F.; Oliva, G.; Polishchuck, R.; Brunetti-Pierri, N.; et al. Transcriptional gene network inference from a massive dataset elucidates transcriptome organization and gene function. Nucleic Acids Res. 2011, 39, 8677–8688. [Google Scholar]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar]
- Arkin, A.; Ross, J. Statistical Construction of chemical reaction mechanisms from measured time-series. J. Phys. Chem. 1995, 99, 970–979. [Google Scholar]
- Arkin, A.; Shen, P.; Ross, J. A test case of correlation metric construction of a reaction pathway from measurements. Science 1997, 277, 1275–1279. [Google Scholar]
- Wahl, S.; Haunschild, M.; Oldiges, M.; Wiechert, W. Unravelling the regulatory structure of biochemical networks using stimulus response experiments and large-scale model selection. Syst. Biol. 2006, 153, 275–285. [Google Scholar]
- Villaverde, A.F.; Ross, J.; Morán, F.; Banga, J.R. MIDER: Network inference with Mutual Information Distance and Entropy Reduction. 2013. Available online: http://www.iim.csic.es/gingproc/mider.html/ (accessed on 6 May 2013).
- Lecca, P.; Morpurgo, D.; Fantaccini, G.; Casagrande, A.; Priami, C. Inferring biochemical reaction pathways: The case of the gemcitabine pharmacokinetics. BMC Syst. Biol. 2012, 6, 51:1–51:21. [Google Scholar]
- Székely, G.; Rizzo, M.; Bakirov, N. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar]
- Szekely, G.; Rizzo, M. Brownian distance correlation. Ann. Appl. Stat. 2009, 3, 1236–1265. [Google Scholar]
- Roy, A.; Post, C. Detection of long-range concerted motions in protein by a distance covariance. J. Chem. Theory Comput. 2012, 8, 3009–3014. [Google Scholar]
- Kong, J.; Klein, B.; Klein, R.; Lee, K.; Wahba, G. Using distance correlation and SS-ANOVA to assess associations of familial relationships, lifestyle factors, diseases, and mortality. Proc. Natl. Acad. Sci. USA 2012, 109, 20352–20357. [Google Scholar]
- Kumari, S.; Nie, J.; Chen, H.; Ma, H.; Stewart, R.; Li, X.; Lu, M.; Taylor, W.; Wei, H. Evaluation of gene association methods for coexpression network construction and biological knowledge discovery. PLoS One 2012, 7, e50411:1–e50411:17. [Google Scholar]
- Reshef, D.; Reshef, Y.; Finucane, H.; Grossman, S.; McVean, G.; Turnbaugh, P.; Lander, E.; Mitzenmacher, M.; Sabeti, P. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar]
- Kinney, J.; Atwal, G. Equitability, mutual information, and the maximal information coefficient. arXiv 2013, arXiv:1301. 7745. [Google Scholar]
- Heller, R.; Heller, Y.; Gorfine, M. A consistent multivariate test of association based on ranks of distances. arXiv 2012, arXiv:1201. 3522. [Google Scholar]
- Reshef, D.; Reshef, Y.; Mitzenmacher, M.; Sabeti, P. Equitability analysis of the maximal information coefficient, with comparisons. arXiv 2013, arXiv:1301. 6314. [Google Scholar]
- Lopes, F.; de Oliveira, E.; Cesar, R. Inference of gene regulatory networks from time series by Tsallis entropy. BMC Syst. Biol. 2011, 5, 61:1–61:13. [Google Scholar]
- Zhao, W.; Serpedin, E.; Dougherty, E.R. Inferring gene regulatory networks from time series data using the minimum description length principle. Bioinformatics 2006, 22, 2129–2135. [Google Scholar]
- Dougherty, J.; Tabus, I.; Astola, J. Inference of gene regulatory networks based on a universal minimum description length. EURASIP J. Bioinform. Syst. Biol. 2008, 2008, 482090:1–482090:11. [Google Scholar]
- Chaitankar, V.; Ghosh, P.; Perkins, E.; Gong, P.; Deng, Y.; Zhang, C. A novel gene network inference algorithm using predictive minimum description length approach. BMC Syst. Biol. 2010, 4, S7:1–S7:12. [Google Scholar]
- Basso, K.; Margolin, A.; Stolovitzky, G.; Klein, U.; Dalla-Favera, R.; Califano, A. Reverse engineering of regulatory networks in human B cells. Nat. Genet. 2005, 37, 382–390. [Google Scholar]
- Margolin, A.; Wang, K.; Lim, W.; Kustagi, M.; Nemenman, I.; Califano, A. Reverse engineering cellular networks. Nat. Protoc. 2006, 1, 662–671. [Google Scholar]
- Margolin, A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.; Califano, A. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinform. 2006, 7, S7:1–S7:15. [Google Scholar]
- Zoppoli, P.; Morganella, S.; Ceccarelli, M. TimeDelay-ARACNE: Reverse engineering of gene networks from time-course data by an information theoretic approach. BMC Bioinform. 2010, 11, 154:1–154:15. [Google Scholar]
- Zhao, W.; Serpedin, E.; Dougherty, E. Inferring connectivity of genetic regulatory networks using information-theoretic criteria. IEEE ACM Trans. Comput. Biol. Bioinformatics 2008, 5, 262–274. [Google Scholar]
- Faith, J.; Hayete, B.; Thaden, J.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.; Gardner, T. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5, e8:1–e8:13. [Google Scholar]
- Friedman, N.; Linial, M.; Nachman, I.; Pe'er, D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000, 7, 601–620. [Google Scholar]
- Michoel, T.; de Smet, R.; Joshi, A.; van de Peer, Y.; Marchal, K. Comparative analysis of module-based versus direct methods for reverse-engineering transcriptional regulatory networks. BMC Syst. Biol. 2009, 3, 49:1–49:13. [Google Scholar]
- Meyer, P.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-theoretic inference of large transcriptional regulatory networks. EURASIP J. Bioinform. Syst. Biol. 2007, 2007, 79879:1–79879:9. [Google Scholar]
- Tourassi, G.; Frederick, E.; Markey, M.; Floyd, J. Application of the mutual information criterion for feature selection in computer-aided diagnosis. Med. Phys. 2001, 28, 2394–2402. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar]
- Meyer, P.; Lafitte, F.; Bontempi, G. Minet: A R/Bioconductor package for inferring large transcriptional networks using mutual information. BMC Bioinform. 2008, 9, 461:1–461:10. [Google Scholar]
- Meyer, P.; Marbach, D.; Roy, S.; Kellis, M. Information-theoretic inference of gene networks using backward elimination. Proceedings of the IASTED International Conference on Computational Bioscience (CompBio), BIOCOMP, Cambridge, MA, USA, 1–3 November 2010; pp. 1–6.
- Luo, W.; Hankenson, K.; Woolf, P. Learning transcriptional regulatory networks from high throughput gene expression data using continuous three-way mutual information. BMC Bioinform. 2008, 9, 467:1–467:15. [Google Scholar]
- Watkinson, J.; Liang, K.; Wang, X.; Zheng, T.; Anastassiou, D. Inference of regulatory gene interactions from expression data using three-way mutual information. Ann. N.Y. Acad. Sci. 2009, 1158, 302–313. [Google Scholar]
- Stolovitzky, G.; Prill, R.; Califano, A. Lessons from the DREAM2 Challenges. Ann. N.Y. Acad. Sci. 2009, 1158, 159–195. [Google Scholar]
- Wang, X.; Qi, Y.; Jiang, Z. Reconstruction of transcriptional network from microarray data using combined mutual information and network-assisted regression. IET Syst. Biol. 2011, 5, 95–102. [Google Scholar]
- Bonneau, R.; Reiss, D.; Shannon, P.; Facciotti, M.; Hood, L.; Baliga, N.; Thorsson, V. The Inferelator: An algorithm for learning parsimonious regulatory networks from systems-biology data sets. de novo. Genome Biol. 2006, 7, R36:1–R36:16. [Google Scholar]
- Bonneau, R.; Facciotti, M.; Reiss, D.; Schmid, A.; Pan, M.; Kaur, A.; Thorsson, V.; Shannon, P.; Johnson, M.; Bare, J.; et al. A predictive model for transcriptional control of physiology in a free living cell. Cell 2007, 131, 1354–1365. [Google Scholar]
- Greenfield, A.; Madar, A.; Ostrer, H.; Bonneau, R. DREAM4: Combining genetic and dynamic information to identify biological networks and dynamical models. PLoS One 2010, 5, e13397:1–e13397:14. [Google Scholar]
- De La Fuente, A.; Bing, N.; Hoeschele, I.; Mendes, P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 2004, 20, 3565–3574. [Google Scholar]
- Bing, N.; Hoeschele, I. Genetical genomics analysis of a yeast segregant population for transcription network inference. Genetics 2005, 170, 533–542. [Google Scholar]
- Çakır, T.; Hendriks, M.; Westerhuis, J.; Smilde, A. Metabolic network discovery through reverse engineering of metabolome data. Metabolomics 2009, 5, 318–329. [Google Scholar]
- Pearl, J. An introduction to causal inference. Int. J. Biostat. 2010, 6, 7:1–7:61. [Google Scholar]
- Rice, J.; Tu, Y.; Stolovitzky, G. Reconstructing biological networks using conditional correlation analysis. Bioinformatics 2005, 21, 765–773. [Google Scholar]
- Opgen-Rhein, G.; Strimmer, K. From correlation to causation networks: A simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Syst. Biol. 2007, 1, 37:1–37:10. [Google Scholar]
- Mathai, P.; Martins, N.; Shapiro, B. On the detection of gene network interconnections using directed mutual information. Proceedings of the Information Theory and Applications Workshop, La Jolla, CA, USA, 29 January–2 February 2007; pp. 274–283.
- Rao, A.; Hero, A.; States, D.; Engel, J. Using directed information to build biologically relevant influence networks. J. Bioinform. Comput. Biol. 2008, 6, 493–519. [Google Scholar]
- Kaleta, C.; Göhler, A.; Schuster, S.; Jahreis, K.; Guthke, R.; Nikolajewa, S. Integrative inference of gene-regulatory networks in Escherichia coli using information theoretic concepts and sequence analysis. BMC Syst. Biol. 2010, 4, 116:1–116:11. [Google Scholar]
- Quinn, C.; Coleman, T.; Kiyavash, N.; Hatsopoulos, N. Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. J. Comput. Neurosci. 2011, 30, 17–44. [Google Scholar]
- Emmert-Streib, F. Influence of the experimental design of gene expression studies on the inference of gene regulatory networks: Environmental factors. PeerJ 2013, 1, e10:1–e10:20. [Google Scholar]
- De Matos Simoes, R.; Emmert-Streib, F. Bagging statistical network inference from large-scale gene expression data. PLoS One 2012, 7, e33624:1–e33624:11. [Google Scholar]
- Altay, G.; Emmert-Streib, F. Inferring the conservative causal core of gene regulatory networks. BMC Syst. Biol. 2010, 4, 132:1–132:13. [Google Scholar]
- Marbach, D.; Prill, R.; Schaffter, T.; Mattiussi, C.; Floreano, D.; Stolovitzky, G. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA 2010, 107, 6286–6291. [Google Scholar] [Green Version]
- Prill, R.; Saez-Rodriguez, J.; Alexopoulos, L.; Sorger, P.; Stolovitzky, G. Crowdsourcing network inference: The DREAM predictive signaling network challenge. Sci. Signal. 2011, 4, mr7:1–mr7:6. [Google Scholar]
- Marbach, D.; Costello, J.; Küffner, R.; Vega, N.; Prill, R.; Camacho, D.; Allison, K.; Kellis, M.; Collins, J.; Stolovitzky, G.; et al. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar]

© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Villaverde, A.F.; Ross, J.; Banga, J.R. Reverse Engineering Cellular Networks with Information Theoretic Methods. Cells 2013, 2, 306-329. https://doi.org/10.3390/cells2020306
Villaverde AF, Ross J, Banga JR. Reverse Engineering Cellular Networks with Information Theoretic Methods. Cells. 2013; 2(2):306-329. https://doi.org/10.3390/cells2020306
Chicago/Turabian StyleVillaverde, Alejandro F., John Ross, and Julio R. Banga. 2013. "Reverse Engineering Cellular Networks with Information Theoretic Methods" Cells 2, no. 2: 306-329. https://doi.org/10.3390/cells2020306
APA StyleVillaverde, A. F., Ross, J., & Banga, J. R. (2013). Reverse Engineering Cellular Networks with Information Theoretic Methods. Cells, 2(2), 306-329. https://doi.org/10.3390/cells2020306