Mechanical Properties of Endothelial Cells: A Key to Physiology, Drug Testing and Nanostructure Interaction
Highlights
- Endothelial elasticity is a physical parameter that describes physiological changes in cells.
- Changes in endothelial cell mechanical properties are largely associated with cellular cytoskeleton remodeling.
- Force spectroscopy is a relevant method for testing drugs on the endothelium.
- Nanostructures affect the mechanical properties of endothelial cells.
Abstract
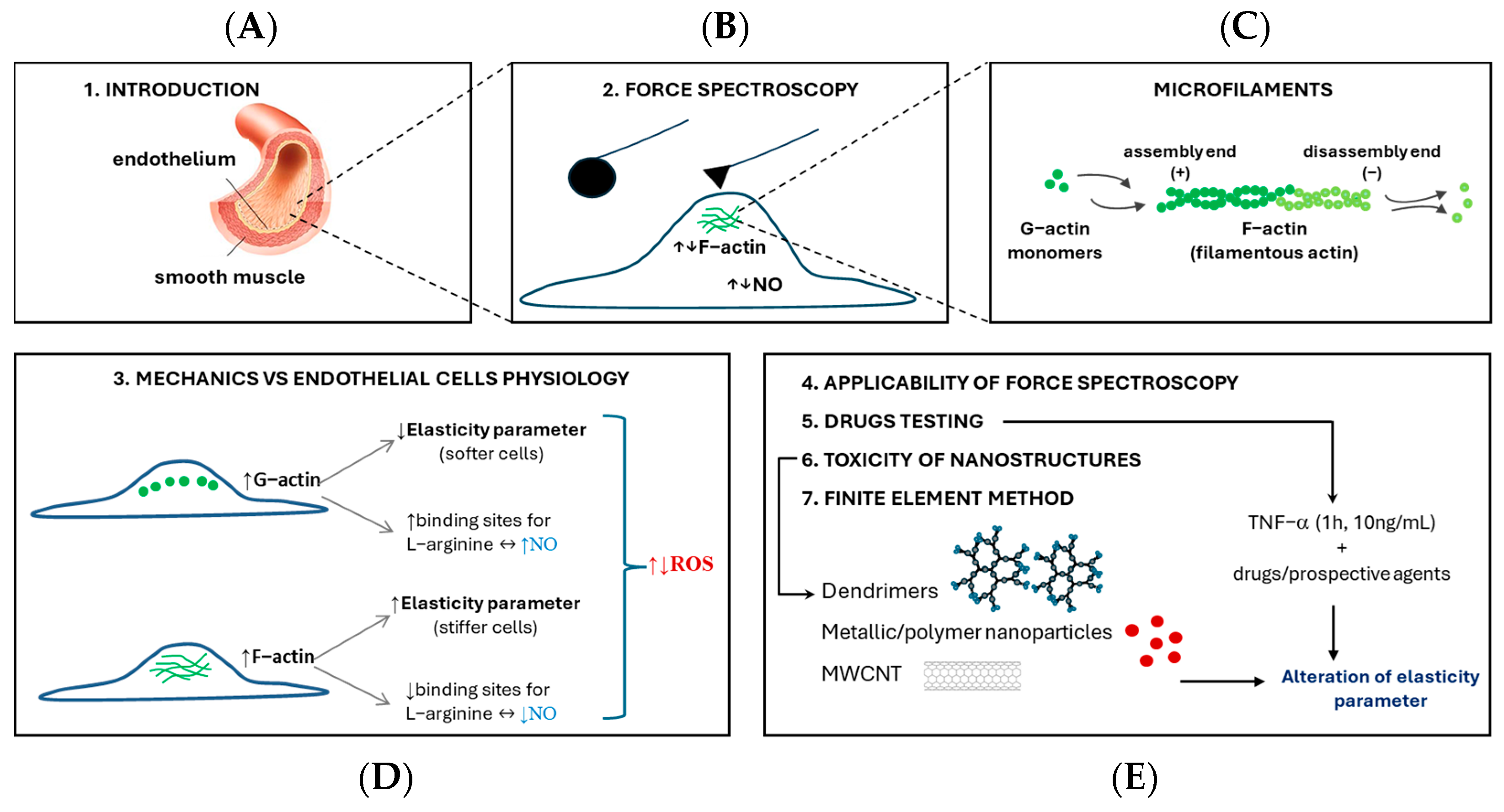
1. Introduction
2. Different Approaches to Force Spectroscopy Measurements and Analysis
2.1. Introduction to Force Spectroscopy Technique
2.2. Comparison of Force Spectroscopy Study with Different Probes Geometries and Materials
2.3. Substrate Influence on Force Spectroscopy Measurements
2.4. Elasticity and Viscoelasticity of Cells
2.5. Limitation of Force Spectroscopy Study
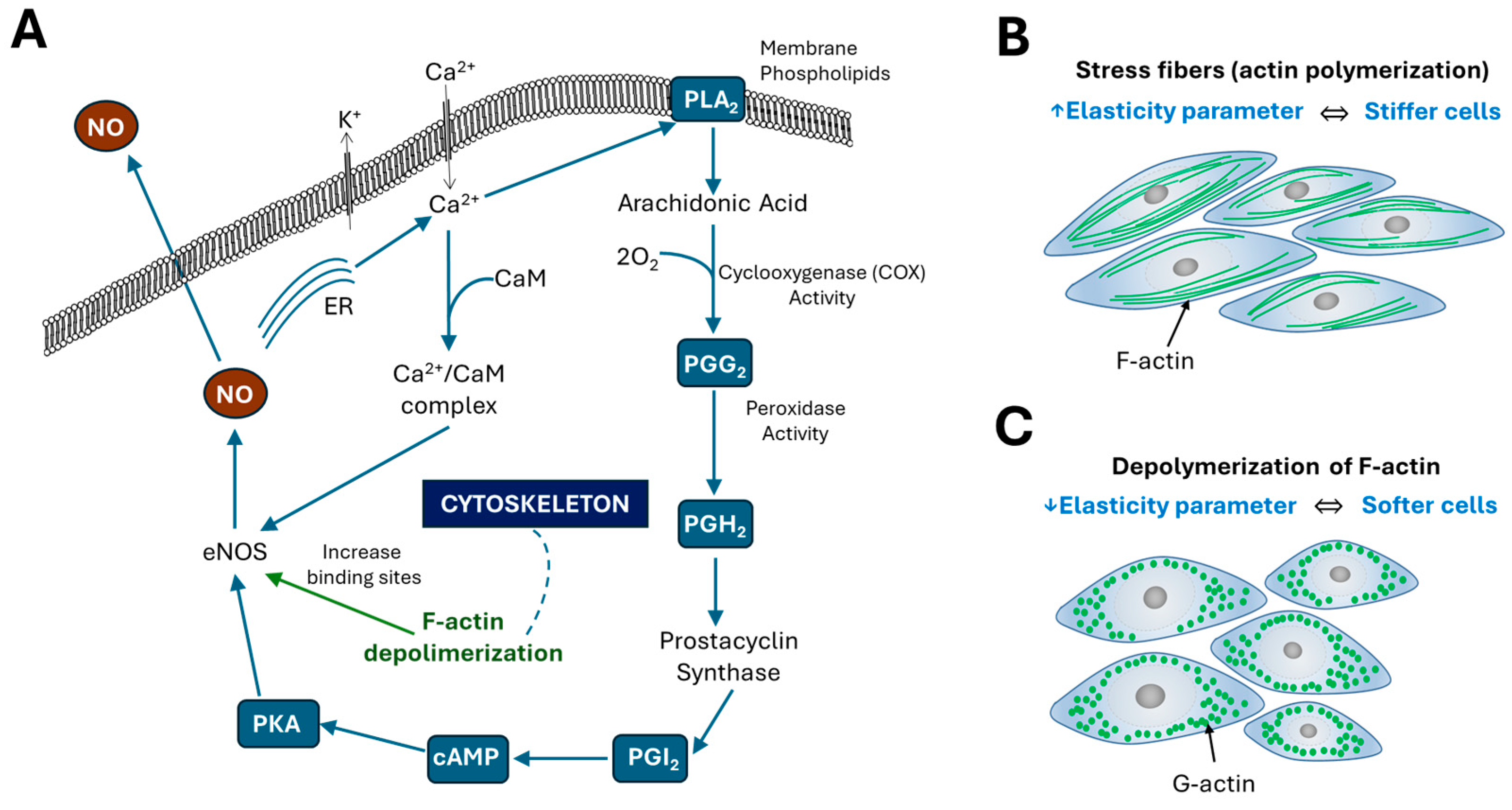
3. How Changes in the Mechanical Properties of Cells Affect Their Physiology
3.1. Mechanical Environment of the Endothelium
3.2. Elasticity of Endothelial Cells
4. The Applicability of Atomic Force Spectroscopy in the Study of Endothelial Cells
5. From Cytokine to Drugs—How to Test Potential Agents Based on Elasticity Measurements
6. Toxicity of Nanostructures Versus Cell Elasticity
6.1. Impact of Carbon Nanotubes on Endothelial Cell Elasticity
6.2. Alteration in Endothelial Elasticity Induced by Metallic and Polymer Nanoparticles
6.3. Effect of Dendrimers on Cell Elasticity
7. Finite Element Method in Endothelial Cell Mechanical Response
7.1. Modeling of Cytoskeletal Architecture
7.2. Viscoelastic and Hyperelastic Modeling
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| AFS | Atomic force spectroscopy |
| ECs | Endothelial cells |
| HMEC | Human microvascular endothelial cells |
| HUVEC | Human umbilical vein endothelial cells |
| SNP | Silver nanoparticles |
| MWCNT | Multi-walled carbon nanotubes |
| PAMAM | Polyamidoamine dendrimers |
| CAT | Cationic amino acid transporters |
| NO | Nitric oxide |
| eNOs | Endothelial nitric oxide synthase |
| PGI2 | Prostacyclin |
| AA | Arachidonic acid |
| PKA | Protein kinase A |
| PLA2 | Phospholipase A2 |
| PGG2 | Prostaglandin G2 |
| PGH2 | Prostaglandin H2 |
| COX | Cyclooxygenase |
| ROS | Reactive oxygen species |
| PAF | Platelet-activating factor |
| ET-1 | Endothelin-1 |
| ENaC | Endothelial sodium channels |
| TNF-α | Tumor necrosis factor—α |
| Sd | Summit density |
| DOX | Doxorubicin |
| DNR | Daunorubicin |
| FEM | Finite Element Method |
| AFs | Actin filaments |
| MTs | Microtubules |
| IFs | Intermediate filaments |
References
- Safran, S.A.; Gov, N.; Nicolas, A.; Schwarz, U.S.; Tlusty, T. Physics of cell elasticity, shape and adhesion. Phys. A Stat. Mech. Its Appl. 2005, 352, 171–201. [Google Scholar] [CrossRef]
- De Santis, G.; Lennon, A.B.; Boschetti, F.; Verhegghe, B.; Verdonck, P.; Prendergast, P.J. How can cells sense the elasticity of a substrate? an analysis using a cell tensegrity model. Eur. Cells Mater. 2011, 22, 202–213. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Liu, Y.; Li, B.; Li, J.; Yan, S.; Chen, H. Cell elasticity measurement and sorting based on microfluidic techniques: Advances and applications. Biosens. Bioelectron. 2025, 271, 116985. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Blood Vessels and Endothelial Cells, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Krüger-Genge, A.; Blocki, A.; Franke, R.P.; Jung, F. Vascular Endothelial Cell Biology: An Update. Int. J. Mol. Sci. 2019, 20, 4411. [Google Scholar] [CrossRef]
- Jufri, N.F.; Mohamedali, A.; Avolio, A.; Baker, M.S. Mechanical stretch: Physiological and pathological implications for human vascular endothelial cells. Vasc. Cell 2015, 7, 8. [Google Scholar] [CrossRef]
- Klar, A.; Lin, Y.; Immanuel, J.; Yun, S. Vascular Inflammatory Diseases and Endothelial Phenotypes. Cells 2023, 12, 1640. [Google Scholar] [CrossRef]
- Eyckmans, J.; Boudou, T.; Yu, X.; Chen, C.S. A hitchhiker’s guide to mechanobiology. Dev. Cell 2011, 21, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Geiger, B.; Spatz, J.P.; Bershadsky, A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009, 10, 21–33. [Google Scholar] [CrossRef]
- Tzima, E.; Irani-Tehrani, M.; Kiosses, W.B.; Dejana, E.; Schultz, D.A.; Engelhardt, B.; Cao, G.; DeLisser, H.; Schwartz, M.A. A mechanosensory complex that mediates the endothelial cell response to fluid shear stress. Nature 2005, 437, 426–431. [Google Scholar] [CrossRef]
- Favero, G.; Paganelli, C.; Buffoli, B.; Rodella, L.F.; Rezzani, R. Endothelium and Its Alterations in Cardiovascular Diseases: Life Style Intervention. Biomed. Res. Int. 2014, 2014, 801896. [Google Scholar] [CrossRef]
- Sato, H.; Kataoka, N.; Kajiya, F.; Katano, M.; Takigawa, T.; Masuda, T. Kinetic study on the elastic change of vascular endothelial cells on collagen matrices by atomic force microscopy. Colloids Surf. B Biointerfaces 2004, 34, 141–146. [Google Scholar] [CrossRef]
- Seo, Y.; Jhe, W. Atomic force microscopy and spectroscopy. Rep. Prog. Phys. 2008, 71, 16101. [Google Scholar] [CrossRef]
- Pimenta-Lopes, C.; Suay-Corredera, C.; Velázquez-Carreras, D.; Sánchez-Ortiz, D.; Alegre-Cebollada, J. Concurrent atomic force spectroscopy. Commun. Phys. 2019, 2, 91. [Google Scholar] [CrossRef]
- Müller, D.J.; Dumitru, A.C.; Lo Giudice, C.; Gaub, H.E.; Hinterdorfer, P.; Hummer, G.; De Yoreo, J.J.; Dufrêne, Y.F.; Alsteens, D. Atomic Force Microscopy-Based Force Spectroscopy and Multiparametric Imaging of Biomolecular and Cellular Systems. Chem. Rev. 2021, 121, 11701–11725. [Google Scholar] [CrossRef]
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 1999, 104, 1–104. [Google Scholar] [CrossRef]
- Szczygiel, A.M.; Brzezinka, G.; Targosz-Korecka, M.; Chlopicki, S.; Szymonski, M. Elasticity changes anti-correlate with NO production for human endothelial cells stimulated with TNF-α. Pflug. Arch. 2012, 463, 487–496. [Google Scholar] [CrossRef]
- Radmacher, M. Studying the Mechanics of Cellular Processes by Atomic Force Microscopy. Methods Cell Biol. 2007, 83, 83015–83019. [Google Scholar] [CrossRef]
- Szymonski, M.; Targosz-Korecka, M.; Malek-Zietek, K.E. Nano-mechanical model of endothelial dysfunction for AFM-based diagnostics at the cellular level. Pharmacol. Rep. 2015, 67, 728–735. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, A.M.; Sokolowska, P.; Zimon, A.; Grala, M.; Rosowski, M.; Siatkowska, M.; Komorowski, P.; Walkowiak, B. Dysfunction of endothelial cells exposed to nanomaterials assessed by atomic force spectroscopy. Micron 2021, 145, 103062. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, A.; Jakubowska, A.; Kucinska, M.; Wasiak, T.; Komorowski, P.; Makowski, K.; Walkowiak, B. Sensing of silver nanoparticles on/in endothelial cells using atomic force spectroscopy. J. Mol. Recognit. 2018, 31, e2723. [Google Scholar] [CrossRef]
- Hertz, H. Uber die Beruhrung fester elastischer Korper. J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A.; Stylianou, A. The Young’s Modulus as a Mechanical Biomarker in AFM Experiments: A Tool for Cancer Diagnosis and Treatment Monitoring. Sensors 2025, 25, 3510. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, R.A.; Vitorino, M.V.; Godinho, C.P.; Bourbon-Melo, N.; Robalo, T.T.; Fernandes, F.; Rodrigues, M.S.; Sá-Correia, I. Yeast adaptive response to acetic acid stress involves structural alterations and increased stiffness of the cell wall. Sci. Rep. 2021, 11, 12652. [Google Scholar] [CrossRef]
- Guz, N.; Dokukin, M.; Kalaparthi, V.; Sokolov, I. If Cell Mechanics Can Be Described by Elastic Modulus: Study of Different Models and Probes Used in Indentation Experiments. Biophys. J. 2014, 107, 564–575. [Google Scholar] [CrossRef] [PubMed]
- Okajima, T. Atomic Force Microscopy: Imaging and Rheology of Living Cells. In Nano/Micro Science and Technology in Biorheology; Kita, R., Dobashi, T., Eds.; Springer: Tokyo, Japan, 2015. [Google Scholar] [CrossRef]
- Zemła, J.; Bobrowska, J.; Kubiak, A.; Zieliński, T.; Pabijan, J.; Pogoda, K.; Bobrowski, P.; Lekka, M. Indenting soft samples (hydrogels and cells) with cantilevers possessing various shapes of probing tip. Eur. Biophys. J. 2020, 49, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.; Dokukin, M.E.; Guz, N.V. Method for quantitative measurements of the elastic modulus of biological cells in AFM indentation experiments. Methods 2013, 60, 202–213. [Google Scholar] [CrossRef]
- Oberleithner, H.; Callies, C.; Kusche-Vihrog, K.; Schillers, H.; Shahin, V.; Riethmuller, C.; MacGregor, G.A.; de Wardener, H.E. Potassium softens vascular endothelium and increases nitric oxide release. Proc. Natl. Acad. Sci. USA 2009, 106, 2829–2834. [Google Scholar] [CrossRef]
- Kulkarni, S.G.; Pérez-Domínguez, S.; Radmacher, M. Influence of cantilever tip geometry and contact model on AFM elasticity measurement of cells. J. Mol. Recognit. 2023, 36, e3018. [Google Scholar] [CrossRef]
- Brill-Karniely, Y. Mechanical measurements of cells using AFM: 3D or 2D physics? Front. Bioeng. Biotechnol. 2020, 8, 605153. [Google Scholar] [CrossRef]
- Wang, L.; Tian, L.; Zhang, W.; Wang, Z.; Liu, X. Effect of AFM nanoindentation loading rate on the characterization of mechanical properties of vascular endothelial cell. Micromachines 2020, 11, 562. [Google Scholar] [CrossRef]
- Weber, A.; Iturri, J.; Benitez, R.; Toca-Herrera, J.L. Measuring biomaterials mechanics with atomic force microscopy. 1. Influence of the loading rate and applied force (pyramidal tips). Microsc. Res. Tech. 2019, 82, 509–517. [Google Scholar] [CrossRef]
- Harris, A.R.; Charras, G.T. Experimental validation of atomic force microscopy-based cell elasticity measurements. Nanotechnology 2011, 22, 345102. [Google Scholar] [CrossRef]
- Carl, P.; Schillers, H. Elasticity measurement of living cells with an atomic force microscope: Data acquisition and processing. Pflug. Arch. 2008, 457, 551–559. [Google Scholar] [CrossRef]
- Rico, F.; Roca-Cusachs, P.; Navajas, D. Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips. Phys. Rev. E 2005, 72, 21914. [Google Scholar] [CrossRef]
- Darling, E.M.; Topel, M.; Guilak, F. Viscoelastic properties of human mesenchymally-derived stem cells and primary osteoblasts, chondrocytes, and adipocytes. J. Biomech. 2008, 41, 454–464. [Google Scholar] [CrossRef]
- Bar, A.; Targosz-Korecka, M.; Suraj, J.; Proniewski, B.; Jasztal, A.; Marczyk, B.; Sternak, M.; Przybyło, M.; Kurpińska, A.; Walczak, M.; et al. Degradation of Glycocalyx and Multiple Manifestations of Endothelial Dysfunction Coincide in the Early Phase of Endothelial Dysfunction Before Atherosclerotic Plaque Development in Apolipoprotein E/Low-Density Lipoprotein Receptor-Deficient Mice. J. Am. Heart Assoc. 2019, 8, e011171. [Google Scholar] [CrossRef]
- Oberleithner, H.; Peters, W.; Kusche-Vihrog, K.; Korte, S.; Schillers, H.; Kliche, K.; Oberleithner, K. Salt overload damages the glycocalyx sodium barrier of vascular endothelium. Pflugers Arch. 2011, 462, 519–528. [Google Scholar] [CrossRef] [PubMed]
- Wiesinger, A.; Peters, W.; Chappell, D.; Kentrup, D.; Reuter, S.; Pavenstädt, H.; Oberleithner, H.; Kümpers, P. Nanomechanics of the endothelial glycocalyx in experimental sepsis. PLoS ONE 2013, 8, e80905. [Google Scholar] [CrossRef]
- Trache, A.; Xie, L.; Huang, H.; Glinsky, V.V.; Meininger, G.A. Applications of Atomic Force Microscopy for Adhesion Force Measurements in Mechanotransduction. In Nanoscale Imaging; Lyubchenko, Y., Ed.; Methods in Molecular Biology; Humana Press: New York, NY, USA, 2018; Volume 1814. [Google Scholar] [CrossRef]
- Variola, F. Atomic force microscopy in biomaterials surface science. Phys. Chem. Chem. Phys. 2015, 17, 2950–2959. [Google Scholar] [CrossRef] [PubMed]
- Toca-Herrera, J.L. Atomic force microscopy meets biophysics, bioengineering, chemistry, and materials science. ChemSusChem 2019, 12, 603–611. [Google Scholar] [CrossRef]
- Jaddivada, S.; Gundiah, N. Physical biology of cell–substrate interactions under cyclic stretch. Biomech. Model. Mechanobiol. 2024, 23, 433–451. [Google Scholar] [CrossRef]
- Califano, J.P.; Reinhart-King, C.A. A Balance of Substrate Mechanics and Matrix Chemistry Regulates Endothelial Cell Network Assembly. Cell. Mol. Bioeng. 2008, 1, 122–132. [Google Scholar] [CrossRef]
- Ding, Y.; Li, C.Y.; Niu, X.; Wang, G.-F. Effects of surface energy and substrate on modulus determination of biological films by conical indentation. Sci. China Technol. Sci. 2024, 67, 1757–1764. [Google Scholar] [CrossRef]
- Vichare, S.; Sen, S.; Inamdar, M.M. Cellular mechanoadaptation to substrate mechanical properties: Contributions of substrate stiffness and thickness to cell stiffness measurements using AFM. Soft Matter 2014, 10, 1174–1181. [Google Scholar] [CrossRef]
- Rheinlaender, J.; Dimitracopoulos, A.; Wallmeyer, B.; Kronenberg, N.M.; Chalut, K.J.; Gather, M.C.; Betz, T.; Charras, G.; Franze, K. Cortical cell stiffness is independent of substrate mechanics. Nat. Mater. 2020, 19, 1019–1025. [Google Scholar] [CrossRef]
- Cappella, B. Physical Principles of Force–Distance Curves by Atomic Force Microscopy. In Mechanical Properties of Polymers Measured Through AFM Force-Distance Curves; Springer Laboratory; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Han, R.; Chen, J. A modified Sneddon model for the contact between conical indenters and spherical samples. J. Mater. Res. 2021, 36, 1762–1771. [Google Scholar] [CrossRef]
- Fu, G.; Fischer-Cripps, A.C. On Sneddon’s boundary conditions used in the analysis of nanoindentation data. J. Mater. Sci. 2005, 40, 1789–1791. [Google Scholar] [CrossRef]
- Li, M.; Liu, L.; Xi, N.; Wang, Y. Atomic force microscopy studies on cellular elastic and viscoelastic properties. Sci. China Life Sci. 2018, 61, 57–67. [Google Scholar] [CrossRef]
- Wala, J.; Das, S. Mapping of biomechanical properties of cell lines on altered matrix stiffness using atomic force microscopy. Biomech. Model. Mechanobiol. 2020, 19, 1523–1536. [Google Scholar] [CrossRef]
- Villarreal, L.; Fontes-Silva, M.; Mendaro, L.; Romanelli, G.; Benech, J.C. Mechanics and disease of heart cells/cardiomyocytes explored through atomic force microscopy. Biophys. Rev. 2025, 17, 347–358. [Google Scholar] [CrossRef]
- Fletcher, D.A.; Mullins, R.D. Cell mechanics and the cytoskeleton. Nature 2010, 463, 485–492. [Google Scholar] [CrossRef]
- Pegoraro, A.F.; Janmey, P.; Weitz, D.A. Mechanical properties of the cytoskeleton and cells. Cold Spring Harb. Perspect. Biol. 2017, 9, a022038. [Google Scholar] [CrossRef]
- Trickey, W.R.; Vail, T.P.; Guilak, F. The role of the cytoskeleton in the viscoelastic properties of human articular chondrocytes. J. Orthop. Res. 2004, 22, 131–139. [Google Scholar] [CrossRef]
- Chim, Y.H.; Mason, L.M.; Rath, N.; Olson, M.F.; Tassieri, M.; Yin, H. A one-step procedure to probe the viscoelastic properties of cells by Atomic Force Microscopy. Sci. Rep. 2018, 8, 14462. [Google Scholar] [CrossRef]
- Mba, E.J.; Okeke, F.O.; Igwe, A.E.; Ozigbo, C.A.; Oforji, P.I.; Ozigbo, I.W. Evolving trends and challenges in sustainable architectural design; a practice perspective. Heliyon 2024, 10, e39400. [Google Scholar] [CrossRef]
- Bishawi, M.; Lee, F.H.; Abraham, D.M.; Glass, C.; Blocker, S.J.; Cox, D.J.; Brown, Z.D.; Rockman, H.A.; Mao, L.; Slaba, T.C.; et al. Late onset cardiovascular dysfunction in adult mice resulting from galactic cosmic ray exposure. iScience 2022, 25, 104086. [Google Scholar] [CrossRef]
- Alsteens, D. Probing living cell dynamics and molecular interactions using atomic force microscopy. Biophys. Rev. 2024, 16, 663–677. [Google Scholar] [CrossRef]
- Radmacher, M.; Fritz, M.; Cleveland, J.P.; Walters, D.A.; Hansma, P.K. Imaging adhesion forces and elasticity of lysozyme adsorbed on mica with the atomic force microscope. Langmuir 1994, 10, 3809–3814. [Google Scholar] [CrossRef]
- Norman, M.D.A.; Ferreira, S.A.; Jowett, G.M.; Bozec, L.; Gentleman, E. Measuring the elastic modulus of soft culture surfaces and 3D hydrogels using atomic force microscopy. Nat. Protoc. 2021, 16, 2418–2449. [Google Scholar] [CrossRef]
- Lam, C.D.; Park, S. Nanomechanical characterization of soft nanomaterial using atomic force microscopy. Mater. Today Bio 2025, 31, 101506. [Google Scholar] [CrossRef]
- Gong, S.; Li, Y.; Yan, K.; Shi, Z.; Leng, J.; Bao, Y.; Ning, K. The Crosstalk Between Endothelial Cells, Smooth Muscle Cells, and Macrophages in Atherosclerosis. Int. J. Mol. Sci. 2025, 26, 1457. [Google Scholar] [CrossRef]
- Plodinec, M.; Loparic, M.; Aebi, U. Atomic force microscopy for biological imaging and mechanical testing across length scales. Cold Spring Harb. Protoc. 2010, 2010, pdb.top86. [Google Scholar] [CrossRef]
- Ushiki, T.; Hitomi, J.; Umemoto, T.; Yamamoto, S.; Kanazawa, H.; Shigeno, M. Imaging of living cultured cells of an epithelial nature by atomic force microscopy. Arch Histol Cytol. 1999, 62, 47–55. [Google Scholar] [CrossRef]
- Domingues, L. (Ed.) PCR: Methods and Protocols; Methods in Molecular Biology; Springer: New York, NY, USA, 2017; Volume 1620. [Google Scholar] [CrossRef]
- Abu Qubaa, A.A.; Schaumann, G.E.; Karagulyan, M.; Diehl, D. Quality control of direct cell–mineral adhesion measurements in air and liquid using inverse AFM imaging. RSC Adv. 2021, 11, 5384–5392. [Google Scholar] [CrossRef]
- Cines, D.B.; Pollak, E.S.; Buck, C.A.; Loscalzo, J.; Zimmerman, G.A.; McEver, R.P.; Pober, J.S.; Wick, T.M.; Konkle, B.A.; Schwartz, B.S.; et al. Endothelial cells in physiology and in the pathophysiology of vascular disorders. Blood 1998, 91, 3527–3561. [Google Scholar]
- Aird, W.C. Endothelial Cell Heterogeneity. Cold Spring Harb. Perspect. Med. 2012, 2, a006429. [Google Scholar] [CrossRef]
- Hennigs, J.K.; Matuszcak, C.; Trepel, M.; Körbelin, J. Vascular Endothelial Cells: Heterogeneity and Targeting Approaches. Cells 2021, 10, 2712. [Google Scholar] [CrossRef]
- Mitchell, J.A.; Ali, F.; Bailey, L.; Moreno, L.; Harrington, L.S. Role of nitric oxide and prostacyclin as vasoactive hormones released by the endothelium. Exp. Physiol. 2008, 93, 141–147. [Google Scholar] [CrossRef]
- Jin, R.C.; Loscalzo, J. Vascular nitric oxide: Formation and function. J. Blood Med. 2010, 1, 147–162. [Google Scholar] [CrossRef]
- Chang, Z.; Li, L.Y.; Shi, Z.J.; Liu, W.; Xu, G.K. Beyond stiffness: Multiscale viscoelastic features as biomechanical markers for assessing cell types and states. Biophys. J. 2024, 123, 1869–1881. [Google Scholar] [CrossRef]
- Natale, C.F.; Lafaurie-Janvore, J.; Ventre, M.; Babataheri, A.; Barakat, A.I. Focal adhesion clustering drives endothelial cell morphology on patterned surfaces. J. R. Soc. Interface 2019, 16, 20190263. [Google Scholar] [CrossRef]
- Sales, A.; Holle, A.W.; Kemkemer, R. Initial contact guidance during cell spreading is contractility-independent. Soft Matter 2017, 13, 5158–5167. [Google Scholar] [CrossRef]
- Baptista, D.; Teixeira, L.; van Blitterswijk, C.; Giselbrecht, S.; Truckenmüller, R. Overlooked? Underestimated? Effects of substrate curvature on cell behavior. Trends Biotechnol. 2019, 37, 838–854. [Google Scholar] [CrossRef]
- Sen, S.; Engler, A.J.; Discher, D.E. Matrix strains induced by cells: Computing how far cells can feel. Cell. Mol. Bioeng. 2009, 2, 39–48. [Google Scholar] [CrossRef]
- Tusan, C.G.; Man, Y.H.; Zarkoob, H.; Johnston, D.A.; Andriotis, O.G.; Thurner, P.J.; Yang, S.; Sander, E.A.; Gentleman, E.; Sengers, B.G.; et al. Collective cell behavior in mechanosensing of substrate thickness. Biophys. J. 2018, 114, 2743–2755. [Google Scholar] [CrossRef]
- Campinho, P.; Vilfan, A.; Vermot, J. Blood flow forces in shaping the vascular system: A focus on endothelial cell behavior. Front. Physiol. 2020, 11, 552. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, K.; Mitra, K.; Bit, A. Influence of Non-Newtonian Viscosity on Flow Structures and Wall Deformation in Compliant Serpentine Microchannels: A Numerical Study. Micromachines 2023, 14, 1661. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.H.C.; Goldschmidt-Clermont, P.; Wille, J.; Yin, F.C.P. Specificity of endothelial cell reorientation in response to cyclic mechanical stretching. J. Biomech. 2001, 12, 1563–1572. [Google Scholar] [CrossRef] [PubMed]
- Moretti, M.; Prina-Mello, A.; Reid, A.J.; Barron, V.; Prendergast, P.J. Endothelial cell alignment on cyclically-stretched silicone surfaces. J. Mater. Sci. Mater. Med. 2004, 15, 1159–1164. [Google Scholar] [CrossRef]
- Ohashi, T.; Sugaya, Y.; Sakamoto, N.; Sato, M. Relative contribution of physiological hydrostatic pressure and fluid shear stress to endothelial monolayer integrity. Biomed. Eng. Lett. 2016, 6, 31–38. [Google Scholar] [CrossRef]
- Ohashi, T.; Sugaya, Y.; Sakamoto, N.; Sato, M. Hydrostatic pressure influences morphology and expression of VE-cadherin of vascular endothelial cells. J. Biomech. 2007, 40, 2399–2405. [Google Scholar] [CrossRef]
- Dessalles, C.A.; Leclech, C.; Castagnino, A.; Barakat, A.I. Integration of substrate- and flow-derived stresses in endothelial cell mechanobiology. Commun. Biol. 2021, 4, 764. [Google Scholar] [CrossRef]
- Hogan, B.; Shen, Z.; Zhang, H.; Misbah, C.; Barakat, A.I. Shear stress in the microvasculature: Influence of red blood cell morphology and endothelial wall undulation. Biomech. Model. Mechanobiol. 2019, 18, 1095–1109. [Google Scholar] [CrossRef] [PubMed]
- Francesco Boselli, F.; Freund, J.B.; Vermot, J. Blood flow mechanics in cardiovascular development. Cell. Mol. Life Sci. 2015, 72, 2545–2559. [Google Scholar] [CrossRef]
- Papaioannou, T. Vascular wall shear stress: Basic principles and methods. Hell. J. Cardiol. 2005, 46, 9–15. [Google Scholar]
- Rotsch, C.; Radmacher, M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: An atomic force microscopy study. Biophys. J. 2000, 78, 520–535. [Google Scholar] [CrossRef] [PubMed]
- Waschke, J.; Curry, F.E.; Adamson, R.H.; Drenckhahn, D. Regulation of actin dynamics is critical for endothelial barrier functions. Am. J. Physiol. Heart Circ. Physiol. 2005, 288, H1296–H1305. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Innate Immunity; Garland Publishing Inc.: New York, NY, USA, 2002. [Google Scholar]
- Petrache, I.; Verin, A.D.; Crow, M.T.; Birukova, A.; Liu, F.; Garcia, J.G.N. Differential effect of MLC kinase in TNF-α-induced endothelial cell apoptosis and barrier dysfunction. Am. J. Physiol. Lung Cell Mol. Physiol. 2001, 280, L1168–L1178. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Edwards-Bennett, S.; Bubb, M.R.; Block, E.R. Regulation of endothelial nitric oxide synthase by the actin cytoskeleton. Am. J. Physiol. Cell Physiol. 2003, 284, C1542–C1549. [Google Scholar] [CrossRef]
- Nesher, N.; Frolkis, I.; Schwartz, D.; Chernichovski, T.; Levi, S.; Pri-Paz, Y.; Chernin, G.; Shtabsky, A.; Ben-Gal, Y.; Paz, Y.; et al. L-arginine improves endothelial function, independently of arginine uptake, in aortas from chronic renal failure female rats. Am. J. Physiol. Renal Physiol. 2014, 15, F449–F456. [Google Scholar] [CrossRef]
- Searles, C.D.; Ide, L.; Davis, M.E.; Cai, H.; Weber, M. Actin cytoskeleton organization and posttranscriptional regulation of endothelial nitric oxide synthase during cell growth. Circ. Res. 2004, 95, 488–495. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, A.M.; Brzezinka, G.D.; Khurana, K.; Targosz-Korecka, M.; Szymonski, M. Nanomechanical sensing of the endothelial cell response to anti-inflammatory action of 1-methylnicotinamide chloride. Int. J. Nanomed. 2013, 8, 2757–2767. [Google Scholar] [CrossRef] [PubMed]
- Fels, J.; Callies, C.; Kusche-Vihrog, K.; Oberleithner, H. Nitric oxide release follows endothelial nanomechanics and not vice versa. Pflugers Arch. 2010, 460, 915–923. [Google Scholar] [CrossRef] [PubMed]
- Schildknecht, S.; Daiber, A.; Ghisla, S.; Cohen, R.A.; Bachschmid, M.M. Acetaminophen inhibits prostanoid synthesis by scavenging the PGHS-activator peroxynitrite. FASEB J. 2008, 22, 215–224. [Google Scholar] [CrossRef]
- Hink, U.; Münzel, T. COX-2, Another Important Player in the Nitric Oxide–Endothelin Cross-Talk. Circ. Res. 2006, 98, 1344–1346. [Google Scholar] [CrossRef]
- Filippini, A.; D’Amore, A.; D’Alessio, A. Calcium Mobilization in Endothelial Cell Functions. Int. J. Mol. Sci. 2019, 20, 4525. [Google Scholar] [CrossRef]
- Munaron, L. Intracellular calcium, endothelial cells and angiogenesis. Recent Pat. Anticancer Drug Discov. 2006, 1, 105–119. [Google Scholar] [CrossRef]
- Fleming, I.; Busse, R. Signal transduction of eNOS activation. Cardiovasc. Res. 1999, 43, 532–541. [Google Scholar] [CrossRef]
- Himmel, H.M.; Whorton, A.R.; Strauss, H.C. Intracellular Calcium, Currents, and Stimulus-Response Coupling in Endothelial Cells. Hypertension 1993, 21, 112–127. [Google Scholar] [CrossRef]
- Levin, R.I.; Weksler, B.B.; Marcus, A.J.; Jaffe, E.A. Prostacyclin production by endothelial cells. In Advances in Prostaglandin, Thromboxane, and Leukotriene Research; Springer: Berlin/Heidelberg, Germany, 1982; Volume 9, pp. 355–358. [Google Scholar]
- Wang, D.; DuBois, R.N. The role of prostaglandin E2 in tumor-associated immunosuppression. Nat. Rev. Cancer 2020, 10, 116–129. [Google Scholar]
- Smith, W.L.; Langenbach, R. Cyclooxygenase pathways: From arachidonic acid to prostaglandins and beyond. FASEB J. 2001, 15, 1731–1742. [Google Scholar]
- Fleming, I. Molecular mechanisms underlying the activation of eNOS. Pflügers Arch.–Eur. J. Physiol. 2010, 459, 793–806. [Google Scholar] [CrossRef]
- Pacher, P.; Beckman, J.; Liaudet, L. Nitric Oxide and Peroxynitrite in Health and Disease. Physiol. Rev. 2008, 87, 315–424. [Google Scholar] [CrossRef]
- Sies, H.; Jones, D.P. Reactive oxygen species (ROS) as pleiotropic physiological signalling agents. Nat. Rev. Mol. Cell Biol. 2020, 21, 363–383. [Google Scholar] [CrossRef]
- Chiang, M.Y.M.; Yangben, Y.; Lin, N.J.; Zhong, J.L.; Yang, L. Relationships among cell morphology, intrinsic cell stiffness and cell substrate interactions. Biomaterials 2013, 34, 9754–9762. [Google Scholar] [CrossRef] [PubMed]
- Vahabi, S.; Salman, B.N.; Javanmard, A. Atomic Force Microscopy Application in Biological Research: A Review Study. Iran. J. Med. Sci. 2013, 38, 76–83. [Google Scholar] [PubMed]
- Matias, Z.; Lopes, C.S.; Santos, N.C.; Carvalho, F.A. Nanotechnology meets medicine: Applications of atomic force microscopy in disease. Biophys. Rev. 2025, 17, 359–384. [Google Scholar] [CrossRef] [PubMed]
- Giergiel, M.; Małek-Ziętek, K.E.; Konior, J.; Targosz-Korecka, M. Endothelial glycocalyx detection and characterization by means of atomic force spectroscopy: Comparison of various data analysis approaches. Micron 2021, 151, 103153. [Google Scholar] [CrossRef]
- Marsh, G.; Waugh, R.E. Quantifying the Mechanical Properties of the Endothelial Glycocalyx with Atomic Force Microscopy. J. Vis. Exp. 2013, 72, e50163. [Google Scholar] [CrossRef]
- Kolesov, D.; Astakhova, A.; Galdobina, M.; Moskovtsev, A.; Kubatiev, A.; Sokolovskaya, A.; Ukrainskiy, L.; Morozov, S. Scanning Probe Microscopy Techniques for Studying the Cell Glycocalyx. Cells 2023, 12, 2778. [Google Scholar] [CrossRef]
- Zapotoczny, B.; Szafranska, K.; Owczarczyk, K.; Kus, E.; Chlopicki, S.; Szymonski, M. Atomic Force Microscopy Reveals the Dynamic Morphology of Fenestrations in Live Liver Sinusoidal Endothelial Cells. Sci. Rep. 2017, 7, 7994. [Google Scholar] [CrossRef]
- Borah, D.; Blacharczyk, O.; Szafranska, K.; Czyzynska-Cichon, I.; Metwally, S.; Szymanowski, K.; Hübner, W.; Kotlinowski, J.; Dobosz, E.; McCourt, P.; et al. Mimicking the Liver Sinusoidal Endothelial Cell Niche In Vitro to Enhance Fenestration in a Genetic Model of Systemic Inflammation. Cells 2025, 14, 621. [Google Scholar] [CrossRef]
- Czyzynska-Cichon, I.; Giergiel, M.; Kwiatkowski, G.; Kurpinska, A.; Wojnar-Lason, K.; Kaczara, P. Protein disulfide isomerase A1 regulates fenestration dynamics in primary mouse liver sinusoidal endothelial cells (LSECs). Redox Biol. 2024, 72, 103162. [Google Scholar] [CrossRef]
- Kopacz, A.; Kloska, D.; Bar, A.; Targosz-Korecka, M.; Cysewski, D.; Awsiuk, K. Endothelial miR-34a deletion guards against aneurysm development despite endothelial dysfunction. BBA-Mol. Basis Dis. 2025, 1871, 167812. [Google Scholar] [CrossRef] [PubMed]
- Kubisiak, A.; Dabrowska, A.; Botwina, P.; Twardawa, P.; Kloska, D.; Kołodziej, T. Remodeling of intracellular architecture during SARS-CoV-2 infection of human endothelium. Sci. Rep. 2024, 14, 29784. [Google Scholar] [CrossRef] [PubMed]
- Huaqi, T.; Tom, M.J.E.; Mehrad, B.; Alireza, M. Revealing Mechanopathology Induced by Dengue NS1 Using Organ Chips and Single-Cell Force Spectroscopy. ACS Biomater. Sci. Eng. 2025, 11, 2448–2455. [Google Scholar] [CrossRef] [PubMed]
- Targosz-Korecka, M. Diabetes and Endothelial Nanomechanics. In Mechanics of Cells and Tissues in Diseases; De Gruyter: Berlin, Germany, 2023; Volume 2, Biomedical Applications. [Google Scholar] [CrossRef]
- Dróżdż, A.; Kołodziej, T.; Wróbel, S.; Misztal, K.; Targosz-Korecka, M.; Drab, M.; Jach, R.; Rząca, C.; Surman, M.; Przybyło, M.; et al. Large extracellular vesicles do not mitigate the harmful effect of hyperglycemia on endothelial cell mobility. Eur. J. Cell Biol. 2022, 101, 151266. [Google Scholar] [CrossRef]
- Targosz-Korecka, M.; Jaglarz, M.; Malek-Zietek, K.E.; Gregorius, A.; Zakrzewska, A.; Sitek, B. AFM-based detection of glycocalyx degradation and endothelial stiffening in the db/db mouse model of diabetes. Sci. Rep. 2017, 7, 15951. [Google Scholar] [CrossRef]
- Wang, K.; Ge, Y.; Yang, Y.; Li, Z.; Liu, J.; Xue, Y.; Zhang, Y.; Pang, X.; Ngan, A.H.W.; Tang, B. Vascular endothelial cellular mechanics under hyperglycemia and its role in tissue regeneration. Regen. Biomater. 2024, 11, rbae004. [Google Scholar] [CrossRef] [PubMed]
- Petrov, M.; Makarova, N.; Monemian, A.; Pham, J.; Lekka, M.; Sokolov, I. Detection of Human Bladder Epithelial Cancerous Cells with Atomic Force Microscopy and Machine Learning. Cells 2025, 14, 14. [Google Scholar] [CrossRef] [PubMed]
- Lekka, M. Discrimination Between Normal and Cancerous Cells Using AFM. BioNanoScience 2016, 6, 65–80. [Google Scholar] [CrossRef] [PubMed]
- Laurent, V.M.; Duperray, A.; Rajan, V.S.; Verdier, C. Atomic Force Microscopy Reveals a Role for Endothelial Cell ICAM-1 Expression in Bladder Cancer Cell Adherence. PLoS ONE 2014, 9, e98034. [Google Scholar] [CrossRef] [PubMed]
- Csonti, K.; Fazakas, C.; Molnár, K.; Wilhelm, I.; Krizbai, I.A.; Végh, A.G. Breast adenocarcinoma cells adhere stronger to brain pericytes than to endothelial cells. Colloids Surf. B Biointerfaces 2024, 234, 113751. [Google Scholar] [CrossRef]
- Kusche-Vihrog, K.; Sobczak, K.; Bangel, N.; Wilhelmi, M.; Nechyporuk-Zloy, V.; Schwab, A.; Schillers, H.; Oberleithner, H. Aldosterone and amiloride alter ENaC abundance in vascular endothelium. Pflug. Arch. 2008, 455, 849–857. [Google Scholar] [CrossRef]
- Oberleithner, H.; Riethmüller, C.; Schillers, H.; MacGregor, G.A.; De Wardener, H.E.; Hausberg, M. Plasma sodium stiffens vascular endothelium and reduces nitric oxide release. Proc. Natl. Acad. Sci. USA 2007, 104, 16281–16286. [Google Scholar] [CrossRef]
- Oberleithner, H.; Riethmüller, C.; Ludwig, T.; Hausberg, M.; Schillers, H. Aldosterone remodels human endothelium. Acta Physiol. 2006, 187, 305–312. [Google Scholar] [CrossRef]
- Fels, J.; Oberleithner, H.; Kusche-Vihrog, K. Ménage à trois: Aldosterone, sodium and nitric oxide in vascular endothelium. Biochim. Biophys. Acta 2010, 1802, 1193–1202. [Google Scholar] [CrossRef]
- Kolodziejczyk, A.M.; Targosz-Korecka, M.; Szymonski, M. Nanomechanical testing of drug activities at the cellular level: Case study for endothelium-targeted drugs. Pharmacol. Rep. 2017, 69, 1165–1172. [Google Scholar] [CrossRef]
- Wojcik, T.; Buczek, E.; Majzner, K.; Kolodziejczyk, A.; Miszczyk, J.; Kaczara, P.; Kwiatek, W.; Baranska, M.; Szymonski, M.; Chlopicki, S. Comparative endothelial profiling of doxorubicin and daunorubicin in cultured endothelial cells. Toxicol. Vitr. 2015, 29, 512–521. [Google Scholar] [CrossRef]
- Le Bot, M.A.; Bégué, J.M.; Kernaleguen, D.; Robert, J.; Ratanasavanh, D.; Airiau, J.; Riché, C.; Guillouzo, A. Different cytotoxicity and metabolism of doxorubicin, daunorubicin, epirubicin, esorubicin and idarubicin in cultured human and rat hepatocytes. Biochem. Pharmacol. 1988, 37, 3877. [Google Scholar] [CrossRef]
- Kołodziejczyk, A.M.; Kucińska, M.; Jakubowska, A.; Siatkowska, M.; Sokołowska, P.; Kotarba, S.; Makowski, K.; Komorowski, P.; Walkowiak, B. Microscopic Analysis of the Nanostructures Impact on Endothelial Cells. Eng. Biomater. 2020, 154, 2–8. [Google Scholar] [CrossRef]
- Dong, C.; Eldawud, R.; Sargent, L.M.; Kashon, M.L.; Lowry, D.; Rojanasakul, Y.; Dinu, C.Z. Carbon nanotube uptake changes the biomechanical properties of human lung epithelial cells in a time-dependent manner. J. Mater. Chem. B 2015, 3, 3983–3992. [Google Scholar] [CrossRef]
- Kolodziejczyk, A.M.; Kucinska, M.; Jakubowska, A.; Sokolowska, P.; Rosowski, M.; Tkacz-Szczesna, B.; Komorowski, P.; Makowski, K.; Walkowiak, B. Endothelial cell aging detection by means of atomic force spectroscopy. J. Mol. Recognit. 2020, 33, e2853. [Google Scholar] [CrossRef]
- Oliveira, V.R.; Uriarte, J.J.; Falcones, B.; Jorba, I.; Zin, W.A.; Farré, R.; Navajas, D.; Almendros, I. Biomechanical Response of Lung Epithelial Cells to Iron Oxide and Titanium Dioxide Nanoparticles. Front. Physiol. 2019, 10, 1047. [Google Scholar] [CrossRef]
- Grala, M.; Kołodziejczyk, A.M.; Białkowska, K.; Walkowiak, B.; Komorowski, P. Assessment of the influence of gold nanoparticles stabilized with PAMAM dendrimers on HUVEC barrier cells. Micron 2023, 168, 103430. [Google Scholar] [CrossRef]
- Fattahi, P.; Yeh, Y.T.; Zhao, T.; Younesi, M.; Huang, C.; Terrones, M.; Zheng, S.; Brown, J.L.; Huh, D.D.; Zhang, S.; et al. Endothelial Cell Selectivity to Nanoparticles Depends on Mechanical Phenotype. Adv. Mater. Interfaces 2023, 10, 2300137. [Google Scholar] [CrossRef]
- Kołodziejczyk, A.M.; Grala, M.M.; Zimon, A.; Białkowska, K.; Walkowiak, B.; Komorowski, P. Investigation of HUVEC response to exposure to PAMAM dendrimers–changes in cell elasticity and vesicles release. Nanotoxicology 2022, 16, 375–392. [Google Scholar] [CrossRef]
- Boyoglu, C.; He, Q.; Willing, G.; Boyoglu-Barnum, S.; Dennis, V.A.; Pillai, S.; Singh, S.R. Microscopic studies of various sizes of gold nanoparticles and their cellular localizations. Int. Sch. Res. Not. 2013, 2013, 123838. [Google Scholar] [CrossRef]
- Mecke, A.; Majoros, I.J.; Patri, A.K.; Baker, J., Jr.; Holl, M.M.B.; Orr, B.G. Lipid Bilayer Disruption by Polycationic Polymers: The Roles of Size and Chemical Functional Group. Langmuir 2005, 21, 10348–10354. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Larson, R.G. Molecular Dynamics Simulations of PAMAM Dendrimer-Induced Pore Formation in DPPC Bilayers with a Coarse-Grained Model. J. Phys. Chem. B 2006, 110, 18204–18211. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.V.; Leroueil, P.R.; Orr, B.G.; Banaszak Holl, M.M.; Andricioaei, I. Poly(Amidoamine) Dendrimers on Lipid Bilayers II: Effects of Bilayer Phase and Dendrimer Termination. J. Phys. Chem. B 2008, 112, 9346–9353. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Ohashi, T.; Sugawara, H.; Ishii, Y. 3-D Stress Distribution in Cultured Endothelial Cells Exposed to Shear Stress. In Proceedings of the First Joint BMES/EMBS Conference: Serving Humanity, Atlanta, GA, USA, 13–16 October 1999. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Yamamoto, Y.; Liu, H. Computational mechanical model studies on the spontaneous emergent morphogenesis of the cultured endothelial cells. J. Biomech. 2000, 33, 115–126. [Google Scholar] [CrossRef]
- Ohashi, T.; Ishii, Y.; Ishikawa, Y.; Matsumoto, T.; Sato, M. Experimental and numerical analyses of local mechanical properties measured by atomic force microscopy for sheared endothelial cells. Bio-Med. Mater. Eng. 2002, 12, 319–327. [Google Scholar]
- Jean, R.P.; Chen, C.S.; Spector, A.A. Finite-element analysis of the adhesion-cytoskeleton-nucleus mechanotransduction pathway during endothelial cell rounding: Axisymmetric model. J. Biomech. Eng. 2005, 127, 594–600. [Google Scholar] [CrossRef]
- Ferko, M.C.; Bhatnagar, A.; Garcia, M.B.; Butler, P.J. Finite-element stress analysis of a multicomponent model of sheared and focally-adhered endothelial cells. Ann. Biomed. Eng. 2007, 35, 208–223. [Google Scholar] [CrossRef]
- Deguchi, S.; Fukamachi, H.; Hashimoto, K.; Iio, K.; Tsujioka, K. Measurement and finite element modeling of the force balance in the vertical section of adhering vascular endothelial cells. J. Mech. Behav. Biomed. Mater. 2009, 2, 173–185. [Google Scholar] [CrossRef]
- Wood, S.T.; Dean, B.C.; Dean, D. A Computational Approach to Understand Phenotypic Structure and Constitutive Mechanics Relationships of Single Cells. Ann. Biomed. Eng. 2013, 41, 630–644. [Google Scholar] [CrossRef]
- Vargas-Pinto, R.; Gong, H.; Vahabikashi, A.; Johnson, M. The Effect of the Endothelial Cell Cortex on Atomic Force Microscopy Measurements. Biophys. J. 2013, 105, 300–309. [Google Scholar] [CrossRef]
- Jakka, V.V.S.V.; Bursa, J. Finite Element Simulations of Mechanical Behaviour of Endothelial Cells. Biomed. Res. Int. 2021, 2021, 8847372. [Google Scholar] [CrossRef] [PubMed]
- Jakka, V.V.S.V.; Bursa, J. Impact of physiological loads of arterial wall on nucleus deformation in endothelial cells: A computational study. Comput. Biol. Med. 2022, 143, 105266. [Google Scholar] [CrossRef]
- Yang, W.; Lacroix, D.; Tan, L.P.; Chen, J. Revealing the nanoindentation response of a single cell using a 3D structural finite element model. J. Mater. Res. 2021, 36, 2591–2600. [Google Scholar] [CrossRef]
- Ohashi, T.; Seo, S.; Matsumoto, T.; Sato, M. Structural optimization analysis of endothelial cell remodeling to fluid flow. In Proceedings of the Second Joint EMBS/BMES Conference, Houston, TX, USA, 23–26 October 2002. [Google Scholar]
- Yamada, H.; Mouri, N.; Nobuhara, S. Three-dimensional morphometry of single endothelial cells with substrate stretching and image-based finite element modeling. EURASIP J. Adv. Signal Process. 2009, 2010, 616091. [Google Scholar] [CrossRef]
- Kang, I.; Panneerselvam, D.; Panoskaltsis, V.P.; Eppell, S.J.; Marchant, R.E.; Doerschuk, C.M. Changes in the hyperelastic properties of endothelial cells induced by tumor necrosis factor-α. Biophys. J. 2008, 94, 3273–3285. [Google Scholar] [CrossRef]
- Wei, F.; Yang, H.; Liu, L.; Li, G. A novel approach for extracting viscoelastic parameters of living cells through combination of inverse finite element simulation and Atomic Force Microscopy. Comput. Methods Biomech. Biomed. Eng. 2016, 20, 373–384. [Google Scholar] [CrossRef]
- Li, S.; Lei, L.; Hu, Y.; Zhang, Y.; Zhao, S.; Zhang, J. A fully coupled framework for in silico investigation of in-stent restenosis. Comput. Methods Biomech. Biomed. Eng. 2018, 2, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Mollaeian, K.; Ren, J. Finite element modeling of living cells for AFM indentation-based biomechanical characterization. Micron 2019, 116, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Tian, L.; Wang, Y.; Zhang, W.; Wang, Z.; Liu, X. Determination of viscohyperelastic properties of tubule epithelial cells by an approach combined with AFM nanoindentation and finite element analysis. Micron 2020, 129, 102779. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Zhao, L.; Huang, Q.; Kong, L.; Wang, G.; Ye, Z. Single cell mechanics analyzed by atomic force microscopy and finite element simulation. Phys. Scr. 2024, 99, 45510. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, C.; Wu, C.; Zhang, W. A Fitted Model for Calculating Cellular Viscoelastic Parameters. J. Biomech. 2025, 190, 112878. [Google Scholar] [CrossRef]

| Cell Line and Nanostructures | Indentation Probe | Outcomes | Source |
|---|---|---|---|
| EA.hy926 cell line + Multi-walled carbon nanotubes (4 and 12 μg/mL)/Silver nanoparticles (3 and 3.6 μg/mL)/PAMAM dendrimers of 4th generation (0.4 and 0.8 μmol/L) | PFQNM-LC (Bruker); glass spheres (Nova Scan) | MWCNTs: ↑ E of 110% in parallel with an increase in ROS levels and alteration in actin cytoskeleton | [20] |
| SNP: ↓ E of 43% (3 μg/mL), ↑ E of 112% (3.6 μg/mL) accompanied by thickening of actin fibers | |||
| PAMAM G4: ↓ E of 14% (0.8 μmol/L) and increase in apoptotic cells accompanied by an elevated level of ROS production | |||
| BEAS-2B cell line + Multi-walled carbon nanotubes (24 µg/cm2) | Sharp probe | ↑ E of 29% relative to control cells | [141] |
| EA.hy926 cell line + Silver nanoparticles (3, 3.6 and 16 μg/mL) | PFQNM-LC (Bruker); glass spheres (Nova scan) | Dose-dependent increase in E (of 14, 20 and 42% for selected SNPs concentrations, respectively) and polymerization of F-actin fibers in the central parts of the cells. | [21] |
| EA.hy926 cell line + Silver nanoparticles (1, 3, 3.6 and 16 μg/mL) | PFQNM-LC (Bruker) | Reduction in E of 16% (after 24 h incubation of 3 μg/mL SNPs); Increase in E (of 90 and 150% after one-hour incubation of 1 and 3 μg/mL of SNP) accompanied by the elevated ROS level | [142] |
| A-549 alveolar epithelial cells + Fe2O3 and TiO2 nanoparticles (10 μg/mL—no cytotoxic effect) | Spherical tip (Nova Scan) | Decreased cell stiffness compared to control cells of 28% and 24% for Fe2O3 and TiO2, respectively | [143] |
| HUVEC cell line + PAMAM dendrimers of 2nd (1.08, 1.90 and 2.7 μmol/L), 4th (0.15, 0.45 and 0.95 μmol/L) and 7th (0.17, 0.35 and 0.65 μmol/L) generation | MLCT-SPH-spherical (Bruker); PFQNM-LC (Bruker) | PAMAM G2: dose-dependent decrease in E (of 19, 30 and 56% for selected concentrations, respectively); PAMAM G4: dose-dependent decrease in E (of 20, 59 and 67% for selected concentrations, respectively) PAMAM G7: ↓ E of 33% (0.35 μmol/L); ↑ E of 102% (0.65 μmol/L); | [146] |
| HUVEC + gold nanoparticles stabilized with PAMAM dendrimers (no cytotoxic: 0.5 and 0.7 μg/mL; and 1.1 μg/mL—80% cellular viability) | PFQNM-LC (Bruker) | ↓ E of 34% for 0.5 μg/mL ↓ E of 24% for 0.7 μg/mL ↑ E of 28% for 1.1 μg/mL | [144] |
| Modeling Approach | Cytoskeletal Components | Main Results | Unique Contribution | Source |
|---|---|---|---|---|
| 3D FEM with fluid–structure interaction | F-actin | Stress distribution correlates with F-actin localization | Early integration of AFM and FEM for shear stress analysis | [151] |
| CFD with dynamic cell modeling | Implicit cytoskeletal adaptation | Cell elongation and alignment reduce wall shear stress | Mechanically optimized morphogenesis simulation | [152] |
| AFM + FEM with axisymmetric model | F-actin | Shear stress increases stiffness and reorganizes cytoskeleton | Spatial stiffness mapping under flow | [153] |
| Axisymmetric FEM | AFs (discrete and continuum) | Cytoskeletal tension drives nuclear deformation | Mechanotransduction pathway modeling | [154] |
| Multicomponent FEM with FA mapping | Cytoplasm, nucleus, FAs | Stress amplification near FAs and nucleus | Quantified stress heterogeneity due to adhesion sites | [155] |
| 3D FEM with vertical force balance | AFs, MTs | Actin compresses vertically; MTs resist compression | First model of vertical intracellular mechanics | [156] |
| 3D FEM from confocal images | Actin stress fibers as truss elements | Spatial arrangement of fibers affects stiffness | Validated image-based FEM pipeline | [157] |
| FEM with two-layer cortex model | Actin cortex | Sharp AFM tips overestimate stiffness due to cortex | Demonstrated cortical dominance in AFM measurements | [158] |
| Hybrid FEM with bendotensegrity | AFs, MTs, IFs | AFs dominate stiffness; MTs contribute under tension | Realistic modeling of cytoskeletal flexure | [159] |
| 3D FEM in arterial wall context | AFs, MTs, IFs | Shear stress and axial stretch amplify nuclear strain | Integration of cell mechanics with vascular loading | [160] |
| 3D FEM with detailed cytoskeletal geometry | AFs, MTs, actin cortex | Probe geometry affects stiffness measurement | Spatially resolved stiffness mapping via FEM | [161] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kołodziejczyk, A.M.; Kołodziejczyk, Ł.; Karwowski, B. Mechanical Properties of Endothelial Cells: A Key to Physiology, Drug Testing and Nanostructure Interaction. Cells 2025, 14, 1659. https://doi.org/10.3390/cells14211659
Kołodziejczyk AM, Kołodziejczyk Ł, Karwowski B. Mechanical Properties of Endothelial Cells: A Key to Physiology, Drug Testing and Nanostructure Interaction. Cells. 2025; 14(21):1659. https://doi.org/10.3390/cells14211659
Chicago/Turabian StyleKołodziejczyk, Agnieszka Maria, Łukasz Kołodziejczyk, and Bolesław Karwowski. 2025. "Mechanical Properties of Endothelial Cells: A Key to Physiology, Drug Testing and Nanostructure Interaction" Cells 14, no. 21: 1659. https://doi.org/10.3390/cells14211659
APA StyleKołodziejczyk, A. M., Kołodziejczyk, Ł., & Karwowski, B. (2025). Mechanical Properties of Endothelial Cells: A Key to Physiology, Drug Testing and Nanostructure Interaction. Cells, 14(21), 1659. https://doi.org/10.3390/cells14211659







