Investigating Two Modes of Cancer-Associated Antigen Heterogeneity in an Agent-Based Model of Chimeric Antigen Receptor T-Cell Therapy
Abstract
Simple Summary
Abstract
1. Introduction
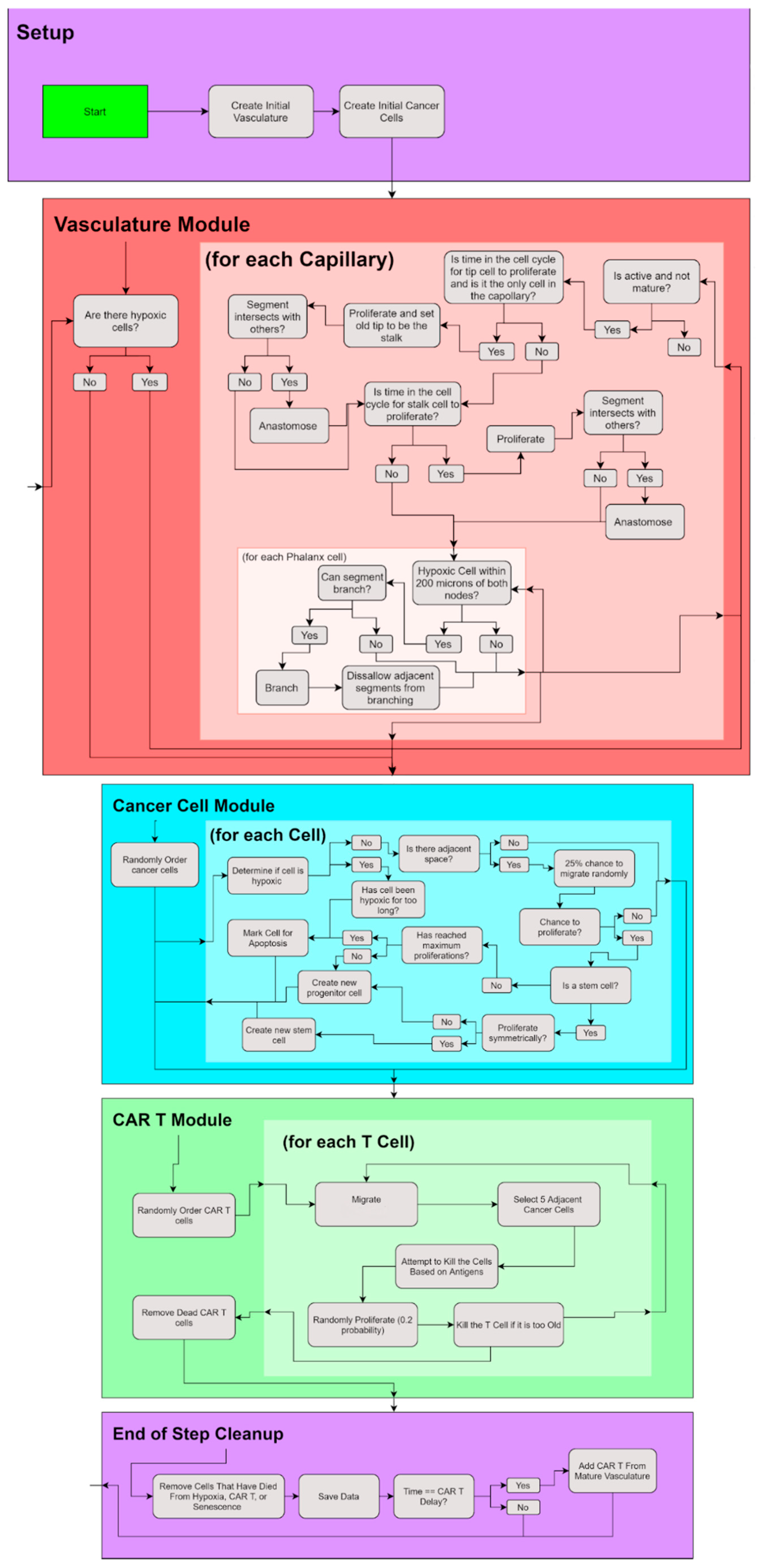
2. Materials and Methods
2.1. Cancer Cell Module
2.2. Vasculature Module
2.3. CAR T—Cell Module
2.4. Statistics
3. Results
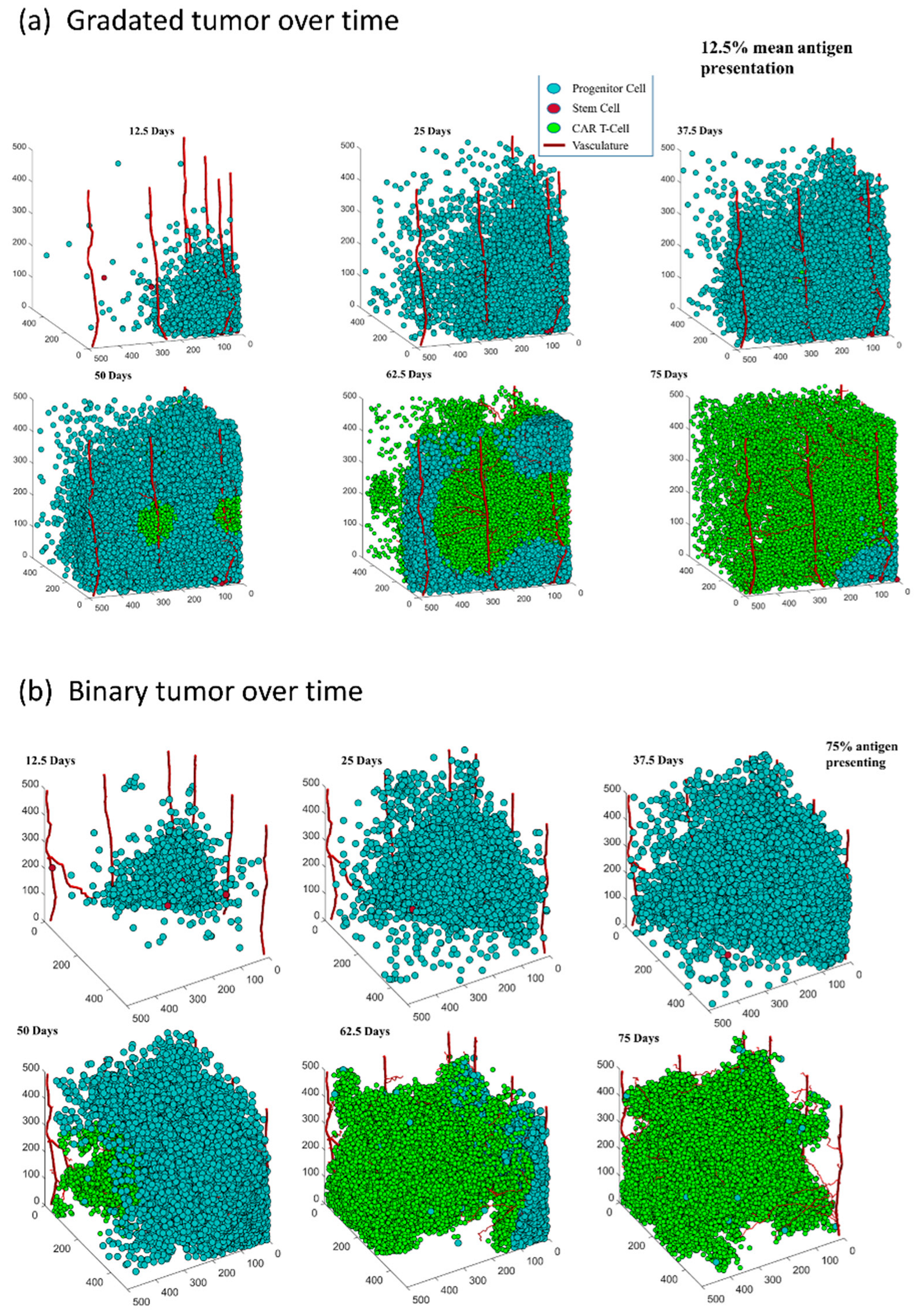
3.1. Both Models of CAR T-Cell Therapy Can Successfully Reduce the Size of Tumor
3.2. The Distribution of Antigen Presenting Cells Effects the Rate of Tumor Reduction in Both Antigen Distribution Models
3.2.1. Gradated Heterogeneity Antigen Model
3.2.2. Binary Heterogeneity Antigen Model
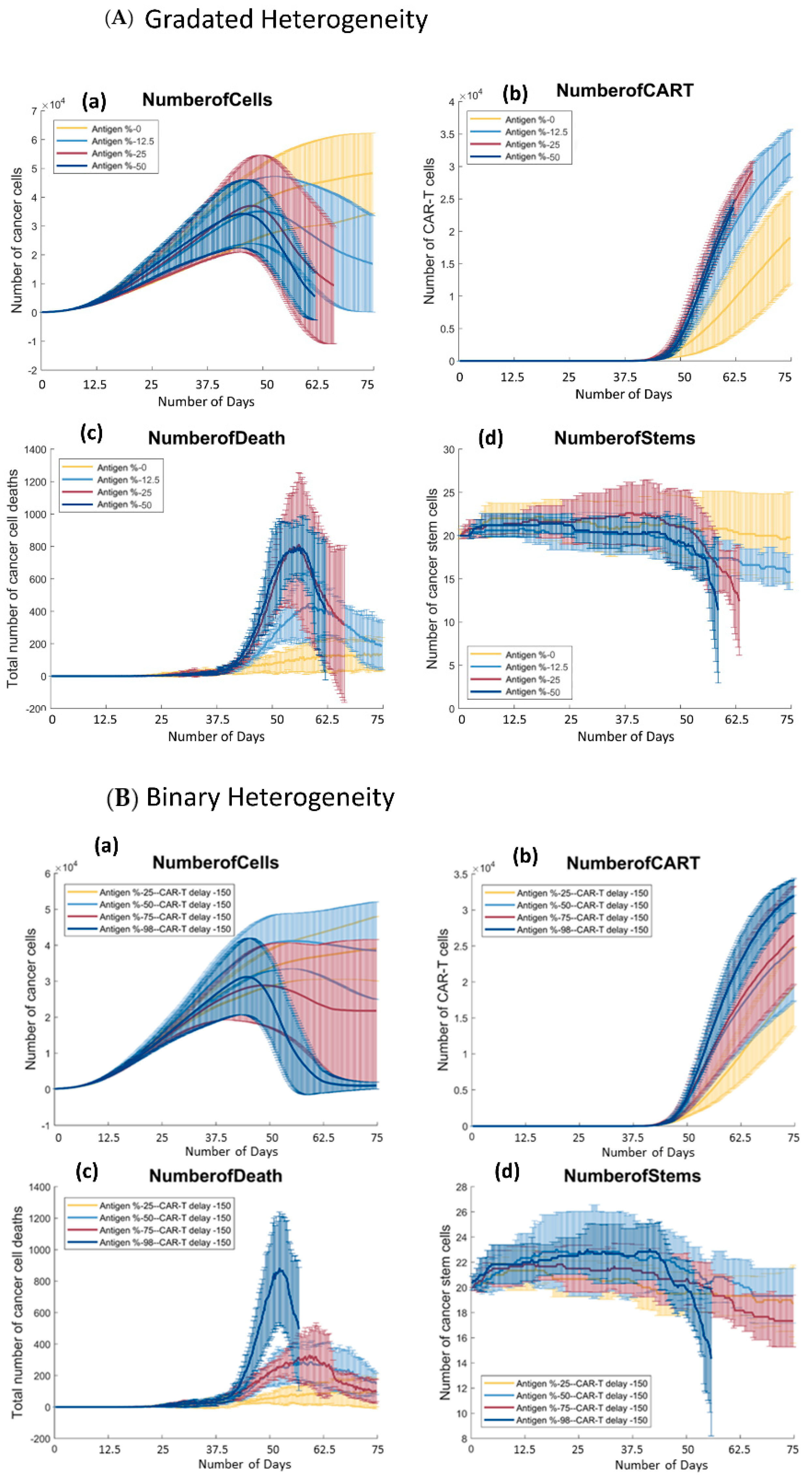
3.3. There Is a Positive Trend between the Number of Antigen Presenting Cells and the Growth of CAR T-Cells in Both Models
3.4. There Is a Positive Trend between the Percentage of Antigen Expression and the Number of Cancer Cells Killed by CAR T-Cells throughout the Simulation in Both Models of Antigen Distribution
3.4.1. Gradated Heterogeneity Antigen Model
3.4.2. Binary Heterogeneity Antigen Model
3.5. In Both Models, There Are Parameter Values in which Cancer Stem Cells Get Eliminated
3.5.1. Gradated Heterogeneity Antigen Model
3.5.2. Binary Heterogeneity Antigen Model
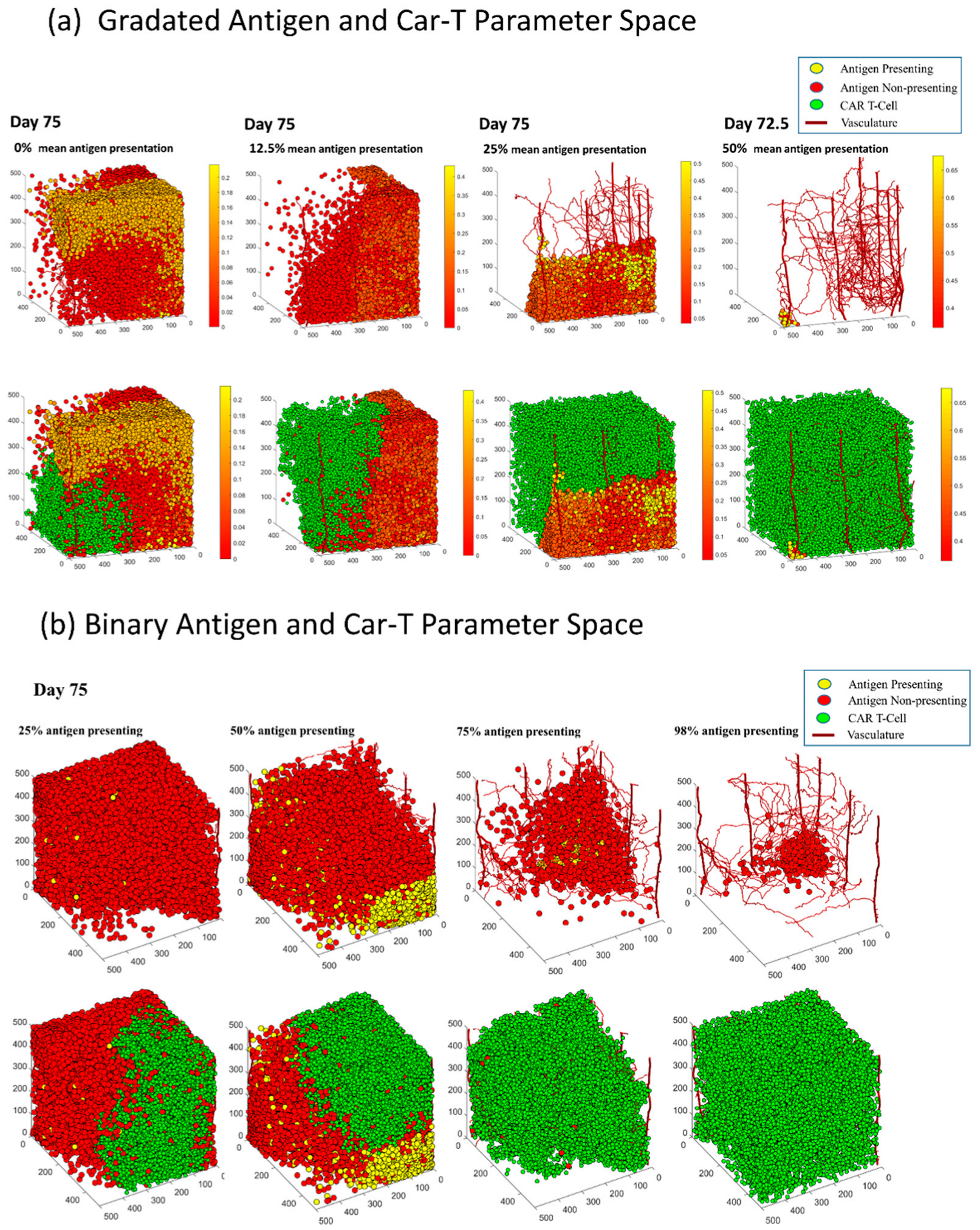
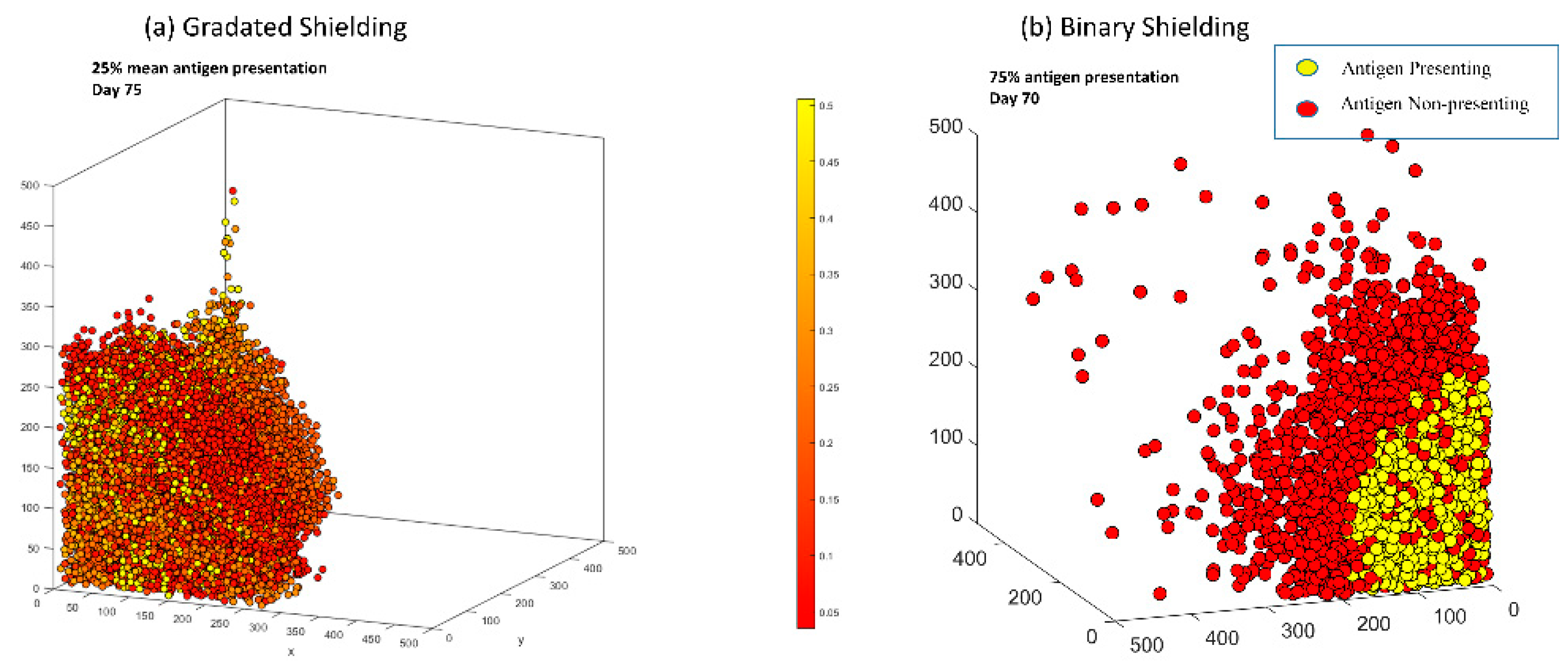
3.6. In Both Models, Antigen Presenting Cells Can Form a Shield over Antigen Non-Presenting Cells That Blocks CAR T-Cells from Killing Vulnerable Cancer Cells
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hanahan, D.; Weinberg, R.A. The hallmarks of cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.T.; Heneghan, H.M.; Winter, D.C. Systematic review and meta-analysis of outcomes following pathological complete response to neoadjuvant chemoradiotherapy for rectal cancer. Br. J. Surg. 2012, 99, 918–928. [Google Scholar] [CrossRef]
- Niikura, N.; Shimomura, A.; Fukatsu, Y.; Sawaki, M.; Ogiya, R.; Yasojima, H.; Fujisawa, T.; Yamamoto, M.; Tsuneizumi, M.; Kitani, A.; et al. Durable complete response in HER2-positive breast cancer: A multicenter retrospective analysis. Breast Cancer Res. Treat. 2018, 167, 81–87. [Google Scholar] [CrossRef]
- Riggio, A.I.; Varley, K.E.; Welm, A.L. The lingering mysteries of metastatic recurrence in breast cancer. Br. J. Cancer 2021, 124, 13–26. [Google Scholar] [CrossRef]
- Xiang, L.S.; Gilkes, D.M.; Chaturvedi, P.; Luo, W.B.; Hu, H.X.; Takano, N.; Liang, H.J.; Semenza, G.L. Ganetespib blocks HIF-1 activity and inhibits tumor growth, vascularization, stem cell maintenance, invasion, and metastasis in orthotopic mouse models of triple-negative breast cancer. J. Mol. Med. 2014, 92, 151–164. [Google Scholar] [CrossRef]
- Hollmén, M.; Roudnicky, F.; Karaman, S.; Detmar, M. Characterization of macrophage—Cancer cell crosstalk in estrogen receptor positive and triple-negative breast cancer. Sci. Rep. 2015, 5, 9188. [Google Scholar] [CrossRef] [PubMed]
- Breast Cancer Facts & Figures 2019–2020|Enhanced Reader. Available online: Moz-extension://da48656a-2698-4b3a-98bc-9c2244237ce0/enhanced-reader.html?openApp&pdf=https%3A%2F%2Fwww.cancer.org%2Fcontent%2Fdam%2Fcancer-org%2Fresearch%2Fcancer-facts-and-statistics%2Fbreast-cancer-facts-and-figures%2Fbreast-cancer-facts-and-figures-2019-2020.pdf (accessed on 19 July 2022).
- Liu, L.; Wang, Y.; Miao, L.; Liu, Q.; Musetti, S.; Li, J.; Huang, L. Combination Immunotherapy of MUC1 mRNA Nano-vaccine and CTLA-4 Blockade Effectively Inhibits Growth of Triple Negative Breast Cancer. Mol. Ther. 2018, 26, 45–55. [Google Scholar] [CrossRef]
- Dees, S.; Ganesan, R.; Singh, S.; Grewal, I.S. Emerging CAR-T cell therapy for the treatment of triple-negative breast cancer. Mol. Cancer Ther. 2020, 19, 2409–2421. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Yazdanifar, M.; Das Roy, L.; Whilding, L.M.; Gavrill, A.; Maher, J.; Mukherjee, P. CAR T cells targeting the tumor MUC1 glycoprotein reduce triple-negative breast cancer growth. Front. Immunol. 2019, 10, 1149. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, R.; Chowdhury, C.R.; Arega, S.; Sen, P.; Ganguly, P.; Ganguly, N. CAR T cell therapy: A new era for cancer treatment (Review). Oncol. Rep. 2019, 42, 2183–2195. [Google Scholar] [CrossRef] [PubMed]
- Feins, S.; Kong, W.; Williams, E.F.; Milone, M.C.; Fraietta, J.A. An introduction to chimeric antigen receptor (CAR) T-cell immunotherapy for human cancer. Wiley Online Libr. 2019, 94, S3–S9. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.; Wickman, E.; DeRenzo, C.; Gottschalk, S. CAR T Cell Therapy for Solid Tumors: Bright Future or Dark Reality? Mol. Ther. 2020, 28, 2320–2339. [Google Scholar] [CrossRef] [PubMed]
- Newick, K.; O’brien, S.; Moon, E.; Albelda, S.M. CAR T Cell Therapy for Solid Tumors. Annu. Rev. Med. 2016, 68, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Szeto, G.L.; Finley, S.D. Integrative Approaches to Cancer Immunotherapy. Trends Cancer 2019, 5, 400–410. [Google Scholar] [CrossRef] [PubMed]
- Norton, K.-A.; Gong, C.; Jamalian, S.; Popel, A.S. Multiscale agent-based and hybrid modeling of the tumor immune microenvironment. Processes 2019, 7, 37. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Butner, J.D.; Cristini, V.; Deisboeck, T.S. Integrated PK-PD and agent-based modeling in oncology. J. Pharmacokinet. Pharmacodyn. 2015, 42, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Barros, L.R.C.; de Jesus Rodrigues, B.; Almeida, R.C. CAR-T cell Goes on a Mathematical Model. J. Cell. Immunol. 2020, 2, 31–37. [Google Scholar] [CrossRef]
- Sahoo, P.; Yang, X.; Abler, D.; Maestrini, D.; Adhikarla, V.; Frankhouser, D.; Cho, H.; Machuca, V.; Wang, D.; Barish, M.; et al. Mathematical deconvolution of CAR T-cell proliferation and exhaustion from real-time killing assay data. J. R. Soc. Interface 2020, 17, 20190734. [Google Scholar] [CrossRef]
- Cess, C.G.; Finley, S.D. Multi-scale modeling of macrophage—T cell interactions within the tumor microenvironment. PLoS Comput. Biol. 2020, 16, e1008519. [Google Scholar] [CrossRef] [PubMed]
- Schacht, C.; Meade, A.; Banks, H.T.; Enderling, H.; Abate-Daga, D. Estimation of probability distributions of parameters using aggregate population data: Analysis of a CAR T-cell cancer model. Math. Biosci. Eng. 2019, 16, 7299–7326. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Zheng, X.; Lin-Schmidt, X.; Chen, W.; Carpenter, T.J.; Zong, A.; Wang, W.; Heald, D.L. Development of a quantitative relationship between CAR-affinity, antigen abundance, tumor cell depletion and CAR-T cell expansion using a multiscale systems PK-PD model. MAbs. 2020, 12, 1688616. [Google Scholar] [CrossRef]
- Mostolizadeh, R.; Afsharnezhad, Z.; Marciniak-Czochra, A. Mathematical model of chimeric anti-gene receptor (CAR) T cell therapy with presence of cytokine. Numer Algebr. Control. Optim. 2018, 8, 63. [Google Scholar] [CrossRef]
- Gong, C.; Milberg, O.; Wang, B.; Vicini, P.; Narwal, R.; Roskos, L.; Popel, A.S. A computational multiscale agent-based model for simulating spatio-temporal tumour immune response to PD1 and PDL1 inhibition. J. R. Soc. Interface 2017, 14, 20170320. [Google Scholar] [CrossRef]
- Storey, K.M.; Jackson, T.L. An Agent-Based Model of Combination Oncolytic Viral Therapy and Anti-PD-1 Immunotherapy Reveals the Importance of Spatial Location When Treating Glioblastoma. Cancers 2021, 13, 5314. [Google Scholar] [CrossRef]
- Kather, J.N.; Poleszczuk, J.; Suarez-Carmona, M.; Krisam, J.; Charoentong, P.; Valous, N.A.; Weis, C.A.; Tavernar, L.; Leiss, F.; Herpel, E.; et al. In silico modeling of immunotherapy and stroma-targeting therapies in human colorectal cancer. Cancer Res. 2017, 77, 6442–6452. [Google Scholar] [CrossRef]
- Curtis, L.T.; Frieboes, H.B. Modeling of Combination Chemotherapy and Immunotherapy for Lung Cancer. In Proceedings of the Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Berlin, Germany, 23–27 July 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; Volume 2019, pp. 273–276. [Google Scholar]
- Prybutok, A.N.; Yu, J.S.; Leonard, J.N.; Bagheri, N. Mapping CAR T-Cell Design Space Using Agent-Based Models. Front. Mol. Biosci. 2022, 9, 621. [Google Scholar] [CrossRef]
- Fischel, H.; Giorgadze, T.; Tessier, A.; Norton, K.A. Computational Modeling of Chimeric Antigen Receptor (CAR) T-Cell Therapy of a Binary Model of Antigen Receptors in Breast Cancer. In Proceedings of the Proceedings-2021 IEEE International Conference on Bioinformatics and Biomedicine, BIBM 2021, Houston, TX, USA, 9–12 December 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 3267–3274. [Google Scholar]
- Norton, K.-A.; Wallace, T.; Pandey, N.B.; Popel, A.S. An agent-based model of triple-negative breast cancer: The interplay between chemokine receptor CCR5 expression, cancer stem cells, and hypoxia. BMC Syst. Biol. 2017, 11, 68. [Google Scholar] [CrossRef]
- Norton, K.-A.A.; Popel, A.S. Effects of endothelial cell proliferation and migration rates in a computational model of sprouting angiogenesis. Sci. Rep. 2016, 6, 36992. [Google Scholar] [CrossRef]
- Ventoso, M.; Norton, K.A. Simulating an Immune Response with a Combined Agent-Based Model of a Triple-Negative Breast Cancer Tumor and Vascular Network. In Proceedings of the Proceedings-2020 IEEE International Conference on Bioinformatics and Biomedicine, BIBM 2020, Seoul, Korea, 16–19 December 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 1303–1310. [Google Scholar]
- Norton, K.A.; Jin, K.; Popel, A.S. Modeling triple-negative breast cancer heterogeneity: Effects of stromal macrophages, fibroblasts and tumor vasculature. J. Theor. Biol. 2018, 452, 56–68. [Google Scholar] [CrossRef]
- Lin, S.; Wan, S.; Sun, L.; Hu, J.; Fang, D.; Zhao, R.; Yuan, S.; Zhang, L. Chemokine C-C motif receptor 5 and C-C motif ligand 5 promote cancer cell migration under hypoxia. Cancer Sci. 2012, 103, 904–912. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.J.; Gatenby, R.A. Adaptive Landscapes and Emergent Phenotypes: Why Do Cancers Have High Glycolysis? J. Bioenerg. Biomembr. 2007, 39, 251–257. Available online: https://www.deepdyve.com/lp/springer-journals/adaptive-landscapes-and-emergent-phenotypes-why-do-cancers-have-high-QoDS8UGc6Q (accessed on 2 July 2021).
- Harris, T.H.; Banigan, E.J.; Christian, D.A.; Konradt, C.; Wojno, E.D.T.; Norose, K.; Wilson, E.H.; John, B.; Weninger, W.; Luster, A.D.; et al. Generalized Lévy walks and the role of chemokines in migration of effector CD8 + T cells. Nature 2012, 486, 545–548. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Ayyar, V.S.; Zheng, X.; Chen, W.; Zheng, S.; Mody, H.; Wang, W.; Heald, D.; Singh, A.P.; Cao, Y. Model-Based Cellular Kinetic Analysis of Chimeric Antigen Receptor-T Cells in Humans. Clin. Pharmacol. Ther. 2021, 109, 716–727. [Google Scholar] [CrossRef] [PubMed]
- Weigelin, B.; den Boer, A.T.; Wagena, E.; Broen, K.; Dolstra, H.; de Boer, R.; Figdor, C.; Textor, J.; Friedl, P. Cancer cell elimination by cytotoxic T cell cooperation and additive damage. bioRxiv 2020. [Google Scholar] [CrossRef]
- Norton, K.-A.; Popel, A.S. An agent-based model of cancer stem cell initiated avascular tumour growth and metastasis: The effect of seeding frequency and location. J. R. Soc. Interface 2014, 11, 20140640. [Google Scholar] [CrossRef]
- Yang, P.; Cao, X.; Cai, H.; Feng, P.; Chen, X.; Zhu, Y.; Yang, Y.; An, W.; Yang, Y.; Jie, J. The exosomes derived from CAR-T cell efficiently target mesothelin and reduce triple-negative breast cancer growth. Cell. Immunol. 2021, 360, 104262. [Google Scholar] [CrossRef]
- Tchou, J.; Wang, L.C.; Selven, B.; Zhang, H.; Conejo-Garcia, J.; Borghaei, H.; Kalos, M.; Vondeheide, R.H.; Albelda, S.M.; June, C.H.; et al. Mesothelin, a novel immunotherapy target for triple negative breast cancer. Breast Cancer Res. Treat. 2012, 133, 799–804. [Google Scholar] [CrossRef]
- Wei, H.; Wang, Z.; Kuang, Y.; Wu, Z.; Zhao, S.; Zhang, Z.; Li, H.; Zheng, M.; Zhang, N.; Long, C.; et al. Intercellular Adhesion Molecule-1 as Target for CAR-T-Cell Therapy of Triple-Negative Breast Cancer. Front. Immunol. 2020, 11, 2272. [Google Scholar] [CrossRef]
- Ruella, M.; Maus, M.V. Catch me if you can: Leukemia Escape after CD19-Directed T Cell Immunotherapies. Comput. Struct. Biotechnol. J. 2016, 14, 357–362. [Google Scholar] [CrossRef]
- Zhang, Q.; Ping, J.; Huang, Z.; Zhang, X.; Zhou, J.; Wang, G.; Liu, S.; Ma, J. CAR-T Cell Therapy in Cancer: Tribulations and Road Ahead. J. Immunol. Res. 2020, 2020. [Google Scholar] [CrossRef]
- Wang, X.; Osada, T.; Wang, Y.; Yu, L.; Sakakura, K.; Katayama, A.; McCarthy, J.B.; Brufsky, A.; Chivukula, M.; Khoury, T.; et al. CSPG4 protein as a new target for the antibody-based immunotherapy of triple-negative breast cancer. J. Natl. Cancer Inst. 2010, 102, 1496–1512. [Google Scholar] [CrossRef]
- Rafiq, S.; Hackett, C.S.; Brentjens, R.J. Engineering strategies to overcome the current roadblocks in CAR T cell therapy. Nat. Rev. Clin. Oncol. 2020, 17, 147–167. [Google Scholar] [CrossRef]
- Andrea, A.E.; Chiron, A.; Mallah, S.; Bessoles, S.; Sarrabayrouse, G.; Hacein-Bey-Abina, S. Advances in CAR-T Cell Genetic Engineering Strategies to Overcome Hurdles in Solid Tumors Treatment. Front. Immunol. 2022, 13, 309. [Google Scholar] [CrossRef]
- Huang, M.; Deng, J.; Gao, L.; Zhou, J. Innovative strategies to advance CAR T cell therapy for solid tumors. Am. J. Cancer Res. 2020, 10, 1979–1992. [Google Scholar]
- León-Triana, O.; Pérez-Martínez, A.; Ramírez-Orellana, M.; Pérez-García, V.M. Dual-Target CAR-Ts with On-and Off-Tumour Activity May Override Immune Suppression in Solid Cancers: A Mathematical Proof of Concept. Cancers 2021, 13, 703. [Google Scholar] [CrossRef]
- Cui, X.; Liu, R.; Duan, L.; Cao, D.; Zhang, Q.; Zhang, A. CAR-T therapy: Prospects in targeting cancer stem cells. Wiley Online Libr. 2021, 25, 9891–9904. [Google Scholar] [CrossRef] [PubMed]
- Alhabbab, R.Y. Targeting Cancer Stem Cells by Genetically Engineered Chimeric Antigen Receptor T Cells. Front. Genet. 2020, 11, 312. [Google Scholar] [CrossRef] [PubMed]
- Jeong, Y.K.; Siegler, E.L.; Siriwon, N.; Wang, P. Therapeutic strategies for targeting cancer stem cells Quick Response Code. Artic. J. Cancer Metastasis Treat. 2016. [Google Scholar] [CrossRef]
- Masoumi, J.; Jafarzadeh, A.; Abdolalizadeh, J.; Khan, H.; Philippe, J.; Mirzaei, H.; Mirzaei, H.R. Cancer stem cell-targeted chimeric antigen receptor (CAR)-T cell therapy: Challenges and prospects. Acta Pharm. Sin. B 2021, 11, 1721–1739. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgadze, T.; Fischel, H.; Tessier, A.; Norton, K.-A. Investigating Two Modes of Cancer-Associated Antigen Heterogeneity in an Agent-Based Model of Chimeric Antigen Receptor T-Cell Therapy. Cells 2022, 11, 3165. https://doi.org/10.3390/cells11193165
Giorgadze T, Fischel H, Tessier A, Norton K-A. Investigating Two Modes of Cancer-Associated Antigen Heterogeneity in an Agent-Based Model of Chimeric Antigen Receptor T-Cell Therapy. Cells. 2022; 11(19):3165. https://doi.org/10.3390/cells11193165
Chicago/Turabian StyleGiorgadze, Tina, Henning Fischel, Ansel Tessier, and Kerri-Ann Norton. 2022. "Investigating Two Modes of Cancer-Associated Antigen Heterogeneity in an Agent-Based Model of Chimeric Antigen Receptor T-Cell Therapy" Cells 11, no. 19: 3165. https://doi.org/10.3390/cells11193165
APA StyleGiorgadze, T., Fischel, H., Tessier, A., & Norton, K.-A. (2022). Investigating Two Modes of Cancer-Associated Antigen Heterogeneity in an Agent-Based Model of Chimeric Antigen Receptor T-Cell Therapy. Cells, 11(19), 3165. https://doi.org/10.3390/cells11193165




