Application of Lacunarity for Quantification of Single Molecule Localization Microscopy Images
Abstract
1. Introduction
2. Materials and Methods
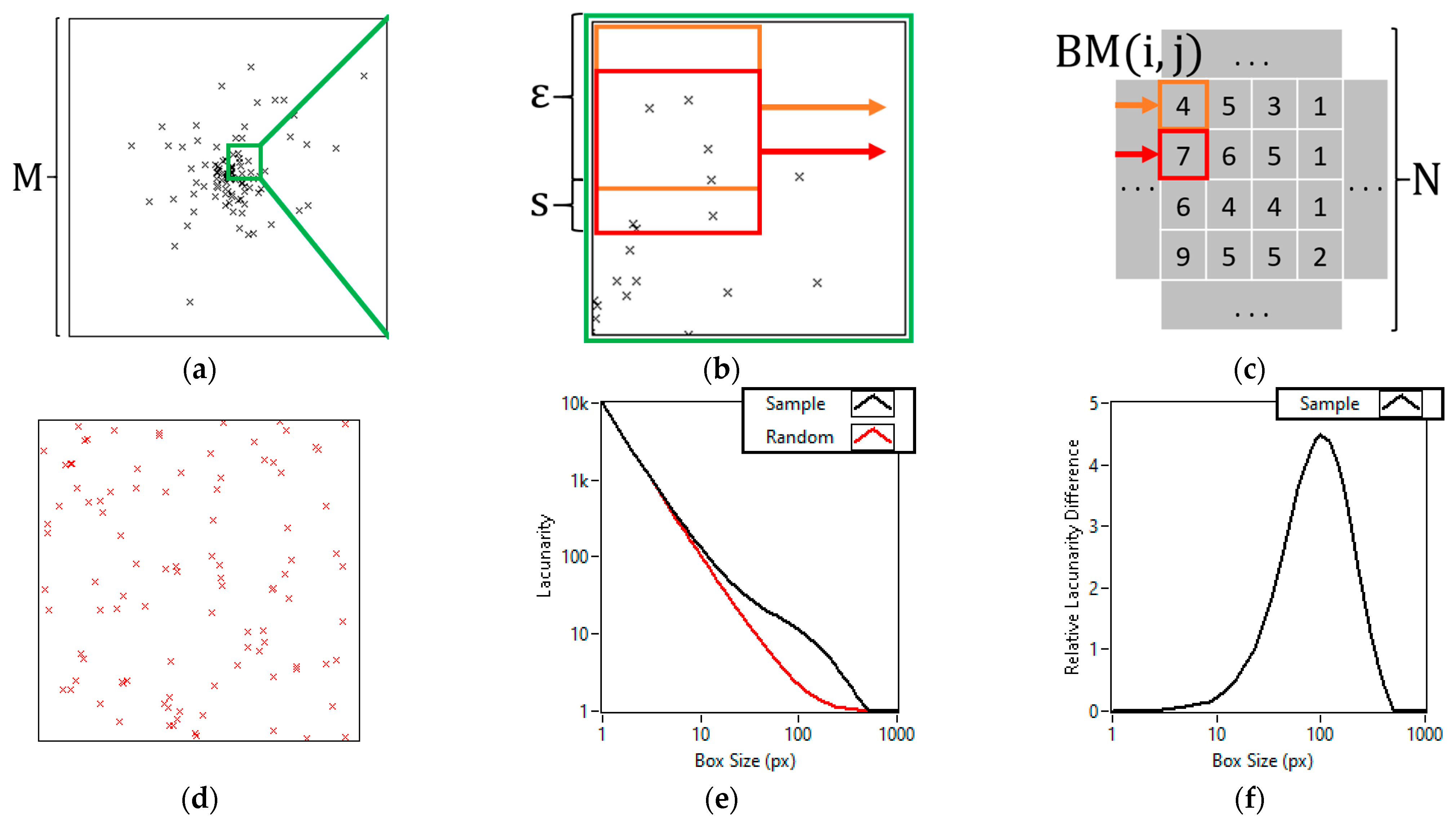
2.1. Lacunarity Calculation
2.2. TestSTORM Simulation
2.3. DNA DSB dSTORM Images
3. Results
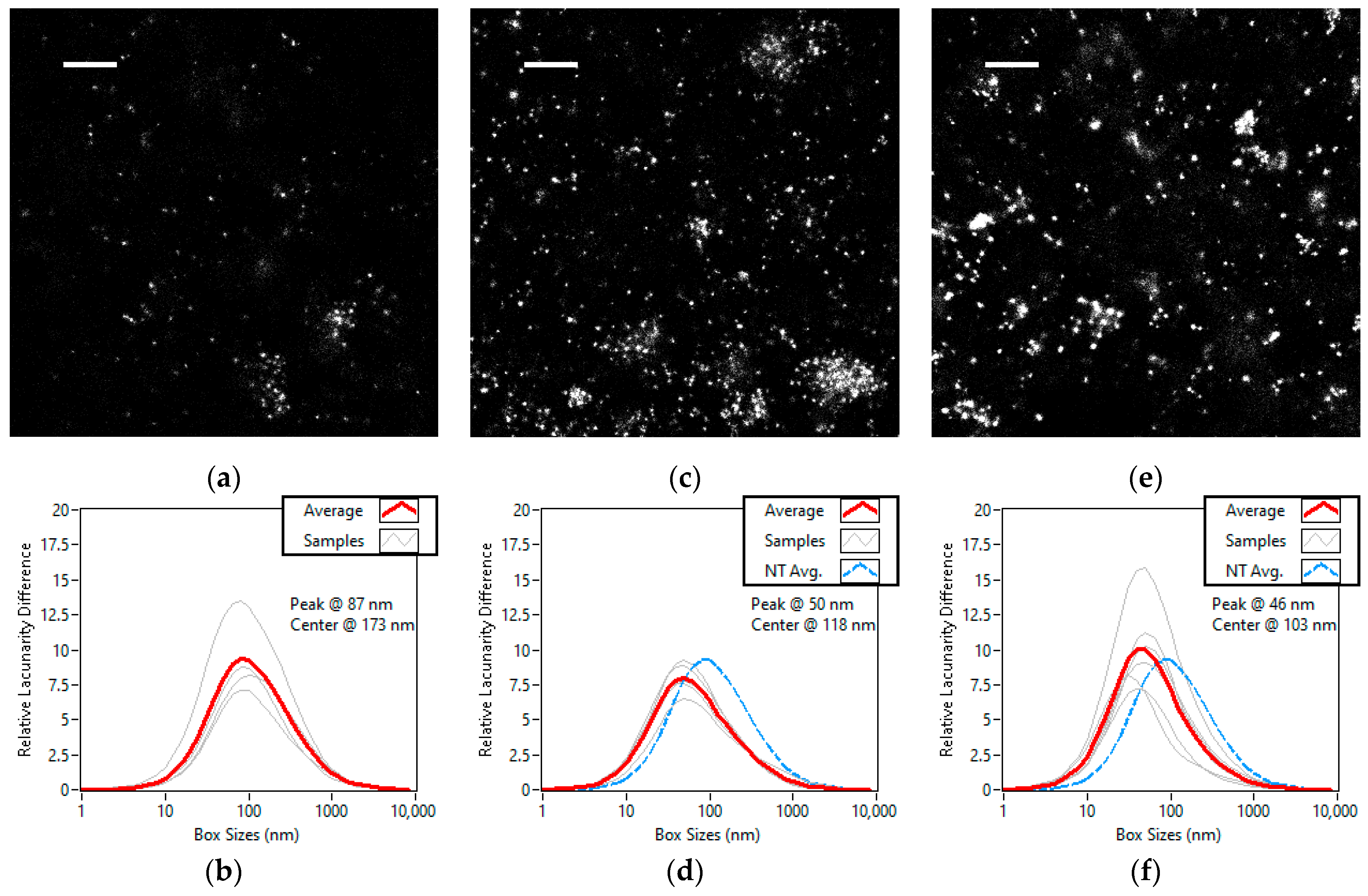
3.1. Lacunarity Behaviour Examined through TestSTORM Simulations
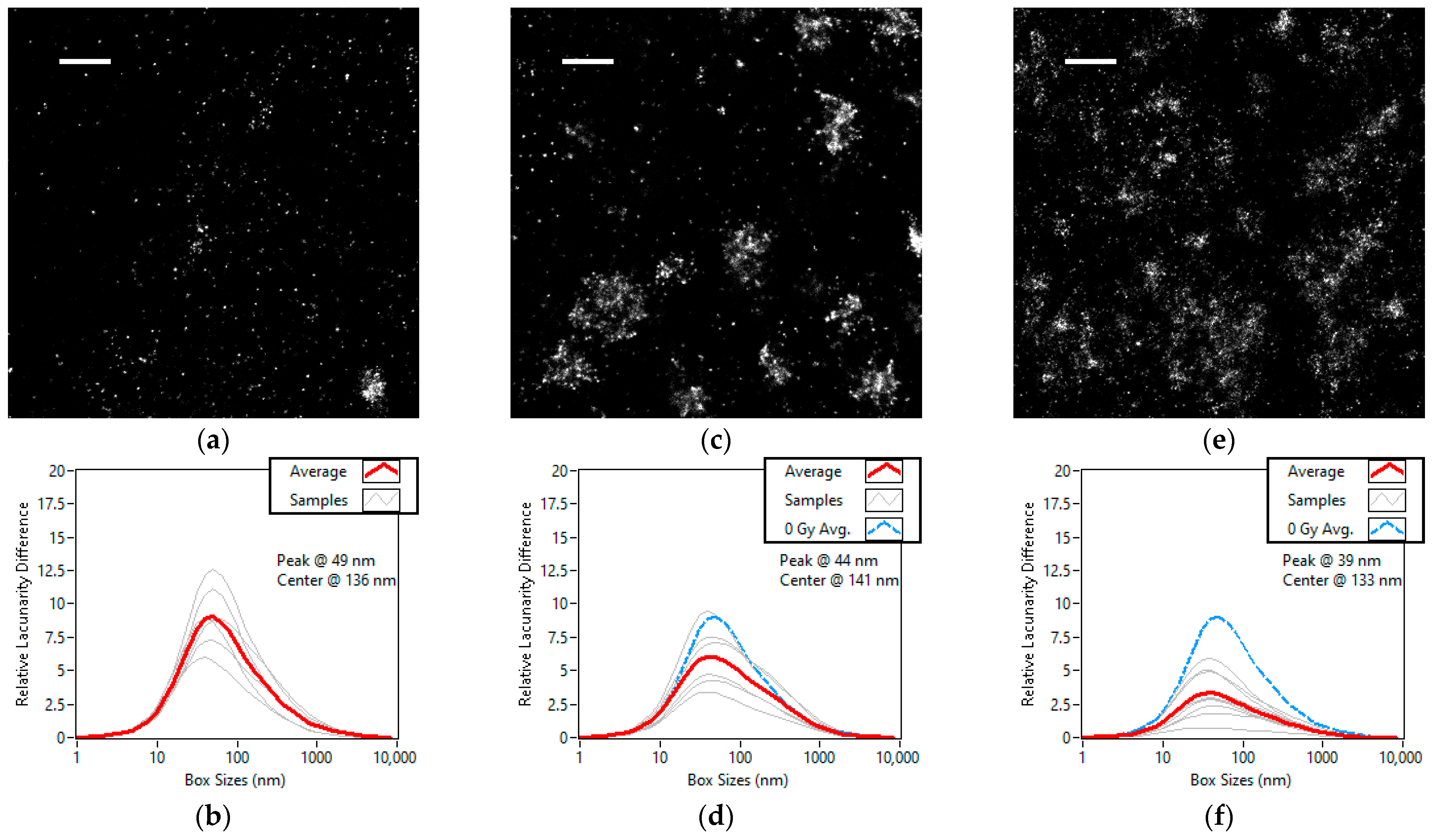
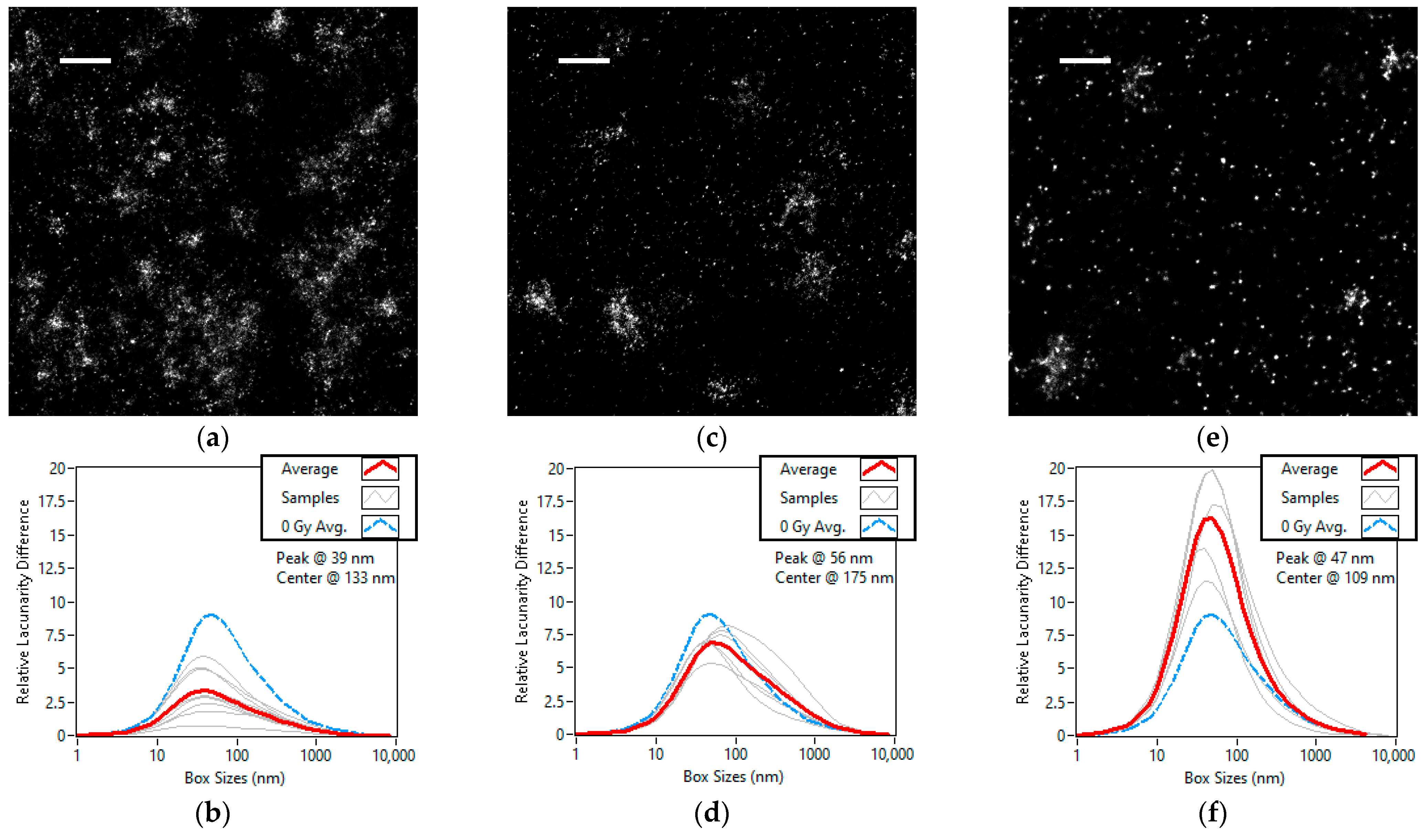
3.2. Dose Dependent Lacunarity Study of the X-ray Radiation Treated Cell Line
3.3. Kinetic Lacunarity Study of the X-ray Radiation Treated Cell Line
3.4. Lacunarity Study of Chemically Treated Cell Lines
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rossmann, K. Point spread-function, line spread-function, and modulation transfer function: Tools for the study of imaging systems. Radiology 1969, 93, 257–272. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999; pp. 484–499. [Google Scholar]
- Gustafsson, M.G. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2000, 198, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Lelek, M.; Gyparaki, M.T.; Beliu, G.; Schueder, F.; Griffié, J.; Manley, S.; Jungmann, R.; Sauer, M.; Lakadamyali, M.; Zimmer, C. Single-molecule localization microscopy. Nat. Rev. Methods Prim. 2021, 1, 39. [Google Scholar] [CrossRef]
- Rust, M.J.; Bates, M.; Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 2006, 3, 793–796. [Google Scholar] [CrossRef]
- Heilemann, M.; Van De Linde, S.; Schüttpelz, M.; Kasper, R.; Seefeldt, B.; Mukherjee, A.; Tinnefeld, P.; Sauer, M. Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes. Angew. Chem. Int. Ed. 2008, 47, 6172–6176. [Google Scholar] [CrossRef]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef]
- Dickson, R.M.; Cubitt, A.B.; Tsien, R.Y.; Moerner, W.E. On/off blinking and switching behaviour of single molecules of green fluorescent protein. Nature 1997, 388, 355–358. [Google Scholar] [CrossRef]
- Sharonov, A.; Hochstrasser, R.M. Wide-field subdiffraction imaging by accumulated binding of diffusing probes. Proc. Natl. Acad. Sci. USA 2006, 103, 18911–18916. [Google Scholar] [CrossRef]
- Fölling, J.; Bossi, M.; Bock, H.; Medda, R.; Wurm, C.A.; Hein, B.; Jakobs, S.; Eggeling, C.; Hell, S.W. Fluorescence nanoscopy by ground-state depletion and single-molecule return. Nat. Methods 2008, 5, 943–945. [Google Scholar] [CrossRef]
- Balzarotti, F.; Eilers, Y.; Gwosch, K.C.; Gynnå, A.H.; Westphal, V.; Stefani, F.D.; Elf, J.; Hell, S.W. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science 2017, 355, 606–612. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.L.; Tschanz, A.; Krupnik, L.; Ries, J. Quantitative data analysis in single-molecule localization microscopy. Trends Cell Biol. 2020, 30, 837–851. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, P.; Jovanovic-Talisman, T.; Skoko, D.; Renz, M.; Veatch, S.L.; Lippincott-Schwartz, J. Probing protein heterogeneity in the plasma membrane using PALM and pair correlation analysis. Nat. Methods 2011, 8, 969–975. [Google Scholar] [CrossRef] [PubMed]
- Owen, D.M.; Rentero, C.; Rossy, J.; Magenau, A.; Williamson, D.; Rodriguez, M.; Gaus, K. PALM imaging and cluster analysis of protein heterogeneity at the cell surface. J. Biophotonics 2010, 3, 446–454. [Google Scholar] [CrossRef]
- Nicovich, P.R.; Owen, D.M.; Gaus, K. Turning single-molecule localization microscopy into a quantitative bioanalytical tool. Nat. Protoc. 2017, 12, 453–460. [Google Scholar] [CrossRef]
- Pike, J.A.; Khan, A.O.; Pallini, C.; Thomas, S.G.; Mund, M.; Ries, J.; Poulter, N.S.; Styles, I.B. Topological data analysis quantifies biological nano-structure from single molecule localization microscopy. Bioinformatics 2020, 36, 1614–1621. [Google Scholar] [CrossRef]
- Baddeley, D.; Cannell, M.B.; Soeller, C. Visualization of localization microscopy data. Microsc. Microanal. 2010, 16, 64–72. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Inkdd 1996, 96, 226–231. [Google Scholar]
- Andronov, L.; Orlov, I.; Lutz, Y.; Vonesch, J.L.; Klaholz, B.P. ClusterViSu, a method for clustering of protein complexes by Voronoi tessellation in super-resolution microscopy. Sci. Rep. 2016, 6, 24084. [Google Scholar] [CrossRef]
- Varga, D.; Majoros, H.; Ujfaludi, Z.; Erdélyi, M.; Pankotai, T. Quantification of DNA damage induced repair focus formation via super-resolution dSTORM localization microscopy. Nanoscale 2019, 11, 14226–14236. [Google Scholar] [CrossRef]
- Sun, M.; Huang, J.; Bunyak, F.; Gumpper, K.; De, G.; Sermersheim, M.; Liu, G.; Lin, P.H.; Palaniappan, K.; Ma, J. Superresolution microscope image reconstruction by spatiotemporal object decomposition and association: Application in resolving t-tubule structure in skeletal muscle. Opt. Express 2014, 22, 12160–12176. [Google Scholar] [CrossRef] [PubMed]
- Pageon, S.V.; Nicovich, P.R.; Mollazade, M.; Tabarin, T.; Gaus, K. Clus-DoC: A combined cluster detection and colocalization analysis for single-molecule localization microscopy data. Mol. Biol. Cell 2016, 27, 3627–3636. [Google Scholar] [CrossRef] [PubMed]
- Levet, F.; Julien, G.; Galland, R.; Butler, C.; Beghin, A.; Chazeau, A.; Hoess, P.; Ries, J.; Giannone, G.; Sibarita, J.B. A tessellation-based colocalization analysis approach for single-molecule localization microscopy. Nat. Commun. 2019, 10, 2379. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: San Francisco, CA, USA, 1983; pp. 310–319. [Google Scholar]
- Sebők, D.; Vásárhelyi, L.; Szenti, I.; Vajtai, R.; Kónya, Z.; Kukovecz, Á. Fast and accurate lacunarity calculation for large 3D micro-CT datasets. Acta Mater. 2021, 214, 116970. [Google Scholar] [CrossRef]
- García-Farieta, J.E.; Casas-Miranda, R.A. Effect of observational holes in fractal analysis of galaxy survey masks. Chaos Solitons Fractals 2018, 111, 128–137. [Google Scholar] [CrossRef]
- Valous, N.A.; Sun, D.W.; Allen, P.; Mendoza, F. The use of lacunarity for visual texture characterization of pre-sliced cooked pork ham surface intensities. Food Res. Int. 2010, 43, 387–395. [Google Scholar] [CrossRef]
- Drăghici, C.C.; Andronache, I.; Ahammer, H.; Peptenatu, D.; Pintilii, R.D.; Ciobotaru, A.M.; Simion, A.G.; Dobrea, R.C.; Diaconu, D.C.; Vișan, M.C.; et al. Spatial evolution of forest areas in the northern Carpathian Mountains of Romania. Acta Montan. Slovaca 2017, 22, 95–106. [Google Scholar]
- Nichita, M.V.; Paun, M.A.; Paun, V.A.; Paun, V.P. Fractal analysis of brain glial cells. Fractal dimension and lacunarity. Univ. Politeh. Buchar. Sci. Bull. Ser. A Appl. Math. Phys. 2019, 81, 273–284. [Google Scholar]
- Waliszewski, P. The quantitative criteria based on the fractal dimensions, entropy, and lacunarity for the spatial distribution of cancer cell nuclei enable identification of low or high aggressive prostate carcinomas. Front. Physiol. 2016, 7, 34. [Google Scholar] [CrossRef]
- Brunner, S.; Varga, D.; Bozó, R.; Polanek, R.; Tőkés, T.; Szabó, E.R.; Molnár, R.; Gémes, N.; Szebeni, G.J.; Puskás, L.G.; et al. Analysis of Ionizing Radiation Induced DNA Damage by Superresolution dSTORM Microscopy. Pathol. Oncol. Res. 2021, 27, 1609971. [Google Scholar] [CrossRef]
- Rogakou, E.P.; Boon, C.; Redon, C.; Bonner, W.M. Megabase chromatin domains involved in DNA double-strand breaks in vivo. J. Cell Biol. 1999, 146, 905–916. [Google Scholar] [CrossRef] [PubMed]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-stranded breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef] [PubMed]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552. [Google Scholar] [CrossRef] [PubMed]
- Tolle, C.R.; McJunkin, T.R.; Gorsich, D.J. An efficient implementation of the gliding box lacunarity algorithm. Phys. D Nonlinear Phenom. 2008, 237, 306–315. [Google Scholar] [CrossRef]
- Backes, A.R. A new approach to estimate lacunarity of texture images. Pattern Recognit. Lett. 2013, 34, 1455–1461. [Google Scholar] [CrossRef]
- Novák, T.; Gajdos, T.; Sinkó, J.; Szabó, G.; Erdélyi, M. TestSTORM: Versatile simulator software for multimodal super-resolution localization fluorescence microscopy. Sci. Rep. 2017, 7, 951. [Google Scholar] [CrossRef]
- Berzsenyi, I.; Pantazi, V.; Borsos, B.N.; Pankotai, T. Systematic overview on the most widespread techniques for inducing and visualizing the DNA double-strand breaks. Mutat. Res. Rev. Mutat. Res. 2021, 788, 108397. [Google Scholar] [CrossRef]
- Iacovoni, J.S.; Caron, P.; Lassadi, I.; Nicolas, E.; Massip, L.; Trouche, D.; Legube, G. High-resolution profiling of γH2AX around DNA double strand breaks in the mammalian genome. EMBO J. 2010, 29, 1446–1457. [Google Scholar] [CrossRef]
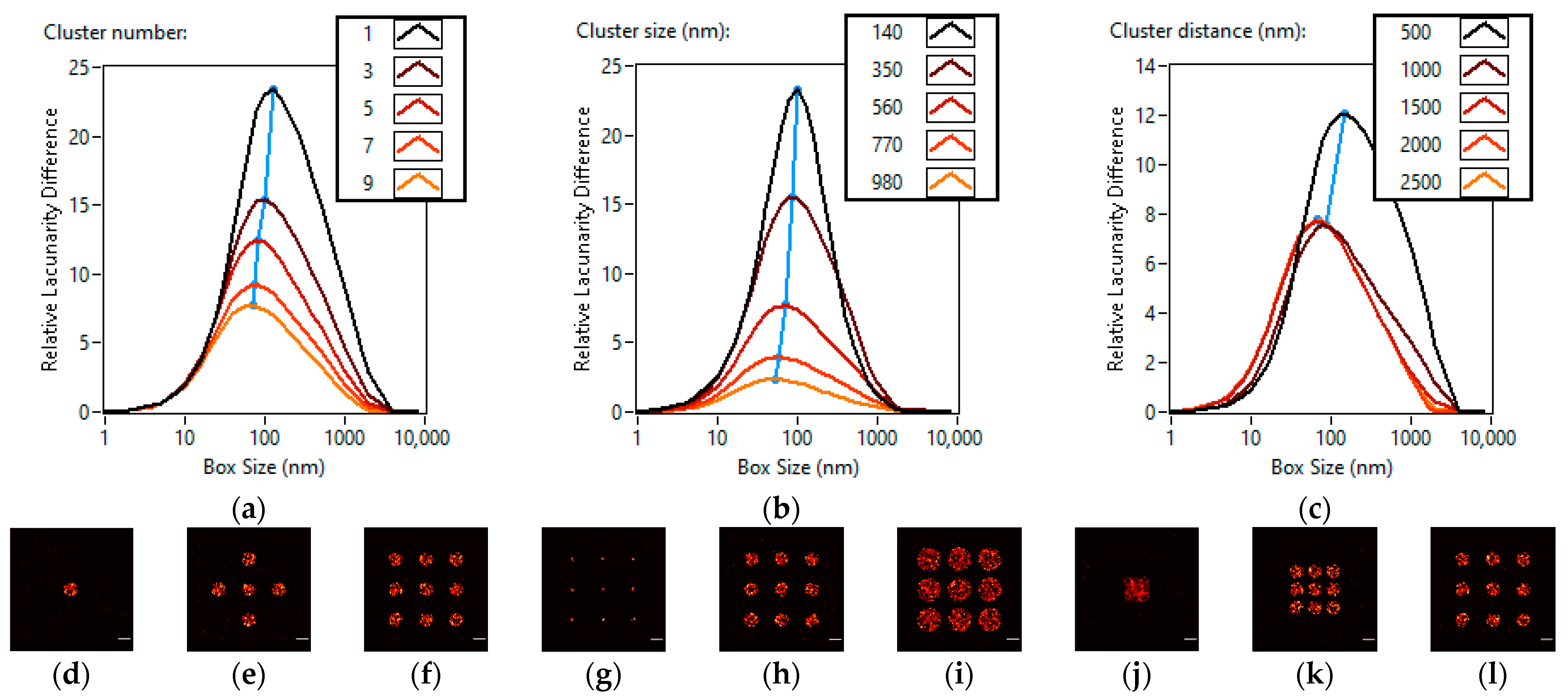
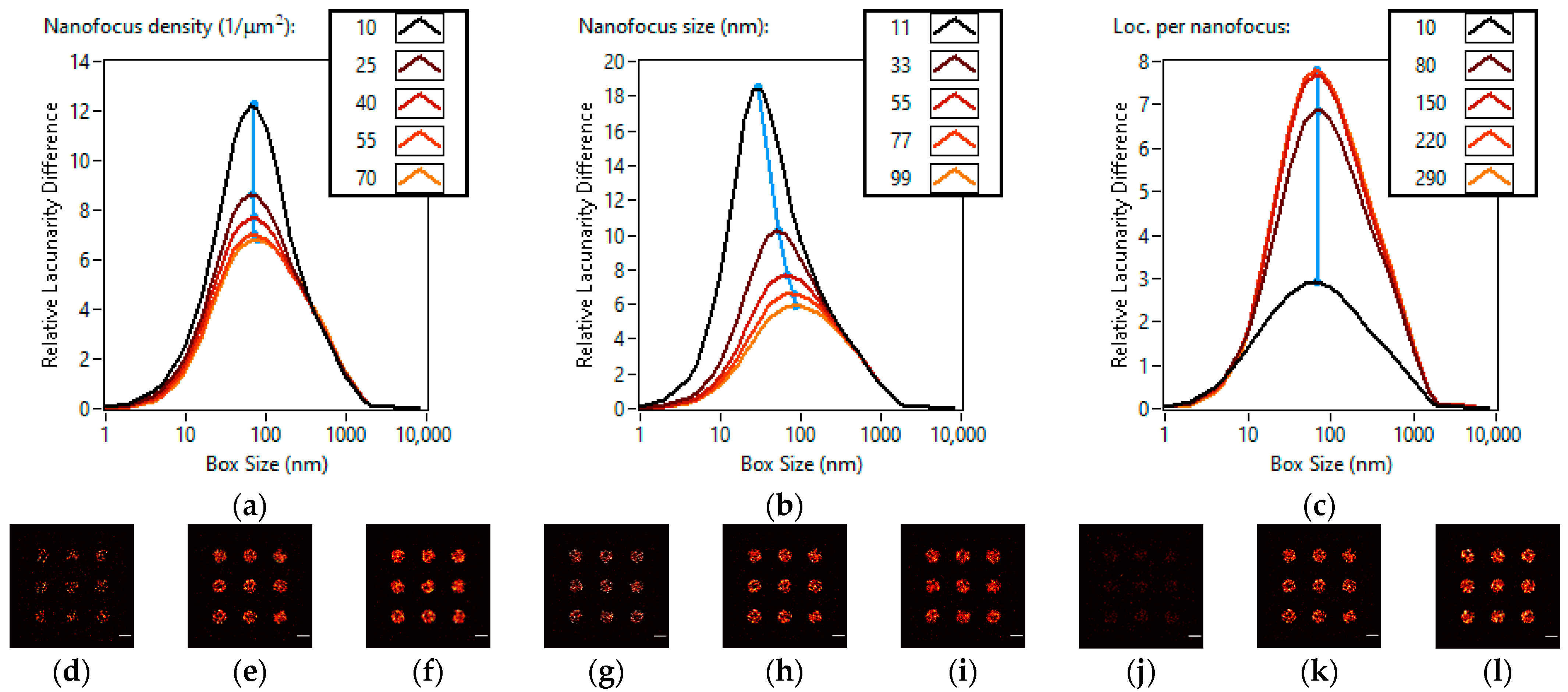
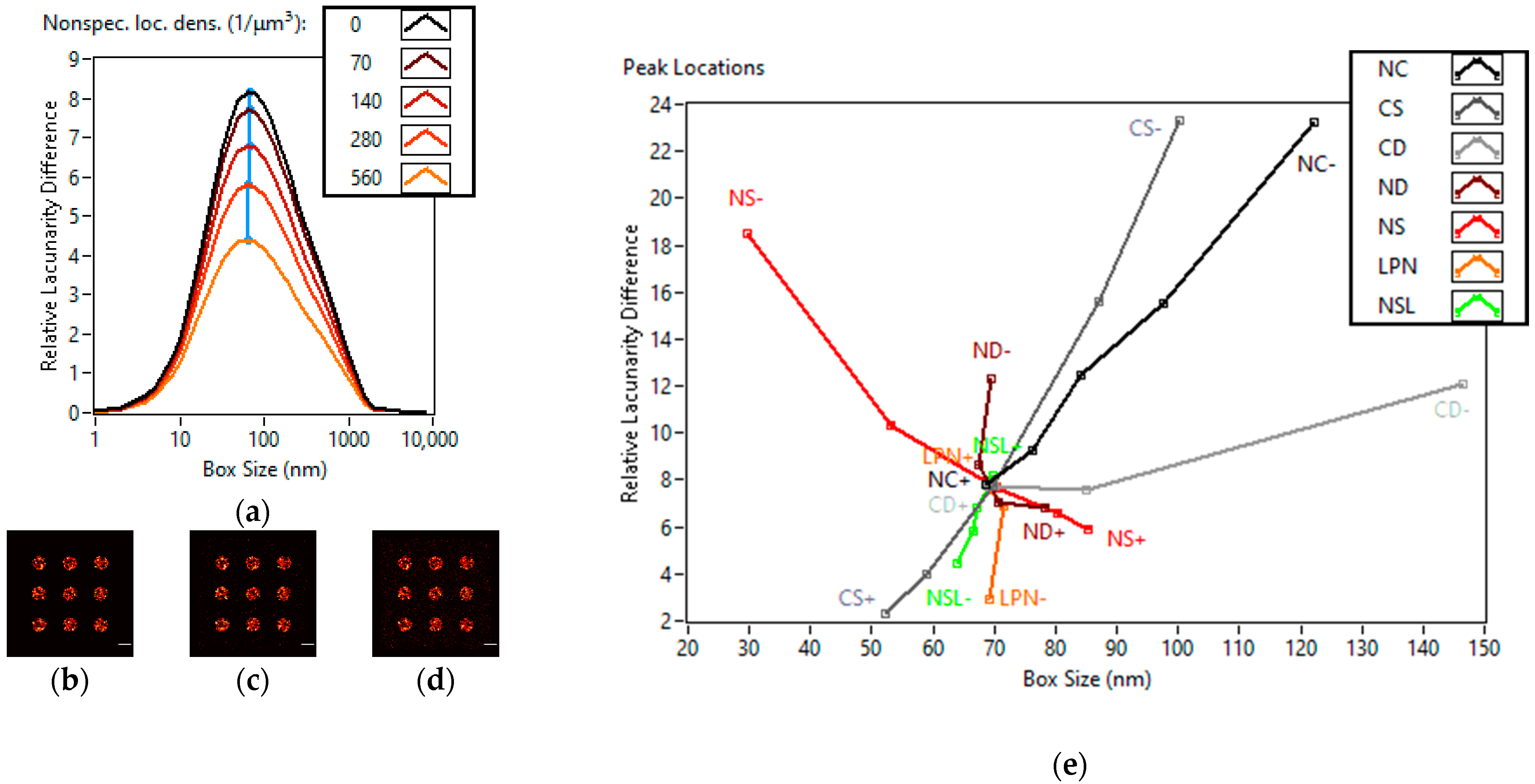
| Names of the Simulation Parameters | Base Values of the Simulation Parameters | Ranges of the Simulation Parameters |
|---|---|---|
| Cluster number | 9 | 1–9 |
| Cluster size (nm) | 560 | 140–980 |
| Cluster distance (nm) | 2500 | 500–2500 |
| Nanofocus density (nanofoci/µm2) | 40 | 10–70 |
| Nanofocus Size (nm) | 55 | 11–99 |
| Localizations per nanofocus (localizations/µm2) | 150 | 10–290 |
| Nonspecific localization density (localizations/µm3) | 70 | 0–560 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, B.B.H.; Varga, D.; Sebők, D.; Majoros, H.; Polanek, R.; Pankotai, T.; Hideghéty, K.; Kukovecz, Á.; Erdélyi, M. Application of Lacunarity for Quantification of Single Molecule Localization Microscopy Images. Cells 2022, 11, 3105. https://doi.org/10.3390/cells11193105
Kovács BBH, Varga D, Sebők D, Majoros H, Polanek R, Pankotai T, Hideghéty K, Kukovecz Á, Erdélyi M. Application of Lacunarity for Quantification of Single Molecule Localization Microscopy Images. Cells. 2022; 11(19):3105. https://doi.org/10.3390/cells11193105
Chicago/Turabian StyleKovács, Bálint Barna H., Dániel Varga, Dániel Sebők, Hajnalka Majoros, Róbert Polanek, Tibor Pankotai, Katalin Hideghéty, Ákos Kukovecz, and Miklós Erdélyi. 2022. "Application of Lacunarity for Quantification of Single Molecule Localization Microscopy Images" Cells 11, no. 19: 3105. https://doi.org/10.3390/cells11193105
APA StyleKovács, B. B. H., Varga, D., Sebők, D., Majoros, H., Polanek, R., Pankotai, T., Hideghéty, K., Kukovecz, Á., & Erdélyi, M. (2022). Application of Lacunarity for Quantification of Single Molecule Localization Microscopy Images. Cells, 11(19), 3105. https://doi.org/10.3390/cells11193105







