Scanner-Based Minirhizotrons Help to Highlight Relations between Deep Roots and Yield in Various Wheat Cultivars under Combined Water and Nitrogen Deficit Conditions
Abstract
1. Introduction
2. Materials and Methods
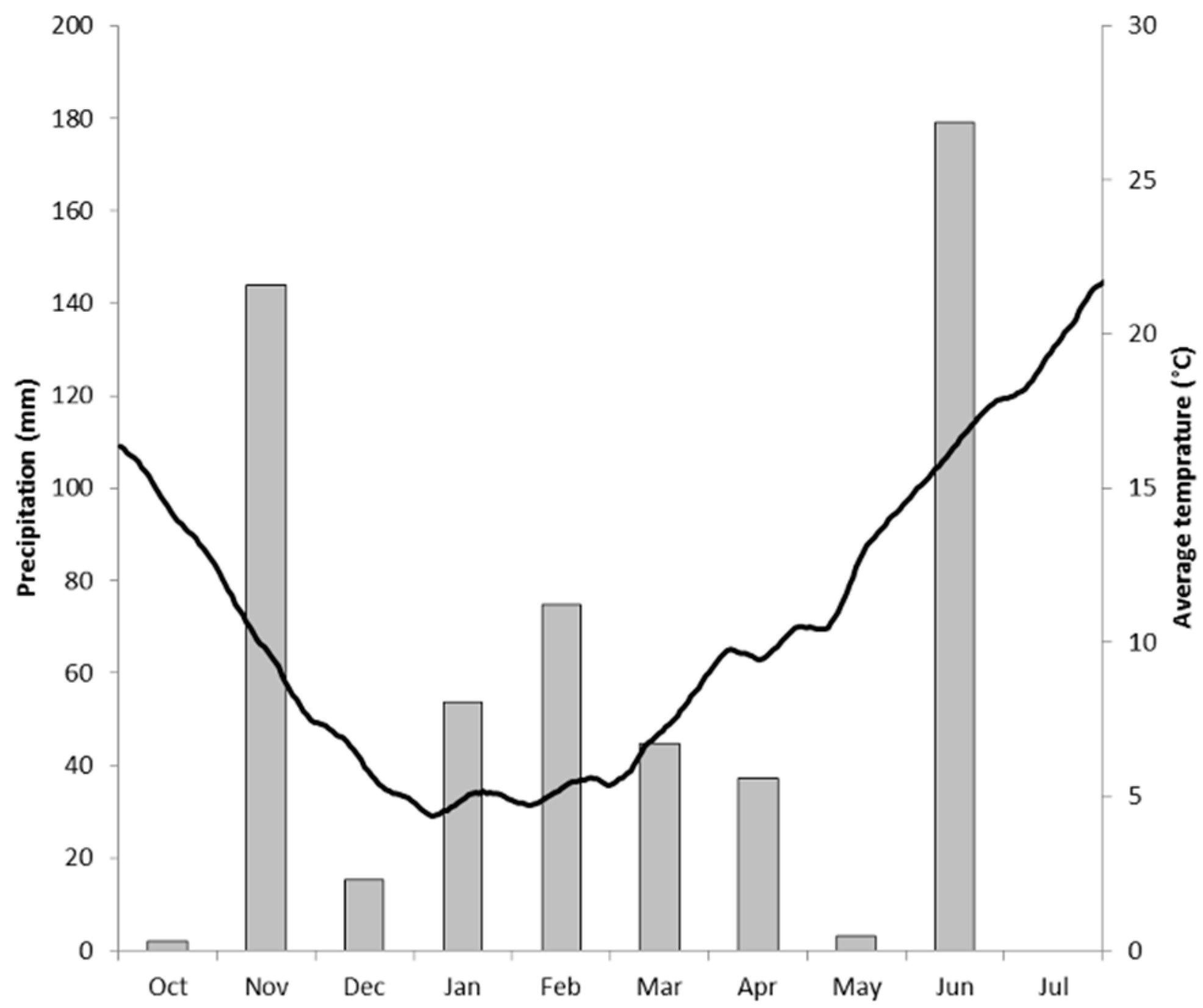
2.1. The Field Site
2.2. Experimental Design
2.3. Crop Management
2.4. Shoot Biomass and N Measurements
2.5. Root Measurements
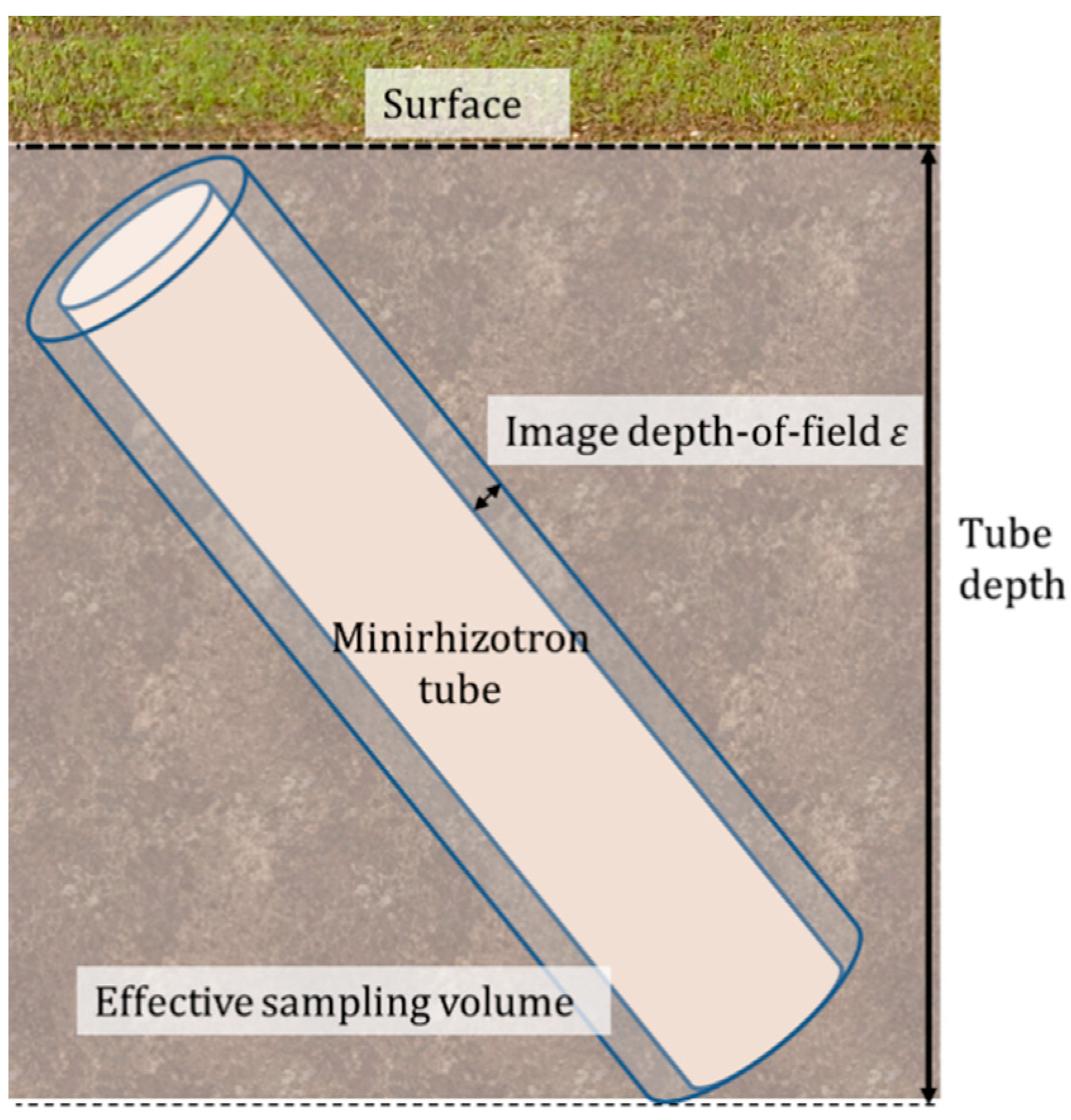
2.5.1. Minirhizotron Installation
2.5.2. Image Processing of Minirhizotron Images
2.5.3. Auger Sampling for Root Biomass
2.5.4. Conversion of Root Length Surface Density to Root Biomass
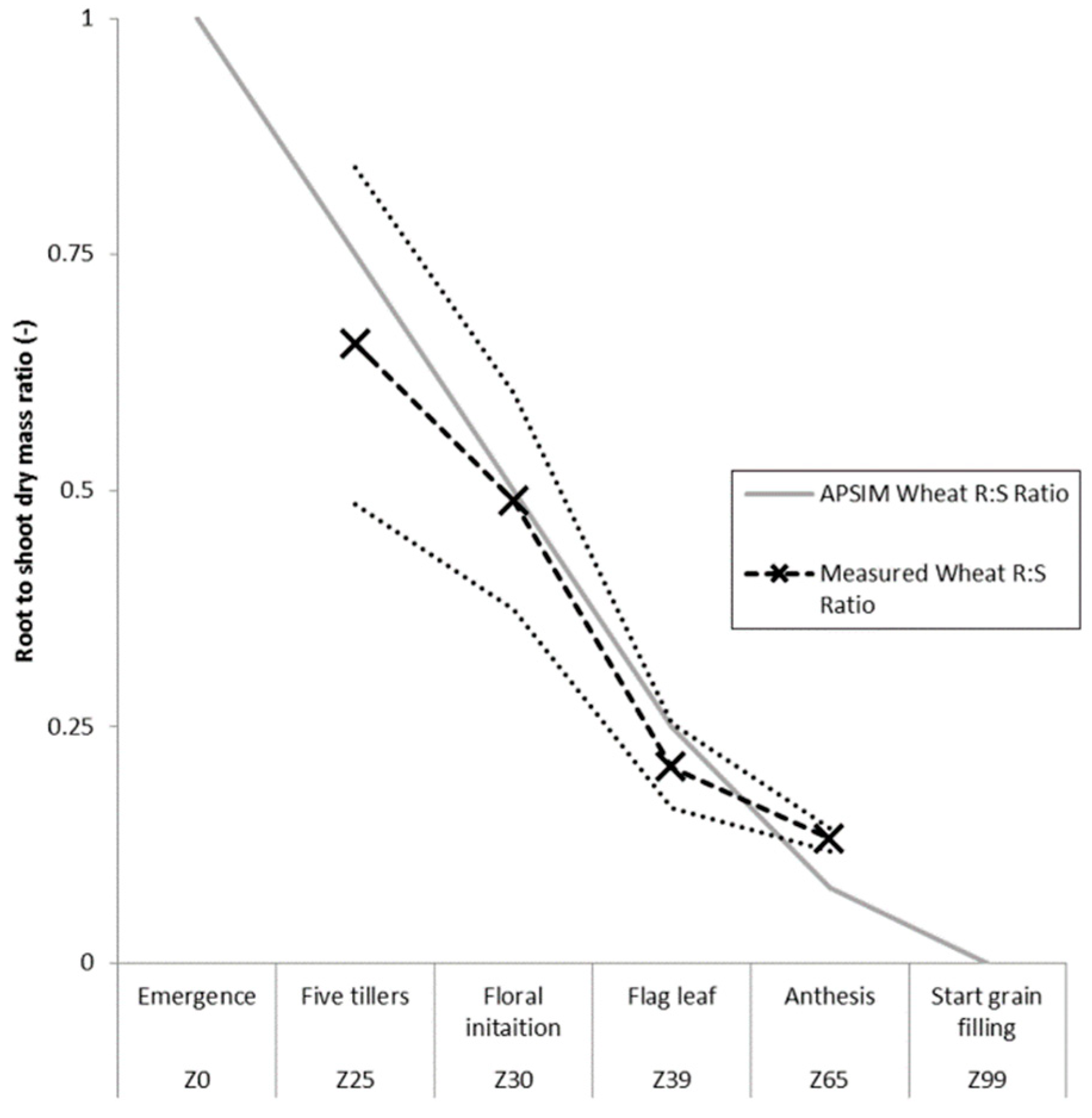
2.6. Root to Shoot Ratio
2.7. Statistical Analyses
3. Results
3.1. Root Length to Biomass Conversion Factor and Root to Shoot Ratio
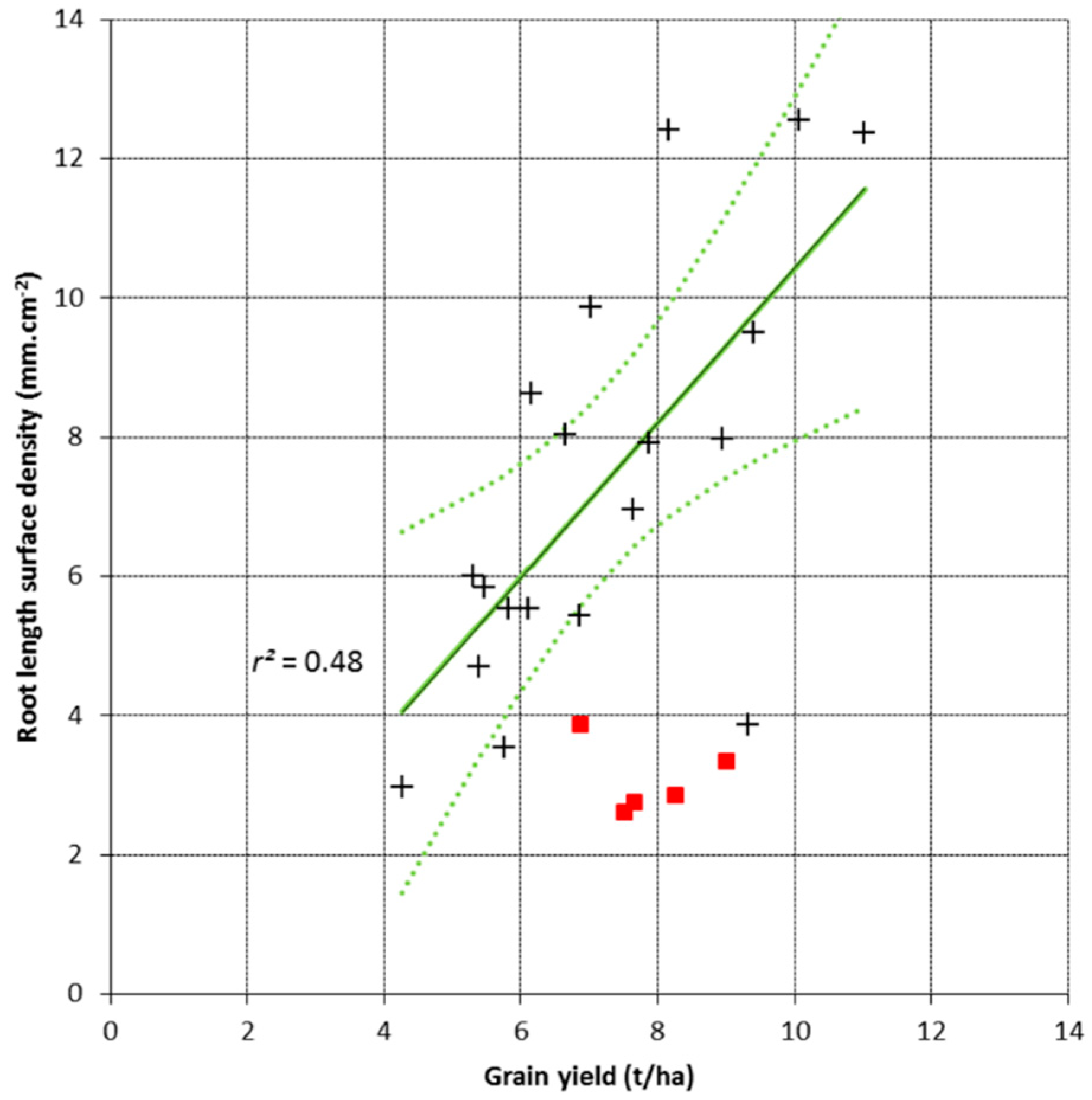
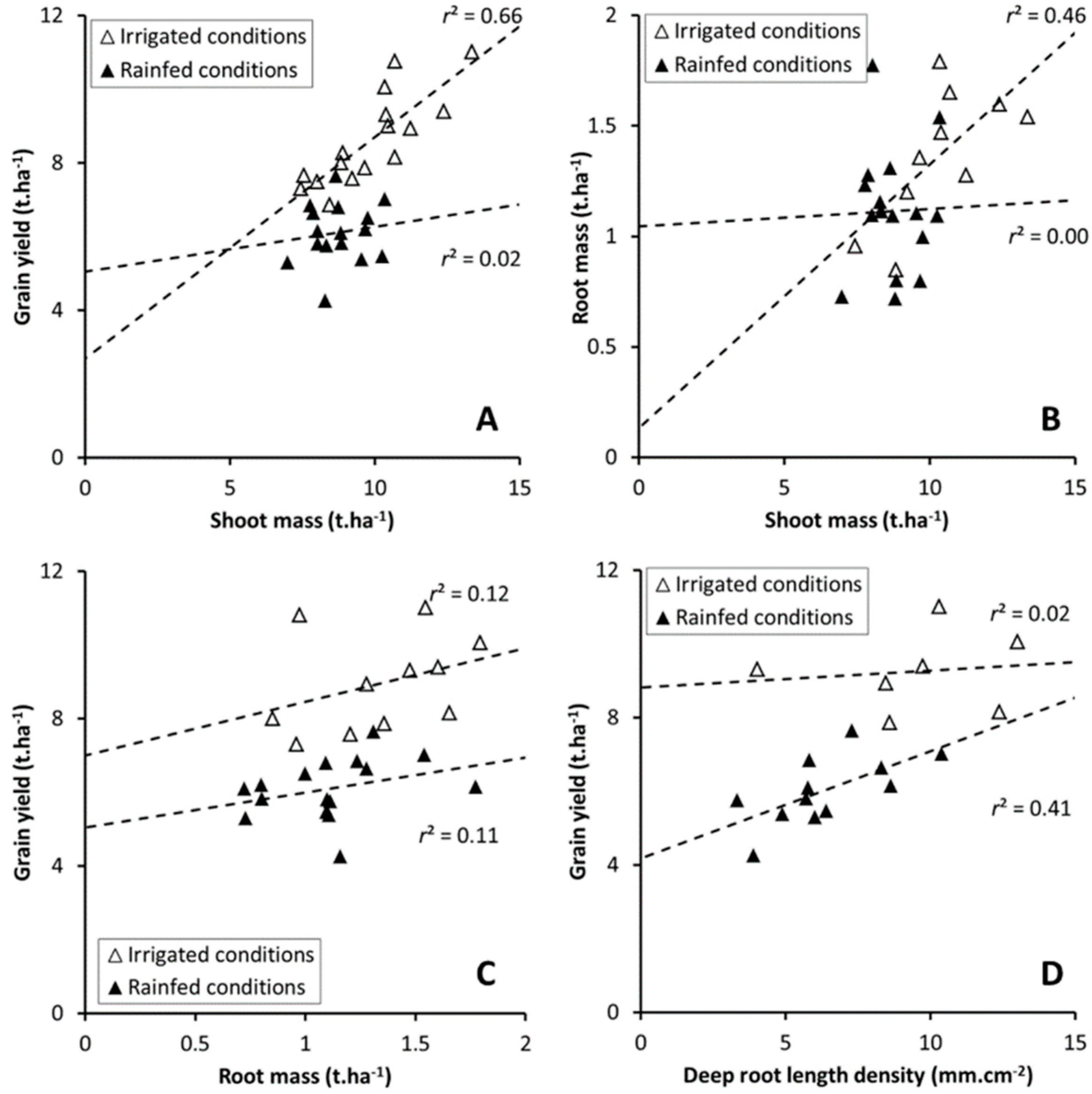
3.2. Root Length Surface Density and Grain Yield
3.3. Impact of Different N and Water Treatments
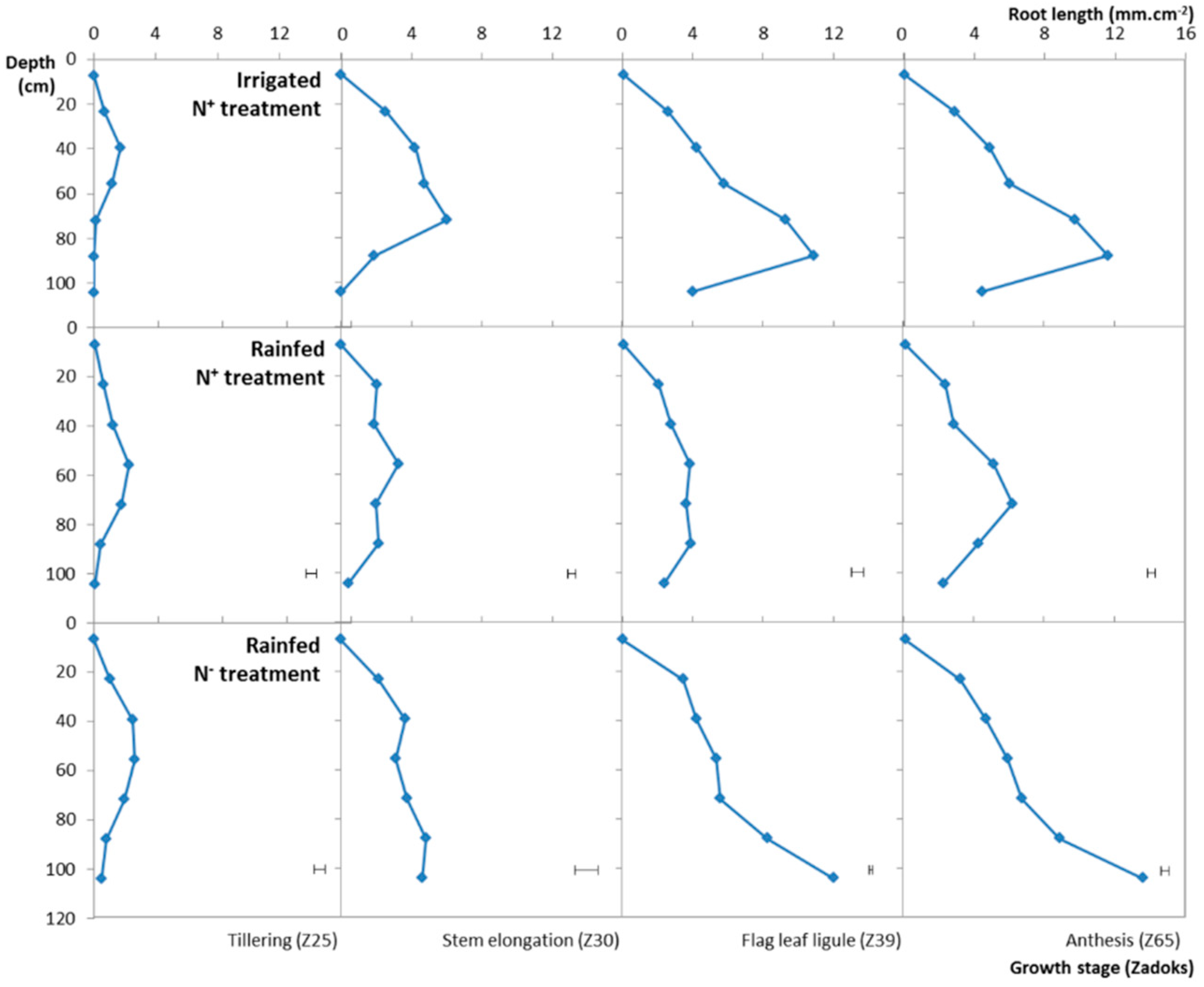
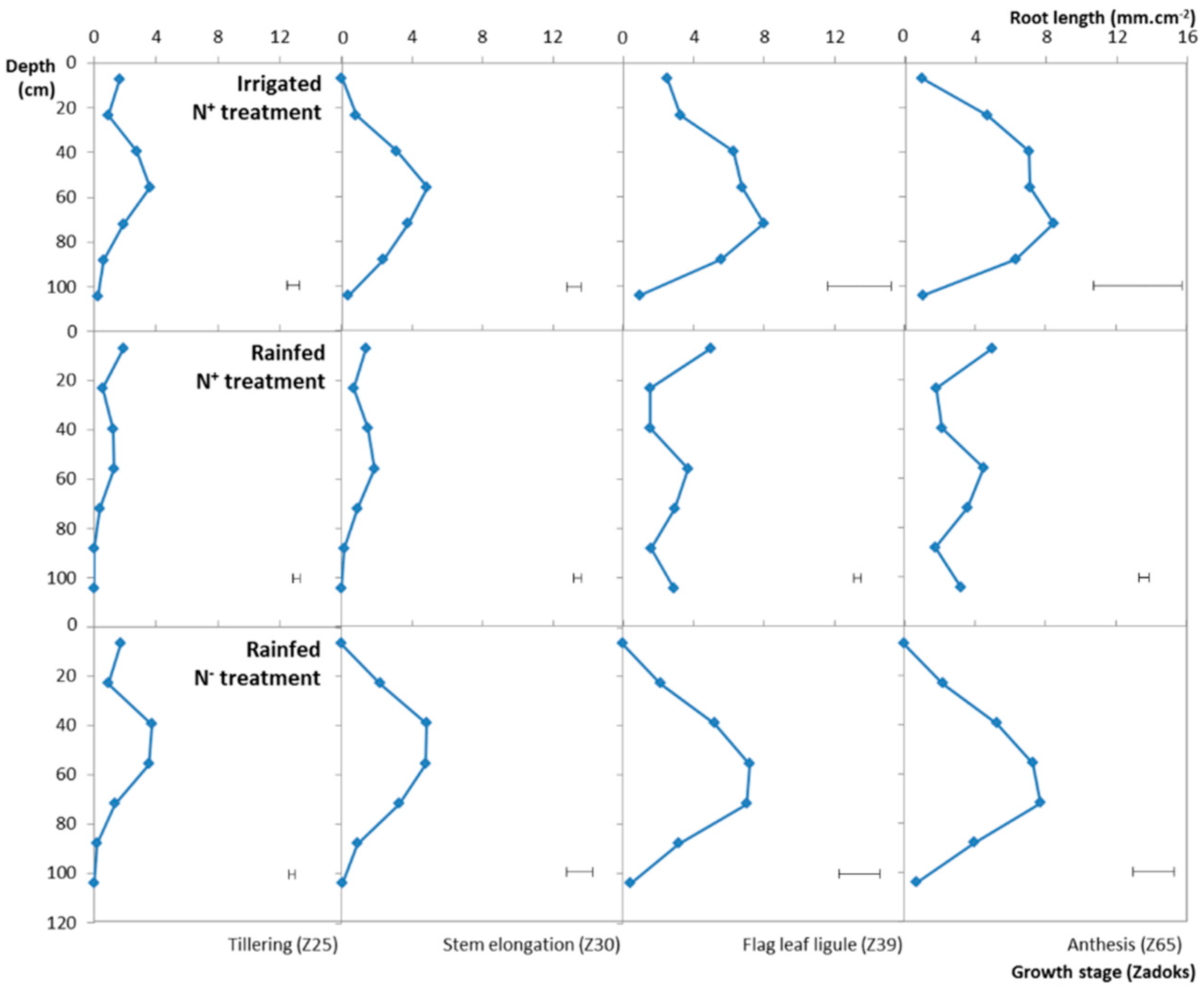
3.4. Variation of the RLSD under the Different Water, N Treatments
3.5. Allometric Relation between Plant Traits
4. Discussion
4.1. Minirhizotron Methodology Reliability
4.2. Effect of Multifactorial Stress on Grain Yield and Root System
4.3. Relevance of Minirhizotron in Field Crop Trials
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alexandratos, N.; Bruinsma, J. World Agriculture towards 2030/2050: The 2012 Revision; ESA Working Paper No. 12-03; FAO: Rome, Italy, 2012. [Google Scholar]
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, M.P.; Pfeiffer, W.H.; Royo, C. Applying physiological strategies to improve yield potential. Durum Wheat Improv. Mediterr. Reg. New Chall. Options Mediterranèennes 2000, 40, 95–103. [Google Scholar]
- Brisson, N.; Gate, P.; Gouache, D.; Charmet, G.; Oury, F.X.; Huard, F. Why are wheat yields stagnating in Europe? A comprehensive data analysis for France. Field Crops Res. 2010, 119, 201–212. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L.; Quiroga, S.; Moneo, M. A regional comparison of the effects of climate change on agricultural crops in Europe. Clim. Change 2012, 112, 29–46. [Google Scholar] [CrossRef]
- Subira, J.; Ammar, K.; Álvaro, F.; Del Moral, L.F.G.; Dreisigacker, S.; Royo, C. Changes in durum wheat root and aerial biomass caused by the introduction of the Rht-B1b dwarfing allele and their effects on yield formation. Plant Soil 2016, 403, 291–304. [Google Scholar] [CrossRef]
- Herder, G.D.; van Isterdael, G.; Beeckman, T.; De Smet, I. The roots of a new green revolution. Trends Plant Sci. 2010, 15, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Waines, J.G.; Ehdaie, B. Domestication and crop physiology: Roots of green-revolution wheat. Ann. Bot. 2007, 100, 991–998. [Google Scholar] [CrossRef]
- Monti, A.; Zatta, A. Root distribution and soil moisture retrieval in perennial and annual energy crops in Northern Italy. Agric. Ecosyst. Environ. 2009, 132, 252–259. [Google Scholar] [CrossRef]
- Manschadi, A.M.; Hammer, G.L.; Christopher, J.T.; deVoil, P. Genotypic variation in seedling root architectural traits and implications for drought adaptation in wheat (Triticum aestivum L.). Plant Soil 2008, 303, 115–129. [Google Scholar] [CrossRef]
- Mathieu, L.; Lobet, G.; Tocquin, P.; Périlleux, C. “Rhizoponics”: A novel hydroponic rhizotron for root system analyses on mature Arabidopsis thaliana plants. Plant Methods 2015, 11, 3. [Google Scholar] [CrossRef]
- Mooney, S.J.; Pridmore, T.P.; Helliwell, J.; Bennett, M.J. Developing X-ray computed tomography to non-invasively image 3-D root systems architecture in soil. Plant Soil 2012, 352, 1–22. [Google Scholar] [CrossRef]
- Metzner, R.; Eggert, A.; van Dusschoten, D.; Pflugfelder, D.; Gerth, S.; Schurr, U.; Uhlmann, N.; Jahnke, S. Direct comparison of MRI and X-ray CT technologies for 3D imaging of root systems in soil: potential and challenges for root trait quantification. Plant Methods 2015, 11, 17. [Google Scholar] [CrossRef] [PubMed]
- Rellán-Álvarez, R.; Lobet, G.; Lindner, H.; Pradier, P.L.M.; Yee, M.C.; Sebastian, J.; Geng, Y.; Trontin, C.; LaRue, T.; Lavelle, A.S. Multidimensional mapping of root responses to soil environmental cues using a luminescence-based imaging system. bioRxiv 2015, 16931. [Google Scholar]
- Eberbach, P.L.; Hoffmann, J.; Moroni, S.J.; Wade, L.J.; Weston, L.A. Rhizo-lysimetry: facilities for the simultaneous study of root behaviour and resource use by agricultural crop and pasture systems. Plant Methods 2013, 9, 3. [Google Scholar] [CrossRef] [PubMed]
- Watt, M.; Moosavi, S.; Cunningham, S.C.; Kirkegaard, J.A.; Rebetzke, G.J.; Richards, R.A. A rapid, controlled-environment seedling root screen for wheat correlates well with rooting depths at vegetative, but not reproductive, stages at two field sites. Ann. Bot. 2013, 112, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.R.; Chaudhary, T.N. Wheat root growth, grain yield and water uptake as influenced by soil water regime and depth of nitrogen placement in a loamy sand soil. Agric. Water Manag. 1983, 6, 365–373. [Google Scholar] [CrossRef]
- Rich, S.M.; Watt, M. Soil conditions and cereal root system architecture: review and considerations for linking Darwin and Weaver. J. Exp. Bot. 2013, 64, 1193–1208. [Google Scholar] [CrossRef]
- Barraclough, P.B.; Weir, A.H.; Kulhmann, H. Factors Affecting the Growth and Distribution of Winter Wheat Roots Under Uk Field Conditions. In Developments in Agricultural and Managed Forest Ecology; McMichael, B.L., Persson, H., Eds.; Elsevier: Amsterdam, The Netherlands, 1991; pp. 410–417. [Google Scholar]
- Kmoch, H.G.; Ramig, R.E.; Fox, R.L.; Koehler, F.E. Root development of winter wheat as influenced by soil moisture and nitrogen fertilization. Agron. J. 1957, 49, 20–26. [Google Scholar] [CrossRef]
- Barraclough, P.B.; Kuhlmann, H.; Weir, A.H. The Effects of Prolonged Drought and Nitrogen Fertilizer on Root and Shoot Growth and Water Uptake by Winter Wheat. J. Agron. Crop Sci. 1989, 163, 352–360. [Google Scholar] [CrossRef]
- Herrera, J.M.; Stamp, P.; Liedgens, M. Dynamics of root development of spring wheat genotypes varying in nitrogen use efficiency. In Wheat Production in Stressed Environments; Springer: Dordrecht, The Netherlands, 2007; pp. 197–201. [Google Scholar]
- Trachsel, S.; Kaeppler, S.M.; Brown, K.M.; Lynch, J.P. Shovelomics: high throughput phenotyping of maize (Zea mays L.) root architecture in the field. Plant Soil 2011, 341, 75–87. [Google Scholar] [CrossRef]
- Maeght, J.L.; Rewald, B.; Pierret, A. How to study deep roots—and why it matters. Front. Plant Sci. 2003, 4, 299. [Google Scholar] [CrossRef] [PubMed]
- Polomski, J.; Kuhn, N.; Waisel, Y.; Eshel, A.; Kafkafi, U. Root research methods. In Plant Roots: Hidden Half; Waisel, Y., Eshel, A., Beeckman, T., Kafkafi, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 295–321. [Google Scholar]
- Wang, M.B.; Zhang, Q. Issues in using the WinRHIZO system to determine physical characteristics of plant fine roots. Acta Ecol. Sin. 2009, 29, 136–138. [Google Scholar] [CrossRef]
- Munoz-Romero, V.; Benítez-Vega, J.; López-Bellido, L.; López-Bellido, R.J. Monitoring wheat root development in a rainfed vertisol: Tillage effect. Eur. J. Agron. 2010, 33, 182–187. [Google Scholar] [CrossRef]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Justes, E.; Mary, B.; Meynard, J.M.; Machet, J.M.; Thelier-Huche, L. Determination of a Critical Nitrogen Dilution Curve for Winter Wheat Crops. Ann. Bot. 1994, 74, 397–407. [Google Scholar] [CrossRef]
- Lobet, G.; Pagès, L.; Draye, X. A Novel Image-Analysis Toolbox Enabling Quantitative Analysis of Root System Architecture. Plant Physiol. 2011, 157, 29–39. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Li, X.R.; Wang, T.; Wang, X.P.; Xue, Q.W.; Liu, L.C. Distribution and Seasonal Dynamics of Roots in a Revegetated Stand of Artemisia ordosica Kracsh in the Tengger Desert (North China). Arid Land Res. Manag. 2008, 22, 195–211. [Google Scholar] [CrossRef]
- Atkinson, D. Spatial and temporal aspects of root distribution as indicated by the use of root observation laboratory. In Ecological Interactions in Soil Special Publication Number 4 of the British Ecological Society; Fitter, A.H., Atkinson, D., Read, D.J., Usher, M.B., Eds.; Blackwell Scientific Publications: Oxford, UK, 1985; pp. 43–65. [Google Scholar]
- Løes, A.K.; Gahoonia, T.S. Genetic variation in specific root length in Scandinavian wheat and barley accessions. Euphytica 2004, 137, 243–249. [Google Scholar] [CrossRef]
- Keating, B.; Carberry, P.; Hammer, G.; Probert, M.; Robertson, M.; Holzworth, D.; Huth, N.; Hargreaves, J.N.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Gregory, P.J. A Periscope Method for Observing Root Growth and Distribution in Field Soil. J. Exp. Bot. 1979, 30, 205–214. [Google Scholar] [CrossRef]
- MerrillE, S.D.; Doering, E.J.; Reichman, G.A. Application of a Minirhizotron with Flexible, Pressurized Walls to a Study of Corn Root Growth 1. In Minirhizotron Observation Tubes: Methods and Applications for Measuring Rhizosphere Dynamics; Taylor, H.M., Ed.; ASA, CSSA, SSSA: Madison, WI, USA, 1987; Volume 50, pp. 131–143. [Google Scholar]
- Upchurch, D.R.; Ritchie, J.T. Root observations using a video recording system in mini-rhizotrons. Agron. J. 1983, 75, 1009–1015. [Google Scholar] [CrossRef]
- Johnson, M.G.; Tingey, D.T.; Phillips, D.L.; Storm, M.J. Advancing fine root research with minirhizotrons. Environ. Exp. Bot. 2001, 45, 263–289. [Google Scholar] [CrossRef]
- Chaudhuri, U.N.; Kirkham, M.B.; Kanemasu, E.T. Root growth of winter wheat under elevated carbon dioxide and drought. Crop Sci. 1990, 30, 853–857. [Google Scholar] [CrossRef]
- Li, F.M.; Liu, X.L.; Li, S.Q. Effects of early soil water distribution on the dry matter partition between roots and shoots of winter wheat. Agric. Water Manag. 2001, 49, 163–171. [Google Scholar] [CrossRef]
- Allard, V.; Martre, P.; Le Gouis, J. Genetic variability in biomass allocation to roots in wheat is mainly related to crop tillering dynamics and nitrogen status. Eur. J. Agron. 2013, 46, 68–76. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Nakhforoosh, A.; Grausgruber, H.; Kaul, H.P.; Bodner, G. Wheat root diversity and root functional characterization. Plant Soil 2014, 380, 211–229. [Google Scholar] [CrossRef]
- Hendricks, J.J.; Hendrick, R.L.; Wilson, C.A.; Mitchell, R.J.; Pecot, S.D.; Guo, D. Assessing the patterns and controls of fine root dynamics: an empirical test and methodological review. J. Ecol. 2006, 94, 40–57. [Google Scholar] [CrossRef]
- Lopes, M.S.; Reynolds, M.P. Partitioning of assimilates to deeper roots is associated with cooler canopies and increased yield under drought in wheat. Funct. Plant Biol. 2010, 37, 147–156. [Google Scholar] [CrossRef]
- Pradhan, G.P.; Prasad, P.V.V.; Fritz, A.K.; Kirkham, M.B.; Gill, B.S. Effects of drought and high temperature stress on synthetic hexaploid wheat. Funct. Plant Biol. 2012, 39, 190. [Google Scholar] [CrossRef]
- Christopher, J.T.; Manschadi, A.M.; Hammer, G.L.; Borrell, A.K. Developmental and physiological traits associated with high yield and stay-green phenotype in wheat. Aust. J. Agric. Res. 2008, 59, 354. [Google Scholar] [CrossRef]
- Barraclough, P.B.; Leigh, R.A. The growth and activity of winter wheat roots in the field: the effect of sowing date and soil type on root growth of high-yielding crops. J. Agric. Sci. 1984, 103, 59–74. [Google Scholar] [CrossRef]
- Passioura, J.B. Grain yield, harvest index, and water use of wheat. J. Aust. Inst. Agric. Sci. 1977, 43, 117–120. [Google Scholar]

| Treatment | Genotype | GY15 (t ha−1) | SDM (t ha−1) | RDM (t ha−1) | R:S (-) | |
|---|---|---|---|---|---|---|
| I + N+ | Miradoux | 8.79 | 10.53 | 1.56 | 0.15 | |
| Apache | 9.04 | 10.85 | 1.24 | 0.11 | ||
| Hystar | 10.33 | 11.84 | 1.67 | 0.14 | ||
| Nogal | 9.12 | 11.02 | 1.48 | 0.13 | ||
| Mean I + N+ | 9.32 | 11.06 | 1.49 | 0.13 | ||
| I + N− | Miradoux | 7.12 | 8.22 | 0.88 | 0.11 | |
| Apache | 8.31 | 8.21 | 0.96 | 0.12 | ||
| Hystar | 9.87 | 9.75 | 0.91 | 0.09 | ||
| Nogal | 7.34 | 8.32 | 1.08 | 0.13 | ||
| Mean I + N− | 8.16 | 8.62 | 0.96 | 0.11 | ||
| I − N+ | Miradoux | 4.91 | 8.30 | 1.13 | 0.14 | |
| Apache | 5.19 | 9.89 | 1.10 | 0.11 | ||
| Hystar | 6.26 | 9.24 | 1.05 | 0.11 | ||
| Nogal | 6.14 | 9.25 | 0.80 | 0.09 | ||
| Mean I − N+ | 5.62 | 9.17 | 1.02 | 0.11 | ||
| I − N− | Miradoux | 5.79 | 7.50 | 0.91 | 0.12 | |
| Apache | 7.17 | 9.06 | 1.39 | 0.15 | ||
| Hystar | 7.65 | 8.26 | 1.29 | 0.16 | ||
| Nogal | 6.06 | 8.42 | 1.25 | 0.15 | ||
| Mean I − N− | 6.67 | 8.31 | 1.21 | 0.14 |
| Treatment | GY15 (t ha−1) | SDM (t ha−1) | RDM (t ha−1) | R:S (-) | ||
|---|---|---|---|---|---|---|
| Source of variance | Fertilization | NS | ** | ** | ** | |
| Irrigation | *** | NS | NS | NS | ||
| G × N | ** | NS | ** | . | ||
| G × I | . | . | . | *** | ||
| N × I | *** | * | *** | *** | ||
| Genotype | * | NS | ** | NS | ||
| Irrigated conditions | Fertilization | NS | * | * | NS | |
| G × N | NS | NS | * | . | ||
| Genotype | NS | . | NS | * | ||
| Rainfed conditions | Fertilization | *** | NS | . | ** | |
| G × N | * | NS | *** | ** | ||
| NNI 20 April 2015 (Z39) | NNI 10 May 2015 (Z65) | TRLSD (mm cm−2) | Minirhizotron Max. Depth (cm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | n | Mean | n | Mean | n | Mean | n | |||
| I + N+ | 1.19 (0.17) c | 8 | 1.25 (0.13) c | 8 | 9.5 (3.0) a | 7 | 95 (16) a | 7 | ||
| I + N− | 0.84 (0.16) a | 8 | 0.85 (0.23) a | 8 | NA | NA | 45 (8) b | 4 | ||
| I − N+ | 0.98 (0.13) b | 8 | 1.03 (0.12) b | 8 | 4.3 (1.6) b | 4 | 96 (21) a | 4 | ||
| I − N− | 0.77 (0.09) a | 8 | 0.70 (0.05) a | 8 | 7.2 (1.8) ab | 8 | 106 (15) a | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Postic, F.; Beauchêne, K.; Gouache, D.; Doussan, C. Scanner-Based Minirhizotrons Help to Highlight Relations between Deep Roots and Yield in Various Wheat Cultivars under Combined Water and Nitrogen Deficit Conditions. Agronomy 2019, 9, 297. https://doi.org/10.3390/agronomy9060297
Postic F, Beauchêne K, Gouache D, Doussan C. Scanner-Based Minirhizotrons Help to Highlight Relations between Deep Roots and Yield in Various Wheat Cultivars under Combined Water and Nitrogen Deficit Conditions. Agronomy. 2019; 9(6):297. https://doi.org/10.3390/agronomy9060297
Chicago/Turabian StylePostic, François, Katia Beauchêne, David Gouache, and Claude Doussan. 2019. "Scanner-Based Minirhizotrons Help to Highlight Relations between Deep Roots and Yield in Various Wheat Cultivars under Combined Water and Nitrogen Deficit Conditions" Agronomy 9, no. 6: 297. https://doi.org/10.3390/agronomy9060297
APA StylePostic, F., Beauchêne, K., Gouache, D., & Doussan, C. (2019). Scanner-Based Minirhizotrons Help to Highlight Relations between Deep Roots and Yield in Various Wheat Cultivars under Combined Water and Nitrogen Deficit Conditions. Agronomy, 9(6), 297. https://doi.org/10.3390/agronomy9060297





